1 Introduction

Ca2+ ions are required in very low and highly controlled concentrations to perform their informational role in Ca2+ signalling during various metabolic activities as its higher concentration is unfavorable to normal cell functioning. The intracellular Ca2+ levels are regulated by simple and classic set of mechanisms by controlling the Ca2+ movement across the plasma membrane of the cell. Thus, the amount of influx and efflux across the cell membranes regulates the intracellular Ca2+ concentration (Berridge et al. 2000, 2003). Ca2+ ions contribute to egg activation upon fertilization (Flacke 2004). Specifically, at egg activation a fertilization Ca2+ wave triggers embryonic development and cell differentiation, high Ca2+ concentrates for a long time can activate programed cell death. Ca2+ ions play such an important role in so many biological processes that it has been branded as “a life and death signal” (Berridge et al. 1998). Ca2+ signaling differentiation which occurs during xenopus oocyte maturation is a cellular mechanism that follows the aforementioned leading to a variety of Ca2+ patterns. Various experimental and theoretical approaches are being developed and employed to generate the information on Ca2+ dynamics in oocyte cells. In the literature, there are experimental investigations reported on Ca2+ signalling in different types of oocytes such as Human oocytes (Ajduk et al. 2008; Tosti and Boni 2004; Tosti 2006; Gosden and Bownes 1995), Mouse oocytes (Toth et al. 2006), Bovine oocytes (Viets et al. 2001; Liang et al. 2011; Yue et al. 1995), Pig oocytes (Petr et al. 2005), Mussel oocytes (Tomkowiak et al. 1997), Hamster oocytes (Igusa and Miyazaki 1983), Porcine oocytes (Machaty et al. 2002) and Xenopus Laevis oocytes (Busa and Nuccitelli 1985; Baran 2006; Takahashi et al. 1987), (Young et al. 1995; Marchant et al. 1999; Stith et al. 1993; Vasilets and Schwarz 1992; Wagner and Keizer 1994). Thus, it is of interest to determine how different factors affect this Ca2+ distribution in the cell. In these experimental studies the research workers have studied the effect of various parameters such as buffers, L-type voltage-gated Ca2+ channel, Na+/Ca2+ exchanger, RyR Ca2+ channel, Na+/K+ pump, IP3R Ca2+ channel on Ca2+ distribution in oocytes all individually. But these experimental investigations are very time consuming and expensive and have several limitations. Many times it is very difficult and almost impossible to perform the experiments on the living cell organisms. A good number of theoretical investigations on Ca2+ distribution in various cells such as neurons (Tripathi and Adlakha 2013; Tewari and Pardasani 2010), astrocytes (Jha and Adlakha 2013; Jha et al. 2014), fibroblasts (Kotwani et al. 2014), acinar cells (Manhas et al. 2014; Manhas and Pardasani 2014) and myocytes (Pathak and Adlakha 2015) are reported in the literature. Also some theoretical studies are reported in the literature for the study of Ca2+ distribution in oocytes for one-dimensional (Jafri et al. 1992; Naik and Pardasani 2013, 2015; Panday and Pardasani 2013) and two-dimensional (Panday and Pardasani 2014; Naik and Pardasani 2015, 2016; Girard et al. 1992) cases. Further, the experimental investigations carried out by research workers in the past on Ca2+ distribution in oocytes are based on only point source of influx. Also most of the theoretical investigations reported in the literature for study of Ca2+ distribution in oocytes are based on point source of influx. The one- and two-dimensional models do not provide complete picture of spatial Ca2+ distribution in the cell. To incorporate more details of structure of oocyte and source geometry, there is a need to develop three-dimensional models of Ca2+ distribution in oocyte. In view of above, the present paper is devoted to the development of three-dimensional finite element model of Ca2+ distribution in oocyte involving excess buffer, point source, line source, RyR Ca2+ channel and SERCA pump for an unsteady-state case. The mathematical formulation and its solution are presented in the next section.

2 Mathematical model and solution

The actual shape of the oocyte varies with the organisms. The oocyte cells are irregular in shapes in some organisms (Matsuzaki et al. 1979), while of cylindrical and spherical shapes (Yi et al. 2005; Brangwynne et al. 2011) in other organisms. For the sake of development of computational model we assume a cytosolic region near the Ca2+ source in oocyte to be cylindrical in shape. The imaging technique has revealed that Ca2+ signals occurs within ≈10 μm cytosolic region below the plasma membrane (Naik and Pardasani 2015; Kotwani et al. 2014). Ca2+ kinetics in oocytes is governed by a set of reaction diffusion equations which can be framed assuming homogeneity, isotropy and Fickian diffusion as well as bimolecular association reaction between buffer and Ca2+ of the form (Smith 1996; Smith et al. 2000)

$$ [{\text{Ca}}^{2 + } ] + [B_{j} ]\mathop \Leftrightarrow \limits_{{k_{j}^{ - } }}^{{k_{j}^{ + } }} [{\text{Ca}}B_{j} ] $$
(1)

where [Ca2+], [B j ] and [CaB j ] represent the cytosolic Ca2+ concentration, free buffer concentration and Ca2+-bound buffer concentration, respectively, and ‘j’ is an index over buffer species, k + j and k − j are association and dissociation rates for jth buffer, respectively. Equation (1) which is given by (Smith 1996; Smith et al. 2000) for one-dimensional case can be modified by incorporating buffer, RyR Ca2+ channel and SERCA pump for three-dimensional unsteady-state case in polar cylindrical coordinates as (Smith 1996; Smith et al. 2000)

$$ \begin{aligned} \frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial t} & = D_{\text{Ca}} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial r}} \right) + \frac{1}{r}\frac{\partial }{\partial \theta }\left( {r\frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial \theta }} \right) + \frac{{\partial^{2} [{\text{Ca}}^{2 + } ]}}{{\partial z^{2} }}} \right) + \sum {R_{j} } \\ & \quad + \sigma_{\text{RyR}} - \sigma_{\text{SERCA}} + \delta a(r_{i} ,\theta_{i} ,z_{i} )*\sigma_{\text{Ca}} \\ \end{aligned} $$
(2)

where reaction term R j is given by

$$ R_{j} = - k_{j}^{ + } [{\text{Ca}}^{2 + } ][B_{j} ] + k_{j}^{ - } [{\text{Ca}}B] $$
(3)

For stationary immobile buffers or fixed buffers \( D_{{B_{j} }} = D_{{{\text{Ca}}B_{j} }} \). Then Eqs. (1)–(3) can be written as (Panday and Pardasani 2014; Naik and Pardasani 2015)

$$ \begin{aligned} \frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial t} & = D_{\text{Ca}} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial r}} \right) + \frac{1}{r}\frac{\partial }{\partial \theta }\left( {r\frac{{\partial \,[{\text{Ca}}^{2 + } ]}}{\partial \theta }} \right) + \frac{{\partial^{2} [{\text{Ca}}^{2 + } ]}}{{\partial z^{2} }}} \right) - k_{j}^{ + } [B_{j} ]_{\infty } ([{\text{Ca}}^{2 + } ] - [{\text{Ca}}^{2 + } ]_{\infty } \\ & \quad + \sigma_{\text{RyR}} - \sigma_{\text{SERCA}} + \delta a(r_{i} ,\theta_{i} ,z_{i} )*\sigma_{\text{Ca}} \\ \end{aligned} $$
(4)

where [B j ]∞ is the buffer concentration at equilibrium and [Ca 2+]∞ is the Ca2+ concentration far from the source. The term σ RyR is flux due to ryanodine receptor given by (Naik and Pardasani 2013, 2015; Tripathi and Adlakha 2013)

$$ \sigma_{\text{RyR}} = V_{\text{RyR}} P_{o} ([Ca^{2 + } ]_{\text{ER}} - [Ca^{2 + } ]) $$
(5)

where V RyR is the ryanodine receptor rate, P o is the open probability of RyR and [Ca2+] ER is the ER Ca2+ concentration.

In cytosol of the oocyte, the Ca2+ ions continuously release through ER membrane and there are SERCA pumps which take Ca2+ from the cytosol to fill the Ca2+ into the ER store. Marko et al. model the SERCA pump efflux by (Panday and Pardasani 2013, 2014; Tripathi and Adlakha 2013; Marhl et al. 2000)

$$ J_{\text{SERCA}} = V_{\text{SERCA}} ([{\text{Ca}}^{2 + } ]) $$
(6)

Incorporating Eqs. (5) and (6) in Eq. (4), we get the proposed mathematical model as

$$ \begin{aligned} \frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial t} & = D_{\text{Ca}} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial r}} \right) + \frac{1}{r}\frac{\partial }{\partial \theta }\left( {r\frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial \theta }} \right) + \frac{{\partial^{2} [{\text{Ca}}^{2 + } ]}}{{\partial z^{2} }}} \right) - k_{j}^{ + } [B_{j} ]_{\infty } ([{\text{Ca}}^{2 + } ] - [{\text{Ca}}^{2 + } ]_{\infty } \\ & \quad + V_{\text{RyR}} P_{o} ([{\text{Ca}}^{2 + } ]_{\text{ER}} - [{\text{Ca}}^{2 + } ] - V_{\text{SERCA}} ([{\text{Ca}}^{2 + } ]) + \delta a(r_{i} ,\theta_{i} ,z_{i} )*\sigma_{\text{Ca}} \\ \end{aligned} $$
(7)

where V SERCA is the maximum Ca2+ uptake through SERCA pump. \( \delta (r,\theta ,z) \) is the unit step function representing the location of the Ca2+ source.

The initial condition for the Ca2+ concentration of the above problem which is equal to its background concentration is expressed as (Panday and Pardasani 2014; Naik and Pardasani 2015; Panday and Pardasani 2013; Tewari and Pardasani 2010)

$$ [{\text{Ca}}^{2 + } ]_{t = 0} = 0.1\;{\mu M} = [{\text{Ca}}^{2 + } ]_{\infty } $$
(8)

The influx through Ca2+ source is employed for two different cases by applying different boundary conditions as given below:

Case 1: The point source of Ca 2+ influx

The point source of Ca2+ influx is assumed to be present at (r = 0, θ = 0, z = 0). Therefore, the boundary condition imposed in this case is given by (Panday and Pardasani 2013, 2014; Naik and Pardasani 2015; Tewari and Pardasani 2010)

$$ \mathop {\lim }\limits_{r \to 0,\theta \to 0,z \to 0} \left( { - 2\pi rD_{Ca} \frac{{\partial [Ca^{2 + } ]}}{\partial \eta }} \right) = \sigma_{Ca} $$
(9)

Case 2: The line source of Ca 2+ influx

The line source of Ca2+ influx is assumed to be present at \( (r = 0, - \frac{\pi }{4} \le \theta \le \frac{\pi }{4},z = 0) \). Therefore, the boundary condition imposed along the curve is given by (Panday and Pardasani 2013, 2014; Naik and Pardasani 2015; Tewari and Pardasani 2010)

$$ \mathop {\lim }\limits_{{r \to 0, - \frac{\pi }{4} \le \theta \le \frac{\pi }{4},z \to 0}} \left( { - 2\pi rD_{\text{Ca}} \frac{{\partial [{\text{Ca}}^{2 + } ]}}{\partial \eta }} \right) = \sigma_{\text{Ca}} $$
(10)

where η is normal to the surface. The other end of the cylinder at z = 10 μm is maintained at the background of 0.1 μM. Thus, we have the other boundary condition as given below

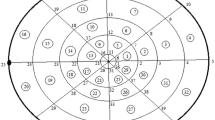
$$ \mathop {\lim }\limits_{r \to 10,\theta \to 0,z \to 10} [{\text{Ca}}^{2 + } ] = 0.1\;{\mu M} = [{\text{Ca}}^{2 + } ]_{\infty } $$
(11)

The cytosolic region is taken as cylindrical shaped region with height 10 μm having radius r = 10 μm. The cytosolic region has been divided into 80 coaxial circular sectoral elements with 96 nodal points as shown in Fig. 1. The left circular base in Fig. 1 is at z = 0 and right circular base in Fig. 1 is at z = 10. In Fig. 1 the numbers within circles represent the element numbers and numbers without circles represent the nodal points.

Fig. 1
figure 1

The three-dimensional discretization of cytosol. The number in circle represents elements and numbers without circles represent nodes. Here e = 1, 2, 3, …, 80 and n = 1, 2, 3, …, 96

Full size image

The discretized variational form of Eq. (7) along with Eqs. (8)–(11) is given by

$$ \begin{aligned} I^{(e)} & = \frac{1}{2}\iiint_{V} {r\left( {\frac{{\partial u^{(e)} }}{\partial r}} \right)}^{2} + \frac{1}{r}\left( {\frac{{\partial u^{(e)} }}{\partial \theta }} \right)^{2} + \left( {\frac{{\partial u^{(e)} }}{\partial z}} \right)^{2} + \left[ {\frac{r}{{\lambda^{2} }}\left( {(u^{(e)} )^{2} - 2u^{(e)} u_{\infty } } \right)^{2} } \right] \\ & \quad + \left[ {\frac{r}{{\xi^{2} }}\left( {(u^{(e)} )^{2} - 2u^{(e)} u_{\text{ER}} } \right)} \right] + \frac{r}{{\omega^{2} }}(u^{(e)} )^{2} + \left[ {\frac{r}{{D_{\text{Ca}} }}\frac{{\partial (u^{(e)} )^{2} }}{\partial t}} \right]{\text{d}}r{\text{d}}\theta {\text{d}}z \\ & \quad - \mu^{(e)} \left[ {\frac{{\sigma_{Ca} u^{(e)} }}{{2D_{\text{Ca}} }}} \right]_{r = 0,\theta = 0,z = 0} - \rho^{(e)} \int_{{ - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}}}^{{{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}}} {\left[ {\frac{{\sigma_{\text{Ca}} u^{(e)} }}{{2D_{\text{Ca}} }}} \right]_{r = 0,z = 0.} } \\ \end{aligned} $$
(12)

where \( \lambda = \sqrt {\frac{{D_{\text{Ca}} }}{{k_{j}^{ + } [B_{j} ]_{\infty } }}} ,\xi = \sqrt {\frac{{D_{\text{Ca}} }}{{V_{\text{RyR}} P_{o} }}} ,\omega = \sqrt {\frac{{D_{\text{Ca}} }}{{V_{\text{SERCA}} }}}. \) Here we have used ‘u’ in lieu of Ca2+ for our convenience and e = 1, 2, 3,…, 80. For the point source of Ca2+ μ (e) = 1 for e = 1, 36 and μ (e) = 0 for rest of elements. The term outside the integral, ρ (e) represents the location of the line source. Here μ (e) = 1 and ρ (e) = 1 represents the location/elements in which the source of Ca2+ is present.

The following trilinear shape function for the Ca2+ concentration within each element has been taken as (Rao 2004; Agrawal et al. 2010)

$$ u^{(e)} = c_{1}^{(e)} + c_{2}^{(e)} r + c_{3}^{(e)} \theta + c_{4}^{(e)} z + c_{5}^{(e)} r\theta + c_{6}^{(e)} \theta z + c_{7}^{(e)} rz + c_{8}^{(e)} r\theta z $$
(13)

Expression (13) can be rewritten as

$$ u^{(e)} = p^{T} c^{(e)} $$
(14)

where p T = [1 r θ z rθ θz rz rθz] and c (e) = [c (e)1 c (e)2 c (e)3 c (e)4 c (e)5 c (e)6 c (e)7 c (e)8 ].

Using nodal condition in Eq. (14) we get

$$ \bar{u}^{(e)} = P^{(e)} c^{(e)} $$
(15)

where

$$ P^{(e)} = \left[ {\begin{array}{*{20}c} 1 & {r_{i} } & {\theta_{i} } & {z_{i} } & {r_{i} \theta_{i} } & {\theta_{i} z_{i} } & {r_{i} z_{i} } & {r_{i} \theta_{i} z_{i} } \\ 1 & {r_{j} } & {\theta_{j} } & {z_{j} } & {r_{j} \theta_{j} } & {\theta_{j} z_{j} } & {r_{j} z_{j} } & {r_{j} \theta_{j} z_{j} } \\ 1 & {r_{k} } & {\theta_{k} } & {z_{k} } & {r_{k} \theta_{k} } & {\theta_{k} z_{k} } & {r_{k} z_{k} } & {r_{k} \theta_{k} z_{k} } \\ 1 & {r_{l} } & {\theta_{l} } & {z_{l} } & {r_{l} \theta_{l} } & {\theta_{l} z_{l} } & {r_{l} z_{l} } & {r_{l} \theta_{l} z_{l} } \\ 1 & {r_{{i^{\prime}}} } & {\theta_{{i^{\prime}}} } & {z_{{i^{\prime}}} } & {r_{{i^{\prime}}} \theta_{{i^{\prime}}} } & {\theta_{{i^{\prime}}} z_{{i^{\prime}}} } & {r_{{i^{\prime}}} z_{{i^{\prime}}} } & {r_{{i^{\prime}}} \theta_{{i^{\prime}}} z_{{i^{\prime}}} } \\ 1 & {r_{{j^{\prime}}} } & {\theta_{{j^{\prime}}} } & {z_{{j^{\prime}}} } & {r_{{j^{\prime}}} \theta_{{j^{\prime}}} } & {\theta_{{j^{\prime}}} z_{{j^{\prime}}} } & {r_{{j^{\prime}}} z_{{j^{\prime}}} } & {r_{{j^{\prime}}} \theta_{{j^{\prime}}} z_{{j^{\prime}}} } \\ 1 & {r_{{k^{\prime}}} } & {\theta_{{k^{\prime}}} } & {z_{{k^{\prime}}} } & {r_{{k^{\prime}}} \theta_{{k^{\prime}}} } & {\theta_{{k^{\prime}}} z_{{k^{\prime}}} } & {r_{{k^{\prime}}} z_{{k^{\prime}}} } & {r_{{k^{\prime}}} \theta_{{k^{\prime}}} z_{{k^{\prime}}} } \\ 1 & {r_{{l^{\prime}}} } & {\theta_{{l^{\prime}}} } & {z_{{l^{\prime}}} } & {r_{{l^{\prime}}} \theta_{{l^{\prime}}} } & {\theta_{{l^{\prime}}} z_{{l^{\prime}}} } & {r_{{l^{\prime}}} z_{{l^{\prime}}} } & {r_{{l^{\prime}}} \theta_{{l^{\prime}}} z_{{l^{\prime}}} } \\ \end{array} } \right] $$
(16)

and

$$ \bar{u}^{(e)} = \left[ {\begin{array}{*{20}c} {u_{i} } \\ {u_{j} } \\ {u_{k} } \\ {u_{l} } \\ {u_{{i^{\prime}}} } \\ {u_{{j^{\prime}}} } \\ {u_{{k^{\prime}}} } \\ {u_{{l^{\prime}}} } \\ \end{array} } \right] $$
(17)

From Eq. (15) we have

$$ c^{(e)} = R^{(e)} \bar{u}^{(e)} $$
(18)

where

$$ R^{(e)} = P^{{(e)^{ - 1} }} $$
(19)

Substituting c (e) from Eq. (18) in Eq. (14), we get

$$ u^{(e)} = P^{T} R^{(e)} \bar{u}^{(e)} $$
(20)

Now the integral I (e) can be written in the form

$$ I^{(e)} = I_{1}^{(e)} + I_{2}^{(e)} + I_{3}^{(e)} - I_{4}^{(e)} - I_{5}^{(e)} - I_{6}^{(e)} $$
(21)

where

$$ I_{1}^{(e)} = \frac{1}{2}\frac{d}{{{\text{d}}t}}\iiint_{V} {\left[ {r\frac{{(u^{(e)} )^{2} }}{{D_{\text{Ca}} }}} \right]}{\text{d}}r{\text{d}}\theta {\text{d}}z $$
(22)
$$ I_{2}^{(e)} = \frac{1}{2}\iiint_{V} {\left[ {r\left( {\frac{{\partial u^{(e)} }}{\partial r}} \right)^{2} + \frac{1}{r}\left( {\frac{{\partial u^{(e)} }}{\partial \theta }} \right)^{2} + \left( {\frac{{\partial u^{(e)} }}{\partial z}} \right)^{2} } \right]{\text{d}}r{\text{d}}\theta {\text{d}}z} $$
(23)
$$ I_{3}^{(e)} = \frac{1}{2}\iiint_{V} {r\left[ {(u^{(e)} )^{2} \left( {\frac{1}{{\lambda^{2} }} + \frac{1}{{\xi^{2} }} + \frac{1}{{\omega^{2} }}} \right)} \right]}\,{\text{d}}r{\text{d}}\theta {\text{d}}z $$
(24)
$$ I_{4}^{(e)} = \frac{1}{2}\iiint_{V} {2ru^{(e)} }\left[ {\frac{{u_{\infty } }}{{\lambda^{2} }} + \frac{{u_{\text{ER}} }}{{\xi^{2} }}} \right]\,{\text{d}}r{\text{d}}\theta {\text{d}}z $$
(25)
$$ I_{5}^{(e)} = \left[ {\frac{{\sigma_{\text{Ca}} }}{{2D_{\text{Ca}} }}u^{(e)} } \right]_{r = 0,\theta = 0,z = 0} $$
(26)
$$ I_{6}^{(e)} = \int_{{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0pt} 4}}}^{{{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}}} {\left[ {\frac{{\sigma_{\text{Ca}} }}{{2D_{\text{Ca}} }}u^{(e)} } \right]}_{r = 0,z = 0.} $$
(27)

The integrals I (e) are evaluated and assembled to obtain I as

$$ I = \sum\limits_{e = 1}^{e = N} {\bar{M}^{(e)} } I^{(e)} \bar{M}^{(e)T} $$
(28)

Now we extremize I with respect to each nodal Ca2+ concentration u i as given below

$$ \frac{{{\text{d}}I}}{{{\text{d}}\overline{u} }} = \sum\limits_{e = 1}^{e = N} {\overline{M}^{(e)} } \frac{{{\text{d}}I^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }}\overline{M}^{(e)T} = 0 $$
(29)

where

$$ \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ . & . & . & . & . & . & . & . \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ . & . & . & . & . & . & . & . \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
(30)

This gives following set of ordinary linear differential equations

$$ [M]_{n \times n} \left[ {\frac{{\partial \bar{u}}}{\partial t}} \right]_{n \times 1} + [K]_{n \times n} [\bar{u}]_{n \times 1} = [F]_{n \times 1}. $$
(31)

Here \( \bar{u} = [u_{1} ,u_{2} ,u_{3} , \ldots ,u_{n} ]^{T} \), M and K are the system matrices and F is system vector. The Crank–Nicolson method (Young and Bang 1997) is employed to solve the system of first-order ordinary differential Eq. (31). A computer program in MATLAB 7.10 is developed to find numerical solution to the entire problem.

3 Results and discussion

In this section, the numerical results for Ca2+ profile are shown in the form of figures explaining the relationships observed between the physiological parameters and intracellular Ca2+ concentration. The numerical values of biophysical parameters used in the model are as stated in Table 1.

Table 1 Values of biophysical parameters (Panday and Pardasani 2013, 2014; Naik and Pardasani 2013, 2016; Tripathi and Adlakha 2013; Marhl et al. 2000)
Full size table

Figures 2 and 3 show the steady-state spatial spread of Ca2+ concentration on the circular plane with EGTA buffer concentration 50 μM and for the two different types of source geometry, i.e., point and line source, respectively, in oocyte cell. Figure 2 shows the distribution of Ca2+ concentration along rand θ direction in oocyte for Case 1: Point source. In Fig. 2, we observe that the Ca2+ concentration is maximum at the point (r = 0, θ = 0, z = 0) about 2.7 μM and it decreases very quickly as we move away along θ = 0 between r = 0 and 2.5 μm from the point source and then decreases gradually between r = 2.5 and 6.5 μm and achieves background concentration at a distance r = 7.5 μm from the point source along θ = 0. Along circumferential direction of the circle of radius r = 0.25 μm, the cytosolic Ca2+ concentration decreases gradually and achieves 2.6 μM at the point θ = π on the circumference. The peak value of the Ca2+ concentration near the source is due to much flux from the Ca2+ source and less active buffers. After some time the buffers becomes more active and thus lowers the Ca2+ concentration in the cell by binding some Ca2+. In Fig. 3 we observe that the Ca2+ concentration is maximum about 4.0 μM at the point (r = 0, θ = 0, z = 0) for Case 2: Line source. For the case of line source, the Ca2+ concentration decreases very quickly as we move away along θ = 0 between r = 0 and 3 μm from the location of line source and then decreases gradually between r = 3 and 6.5 μm and achieves background concentration within r = 8 μm distance at θ = 0 radial direction from the line source. Along circumferential direction of the circle of radius r = 0.25 μm, the cytosolic Ca2+ concentration decreases gradually and achieves 3.9 μM at the point θ = π on the circumference. It is observed from the figures that the Ca2+ concentration in case 2 lasts for a long time as compared to Case 1. This is because in case 2 there is a line source of Ca2+ and there is also an increase in the Ca2+ influx due to flux from the source along the line. Thus, the peak values increase from 2.7 to 3.9 μM in Figs. 2 and 3.

Fig. 2
figure 2

Spatial Ca2+ concentration along r and θ direction in oocyte for Case 1: point source of Ca2+

Full size image
Fig. 3
figure 3

Spatial Ca2+ concentration along r and θ direction in oocyte for Case 2: line source of Ca2+

Full size image

Figure 4 shows the steady-state spatial spread of Ca2+ ion concentration for four different values of buffer concentration of EGTA buffer for point source on Ca2+ profile in oocytes. We observe that the Ca2+ concentration is maximum near the point source about 2.6 μM for the buffer concentration 50 μM and then it starts to decrease sharply between r = 0 and 2.5 μm and decreases gradually between r = 2.5 and 6.5 μm and then becomes constant from r = 6.5 to 10 μm and finally achieves background cytosolic Ca2+ concentration at r = 10 μm. When buffer concentration is 200 μM, the maximum value of Ca2+ concentration near the point source is 0.9 μM and then it decreases sharply between r = 0 and 1.5 μm and decreases gradually between r = 1.5 and 5 μm and the becomes constant from r = 5 to 10 μm and finally achieves background cytosolic Ca2+ concentration at r = 10 μm. We also observe that the cytosolic Ca2+ concentration in oocyte decreases as the buffer concentration increases for the point source of Ca2+ in oocyte. The reason for lower Ca2+ concentration with higher buffer concentration is that the higher concentration of buffer binds more Ca2+ to decrease the value of the Ca2+ concentration.

Fig. 4
figure 4

Spatial Ca2+ concentration along r and θ direction in oocyte for four different values of EGTA buffer and for Case 1: point source of Ca2+

Full size image

Figure 5 shows the spatial intracellular Ca2+ concentration distribution in oocyte in the presence and absence of RyR Ca2+ channel. It is evident from Fig. 5 that the Ca2+ concentration is higher in the presence of RyR which is 3.0 μM and lower in the absence of RyR which is 2.6 μM. This is because the RyR is a Ca2+-releasing channel, thus in its presence it releases the Ca2+ making the concentration higher in the oocyte cell. Figure 5 shows that the Ca2+ concentration is higher from r = 0 to 3 μm in the presence of RyR. While in the absence of RyR there is a slight decrease in the Ca2+ concentration and the concentration is higher from r = 0 to 2.5 μm. From Fig. 5 the contribution of RyR as a Ca2+-releasing channel in Ca2+ signalling in oocyte is clearly visible. Further, the increase in Ca2+ concentration is due to influx from both sources as well as RyR Ca2+ channel as RyR also releases the Ca2+ being the Ca2+ channel in the cell.

Fig. 5
figure 5

Spatial Ca2+ concentration along r and θ direction in oocyte in the absence and presence of RyR and for Case 1: point source of Ca2+

Full size image

Figure 6 shows the spatial intracellular Ca2+ concentration distribution in oocyte in the presence and absence of SERCA pump. From Fig. 6 it is clear that in the absence of pump the Ca2+ concentration is higher as compared to that in its presence. This is because the pump removes the Ca2+ from the cytosol of the cell to make the concentration lower so as to prevent the cell death because the higher Ca2+ concentration is toxic for the cell. The Ca2+ concentration in the absence of pump is about 1.5 μM, while it is up to 1 μM in its presence. The Ca2+ concentration in the absence of pump is higher from r = 0 to r = 1.5 μm and then starts decreasing up to r = 4 μm and then onwards tends to the background concentration of 0.1 μM. However, in the presence of the pump the Ca2+ concentration is higher from r = 0 to 0.9 μm and then starts decreasing up to r = 3 μm and then tends to the background concentration of 0.1 μM. The gap between the peak value as seen in the figure here are more in the case when pump is absent as compared to the case when it is present. This implies that the effect of pump when it is present as compared to that when it is absent is more significant. This is due to the fact that the rate constant of the pump plays an important role in making the balance in the Ca2+ concentration within the cytosol of the cell. The combined effect of pump and buffers is quite significant in lowering down Ca2+ concentration in the cell. Further, the out flux due to pump dominates over the effect of buffers on calcium signalling in oocytes.

Fig. 6
figure 6

Spatial Ca2+ concentration along r and θ direction in oocyte in the absence and presence of SERCA pump for Case 1: point source of Ca2+

Full size image

Figure 7 shows the temporal variation of Ca2+ concentration in oocyte cell in the presence of EGTA buffer for different values of SERCA pump conductance. SERCA pump functions in the sense that it reduces the cytosolic Ca2+ concentration. From Fig. 7 the role of SERCA pump is clearly visible, i.e., with low pump conductance the intracellular Ca2+ concentration is higher and as the pump conductance increases the Ca2+ concentration decreases. For the values of pump conductance, i.e., for V SERCA  = 10, 20, the Ca2+ concentration is 2.5 and 1 μM, respectively. It is evident from Fig. 7 that the effect of pump conductance over cytosolic Ca2+ is very significant for the point source in oocyte. It is observed from the figure that when the pump conductance is high the Ca2+ concentration is low; this is because for higher pump conductance the pump becomes more active, thus reduces the concentration of Ca2+ in the cell. This is because when calcium concentration in the oocyte cell becomes high, which oocyte cell cannot tolerate for longer periods due to its toxicity, the SERCA pump will play an important role in reducing the cytosolic calcium concentration. Thus, the various components of cell become active or inactive as per the requirements of the oocyte for its maturation.

Fig. 7
figure 7

Temporal variation of intracellular Ca2+ distribution in oocyte for different values of pump conductance, i.e., for different values of V SERCA and for Case 1: point source of Ca2+

Full size image

Figure 8 shows the temporal variation of Ca2+ concentration in oocyte cell in the presence of EGTA buffer with different states of ryanodine receptor. The probability P o  = 0 represents the state when receptor Ca2+ channel is closed whereas P o  = 1 represents the state when receptor channel is completely open. Also P o  = 0.5 represents the state when channel is 50% open. For the state P o  = 0.1, the Ca2+ concentration increases from its initial value 0.1 to 1.25 μM. For state P o  = 0.5, the Ca2+ concentration increases from its initial value 0.1 to 2.5 μM very sharply between time t = 0 to 50 ms and then increases gradually up to t = 60 ms and finally tends to the steady state. For the state P o  = 1.0, i.e., when the receptor is completely open, the Ca2+ concentration increases from its initial value 0.1–3.7 μM very sharply between time t = 0 to 70 ms and then increases gradually up to t = 90 ms and finally tends to the steady state. Thus, the cytosolic Ca2+ concentration increases as the value of probability of open state of RyR increases in oocyte. It is evident from Fig. 8 that the effect of probability of open state of RyR over cytosolic Ca2+ is very significant for the point source in oocyte. It is clear from Fig. 8 that Ca2+ concentration is higher when receptor is in open state than the state when the receptor channel is completely closed. The higher concentration of Ca2+ in open state is due to the fact that the receptor releases much Ca2+ to diffuse into the cell.

Fig. 8
figure 8

Temporal variation of intracellular Ca2+ distribution in oocyte at different values of open probability of the RyR, i.e., for different values of ‘P o ’ and for Case 1: point source of Ca2+

Full size image

Figure 9 shows the temporal variation of Ca2+ concentration for two cases of Ca2+ source, i.e., Case 1 and Case 2 in oocyte. For Case 1, the Ca2+ concentration increases from its initial value 0.1 to 3.69 μM very sharply from time t = 0 to 25 ms and then increases gradually from t = 25 to 40 ms and finally becomes 3.7 μM. For Case 2, the Ca2+ concentration increases from its initial value 0.1 to 4.99 μM very sharply between time t = 0 to 80 ms and then increases gradually from t = 80 to 95 ms and finally becomes 5.0 μM. It is evident from Fig. 9 that the effect of source geometry is very significant in oocyte.

Fig. 9
figure 9

Temporal variation of intracellular Ca2+ distribution in oocyte for two cases of source geometry

Full size image

The results shown in Figs. 4, 5, 6, 7 and 8 were obtained for Case 1: Point source of Ca2+. However, similar results have been obtained for Case 2: Line source of Ca2+. The results obtained in this study are in a close agreement with the experimental studies (Naik and Pardasani 2015; Swann 1992; Zhou and Neher 1993; Pathak and Adlakha 2015) and the numerical results obtained by other researchers (Panday and Pardasani 2013, 2014; Kaouri et al. 2014; Hatano et al. 2011; Snyder et al. 2000; Han et al. 2017).

4 Conclusion

The three-dimensional finite element model was proposed and successfully employed to study spatio-temporal calcium distribution in oocytes involving point source, line source, excess buffers, RyR calcium channel and SERCA pump. The effect of source geometry on Ca2+ distribution in oocyte is also studied with the help of the proposed model by incorporating Point and Line source. The results indicate that if buffer concentration increases from 50 to 200 μM then calcium concentration is reduced from 2.6 to 0.9 μM, respectively. It is also concluded from the results that RyR and SERCA pumps have significant effects on calcium distribution in oocytes. The results indicate that in the presence of RyR the oocyte cell is able to maintain high cytosolic calcium concentration which is required for maturation. While in the presence of the SERCA pump the intracellular calcium concentration is lower because the SERCA pump reduces the concentration of calcium to make it up to balanced level to prevent cell death because higher concentration of calcium is toxic for the cell. Further, it can be concluded from results that for Line source the calcium concentration is higher than for Point source in the oocyte cell. Thus, source geometry also has significant effect on calcium distribution in the oocyte cell. The three-dimensional model gives us better picture of calcium variation in oocytes. The finite element method is quite flexible and versatile in the present situation as it has been possible to incorporate the important parameters such as SERCA pump, RyR and buffers in the model. Such models can be developed further to generate information on calcium dynamics in oocyte which can be useful to biomedical scientists for developing protocols for population growth and its control.