Introduction

We are part of a bigger project team that aims to distil the distinctives of mathematics teaching in Singapore classrooms. This team focuses on Singapore mathematics teachers’ use of instructional materials in their work of teaching.

In the course of our data collection, an interview with a teacher—henceforth referred to as Teck Kim—particularly caught our attention. It was conspicuous during the interview that he made numerous references to being “explicit” in his instructional work; it was after data transcription and deliberate scrutiny that we were even more drawn to this aspect of his teaching practice: he mentioned 14 times the word “explicit” during one 45-min interview session alone.

It occurred to us then that making explicit might indeed be an integral part of Teck Kim’s instructional practice. Naturally, among the team members, we further discussed what each of us thought was meant by Teck Kim’s use of “explicit”. While we acknowledged that the term “making explicit” was a common phrase used in the education literature, we could not articulate clearly our interpretations of the term; and with the little we could articulate, we could not agree among ourselves! We then realised that much could be unpacked from Teck Kim’s “making explicit”. We decided to merge this new line of inquiry with the original study of the use of instructional materials: a case study of a Singapore mathematics teacher’s use of instructional materials in making things explicit. Before we describe the details of the case study, we review current literature on the use of “explicit” in teaching mathematics.

“Explicit” in the teaching of mathematics

A search on “explicit” in databases within the field of education research yields a majority of articles on “explicit instruction”. When this term is used in the literature, it generally refers to a method of instruction that most traced its origins from Brophy’s (1988) report. In it, he mentioned the term “explicit” in the context of recommending a way of instruction that would help students in skill attainment: “explicit, detailed explanations and cognitive modeling of strategy implementation that not only demonstrates relevant actions but includes verbalisation of the information processing, decision making, and other self-talk that guides these actions” (p. 261, emphasis added).

Since then, explicit instruction has developed into a particular method of instruction and is studied by a number of researchers (e.g. Christenson et al. 1989; Gersten et al. 2000; Marchand-Martella et al. 2004; Rosenshine 1997; Simmons et al. 1995; Swanson 2001). While there are differences in how they detail the method of explicit instruction, there are concurrences among the writers, and we summarise the broad moves of the instructional sequence as follows: (i) organisation of content into bits that are manageable according to students’ cognitive abilities; (ii) clear teacher demonstrations and explanations; (iii) supported practice of the demonstrated procedures by students; (iv) timely feedback with high levels of teacher involvement especially in the initial stages of practice.

This conception of explicit instruction is seen as closely associated to other methods of instruction such as “teacher-directed instruction” (Doabler et al. 2015) and “direct instruction” (Gersten and Carnine 1984). The former highlights the primary role of the teacher in structuring lesson sequences; the latter focuses on the direct manner in which procedural steps ‘pass from’ teacher to students. Both of these aspects are reflected in the common portraits of explicit instruction as described in (i)–(iv) in the previous paragraph. Positive effects of this kind of explicit instruction were reported in several studies (Brophy and Good 1986; Christenson et al. 1989; Kroesbergen and Van Luit 2003; Rosenshine and Stevens 1986). In particular, the value of explicit instruction in helping students make gain in mathematics achievement is clearer for students with mathematical difficulties but less clear with others who are not considered ‘at risk’ (Doabler et al. 2015).

There are other portrayals of explicit instruction that pare down on the teacher-directed feature and that are more congenial to theories advocating students’ active contribution in knowledge generation. Goeke (2009) stressed the importance of interactions among teachers and students in the instructional process and that “[t]he outcome of learning [in explicit instruction] depends jointly on what information is presented and how the learner processes that information. From this perspective the teacher leads but with a greater emphasis on the ways in which students actively construct and process knowledge” (p. 9).

Selling (2016), however, made a clean break from this tradition of explicit instruction when she defined a different conception of “explicitness” in mathematics teaching as

making what might be implicit in interactions explicit; in other words, making a disciplinary practice explicit means raising the collective awareness (White and Frederiksen 1998; Zohar and Peled 2008) of the existence and importance of such practices, as well as of what it means to engage in those practices while learning and doing mathematics (p. 510).

It is clear that this positioning of explicit is not bounded so strictly by the global theoretical stance taken by the researcher or the teacher. Regardless of the instructional approach taken—whether considered behaviouristic or constructivistic (or of other epistemological origins)—the work of teaching does require the rendering of implicit moves explicit so that the underlying elements can themselves become objects of (collective) inquiry. Selling (2016) described a discourse in class about how the teacher elicited students’ responses towards the reason for \( \frac{1}{2} bh \) as the formula for area of triangle. The discussion led a pair of students to propose viewing the triangle as being inscribed in the associated rectangle of area bh. Using this episode as an illustration, she pointed out that while the process of helping students arrive at the triangle–rectangle connection is canonical practice from the socio-cultural perspective of knowledge-building in classrooms, there remains a need, from a disciplinary perspective, to make explicit what counts as valid argument in their reasoning about the connection.

To us, Selling’s (2016) contribution to the academic discourse of “making explicit” in the work of teaching mathematics opens up a whole new area of study that up to this point in time is too limited to the scope of the explicit teaching method reviewed earlier. She focused on explicitness in the area of mathematics practices. These practices are linked to what mathematicians do, such as defining and justifying. She then examined how teachers use the structures in classroom discourses to make explicit these mathematical practices.

In the study that we report here, we begin with a different starting point: we are not limiting the instructional sphere in which Teacher Teck Kim makes things explicit; rather, in line with the goal of examining the distinctives of Singapore mathematics teacher practices, we study the instructional elements in which he considered necessary for making explicit. In particular, we link his concept of explicitness with his use of instructional materials as an instrument for making things explicit.

Use of instructional materials to make things explicit

In the work of instruction, teachers draw from a variety of resources which include textbooks, teachers’ guides, online material, and electronic devices (Clark-Wilson et al. 2014; Gueudet et al. 2013; Gueudet and Trouche 2009). Also, in the midst of planning and enacting instruction, teachers engage in a variety of activities with curriculum. Remillard (2005) describes the teacher–curriculum relationship as a dynamic transaction in which teachers participate with curricular materials.

Often, these reference resources (hereafter referred to as “base materials”) undergo a process of selection and modification by the teachers to morph into a form that is considered suitable for use in classroom work to advance their instructional goals. It is this latter form—one which is classroom-ready and that carries the teacher’s actual instructional goals—that we term “instructional materials”. Gueudet and Trouche (2009) similarly observed the active role of teachers in transforming base materials into useable forms in classroom instruction: “The resources evolve, are modified, combined; documents develop according to the processes of genesis and bear new resources” (p. 207).

Brown (2000) summarised the role of instructional materials as follows: (i) promotes meaningful communication, hence effective learning; (ii) ensures retention, thus making learning more permanent; (iii) helps to overcome the limitation of classroom by making the inaccessible accessible. They stimulate and motivate students to learn; (iv) encourage participation especially if students are allowed to manipulate materials used (as cited in Arop et al. 2015, p. 67).

For the purpose of this research, we zoomed in further into relevant literature on how teachers utilise instructional materials to make things explicit for the students in their classroom learning. Again, Brophy (1988) played a seminal role in linking instructional materials to explicit instruction. In dealing with students’ misconceptions in particular content, he highlighted the need to use “materials that explain the content in more explicit and detailed terms” (p. 261, emphases added). More recently, Remillard (2000) suggested that for the

“pedagogical change that would support true reform of mathematics instruction, textbooks … need to do more than just set out activities for students to do and terrain for teachers to cover. … [A]s well as being written for students, textbooks need to be written with teachers in mind. In particular, textbook authors need to be more explicit about reasons and purposes for certain content or activities, and to provide opportunities for teachers to engage in decision-making, giving them space to play out some of the introduced possibilities on their own” (cited in Grossman and Thompson 2008, p. 2015, emphasis added).

While this is an acknowledgement of the need to be explicit in crafting materials for teaching, it has only gone as far as interpreting Brophy’s (1988) remark quoted earlier. Important questions remain: What are the specific areas in the teaching of mathematics that we need to be explicit about in the instructional materials? How do teachers actually make things explicit when they transform base materials into instructional materials for actual use in class? Surprisingly, these gaps are not addressed in the current research literature.

We are thus prompted to pursue the lines of inquiry guided by these critical questions with respect to how and what teachers make explicit when crafting instructional materials for their students’ mathematical learning. Returning to Teck Kim, we treated his attempt to make explicit as a case study to help us gain deeper insights into this understudied area of materials–explicit link within the context of his instructional work in teaching a topic in school mathematics. We began with examining his use of “explicit”, and from there, investigate his efforts at explicitation through the use of the instructional materials that he crafted.

Method

Like other participants in the bigger project, Teck Kim was identified as an experienced and competent teacher. “Experienced” is defined as having taught the same mathematical course at the same level for a minimum of 5 years; and “competent” selection is based on recognition by the local professional community as a teacher who is effective in teaching mathematics.

As mentioned briefly at the start of the paper, the choice of Teck Kim as a subject of deeper study of making things explicit was largely due to his own reference to “explicit” as stated in the interviews. In addition, a number of other factors about Teck Kim’s practices lends itself to a rich unpacking of his explicitation work—a characteristic feature of case study: (1) During interviews, he was able to articulate comprehensively his goals for many tasks. This allows us to uncover his intents behind the activities we recorded in his classroom; (2) He produced a full set of handouts for students’ use in class (hereafter referred to as “Notes”) before the start of the module and supplemented these along the way in the form of quizzes and additional practice items. In other words, his work yielded a rich set of instructional materials on which to ground our study; (3) he constantly made references among his goals, his actual activity in class, and his use of instructional materials. This enabled us to study the interactions among these major pieces of his instructional processes.

The class that Teck Kim taught was a Year 11 Normal Academic class. In Singapore, students progress to secondary level based on the scores they obtain at the end of Year 6 in the Primary School Leaving Examination (PSLE) conducted nationwide. Using the PSLE score, pupils are streamed into three ability streams. The streams are known as Express, Normal Academic (NA) and Normal Technical (NT), and the percentage of students in each of these streams are roughly 60, 25 and 15, respectively. A student in the NA course of study is expected to complete in 5 years the same content covered in 4 years for students in the Express Stream.

The module that Teck Kim taught was “Vectors in Two Dimensions” (hereafter referred to as “Vectors”). The contents—as stipulated by the Ministry of Education (2012)—that he had to cover were (i) use of notations, (ii) representing a vector as a directed line segment, (iii) translation by a vector, (iv) position vectors, (v) magnitude of a vector, (vi) use of sum and difference of two vectors to express given vectors in terms of two coplanar vectors, (vii) multiplication of a vector by a scalar and (viii) geometric problems involving the use of vectors. The module was taught over 10 lessons, each about 45 min in duration.

Data

Under instructional materials, Teck Kim used mostly the set of notes he designed. During the course of the lessons, he supplemented by quizzes which performed the role of milestone assessments of student learning. He also drew heavily from the textbook (Chow et al. 2016) he used as base material. These related materials form the first primary source of data.

The next source of data is the interviews we conducted with Teck Kim. We conducted one pre-module interview before his lessons and three post-lesson interviews after each of three lessons he selected—Lessons 04, 08 and 10. All interviews were video recorded. We designed an interview protocol with two sets of questions and probes respectively for the pre-module interview and post-lesson interviews.

The pre-module interview was conducted to find out what Teck Kim’s instructional goals were and how he designed and planned to utilise his instructional materials to fulfil his goals. Some prompts in the pre-module interview were:

  • Please share with me what mathematical goals you intend to achieve for this set of materials that you will be using.

  • How different is this set of materials that you developed compared to those in the textbook?

  • Are there any other specific instructional materials that you are going to prepare for this module?

The post-lesson interviews were conducted to find out if he had met his instructional objectives with the instructional materials he designed and planned to use. Some of the questions were:

  • Did you use all the materials that you had intended to use for the lesson?

  • How did the materials help you achieve your goals for this lesson?

The third source of data is Teck Kim’s enactment of his lessons in the module. We adopted non-participant observer roles during the course of our study—one researcher sat at the back of the class to observe Teck Kim’s lessons. This is so that the researcher will be able—during the post-lesson interviews—to make relevant and specific references to his teaching actions when pursuing certain threads during the interviews. A video camera was also placed at the back of the class to record Teck Kim’s actions. All the 10 lessons were video-recorded.

Analysis of data

We proceeded with the analysis along these stages:

Stage 1: Identification of units of analysis of the notes

We took the sections of the notes as prepared by Teck Kim (e.g. “Introductory Activity”, “What is a Vector?”) as the basic units of our preliminary analysis. We coded the units according to the mathematical contents targeted in each section. We matched the comments in Teck Kim’s pre-module interview according to the references he made to these units. Together with the coded content, we were better able to verify the instructional goals intended for each unit.

It soon became clear to us that the sequence of units in the notes did not cohere exactly with the sequence enacted in Teck Kim’s actual lessons. For example, under Unit 12: “Drawing of Vectors”, the actual coverage of this content strand was over Lessons 07, 08 and 09. In other words, while Teck Kim had proceeded to deal with other aspects of Vectors, he often reverted to contents of a previous unit found in the notes. This means that an approach that separates the analysis of the instructional materials and the analysis of in-class teaching actions would miss out on these rich interactions between these elements. Thus, we proceeded with analysis of the units together with the associated lesson enactments.

Stage 2: Composition of chronological narratives

For some of these selected units with rich related data on Teck Kim’s enactment and interview comments, we crafted chronological narrative (CN) for each of them. In each CN, we integrated a number of data sources—pre-module interview transcriptions, post-lesson transcriptions, tasks in his notes, questions he selected from the textbook, quizzes he designed and his classroom vignettes. The CN for “Column Vectors”, for instance, was composed by first examining the text in the pre-module interview. As we found him commenting at length about how he planned to supplement the base materials with his notes on the unit of “Column Vectors”, we validated his intentions for designing the mathematical tasks and questions by examining pp. 1–4 of his notes. After which, we proceeded to search the video recordings of the related lessons he conducted for evidence to corroborate his use of the instructional materials. We found that he started with the unit at the end of Lesson 01, continued to develop it in Lesson 02 and then revised it in Lesson 04 before setting a 10-min quiz. Thereafter, he explained the answers to the quiz questions and reinforced the unit by highlighting students’ mistakes in Lesson 05. We consolidated the evidence and organised them in a table.

Table 1 presents a simplified version of the CN for “column vectors”.

Table 1 Simplified chronological narrative (CN) for Column Vectors
Full size table

Stage 3: Formation of conjectures related to making things explicit

We begin specifically to look for themes related to how Teck Kim made things explicit by closely examining the CN on “Column Vectors”. This CN was chosen as a first-entry study because it is one where Teck Kim made the most references to “explicit”. This CN became an intensive source of analysis for emerging themes related to explicitation. We underwent many rounds of discussions, conjecturing, refuting and re-conjecturing to a point where there was stability in agreement among the members of the research team—where the conjectures could be substantiated from all the data sources. We repeated this process on two other units of analysis so as to develop our conjectures, refute previous ones, or substantiate/revise those generated earlier.

Stage 4: Testing of conjectures

In the final stage of analysis, we brought the conjectures we obtained in Stage 3 and checked it against all the other CNs. After going through further refutations and refinements of conjectures, we managed to refine the conjectures into a form that contribute to theory generation. In the next section, we present our findings on the processes of analysis under Stages 3 and 4 by first detailing the CN on “Column Vectors”. This is followed by two other CNs on “Development of Column Vectors” and “Proving Collinearity using Vectors” before summarising the findings on the other CNs (see Figs. 1 and 2).

  1. (A)

    Chronological narrative on the unit “Column vectors”

Fig. 1
figure 1

Extract of textbook on the unit of column vectors (source—Chow et al. 2016, p. 117)

Full size image
Fig. 2
figure 2

Extract of Teck Kim’s Notes on the unit of “Column Vectors” (source—Teck Kim’s Notes, p. 1)

Full size image

We observed the following adaptations Teck Kim made in the notes from the textbook: (i) In the textbook, the textual explanation of column vectors was located at a separate section of the textbook for the vector diagram. In Teck Kim’s notes, he merged the textual mode into the visual representation of column vectors. Not only was the label of \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \) placed beside the drawn vector, the explanation of translation of “− 3” and “4” was also summarily fused into the diagram. At this point, we conjecture that this merging of representational modes was the way in which Teck Kim made explicit—in this case the links among the drawn vector, the column vector notation, and the translational significance. (ii) The two examples in the textbook were \( \left(\begin{array}{c}2\\ {}3\end{array}\right) \) and \( \left(\begin{array}{c}-1\\ {}-4\end{array}\right) \). The two examples in Teck Kim’s notes were \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \) and \( \left(\begin{array}{c}-3\\ {}-4\end{array}\right) \). There was a clear departure from the examples given in the textbook: Compared to \( \left(\begin{array}{c}2\\ {}3\end{array}\right) \) and \( \left(\begin{array}{c}-1\\ {}-4\end{array}\right) \), the magnitudes of \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \) and \( \left(\begin{array}{c}-3\\ {}-4\end{array}\right) \) yielded an integer value, not a surd. It was perhaps deliberately chosen to reduce computational complexity so that the focus was on the definition and method of obtaining the magnitude, and not on the computational obstacles that the task might present. Moreover, the choice of \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \) and \( \left(\begin{array}{c}-3\\ {}-4\end{array}\right) \) shows a one-component variation only in the translation in the y-direction, allowing the teacher to focus students’ attention on the translational significance when “4” is replaced with “− 4”, thus highlighting the need to attend carefully to signs. An analysis of Teck Kim’s enactment of this portion of the notes bears this out: He carefully drew students’ attention to the difference between \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \) and \( \left(\begin{array}{c}-3\\ {}-4\end{array}\right) \); he also emphasised the need to be careful with the sign and the difference in the translational significance between negative and positive signs. In other words, Teck Kim used these examples that he crafted to make explicit differences in the case of the sign in the y-direction which may have otherwise been unnoticed by the students. (iii) The task implicit in the textbook required students to “write” the given drawn vector in column vector notation; the task in Teck Kim’s notes required students to do the reverse: to “draw” vector given its column vector notation. From Teck Kim’s pre-module interview, we learnt that this reversal was deliberate:

I also will be getting students to … do more drawing for column vectors. The textbook doesn’t have much drawing of column vectors … so I will give them some spare grids for them to do some drawing. … I want them not to be confused between for example 3, 4; and 4, 3; and minus 3, minus 4; 3, minus 4, that sort of thing and then make comparison of each of these vectors. (Pre-module Interview)

In other words, he made explicit by filling a gap in the textbook. In this case, the gap was the skill of drawing vectors. (iv) The textbook presented the process of calculating the magnitudes of the given vectors, leading to a ‘formula’ of \( \sqrt{x^2+{y}^2} \) for column vector \( \left(\begin{array}{c}x\\ {}y\end{array}\right) \). In its place, Teck Kim’s notes appeared to compress all these into one question: “How would you calculate the magnitude?” On the surface, it appears that Teck Kim was less explicit than the textbook in the computational process of magnitude. But a careful examination into the pre-module interview reveals that the compression of this section into a question was deliberate:

I’m trying to achieve these goals that I have through these notes that I wrote but there’ll be other questions that I will be throwing in between as they are doing certain tasks. But they might not be explicit in the notes itself. They may be in the lesson itself that I would go through these questions to them. … I try to put in these questions so that it is more explicit to … and I will remind myself that these are the questions that I want to ask the students (Pre-module Interview, emphases added).

He meant to use the question to trigger students’ initial thoughts on the matter—which would then serve to ready their frame of mind when the teacher explains the procedure in class:

So how do we know the magnitude? The length of it. What theorem do we use? Pythagoras theorem right? So it’s three steps to the left, four steps down, this is three, this is four, I'm sure you know this length is five. The most famous triangle in Pythagoras. … the symbol for magnitude … is this one [points to modulus]. This is the mathematical symbol. This can be used for the length or the magnitude of the vector AB. (Lesson 02, 6:52)

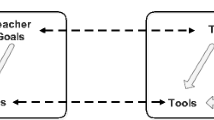
Moreover, Teck Kim also revealed in the interview that the question in the notes helps “to remind myself” the steps or concepts he needed to emphasise in class. In other words, the notes made explicit key ideas to highlight in class. This point is particularly intriguing to us. When we first began the analysis, we were looking specifically for areas Teck Kim made explicit with reference to the textbook materials. In other words, we were examining explicitation by way of the relation from the notes to the base materials. We were surprised that Teck Kim’s idea of “making explicit” was not confined to his notes ➔ base materials link, he was also thinking in terms of the notes ➔ classroom link. Figure 3 presents our provisional diagrammatic representation at this stage of our analyses. The prepositions “from” and “to” in the diagram take reference from the Notes that Teck Kim designed. That is, the way Teck Kim crafted the Notes made explicit elements from the base materials; he also used it to project forward what he intended to make explicit to his classroom enactment.

Fig. 3
figure 3

Notes make explicit base materials and classroom enactment

Full size image
  1. (B)

    Chronological narrative on the unit “Development of column vectors”

We proceed with the analysis of the next section immediately following the introduction of column vectors. We use the analysis in this section to test out and add to the preliminary conjectures forwarded in the previous section.

Following (A), one full textbook page was devoted to more examples of column vectors which consists of two parts: (a) demonstration of writing the given drawn vectors in column vector notation: \( \overrightarrow{AB}=\left(\begin{array}{c}2\\ {}1\end{array}\right) \), \( \overrightarrow{CD}=\left(\begin{array}{c}2\\ {}1\end{array}\right) \), \( \overrightarrow{EF}=\left(\begin{array}{c}3\\ {}0\end{array}\right) \), \( \overrightarrow{GH}=\left(\begin{array}{c}-2\\ {}-1\end{array}\right) \), and \( \overrightarrow{AA}=\left(\begin{array}{c}0\\ {}0\end{array}\right) \); (b) a follow-up task for students to write in column vectors given drawn vectors. Unlike the previous section (a), the answers were not given. For the reader’s reference, the vectors were \( \overrightarrow{KL}=\left(\begin{array}{c}-3\\ {}1\end{array}\right) \), \( \overrightarrow{MN}=\left(\begin{array}{c}-3\\ {}1\end{array}\right) \), \( \overrightarrow{PQ}=\left(\begin{array}{c}0\\ {}2\end{array}\right) \), \( \overrightarrow{RS}=\left(\begin{array}{c}3\\ {}-1\end{array}\right) \), \( \overrightarrow{QQ}=\left(\begin{array}{c}0\\ {}0\end{array}\right) \).

The corresponding section in Teck Kim’s notes consists of five student tasks. Tasks 1–4 required students to ‘draw’ vectors.

Task 1 vectors: \( \left(\begin{array}{c}3\\ {}4\end{array}\right) \), \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \), \( \left(\begin{array}{c}-3\\ {}-4\end{array}\right) \), \( \left(\begin{array}{c}3\\ {}-4.\end{array}\right) \)

Task 2 vectors: \( \left(\begin{array}{c}3\\ {}0\end{array}\right) \), \( \left(\begin{array}{c}-3\\ {}0\end{array}\right) \)

Task 3 vectors: \( \left(\begin{array}{c}0\\ {}3\end{array}\right) \), \( \left(\begin{array}{c}0\\ {}-3\end{array}\right) \)

Task 4 vectors: \( \left(\begin{array}{c}4\\ {}1\end{array}\right) \), \( \left(\begin{array}{c}1\\ {}4\end{array}\right) \)

At the end of each of these four tasks, these same questions were asked:

  • How are they different?

  • What do these vectors have in common?

  • Other observations?

Task 5 was an exact replica of Task (b) from the textbook, with one additional question at the end: “How are the vectors above related?”

The tasks used in the section of Teck Kim’s notes confirms the Conjectures (ii), (iii) and (iv) forwarded in the previous section of analysis.

In this development section, Teck Kim expanded systematically to a whole suite of example tasks: For Task 1, the example set broadened from the \( \left(\begin{array}{c}-3\\ {}4\end{array}\right) \) and \( \left(\begin{array}{c}-3\\ {}-4\end{array}\right) \) in the earlier section to all the positive/negative combinations of \( \left(\begin{array}{c}3\\ {}4\end{array}\right) \). In so doing, students were drawn to observe the similarities and differences among the examples and attend to the difference in the x- and y-directions in translation. Task 2 focused on column vector of the form \( \left(\begin{array}{c}x\\ {}0\end{array}\right) \) and \( \left(\begin{array}{c}-x\\ {}0\end{array}\right) \). This overlapped with the previous emphasis on positive/negative translational significance and yet included the additional focus on “0” in y-direction. Task 3 is similar to Task 2 and shifted the “0” focus to the x-direction. Task 4 drew students’ attention to the differences between \( \left(\begin{array}{c}4\\ {}1\end{array}\right) \) and \( \left(\begin{array}{c}1\\ {}4\end{array}\right) \)—emphasising again the care needed to distinguish translation in the x-direction and the y-direction. Hence, not only is Conjecture (ii) about Teck Kim making explicit differences through examples for students’ attention sustained, we see that the explicitation process was systematic, pointing and reinforcing similarities and differences one at a time, and likely factoring in his knowledge of likely students’ misconceptions. In other words, he made explicit important differences that if left unattended by the students can result in serious obstacles to learning related skills or concepts later. This interpretation is supported by this pre-module interview extract:

I want them not to be confused between for example, 3, 4 and 4, 3, and minus 3, minus 4, 3, minus 4, that sort of thing and then make comparison of each of these vectors. These vectors itself, ah, what is the difference? What is the meaning? And there, actually I can derive the meaning of equal vectors, opposite vectors, ahh ... you know, that sort of things. Vectors ah ... they are actually vectors with the same magnitude but different in direction because the sign may change. That sort of thing I want to put it all into one task so that the students may be able to do the comparison. Again these are not visible in the textbooks which I feel is necessary so that they not just be looking at column vectors but they will look at column vectors with understanding. … So I also want to make that explicit in the task itself so that I'll lay a better foundation. These are not very explicitly taught in the textbook itself so I embedded all these extra tasks to build up the foundation of the students. (Pre-Module Interview)

For Conjecture (iii), the case for the reversal from “writing” to “drawing” as a deliberate way to explicitly fill the gap is clearly strengthened. Also the repeated questions in Task 1–4 and the included question in Task 5 were—like in the previous section (A)—used to trigger students’ preparation to focus on the points which Teck Kim wanted to emphasise in class. This strengthens Conjecture (iv).

But there is more. The analysis of Teck Kim’s response to the questions in class reveals that the questions were not merely used to direct students’ attention to the skill of drawing and to prepare them to attend to the teacher’s explicitation of salient points; Teck Kim was also using these junctures to introduce informally ideas that he would more formally develop later in the module. As an example in Task 1, he used the questions to point students to observe that while all the given vectors are equal in magnitude, some pairs of vectors are parallel but pointing at opposite directions. The concept of negative vectors was then introduced, although he would formally define it in a later section of the notes. Similarly, Task 5 presented some precursor—vectors \( \overrightarrow{KL}=\left(\begin{array}{c}-3\\ {}1\end{array}\right) \), \( \overrightarrow{MN}=\left(\begin{array}{c}-3\\ {}1\end{array}\right) \) , \( \overrightarrow{RS}=\left(\begin{array}{c}3\\ {}-1\end{array}\right) \), and \( \overrightarrow{QQ}=\left(\begin{array}{c}0\\ {}0\end{array}\right) \)—that he would later develop formally the concepts of equal vectors, negative vectors and zero vector. In other words, Teck Kim was using this section of his notes also to transit from the introduction of column vectors to formal definitions of zero vectors, equal vectors and negative vectors. Seen through the interpretative lens of “making things explicit”, Teck Kim was using this section of the notes to introduce implicitly ideas that he planned to make explicit later. Returning to Fig. 3, we can further include a component of explicitation link within the set of notes along its chronological use. Figure 4 revises the model.

Fig. 4
figure 4

Notes make explicit base materials, classroom enactment and previous units within the notes

Full size image
  1. (C)

    Chronological narrative on the unit of “Proving collinearity using vectors”

We examine here the next unit which Teck Kim made significant references to during the interviews. As the themes that emerged are similar to the ones described in the previous section, the description here will be brief, focusing instead on whether and how the analysis of this unit would support the conjectures developed earlier (Fig. 5).

Fig. 5
figure 5

Extract of Teck Kim’s notes on the unit of "Proving collinearity using vectors" (source—Teck Kim’s Notes, p. 13)

Full size image

This task was taken mainly from the textbook. The modifications he made were:

  1. (a)

    the bubbles and the annotations of the bubbles;

  2. (b)

    the text in the rectangular box;

  3. (c)

    the enlarged Triangle ABC.

(a) supports Conjecture (i) stated earlier about explicitising links—in this case, the link between the vector equations (e.g. \( \overrightarrow{AC}=2\overrightarrow{AN} \)) to the ratio of the corresponding magnitudes of the vectors (e.g. \( \frac{AC}{AN}=2 \)). This link was also represented by the placement of the textual information in (b) beside the enlarged diagram in (c).

The combined purpose of (b) and (c) can also be interpreted as a skill—that of reproducing a sufficiently big diagram and transferring ratio information from the text as annotation on the diagram—Teck Kim chose to fill a gap that was not explicit in the textbook material. This was expressed in Conjecture (iii). As to Conjecture (iv), the task stated in the rectangle text box in (b) was Teck Kim’s way of drawing students’ attention to an important point he meant to explicitise in class. In Lesson 10, Teck Kim proceeded to show how the vector and ratio information was “put” into the diagram. Figure 6 is an extract of the whiteboard at 3 min 19 s juncture during the lesson.

Fig. 6
figure 6

The diagram on the whiteboard at 3 min 19 s of Lesson 10

Full size image

To examine the explicitation links across units (i.e. Conjecture (v)), we zoom out to the materials beyond the boundary of this unit. Prior to this unit, the task in Teck Kim’s notes requires that given drawn vectors a and b on grid paper, students are to draw on the same grid paper the following vectors: −\( \frac{1}{3} \)a, − a, − b, a + b, a– b, − a– b, − \( \frac{2}{3} \)a+\( \frac{1}{2} \)b, − \( \frac{1}{2} \)b + (− a). In these examples, the ostensible task was to draw vectors of the form ma + nb, m, n ∈ Q. To complete the task students are required to attend to, among other things, the geometrical meaning of the scalar m and n to the respective vectors. Here, students began to consider—at least implicitly—the ratio of ma to a and nb to b. This ratio derived from the vector representation, as discussed earlier, was made explicit to students in the collinearity task. This is another example of the type of inter-unit link stated in Conjecture (v).

Apart from preparing students for ideas to be made explicit later, the examples in this unit were structured to help others attend to the differences between most adjoining pairs so that they can notice the mathematical points that Teck Kim would want to emphasise. For example, for \( \frac{1}{3} \)a and − a, they are instantiations of ma, the change in value of m from \( \frac{1}{3} \) to − 1 can potentially draw students’ attention to the effects of different values of m—positive, negative, whole number, non-whole numbers—on the geometrical properties of ma. This systematic use of a variety of examples to explicitise differences with a view of adding likely students’ errors supports Conjecture (ii).

  1. (D)

    Summary analyses of the other units in the Notes

In the previous sections, we present the analyses of three units which Teck Kim made the most reference to in the interviews. In this section, we broaden to the whole set of notes. We include in Table 2 only units where there were significant adaptations from the textbook.

Table 2 Units with adaptations
Full size table

Discussion

We began this paper by describing our interest in studying Teck Kim’s use of “explicit” in his instructional practice. Through examining the use of instructional materials that he designed, as shown in the analyses, we summarise our conceptions of Teck Kim’s ‘explicit’ along these lines: explicit–from base, explicit–within materials and explicit–to instruction. These three conceptions correspond roughly to the three arrows shown in Fig. 4.

Explicit–from base

Teck Kim referred extensively from the school-subscribed textbook as his base curricular material. However, the transference from textbook to the instructional materials he used was not merely one of direct lifting nor minor adaptations. He saw the move between these material domains as primarily one of “making explicit”. As evidenced in the findings, this explicitation can be further categorised into: filling gaps in the textbook content, making links between representations given in the textbook, and highlighting critical ideas—without which students may inadvertently develop misconceptions—not emphasised in the textbook.

In a widely referencedFootnote 1 article, Brown (2009) proposed that teachers use base curricular materials in one of these three ways: offload, adapt and improvise. These moves can be seen as points along the continuum of the teacher agency scale. While Teck Kim used curricular materials in all of these three ways, the focus of our study here is on his improvisations. In particular, the findings in this paper contributes directly to the research on what teachers do in improvising from base materials when motivated by the need to make things more explicit to their students.

Greater teacher agency in improvising from base materials presupposes teacher knowledge in a range of domains. If we interpret Teck Kim’s explicit–from base work through the lens of the well-known construct of Mathematical Knowledge for Teaching or MKT (Ball and Bass 2003; Ball et al. 2008; Hill et al. 2008), even without a detailed analyses which is beyond the scope of this study, it is clear that Teck Kim’s moves drew upon various component domains within the MKT model. Cursorily, Specialised Content Knowledge (SCK) and Knowledge of Content and Curriculum (KCC) would support the work of filling gaps in the textbook content; making links between representations would draw from SCK and Knowledge of Content and Teaching (KCT); and highlighting critical ideas with a view of students’ likely misconceptions would touch on Knowledge of Content and Students (KCS). Seen in this way, we think that quality explicit–from base improvisations are not straightforward teacher implements; rather, as exemplified by Teck Kim, they require careful weaving of relevant knowledge strands in a way that fulfils the teacher’s instructional goals.

Moreover, if we zoom in to examine Teck Kim’s practices, we find that there are other techniques applied that are beyond the broad descriptions of the MKT model. For example, the way he structured the sequence of column vector exercises revealed a deliberate attempt to vary items with a view of helping students attend to the differences and similarities across them. This appears to us—regardless of whether the teacher was aware—to be an application of variation theory (Marton and Booth 1997; Watson and Mason 2006). The cardinal premise of the theory is that students’ awareness of change is central to learning; and this awareness is aided by teachers’ structuring of variation during instructional activities, such as thoughtful variation of students’ worked examples. Another example is the attempt to present linked representations in the notes. This can also be interpreted as a distillation of other instructional theories that regard tight intermodal links as facilitating students’ making of connections in learning (e.g. Leong et al. 2015; Moyer-Packenham 2016).

This further unpacking of Teck Kim’s explicit–from base work reveals another layer of complexity that is not widely discussed in the literature: the ways teachers utilise theoretical ideas in the improvisation of reference materials for classroom instruction.

Explicit–within materials

Teck Kim used each unit to focus on one main vector concept. As is usually the case in mathematics, the focused concept is tightly linked to other related ideas. Instead of highlighting all the ideas in one-go within a unit, he used the strategy of foregrounding a particular idea while holding the other related ones as ‘supporting cast’ at the background. As described in the findings, an example of this was the case of negative vectors ‘lurking’ implicitly in his discussion of column vectors; in that unit, he focused on helping students translate the column vector representations into drawn directed segments on the Cartesian plane; this implicit notion of negative vectors illustrated in the tasks was only later foregrounded explicitly in the next unit.

This inter-unit implicit-to-explicit strategy reveals a level of sophistication in the crafting of instructional materials that we had not previously studied. The common anecdotal portrayal of Singapore mathematics teachers’ use of materials is one of numerous similar routine exercise items for students to repetitively practise the same skill to gain fluency. In the case of Teck Kim’s notes, it was not pure repetitive practice that was in play; rather, students were given the opportunity to revisit similar tasks and representations but with added richness of perspective each time. In other words, each revisit allowed students to reinforce previously introduced ideas and to connect to new ones.

From the viewpoint of theories in educational psychology, the behaviourist tradition advocates targeted practice to strengthen skill proficiency; the cognitivists emphasise the need to build connections to aid conceptual learning. Interestingly, Teck Kim’s strategy can be interpreted as a sort of merger of these theoretical streams: the revisitation of similar tasks in sequential units performs both the functions of skill consolidation and concept linkage.

Explicit–to instruction

No matter how well the instructional materials were designed, Teck Kim recognised the limitations to the extent in which the notes by itself can help make things explicit to the students. The explicitation strategy must go beyond the contents contained in the notes. In particular, he used the notes as a springboard to connect to further examples and explanations he would provide during in-class instruction. He drew students’ attention to questions spelt out in the notes, created opportunities for students to formulate initial thoughts and used these preparatory moves to link to the explicit content he subsequently covered in class.

From the point of view of structuring students’ learning experience, the chronology of first prompting their thoughts followed by the teacher’s explicitation inverts the more traditional order of teacher–teach proceeded by student–practice. While the latter tends to foster a passive adherence to teacher-demonstrated steps, the former allows students to carry out their first-cut thought experiments before the teacher points out the salient ideas or demonstrate some canonical methods. This sequence provides students the opportunity to contrast their more naive preliminary ideas against the explicit treatment provided by the teacher—and thus learn to better appreciate the mathematical explicitation.

Also, this explicit–to strategy helps to link two major components of classroom practice: teacher–instruct and student–do. These oversimplifications correspond to two abiding images of mathematics classrooms: (a) the teacher working in the front of the classroom, writing on the board and simultaneously talking to the students about the contents written; and (b) students working (either individually or in groups) on some mathematical tasks presented in some printed materials. We think that these two activities, regardless of pedagogical orientations, take up most of the class time of mathematics lessons around the world. If so, then it is critical that students in these classrooms do not experience teacher–instruct and student–do as disconnected entities. Teck Kim’s use of the strategy to direct students from the questions in the notes (as a form of student–do) to teacher’s in-class explicitation (as a form of teacher–instruct) provides a concrete way to tightly link these two dominant modes of learning in mathematics classrooms.

Conclusion

Few dispute that one major task of mathematics teachers is to “make things explicit” to students. Surprisingly, up till now, research on what this means is scarce and shallow. In the study reported in this paper, we found that the work of making explicit using carefully designed instructional materials is far from a straightforward enterprise. Among others, it draws on a wide range of the teacher’s knowledge domains, it requires a judicious integration of learning theories and it attends to a deliberate tight-linkage between instructional materials and in-class instructional enactment.

The findings reported in this paper are derived from a case study of Teacher Teck Kim’s use of explicit. It nevertheless prompts us to inquire whether the strategies of explicitation in which he used to weave these complex elements together in the design of instructional materials and instruction is the unique practice of one teacher in Singapore. In the next stage of our study, we will broaden our research to other mathematics teachers in the project with a view of pursuing this line of inquiry: What strategies do Singapore mathematics use to “make things explicit” to students?