Algebra serves as a gatekeeper both for university admission and for the numerous jobs that allow for promotion and mobility (Schoenfeld 2002). It is required for graduation from secondary school and admission to most higher education. For instance, many states in the U.S. are now requiring all students to take a course specifically on algebra by eighth grade (Kaput 2008; Usiskin 1999), and “Algebra II” is a high school graduation requirement in 21 states (Achieve 2010), up from 8 states in 2006 (Chazan 2008). The International Commission on Mathematics Instruction (ICMI) reflects the gatekeeper status of algebra internationally: “As the language of higher mathematics, algebra is a gateway to future study and mathematically significant ideas, but it is often a wall that blocks the paths of many” (2001, p. 1). This wall first appears for many students when they begin the transition from arithmetic to algebra in the middle grades (Kilpatrick and Izsak 2008).

One crucial difficulty in this transition to algebraic thinking is the concept of a variable. For example, beginning algebra students, unaware of the multiple functions of letters in mathematical expressions, often only treat a variable as representing an unknown, but fixed, quantity. This can be seen in situations when students, faced with a general algebraic expression or with an equation to simplify, approach the task by choosing some value for the variable, substitute the value for the variable and carry out the resulting arithmetic. It can also be seen in situations where a student encountering a variable in an expression asks, “What is x?”, implying that they do not see the letter as representing any of a set of values for which the expression applies, but rather that it stands for a single value that has not yet been found.

While such student actions may be surprising to those who understand algebra, they reflect conceptions that are perfectly natural for students whose prior experience with letters in mathematical expressions has focussed on finding unknowns in equations, or substituting a single value and then evaluating the resulting variable expressions. To help students make sense of the different and broader meaning of a letter as a variable, not just as an unknown, mathematics educators should be able to distinguish between several uses of algebraic letters and understand the way these several uses develop from one another.

Our purpose is to detail some of the key ideas that are required for the understanding of variable. We first describe an important distinction between three different uses of letters in algebraic expressions—unknowns, variables, and placeholders. Then we tell the story of some of the key ideas that developed in the history of mathematics to allow for our modern understanding of variable. We then describe how students grapple with some of these key ideas, and we provide some examples of student difficulties with them. Finally, we discuss how these ideas show the ways that curricular treatments of the transition from unknowns to variables can help or hinder student understanding.

Unknown, placeholder, variable

In order to clearly portray the transition to thinking with variables, we use the terms unknown, variable, and placeholder to mean different usages of letters in mathematical expressions and equations. Among the mathematical community there is no unanimous agreement about the usages of these terms. In particular, the term variable is commonly used to denote nearly any letter appearing in a mathematical formula or expression. We are not claiming that this usage is incorrect, but in this paper we reserve the term variable for a more specific situation, in order to acknowledge a distinction that is important for making sense of student understandings and of the historical development of algebra. We also briefly discuss the idea of a generalized number. These four terms are meant not to exhaust all of the possible usages of algebraic letters, but rather to highlight several of the usages that are important and noteworthy both historically and for our students.

Unknown

We use the term unknown to mean a determinate quantity. It stands for a particular numerical value (or a few values) that can be determined from the information provided, even if one does not yet know what the value is. In this sense, an unknown is always part of an equation, not just an expression, even if the equation is tacit—the idea is that the unknown value is to be found. In “\( {4} + x = {9} \),” the unknown is the “x” that represents a unique value, and in “\( {x^2} - {3}x = {6} \)” the unknown is the “x,” representing two values. In the following problem, the unknown is “some amount,” and the equation is tacit: “Jack has some amount of apples and then gives 4 of them away. If he now has 3, then how many apples did he start with?”

Variable

We use the term variable in keeping with the usage of Collis (1975), Küchemann (1978), and a number of other researchers, such as Philipp (1992), who terms it a varying quantity. When a letter is used as a variable, “the letter is seen as representing a range of unspecified values, and a systematic relationship is seen to exist between two such sets of values” (Küchemann 1981, p. 104). There are two properties here, both of which are crucial in our historical story and for student learning. First, a variable is indeterminate, rather than determinate, meaning that it does not represent just one (or a few) specific numerical value(s) that can be determined from the information provided. Rather it is capable of assuming any of a (large) set of values, and it stands for a generic element of that set. Thus, for instance, in the equation \( y = - \frac{1}{2} x + 6 \), both x and y are variables. If one becomes specified with a particular value, then the other letter becomes an unknown that can be found.

The second property that distinguishes a variable is that it is a part of a “systematic relationship”—a variable quantity can vary, and when it does there is some other quantity that varies with it. These two quantities are said to co-vary (Carlson et al. 2002). This relation is often, but not always, explicitly stated in terms of an equation. For instance, in “It takes 2n-1 legal moves to move a Hanoi tower of height n to a different peg,” there is an implied relationship between two variable quantities: the height of the tower and the number of moves it takes to shift the tower to a new peg. One is represented in terms of the other; the relationship is m = 2n-1 (or in function notation, m(n) = 2n-1). This relationship can sometimes be hard to discern—if the equation \( y = - \frac{1}{2} x + {6} \) is instead expressed as \( f:x \to - \frac{1}{2} x + {6} \), now in order to see the variation, one must recognize that when the input value x changes, the output value \( - \frac{1}{2} x + {6} \) changes too. One implication of this second property of variables is that a letter appearing in a bald expression, like √x/3, does not function fully as a variable (even though it might colloquially be called a “variable”) unless this expression takes part in some sort of relation, as one changeable quantity represented in terms of another.

Placeholder

We use the word placeholder to mean a letter standing for a number that will be provided in a particular problem or context. A placeholder is often called a given or a constant; in specific instances it is a parameter or a coefficient. Like a variable, a placeholder is indeterminate, but whereas a variable can stand for an entire set of values, here the point is that the equation or expression really stands for an entire set of equations or expressions. For instance, in the equation “\( a{x^2} + bx + c = 0 \),” a, b, and c are placeholders (in particular, coefficients). This equation in fact stands for an entire set of quadratic equations (if a ≠ 0), and it is understood that in a specific context these letters will be replaced with specific numbers.

Notice how inherently vague this is! For instance, in “y = kx,” we understand the k to be a placeholder (in particular, a parameter, holding the place of a specific coefficient)—when it takes on a particular numerical value. The general equation, which now represents an entire set of linear equations, will become one specific linear equation, a relation between the two variable quantities x and y. But how do we know that the k is a placeholder and the x and y are variables? We need extra information from the mathematical context, such as the fact that we are describing a set of lines through the origin on the xy plane. And even if we are not provided with such a context, we would still expect k to be a placeholder from our prior experience. In mathematics tradition, we are accustomed to letters like a, b, c, h, k acting as placeholders and x, y, n acting as variables, and we have seen enough similar-looking situations where k takes on a particular value in a specific instance. Understanding which letters are placeholders and which are variables comes from experience with the practices and contexts of a mathematical community. It is reasonable to expect that students in the middle grades without such experiences would have difficulty making this distinction.

A significant conceptual shift must occur in order for students to be comfortable using placeholders in algebraic expressions rather than just numbers. Anna Sfard tells of the price of being unaware of this shift, when she gave a class of 10th graders an assignment that included equations with placeholders, and the weeks of struggle that ensued (Sfard 1995). As we shall discuss, this conceptual shift is so significant historically that it marked the birth of symbolic algebra. It is worth noting that many students see instances of placeholders only after they have already been working with variables, in the form of equations with parameters such as y = a(x−4)2. This might lead one to think that placeholders are generally more conceptually complex than variables, as this equation is more conceptually complex than y = 3(x−4)2. But this is not quite the context in which placeholders historically emerged and, as we shall describe, the important practice necessary for placeholders—the use of a letter to stand for any of a set of indeterminate quantities rather than a single unknown—is one of two important practices required for the developed idea of variable.

Generalised Number

Although we do not focus on this category, it is important to mention this usage of letters in algebraic expressions. Philipp explains Küchemann’s definition of a generalised number succinctly by saying that it refers to “the use of literal symbols when all replacement values of the literal symbols will result in a true statement, as with identities” (Philipp 1992, p. 160). So the letters in “a(b + c) = ab + ac” serve as generalised numbers, and a student who simplifies 2t + 3t − 9 into 5t − 9 uses the identity 2t + 3t = 5t, in which the letter is a generalised number. Küchemann found that using generalised numbers is more difficult for middle-grades students than using unknowns, but not as difficult as using variables (1978).

Historical development of unknown, placeholder, and variable

Unknowns were used for millennia before placeholders appeared in 1591, marking the true beginning of symbolic algebra and paving the way for the development of the full idea of variable in 1637. In this section we summarise the historical development of the usages of unknown, placeholder, and variable, because this historical story illustrates how the notations and representations with which we are so comfortable enfold a handful of complex practices that are crucial in the development of the idea of variable.

The historical story is quite relevant to our understanding of student learning, but not because we expect students to go through exactly the same development. Some detailed theories account for relationships between the historical development and student conceptual development, such as the theories of epistemological obstacles (Brousseau 1997) and of genetic epistemology (Piaget and Garcia 1989). Our focus here is not on cognitive development, but rather on the changes in usage with which students must gain comfort and proficiency when using variables rather than unknowns, and how these relate to the changes in usage that occurred historically. For our purposes here, it suffices simply to distinguish between two important practices that distinguish variables from unknowns and two historical viewpoint shifts that needed to occur in order for these two practices to emerge.

The two important practices that we focus on are (a) the use of a letter to stand for any of a set of indeterminate quantities, not just a single unknown, and (b) the representation and quantification of the way one quantity changes with respect to another. It is these practices that we claim students must also be able to make sense of in order to work with variables. We also discuss two important shifts in viewpoint that mathematicians needed to make before these two practices could become available: adopting a more general view of a mathematical object and treating qualities as being quantifiable. These shifts in viewpoint are likely not shifts that students must make in order for the two important practices to become available to them, since both of these are shifts away from ancient Greek viewpoints that are no longer significant parts of our cultural milieu.

By differentiating between these two different kinds of change, we can see important relationships between student learning and historical development, while still maintaining the integrity of the historical story by not ignoring important historical developments just because they are not cleanly reflected by our students.

Unknowns

For thousands of years unknowns have been used in mathematical representations, although these usually appeared as words or abbreviated words until the last 400 years. Some of the oldest representations of unknown quantities are found in Old Babylonian cuneiform tablets (c. 1900–1600 BC). For instance, tablet YBC 6967 poses the problem of finding the “igibum” and the “igum,” two unknown values whose product is some power of 60 (the base of the Babylonian number system) and whose difference is 7. In our notation, this means that x−60/x = 7 (i.e., x 2−60 = 7). The solutions to this quadratic equation are lengths of sides of a rectangle (x is 12 and 60/x is 5), found by quite literally completing the square as shown in Fig. 1. The translation and geometric interpretation of this tablet in the figure is from J. Høyrup (2005).

Fig. 1
figure 1

Old Babylonian tablet YBC 6967

Full size image

Greek mathematicians also routinely solved for unknowns, usually lengths that satisfy some sort of geometric criterion or equality, but sometimes unknowns were numbers as well. Methods for finding unknown numbers were generally treated separately from methods for finding unknown lengths. For example, Euclid treats these two topics in entirely separate places in his Elements—the former in Books 7–9 and the latter in Books 2, 5, 6, (for commensurable lengths) and Book 10 (for incommensurable lengths)—even though this often requires him to prove in two places that which looks to us to be only one theorem. As we describe below, this strict separation between lengths and numbers prevented the development both of our generic idea of “number” and of generic methods for manipulating quantities.

The Babylonians and Greeks generally used words rather than symbols when representing and manipulating unknowns, as did Indian and medieval Islamic mathematicians. In such rhetorical methods, the unknown quantity is usually referred to as “thing” or “number,” or “root.” For instance, note the verbal form of al-Khwarizmi’s expression (c. 830 AD) of \( {x^2} + {1}0x = {39} \) and its solution \( x = \sqrt {{{{\left( {\frac{{10}}{2}} \right)}^2} + 39 - }} \left( {\frac{{10}}{2}} \right) \) (that is, x = 3), in which the unknown quantity is the root or number of roots:

What must be the square which, when increased by ten of its own roots, amounts to 39? The solution is this: You halve the number of roots, which in the present instance yields five. This you multiply by itself; the product is 25. Add this to 39; the sum is 64. Now take the root of this, which is eight, and subtract from it half the number of the roots, which is five; the remainder is three. This is the root of the square which you sought for. (Al-Khwarizmi in Katz 2007, p. 543)

By this time, mathematicians in India had also been using rhetorical algebra to do avyaktaganita (“mathematics with invisible (or unknown) [numbers]”)—for instance, in AD 499 Aryabhata used “gulika” (bead) to represent an unknown quantity, and Bhaskara I used “yāvattāvat” (as much as). By Bhaskara II’s time (AD 1150) this algebra was being abbreviated: a term like −2x 4 was written as “yāvava \( \mathop {2}\limits^\cdot \),” an abbreviation of yāvattāvat and varga varga (square square) (Datta and Singh 2001). This use of abbreviations is natural enough, and in the 1400s the Italian abacists did the same thing, using “c” for cosa (thing), “ce” for censo (square), and “R” for radice (root). While abbreviated (or “punctuated”) algebra likely allows for clearer algebraic manipulations than the more cumbersome rhetorical representations of al-Khwarizmi (and of the Greeks, Babylonians, and others), this alone was not enough to facilitate the development of placeholders and variables. Other shifts in viewpoint were also necessary for these developments.

A historical shift necessary for placeholders: the generality of mathematical objects

In order to use a symbol as a placeholder rather than as an unknown, a shift in thinking was needed that allowed a symbol to refer to a more general kind of object. For the ancient Greek mathematicians, the manipulations and representations that could be used for a particular mathematical object depended upon the actual existence and properties of the object itself, the ontology of the mathematical object. For instance, to find an unknown quantity was to be able to actually construct a line of the appropriate length, not to produce a symbol like 3 + √17 or e −4.2. According to Klein, this limited the generality of the methods of manipulation the Greeks could employ:

The problem of the “general” applicability of a method is therefore for the ancients the problem of the “generality” (καθóλου) of the mathematical objects themselves, and this problem they can solve only on the basis of an ontology of mathematical objects. In contrast to this, modern mathematics, and thereby the modern interpretation of ancient mathematics, turns its attention first and last to method as such. It determines its objects by reflecting on the way in which these objects become accessible through a general method. (Klein 1968, p. 122-3)

In our modern practice (which includes the practices developing in Europe in the 16th century), we may always perform a given method or procedure, such as solving a quadratic equation, without worrying about whether the quantities we are manipulating will turn out to be positive, negative, rational, irrational, transcendental, or even imaginary. It does not matter whether these quantities are “real” things that can be drawn or pointed to. Indeed, modern mathematicians prioritise method so much that when a method produces a seemingly nonsensical entity such as √-1, we treat it as a new object and carry on manipulating it anyway, even if it “seems to rest on sophistry rather than on truth” (Bombelli 1966). It is this that allows the modern mathematician to put letters in place of any quantities, determinate or indeterminate, and trust that the manipulations we perform on these letters would work the same way for any of the specific numbers that could live in their places.

But for the Greek mathematicians, there is no general method for manipulating letters that could stand for a multitude of values. Two of the reasons for this are that (a) operations that could be performed with some mathematical objects were not possible with others (such as finding a common denominator or measure), and (b) “no action was allowable that did not have a well-defined geometric referent,” meaning among other things that each intermediate step in a procedure usually could have only positive quantities in the three allowable dimensions of physical space (Kaput 1994, p. 103). In these ways the qualities of the mathematical object being represented by the letter are of crucial importance to the Greek mathematicians.

Hence the idea of indeterminacy, and thus the idea of variable or placeholder, is not part of Greek practice. Even when a letter does appear in a Greek equation or mathematical statement, it is there only to illustrate a determinate quantity that we know something about, even if we do not know its value, not to represent the value of a general indeterminate quantity that we can freely manipulate and later instantiate with any value we like. The Greek practice “does not do two things which constitute the heart of the symbolic procedure: It does not identify the object represented with the means of its representation, and it does not replace the real determinateness of an object with a possibility of making it determinate…” (Klein 1968, p. 223). Klein argues that only by changing these elements of ancient practice was it possible to develop a symbolic algebra able to represent and manipulate indeterminate quantities as placeholders and variables.

The advent of placeholders

Franciscus Vieta (François Viète) is sometimes called the father of symbolic algebra, for his 1591 work In Artem Analyticem Isagoge (Introduction to the Analytical Art) in which he proposes the new practice of representing values that are given in a problem with letters that hold their place. His idea is to “let the given magnitudes be distinguished from the undetermined unknowns by a constant, everlasting, and very clear symbol, as, for instance, by designating the unknown magnitude by means of the letter A or some other vowel E, I, O, U, or Y, and the given magnitudes by means of the letters B, G, and D or the other consonants” (Vieta, in Klein 1968, p. 340).Footnote 1 Vieta then shows how to manipulate these quantities to find the unknown value in terms of the placeholders. The point is that if you show how to solve a quadratic equation using a particular example equation like \( {2}{x^2} + {12} = {1}0x \), then the final answers of x = 2 and x = 3 do not in this form clearly reveal how they emerged from the 2, 12, and 10. But if you show how to solve a quadratic equation where you represent these given quantities with placeholders, like ax 2 + c = bx, then in the solution the letters retain their original appearance so one can see what happens to them in the course of the manipulations. This equation therefore represents an entire set of specific equations, and its solution shows at once the solutions of all of these specific equations. This is what William Oughtred, in 1631, describes as the benefit of this new practice of using placeholders, which he terms the arithmetic of species (“Specious”), rather than only using the arithmetic of particular numbers (the “Numerous”):

This Specious Arithmetic is more applicable to the Analyticall art, (in which by taking the thing sought as knowne, we finde out that we seeke) than that Numerous. For in the Numerous, the numbers with which we worke, are so, as it were, swallowed up into that new which is brought forth, that they quite vanish, not leaving any print or footstep of themselves behinde them. But in the Specious, the species remaine without any change, shewing the processe of the whole worke: and so doe not onely resolve the question in hand; but also teach a generall Theoreme for the solution of like questions in other magnitudes given. (Oughtred, in Fauvel and Gray 1987, p. 302)Footnote 2

This is a huge breakthrough, to represent an entire “number species” with a placeholder letter that can be manipulated as though it were number, as many mathematicians of the time realised. Indeed, at the end of the Isagoge Vieta declares in all capital letters, “THERE IS NO PROBLEM WHICH CANNOT BE SOLVED.”

A historical shift necessary for variable: quantifying change

In addition to the shift in thinking required for the development of placeholders, an additional shift in thinking was important to the development of the notion of variable: the possibility of quantifying and representing continuous variation of one quantity with respect to another. It was only in the 14th century that mathematicians began exploring the idea of “studying change quantitatively, and thus admitting into mathematics the concept of variation” (Edwards 1979, p. 71). This shift is rooted in the Aristotelian distinction between quantities, which vary in extensity, and qualities, which vary in intensity (Kaput 1994). Thus quantities included lengths, areas, volumes, and time, while qualities included a variety of forms subject to variation in intensity, such as velocity, acceleration, and density (Boyer 1968). Only in the 14th century did scholars, including Thomas Bradwardine and William Heytesbury, begin to categorise how these intensities changed or varied, first distinguishing uniform from non-uniform change, then separating the latter category into what we would call linear and non-linear change. These descriptions are long and discursive, generally containing few symbols, graphs, or diagrams, until Nicole Oresme. In the 1350s Oresme represented a linear change in the intensity of a quality with diagrams such as in Fig. 2, in which

Fig. 2
figure 2

Linearly changing intensity. From N. Oresme, De Configurationibus, book I

Full size image

If any three points are taken, the ratio of the distance between the first and the second to the distance between the second and third is as the ratio of the excess in intensity of the first point over that of the second point to the excess of that of the second point over that of the third point, calling the first of those three points the one of greatest intensity. (Oresme, in Clagett 1968, p. 193)Footnote 3

Here, as a thing moves from a to b, its linearly diminishing intensity is quantified and represented by the height of the line, such as the length dc in the figure. By representing a variable intensity as a variable height, the quality becomes a quantity. This representation and quantitative description of qualities in terms of how one quantity varies as another one varies marks an advent of covariational reasoning, one of the two crucial steps in the development of the idea of variable.

The advent of variables

Although the medieval mathematicians took the crucial step by representing and studying qualities as variable quantities, it took several centuries to develop symbolic systems for representing one variable quantity in terms of another. “The idea of variation that Oresme and others were able to cognize could only be expressed notationally in natural language and in his diagrams—no notation of variable yet existed” (Kaput 1994, p. 101). In 1637 Descartes and Fermat independently (!) developed such systems of algebraic geometry, in which we first see the modern usage of a variable as a letter in an equation or system of equations representing a quantity that varies with respect to other varying quantities.

In his Geometrie, Descartes describes his new method of using algebraic symbolism to represent and solve geometric problems. First, in order to construct a particular geometric object, we are to “give names to all the lines [lengths] that seem needful for its construction—to those that are unknown as well as to those that are known” (Descartes 1637, p. 294) Then we have some equations with some unknowns (represented with x, y, z, and other letters from the end of the alphabet) and some knowns (represented with placeholder letters from the beginning of the alphabet, a, b, c, etc.) In Book I Descartes treats the case when there are as many equations as there are unknowns, reducing the equations to a single linear, quadratic, or cubic equation in which the unknown can be solved in terms of the placeholders.

It is in Book II that Descartes treats the case when there are fewer equations than unknowns; here the unknowns become variables, and the resulting equation is a locus that describes the relationship between (two) unknown quantities:

If then we should take successively an infinite number of different values for the line[length] y, we should obtain an infinite number of values for the line x, and therefore an infinity of different points, such as C, by means of which the required curve could be drawn. (Descartes, in Hawking 2005, p. 303)

Here we see what comes to be known as the Cartesian plane, containing a curve that represents two related quantities x and y. Fermat’s system works the same way: in solving a geometric problem algebraically, if one ends up with an equation in two unknowns, the solution is a locus. For Fermat the points of the locus are determined by the motion of one endpoint of a variable line segment (y, y’, etc. in Fig. 3), the other endpoint of which moves on a straight line (x, x’, etc. in Fig. 3). Thus an equation in two variables determines a geometric curve, and vice versa—this is the revolutionary development of algebraic geometry, and the birth of the modern concept of variable. The relationship between the two quantities is apparent in the curve and in the equation, both of which can be seen as representing one varying quantity in terms of the other.

Fig. 3
figure 3

Fermat’s generation of a curve from an equation in two variables—y traces out a locus or curve as x moves in a straight line

Full size image

In summary, in the historical account we have outlined two important new practices that were crucial to the development of the idea of variables. One is the general idea at the heart of the placeholder: a letter can stand for any of a set of indeterminate quantities, not just a single unknown quantity. The second is covariational reasoning, how to represent and quantify the way that one quantity changes with respect to another. Both of these practices were important historically, and are important for students too. In the following section we particularly focus on the first of these two understandings, illustrating it with examples from student work. There are also several specific historical obstacles to the idea of variable requiring historical shifts in viewpoint that we are not claiming to be important obstacles for students. One of these is the Greek focus on the actual existence and tangible properties of the mathematical objects being represented and manipulated, which prevented the general manipulation of an indeterminate quantity that stands for a variety of types of quantities and objects. For the Greeks this obstacle is related to formal proof and geometric construction, neither of which is commonly found in the middle grades. The other is the strict Aristotelian distinction between quantities and qualities. By the middle grades we expect that most students will have enough experience with measurement to be comfortable with the fact that speeds, temperatures, etc. are quantifiable attributes, not just qualities. We included these two specific obstacles in order to make the historical story more complete and coherent, not because we anticipate these to be significant issues for students.

Some student practices

In this section we discuss a few examples of students working with letters in mathematical expressions. We particularly focus on issues that we saw arising as students are in the process of learning the first important practice that a letter can stand for any of a set of indeterminate quantities, not just a single unknown quantity. This element of the difference between unknown and variable marks a crucial step in understanding for students in the middle grades (Asquith et al. 2007; Bardini et al. 2005; Küchemann 1978; Stacey and MacGregor 1997).

Many difficulties students have with the progression from unknown to variable come from prior experiences in elementary grades. Students generally have experience with use of letters as unknowns in their arithmetic and pre-algebra curriculum, and thus by the time they reach the middle grades, most have a good understanding of the concept of an unknown. These experiences are introduced at increasingly early ages, perhaps with the aim of better preparing students for success in algebra. These experiences may contribute to difficulties, as Wagner and Parker caution that “students’ early impressions about variables may impede their construction of a sufficiently general concept” (1999, p. 330).

Some students may also have had school mathematics experiences in which letters are used (non-mathematically) as codes for specific numbers (Stacey and MacGregor 1997), frequently based on the position of the letter in the alphabetic sequence, such as a = 1, b = 2, c = 3, and so on.Footnote 4 Students often have had experience with secret code games or puzzle-like worksheets on which numerical answers are to be coded to letters, using a coding scheme provided in the exercise such as in the Mathimagination and Math with Pizzazz! workbooks that have been in American classroom use since the 1970s (Marcy 1999, 2002; Marcy and Marcy 1973, 2003). The resulting sequence of letters states a common phrase which can easily be identified if the student has found the correct answers and coded them accurately. The code can change from one situation to the next, but at any given time, a single value holds. With experience from such exercises, it is understandable for students to be inclined to treat a letter as representing a single numerical value, rather than as a variable.

Another potential source of confusion is the experiences students have using letters for names (Stacey and MacGregor 1997). For example, if Sara is 12 years younger than her brother Justin, we can represent Justin’s age with the letter J. However, as teachers and students describe this representation, it is common for them to say simply that J represents Justin. While the teacher is aware that J represents Justin’s age, a number, students many confuse J as an abbreviation for Justin himself. This type of misunderstanding persists in secondary grades; for instance, when learners are asked to write an equation in which s and p represent respectively the number of students and professors, they often write 6s = p to represent the fact that there are 6 students for each professor (e.g., Clement 1982 et al.). One reason is that learners think s is the label (so 6s means “6 students,” like 6m means “6 metres”) rather than a letter that denotes a quantity of students, a misunderstanding that is surely aggravated by the ambiguity of our notation.

These are some types of previous experiences on which students may draw when they make sense of new situations. Without either specific instruction on the new (and competing) uses of letters in mathematics or encounters with obviously discrepant situations, students are even more likely to continue to attribute to a letter the familiar meaning of a single unknown value or a code for a specific number. When faced with a symbolic example of generalised arithmetic, they may (inappropriately) wonder how the value for a letter is to be chosen. When told that each letter can represent “any number” they may assume it can represent any one number, as opposed to representing the many possibilities available. Thus the sudden change to the use of letters as variables, which students usually first experience in Grade 6 or 7, can produce great difficulty for students (Bardini et al. 2005). This is particularly problematic if students receive no deliberate instruction in the matter, or if their curricula treat the matter in a fashion that indicates unawareness of the complexity of this important issue, as we shall discuss in Section IV.

“What is x?”

Knowing about the historical story helped us to make sense of some classroom experiences with a few of our students in their transition from unknown to variable. The task in Fig. 4 was given to three 8th graders as part of a teaching experiment focussing on quadratic behaviour. In the previous class session, the students had worked on similar problems with tables of side lengths, perimeters, and areas of rectangles, but without any variables like x. By choosing values in the columns that did not have regular differences, the teacher hoped that the students would be pushed to generate missing values in the table horizontally, relating side lengths within a figure, rather than rather than vertically, continuing the pattern in the sequence of values in the column. The students readily did this, but for our purposes the thing of most interest is their reactions when they got to the last row, which calls for general expressions for the dimensions, area, and perimeter of a rectangle in terms of a variable side length x. Edward reflected the students’ perplexity, asking, “What is x?”

Fig. 4
figure 4

A task for 8th graders dealing with patterns in rectangular areas and perimeters

Full size image

The students were completely unwilling to talk about the entries in the last row in terms of a general x term, despite the teacher’s repeated entreaties. Amal said, “So pretty much, we can make this [the last problem] anything we want, right? The last one, since we don’t know what the small side is?” Marko echoed this: “For x, do we just do whatever we want?”

The teacher asked, “Well, instead of putting a number in, could you just leave it as x?” Then, writing “x” on the bottom line in the Dimensions column, she asked “So if this was, the small side was x, what would the other side be?” Amal responded, “I don’t know, y, something like that.”

As they filled out and discussed the rest of the table except the last row, the students demonstrated that they thought, for these rectangles, the long side is always 2 cm longer than the short side. Nonetheless, when the short side is “x” they did not describe the long side as “x + 2.” Amal was able to write “y” for the longer side, but was very uncomfortable with the uncertainty of what this value is. He finally filled in the last row with the area being 9800. The assisting teacher asked him about this.

  • T2: What’d you write here? Oh, sorry.

  • A: I did x…

  • T2: x by…

  • A: By 100. Because then and then a hundred, x would be 98, and then 100, and this would be the area, and that’s the perimeter.

  • T2: Why is x 98?

  • A: What?

  • T2: Why is x 98?

  • A: I just followed the pattern. Like, because you can pretty much do whatever you want with it, as long as it follows the pattern. So I just followed it because this last one is 96 and 98, so this is the next one up.

Amal finally decided to treat x as standing for the number 98, because he thought this could be the next number in the pattern in that column. Amal said, “I just imagined x was 98.” The teacher looked over at Marko’s paper to see that he has done something similar. When she asked, “What did you get for x?”, Marko responded “70.” On his own, Edward chose a different value, 1,000, to be his smaller side x. Each of the students picked a single specific number with which to replace x.

Although the students saw the relationship between the two rectangle sides and the perimeters and areas, they were unable to represent these relationships in terms of a variable length x for the short side. The letter always stood for a specific value. This interpretation of the role of a letter is also apparent in these students’ work in the next class session.

In this next class session, the students discussed a similar problem with rectangles. In this problem the shorter side is always 4 less than the longer side, rather than 2 less. The teacher wrote an “L” under the column for the longer side and asked the students what the shorter side will be. Edward had already identified the pattern between the sides, and the teacher pointed this out.

  • T1: So if the longer side is L, what’s going to be the shorter side if it’s four less?

  • A: If that was 4 less?

  • T1: How do you say that?

  • A: Um, can we give it a letter?

  • T1: You want to give it a letter?

  • E: No. You…

  • A: What?

  • E: But how can you go, do that?

  • A: What do you mean? I’m saying can you give the short side a letter?

  • E: How can you give the short side a letter? Then you won’t know if we have to figure it out.

  • M: It should be H.

  • A: It’s just, it’s just representative.

  • T1: I just gave the long side a letter.

  • A: Yeah.

  • M: It should be H. For the short side.

  • T1: H? You want to call the short side H?

  • M: Because it’s four letters af, L is four letters after H.

  • T1: L is 4 letters after H? Oh.

  • M: I think. H, I, J, K, L. [counting on his hand]

Amal wanted to represent the short side with its own letter, and Marko proposed “H,” because H is 4 letters previous in the alphabet to L. The letters are thus acting as a code for the numbers. When the teacher asked them to find the area in terms of L, Edward produced the answer “96.” When asked about this, he said that this is because L is the 12th letter of the alphabet. “L” is simply code for the number 12! Thus the area is 8 × 12, or H × L. Edward’s reasoning here is consistent with the interpretation that each letter corresponds to a specific single numerical quantity, a value that can be “deciphered” from its position in the alphabet. The letter is not representing a variable quantity, but an unknown quantity, one whose value is not determined by calculation but by deciphering. The students’ difficulty here is with one of the two important new practices found in the historical development of variables, using a letter to stand for any of a set of indeterminate quantities, not just a single unknown quantity that must be found. The students, particularly Marko and Edward, were unprepared for this new usage of letters, and so continued to search for the unknown value of the letters. This explains the deciphering behaviour, which has been seen in other instances of “coding” (e.g., Wagner 1981), as a way that students fall back on prior understandings of letter as unknown because they are unfamiliar with the new practice of a letter representing a range of quantities.

Marko’s use of the letters L and H here reflects a desire to represent how the two quantities relate to each other, that the short side always stays 4 less than the long side. Thus to some degree he is working with the second important practice, representing how one quantity changes with the other (although the teacher never asked about change explicitly). However, his representation of this is highly unconventional, because he has not become comfortable with the first practice, the representation with a single letter of an indeterminate quantity that can take on a set of values.

During this most recent episode, Amal is much more hesitant to treat L and H as code for “12” and “8,” preferring to simply write the area as L x H. This is similar to his response on the previous day, in which he was comfortable writing x × y, but not x × (x-2). In his expression for the area, he is unwilling to represent H in terms of L, such as “L-4.” Thus, his representation of the area A = L × H of these rectangles does not describe the specific relationship between the long side, short side, and area, but instead only looks like a generic area formula. Amal is not just treating the letters as unknowns to be found, but he still cannot represent one quantity in terms of another. Thus he is not comfortable replacing the “H” with “L-4” in the expression of the rectangle’s area. Filloy et al. (2010) describe this kind of understanding as requiring a second level of representational abstraction—at the first level the value is represented by “H,” while at the second level it is represented by “L-4.” This particular understanding is later necessary when students are solving systems of equations using substitution. In any case, Amal still is not using H or A as a variable, as representing quantities that can be written in terms of L and vary predictably as L varies.

The teachers were not ready for the issue to arise in which students could only treat a letter as standing for a single unknown quantity rather than a set of indeterminate quantities, and it interfered with their plans. Their purpose with the activities was ultimately to have students represent and investigate the covariation between a linear quantity (side length) and a quadratic quantity (area). The teacher essentially wanted to work with the second important practice necessary for the development of variable in our historical story—representing one changing quantity in terms of another—in the context of quadratic behaviour. But the students were stuck on the first important practice, the one that underlies the idea of a placeholder. Only later did the teachers see the difference between their use of letters and that of their students, too late to explicitly familiarise the students with the changes in practice entailed in the transition from using letters as unknowns to using them as variables.

Helping our students

It is understandable that students would have difficulty interpreting letters as representing variable quantities, and difficulty representing one variable quantity in terms of another, if their experiences in elementary school are almost entirely with unknowns, such as “17−m = 12.” Some curricular treatments might hinder the transition to variable by not deliberately acknowledging the important changes in practice that the students must understand when making this transition.

For instance, in one textbook series, the first example of a letter as a variable, not an unknown, occurs near the end of Grade 6, in a lesson (one class period) where the term function is first introduced. The exercises ask students to find a single missing number in tables, by plugging in a single determined value for x. In the section where variables are introduced, near the beginning of Grade 7, the exercises ask students to evaluate numerical expressions with a single specified value for each letter (Fig. 5).

Fig. 5
figure 5

Exercise from Saxon Math, Gr. 7, (Hake 2007b, p. 11)

Full size image

These lessons and exercises may serve to reinforce the idea for students that letters represent unknowns, not variables. In all of these cases each letter in fact stands for a single distinct unchanging value. Students are not asked to discuss the relationship between the two quantities, how to express one quantity in terms of the other, or how the change in one quantity relates to a change in the other. Unless a teacher substantially enhances these lessons, by extending the tables to include multiple missing values, and asking how the quantities and their changes relate to one another, students may persist in seeing letters as unknowns.

A number of textbook treatments indicate more awareness of these issues in the transition from unknown to variable. For instance, in the Math Thematics (Billstein and Williamson 2008) textbook series, variables are first discussed early in Grade 6 in a section that begins by asking students to find and explain the rule that generates new terms in the patterns from previous ones. The section then introduces the difference between a term in the sequence and the term number (index) of that term, and it introduces how to represent these with tables, followed by a number of classroom activities in which students must begin to describe a term of a sequence directly in terms of its term number—for instance, for a simple pattern determining the 90th term. This deliberately directs students to work with the second important practice, representing one changing quantity in terms of another rather than in terms of the previous terms. Students are first asked to represent such a relationship verbally (“you double the term number and then subtract one”), and then they are shown how to represent such a relationship using letters (“t” for term and “n” for term number). An example of such a classroom activity is in Fig. 6.

Fig. 6
figure 6

A classroom activity from the teacher’s edition of Exploration 2 of Chapter 1.2, Math Thematics, Book 1, Teacher’s Edition, MacDougal-Littel, p. 20. (Billstein and Williamson 2008)

Full size image

It is only in this context of two covarying quantities that the term “variable” is defined. Thus this treatment illustrates an awareness of the importance of building the practices of representing one changeable quantity in terms of another, and the explicit recognition that in order to use letters for such a representation, a letter must stand for any of a set of eligible values, not just for an unknown value.

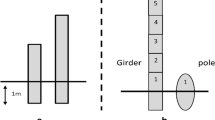
There is evidence that such a usage of variables and variation can be meaningfully available for students as young as eight or nine (Carpenter et al. 2003; Carraher et al. 2006; Fosnot and Jacob 2010). In one classroom study with students in Grades 2–4, students in Grade 3 were shown how to use a “variable number line” to represent one variable quantity in terms of another. Using this tool, they could solve problems like the “Heights” problem in Fig. 7. By the end of the teaching experiment, the students were comfortable representing any of the three characters’ heights in terms of the indeterminate height N of another; they could represent Leslie’s height as N + 6 if Maria’s height was N, and represent Maria’s height as N – 6 if Leslie’s height was called N instead. The students worked only in the context of simple “additive offset” relationships (of the form x + b), but their responses show how, with proper classroom practices, students can build an understanding of algebraic letters that transcends “unknowns” at an early age.

Fig. 7
figure 7

The Heights problem and student work (Carraher et al. 2006, p. 104–106)

Full size image

There are many other recent examples of curricular materials, interventions, and tasks that have been used to help students build an understanding of the use of letters as variables rather than unknowns. Some examples include Fujii and Stephens’ (2008) work with students to use variables as a way to summarise the structural patterns found in groups of related numerical expressions. Gay and Jones (2008) used the context of amusement parks to give students experience representing real-world situations with variables. Tabach and Friedlander (2008) used sequences of visual patterns as a context for the construction of general expressions that represent the structure of the pattern. These approaches stress the importance of providing such experiences early in students’ learning process to prepare them for the transition to variables in the middle grades.

Deliberately focussing on the two practices that are crucial to the development of the use of variables, as shown in the historical development of variables, helps us interpret student difficulties and better prepare students to succeed in the middle-grades transition from unknown to variable. We hope that widespread awareness of these practices will also support teachers and textbooks in purposefully beginning to develop these practices in early grades.