1 Introduction

The exploitation of underground resources and the expansion of underground space are getting deeper in recent years [1, 2]. High in-situ stress of deep engineering projects has much influence on the stability of surrounding rock, which has become a worldwide problem in geotechnical mechanics and engineering [3, 4]. For the blasting excavation process of underground engineering, blasting load makes microcracks expand to macro-cracks, which leads to the reduction of original rock bearing capacity, and results in damage areas [5]. And blasting damage cannot be eliminated by optimizing blasting design [6, 7].

In earlier research of damage zone during tunnel excavation, only the influence of secondary stress field was involved. Andersson and Martin [8] discussed the influence of the thermal stress on the damage of pillar between two tunnels, and the result showed that failure would occur in intact rock under the stress of 80 to 135 MPa. Cai et al. [9] studied the damage threshold of intact rock mass under the influence of the secondary stress field of rock excavation. It was found that crack and damage initiate at 0.3 ~ 0.5 times of rock uniaxial compressive peak stress, which means the damage depth will increase with the stress level increasing. Lim et al. [10] analyzed the microcracking behavior of granite cores within different embedment depths (it also means different in-situ stress levels), and they pointed out that the volume of the microcracking is closely related to the sampling embedment depth. In the researches above, the in-situ stress was involved by static method, and the dynamic process, including blasting load and in-situ stress dynamic adjustment, is ignored.

In recent years, with the development of theories and experimental methods, dynamic disturbance of excavation has been taken into consideration in the researches of damage zone. Chen et al. [11] explored the influence of the coupling effect of blasting load and in-situ stress on damage zone of deep buried tunnel. Significantly, the redistribution of initial stress is the main factor of blasting damage, and the blasting load will increase the damage depth. Yang [12] pointed out that as the stress level increases, the damage depth of surrounding rock decreases obviously, and it begins to increase after the local stress reaches a certain level. For mechanism analysis, Fu et al. [13] thought that the existence of high stress level is equivalent to the increment of the tensile strength when analyzing the mechanism and damage properties of deep tunnel. Mu and Pan [14], Bai et al. [15], and Xie et al. [16] all stated that high in-situ stress has resistance on blasting damage in their researches. Besides, Yang et al. [17] studied the blasting damage under different in-situ stress level by simulation and acoustic wave test, and the result showed that the damage extent of surrounding rock decreases first and then increases with the stress increasing continuously. It was apparent that coupling effect of blasting load and in-situ stress was taken into account or just the resistance effect of in-situ stress on blasting damage was described in those researches. However, these researches only described the manifestation, its mechanism involved rarely.

To expose the mechanism of that the damage distribution and the composition shown much distinction under different in-situ stress levels, the coupling effect of explosion load and in-situ stress is considered. Based on the numerical simulation and theoretical analysis, the resistance effect in-situ stress has on blasting damage is described and its mechanism is elaborated in this paper by both static and dynamic analyses. The results will be helpful in damage mechanism research and optimizing of excavation design of deep engineering.

2 Theoretical Analysis of Rock Response

2.1 Thick-Walled Cylinder

Considering the blasting load applied on the blasthole as static load, the response of surrounding rock under blasting load can be abstracted as a thick cylinder with internal and external pressures. It is appropriate to assume that the inner and outer radii are r and R, and the internal and external pressures are q1 and q2 (Fig. 1). The stress boundary conditions are shown as:

$$\left\{ \begin{gathered} \left( {\tau_{\rho \varphi } } \right)_{\rho = r} = 0 ;\quad \left( {\tau_{\rho \varphi } } \right)_{\rho = R} = 0 \hfill \\ \left( {\sigma_{\rho } } \right)_{\rho = r} = - q_{1};\quad \left( {\sigma_{\rho } } \right)_{\rho = R} = - q_{2} \hfill \\ \end{gathered} \right.$$
(1)
Fig. 1
figure 1

Boundary conditions

Full size image

The general solution of axisymmetric stress in polar coordinates is shown in Eq. (2). Substituting Eq. (2) in Eq. (1), it can be seen that the equation of shear stress in Eq. (1) is satisfied. However, the model for this problem is multibody (Fig. 1), considering the single value condition of displacement, B = 0 can be deduced. Then, the condition of positive stress in this problem is shown in Eq. (3):

$$\left\{ {\begin{array}{*{20}l} {\sigma_{\rho } = \frac{A}{{\rho^{2} }} + B(1 + 2\ln \rho ) + 2C} \hfill \\ {\sigma_{\varphi } = - \frac{A}{{\rho^{2} }} + B(3 + 2\ln \rho ) + 2C} \hfill \\ {\tau_{\rho \varphi } = \tau_{\rho \rho } = 0} \hfill \\ \end{array} } \right.$$
(2)
$$\left\{ {\begin{array}{*{20}l} {\frac{A}{{r^{2} }} + 2C = - q_{1} } \hfill \\ {\frac{A}{{R^{2} }} + 2C = - q_{2} } \hfill \\ \end{array} } \right.$$
(3)

Equation (4) can be deduced from Eq. (3), and the general solution of uniform pressure on cylinder in polar coordinates can be obtained from Eqs. (2) and (4), as shown in Eq. (5):

$$\left\{ {\begin{array}{*{20}l} {A = \frac{{r^{2} R^{2} \left( {q_{2} - q_{1} } \right)}}{{R^{2} - r^{2} }}} \hfill \\ {2C = \frac{{q_{1} r^{2} - q_{2} R^{2} }}{{R^{2} - r^{2} }}} \hfill \\ \end{array} } \right.$$
(4)
$$\left\{ {\begin{array}{*{20}c} {\sigma_{\rho } = - \frac{{\frac{{R^{2} }}{{\rho^{2} }} - 1}}{{\frac{{R^{2} }}{{r^{2} }} - 1}}q_{1} - \frac{{1 - \frac{{r^{2} }}{{\rho^{2} }}}}{{1 - \frac{{r^{2} }}{{R^{2} }}}}q_{2} } \\ {\sigma_{\varphi } = \frac{{\frac{{R^{2} }}{{\rho^{2} }} + 1}}{{\frac{{R^{2} }}{{r^{2} }} - 1}}q_{1} - \frac{{1 + \frac{{r^{2} }}{{\rho^{2} }}}}{{1 - \frac{{r^{2} }}{{R^{2} }}}}q_{2} } \\ \end{array} } \right.$$
(5)

2.2 Blasthole under Blasting Load

For a single blasthole in infinite rock mass, R can be considered as infinity and r as the radius of blasthole. Then, q1 is 0, and q2 is in-situ stress. The secondary stress field after excavation can be expressed as:

$$\left\{ \begin{gathered} \sigma_{\rho 1} = \left( {\frac{{r_{1}^{2} }}{{\rho^{2} }} - 1} \right)q_{2} \hfill \\ \sigma_{\varphi 1} = - \left( {1 + \frac{{r_{1}^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \end{gathered} \right.$$
(6)

For the tunnel without initial stress, and the inner wall of the tunnel is applied with blasting load, R can be considered as infinity and r as the radius of blasthole, q1 is the peak value of load, q2 is 0. The secondary stress field caused by peak blasting load can be expressed as:

$$\left\{ \begin{gathered} \sigma_{\rho 2} = - \frac{{r_{1}^{2} }}{{\rho^{2} }}q_{1} \hfill \\ \sigma_{\varphi 2} = \frac{{r_{1}^{2} }}{{\rho^{2} }}q_{1} \hfill \\ \end{gathered} \right.$$
(7)

The surrounding rock is considered as a linear elastomer to simplify the theoretical analysis, so the multiple stress fields can be linearly superimposed. The secondary stress field of deep buried tunnel with internal load can be expressed as:

$$\left\{ \begin{gathered} \sigma_{\rho 3} = - \frac{{r_{1}^{2} }}{{\rho^{2} }}q_{1} + \left( {\frac{{r_{1}^{2} }}{{\rho^{2} }} - 1} \right)q_{2} \hfill \\ \sigma_{\varphi 3} = \frac{{r_{1}^{2} }}{{\rho^{2} }}q_{1} - \left( {1 + \frac{{r_{1}^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \end{gathered} \right.$$
(8)

2.3 Smooth Blasthole under Blasting Load

For the detonation of smooth blasting, blastholes are located in the secondary stress field caused by the detonation of the breaking holes. Assume that the radius of the surface of the outermost main blasting hole is R0 and the thickness of the smooth blasting layer is Ls. Ignoring the influence of the cavity of blasthole, the stress state at the blasthole can be inferred from Eq. (6):

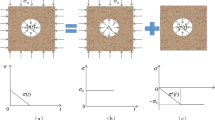
$$\left\{ \begin{gathered} \sigma_{\rho 0} = \left( {\frac{{r^{2} }}{{\rho^{2} }} - 1} \right)q_{2} = \left( {\frac{{r_{0}^{2} }}{{\left( {r_{0} + L_{s} } \right)^{2} }} - 1} \right)q_{2} \hfill \\ \sigma_{\varphi 0} = - \left( {1 + \frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} = - \left( {1 + \frac{{r_{0}^{2} }}{{\left( {r_{0} + L_{s} } \right)^{2} }}} \right)q_{2} \hfill \\ \end{gathered} \right.$$
(9)

The stress state of surrounding rocks around the smooth blasthole can be simplified as the state shown in Fig. 2. To give an analytical solutions of this problem, the stress state in Fig. 2 can be decomposed into two as shown in Fig. 3. As the blasthole size is negligibly small compared to the excavation scale, the two stress states in Fig. 3 can be analyzed by means of the “small orifice problem”, and the elastic solution had been discussed by Xu [18]. For Fig. 3a, b, the solutions can be expressed as:

$$\left\{ \begin{gathered} \sigma_{\rho 4} = - \left( {\frac{{r^{2} }}{{\rho^{2} }} - 1} \right)\left( {\frac{{\sigma_{\rho 0} + \sigma_{\varphi 0} }}{2}} \right) \hfill \\ \sigma_{\varphi 4} = \left( {1 + \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {\frac{{\sigma_{\rho 0} + \sigma_{\varphi 0} }}{2}} \right) \hfill \\ \end{gathered} \right.$$
(10)
$$\left\{ \begin{gathered} \sigma_{\rho 5} = \left( {\frac{{\sigma_{\rho 0} - \sigma_{\varphi 0} }}{2}} \right)\cos 2\varphi \left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 - 3\frac{{r^{2} }}{{\rho^{2} }}} \right) \hfill \\ \sigma_{\varphi 5} = - \left( {\frac{{\sigma_{\rho 0} - \sigma_{\varphi 0} }}{2}} \right)\cos 2\varphi \left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right) \hfill \\ \tau_{\rho \varphi 5} = \tau_{\varphi \rho } = - \sin 2\varphi \left( {\frac{{\sigma_{\rho 0} - \sigma_{\varphi 0} }}{2}} \right)\left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right) \hfill \\ \end{gathered} \right.$$
(11)
Fig. 2
figure 2

Stress filed around smooth blasthole

Full size image
Fig. 3
figure 3

Decomposition of stress filed: a compression on both sides, b compression on the one side and tension on the other

Full size image

The stress state of Fig. 2 can be solved from the superimposition of Eqs. (10) and (11), followed by the substitution of Eq. (9), as shown in Eq. (13). Taking the blasting load into account, the response of surrounding rock of smooth blasthole is shown in Eq. (14):

$$\left\{ \begin{gathered} \sigma_{\rho 6} = - \left( {\frac{{r^{2} }}{{\rho^{2} }} - 1} \right)\left( {\frac{{\sigma_{\rho 0} + \sigma_{\varphi 0} }}{2}} \right) + \left( {\frac{{\sigma_{\rho 0} - \sigma_{\varphi 0} }}{2}} \right)\cos 2\varphi \left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 - 3\frac{{r^{2} }}{{\rho^{2} }}} \right) \hfill \\ \sigma_{\varphi 6} = \left( {1 + \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {\frac{{\sigma_{\rho 0} + \sigma_{\varphi 0} }}{2}} \right) - \left( {\frac{{\sigma_{\rho 0} - \sigma_{\varphi 0} }}{2}} \right)\cos 2\varphi \left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right) \hfill \\ \tau_{\rho \varphi 6} = \tau_{\varphi \rho 5} = - \sin 2\varphi \left( {\frac{{\sigma_{\rho 0} - \sigma_{\varphi 0} }}{2}} \right)\left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right) \hfill \\ \end{gathered} \right.$$
(12)
$$\left\{ \begin{gathered} \sigma_{\rho 6} = \left( {\frac{{r^{2} }}{{\rho^{2} }} - 1} \right)q_{2} + \frac{{r_{0}^{2} \cos 2\varphi }}{{\left( {r_{0} + L_{s} } \right)^{2} }}\left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 - 3\frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \sigma_{\varphi 6} = - \left( {1 + \frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} - \frac{{r_{0}^{2} \cos 2\varphi }}{{\left( {r_{0} + L_{s} } \right)^{2} }}\left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \tau_{\rho \varphi 6} = \tau_{\varphi \rho 5} = - \frac{{r_{0}^{2} \sin 2\varphi }}{{\left( {r_{0} + L_{s} } \right)^{2} }}\left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \end{gathered} \right.$$
(13)
$$\left\{ \begin{gathered} \sigma_{\rho 7} = - \frac{{r^{2} }}{{\rho^{2} }}q_{1} + \left( {\frac{{r^{2} }}{{\rho^{2} }} - 1} \right)q_{2} + \frac{{r_{0}^{2} \cos 2\varphi }}{{\left( {r_{0} + L_{s} } \right)^{2} }}\left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 - 3\frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \sigma_{\varphi 7} = \frac{{r^{2} }}{{\rho^{2} }}q_{1} - \left( {1 + \frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} - \frac{{r_{0}^{2} \cos 2\varphi }}{{\left( {r_{0} + L_{s} } \right)^{2} }}\left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \tau_{\rho \varphi 7} = - \frac{{r_{0}^{2} \sin 2\varphi }}{{\left( {r_{0} + L_{s} } \right)^{2} }}\left( {1 - \frac{{r^{2} }}{{\rho^{2} }}} \right)\left( {1 + 3\frac{{r^{2} }}{{\rho^{2} }}} \right)q_{2} \hfill \\ \end{gathered} \right.$$
(14)

3 Mechanism Analysis of the Smooth Blasting Damage

3.1 Criterion

For the simulation of blasting damage, the key is to determine the damage criterion. Most damage variables defined by existing damage models are the function of crack density. And the crack density is usually determined by probability distribution [19]. Thus, there are lots of obstruction in parameter determination. In this paper, the widely used criteria, Mohr–Coulomb criterion, the first strength criterion and the maximum compressive stress criterion, are adopted at the same time.

Mohr–Coulomb criterion is a criterion widely used in geotechnical field. It describes the change of shear strength with the normal stress changing, as shown in Eq. (15):

$$\tau = c + \sigma \tan \varphi$$
(15)

where τ is the shear stress, σ is the normal stress, φ is the internal friction angle, and c is the cohesion.

At the same time, the tension zone shows obedience to first strength criterion. When the maximum tensile stress σ3 reaches the tensile strength σt, the tensile damage appears. The discriminant is shown in Eq. (16):

$$\sigma_{3} + \sigma_{t} \le 0$$
(16)

where σt is the tensile strength.

In the compression zone, when the maximum compressive stress σ1 reaches the compressive strength σc, the compressive damage appears (Eq. 13).

$$\sigma_{1} - \sigma_{c} \ge 0$$
(17)

where σc is the compressive strength.

In summary, the envelope of the damage criterions of this paper is shown in Fig. 4. The upper left area of the curve is the damaged zone. When the stress path of an element across the envelope gets into the damaged zone, the element is thought to be damaged.

Fig. 4
figure 4

Envelope of the damage criterion

Full size image

3.2 Yield limits

The stress state expressed by Eq. (14) is drawn as the Mohr circle in Fig. 5. It is worth mentioning that the minus indicates compressive stress, while positive number means tensile stress in Eq. (14), which is contrary to symbolic definition of the result shown in Fig. 5. Therefore, it is necessary to change the sign of Eq. (14) while drawing the result into Fig. 5. The broken line MNOP is the envelope of yield criterions, and it intersects with σ axis at points H and I; they represent the tensile strength and compressive strength of the material. Point A and B can be determined by the stress state calculated by Eq. (14). Then, the stress state can be represented by the circle whose diameter is AB. The length of HE, GD and IF can be regarded as the yield limit of tensile failure, shear failure and compression failure of the stress state shown in Fig. 4. Then, the three yield limits can be expressed as follows:

$$\left\{ \begin{gathered} f_{{{\text{yl}}1}} = \sigma_{3} + \sigma_{t} \hfill \\ f_{{{\text{yl}}2}} = \sigma_{c} - \sigma_{1} \hfill \\ f_{{{\text{yl}}3}} = \frac{{\left| {\frac{{\sigma_{1} + \sigma_{3} }}{2}\tan \varphi + c} \right|}}{{\left( {\tan^{2} \varphi + 1} \right)2}} - \frac{{\sigma_{1} - \sigma_{3} }}{2} \hfill \\ \end{gathered} \right.$$
(18)
Fig. 5
figure 5

Schematic of yield limits

Full size image

When fyl > 0, fyl represents the yield limit. And “ fyl < 0” means that the stress state has made the material into yield state.

Circular tunnel is selected for analyzing. Material parameters of rock mass are listed in Table 1. The diameter of excavation outline is 6000 mm, the diameter of smooth blasthole is 45 mm, while their spacing is 500 mm, and the thickness of smooth blasting layer is  600 mm. The point located in the blasthole wall with a depth of 100 mm is taken for analysis, which means that ρ = 100 mm and φ = 0° in Eq. (14). Therefore, the shear stress at the selected position is zero. The principal stress can be calculated by Eq. (19):

$$\left\{ {\begin{array}{*{20}c} {\sigma_{1} = \max (\sigma_{\rho 7} ,\sigma_{\varphi 7} )} \\ {\sigma_{3} = \min (\sigma_{\rho 7} ,\sigma_{\varphi 7} )} \\ \end{array} } \right.$$
(19)
Table 1 Material parameters of rock mass
Full size table

3.3 Theoretical results and discussing

Substituting Eq. (19) in Eq. (18), the laws of yield limits varying with in-situ stress and peak explosive load can be observed, as shown in Figs. 6, 7 and 8. When in-situ stress is 0 MPa, with the increasing of peak blasting load, the yield limit of tensile stress decreases. The tensile stress limit of rock mass has reached, while blasting load is small (72 MPa). With the increasing of in-situ stress, the tensile yield limit increases; with the increasing of blasting load, the tensile yield limit decreases after increment, and the variation of the increasing part is positively correlated to the in-situ stress. When in-situ stress is 0 MPa, the compressive yield limit decreases with the increasing of blasting load; when in-situ stress exists, the compressive yield limit decreases with the increasing of in-situ stress; with the increasing of blasting load, the compressive yield limit decreases after increment, but the variation of increasing part is smaller than the decrement caused by in-situ stress. Therefore, with the increasing of in-situ stress, the compressive yield limit decreases in general. When in-situ stress is 0 MPa, the shear yield limit tends to decrease with the increasing of blasting load. The existence of in-situ stress does not affect the initial shear stress yield limit much; with the increasing of peak load, the shear stress yield limit first increases and then decreases, and the increment is positively related to the in-situ stress.

Fig. 6
figure 6

Tensile yield limit

Full size image
Fig. 7
figure 7

Compressive yield limit

Full size image
Fig. 8
figure 8

Shear yield limit

Full size image

In brief, the existence of in-situ stress can increase the tensile and shear yield limits of rock mass and reduce the compressive yield limits to a certain extent. However, the compressive strength of rock mass is often much larger than the tensile and shear strength, and the influence of in-situ stress on the yield limit of rock mass is mainly reflected on the tensile and shear yield limit. On the whole, in-situ stress will increase the yield limit of surrounding rock to a certain extent, which is not conducive to the fragmentation of rock mass.

To have a better illustration on the effect of in-situ stress and blasting load on yield limit, the Mohr circles of 10 MPa for in-situ stress and 0 MPa, 130 MPa and 400 MPa for peak loads are shown in Fig. 9, and the Mohr circles of 400 MPa for peak blasting load and 0 MPa, 10 MPa, 20 MPa and 30 MPa for in-situ stress are shown in Fig. 10. It can be seen that with the increasing of blasting load, the radius of Mohr circle increases after decreases when the in-situ stress level remains the same. At the same time, the tensile yield limit, shear yield limit and compressive yield limit decrease first and then increase. And when blasting load remains the same, the Mohr circle radius decreases with the increasing of in-situ stress. At the same time, tensile yield limit and shear yield limit increase and the compressive yield limit decreases. For blasting damage, tension-shear damage often takes up the main part, so the existence of in-situ stress increases the yield limit of rock mass to a certain extent in general, thus making that blasting damage extent decreases with the increasing of in-situ stress.

Fig. 9
figure 9

Stress state with different peak load

Full size image
Fig. 10
figure 10

Stress state with different in-situ stress

Full size image

The relations of in-situ stress, depth of measuring point, peak load and yield limit are shown in Figs. 11, 12 and 13, where the horizontal axis is the depth of measuring point and the peak blasting load, the vertical axis is the in-situ stress, and the color axis is yield limit. For the color axis, the color represents the relative location between the Mohr circle and criterion envelope, the blues means they are disjoint, the reds means they are intersecting and the whites means they are tangent. Sections are made at depths of 100 mm, peak loads of 2000 MPa and in-situ stresses of 0 MPa. It can be seen that the responses of the tensile yield limit and shear yield limit to the depth changing of measuring point, in-situ stress and blasting load are similarity. The two yield limits increase with the increasing of in-situ stress, the depth of measuring point and blasting load. The compressive yield limit decreases with the increasing of in-situ stress and the depth of measuring point; and it decreases with the increasing of blasting load overall. But it increases first and then decreases with the increasing of blasting load when in-situ stress exists. The damage area caused by deep tunnel excavation is mostly made up of tension-shear damage, which means that with the increasing of in-situ stress, the yield limit of rock mass will increase, and the damage area caused by excavation with the same blasting design will gradually decrease. Meanwhile, in order to get the same fragmenting effect (damage depth), the blasting load must be increased by increasing the amount of explosive or using high-energy explosive.

Fig. 11
figure 11

Tensile yield limit

Full size image
Fig. 12
figure 12

Compressive yield limit

Full size image
Fig. 13
figure 13

Shear yield limit

Full size image

4 Numerical Simulation on the Effects

4.1 Simulation Method and Verification

In order to explain the effect of in-situ stress on blasting damage more visible, the process is explained by numerical simulation with FLAC3D. The yield criteria are shown in Sect. 3 and the material parameters are shown in Table 1. The blasting load is applied on the blasthole. The model size is 12 m × 12 m, with a circular tunnel located in the middle whose excavation radius is 2000 mm. The diameter of smooth blastholes is 40 mm, and the distance between the holes is 500 mm, as shown in Fig. 14. And the model where blasting load is applied is shown in Fig. 15.

Fig. 14
figure 14

Model size

Full size image
Fig. 15
figure 15

The position where load applied

Full size image

Triangular curve is adopted for blasting load in simulation, as shown in Fig. 16. Considering the blasting design of general tunnel excavation, the rising time tr is 0.5 ms, the positive pressure action time tb is 5 ms, and the peak load is 424 MPa.

Fig. 16
figure 16

Time-history curve of blasting load

Full size image

Both blasthole load and equivalent load are adopted in simulation. When the blasting load is equivalent to the excavation surface, the equivalent load [20,21,22] is:

$$P_{be}= \frac{2r}{{L_{s} }}P_{b0}$$
(20)

where Ls is the distance between the holes. Therefore, the equivalent load applied on the excavation face is 34 MPa.

To verify the simulation method, a single blasthole model is established and the result of theoretical calculation is compared. The model is a semicircle and its radius is 5 m with a Φ40 mm blasthole at the center (Fig. 17). The input diameters are the same as the main simulation in Table 1. The result is shown as Fig. 18.

Fig. 17
figure 17

Model to verify the simulation method

Full size image
Fig. 18
figure 18

Simulation result

Full size image

According to Chapman–Jouguet theory and Mises criterion, Dai Jun [23] discussed the radius of fractured zone. When the charging column is small and the decoupling coefficient is small, the radius of fracture zone is as follows:

$$R_{2} = \left( {\frac{{\sigma_{R} B}}{{\sqrt 2 \sigma_{td} }}} \right)^{{\frac{1}{\beta }}} \left( {\frac{{\rho_{0} D^{2} nK^{ - 2r} l_{e} B}}{{8\sqrt 2 \sigma_{cd} }}} \right)^{\frac{1}{a}} r_{b}$$
(21)
$$B = [(1 + b)^{2} + (1 + b^{2} ) - 2(1 - \mu_{d} )(1 - b)^{2} ]^{\frac{1}{2}}$$
(22)
$$\sigma_{R} = \frac{{\sqrt 2 \sigma_{cd} }}{B}$$
(23)
$$a = 2 + \frac{{\mu_{d} }}{{1 - \mu_{d} }}$$
(24)
$$\beta = 2 - \frac{{\mu_{d} }}{{1 - \mu_{d} }}$$
(25)
$$b = \frac{{\mu_{d} }}{{1 - \mu_{d} }}$$
(26)

where ρ0 is the explosive density, n is the pressure increasing coefficient, taken as 10, le is the axial decoupling coefficient, rb is the blasthole radius, a is the load propagation attenuation coefficient inside the crushing circle, β is the load propagation attenuation coefficient outside the crushing circle, b is the lateral stress coefficient, σcd is the dynamic tensile strength of rock, and μd is the dynamic Poisson's ratio of rock. Within the loading rate range of engineering blasting, μd can be considered as 0.8μ.

According to the parameters in Table 1, it can be calculated that when the borehole diameter is 40 mm and the uncoupling coefficient is 1.25, the loading rate in the crushing ring is 103 s−1 and the loading rate outside the crushing ring is 102.5 s−1. The radius of explosive fracture zone is about 0.751 m. Compared to the theoretical result (0.751 m), the simulation result (0.772 m) is lager by 2.8%. It can be considered that the simulation method in this paper has got the effect in line with the theory while simulating blasting damage, and the practicability of the simulation method in this paper has been verified.

4.2 Numerical Results and Discussion

The damage depth and damage area are counted after simulating with different in-situ stresses, as shown in Figs. 19 and 20. And blasting damages are compared under the in-situ stress of 1 MPa, 2.5 MPa and 5 MPa in Figs. 21, 22 and 23.

Fig. 19
figure 19

Change of damage depth with stress level

Full size image
Fig. 20
figure 20

Change of damage area with stress level

Full size image
Fig. 21
figure 21

Comparison of damage extent with 1 MPa in-situ stress

Full size image
Fig. 22
figure 22

Comparison of damage extent with 2.5 MPa in-situ stress

Full size image
Fig. 23
figure 23

Comparison of damage extent with 5 MPa in-situ stress

Full size image

It can be seen that damage area caused by equivalent load is more uniform, while the damage area caused by blasthole load is hump like. And the damage area caused by blasthole load can better reflect the distribution of damage area. With the increasing of in-situ stress, the damage depth and damage area show a first decreasing and then increasing trend. And the damage depth and damage area minimum value are reached at about 5 MPa in-situ stress. When the stress level continues to increase, the damage depth and damage area with dynamic load are getting close to that without dynamic load. So, it can be inferred that the damage is mainly controlled by blasting load when stress level is low, and it is mainly affected by the redistribution of in-situ stress when stress level is high enough.

Figures 24 and 25 show the statistics of the proportion of every damage type. Shear damage area is the main component of blasting damage area under all stress levels. The proportion of compressive damage under most stress level is less than 10%, and it is much smaller than the other two. With the increasing of stress level, proportion of compressive damage tends to increase. Tensile damage is greatly affected by stress level. In the absence of in-situ stress, the proportion of tensile damage area exceeds 70%. With the increasing of stress level, the proportion of tensile damage area decreases rapidly. When hydrostatic pressure is 12.5 MPa, it is less than 10%. In conclusion, under the condition of low in-situ stress level (less than 12.5 MPa), blasting mainly causes tensile-shear damage, while the local stress level continues to increase, compressive-shear damage tends to be the most important part.

Fig. 24
figure 24

Statistics of damage area

Full size image
Fig. 25
figure 25

Statistics of ratio of different damage type

Full size image

Through the center of the Mohr circle, vertical line of Mohr criterion is made. The vertical line intersects with Mohr circle at two points, and the one close to the Mohr criterion is taken as characteristic points. The point at tunnel wall with a depth of 100 mm is chosen for measuring, and its characteristic point’s path under 5 MPa in-situ stress is recorded in Fig. 26. The trend of the stress path is consistent with the analyses above. Because the peak value of equivalent load on the excavation surface (34 MPa) is greatly reduced compared to the blasthole load (1.62 GPa), the change extent of stress path caused by equivalent load is less than that caused by blasthole load, and the influence mostly falls on the part where the yield limit increases. Therefore, when the in-situ stress level reaches a certain degree, equivalent load cannot make the path cross the criterion, and the damage area fades. With the continuous increasing of in-situ stress, the damage depth will increase continuously. The reason is that the damage is mainly controlled by the secondary stress field of the excavation. So the greater the in-situ stress level is, the greater the damage depth is.

Fig. 26
figure 26

Stress path of points at side wall with a depth of  200 mm

Full size image

5 Conclusion

In this study, the effects of in-situ stress on blasting damage during deep tunnel excavation were analyzed, and the exploration of its mechanism was developed. The following conclusions can be drawn:

  1. (1)

    With the increasing of in-situ stress, the damage depth and damage area show a first decreasing and then increasing trend with a dividing point of 12.5 MPa. In the decreasing part, blasting load is the dominant factor, while the secondary stress field influences the increasing part.

  2. (2)

    The existence of in-situ stress can increase the tensile and shear yield limits of rock mass and reduce the compressive yield limits to a certain extent. Moreover, the major constituent of blasting damage is tensile-shear damage, so the in-situ stress shows the resistance on the blasting damage.

  3. (3)

    Under the condition of low in-stress stress level (less than 12.5 MPa), blasting mainly causes tensile-shear damage, while local stress level continues to increase, compressive-shear damage tends to be the most important part.