Thermal performance analysis of a long-span suspension bridge with long-term monitoring data

Abstract

Thermal performance analysis such as calculating thermal stress from monitoring data is important for structural safety evaluation. These temperature characteristics of long-span bridges are more complicated due to their temperature distribution, structural configuration and boundary conditions. In this study, the method of structural thermal performance analysis is proposed by processing and analyzing the long-term monitoring data and it is applied to study the thermal and mechanical behavior of a long-span suspension bridge under daily operating conditions. First, statistical analysis of strain data and temperature data is performed on the main girder. Second, thermal analysis and temperature-induced stress calculation are proposed, in which the different kinds of thermal loads including uniform temperature, linear/nonlinear temperature gradient and partial constraints in axial/rotation directions are considered. Other parameters such as restrained stiffness, deformation, etc., are derived. Third, the proposed method is verified and used in the temperature-induced stress calculation on the studied bridge.

1 Introduction

The thermal effect is widely regarded as one of the most significant and negative effects on bridges and high-rise structures. The changes in structural temperature and temperature distribution on structure lead to the whole deformations and movements, stresses, cracks, etc. It has been reported that the environmental thermal stress may have a more significant impact on structural behaviors compared with vehicle loadings [1,2,3,4,5,6,7,8].

Temperature load has great influence on the static/dynamic responses of the long-span bridge. First, the temperature change induces the change of structural dynamic characteristics. Liu and DeWolf [9] reported that the first three frequencies of a curved concrete box bridge decreased by 0.8%, 0.7%, and 0.3%, respectively, per degree Celsius increase in temperature. Second, the temperature load is the main factor leading to the deformation of long-span bridges. Koo et al. [10] presented that structural temperature leading to thermal expansion of the deck, main cables, and additional stays is the major factor on global deformation, whereas vehicle load and wind are usually secondary factors. Third, bridge structures are subject to complex thermal stresses which vary continuously with time. However, only a limited number of studies have been devoted to the long-span bridges. Earlier procedures for determining thermal stresses in composite-girder concrete and steel bridges were presented by Zuk [11]. It has been reported that the magnitude of tensile stress in the deck can be relatively high compared with traffic loading-induced stress [12, 13]. Song et al. [14] found that the tensile stress caused by the solar temperature differential can be quite large (4.41 MPa) compared with the tensile strength of concrete. Therefore, the calculation of thermal stress levels due to time-variable and space-variable thermal loads is more significant in the bridge design considering the aspects of the maximum stress limitation.

The mechanism between thermal stress and measured strain under temperature loads is in urgent need of research to understand the thermal behavior of long-span bridges. In terms of finite element simulation, the distribution of temperature and induced strain/stress has been studied by performing finite element analysis of long-span bridges [15, 16]. But there are still too many assumptions in the numerical model, such as the temperature distribution is constant along the longitudinal direction of the girder. In the field measurement, Xia et al. [17] calculated the thermal stress in each component through the formula of elastic mechanics, and the maximum thermal stress is about 10.0 MPa. The other method of thermal stress calculation depends on an accurate prediction of the temperature distribution [18, 19]. In addition, the time history of structural stress is obtained by simply multiplying the measured strain data by the elastic modulus of steel [20]. Obviously, this calculation is not accurate enough. Ni et al. [21] thought that the temperature-induced stress is often ignored by assuming that the bridge is freely constrained, in which the thermal-induced strain is totally transformed to structural deformation and no stress is induced.

Despite investigating for a long time, challenging problems still exist in the field of long-span bridge thermal performance analysis. Bridge owners and researchers are interested in unsolved problems such as the thermal behavior of long-span bridges under operational conditions; the mechanism between structural deformation, especially thermal stress and measured strain under temperature loads that include a nonlinear temperature gradient; and the calculation of a temperature-induced stress distribution from the measured strain of long-span bridges.

If temperature effects are not fully understood, then false identification of structural condition may occur. Static load test has also been performed on the studied bridge, in which the measured static strain of the main girder reached 156 με under a truck train load of 17,680 kN. In the condition of static test, structural stress can be calculated directly from measured strains. It is found from the long-term ambient test data of the studied bridge that the temperature-induced strain reached 150 με in operational conditions. It is seen that the strains measured in the static test and in the ambient vibration test are comparable, but it is impossible that their induced stress are in a same level. Thermal strain will not convert fully to structural stress because it will partially release due to the partial constraints of real bridges. Then, the questions arising are, how to calculate the thermal stress distribution for the real bridges which depends on the boundary condition and the type of temperature load, and what’s the role of the thermal stress contributing to structural mechanical performance during evaluating the safety condition of long-span bridges.

The objective of this article is to study the thermal stress distribution of a long-span suspension through the long-term monitoring data, in which the thermal analysis method considering the structure model with various boundary conditions and temperature load types is proposed. The structure of the article is as follows: first, the studied long-span suspension bridge and its structural health-monitoring system are briefly described. Statistical analysis of the one-year monitoring data is performed. Second, the thermal analysis method considering the structures with various boundary conditions and temperature load types are proposed, and it is verified by a numerical example. Third, the temperature-/vehicle- induced stress are calculated and analyzed based on the long-term monitoring data. Finally, the conclusions are given.

2 The studied bridge and statistical analysis of the long-term monitoring data

2.1 Structural health monitoring (SHM) system of the studied bridge

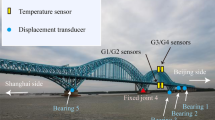
The studied suspension bridge has a main span length of 1385 m over the Yangtze River in Jiangsu, China (Fig. 1). Its main span has a welded streamlined constant depth steel box girder of 3 m height and 36.9 m width which utilized the asphalt concrete pavement, and a navigation clearance of 50 m. The bridge has two reinforced concrete towers of 190 m height, and main cables are anchored in gravity anchorages. The air temperature changes from −6.1 to 37.2 °C in year and an annual average temperature is about 16.9 °C. An SHM system is designed and installed on the bridge in 2005 [22]. The sensor layout of the current SHM system includes 170 sensors, such as accelerometers (AS), Fiber Bragg grating sensors (FBG), displacement sensors (DIS), global positioning system (GPS) receivers, shear pins, ultrasonic anemometer, etc. Main sensors as shown in Fig. 1. A total of 116 FBG are installed on the upper deck and lower deck (Fig. 1b) at nine equidistant cross sections of the main span to measure strain (FBGS) and temperature (FBGT). Other types of sensors are also installed on the bridge as shown in Fig. 1a, but their output data are not used in this article. The measured strain and temperature data in the year of 2005 (the first year from installing the SHM system) are used to investigate thermal performance analysis of the studied bridge.

Fig. 1

Sensors layout of the studied bridge: a sensors layout; b typical cross-section

2.2 Statistical analysis of measured temperatures and strains

The structural strain is an important indicator for condition assessment of bridges. The statistical analysis of the measured temperature and strain is shown in Fig. 2. Figure 2a shows the typical strain and temperature time histories on the lower deck, illustrating that the trend of the measured strain is consistent with the temperature change. From the measured data, the temperature-induced strain could exceed 150 με. Figure 2b shows the typical strain and temperature time histories on the upper deck, displaying that the trend of the measured strain is opposite with the temperature change. Figure 2c shows the regression analysis results of the long-term monitoring data on the upper deck of the mid-span. The upper controlled line (UCL) and the lower controlled line (LCL) represent upper and lower limits of the 0.95 confidence interval of the measured values, respectively. The results show that temperature changing is a major cause leading to deformation of long-span suspension bridge. In addition, a controlled static load testing was carried on the studied bridge in July 2014, and the results are plotted in Fig. 2c. The measured strain is around − 20 με as represented by circles when no trucks on the bridge in the static test. After that, 52 weighed trucks (52 × 340 kN = 17680 kN) placed to the mid-span of the bridge, and the measured strain of the girder reached 156 με as represented by rectangular.

Fig. 2

Statistical analysis results: a strain and temperature on the lower deck; b strain and temperature on the upper deck; c the relationship between strain and temperature

In the operation condition, it should be noted that the measured strain consists of lower frequency strain induced by temperature-induced strain and the higher frequency strain mainly induced by vehicular. Figure 3a shows a typical measured strain during a day, which is decomposed to the temperature-induced strain (Fig. 3b) and the vehicle-induced strain (Fig. 3c) by the Ensemble Empirical Mode Decomposition (EEMD) technology [23, 24]. It is seen that the temperature-induced strain can reach 150 με under the maximum temperature gradient in common operation environment. However, the traffic-induced maximum strain does not exceed 100 με.

Fig. 3

Strain decomposition: a measured strain; b temperature-induced strain; c vehicle-induced strain

Despite thermal performance has been investigated for a long time, challenging problems still exist in the long-span bridge. For instance, during a long-term ambient test, monitoring data indicated that the temperature-induced strain could reach 150 με, which is close to the static strain under the static load testing. Although the two states are similar which produce large strain and deformation, however, their mechanisms are totally different. Therefore, how much does the structural stress caused by temperature load and vehicle load, respectively, under normal operation?

3 Structural thermal performance analysis method

Structural stress is a direct indicator for structural safety evaluation. Vehicle-induced stress can be directly calculated from the measured vehicle-strain by multiplying it with the elastic modulus, but the temperature-induced stress cannot be directly calculated from the temperature-induced strain and their complex relation depends on the types of temperature distribution, structural configuration, and boundary conditions. The main girder of a long-span suspension bridge is modeled by a simply supported beam with partial axial and rotational constraints [25]. Following sections will study the thermal analysis of the beam model with different constraints under each temperature type, respectively.

3.1 Thermal analysis with the uniform temperature distribution

The simply supported beam model with the change of uniform temperature distribution, $\Delta T_{\text{U}}$ as shown in Fig. 4a. It has a length of $L$, and it expands $\delta_{\text{U}}$ under the change of uniform temperature load due to no axial constraints. Although there is strain ($\varepsilon_{\text{U}}$) occur, there is no thermal stress induced.

Fig. 4

Simply supported beam with uniform thermal load: a the beam with no axial constraint; b the beam with axial constraint

When the simply supported beam is restrained by a partial axial spring with the stiffness of $k_{\text{R}}$ as shown in Fig. 4b, the expanding displacement induced by the uniform thermal load is not $\delta_{\text{U}}$ because part of it, $\delta_{\text{U}}^{{'{\text{N}}}}$, will be restrained by the axial spring constraint. The longitudinal displacement of the simply supported beam with a partial axial constraint is,

$$\delta_{\text{UR}} = \delta_{\text{U}} - \delta_{\text{U}}^{{'{\text{N}}}}$$

(1)

where $\delta_{\text{UR}}$ is the axial deformation which can be measured by displacement meters, $\delta_{\text{U}}$ is the longitudinal thermal expansion of the beam with no axial constraint, it is calculated by $\alpha \Delta T_{\text{U}} L$, α is the expansion coefficient, and $\delta_{\text{U}}^{{'{\text{N}}}}$ is restrained axial deformation by the axial spring constraint and is calculated,

$$\delta_{\text{U}}^{{'{\text{N}}}} = F_{\text{s}} L/EA$$

(2)

where $F_{s}$ is the axial restrained force, $E$ is the elastic modulus, and A is the cross-sectional area. The strains have the same relationship as Eq. (1),

$$\varepsilon_{\text{UR}} = \varepsilon_{\text{U}} - \varepsilon_{\text{U}}^{{'{\text{N}}}}$$

(3)

where $\varepsilon_{\text{UR}}$ is the measured strain, $\varepsilon_{\text{U}}$ is the unconstrained strain, and $\varepsilon_{\text{U}}^{{'{\text{N}}}}$ is the restrained strain which will induce structural stress and as denoted by dashed line in Fig. 3b. The induced thermal stress is calculated,

$$\sigma_{\text{U}}^{{'{\text{N}}}} = E\varepsilon_{\text{U}}^{{'{\text{N}}}} = E(\varepsilon_{\text{U}} - \varepsilon_{\text{UR}} ).$$

(4)

The other parameters such as axial restrained force and restrained stiffness can be calculated by, $F_{\text{s}} = k_{\text{R}} \delta_{\text{UR}}$, $k_{\text{R}} = \frac{{EA(\delta_{\text{U}} - \delta_{\text{UR}} )}}{{\delta_{\text{UR}} L}}$. Where $F_{\text{s}}$ is the axial restrained force, and $k_{\text{R}}$ is the axial restrained stiffness. When the measured displacement, $\delta_{\text{UR}}$, equal to zero, it means that the restrained stiffness tends to infinity.

3.2 Thermal analysis with the linear temperature gradient

The model is subjected to a linear temperature gradient, $T_{\text{L}}$, which linear change along the cross-section as shown in Fig. 5a. The unrestrained rotation is caused by deformation when there are no rotational restraints at beam ends. The rotation can be calculated,

Fig. 5

Simply supported beam with linear temperature gradient: a the beam with no bending constraints; b the beam with bending constraints

$$\theta_{\text{T}} = \frac{{\alpha (T_{1} - T_{2} )L}}{2h}$$

(5)

where $\theta_{\text{T}}$ is the rotation at the beam ends. $h$ is height of cross-section, $T_{1}$, $T_{2}$ are the temperature of the top and bottom surface, respectively, and $T_{1} = - T_{2}$. The measured strain along the depth of cross-section can be calculated,

$$\varepsilon_{\text{L}} = \alpha T_{\text{L}}$$

(6)

where $\varepsilon_{\text{L}}$ and $T_{\text{L}}$ are the bending strain and linear temperature gradient along the depth of cross-section, respectively. The liner temperature gradient completely generates the bending deformation, but do not produce the thermal stress in the beam.

Considering the beam model with a rotation spring at two ends, respectively, the rotational stiffness is $k_{\text{s}}$ as shown in Fig. 5b. Some bending deformation will be restrained by the rotation springs, the actual rotation at two ends can be calculated,

$$\theta_{\text{U}} = \frac{{(\varepsilon_{\text{LR1}} - \varepsilon_{\text{LR2}} )L}}{2h}$$

(7)

where $\theta_{\text{U}}$ is rotation caused by final deformation at the beam ends, $\varepsilon_{\text{LR}}$ is the measured strain along the depth of cross-section, and $\varepsilon_{\text{LR1}}$ and $\varepsilon_{\text{LR2}}$ are the measured strains at the upper and lower surface of the beam, respectively. The retrained rotation at beam ends of the simply supported beam with partial spring constraints is,

$$\theta_{\text{R}}^{ '} = \theta_{\text{T}} - \theta_{\text{U}}$$

(8)

where $\theta_{\text{R}}^{ '}$ is restrained rotation, $\theta_{\text{T}}$ is free rotation at the beam end with no spring constraints, and $\theta_{\text{U}}$ is measured rotation at beam ends with spring constraints. The bending strains have same relationship,

$$\varepsilon_{\text{L}}^{{'{\text{M}}}} = \varepsilon_{\text{L}} - \varepsilon_{\text{LR}}$$

(9)

where $\varepsilon_{\text{L}}^{{ ' {\text{M}}}}$ is restrained bending strain caused by spring constraints, $\varepsilon_{\text{L}}$ is free bending strain under no spring constraints, and $\varepsilon_{\text{LR}}$ is measured bending stain with spring constraints. Therefore, the restrained bending stress is equal to,

$$\sigma_{\text{T}}^{{ ' {\text{M}}}} = E\varepsilon_{\text{L}}^{{ ' {\text{M}}}} = \frac{{2E(\theta_{\text{T}} - \theta_{\text{U}} )}}{L}y_{0}$$

(10)

where $\sigma_{\text{T}}^{{ ' {\text{M}}}}$ is restrained bending stress with partial spring constraints, and $y_{0}$ is the distance to the neutral axis.

The relationships among restrained rotation, restrained bending moment and spring stiffness are as follow: $\theta_{\text{R}}^{'} = \frac{{M_{\text{s}} L}}{2EI}$, $M_{\text{s}} = k_{\text{s}} \theta_{\text{U}}$, $k_{\text{s}} = \frac{{2EI(\theta_{\text{T}} - \theta_{\text{U}} )}}{{\theta_{\text{U}} L}}$. Where $M_{\text{s}}$ is restrained bending moment. $I$ is moment of inertia of section. $k_{\text{s}}$ is rotational spring stiffness. When the rotational stiffness of springs at the beam ends tend to infinity, the $\theta_{\text{U}}$ will be equal to zero and temperature-induced bending stress was completely retrained in the beam.

3.3 Thermal analysis with the nonlinear distributed temperature

First, the calculating process of self-equilibrating temperature stress is briefly introduced. The structure is first assumed to be fully restrained against rotation and translation. The thermal stress is determined by Eq. (11).

$$\sigma_{\text{RT}} \left( y \right) = E \cdot \alpha \cdot T(y)$$

(11)

where $\sigma_{\text{RT}} \left( y \right)$ is the thermal stress, E is the elastic modulus, and $T(y)$ is the nonlinear temperature gradient along the cross-section. The equivalent of axial force and bending moment on the cross-section can be calculated from $\sigma_{\text{RT}} \left( y \right)$ as follows:

$$N_{\text{T}} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{\text{RT}} \left( y \right) \cdot b\left( y \right){\text{d}}y$$

(12)

$$M_{\text{T}} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{\text{RT}} \left( y \right) \cdot b\left( y \right) \cdot y_{0} {\text{d}}y$$

(13)

where $N_{\text{T}}$ is the equivalent axial force. $M_{\text{T}}$ is the equivalent bending moment. $b(y)$ is the cross-sectional width that changes with y, and $y_{0}$ is the distance to the neutral axis. $h$ is the height of cross-section.

If the axial and rotational constraints are released completely, then the axial force and bending moment defined in Eqs. (12) and (13) will be released. The axial and bending deformation as shown in Fig. 6a, which will induce the following strains:

Fig. 6

Simply supported beam with nonlinear temperature gradient: a the beam with no constraints; b the beam with constraints

$$\varepsilon_{\text{T}}^{\text{N}} = \frac{{N_{\text{T}} }}{EA}$$

(14)

$$\varepsilon_{\text{T}}^{\text{M}} = \frac{{M_{\text{T}} \cdot y_{0} }}{{{\text{EI}}_{\text{Z}} }}$$

(15)

where A is the cross-sectional area, and ${\text{EI}}_{\text{Z}}$ is the bending stiffness. The total strain caused by the nonlinear temperature gradient under no constraints can be expressed by $\varepsilon \left( {\text{y}} \right) = \varepsilon_{\text{T}}^{\text{N}} + \varepsilon_{\text{T}}^{\text{M}}$.

It should be noted that the thermal stress $\sigma_{\text{RT}} \left( y \right)$ defined in Eq. (11) converts to deformation $\alpha T(y)L$. However, $\alpha T(y)$ does not agree with the planar cross-section assumption because $T(y)$ is a nonlinear curve in the cross-sectional depth. Therefore, a self-restrained strain will be induced to maintain the planar cross-section, which is calculated from:

$$\varepsilon '_{\text{SE}} \left( y \right) = \varepsilon_{\text{T}}^{\text{N}} + \varepsilon_{\text{T}}^{\text{M}} - \alpha \cdot T(y).$$

(16)

Self-equilibrating temperature stress is calculated from Eq. (17),

$$\sigma '_{\text{SE}} \left( y \right) = E\varepsilon '_{\text{SE}} \left( y \right).$$

(17)

The equivalent of axial force and bending moment will generate the axial deformation and bending deformation under the nonlinear temperature gradient. When the partial constraints exist in the beam ends (Fig. 6b), the partial deformation will be restrained. The internal relations of axial deformation and bending deformation are derived, respectively.

$$\varepsilon_{\text{T}}^{{'{\text{N}}}} = \varepsilon_{\text{T}}^{\text{N}} - \varepsilon_{\text{TR}}^{\text{N}}$$

(18)

$$\varepsilon_{\text{T}}^{{'{\text{M}}}} = \varepsilon_{\text{T}}^{\text{M}} - \varepsilon_{\text{TR}}^{\text{M}}$$

(19)

where $\varepsilon_{\text{T}}^{{'{\text{N}}}}$ and $\varepsilon_{\text{T}}^{{'{\text{M}}}}$ are retrained axial strain and restrained bending strain, respectively, and generate the restrained stresses, $E\varepsilon_{\text{T}}^{{'{\text{N}}}}$ and $E\varepsilon_{\text{T}}^{{'{\text{M}}}}$. $\varepsilon_{\text{T}}^{\text{N}}$ and $\varepsilon_{\text{T}}^{\text{M}}$ are the axial stain and bending strain induced by $N_{\text{T}}$ and $M_{\text{T}}$ without partial constraints. $\varepsilon_{\text{TR}}^{\text{N}}$ and $\varepsilon_{\text{TR}}^{\text{M}}$ are measured strains with partial constraints.

Therefore, the axial spring stiffness and bending spring stiffness are calculated by, $k_{\text{R}} = \frac{{N_{\text{T}} L - EA\delta_{\text{UR}} }}{{\delta_{\text{UR}} L}}$, $k_{\text{s}} = \frac{{M_{\text{T}} L - 2\theta_{\text{U}} EI}}{{\theta_{\text{U}} L}}$. Where $k_{\text{R}}$, $k_{\text{s}}$ are the axial spring stiffness and bending spring stiffness, respectively. $N_{\text{T}}$ is the equivalent axial force. $M_{\text{T}}$ is the equivalent bending moment. $\theta_{\text{U}}$ is measured rotation at the beam ends with partial constraints. $\delta_{\text{UR}}$ is measured axial deformation at the beam ends with partial constraints.

Therefore, the thermal stress of the simply supported beam with partial constraints under nonlinear temperature gradient is as follow:

$$\sigma '_{\text{RSE}} \left( y \right) = \sigma '_{\text{SE}} \left( y \right) + E\varepsilon_{\text{T}}^{{ ' {\text{N}}}} + E\varepsilon_{\text{T}}^{{ ' {\text{M}}}}$$

(20)

where $\sigma '_{\text{RSE}} \left( y \right)$ is the thermal stress under nonlinear temperature gradient with partial constraints, and $E\varepsilon_{\text{T}}^{{ ' {\text{N}}}}$, $E\varepsilon_{\text{T}}^{{ ' {\text{M}}}}$ are the axial restrained stress and bending restrained stress, respectively.

Based on the above theoretical analysis, the research framework of this article is summarized as follows as shown in Fig. 7. (1) Temperature decomposition. A suspension bridge can be simplified as a simply supported beam model for analysis of temperature-induced response. The structural temperature $T_{\text{total}}$ decomposes the three parts: uniform temperature $\Delta T_{\text{U}}$, linear temperature gradient ($T_{\text{L}}$) and nonlinear temperature gradient ($T(y)$). (2) Strain decomposition without partial constraints, the three-temperature model generate the deformation (or strain $\varepsilon_{\text{T}}^{\text{F}}$), the nonlinear temperature induces self-equilibrating temperature stress ($\sigma '_{\text{SE}}$). (3) Strain decomposition within partial constraints. When the beam within partial constraints, the deformations will be restrained. This moment, the measured strain and restrained strain are the $\varepsilon_{\text{TR}}^{\text{F}}$ and $\varepsilon '_{\text{R}}$, respectively. The dashed line shows the restrained strain, generating the stress. The solid line shows the measured strain, not generating the stress. (4) Finally, stress decomposition, the total thermal stress can be expressed $\sigma '_{\text{TRSE}} (y)$, which is equal to restrained stress ($\sigma '_{\text{R}}$) plus self-equilibrating temperature stress ($\sigma '_{\text{SE}}$). Structural strain and temperature load are observed from the SHM system, and structural stress, deformation, and boundary stiffness can be calculated on the proposed method.

Fig. 7

The summary of analysis procedure

4 Stress analysis in the studied bridge

4.1 Numerical calculation and verification

Numerical thermal analysis results of the studied bridge were used to validate the proposed method. The bridge was modeled and analyzed in the ANSYS 14.5 [26] software as shown in Fig. 8. The steel box girder is simulated by the elastic shell elements 63. The nonlinear elements of link 10 are used in the main cables and hangers. The bridge towers are simulated by the solid elements. The mass density of the girder is 7850 kg/m³. The vertical and lateral bending moment of inertias is 1.844 and 93.318 m⁴, respectively. The elasticity modulus of the wire rope and the parallel wire strand (PWS) are $1.4 \times 10^{5}$ and $2.0 \times 10^{5} \,{\text{MPa}}$, respectively. The temperature load at any time of the day can be expressed by the function and is loaded on the bridge deck surface.

Fig. 8

The finite element model of the studied bridge

$$T\left( t \right) = 0.5(T_{\hbox{max} } + T_{\hbox{min} } ) + 0.5(T_{\hbox{max} } - T_{\hbox{min} } ) \times \sin [(t - 9) \times \pi /12]$$

(21)

where $T_{\hbox{max} }$ and $T_{\hbox{min} }$ are the highest and lowest temperatures in a day, respectively. $t$ is the time of day.

The detailed steps of temperature-induced stress calculation are as follows:

• 1. The time-history curves of temperature and strain were extracted on one cross-section as shown in Fig. 9. The measured temperature is decomposed to uniform temperature ($\Delta T_{\text{U}}$) and nonlinear temperature gradient ($T(y)$). The axial strain and bending strain can be obtained by measured strain of topper deck and lower deck.

  Fig. 9

  

  Strain and temperature on the upper deck and lower deck, respectively

• 2. The restrained axial stress and bending stress calculation. The free axial strain can be calculated from $\alpha \Delta T_{\text{U}}$ and Eq. (14). The restrained axial stress can be estimated on multiplying elastic modulus by the difference value between free axial strain and measured axial strain. The free bending strain calculated on Eqs. 6 and 15. The restrained bending stress can be estimated on multiplying elastic modulus by the difference value between free bending strain and measured bending strain.

• 3. Self-equilibrating thermal stress calculated on Eq. (17). The temperature-induced stress equal to restrained stress plus the self-equilibrating thermal stress. Finally, the calculation results and theoretical results are compared in Fig. 10.

  Fig. 10

  

  The thermal stress calculation

4.2 The stresses calculation and comparison

After the proposed method was verified by finite element model, the temperature-induced stress calculation for the studied bridge was based on measured strain and temperature. The following steps are performed to demonstrate the temperature-induced stress calculation by taking the mid-span of the main girder as the example:

• 1. Temperature load analysis. The measured temperature at middle span was decomposed to uniform temperature ($\Delta T_{\text{U}}$) and nonlinear temperature gradient (T(y)) as shown in Fig. 11a.

  Fig. 11

  

  Thermal stress calculation: a self-equilibrating thermal stresses; b axial restrained stress; c total thermal stress

• 2. Self-equilibrating thermal stress calculation. For the fully constrained structure, the nonlinear temperature gradient generates the thermal stress $\sigma_{\text{RT}} \left( y \right)$ as calculated by Eq. (11), and the axial force and bending moment and calculated from Eqs. (12) and (13). When the longitudinal and rotational constraints are fully released, the above calculated axial force and bending moment will be released, which will induce strains $\varepsilon_{\text{T}}^{\text{N}}$ and $\varepsilon_{\text{T}}^{\text{M}}$ as calculated from Eqs. (14) and (15). The axial force and bending moment are subtracted from the fully restrained thermal stress to give self-equilibrating thermal stresses as shown in Fig. 11a. The minus sign represents a compressive stress in Fig. 11.

• 3. Calculation of thermal stress caused by redundant constraints. The longitudinal direction of the studied bridge is modeled by partial constraints. The free axial strain of $\varepsilon_{\text{U}}$, $\varepsilon_{\text{T}}^{\text{N}}$ were calculated from $\alpha T$ and Eq. (14). The measured axial strain of $\varepsilon_{\text{UR}}$, $\varepsilon_{\text{TR}}^{\text{N}}$ were obtained from topper deck and lower deck. So the restrained axial stress is shown in Fig. 11b. It is necessary to be pointed out here that the boundary of studied bridge is a simple supported condition, and there is no axial constraint in design. However, the structure of the suspension bridge is rather complicated and there may be practical restrained axial stress in the local cross-section. From the calculation results, the local restrained axial stress is relatively small, only 2.4 MPa. The rotation boundary is free for the studied bridge, thus the restrained bending stress is zero. In addition, the proposed method can be applied to the calculation of other parameters of the bridge, such as boundary stiffness, constrained strain, deformation, etc.

• 4. Total thermal stress calculation. The total thermal stress of the middle span under uniform temperature and the nonlinear temperature gradient were calculated as shown in Fig. 11c. The total thermal stress could reach 13.8 MPa on the upper deck, and 7 MPa on the lower deck. The thermal stress of other sections can be calculated using the measured temperature and strains on those sections.

In summary, compared with the traditional thermal stress formula ($\sigma = (\varepsilon - \alpha T)$), the work in this article is not only to calculate temperature-induced stress, but also to analyze the monitoring strain data deeply as shown in Fig. 7. This work decomposed the monitoring strain data in detail and clearly explained the physical meaning corresponding to each component, and the significance of the work makes it easier for engineers to understand the temperature effect.

Finally, the strain and temperature data from April 1, 2006 to April 10, 2006 are processed for stress calculation. The stresses time history at the upper/lower deck of mid-span induced by vehicle and temperature as shown in Fig. 12. Figure 12a shows the vehicle-induced stress and temperature-induced stress on the upper deck. Vehicle-induced stress is about − 15–10 MPa under normal operation. Temperature-induced stress has obvious cyclical fluctuations. When the temperature of deck rises to the maximum in a day, maximum temperature-induced stress also appears. During the 0–24 h, the change of temperature-induced stress is only − 2–4 MPa, which is less than the vehicle-induced stress. During the 24–48 h, the change of temperature-induced stress is − 28–2 MPa, which is more than the vehicle-induced stress. When the temperature of upper deck is less than 17 °C, the temperature-induced stress will be less than vehicle-induced stress. When the temperature of upper deck is above 41 °C, the temperature-induced stress may be more than 30 MPa. Figure 12b shows the vehicle-induced stress and temperature-induced stress on the lower deck. Vehicle-induced stress is about − 7–15 MPa and temperature-induced stress is about − 12.5–9 MPa. The effect lower deck is mainly subjected to vehicle loads. This is a common method of temperature-induced stress and vehicle-induced stress analysis, which can quantitatively analyze the proportion of stress generated by each load. But no more deep information can be extracted from this calculation. The method presented in this article can provide more valuable information to evaluate structural performance, such as temperature-induced deformation, restrained force, boundary constraints and so on.

Fig. 12

Temperature-induced stress and vehicle-induced stress time history: a stress on the upper deck; b stress on the lower deck

5 Conclusions

The thermal analysis of large span bridges has the important engineering value for evaluating the safety performance. This article studies the temperature characteristics of the long-span bridge from monitoring data and theoretical analysis. The present study comes to the following conclusions:

The statistical analysis of temperature and strain at mid-span was performed. The temperature load is a major cause leading to deformation of suspension bridge during the long-term operation. The theory of thermal stress calculations with a proposed model under different temperature gradients and different boundary conditions were deduced in detail. Compared with the traditional thermal stress formula ($\sigma = (\varepsilon - \alpha T)$), the proposed method is not only to calculate thermal stress, but also to analyze the monitoring strain data deeply (as shown in Fig. 7). It decomposes the monitoring strain data in detail and clearly explains the physical meaning corresponding to each component, and specifically reveals the relationships between measured strain and thermal stress, deformation and boundary stiffness of the structure with different boundary conditions under different temperature gradients. The significance of the work makes it easier for engineers to understand the temperature effect.