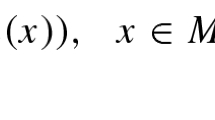Compactness of embedding of generalized higher order Lipschitz classes

Abstract

In this paper sufficient conditions for continuous and compact embeddings of generalized higher order Lipschitz classes on a compact subset of n-dimensional real Euclidean spaces are obtained.

1 Introduction

Embedding theorems in function spaces have been studied in [1, 2, 9, 11]. A comprehensive introduction to the theory of embedding of function spaces and historical references may be found in [11].

Hölder-type spaces and their embeddings play a significant role in mathematical analysis and in applications. They are useful in various questions arising in the theory of partial differential equations and the branches of analysis associated with it.

In a series of papers [3, 4, 6, 7] embeddings of Hölder spaces of real continuous functions over a one-dimensional compact interval were carried out.

The principal goal of this paper is to derive more general results, namely we establish sufficient conditions for continuous and compact embeddings of generalized higher order Lipschitz classes on a compact subset of n dimensional real Euclidean spaces.

2 Preliminaries

In this section we will gather together some basic notation and statements which will be used later in the paper. Additional information can be found for example in [5, 8].

Definition 2.1

Let $(X,\Vert \cdot \Vert _X)$ and $(Y,\Vert \cdot \Vert _Y)$ two normed spaces. We say that the space X is continuously embedded into Y and denote this by

$$\begin{aligned} X \hookrightarrow Y \end{aligned}$$

if it holds that $X \subset Y$ and there exists a $K>0$ such that

$$\begin{aligned} \Vert x\Vert _{Y} \le K\Vert x\Vert _{X},\quad \forall x\in X. \end{aligned}$$

Moreover, we say that the space X is compactly embedded into Y and denote this by

$$\begin{aligned} X \hookrightarrow \hookrightarrow Y \end{aligned}$$

if it holds that $X \subset Y$ and every bounded set in $(X,\Vert \cdot \Vert _X)$ is relatively compact in $(Y,\Vert \cdot \Vert _Y)$.

As usual, ${\mathbb {R}}^n$ denotes the Euclidean n-dimensional space. Let ${\mathbf {E}}$ be a closed subset of ${\mathbb {R}}^n, n\ge 1$, with coordinates $x = (x_1, \ldots , x_n)$. For $k\le n$ we write $j=(j_1, \ldots , j_k)$ a k-dimensional multi-index of order $|j| = j_1 +\cdots +j_k$, where $j_1, \ldots ,j_k$ are non-negative integers. We also use the symbol

$$\begin{aligned} \partial ^{(j)}:=\frac{\partial ^{|j|}}{\partial x_1^{j_1}\partial x_2^{j_2} \ldots \partial x_k^{j_k}}, \end{aligned}$$

for the higher order partial derivatives.

Various positive constants are denoted by C, their values may change from one occurrence to another.

This paper is wholly concerned with the so called higher order Lipschitz classes, which are directly related to a very deep theorem in real analysis due to H. Whitney, see [10, pag. 177].

Let $k<\gamma \le k+1$. We shall say that a real valued function f, defined in ${\mathbf {E}}$, belongs to ${\text{ Lip }}({\mathbf {E}},\gamma )$ if there exist real valued bounded functions $f^{(j)}$, $0<|j|\le k$, defined on ${\mathbf {E}}$, with $f^{(0)}=f$, and so that

$$\begin{aligned} f^{(j)}(x)=\sum _{|j+l|\le k}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y),\,\,x,y\in {\mathbf {E}}\end{aligned}$$

(2.1)

where

$$\begin{aligned} |f^{(j)}(x)|\le C,\,\,\,|R_j(x,y)|\le C|x-y|^{\gamma -|j|},\,\,x,y\in {\mathbf {E}}, |j|\le k, \end{aligned}$$

(2.2)

being C is a positive constant.

The norm in ${\text{ Lip }}({\mathbf {E}},\gamma )$ is defined as the smallest C satisfying (2.2), which will be denoted by $\Vert \cdot \Vert _{\gamma }$.

From now on we restrict ourselves to the case of ${\mathbf {E}}$ being compact with diameter d.

Theorem 2.2

The norm space $({\text{ Lip }}({\mathbf {E}},\gamma ),\Vert \cdot \Vert _{\gamma })$ is a Banach space.

Proof

Will be enough to prove that for any sequence $f_n\in {\text{ Lip }}({\mathbf {E}},\gamma )$ with $\sum _{n = 1}^{\infty }\Vert f_{n}\Vert _{\gamma } < +\infty$ we have $\sum _{n = 1}^{\infty }f_{n} = f \in Lip({\mathbf {E}},\gamma )$ (see [8, Theorem 1.1, pag. 211]).

Let be $\lbrace f_{n}\rbrace \subset Lip({\mathbf {E}},\gamma )$, then obviously we have $\Vert f_{n}^{(j)}\Vert _\infty \le \Vert f_{n}\Vert _{\gamma }$ and hence

$$\begin{aligned} \sum _{n = 1}^{\infty }\Vert f_{n}^{(j)}\Vert _\infty \le \sum _{n = 1}^{\infty }\Vert f_{n}\Vert _{\gamma } < +\infty . \end{aligned}$$

The Banach structure of the space of continuous functions $C({\mathbf {E}})$ yields

$$\begin{aligned} \sum _{n = 1}^{\infty } f^{(j)}_{n} = f^{(j)} \in C({\mathbf {E}}) \end{aligned}$$

and in particular $\sum _{n = 1}^{\infty } f_{n} = f \in C({\mathbf {E}})$.

Moreover, taking into account that

$$\begin{aligned} R^{n}_{j}(x,y)=f_{n}^{(j)}(x) -\sum _{\vert j + l\vert \le k}\dfrac{f_{n}^{(j + l)}(y)}{l!}(x - y)^{l} \end{aligned}$$

satisfies

$$\begin{aligned} \vert R^{n}_{j}(x,y)\vert \le \Vert f_{n}\Vert _{\gamma }d^{\gamma - \vert j\vert }, \end{aligned}$$

then

$$\begin{aligned} \sum _{n = 1}^{\infty }\Vert R^{n}_{j}(x,y)\Vert _\infty \le \sum _{n = 1}^{\infty }\Vert f_{n}\Vert _{\gamma }d^{\gamma - \vert j\vert } \le d^{\gamma - \vert j\vert }\sum _{n = 1}^{\infty }\Vert f_{n}\Vert _{\gamma } < +\infty \end{aligned}$$

and consequently

$$\begin{aligned} \sum _{n = 1}^{\infty }R^{n}_{j}(x,y) = R_{j}(x,y) \in C({\mathbf {E}}\times {\mathbf {E}}). \end{aligned}$$

At this point is a matter of direct calculations to derive that $f \in Lip({\mathbf {E}},\gamma )$ as well as that $\sum _{n = 1}^{\infty } f_{n} = f$ in the Lipschitz norm $\Vert \cdot \Vert _{\gamma }$. $\square$

In general, an element of ${\text{ Lip }}({\mathbf {E}},\gamma )$ should be interpreted as a collection

$$\begin{aligned} \{f^{(j)}{:}\,{\mathbf {E}}\mapsto {\mathbb {R}},\,|j|\le k\}. \end{aligned}$$

When $0<\gamma \le 1$, the Lipschitz class becomes the usual class $C_b^{0,\gamma }({\mathbf {E}})$ of bounded Hölder continuous functions in ${\mathbf {E}}$.

Remark 2.3

[10] We remark that the function $f^{(0)}=f$ does not necessarily determine the functions $f^{(j)}$ for arbitrary ${\mathbf {E}}$, but for ${\mathbf {E}}={\mathbb {R}}^n$ the functions $f^{(j)}$ are uniquely determined by $f^{(0)}$ and ${\text{ Lip }}({\mathbb {R}}^n,\gamma )$ actually consists of continuous and bounded functions f with continuous and bounded partial derivatives $\partial ^{(j)}f$ up to the order k. Moreover, for $|j|=k$ the functions $\partial ^{(j)}f$ belongs to the space ${\text{ Lip }}({\mathbb {R}}^n,\gamma -k)$.

Let us recall that a non-negative function $\omega$ is said to be almost increasing (or almost decreasing) if there exists a constant $C\ge 1$ such that $\omega (x)\le C\omega (y)$ for all $x\le y$ ($y\le x$, respectively).

A modulus of continuity is a positive almost increasing function $\omega {:}\,[0,\infty )\mapsto [0,\infty )$ with $\lim _{t\rightarrow 0} \omega (t)=0$. Here we shall mainly consider such a functions in bounded intervals of the form (0, d], with $d>0$.

In our future considerations we need to introduce the following special class of modulus of continuity:

Definition 2.4

We denote by $H^{k}(0,d]$ the set of all modulus of continuity $\omega$ in (0, d] satisfying the conditions

• (a) $\lim _{t \rightarrow 0+}\frac{\omega (t)}{t^{k}} = 0$

• (b) $\lim _{t \rightarrow 0+}\frac{\omega (t)}{t^{k + 1}} = \infty .$

With the help of $H^{k}(0,d]$ (we shall write it $H^{k}$ for brevity) a natural generalization of the higher order Lipschitz classes in terms of modulus of continuity may be considered.

Given $\omega \in H^{k}$, a real valued function f, defined in ${\mathbf {E}}$, is said to belong to ${\text{ Lip }}({\mathbf {E}},\omega )$ if there exist real valued bounded functions $f^{(j)}$, $0<|j|\le k$, defined on ${\mathbf {E}}$, with $f^{(0)}=f$, and so that

$$\begin{aligned} f^{(j)}(x)=\sum _{|j+l|\le k}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y),\,\,x,y\in {\mathbf {E}}\end{aligned}$$

(2.3)

where

$$\begin{aligned} |f^{(j)}(x)|\le C,\,\,\,|R_j(x,y)|\le C\frac{\omega (|x-y|)}{|x-y|^{|j|}},\,\,x,y\in {\mathbf {E}}, |j|\le k, \end{aligned}$$

(2.4)

being C a positive constant.

This time the norm in ${\text{ Lip }}({\mathbf {E}},\omega )$ is denoted by $\Vert \cdot \Vert _\omega$ and corresponds to the smallest C satisfying (2.4). We will refer to ${\text{ Lip }}({\mathbf {E}},\omega )$ as the generalized Lipschitz classes. Similar arguments to those employed in Theorem 2.2 yields the Banach structure of the norm space $({\text{ Lip }}({\mathbf {E}},\omega ),\Vert \cdot \Vert _\omega )$.

Direct calculations shows that if $f\in {\text{ Lip }}({\mathbf {E}},\omega )$, then $f^{(j)}\in {\text{ Lip }}({\mathbf {E}},\omega _j)$ with $\omega _j(t)=t^{-|j|}\omega (t)$ and $0\le |j|\le k$. This fact allows us to redefine the generalized Lipschitz norm in more precise terms:

$$\begin{aligned} \Vert f\Vert _{\omega } = \sup _{0 \le \vert j\vert \le k}\left( \Vert f^{(j)}\Vert _\infty , \vert f^{(j)}\vert _{\omega } \right) , \end{aligned}$$

where $\Vert {\cdot }\Vert _\infty$ denotes the standard uniform norm and

$$\begin{aligned} \vert f^{(j)}\vert _{\omega } := \sup _{\begin{array}{c} x, y \in {\mathbf {E}}\\ x \ne y \end{array}}\dfrac{\vert R_{j}(x,y)\vert }{\omega _j(\vert x - y\vert )}, \end{aligned}$$

3 Continuous embeddings of Lipschitz classes

Theorem 3.1

If $\gamma _1<\gamma _2$, then ${\text{ Lip }}({\mathbf {E}},\gamma _2)\hookrightarrow {\text{ Lip }}({\mathbf {E}},\gamma _1)$

Proof

If $k<\gamma _1<\gamma _2\le k+1$, then the proof easily follows from the trivial inequality

$$\begin{aligned} |x-y|^{\gamma _2-|j|}\le C|x-y|^{\gamma _1-|j|}, \end{aligned}$$

where C is a constant independent of x and y.

Hence suppose $k_1<\gamma _1\le k_1+1<\gamma _2$ and let $k_2<\gamma _2\le k_2+1$.

Let be $f\in {\text{ Lip }}({\mathbf {E}},\gamma _2)$, then we have

$$\begin{aligned} f^{(j)}(x)=\sum _{|j+l|\le k_2}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y),\,\,x,y\in {\mathbf {E}}\end{aligned}$$

(3.1)

with

$$\begin{aligned} \begin{array}{ccccc} \vert f^{(j)}\vert \le M&and&\vert R_{j}(x,y)\vert \le M\vert x - y\vert ^{\gamma _{2} - \vert j\vert },&\forall x,y \in {\mathbf {E}},&\vert j\vert \le k_{2}. \end{array} \end{aligned}$$

On the other hand, we can rewrite (3.1) as

$$\begin{aligned} f^{(j)}(x)=\sum _{|j+l|\le k_1}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+\sum _{k_1+1\le |j+l|\le k_2}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y).\nonumber \\ \end{aligned}$$

(3.2)

Since $\gamma _1-|j|\le |l|$, a direct calculation shows that the remaining function

$$\begin{aligned} \mathbf{R}_j(x,y):=\sum _{k_1+1\le |j+l|\le k_2}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y) \end{aligned}$$

satisfies the estimate

$$\begin{aligned} |\mathbf{R}_j(x,y)|\le C\,M|x-y|^{\gamma _1-|j|}, \end{aligned}$$

where C is a constant independent of x and y. This fact, together with (3.2) and the boundedness of all the functions $f^{(j)}$, $0\le |j|\le k_1$ imply that $f\in {\text{ Lip }}({\mathbf {E}},\gamma _1)$.

On the other hand, a carefully look to our previous considerations shows that

$$\begin{aligned} \Vert f\Vert _{\gamma _1}\le C\Vert f\Vert _{\gamma _2}, \end{aligned}$$

with a constant C independent of f, and the proof is complete. $\square$

Now we turn to the embeddings of generalized Lipschitz classes.

Theorem 3.2

Let be $\omega _1,\omega _2\in H^{k}$ such that

$$\begin{aligned} \lim _{t\rightarrow 0^{+}}\dfrac{\omega _{2}(t)}{\omega _{1}(t)} = 0, \end{aligned}$$

(3.3)

then ${\text{ Lip }}({\mathbf {E}},\omega _{2}) \hookrightarrow {\text{ Lip }}({\mathbf {E}},\omega _{1})$.

Proof

To prove the inclusion ${\text{ Lip }}({\mathbf {E}},\omega _{2}) \subset {\text{ Lip }}({\mathbf {E}},\omega _{1})$ we just need to show that

$$\begin{aligned} \frac{\omega _2(|x-y|)}{|x-y|^{|j|}}\le C \frac{\omega _1(|x-y|)}{|x-y|^{|j|}}, \end{aligned}$$

a fact that it is obviously implied by (3.3). At the same time, the condition (3.3) yields in a similar way the continuity condition $\Vert f\Vert _{\omega _1}\le C \Vert f\Vert _{\omega _2}$, for $f\in Lip(\omega _{2}, F)$. $\square$

Theorem 3.3

Let be $\omega _{1} \in H^{k_{1}}$, $\omega _{2} \in H^{k_{2}}$ and $k_{1} < k_{2}$, then ${\text{ Lip }}({\mathbf {E}},\omega _{2}) \hookrightarrow {\text{ Lip }}({\mathbf {E}},\omega _{1})$.

Proof

The proof reduces to use the previous theorem together with the arguments employed in Theorem 3.1. To this end we note that

$$\begin{aligned} \frac{\omega _{2}(t)}{\omega _{1}(t)}=\frac{\omega _{2}(t)}{t^{k_2}}\frac{t^{k_2}}{\omega _1(t)}. \end{aligned}$$

Now, condition $k_1<k_2$ yields (3.3).

Let be $f\in {\text{ Lip }}({\mathbf {E}},\omega _2)$, then we have

$$\begin{aligned} f^{(j)}(x)=\sum _{|j+l|\le k_2}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y),\,\,x,y\in {\mathbf {E}}, \end{aligned}$$

which may be rewritten as

$$\begin{aligned} f^{(j)}(x)=\sum _{|j+l|\le k_1}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+\mathbf{R}_j(x,y), \end{aligned}$$

where

$$\begin{aligned} \mathbf{R}_j(x,y):=\sum _{k_1+1\le |j+l|\le k_2}\frac{f^{(j+l)}(y)}{l!}(x-y)^l+R_j(x,y). \end{aligned}$$

At this point, the continuous embedding of ${\text{ Lip }}({\mathbf {E}},\omega _{2})$ in ${\text{ Lip }}({\mathbf {E}},\omega _{1})$ easily follows from (3.3) and the arguments developed in the proof of Theorem 3.1. $\square$

4 Compact embeddings of Lipschitz classes

In this subsection we show how, under conditions of Theorems 3.2 or 3.3, the embeddings of Lipschitz classes is not just continuous, but also compact. This says, in particular, that condition $\gamma _1<\gamma _2$ in Theorem 3.1 implies also the compactness of the embeddings of ${\text{ Lip }}({\mathbf {E}},\gamma _2)$ in ${\text{ Lip }}({\mathbf {E}},\gamma _1)$.

Before proving the main theorem we will need a couple of lemmas.

Lemma 4.1

Let be $\omega _{1},\omega _{2}\in H^{k}$ satisfying (3.3) and let be $f\in {\text{ Lip }}({\mathbf {E}},\omega _{2})$. Then, for $\varepsilon >0$ there exists $\delta >0$ such that

$$\begin{aligned} \vert f^{(j)}\vert _{\omega _{1}} \le C\max \left\{ \varepsilon \vert f^{(j)}\vert _{\omega _{2}}, \dfrac{1}{\omega _{1}(\delta )}{\sum _{\vert j + l\vert \le k}\dfrac{\Vert f^{(j + l)}\Vert _\infty }{l!}d^{\vert j + l\vert }}\right\} \end{aligned}$$

for every $0\le |j|\le k$, where the constant $C\ge 2$ depends only on $\omega _2$.

Proof

From (3.3), for any $\varepsilon >0$ there exists $\delta >0$ such that

$$\begin{aligned} \frac{\omega _2(t)}{\omega _1(t)}<\varepsilon , \forall \, t\in (0,\delta ). \end{aligned}$$

(4.1)

Next, we have

$$\begin{aligned} \begin{aligned} \vert f^{(j)}\vert _{\omega _{1}}&= \sup _{\begin{array}{c} x, y \in F\\ x \ne y \end{array}}\dfrac{\vert R_{j}(x,y)\vert }{\omega _{1}(\vert x - y\vert )\vert x - y\vert ^{- \vert j\vert }} \\&= \max \left\{ \sup _{0<\vert x - y\vert<\delta }\dfrac{\vert R_{j}(x,y)\vert }{\omega _{1}(\vert x - y\vert )\vert x - y\vert ^{- \vert j\vert }}, \right. \\&\quad \left. \sup _{\delta \le \vert x - y\vert \le d}\dfrac{\vert R_{j}(x,y)\vert }{\omega _{1}(\vert x - y\vert )\vert x - y\vert ^{- \vert j\vert }} \right\} \\&\le \max \left\{ \sup _{0<\vert x - y\vert <\delta }\Bigl (\dfrac{\omega _{2}(\vert x - y\vert )}{\omega _{1}(\vert x - y\vert )}\cdot \dfrac{\vert R_{j}(x,y)\vert }{\omega _{2}(\vert x - y\vert )\vert x - y\vert ^{- \vert j\vert }}\Bigr ), \right. \\&\quad \left. \dfrac{C_1}{\omega _{1}(\delta )}\sup _{\delta \le \vert x - y\vert \le d}{\vert R_{j}(x,y)\vert d^{\vert j\vert }} \right\} , \end{aligned} \end{aligned}$$

where $C_1\ge 1$ is the constant related to the almost decreasing function $\dfrac{1}{\omega _1(t)}$ in (0, d].

Then, in virtue of (4.1) and after some simple estimates we have

$$\begin{aligned} \vert f^{(j)}\vert _{\omega _{1}} \le C\max \left\{ \varepsilon \vert f^{(j)}\vert _{\omega _{2}}, \dfrac{1}{\omega _{1}(\delta )}{\sum _{\vert j + l\vert \le k}\dfrac{\Vert f^{(j + l)}\Vert _\infty }{l!}d^{\vert j + l\vert }}\right\} , \end{aligned}$$

with $C:=2C_1$. $\square$

The following Lemma may be obtained in a quite similar way.

Lemma 4.2

Let be $\omega _{1} \in H^{k_{1}}$, $\omega _{2} \in H^{k_{2}}$, $k_{1} < k_{2}$ and let be $f\in {\text{ Lip }}({\mathbf {E}},\omega _{2})$. Then for every $\varepsilon > 0$ exists a $\delta \in (0, d)$ such that

$$\begin{aligned} \begin{aligned} \vert f^{(j)}\vert _{\omega _{1}}&\le C\max \left\{ {\sum _{k_1+1\le \vert j + l\vert \le k_2}\dfrac{\Vert f^{(j + l)}\Vert _\infty }{l!}d^{\vert j + l\vert -(k_1+1)}}\right. \\&\left. \quad +\,\varepsilon \vert f^{(j)}\vert _{\omega _{2}}, \dfrac{1}{\omega _{1}(\delta )}{\sum _{\vert j + l\vert \le k_1}\dfrac{\Vert f^{(j + l)}\Vert _\infty }{l!}d^{\vert j + l\vert }}\right\} \end{aligned} \end{aligned}$$

for every $0\le |j|\le k$, where the constant $C\ge 2$ depends only on $\omega _2$.

We are now in position of stating and proving our main result.

Theorem 4.3

Let be $\omega _{i} \in H^{k_{i}}$, $i=1,2$. If $k_{1} = k_{2}$ and

$$\begin{aligned} \lim _{t\rightarrow 0^{+}} \dfrac{\omega _{2}(t)}{\omega _{1}(t)} = 0, \end{aligned}$$

or if $k_{1} < k_{2}$, then $Lip(\omega _{2}, F) \hookrightarrow \hookrightarrow Lip(\omega _{1}, F)$.

Proof

We will prove that the unit ball $B_{\omega _2}$ of ${\text{ Lip }}({\mathbf {E}},\omega _{2})$ is relatively compact in ${\text{ Lip }}({\mathbf {E}},\omega _{1})$. Making use of the classical Arzela theorem it is a matter of fact to see that the Lipschitz classes are compactly embedded in $C({\mathbf {E}})$. Then, from any sequence $\{f_n\}$ of $B_{\omega _2}$, a subsequence $\{f_{n_p}\}$ may be chosen such that $\{f_{n_p}^{(j)}\}$ is convergent in $\Vert \cdot \Vert _\infty$ for any $0\le |j|\le k_2$. The point is now to prove that such a subsequence is a Cauchy sequence in ${\text{ Lip }}({\mathbf {E}},\omega _{1})$. This together with the Banach property of ${\text{ Lip }}({\mathbf {E}},\omega _{1})$ would yield the result.

First assume $k_{1} = k_{2}$ and

$$\begin{aligned} \lim _{t\rightarrow 0^{+}} \dfrac{\omega _{2}(t)}{\omega _{1}(t)} = 0. \end{aligned}$$

Let be $\varepsilon >0$ arbitrarily chosen and take $\delta$ as in Lemma 4.1. Since $\{f_{n_p}^{(j)}\}\subset B_{\omega _2}$ is convergent in $\Vert \cdot \Vert _\infty$ for any $0\le |j|\le k_2$, then there exists $N>0$ such that for $p,m>N$

$$\begin{aligned} {\sum _{\vert j + l\vert \le k}\dfrac{\Vert f_{n_p}^{(j + l)}-f_{n_m}^{(j + l)}\Vert _\infty }{l!}d^{\vert j + l\vert }}\le {\varepsilon }\,{\omega _1(\delta )} \end{aligned}$$

for any $j,\,|j|\le k_2$.

This together with the estimate of Lemma 4.1 yield the Cauchy property of $\{f_{n_p}\}$ and we are done.

The case $k_{1} < k_{2}$ may be carried out in a similar way, but this time invoking Lemma 4.2. $\square$