1 Introduction

Confusion and diffusion are considered as the two fundamental operations to ensuring the security encryption. S-box, commonly as the unique nonlinear component, is used to enforce confusion in block-ciphers with the substitution-permutation network structure. S-box is also widely discussed in linear and differential attacks against block ciphers [1].

Mathematically, a \(m \times n\) S-box is a nonlinear substitution mapping function S(x):GF(2 m) → GF(2 m) which is also written as the Boolean function formulation: f(x) = (f 1(x), f 2(x),…, f m (x)). There have been abundant S-box construction techniques such as algebra-based ones, small-to-larger ones, pseudo-random-based ones and heuristic-approaches-based ones.

It is noticed that chaotic system and cryptography overlaps some characteristics which can lead to developing secure chaos-based cryptosystem. Sensitivity to initial conditions, ergodicity, and pseudorandom behavior of chaotic systems, fulfill the analogous requirements for a good cryptosystem. The comparability motivated researchers to design S-box using chaotic systems. Matthews is the pioneer to enlighten chaotic encryption algorithm in 1989 [2]. Jakimoski and Kocarev [3, 4] used the logistic chaotic map to design S-box. Tang et al. [5] introduced a method to design S-box using discretized chaotic map with good performance. In [6], the tent map was used to generate dynamic S-box for block ciphers. Chaotic Lorenz system was employed to construct S-box in [7]. In sequence, Duffing chaotic system was used to design 8 × 8 S-box [8]. Chaotic baker map is used to obtain S-box [9]. With the development of hyperchaotic systems, the hyperchaotic Lorenz system was introduced to design S-box [10].

Recently, Liu et al. [11] introduced an efficient scheme for constructing S-box based on the 3D-4wing autonomous chaotic system. Due to owning more than one positive Lyapunov exponent, multi-wing chaotic systems exhibit eminence behaviors with high sensitivity to initial conditions, randomness, strong spatiotemporal complexity which make them possible to construct S-box with better performance. In the last decade, multi-wing chaotic systems were deeply studied [12–16]. In [11], the scheme batched generated 8 × 8 S-boxes and the optimal S-box is selected according to cryptographic properties. The results were compared with the existing chaos-based schemes [17–24]. The improved security performance showed the superiority of the 3D-4wing chaotic system, the batched generation manner and optimum selection strategy used in [11]. Unfortunately, S-boxes that are based on hyperchaotic chaos still do not achieve the performance as high as those used in traditional block ciphers such as AES, Camellia, SEED etc. which leaves the possible further improvement space.

In this paper, a batch of cryptographically strong S-box is efficiently generated using the recently discovered 4D hyperchaotic system. The cryptographic strength of the preferred S-box is examined using typical criteria including bijectivity, nonlinearity, differential approximation probability, bits independence criterion and strict avalanche criterion.

This paper is organized as follows. In Sect. 2, the 4D hyperchaotic memristive system is discussed in detail. In Sect. 3, the proposed algorithm is explained detailedly. In Sect. 4, the performance of generated 8 × 8 S-box is investigated by the standard evaluation criterions and the comparison with other chaotic based S-boxes are performed. Finally, the conclusion is drawn and future work is forecasted in Sect. 5.

2 Review of the 4D-4Wing Hyperchaotic System

In recent years, hyperchaotic systems have been deeply investigated in many engineering fields, such as lasers [25], nonlinear circuits [26], synchronization [27], control [28] and secure communications [10, 11, 29] respectively. In [30], a new four-wing hyperchaotic system generated from a 4D memristive system was discovered with richer dynamical behavior than that of most of the known memristive systems [31–35]. The system is described as follow:

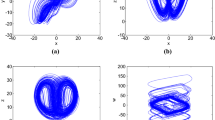
$$\left\{ \begin{aligned} &\dot{x} = ax + byz \hfill \\ &\dot{y} = cy + dxz - kyW(u) \hfill \\ &\dot{z} = ez + fxy + gxu \hfill \\ &\dot{u} = - y \hfill \\ \end{aligned} \right.$$
(1)

where a, b, c, d, e, f, g, k, m, n are system parameters, \(W\left( u \right) = m + 3nu^{2}\), and \(k,g,m,n( \in R^{ + } )\). When \(a = 0.35,b = - 10,c = - 0.6,d = 0.3,e = - 1.6,f = 2,g = 0.1,m = 0.1,n = 0.01\) and \(k \in \left( {0,2.5} \right)\), then the system shows sophisticated hyperchaotic behaviors. It is found that the system has four Lyapunov exponents, \({\text{LE}}_{1} = 0.0905,{\text{LE}}_{2} = 0.0147,{\text{LE}}_{3} = - 0.0001\), and \({\text{LE}}_{4} = - 1.9862\). It exhibits line equilibrium and makes it harder to analyze than the classical dynamical system. Different projection planes are depicted in Fig. 1a–f respectively.

Fig. 1
figure 1

Four-wing hyper-chaotic phase portraits of system (1) with control parameters \(a = 0.35,b = - 10,c = - 0.6,d = 0.3,\) \(e = - 1.6,\,f = 2,\,g = 0.1,\,m = 0.1,\,n = 0.01\) and \(k = 0.2\). a Projection on the x–y plane. b Projection on the x–z plane. c Projection on the y–z plane. d Projection on the x–u plane. e Projection on the z–u plane. f 3-D view in the x–y–z space

Full size image

The more sophisticated dynamic behavior can be observed just by the simple nonlinear combination like t 1 = xy and t 2 = zu. Figure 2a shows the dynamics of the new system with the state variable xy and zu. Figure 2b gives the curve t1 varying with time. The curve of t 2 is similar to that of t 1, so we do not provide it here.

Fig. 2
figure 2

The dynamics of t 1 = xy and t 2 = zu, and the t 1. a The oribit of t 1–t 2. b t 1 curve varying with time

Full size image

Figure 3 shows the histograms of t 1 and t 2, the two histogram shapes are very close to Laplace distribution with zero mean value defined by Eq. (2)

Fig. 3
figure 3

The histograms of t 1 and t 2. a The histogram of t 1. b The histogram of t 2

Full size image
$$p(x) = \frac{1}{2\beta }\exp \left( { - \left| {\frac{x}{\beta }} \right|} \right)$$
(2)

After further fitness analysis, we find that β = 0.1884, 0.2456 for t 1 and t 2 with low root-mean-square errors.

3 Generate Candidate S-Boxes Based on 4D-4Wing Hyperchaotic System

S-boxes generation steps are shown in Fig. 4 and the process is described as follows.

Fig. 4
figure 4

S-boxes generation process

Full size image

  • Step 1 Set the initial values (x 0, y 0, z 0, u 0) of System (1) and it's parameters a, b, c, d, e, f, g, m, n.

  • Step 2 Set the iteration step τ and iteration round N, perform the iteration of System (1), obtain four state variable sequences {x 1, x 2,…,x N },{y 1, y 2,…,y N },{z 1, z 2,…,z N } and {u 1, u 2,…,u N }, discard the transient part total k-1 beginning variables of the four sequence. Ultimately, x = {x k, x k+1,…,x N }, y = {y k , y k+1,…,y N },z = {z k , z k+1,…,z N } and u = {u k , u k+1,…,u N } are obtained.

  • Step 3 Generate two new sequences t 1 = {x k· y k , x k+1· y k+1,…, x N· y N } and t 2 = {z k· u k , z k+1· u k+1,…, z N· u N } based on x, y, z and u.

  • Step 4 Set the sampling step as s (sL = N-k + 1 and L is divisible by 8) to sample t 1 and t 2 to w = {x k· y k , x k+s· y k+s, x k+2s· y k+2s,…, x N· y N } and v = {z k· u k , z k+s· u k+s, z k+2s· u k+2s,…, z N· u N }. The sampling procedure is used to assure the unpredictability of chaotic sequence.

  • Step 5 Convert w = {w 1, w 2,…, w L } and v = {v 1, v 2,…, v L } to the corresponding binary sequence w′ = {w′1, w′2,…, w′ L } and v′ = {v′1, v′2,…, v′ L } by Eq. (3).

$$w^{\prime}_{i} = \left\{ {\begin{array}{*{20}c} 0 & {w_{i} < 0} \\ 1 & {w_{i} \ge 0} \\ \end{array} } \right.\quad v^{\prime}_{i} = \left\{ {\begin{array}{*{20}c} 0 & {v_{i} < 0} \\ 1 & {v_{i} \ge 0} \\ \end{array} } \right.,\quad i = 1,2, \ldots ,L$$
(3)

  • Step 6 Assume L = 8· n, convert the binary seqences w′ = {w′1, w′2,…, w′ L } and v′ = {v′1, v′2,…, v′ L } to 8-bit integer sequnce p = {p 1, p 2,…, p n } and q = {q 1, q 2,…, q n } by Eq. (4).

$$\left\{ {\begin{array}{*{20}c} {p_{i} = \sum\limits_{j = 0}^{7} {w^{\prime}_{j + 8(i - 1)} \cdot 2^{j} } } \\ {q_{i} = \sum\limits_{j = 0}^{7} {v^{\prime}_{j + 8(i - 1)} \cdot 2^{j} } } \\ \end{array} } \right.\quad i = 1,2, \ldots ,n$$
(4)

  • Step 7 Generate C candidate S-boxes by swapping operation on the initial B 0 = {0,1,2,…,255}. For the S-box B i , use p and q to perform swap operation on B 0 iteratively. The j-time swap on B 0 is defined by Eq. (5), then B i is generated after A times iterative swaps.

$$B_{0} (p_{(i - 1)A + j} ) \leftrightarrow B_{0} (q_{(i - 1)A + j} )$$
(5)

For example, to generate the first candinate S-box B 1 , when p 1 = 2, q 1 = 254 and when p 2 = 3, q 1 = 2 the first two round swap operation can be illustrated by Fig. 5.

Fig. 5
figure 5

Example of the swap operation

Full size image

Finally, it should be noticed that according to the above statement, the required iteration round N is determined by Eq. (6).

$$N = 8s \cdot A \cdot C + k - 1$$
(6)

4 Performance Analysis of the Generated S-Boxes

4.1 Typical Evaluation Criteria for S-Box

There are many design criteria of S-boxes according to [36, 37]. In this paper, five typical evaluation criteria are taken into consideration including nonlinearity, differential uniformity, strict avalanche criterion, output bits independence criterion and bijective property for benchmark.

4.1.1 Bijectivity

A m × m S-box is a bijective mapping referring to an m-bit permutation. The set of all m-bit permutation is known as the symmetric group on 2 m objects with total (2 m)! ones. And among those (2 m)! S-boxes, the overwhelming majority is worse in cryptographic meaning. In this paper, all S-boxes are constructed by permuting the identical mapping {0,1,…,255}, which guarantees the bijectivity of our generated S-boxes is invariably tenable.

4.1.2 Strict Avalanche Criterion

Strict Avalanche Criterion(SAC) was firstly introduced by Webster and Tavares [37]. For a Boolean function f(x):GF(2n) → GF(2), SAC means that the change of one single bit of x will change the output bit with the probability equal to 0.5, which is an important characteristic resisting cryptanalysis. SAC can be described via dependency matrix [37]. The ideal value is 0.5 for each element of dependency matrix. Commonly, the minimum, maximum and mean values of the dependency matrix (αmin, αmax, αmean) are taken as evaluation criteria.

4.1.3 Nonlinearity

Nonlinearity directly determines the strength of cryptosystem against linear cryptanalysis. For a Boolean function f(x):GF(2n) → GF(2), the nonlinearity can be measured by the Hamming distance to the set of all linear functions on GF(2n). It is can be defined by Eq. (7) via Walsh transform.

$$N_{f} = 2^{n - 1} - \frac{1}{2}\mathop {\hbox{max} }\limits_{{\omega \in GF(2^{n} )}} |S_{ < f > } (\omega )|,$$
(7)

where \(S_{ < f > } (\omega )\) is the Walsh spectrum of the Boolean function f. It is defined by the following equation.

$$S_{ < f > } (\omega ) = \sum\limits_{{x \in GF(2^{n} )}} {( - 1)^{f(x) \oplus x.\omega } } ,$$
(8)

where \(\omega \in GF(2^{n} )\) and \(x \cdot \omega\) denotes the dot product bit by bit. The nonlinearity of a Boolean function on GF(2n) is known to have the upper bound of 2n−1–2n/2−1 when n is even [38]. For 8 × 8 S-boxes discussed in this paper, the value of nonlinearity of anyone of the eight in an S-box will not exceed 120. Here, the minimum, maximum and average nonlinearity values of the eight Boolean function (ηmin, ηmax, ηmean) are taken as the evaluation criteria.

4.1.4 Differential Uniformity

The differential analysis is the commonly used manner of block cipher cryptanalysis. S-box is expected to have differential uniformity, which means an input Δx should uniquely map to an output Δy. The differential approximation probability δ is a measure of differential uniformity.

$$\delta = \mathop {\hbox{max} }\limits_{\Delta x \ne 0,\Delta y} \left\{ {\frac{{\# \left\{ {x \in GF(2^{m} )|{\mathbf{f}}(x) \oplus {\mathbf{f}}(x \oplus \Delta x) = \Delta y} \right\}}}{{2^{m} }}} \right\},$$
(5)

where # denotes the cardinality of the set. The low value of δ is the indication of better S-box.

4.1.5 Bit Independence Criterion

Bit independence criterion is another important criterion to design S-box. It is stated that, for a given set of avalanche vectors generated by the complementing of a single input bit, all the avalanche variables should be pairwise independent. The degree of independence is measured by the correlation coefficient of avalanche vectors. According to [36], for S-box, f(x) = (f 1(x), f 2(x),…, f m (x)), it is pointed out that if f(x) met BIC, f i ⊕ f j (i ≠ j, i, j ∈ {1,2,…,m}) should have high nonlinear value and ideal dependence matrix with each element near 0.5. Here, the mean nonlinearity of total 56 Boolean functions β n , and mean value of all dependency matrix element β d are taken as the evaluation criteria.

4.2 Performance Analysis of the Preferred S-Box

In this paper, the initial values (x 0, y 0, z 0, u 0) is set to (1,1,1,1), the iteration step τ is set to 0.01, the sampling step s is set to 1000, the skip length is set to 1,000,000 the swap time A is set to 213. There are totally 1024 S-boxes are generated. After those 1024 S-boxes are generated, the best one is selected as the preferred S-box according to the value of (αmin, αmax, αmean), (ηmin, ηmax, ηmean), δ, β n and β d . Table 1 gives the preferred S-box arranged to the 16 × 16 matrix column by column.

Table 1 The preferred S-box generated by the proposed method
Full size table

We compare the proposed scheme with the state-of-the-art chaos-based schemes, the comparative results are shown in Table 2. It should be noticed that the value of β n of the method in [10] is not given because the specific S-box was not given in the original paper. Integrating all the evaluation criteria, the result given in [11] is the current best one. It is evident that the mean value for nonlinearity is preeminent to all others. Comparatively, the result of SAC is also got improvement with αmean is very close to 0.5, and better than the others. On the aspect of BIC, β n is better than that of [11] with βd decreasing just about 0.1%.

Table 2 Comparison of recent chaos-base designed S-Boxes with the proposed S-Box
Full size table

5 Conclusion

In this paper, the new 4D 4-wing hyperchaotic system is used to generate S-boxes. The hyperchaotic system with more sophisticated behaviors provides sufficient randomness to generate the swap position pairs. The generated and preferred S-box is proved to have good cryptographic strength according to the performance analysis and comparison with the-state-of-art chaos-based schemes. However, its performance is still lower than those widely used in commercial standard block ciphers. Hence, in the future work, we will continue exploring the chaos-based S-box design methods and combine it with heuristic optimization methods to find better ones.