1 Introduction

A burst is a rapid energy release phenomenon that produces a blast wave and hot gasses (Mirtaheri et al. 2011). During the detonation process, the hot gasses expanded and occupied the space around it, which lead to a wave like propagation that was transmitted spherically through the unbounded surrounding medium (Shim et al. 2013). Along with the produced gasses, the air around the blast, which was for air blasts, also expanded and the molecules piled-up resulted in what is known as a blast wave and a shock front (Cerik 2017). The explosive loads can produce a significant amount of damage to the structural elements, which might lead to a total or a partial structural system failure without any proportionality between the initial and the ultimate devastation. (Mohammadzadeh and Noh 2015).

There has been a considerable amount of research involving the literature conducted on the design and the analysis of structures as well as the structural elements subjected to the various types of loads, such as wind, earthquakes, hydrodynamics, and bending (Mohammadzadeh et al. 2012; Mohammadzadeh and Noh 2013; Choi et al. 2018; Mohammadzadeh 2016). However, there are a few studies about the structures subjected to explosive loads. There are also some performed experimental work (Clubley 2014; Rolfe et al. 2017), and some employed analytical and numerical approaches (Markose, and Rao 2017; Gharababaei et al. 2010; Al-Thairy 2018) to investigate the structural responses exposed to blast loading.

Kim and Lee (2015) performed a set of numerical, analytical and experimental work to evaluate the blast-resistant performance of an earth covered magazine, which was fabricated using corrugated steel plates. For the numerical investigations, they employed LS-DYNA. The results showed that the bolted joints of the corrugated steel plates did not suffer any fracture, displacement, or destruction of the steel surrounding the bolts. Lee and Shin (2016) extended and developed a single degree of freedom elastic–plastic design charts for protective structures subjected to blast loads. They justified their work by using the existing design charts and the finite element method through LS-DYNA. Tsavdaridis et al (2017) investigated the behavior of steel web-perforated beams with numerous shaped single openings located close to the beam-to-column connections under monotonic and cyclic loading by employing a numerical approach through the finite element (FE) package ANSYS. The results showed that larger web cut-outs are capable of moving the plastic hinge away from the column face and the complete joint penetration (CJP) weld. Also, the inter-story drifts could be controlled with a rational use of the beam web perforation size, shape, and distance from the face. Mohammadzadeh and Noh (2017) investigated the dynamic responses of the sandwich plates that have the functionally graded material (FGM) face sheets that rest on the elastic foundation subjected to the blast loads analytically and numerically. They employed Hamilton’s principle and the higher order shear deformation theory in order to gain the differential equations of motion. The obtained results from the presented analytical scheme were compared with the results from the numerical approach through ABAQUS in order to evaluate the validity of the method. Yuan and Tan (2013) performed a numerical investigation of the deformation and the failure of the fully clamped rectangular plates that were subjected to a zero-period impulsive load. They also performed numerical nonlinear analyses of the rectangular plate to perceive the central deflection for the different aspect ratios. Mirzababaie Mostofi et al. (2016) presented an approximated theoretical analysis of the inelastic behavior of the fully clamped thin quadrangular plates that were subjected to two different distributions of impulsive loading. The obtained models could predict the culminating deflections of the quadrangular plate loaded of the uniformly distributed and localized loadings.

Having looked at the studies available in the literature, it could be inferred that performing the blast-related research work would be costly and face many hazards. Accordingly, employing the analytical and the numerical approaches could be a potential alternative. Some methods presented in literature were difficult to understand and very complicated to use, and some of them had limited uses for specific cases. Therefore, the need for a simplified comprehensive study that considered the most effective burst-related effective parameters on plated structures arose.

The volume of knowledge in this area motivated this study to provide a simplified comprehensive analytical method that investigated the isotropic plates that were exposed to detonation considering a range of explosive charges. The effects of the most important parameters, such as sheet thickness, aspect ratio, and the explosive charge weight on the behavior of the plated structures subjected to the explosion, were investigated through parametric studies in order to provide a good insight and an understanding of the problem. This method can be employed for the research and the design purposes as well as show reliable results for the deflection and the time history of the plates.

An analytical approach for the investigation of the dynamic responses of the isotropic rectangular plates subjected to the blast loads is presented in this research. First, Navier’s solution was employed to construct and provide the analytical approach. By considering the distribution of the applied load independent of the position on the plate surface, the general equation of the displacement was obtained. Afterwards, the largest deflection and the utmost bending moments around the x and y-axes were obtained for the center point of the plate. In addition, the numerical investigations of the plates subjected to the blast loads were performed through the commercial finite element method (FEM) package ABAQUS. Finally, some problems were solved by the methods of this study and FEM. After that, in order to show the applicability and the validity of the suggested approach, the comparisons were made among the results of the current method, the literature, and the FEM.

2 The Derivation of the Analytical Equation of Displacement

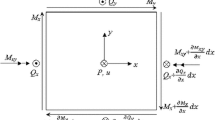
A rectangular isotropic plate having a length of a and a width c, is illustrated in Fig. 1. The abscissa is allocated to x and the ordinate is specified for y.

Fig. 1
figure 1

Schematic of plate

Full size image

The distribution of the blast wave pressure over the surface of the plate was assumed as a function of time, which is represented in Eq. (1) (Goel et al. 2012):

$$P\left( t \right) = P_{{s0^{ + } }} \left( {1 - \frac{t}{{t_{{0^{ + } }} }}} \right)\exp \left( {\frac{{ - b\left( {t - t_{a} } \right)}}{{t_{{0^{ + } }} }}} \right),$$
(1)

where \(P\left( t \right)\) is the time dependent pressure (MPa), \(P_{{s0^{ + } }}\) peak overpressure (MPa), t time, \(t_{{0^{ + } }}\) the positive phase duration (ms), b is the dimensionless wave decay coefficient, and \(t_{a}\) is the wave arrival time in ms. The illustration of the expansion of a typical blast wave pressure in its surroundings is given in Fig. 2.

Fig. 2
figure 2

An illustration of a typical blast wave expansion into the around media

Full size image

In Fig. 2, \(P_{a}\) represents the ambient atmospheric pressure while the maximum negative pressure is symbolized with \(P_{{S^{ - } }}\).

This study aims to achieve an analytical expression for the extreme deflection of the plate due to the blast pressure, which is represented by Eq. (1), considering only the elastic range. This study does not account for the damping, because the previous study showed that it didn’t have a substantial effect on the ultimate displacement of the plates exposed to the explosive forces (Mohammadzadeh and Noh 2015).

2.1 A Definition of the Problem

2.1.1 The Governing Differential Equation of Motion

The governing differential equation of the plate can be expressed as follows (Ventsel and Krauthammer 2001):

$$\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }} + \frac{\rho h}{D}\frac{{\partial^{2} w}}{{\partial t^{2} }} = \frac{P\left( t \right)}{D} ,$$
(2)

where \(w\) is the plane-normal displacement, t is time, ρ is the mass density per unit volume, h is the thickness of the plate, and D is the flexural rigidity, which can be defined as given in Eq. (3):

$$D = \frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}} ,$$
(3)

where \(E\) is the modulus of elasticity, \(\nu\) is Poisson’s ratio.

2.1.2 The Boundary Conditions

The simply supported boundary conditions are expressed as follows:

  • w = 0, \(M_{x} = 0\) for x = 0 and x = a,

  • w = 0, \(M_{y} = 0\) for y = 0 and y = c,

  • w = 0, \(M_{x} = 0\), \(M_{y} = 0\) at t = 0.

where \(M_{x}\) and \(M_{y}\) are the moments about the y and x axes represented by Eqs. (4) and (5), respectively,

$$M_{x} = - D\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right),$$
(4)
$$M_{y} = - D\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) .$$
(5)

Having w = 0, \(\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0\) and \(\frac{{\partial^{2} w}}{{\partial y^{2} }} = 0\) along the edge, the boundary conditions are represented as follows:

  • w = 0, \(\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0\) for x = 0 and x = a,

  • w = 0, \(\frac{{\partial^{2} w}}{{\partial y^{2} }} = 0\) for y = 0 and y = c,

  • w = 0, \(\frac{\partial w}{\partial t} = 0\) at t = 0.

2.2 A Solution for the Displacement w

The external load, \(P\left( {x,y,t} \right),\) is expressed in the form of a series as given in Eq. (6):

$$P\left( {x,y,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } f_{mn} \left( t \right)W_{mn} \left( {x,y} \right).$$
(6)

where \(f_{mn} \left( t \right)\) is the time-dependent part of the applied load, and \(W_{mn} \left( {x,y} \right)\) is the displacement-dependent part of the equation, which is defined later in Eq. (12).

The plate deflection should be defined in terms of the time and the plate geometry to include the dynamics of the method. The time and the position deflection of the plate w is represented by the function given in Eq. (7):

$$w\left( {x,y,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } F_{mn} \left( t \right)W_{mn} \left( {x,y} \right),$$
(7)

where the function \(F_{mn} \left( t \right)\) is the time dependent part of the deflection and n are the mode shaped numbers that express the number of half waves of vibration along with the x and the y directions, respectively. As illustrated by Eq. (7), there are two functions. The first one is \(F_{mn} \left( t \right)\), which is the time dependent part that states the change in the blast wave intensity and the change in the plate displacement with respect to time. The other equation is \(W_{mn} \left( {x,y} \right)\), which expresses the displacement over the area of the plate. \(F_{mn} \left( t \right)\) is illustrated below.

$$F_{mn} \left( t \right) = A_{mn} \cos \omega_{mn} t + B_{mn} \sin \omega_{mn} t + F_{mn}^{\left( p \right)} \left( t \right),$$
(8)

where \(F_{mn}^{\left( p \right)} \left( t \right)\) is a particular solution from Eq. (2). The constants \(A_{mn}\) and \(B_{mn}\) are determined.

2.2.1 The Particular Solution

The function \(F_{mn}\) given in Eq. (8) satisfies the following expression:

$$\ddot{F}_{mn} \left( t \right) + \omega_{mn}^{2} F_{mn} \left( t \right) = \frac{1}{\rho h}f_{mn} \left( t \right),$$
(9)

where \(\ddot{F}_{mn}\) is the second time derivative of \(F_{mn} \left( t \right)\), \(\omega_{mn}\) is the frequency, and \(f_{mn} \left( t \right)\) is an arbitrary expression that is defined in this study as Eq. (10) where the particular solution for \(F_{mn}^{\left( p \right)} \left( t \right)\) can be found as:

$$f_{mn} \left( t \right) = exp\left( {\frac{{ - b\left( {t - t_{a} } \right)}}{{t_{0}^{ + } }}} \right),$$
(10)

Equation (9) is rewritten as follows:

$$\ddot{F}_{mn} + \omega_{mn}^{2} F_{mn} = \frac{1}{\rho h}\cdot exp\left( {\frac{{ - b\left( {t - t_{a} } \right)}}{{t_{0}^{ + } }}} \right).$$
(11a)

To find the particular solution, \(F_{mn}\) is set as

$$F_{mn} = A exp\left( {\frac{{ - b\left( {t - t_{a} } \right)}}{{t_{0}^{ + } }}} \right).$$
(11b)

By substituting Eq. (11b) into Eq. (11a) the constant A is provided and is as follows:

$$A = \frac{1}{{\rho h\left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{mn}^{2} } \right)}},$$
(11c)

Then, by substituting A into Eq. (11b), the particular solution of Eq. (2) is obtained as follows:

$$F_{mn}^{\left( p \right)} \left( t \right) = \frac{{exp\left( {\frac{{ - b\left( {t - t_{a} } \right)}}{{t_{0}^{ + } }}} \right)}}{{\rho h\left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{mn}^{2} } \right)}}.$$
(11d)

2.2.2 The Determination of the Constants \(A_{mn}\) and \(B_{mn}\)

As previously mentioned, in order to solve the governing differential equation of the motion, the Navier solution was taken into account. Accordingly, it was supposed that the solution of the equation of motion, and the plate displacement, are a function of time and displacement, which is elementary geometry. Based on the Navier method, the displacement dependent section \(W_{mn} \left( {x,y} \right),\) can be expressed in the form of a trigonometric series that accounts for the fundamental mode, which is represented Eq. (12). Evidently, it was defined in a method to satisfy the boundary conditions. The guidelines given in (Chopra 2001, and Reddy 2006) were employed for proposing Eq. (12).

$$W_{mn} \left( {x,y} \right) = G_{mn} {\text{sin}}\alpha_{m} x\sin \beta_{n} y$$
(12)

where \(\alpha_{m} = \frac{m\pi }{a} , \beta_{n} = \frac{n\pi }{c}\;{\text{and }}\;G_{mn}\) is the Fourier coefficient, which can be determined by the following expression given in Eq. (12a):

$$G_{mn} = \frac{4}{ac}\mathop \smallint \limits_{0}^{a} \mathop \smallint \limits_{0}^{c} p_{0} \left( {x, y} \right)\sin \alpha_{m} x\sin \beta_{n} ydxdy.$$
(12a)

The deflection of the plate can be represented by substituting Eq. (8) into Eq. (7):

$$w = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left[ {A_{mn} \cos \omega_{mn} t + B_{mn} \sin \omega_{mn} t + F_{mn}^{\left( p \right)} \left( t \right)} \right]W_{mn} \left( {x,y} \right).$$
(13)

The distribution of the applied load on the plate, \(p_{0} \left( {x, y} \right)\), is the independent of position on the plate, thus:

$$p_{0} \left( {x, y} \right) = P\left( t \right)$$
(14)

By applying the boundary conditions w = 0 and \(\frac{\partial w}{\partial t} = 0\) at t = 0, which states that the plate is at rest at an initial moment, we can evaluate the constants \(B_{mn}\) and \(A_{mn}\) as given in Eqs. (15) and (16), respectively:

$$B_{mn} = \frac{b}{{t_{0}^{ + } \omega_{mn} }}\cdot \frac{{exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{mn}^{2} } \right)}} ,$$
(15)
$$A_{mn} = - \frac{{exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{mn}^{2} } \right)}} .$$
(16)

2.3 The Determination of the Displacement and the Bending Moment Expressions

We can rewrite the equation of the deflection of the plate by substituting Eqs. (11d), (15) and (16) into Eq. (12) as follows:

$$w = \frac{{exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \frac{1}{{\left( {1 + \left( {\frac{{t_{0}^{ + } \omega_{mn} }}{b}} \right)^{2} } \right)}}\left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{mn} }} + exp\left( {\frac{ - bt}{{t_{0}^{ + } }}} \right)} \right]G_{mn} \sin \alpha_{m} x\sin \beta_{n} y.$$
(17)

The parameter \(G_{mn}\) vanishes when m and n, possess even numbers while it has the amount of \(\left( {{\raise0.7ex\hbox{${16P\left( t \right)}$} \!\mathord{\left/ {\vphantom {{16P\left( t \right)} {mn\pi^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${mn\pi^{2} }$}}} \right)\) for the odd values of m and n. Equation (17) can be rewritten as follows:

$$w = \frac{{16P\left( t \right)exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} }}\mathop \sum \limits_{{m = 1,3, \ldots }}^{\infty } \mathop \sum \limits_{{n = 1,3, \ldots }}^{\infty } \frac{1}{{mn\left( {1 + \left( {\frac{{t_{0}^{ + } \omega_{mn} }}{b}} \right)^{2} } \right)}}\left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{mn} }} + exp\left( {\frac{ - bt}{{t_{0}^{ + } }}} \right)} \right]\sin \alpha_{m} x\sin \beta_{n} y.$$
(18)

The time dependent sections of the equation of deflection are set to \(F\left( t \right)\) as given hereunder:

$$F\left( t \right) = \frac{1}{{mn\left( {1 + \left( {\frac{{t_{0}^{ + } \omega_{mn} }}{b}} \right)^{2} } \right)}}.\left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{mn} }} + exp\left( {\frac{ - bt}{{t_{0}^{ + } }}} \right)} \right].$$
(19)

By substituting the expression of deflection into Eqs. (4) and (5), the maximum bending moments can be found as:

$$M_{x} = \frac{{16DP\left( t \right)exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} }}\mathop \sum \limits_{{m = 1,3, \ldots }}^{\infty } \mathop \sum \limits_{{n = 1,3, \ldots }}^{\infty } F\left( t \right)\left( {\frac{{m^{2} \pi^{2} }}{{a^{2} }} + \nu \frac{{n^{2} \pi^{2} }}{{c^{2} }}} \right)\sin \frac{m\pi }{a}x\sin \frac{n\pi }{c}y,$$
(20)
$$M_{y} = \frac{{16DP\left( t \right)exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} }}\mathop \sum \limits_{{m = 1,3, \ldots }}^{\infty } \mathop \sum \limits_{{n = 1,3, \ldots }}^{\infty } F\left( t \right)\left( {\nu \frac{{m^{2} \pi^{2} }}{{a^{2} }} + \frac{{n^{2} \pi^{2} }}{{c^{2} }}} \right)\sin \frac{m\pi }{a}x\sin \frac{n\pi }{c}y.$$
(21)

2.4 The Maximum Displacement and the Bending Moments

It can be seen that the maximum deflection and the bending moments occur at the center of the plate. By substituting \(x = \frac{a}{2}\) and \(y = \frac{c}{2}\) into Eq. (18) and considering the fundamental mode, m = 1 and n = 1, the corresponding maximum plate deflection can be expressed by Eq. (22):

$$w_{max} = \frac{{16P\left( t \right)exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{11}^{2} } \right)}}\left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{11} }} + exp\left( {\frac{ - bt}{{t_{0}^{ + } }}} \right)} \right].$$
(22)

The time at which the maximum deflection of the plate occurs is indicated by \(t_{max}\), which is obtained from \(\frac{\partial W}{\partial t} = 0\). The evaluation of Eq. (22) at \(t_{max}\) results in Eq. (23):

$$w_{max} = \frac{{16P_{{s0^{ + } }} exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{11}^{2} } \right)}}.\left( {1 - \frac{{t_{max} }}{{t_{{0^{ + } }} }}} \right).exp\left( {\frac{{ - b\left( {t_{max} - t_{a} } \right)}}{{t_{0}^{ + } }}} \right) \left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{11} }} + exp\left( {\frac{{ - bt_{max} }}{{t_{0}^{ + } }}} \right)} \right]$$
(23)

Similarly, the bending moments of the plate center and at \(t = t_{max}\) can be evaluated as follows:

$$\left( {M_{x} } \right)_{max} = \frac{{16P_{{s0^{ + } }} exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{11}^{2} } \right)}}.\left( {1 - \frac{{t_{max} }}{{t_{{0^{ + } }} }}} \right).exp\left( {\frac{{ - b\left( {t_{max} - t_{a} } \right)}}{{t_{0}^{ + } }}} \right) \left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{11} }} + exp\left( {\frac{{ - bt_{max} }}{{t_{0}^{ + } }}} \right)} \right].\left( {\frac{{\pi^{2} }}{{a^{2} }} + \nu \frac{{\pi^{2} }}{{c^{2} }}} \right),$$
(24)
$$\left( {M_{y} } \right)_{max} = \frac{{16P_{{s0^{ + } }} exp\left( {\frac{{bt_{a} }}{{t_{0}^{ + } }}} \right)}}{{\rho h\pi^{2} \left( {\left( {\frac{b}{{t_{0}^{ + } }}} \right)^{2} + \omega_{11}^{2} } \right)}}.\left( {1 - \frac{{t_{max} }}{{t_{{0^{ + } }} }}} \right).exp\left( {\frac{{ - b\left( {t_{max} - t_{a} } \right)}}{{t_{0}^{ + } }}} \right) \left[ { - 1 + \frac{b}{{t_{0}^{ + } \omega_{11} }} + exp\left( {\frac{{ - bt_{max} }}{{t_{0}^{ + } }}} \right)} \right].\left( {\nu \frac{{\pi^{2} }}{{a^{2} }} + \frac{{\pi^{2} }}{{c^{2} }}} \right).$$
(25)

3 The Finite Element Approach

The numerical approach through the FEM approach were abundantly employed to investigate and to conduct an analysis of the wide variety structures and systems (Israel and Tovar 2013; Takahashi and Watanabe 2010; Amini et al. 2010; Chen and Shi 2016; Rajendran and Narasimhan 2006). Some studies used the commercial FEM package, such as the LS-DYNA and the ABAQUS, as given by (Mohammadzadeh and Noh 2014, 2016; Li et al. 2017; Rajendran and Lee 2009). Some also employed the finite element method to investigate a variety of structures subjected to the compression, the blast, and the impact loads, and some examined and investigated the FEM while analyzing structures subjected to extreme loads (Nam et al. 2008; Devi and Amanat 2015; Huang and Richard Liew 2016; Imbalzano et al. 2018).

In this study, the dynamic analysis of plate subjected to blast loads, which included the time dependent deformations, was performed numerically by using the commercially finite element software ABAQUS. For this purpose, the guidelines given in (Li et al. 2017; Farzin and Dibajian 2012) were applied.

The numerical investigations were performed to find the maximum deflection of the simply supported plate and to validate the analytical method presented in this study by making comparisons between the numerical and the analytical results. For the analyses, various aspect ratios (AR) of AR = 1, AR = 2 and AR = 4 and the simply supported boundary conditions were considered. The plate thickness varied in range from 50 mm to 100 mm with a stepwise increase of 10 mm. The plate was subjected to explosive charges of various weights of 2 kg, 20 kg, 50 kg, 75 kg, 100 kg, 150 kg and 200 kg. As the nonlinear material behavior of steel was not taken into account for the analytical approach, Young’s modulus E = 210 GPa and Poisson’s ratio \(\nu = 0.3\), was applied for the elastic properties of steel only for the numerical analysis.

The blast load was applied to the plate in the form of pressure. As the blast wave magnitude varied with respect to time, the amplitude should be defined for the pressure to have a time dependent applied load. Figures 3 and 4 show illustrations of the positive phase of the applied blast load, obtained by employing Eq. (1), which correspond to the charges of 2 kg and 200 kg, respectively. A modeled plate with the applied boundary conditions and the load is depicted in Fig. 5. To solve the problem, the dynamic explicit procedure was chosen as explicit solutions are suitable for the short duration events where the effects of the stress waves are important. During the dynamic explicit FEM analysis, the time varying load was applied to the plate structure with respect to the time step. In this type of analysis, the time step should be small enough to achieve accurate results. As the relatively thick plates were studied in this research work, the solid elements were adopted, which is unlike the thin plates where the shell elements were commonly employed to model the plates. The solid elements in the ABAQUS include first-order (linear) interpolation elements and second-order (quadratic) interpolation elements that are in one, two, or three dimensions. The triangles and the quadrilaterals are available in two dimensions, and the tetrahedra, the triangular prisms, and the hexahedra, which are bricks, are provided in three dimensions. The second-order elements provide higher accuracy than the first-order elements. They capture stress concentrations more effectively and are superior for modeling geometric features. For the element stiffness, the full-integration and the reduced-integration elements are available in the Abaqus library. The reduced integration reduces running time, which is especially true in three dimensions. For example, the element type C3D20 has 27 integration points, while the C3D20R has only 8. Therefore, the element assembly for the C3D20 is roughly 3.5 times more costly than for the C3D20R. The reduced integration is also referred as the uniform strain or the centroid strain elements with hourglass control. The second-order reduced-integration elements in the ABAQUS generally yield more accurate results than the corresponding fully integrated elements. Considering all the explanations above, the 20-node quadratic (brick) elements with reduced integration formulation, which is the C3D20R, was adopted to model the plates used in this study.

Fig. 3
figure 3

The load pattern for a charge of 2 kg

Full size image
Fig. 4
figure 4

The load pattern for a charge of 200 kg

Full size image
Fig. 5
figure 5

An illustration of the applied load and the boundary conditions of the plate

Full size image

The blast load was uniformly applied to the plate area as the explosive wave pressure, which is represented by Eq. (1). The wave decay coefficient b can be defined as follows (Goel et al. 2012):

$$b = Z^{2} - 3.7Z + 4.2,$$
(26)

where \({\text{Z}} = R/W^{1/3}\), ‘W’ is the charge (explosive) weight and R is the standoff distance, which is the distance from the detonation source to the point of interest. The correlation between the positive phase duration, \(t_{{0^{ + } }}\), and R, is expressed in Eq. (27) (Manmohan Dass Goel et al. 2012):

$$log_{10} \left[ {\frac{{t_{{0^{ + } }} }}{{W^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}} \right] \approx - 2.75 + 0.27log_{10} \left[ {\frac{R}{{W^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}} \right].$$
(27)

The impulse (I), the area under the pressure-time curve, is an important parameter for the burst damage capability. It can be obtained by using Eq. (28) (Goel et al. 2012):

$$I_{{s0^{ + } }} = 200\frac{{W^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}{{R^{2} }},$$
(28)

The positive peak overpressure, \(P_{{s0^{ + } }}\), is calculated from Eq. (29) (Goel et al. 2012):

$$P_{{s0^{ + } }} = 0.085\frac{{W^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}{R} + 0.3\left( {\frac{{W^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}{R}} \right)^{2} + 0.8\left( {\frac{{W^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}{R}} \right)^{3} .$$
(29)

By applying Eqs. (27)–(29), the values of \(t_{{0^{ + } }}\), \(I_{{s0^{ + } }}\) and \(P_{{s0^{ + } }}\) were calculated, respectively. The influence of the so-called negative phase depends on the scaled distance, Z. For the scaled distances, Z, if the value is less than 50, the influence of the negative phase can be neglected (Goel et al. 2012). Consideration of the stand-off distance when R = 1.0 m resulted in the values of Z being much smaller than 50, so the positive phase was only considered.

4 The Analysis Results and Discussions

The thick plates have been extensively used in a variety of industries and structures, such as carrier containers, ship upper hull structures, boiler wall plates, pressure vessels in the nuclear industry, bridges, and wind power towers. Because these structures may be subjected to blast loads and shock waves, this study only investigated the responses of the thick plates to the blast loads.

The attempt was made to find the deflection of the plate along with pthe lane-normal-direction by applying both analytical and numerical methods. In the first step, the verification of the derived analytical solution was evaluated. After that, the effects of the charge weight, the plate thickness, and the plate aspect ratio were investigated by employing both the analytical and the numerical approaches. Finally, the results of the two methods were investigated separately, and a comparison between the results of both the methods was made.

4.1 A Verification Analysis of the Suggested Formulae

4.1.1 A Comparison of the Time Histories

This section main focus was to assess the validity of the analytical method presented in this study, and to investigate the effects of the loading duration \(t_{d}\) on the dynamic responses of the blast loaded plate. It has been observed that the nature of the dynamic responses of a system varied with respect to the duration of the applied pulse, \(t_{d}\). If the duration of the applied impulsive load, \(t_{d} ,\) is smaller than half of the natural period of the plates, \(t_{d} < \frac{{T_{n} }}{2}\), the maximum response of the plate develops in the free vibration phase. The opposite occurs if \(t_{d} > \frac{{T_{n} }}{2}\), and the maximum response of the plate develops in forced vibration phase (Chopra 2001).

To fulfill the purposes of this section, two example problems were provided where the time histories of blast loaded plates were obtained. In the first example, which was designed to illustrate the condition of \(t_{d} < \frac{{T_{n} }}{2}\), a plate that had an aspect ratio of AR = 2 and a thickness of 15 mm was subjected to a blast load from a 200 g explosive charge was considered. The duration of the loading was td= 1.2 ms, and the natural period of the plate was \(T_{n} = 5.4\;{\text{ms}}\). As \(t_{d} = 1.2\;{\text{ms}} < \frac{{T_{n} }}{2} = 2.7\;{\text{ms}}\), the maximum response developed in the free vibration phase. The time step of the analysis was \(\Delta t = 0.2\;{\text{ms}}\). In order to verify the validity of the analytical method presented in this study, the time histories of the blast loaded plate were obtained and plotted in the comparative graphs in conjunction with those obtained from the numerical method. Figure 6 shows the comparative time histories corresponding to the first example problem, at plate center x = a/2 and y = c/2, obtained from both the analytical and the numerical approaches.

Fig. 6
figure 6

The time history of the plate that has a 15 mm thickness subjected to blast load from a 200 g charge (AR = 2)

Full size image

The graph with the solid circles shows the time history obtained from the analytical approach while the graph with the hollow circles illustrates the time history obtained by the numerical method. As the loading ended, the plate sustained free vibration, which commenced by the displacement and the velocity of the mass at the end of the force pulse, \(t = t_{d}\). The plates oscillated during its natural period, Tn, around its original equilibrium position. As can be seen from Fig. 6, there wasn’t any peak developed during the forced vibration phase, and the loading duration, which is in agreement with (Chopra 2001; Tavakoli and Kiakojouri 2014).

In the next step, the condition of \(t_{d} > \frac{{T_{n} }}{2}\) was investigated. For this purpose, the time histories of the plates that had an aspect ratio of AR = 2 and thicknesses of 50 mm and 100 mm were subjected to a blast load from a 5 kg explosive charge were obtained in the second example. The duration of the pulse loading was \(t_{d} = t_{{0^{ + } }} = 2.63\;{\text{ms}}\). The natural period of the plate that had a 50 mm thickness was Tn= 1.6 ms while the plate that had a 100 mm thickness was Tn = 0.81 ms. As can be seen from the numerical values of \(t_{d}\) and Tn, these examples met the condition of \(t_{d} > \frac{{T_{n} }}{2}\). It is appropriate to note that the time step of \(\Delta t = 0.18\;{\text{ms}}\) was considered for the analyses. The time histories of the plates that had thicknesses of 50 mm and 100 mm are provided in Figs. 7 and 8, respectively.

Fig. 7
figure 7

A plot of the time history for the plate that had a 50 mm thickness and was subjected to blast load from a charge of 5 kg (AR = 2)

Full size image
Fig. 8
figure 8

A plot of the time history for the plate that had a 100 mm thickness and was subjected to blast load from a charge of 5 kg (AR = 2)

Full size image

The graph with solid circles illustrates the time history of the plates, at plate center x = a/2 and y = c/2, obtained from the analytical approach. The graph with the hollow circles shows the time history generated from the numerical approach. As can be seen from Figs. 7 and 8, the maximum dynamic responses of the plates were developed in the forced vibration phase. This means that the maximum plane-normal displacement of the plate occurred within the loading duration, \(t_{d} = 2.63\;{\text{ms}}\). These results are in the agreement with (Chopra 2001; Tavakoli and Kiakojouri 2014). Figures 7 and 8 illustrate that the numerical approach underestimated the plate deflection that corresponded to a thickness of 50 mm while the time history of the plate that had a 100 mm thickness showed that the numerical approach slightly overestimated the plate deflection.

4.1.2 A Comparison of Maximum Responses

A simply supported isotropic plate that had an AR = 2 and a 60 mm thickness was subjected to an impulsive load due from an explosive charge that had a 200 kg weight. To validate the analytical approach, the maximum plane-normal deflection of the plate was compared to the result obtained from the numerical analysis. To perform the analysis, the time step length of \(\Delta t = 0.18\;{\text{ms}}\) was considered. Table 1 shows the maximum plate deflection, and the corresponding occurrence time obtained from both methods.

Table 1 The plate deflection obtained by the analytical and the numerical methods (AR = 2)
Full size table

As can be seen from the last column of Table 1, the variation between the results of the analytical and the numerical approaches was small (5.97%), so a good agreement between both methods was achieved. With this result, it can be asserted that the equation of the plate displacement is adopted and can possibly be applied to practical situations.

4.2 A Comparison of the Influence of the Structural Geometrical Parameters on the Response of the Plates

In order to investigate the characteristics of the behavior of the plates subjected to the blast load, in this section, the varying geometrical features of the plate, such as the plate thickness and the aspect ratio, were taken into account. By means of the estimation of the behavior of the plate due to the various geometrical conditions, it was conducted to not only to grasp the behavioral characteristics but also to validate the legitimacy of the proposed analytical formulae while estimating the behavior of the plates subjected to the blast load.

4.2.1 The Results Based on the Suggested Analytical Scheme

In this section, the plate deflection in the plane-normal-direction was obtained by using Eq. (22). To provide a better criterion for the investigation of the plate responses to the applied blast load, the plate deflection was normalized as a fraction to the plate thickness, w/h. Also, different dimensions were considered for the plate. Three numerical values, which were AR = 1, 2 and 4, were considered for plate aspect ratios. The thickness of the plate varied in the range from 50 mm to 100 mm. First, the effect of the aspect ratio on the plate deflection was studied, and then it was followed by an investigation of the effect of the plate thickness on the plate deflection for the blast loads due to the various charge weights.

4.2.1.1 The Aspect Ratio

Throughout this study, an equation was obtained to calculate the plate deflection along the thickness direction. In this section, the deflections of the plates that had thicknesses of 50 mm and 100 mm were calculated for AR = 1, 2 and 4, in order to assay the effect of the aspect ratio on the plate deflection that was subjected to the explosive loads, which resulted from charges that had weights in a range from 2 kg to 200 kg. In the following graphs, the dashed lines, which show the perfectly linear paths, were used to distinguish the variation of the results from the linear behavior.

Figure 9 shows the normalized deflections of a plate that had a 50 mm thickness at t = 0. 6 ms for AR = 1, 2 and 4, and Fig. 10 represents the plate that had a thickness of 100 mm at t = 0.49 ms.

Fig. 9
figure 9

The normalized deflection of a plate that had a 50 mm thickness with a varying charge weight

Full size image
Fig. 10
figure 10

The normalized deflection of a plate that had a 100 mm thickness with a varying charge weight

Full size image

As can be seen from Figs. 9 and 10, the smallest aspect ratio resulted in the largest the w/h. It can be inferred that as the plate shape tended to resemble a square, it was more affected by the blast load, so a larger deflection occurred. On the other hand, as the plate tended to resemble a strip shape, the deflection of the plate in the plane-normal-direction was reduced. It can be observed that the plate deflection was almost linear in terms of the charge weight.

4.2.1.2 The Plate Thickness

In order to understand the behavior of the plate from the viewpoint of the plate thickness, a range of thicknesses from 50 mm to 100 mm was allocated to the plate. Two aspect ratios, AR = 1 and 4, with different blast magnitudes due to various charges were considered. The variations of the normalized deflections with respect to the charge weight are given in Figs. 11 and 12, respectively.

Fig. 11
figure 11

The normalized deflection of the plate versus the charge weight for various plate thicknesses (AR = 1)

Full size image
Fig. 12
figure 12

The normalized deflection of the plate versus the charge weight for various plate thicknesses (AR = 4)

Full size image

As can be seen from Figs. 11 and 12, the general relationship between the normalized deflection and the charge weight was almost linear. To provide a better understanding of the effects of the plate thickness on the plate deflection, two graphs are given in Figs. 13 and 14 that represent the change of the plate deflection with respect to the plate thickness.

Fig. 13
figure 13

The normalized deflection of a plate versus the plate thickness for various charge weights (AR = 1)

Full size image
Fig. 14
figure 14

The normalized deflection of a plate versus the plate thickness for various charge weights (AR = 4)

Full size image

As can be observed from Figs. 13 and 14, the trend of change in the deflection with respect to the thickness was nonlinear. One of the reasons for this nonlinearity is the fact that the deflection of the plates is a cubic function of the plate thickness h.

4.2.2 The Results Based on the Numerical Method of the FEM

The plate dynamic responses were obtained numerically by applying the commercially available finite element package, ABAQUS. The parameter, w/h, was used to show the effects of the plate thickness on the responses of the plate. The same example plates were considered and were used in the section that contains the analytical solution.

4.2.2.1 The Aspect Ratio

To investigate the effects of the aspect ratio on the plate deflection, two different thicknesses of 50 mm and 100 mm were considered in conjunction with the three aspect ratios, which were AR = 1, 2 and 4. It is worth noting that the data plotted in Fig. 15 was obtained at t = 0.72 ms, while the data in Fig. 16 was obtained at t = 0.405 ms.

Fig. 15
figure 15

The normalized deflection of a plate that had a 50 mm thickness with a varying charge weight

Full size image
Fig. 16
figure 16

The normalized deflection of a plate that had a 100 mm thickness with a varying charge weight

Full size image

As illustrated from Fig. 15, which shows the normalized displacement of the plate that had a thickness of 50 mm, w/h changed almost linearly with respect to the charge weight. The plate of AR = 4 resulted in the smallest values of w/h, while the plate of AR = 1 provided the largest amount of w/h. The variation of the normalized deflection of the plate with a 100 mm thickness versus a charge weight is illustrated in Fig. 16. The trend of the graph was almost linear for all the aspect ratios. The largest deflection was obtained from the plate when AR = 1 while the smallest deflection was from the plate when AR = 4.

4.2.2.2 The Plate Thickness

A range of thicknesses from 50 mm to 100 mm were considered as well as the two aspect ratios of AR = 1 and 4, as for the analytical solution. The normalized plate deflection, w/h, versus the charge weight is given in Figs. 17 and 18 for AR = 1 and 4, respectively.

Fig. 17
figure 17

The normalized deflection of the plate versus charge weight for various plate thicknesses (AR = 1)

Full size image
Fig. 18
figure 18

The normalized deflection of the plate versus charge weight for various plate thicknesses (AR = 4)

Full size image

Figure 17 shows the changes in w/h with respect to the charge weight for the plate that had an AR = 1. The graph with the hollow circles shows the deflections of the plate of thickness of 100 mm, which are the smallest values. The largest values of the deflection were obtained from the plate that had a 50 mm thickness. The variation of the normalized deflections of the plate that had an AR = 4 is shown in Fig. 18. For all the thicknesses, w/h almost linearly increased with an increasing charge weight. The largest amounts of deflection were achieved with a thickness of 50 mm, which is the graph that has solid circles while the thickness of 100 mm exhibited the smallest amount of deflection, which is the graph that has hollow circles.

Figures 19 and 20 show the changes in the plate deflection with respect to the plate thickness for the different charges of 2 kg, 20 kg, 75 kg, 150 kg and 200 kg and for the aspect ratios AR = 1 and AR = 4, respectively.

Fig. 19
figure 19

The normalized deflection of the plate versus the plate thickness for the various charge weights (AR = 1)

Full size image
Fig. 20
figure 20

The normalized deflection of the plate versus the plate thickness for the various charge weights (AR = 4)

Full size image

From graphs given in Figs. 19 and 20, nonlinear trends for a change in the deflection with respect to the plate thickness were observed. As the thickness of the plate decreased the plate deflection increases. It held for all the cases with various charge weights.

4.2.3 A Comparison Between the Analytical and the Numerical Results

To perform a comparison between the results of both the analytical and the numerical solutions, the guidelines and the concepts given in (Tavakoli and Kiakojouri 2014; Larcher 2007; Rashid and James 2009; Jones 2012; Rajendran and Narasimhan 2006; Ngo et al. 2007; Wierzbicki and Nurick 1996) were used.

The dynamic responses of the simply supported plates subjected to impulsive loads due to the burst of explosives with a range of weights from 2 kg to 200 kg, are given in Tables 2 and 3 for the thicknesses of 50 mm and 100 mm, respectively. From the results given in Table 2, it can be seen that the FEM underestimated the amount of the deflection of the plate with a 50 mm thickness while the plate with a thickness 100 mm, the ABAQUS overestimated the amounts of the maximum deflections, which are given in Table 3. The last column of both Tables 2 and 3 show the difference between the analytical and the numerical solutions. The column on the end shows the proportion of the numerical solution to the analytical solution. It indicates whether the numerical approach underestimated or overestimated the maximum deflection of the plate obtained from the analytical approach.

Table 2 The deflections of a plate with a 50 mm thickness in the plane-normal-direction obtained from the analytical solution and an FEM of AR = 2
Full size table
Table 3 The deflections of a plate with a 100 mm thickness in the plane-normal-direction obtained from the analytical solution and an FEM of AR = 2
Full size table

Based on the values given in the last column of Tables 2 and 3, the entitled error that represents the difference between the results of the analytical and the numerical methods, it was observed that the analytical solutions and the numerical solutions were in a good agreement. To provide a better illustration, two comparative graphs that include the analytical and the numerical solutions with thicknesses of 50 mm and 100 mm are given in Figs. 21 and 22, respectively.

Fig. 21
figure 21

A comparative graph for a plate with a 50 mm thickness (AR = 2)

Full size image
Fig. 22
figure 22

A comparative graph for a plate with a 50 mm thickness (AR = 2)

Full size image

5 Concluding Remarks

This study presented the analytical formulae to investigate the dynamic responses of the simply supported isotropic plates subjected to the blast and impulsive loads. The Navier’s solution was employed to the governing differential equation of motion of the plate to predict the plate deflection in the plane-normal-direction and the internal moments as well. The validity of the proposed method was evaluated and verified by means of the commercially available finite element package ABAQUS.

Firstly, for the method verification, two types of analyses were performed with respect to the natural frequency of the plate. The first one was the case where one-half of the natural period of the plate was smaller than the duration time of the applied loading, and the second analysis was when the condition was opposite. The characteristic behaviors of each case were reproduced successfully with a good agreement between the proposed scheme and the numerical analysis. The maximum response of the blast loaded plate and the corresponding occurrence time obtained from presented analytical approach were in a good agreement with those obtained from the numerical approach.

To show the versatility of the proposed scheme, the parametric studies that took into account various structural parameters, such as the aspect ratio of the plate, the plate thickness, and the charge weight, were also performed. The investigation of the effects of the charge weight on the normalized maximum displacement of the plate (w/h), illustrated that as the charge weight increased the normalized displacement of the plate increased with a slight nonlinearity for the given aspect ratio and the plate thickness. The nonlinearity in the response in terms of the plate thickness for a specific charge weight was relatively severe. This was expected in advance since the stiffness of the plates was a cubic function of the thickness.

By making a comparison between the results of the proposed scheme and the numerical analyses for the plate that had thicknesses of 50 mm and 100 mm, which were the thinnest and the thickest plates in this study, it was found that the errors between the results of the proposed scheme and the numerical analyses were as small as about 5%, where the proposed scheme was overestimated for the 50 mm-thickness plate and underestimated for the 100 mm thickness plate.

Based on the foregoing observations on the performance of the proposed formulae, it was ascertained that the proposed formulae for the plate that was subjected to a blast load were not only acceptable as an engineering estimation but also practical in anticipating the responses.

In this study, the analytical formulae to calculate the maximum displacements and the bending moments of the plate that were subjected to the blast loads were presented. A good point of this method is that it is easy to use, especially for engineers, in order to have a good understanding of the problem and to provide them with a good tool for the design purposes. It is also helpful for researchers for pre-investigations, and it can provide them with a quick insight into the aim problem. Because this method considered the linear mechanical properties, it overestimated the plate responses. To get more accurate results and to have an in-depth insight into the behavior of the blast loaded plates, it is required to take into account the nonlinearities in further studies.