1 Introduction

In a given network, different nodes hold different importance based on the given application context. Researchers have defined various centrality measures such as degree centrality (Shaw 1954), semi-local centrality (Chen et al. 2012), closeness centrality (Sabidussi 1966), betweenness centrality (Freeman 1977), eigenvector centrality (Stephenson and Zelen 1989), Katz centrality (Katz 1953), and PageRank (Brin and Page 1998) to capture the importance of the influential nodes. In this work, we focus on closeness centrality capturing each node’s reachability to the entire network. For example, it can be used to identify the central location within a city to place a new public service so that it is easily accessible to everyone or to deploy a computer virus to infect a high number of computers quickly. In such applications, the nodes that can access the entire network relatively faster are ranked high.

The concept of closeness was first proposed by Sabidussi, where the closeness centrality of a node is computed as the inverse of the sum of the distances with all the other nodes (Sabidussi 1966). In 1978, Freeman proposed the normalized definition of closeness centrality as \(C(u) = \frac{n-1}{\sum _{\forall v}d(u,v)}\), where n represents total number of nodes, and d(u, v) represents the shortest distance between two nodes u and v, applicable to connected networks or a connected component (Freeman 1978).

A standard methodology to compute the closeness centrality of a node would execute breadth-first traversal (BFT) (Cormen et al. 2001) from the respective node. The time complexity to compute the closeness centrality of a node is O(m), where m represents total number of edges in the network. Then, to measure the relative importance of a node, the node’s closeness rank is computed based on its closeness centrality value. The classical method of computing the closeness centrality rank of a node, first computes the closeness centrality value of all nodes, and then compare its closeness value with others to determine the closeness rank of the node. The time complexity of the first step is \(O(n \cdot m)\) to compute the closeness centrality of all nodes; for the second step, it is O(n) to compare the centrality value of the given node with all other nodes. So, the overall time complexity of this process is \(O(n \cdot m)+O(n)= O(n \cdot m)\), which is very high. This high complexity method is infeasible to use in real-life applications of large size networks.

Fig. 1
figure 1

Reverse rank versus closeness centrality follows sigmoid curve

Full size image

In literature, there are several methods to approximate the closeness centrality value of the nodes (Cohen et al. 2014; Eppstein and Wang 2004; Rattigan et al. 2006). A limitation of these methods is the requirement to approximate the closeness centrality value of all the nodes of the network to estimate the rank of a single node. It is infeasible given the large size of the real-world networks and calls for efficient ways of estimating the closeness centrality rank of a node of interest.

We introduced such methodology in our previous work (Saxena et al. 2017b, c), where our studies were limited to social networks. The current research performs a deeper analysis and extends them to four categories of the networks introduced by Newman: 1. Biological, 2. Information, 3. Technological, and 4. Social (Newman 2003). First, we study the structural behavior of closeness centrality on the given networks, through the correlation between closeness and degree, depicting how the closeness centrality of the nodes changes from the central node to periphery nodes. The central node is picked out of the nodes having the highest closeness centrality. We further observe that the reverse rank versus closeness centrality approximately follows a sigmoid curve for many real-world networks as shown in Fig. 1. In reverse ranking, the node having the lowest closeness value has the highest rank, namely 1, and the node having the highest closeness value has the lowest rank. This observed sigmoid curve further helps us estimate the closeness rank of a node without computing the closeness value of all the nodes.

Next, we use these observations to propose heuristic and randomized heuristic methods to fast estimate the closeness centrality rank of a node. The complexity of the proposed methods is O(m), which is a significant improvement over the classical ranking method. The accuracy of the proposed methods is measured using absolute and weighted error functions, where the weighted error depends on the quartile of the node (whose rank is estimated) that it belongs to. Results show that the proposed methods can be used efficiently for large size networks.

To the best of our knowledge, our research is the first work in this direction. The rest of this paper is organized as follows. We begin with the literature on closeness centrality. Sections 3 and 4 explain datasets and terminologies used in the paper, respectively. In Section 5, we study the behavior of closeness centrality that helps to construct the closeness rank estimation methods. In Section 6, we propose methods to estimate the closeness rank and discuss their complexity analysis. In Section 7, the simulation results are discussed. The paper is concluded in Sect. 8. The proposed work further opens up various future directions which are discussed in the last section.

2 Related work

Closeness centrality of a node denotes its reachability to each node of the given network. In undirected and unweighted networks, the reachability of two nodes only considers the minimum number of hops to travel from one node to another, namely the distance between the nodes. But in other types of networks such as weighted or directed networks, the reachability also depends on the edge weight and direction of the connection (i.e., the generalized notion of distance). The closeness centrality has been extended to different types of networks such as weighted networks (Ruslan and Sharif 2015), directed networks (Du et al. 2015), disconnected networks (Rochat 2009), multilayer networks (Barzinpour et al. 2014), and overlapped community structure (Szczepański et al. 2016).

Closeness centrality has been applied to study collaboration networks (Newman 2001; Yan and Ding 2009), brain network (Sporns et al. 2007), network traversal techniques (Carbaugh et al. 2017), human navigation (Sudarshan Iyengar et al. 2012), community detection (Jarukasemratana et al. 2014), identification of the community of a node using the community information of other nodes (Zhang et al. 2012), closeness preferential attachment (CPN) model to generate synthetic networks (Ko et al. 2008), and so on.

Due to the high complexity of computing the closeness centrality in large-scale networks, researchers have addressed the following problems related to closeness centrality:

  1. 1.

    Update closeness centrality in dynamic networks,

  2. 2.

    Approximation algorithms for closeness centrality,

  3. 3.

    Identify top-k nodes with respect to closeness,

  4. 4.

    Consider parallel or distributed computing,

  5. 5.

    Correlation with other centrality measures, and so on.

2.1 Updates in dynamic networks

Real-world networks are highly dynamic, and the computation of closeness centrality of all nodes for each change in the network will be a cumbersome task. In dynamic networks, for each update, the closeness centrality of some nodes may remain unaffected. Therefore, Kas et al. used the set of affected nodes to update the closeness centrality whenever there is any addition, removal, or modification of nodes or edges (Kas et al. 2013). Yen also proposed CENDY algorithm (Closeness centrality and avErage path leNgth in DYnamic networks) to update closeness centrality whenever the edge’s existence is updated (Yen et al. 2013). Sariyuce et al. proposed a method to update closeness centrality using the level difference information of breadth-first traversal (Sariyuce et al. 2013).

2.2 Approximation methods

As the classical method to compute closeness centrality requires the entire network, so, researchers have looked for approximation methods. Cohen et al. (2014) proposed a sampling-based method to approximate closeness centrality in directed and undirected networks. Eppstein et al. proposed a randomized approximation algorithm with time complexity \(O(\frac{logn}{\epsilon ^2} \cdot m)\) for the closeness centrality within an additive error of \(\epsilon \cdot \varDelta\), where \(\varDelta\) is the diameter of the network (Eppstein and Wang 2004). Rattigan used the concept of network structure index (NSI) to approximate the values of different centrality measures that are based on the shortest paths in the given network (Rattigan et al. 2006). Some other approximation methods for closeness centrality include (Chan et al. 2009; Brandes and Pich 2007; Pfeffer and Carley 2012).

2.3 Identifying the top-k nodes

In most real-life applications, the focus is on only identifying the top nodes having the highest closeness centrality. Okamoto et al. proposed a method to identify the k highest closeness centrality nodes using a hybrid of approximate and exact algorithms (Okamoto et al. 2008). Ufimtsev proposed an algorithm to identify high closeness centrality nodes using group testing (Ufimtsev and Bhowmick 2014). Olsen et al. presented an efficient technique to find the k most central nodes based on closeness centrality (Olsen et al. 2014), using intermediate results of centrality computation to minimize the computation time. Bergamini et al. proposed a faster method to identify top-k nodes in undirected networks by approximating the upper bound on closeness centrality using breadth-first traversal (BFT) (Bergamini et al. 2016).

Kim et al. proposed an estimation driven closeness centrality based ranking algorithm named RankCCWSSN (Rank Closeness Centrality Workflow-supported Social Network) to identify top-k nodes in large-scale workflow-supported social networks (Kim et al. 2016). They showed that the time efficiency of the proposed method is about \(50\%\) than the traditional method. This method can easily be extended to weighted workflow-supported social networks.

2.4 Other works

Wehmuth and Ziviani studied the correlation of closeness centrality with the local neighborhood volume of the node (Wehmuth and Ziviani 2012). The local neighborhood volume of a node is defined as,

$$\begin{aligned} Vol(H_h^u) = \sum _{v \epsilon H_h^u} deg(v) \end{aligned}$$

where deg(v) is the degree of node v, and h is the level of breadth-first traversal (BFT). \(H_h^u\) denotes the set of all nodes that belong to h level BFT of node u. By definition, the volume of a node gives us the sum of the degree of all nodes that belong to h-level BFT of the given node. The ranking based on local neighborhood volume is named as DACCER (Distributed Assessment of the Closeness CEntrality Ranking). It is observed that DACCER ranking using \(h=2\) is highly correlated with closeness centrality ranking. Lu et al. extended this method and proposed MDACCER (Modified Distributed Assessment of the Closeness CEntrality Ranking) to compute closeness centrality in a parallel environment like General Purpose Graphics Processing Units (GPGPUs) (Lu et al. 2015).

Bader et al. proposed parallel algorithm to compute closeness centrality, where a BFT is executed from each vertex as a root (Bader and Madduri 2006). Lehmann and Kaufmann proposed a method for decentralized computation of closeness centrality (Lehmann and Kaufmann 2003). Wang et al. proposed a distributed algorithm that estimates closeness centrality with \(91\%\) accuracy on random geometric, Erdős-Rényi, and Barabási-Albert graphs (Wang and Tang 2015).

Table 1 Datasets
Full size table

2.5 Nodes’ rank estimation methods

To our knowledge, there is no research on estimating the rank of a node using its closeness centrality other than the standard method already presented in the introduction. We have proposed faster methods to estimate the degree rank of a node using structural properties of the network or sampling techniques (Saxena et al. 2017a). The first proposed degree rank method exploits the power law characteristic (Barabási and Albert 1999) and computes the rank of a node in O (1) time (Saxena et al. 2015b). We further computed the variance in the rank estimation and showed that it increases with the rank (Saxena et al. 2015a), thus having a better estimate of the rank of higher degree nodes. Next, we proposed sampling-based methods to estimate the degree rank using uniform, random walk, and metropolis-hastings random walk sampling (Saxena et al. 2017d). In (Saxena and Iyengar 2018), authors proposed a method to estimate the k-shell value of the node and the proposed estimator is further used to fast estimate the coreness ranking. These works focused on directly estimating the rank of a node without having the entire network. Further details related to this project are available at (Saxena and Iyengar 2017). We now propose to extend the idea of ranking based on closeness centrality, i.e., a global centrality measure.

3 Datasets

Newman categorized the real-world scale-free networks into four main categories: (1) Biological, (2) Information, (3) Technological, and (4) Social (Newman 2003). We study the behavior of closeness centrality on diverse networks belonging to all these categories. For this study, the directed networks are converted into undirected, and in case of disconnected networks, only the largest connected component is considered. The networks are summarized in Table 1.

4 Terminology

Let G(V, E) represent a network where V is the set of nodes, and E is the set of edges. Table 2 explains the further terminology used in the paper.

Table 2 Terminologies
Full size table

5 Closeness centrality behavior

In this section, we study the behavioral characteristics of closeness centrality and its correlation with the network structure.

5.1 Closeness centrality vs. reverse rank

In the real-world scale-free networks we have considered in this work, we observed that the reverse rank versus closeness centrality of nodes follows a sigmoid curve. In reverse ranking, a node having the highest closeness value will have the smallest rank n (where n is the total number of nodes) and the node having the lowest closeness value will have the rank 1. Real-world scale-free networks have a dense central region and the nodes belonging to the central region are highly connected with each other and also with rest of the nodes. The nodes belonging to the outermost peripheral layers have the smallest closeness values. The closeness centrality of all other nodes lies in this range and increases sharply as we move from the periphery to the center. This phenomenon gives rise to a sigmoidal curve. Figure 2 shows sigmoidal curves for different types of the networks, where the x-axis represents closeness centrality and the y-axis represents the reverse rank of the nodes.

Studying this sigmoidal curve, we find that the 4-parameter logistic equation is a good fit to the curve as seen in Fig. 5. Its equation is given as

$$\begin{aligned} R_{\rm rev}(u) = n + \frac{1-n}{1+\left( \frac{C(u)}{c_{\rm mid}}\right) ^p}, \end{aligned}$$
(1)

where \(c_{\rm mid}\) represents closeness centrality of the middle ranked node in the network, n represents total number of nodes, and p denotes slope of the logistic curve at the middle point (also called hill’s slope). These parameters are displayed in Fig. 1. In most of the networks this curve is observed to be symmetric, and for social networks, the curve is observed to be very smooth. In Sect. 6, we will show how we can use this logistic equation to estimate the closeness rank of a node.

Fig. 2
figure 2

Reverse rank versus closeness centrality. a Biological: C. Elegans, b biological: reactome, c biological: yeast, d information: citeseer, e information: Spanish Book, f information: US Airport, g technological: Linux, h technological: internet, i technological: Gnutella, j social: brightkite, k social: DBLP, l social: digg

Full size image

5.2 Closeness centrality vs. degree

Researchers have studied the correlation of closeness with different centrality measures (Tallberg 2000; Ko et al. 2008; Brandes et al. 2016). Here, we analyze the correlation of closeness and degree of the nodes. Figure 3 shows that there is no general correlation between closeness centrality and the degree. However, we observe that the highest degree node either has the highest closeness centrality or it approximates it well. This characteristic can be used to estimate the highest closeness centrality, by identifying the node having the highest degree and computing its closeness centrality. Further details are explained in Sect. 6.1.

Fig. 3
figure 3

Degree versus closeness centrality. a Biological: C. Elegans, b biological: reactome, c biological: yeast, d information: Citeseer, e information: Spanish Book, f information: US Airport, g technological: Linux, h technological: internet, i technological: Gnutella, j social: brightkite, k social: DBLP, l social: digg

Full size image

5.3 Closeness centrality pattern from center to periphery

We further study how the closeness centrality varies as we move from the central node to the periphery. The nodes having the highest closeness centrality are called the central nodes. We pick one node uniformly at random out of the central nodes as the central node for the simulation. To study this pattern, breadth first traversal (BFT) is executed from the central node until all nodes are traversed. Figure 4 presents the change in closeness centrality of nodes as a function of distance from the central node. The results show that the nodes falling on the outermost periphery layer (last BFT level) have the minimum closeness centrality. We also observe that the outermost level of the BFT (also referred as the outermost periphery) is very sparse, about \(\sim (1-20)\) nodes. We use this characteristic to predict the minimum closeness centrality in the network. This pattern is not so prominent in small size networks such as C. Elegans and Yeast.

Fig. 4
figure 4

Closeness centrality versus BFT level from the central node. a Biological: C. Elegans, b biological: reactome, c biological: yeast, d information: Citeseer, e information: Spanish Book, f information: US Airport, g technological: Linux, h technological: internet, i technological: Gnutella, j social: brightkite, k social: DBLP, l social: digg

Full size image

6 Estimating the closeness rank

The Closeness Centrality rank of a node u is defined as, \(R_{act}(u) = \sum _{v} X_{uv} + 1\), where \(X_{uv} = 1,\) if \(C(v)> C(u)\), otherwise \(X_{uv} = 0\). It has been referred as actual closeness rank throughout the paper. The node having the highest closeness value has the rank number 1. All nodes having the same closeness value hold the same rank. The node that either we are interested in finding the rank of, or it is interested in computing its own rank (such as a person in a social network ranking him/herself) is called the interested node.

We use the observed structural behavior of closeness centrality to propose fast heuristic methods to estimate the closeness rank of a node. We discuss these methods in the following subsections. The proposed methods are simulated on the social networks, discussed in Table 1.

6.1 A heuristic method for closeness ranking

We observed in Sect. 5.1 that in large networks, the reverse rank follows a sigmoid curve as a function of closeness centrality. We now use this behavioral characteristic to estimate the closeness rank of a node. Once both parameters of the logistic Equation 1 are estimated, the closeness rank of a node can be estimated in O(1) time. Next, we will discuss methods to estimate both of these parameters: (1) closeness centrality of the middle-ranked node (\(c_{mid}\)) and (2) slope of the logistic curve (p).

6.1.1 Estimate closeness centrality of middle ranked node \((c_{mid})\)

In this section, we use this observed sigmoid curve information to compute the value of \(c_{mid}\), namely the closeness centrality of the median ranked node. Recall that Property 5.2 says that the maximum closeness centrality can be estimated using the standard computation method on the highest degree node. The highest degree node is discovered while estimating the closeness centrality of the interested node.

Observation 1

The maximum closeness centrality can be estimated as, \(c'_{max}=C(u)\) where \(deg(u) \ge deg(v), \forall v \in V(G)\).

Figure 4 shows that the nodes having the maximum distance from the central node have minimum closeness centrality. So, we can keep track of the nodes falling on the outermost level of BFT while computing the maximum closeness centrality.

Let w be a node in the network chosen uniformly at random from all the nodes farthest away from u (i.e. d(u, w) is maximum) for u identified as a central node in Observation 1. Using the Property 5.3, the minimum closeness centrality can be estimated by using following observation.

Observation 2

The minimum closeness centrality can be estimated as, \(c'_{min}=C(w)\), \(\exists w\) where d(w, u) is max, for u identified in Observation 1.

We now use Observations 1 and 2 to estimate the closeness centrality of the middle ranked node.

Proposition 1

In the case where the reverse rank versus closeness centrality curve is symmetric, the closeness centrality of the middle-ranked node, \(c_{mid}\), can be computed as \(\displaystyle c_{mid}=\frac{c_{max}+c_{min}}{2}\).

Proof

If the sigmoid curve is symmetric, then using Fig. 1 we note that: The distance from A to C is \(c_{max} - c_{min}\), and the distance from A to B is \(\frac{c_{max} - c_{min}}{2}\). The distance of B from the origin point can be computed as,

$$\begin{aligned} \displaystyle c_{mid} = c_{min} + \frac{c_{max}-c_{min}}{2} = \frac{c_{min}+c_{max}}{2}, \end{aligned}$$
(2)

as desired. \(\square\)

6.1.2 Estimate slope of the sigmoid curve (p)

In real-world social networks, the slope of the sigmoid curve is measured using scaled Levenberg-Marquardt algorithm (Moré 1978) with 1000 iterations and 0.0001 tolerance. We observe that the slope ranges from 10-15. The slope for the discussed datasets is shown in Table 3.

Table 3 Networks versus their p values
Full size table

The average of these values is used as the value for p in the simulation. We empirically observed that the slight variation in the estimation of p does not cause more error in the ranking.

6.1.3 Estimate closeness rank

After estimating all the needed parameters for the sigmoid curve, the closeness rank of the interested node u can be estimated using Proposition 2.

Proposition 2

In a network G, the closeness rank of a node u can be computed as, \(\displaystyle R_{act}(u)=1 + \frac{n - 1}{1+\left( \frac{C(u)}{c_{mid}}\right) ^p}\).

Proof

Using Equation 1, the reverse rank of a node u can be computed as,

$$\begin{aligned} R_{\rm rev}(u)= n + \frac{1-n}{1+\left( \frac{C(u)}{c_{\rm mid}}\right) ^p}. \end{aligned}$$

The actual rank of a node can be estimated by subtracting its reverse rank from the total number of nodes plus 1. We thus have that, approximately,

$$\begin{aligned} R_{\rm act}(u)= & {} n-R_{\rm rev}(u)+1\\ R_{act}(u)= & {} n- n - \frac{1-n}{1+\left( \frac{C(u)}{c_{\rm mid}}\right) ^p}+1,\\ \end{aligned}$$

which can be simplified to

$$\begin{aligned} R_{\rm act}(u)=1 + \frac{n-1}{1+(\frac{C(u)}{c_{\rm mid}})^p}, \end{aligned}$$
(3)

as desired. \(\square\)

Thus, we can now estimate the rank of a node in a network G using Corollary 1.

Corollary 1

In a network G, the closeness rank of a node u can be estimated as, \(\displaystyle R_{est}(u)=1+\frac{n-1}{1+\left( \frac{C(u)}{c'_{mid}}\right) ^{p'}}\), where \(c'_{mid}\) and \(p'\) are the estimated values of closeness centrality of middle ranked node and slope of the sigmoidal closeness centrality curve respectively.

Algorithm 1 presents the combined method to estimate the closeness rank of a node. The \({\rm closeness}\_{\rm centrality}(G,u)\) method returns the closeness centrality of node u. Moreover, \({\rm closeness}\_{\rm centrality}1(G,u)\) method returns three outputs: the closeness centrality C(u) of node u, the node v having the highest degree in the network, and the network size n. Then \({\rm closeness}\_{\rm centrality}2(G,v)\) method returns the closeness centrality of node v, and a list of the nodes having maximum distance from the node v. Furthermore, \({\rm random}\_{\rm choice}(cmin\_list)\) function returns a value uniformly at random from the given list \({\rm cmin}\_list\). Notice that \({\rm closeness}\_{\rm centrality}(G,u)\), \({\rm closeness}\_{\rm centrality}1(G,u)\), as well as \({\rm closeness}\_{\rm centrality}2(G,u)\) methods can be implemented by modifying the BFT algorithm as they just need to keep track of few variables.

figure a

6.1.4 Complexity analysis

In this section, we discuss the time complexity of the proposed heuristic method that is explained in Algorithm 1. The time complexity of step 1 is O(m) as it executes one BFT and keeps track of the highest degree node while executing the BFT. The time complexity of step 2 is O(m) as it executes BFT from the node w and returns the list of nodes that are traversed during the last level of BFT. The time complexity of step 3 is O(m), as we assume that \(random\_choice(cmin\_list)\) function returns a value in constant time as the size of the list is very small. Step 4 and 5 take O(1) time. So, the overall complexity of the proposed method is \(O(m) + O(m) + O(m) + 2\cdot O(1) = O(m)\). As mentioned, this is a great improvement over the classical ranking method that takes \(O(n \cdot m)\) time. The space complexity of BFT is O(n) in the worst case scenario, so, the space complexity of step 1, 2, and 3 is O(n). The space complexity of step 4 and 5 is O(1). Thus, the overall space complexity of the proposed algorithm is O(n).

6.2 The randomized heuristic method

The accuracy of the estimated rank using heuristic method depends on the accuracy of the \(c_{mid}\) estimator. So, we propose an improved \(c_{mid}\) estimator to increase the accuracy of the proposed method, when the sigmoid curve is not symmetric.

In the heuristic method, we assumed that the sigmoid curve is symmetric. But in some real-world networks, the sigmoid curve might not be symmetric, as seen in Fig. 5 (d), (h), (j). In these cases, the heuristic method gives a large error. We thus propose an improved randomized method that uses uniformly random samples to estimate the value of \(c_{mid}\). The improved method picks k nodes uniformly at random and computes their closeness centrality values. The average of these k closeness values is used as the estimated value of \(c_{mid}\). Our results show that the estimated value of \(c_{mid}\) is very close to its actual value. The complete algorithm is explained in Algorithm 2. Further details are explained in the Results section.

figure b
Fig. 5
figure 5

Actual, best-fit, and estimated (using heuristic method) reverse rank versus closeness centrality curve. a Brightkite, b DBLP, c Digg, d Enron, e Epinion, f Facebook, g Gowalla, h Google+, i Slashdot, j Twitter

Full size image

6.2.1 Complexity analysis

In RandomizedClosenessRank(G, u, p, k) algorithm, the time complexity of \(closeness\_centrality3(G,u)\) method is O(m) as it returns the closeness centrality of node u and the total number of nodes. In the for loop, k nodes are chosen uniformly at random and their closeness centrality is computed, rendering the time complexity of \(O(k \cdot m)\). The time complexity of step 6 and 7 is O(1). Thus, the overall time complexity of the proposed method is \(O(m) + O(k \cdot m) + O(1) = O(k \cdot m)\). As \(k<< n < m\), the time complexity of the proposed method is O(m). The space complexity of the algorithm is \(O(k) + O(n)\) as we store the closeness values of k randomly picked nodes. In practical implementation \(k<< n\), so, the space complexity is O(n).

7 Simulation results

In this section, we discuss error functions and simulation results on real-world social networks.

Table 4 Error in the estimated closeness rank using heuristic and randomized heuristic (for \(k=10\) and \(k=50\)) methods
Full size table

7.1 Error functions

We compute the accuracy of the proposed methods using absolute and weighted error functions that we discuss below:

  1. 1.

    Absolute Error: We compute the absolute error of the closeness centrality rank estimation of a node u as,

    $$\begin{aligned} Err_{abs}(u) = |R_{est}(u) - R_{act}(u)|. \end{aligned}$$
    (4)

    Then, we compute the percentage average absolute error as

    $$\begin{aligned} Err_{paae} = \frac{\text {average absolute error}}{\text {network size}} \cdot 100\%, \end{aligned}$$

    where the \({average \; absolute \; error}\) is computed by taking the average of absolute error for each node.

  2. 2.

    v In real life applications, the importance of the rank depends on the total number of nodes and where does the node stand. For example, a \(100_{th}\) rank is admirable if it is \(100_{th}\) out of 100, 000 people, but not good enough if it is out of 500 people. So, the significance of the error depends on percentile of the node as well as on the network size. The proposed weighted error function considers both of these parameters, and it is defined as:

    $$\begin{aligned} Err_{wtd}(u) = \frac{Err_{abs}(u)}{n} \times percentile(u) \%. \end{aligned}$$

    The percentile of a node u can be calculated as, \(percentile(u) = \frac{n - R_{act}(u) +1}{n} \times 100\). The weighted error increases linearly with the percentile of the node for a given network, and decreases with the network size.

7.2 Discussion

We simulate the proposed methods on all social networks discussed in Table 1. We compute the absolute and weighted errors for each node and average them over all nodes to compute the overall error of the proposed methods. Table 4 shows the errors, and we follow with a discussion.

We compute the best fit error by using the best-fit logistic curve on the reverse rank versus closeness centrality curve. The parameters of the best fit curve are computed using the scaled Levenberg-Marquardt method with 1000 iterations and 0.0001 tolerance (Moré 1978). Then we use Equation 3 to compute the rank of nodes. Our results show that the error computed using best-fit parameters is very low, and the sigmoid pattern can be efficiently used to estimate the closeness rank of the nodes.

The error for heuristic and randomized heuristic methods is shown for \(p=13.38\), and it varies with the p value. Figure 5 shows the reverse rank versus closeness centrality plots for the best fit and estimated parameters using the heuristic method. The heuristic method gives a high error on some of the real-world networks either due to the error in the estimation of the parameters of the logistic curve, or due to the curve not being smooth.

Next, we show that the improved randomized heuristic method presents an improvement over the heuristic method. To compute the error, each experiment is repeated 40 times for both \(k=10\) and \(k=50\), and Table 4 shows the average errors for both. The complexity to estimate the closeness rank of a node is the same as computing its closeness centrality; this is a considerable improvement over the classical ranking method.

In Table 5, we show Kendall’s tau \((\tau )\) (Kendall 1945) and Spearman correlation coefficient \((\rho )\) (Zar 1972) for the actual versus estimated ranks using heuristic and randomized heuristic \((k= 10\) and 50) methods. The values are rounded off by two decimal places. The correlation coefficients show that the proposed methods can be used efficiently to estimate the closeness rank of the nodes.

Table 5 Kendall’s Tau and Spearman correlation coefficient for actual and estimated closeness rank using heuristic and randomized heuristic (for \(k=10\) and \(k=50\)) methods
Full size table

We further study the changes in error as a function of the rank of the nodes. Figures 6 and 7show both the absolute and weighted error results for Brightkite and DBLP network, respectively. The plots consistently show that the error increases at first with the increase of the rank, and then the error decreases till the smallest rank is achieved. Thus, the proposed methods better estimate the rank of the higher and the lower ranked nodes, while producing a larger error for middle ranked nodes due to the estimation error of p and cmid. Similar results are observed for rest of the networks, not displayed here.

Fig. 6
figure 6

PAAE versus closeness rank. a Brightkite network, b DBLP network

Full size image
Fig. 7
figure 7

Weighted error versus closeness rank. a Brightkite network. b DBLP network

Full size image

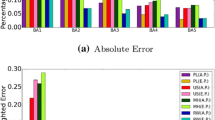
Next, we show how does the performance of the proposed methods change with the network size. To study this, we generate BA networks (Barabási and Albert 1999) of varying sizes having average degree 14.00 and execute the proposed methods on these networks. The methods are executed on a system having Intel(R) Xeon(R) CPU E5-2670 v2 @ 2.50GHz Processor with ten cores, and 96GB RAM is allocated to 20 Cores. The results are shown in Fig. 8 where the x-axis shows the network size and the y-axis shows the running time in seconds. To plot the results, the randomized algorithm is executed 50 times from the randomly chosen interested node and the average time is computed. The results show that the proposed methods can be efficiently used to compute the closeness rank of a node in large real-world scale-free networks.

Fig. 8
figure 8

Running time versus network size (BA Network) for the proposed ranking methods

Full size image

We further compare the proposed methods with DACCER ranking method using h=2 (The detailed method is explained in sect. 2). The correlation coefficients using DACCER ranking are shown in Table 5. The results show that DACCER ranking method does not have good correlation with closeness rank as compared to the proposed methods. The DACCER method also has one more disadvantage that to compute DACCER rank of one node we need to compute the DACCER/approximated closeness value of each node and then compare these values to get the rank of the interested node. So, the overall complexity of this method is high as compared to the proposed methods.

8 Conclusion

In the present work, we studied the behavior of closeness ranking and observed that the reverse rank of the nodes follows a sigmoid pattern as a function of the closeness centrality of the nodes. We further analyzed the correlation of closeness centralities and the nodes’ degrees and the behavior of the closeness centrality of the nodes as a function of the distance from the central node of the network.

We used these observed characteristics of closeness centrality to propose a heuristic method to estimate the closeness rank of a node. The complexity of the proposed method is O(m), which is a great improvement over the classical ranking method which takes \(O(n \cdot m)\) time. The proposed method is further improved using uniformly random node samples, where the closeness centrality values of k sampled nodes are used to estimate the parameter \((c_{mid})\) of the sigmoid curve. The complexity of the improved method is \(O(k \cdot m) \approx O(m)\) as (\(k<< n\)). The accuracy of the proposed methods is verified using absolute and weighted error functions. We further study the correlation of the actual and estimated rank using Kendall’s Tau and Spearman correlation coefficients. Our results show that the proposed methods can be efficiently used to estimate the closeness rank of a node.

9 Future directions

In the proposed methods, we estimate the slope of the sigmoid curve as the average of the slopes observed in real-world networks. The slope of the curve denotes how sharply the closeness centrality increases for all middle layered nodes from periphery to central region. The slope depends on the density of the network and how the density changes from periphery to the center. We briefly studied the correlation of the slope of the sigmoid curve (p) with the density of the network. Figure 9 shows the slope versus density for BA networks (Barabási and Albert 1999) having 40, 000 nodes. We observe that the slope increases with the density, reaches its maximum value, and then it further decreases with the increase in the density. This correlation can be used to propose an estimator for p value.

Fig. 9
figure 9

Slope vs. density on BA networks

Full size image

The proposed method can be modified to apply on real-world dynamic networks as they do not need to store the network and give good performance for the highly ranked nodes which are generally of interest. The APIs of online networks can be used to run the BFT and compute the closeness centrality of the interested node. To further compute other parameters, we need to find out the highest degree node and periphery nodes; one can propose efficient random walk based methods to find out these nodes without gathering the entire network and compute the required parameters. Once all parameters are computed, the closeness rank of the node can be computed using the proposed formula.

The proposed methods can also be improved by estimating the closeness centrality of a node using its local information without having the entire network. These methods are desired due to the fast growth of the networks, as the time complexity of the proposed methods would improve. The methods introduced in this work could also be extended to other types of networks such as weighted networks, directed networks, and multilayered networks.

The rank estimation of a node based on other centrality measures such as betweenness centrality, coreness, and PageRank still remains an open problem.