Large-Eddy Simulations of Flow in the FDA Benchmark Nozzle Geometry to Predict Hemolysis

Abstract

Purpose

Modeling of hemolysis due to fluid stresses faces significant methodological challenges, particularly in geometries with turbulence or complex flow patterns. It is currently unclear how existing phenomenological blood-damage models based on laminar viscous stresses can be implemented into turbulent computational fluid dynamics simulations. The aim of this work is to generalize the existing laminar models to turbulent flows based on first principles, and validate this generalization with existing experimental data.

Methods

A novel analytical and numerical framework for the simulation of flow-induced hemolysis based on the intermittency-corrected turbulent viscous shear stress (ICTVSS) is introduced. The proposed large-eddy simulation framework is able to seamlessly transition from laminar to turbulent conditions in a single flow domain by linking laminar shear stresses to dissipation of mechanical energy, accounting for intermittency in turbulent dissipation, and relying on existing power-law hemolysis models. Simulations are run to reproduce previously published hemolysis data with bovine blood in a benchmark geometry. Two sets of experimental data are relied upon to tune power-law parameters and justify that tuning. The first presents hemolysis measurements in a simple laminar flow, and the second is hemolysis in turbulent flow through the FDA benchmark nozzle. Validation is performed by simulation of blood injected into a turbulent jet of phosphate-buffered saline, with modifications made to account for the local concentration of blood.

Results

Hemolysis predictions are found to be very sensitive to power-law parameters in the turbulent case, though a set of parameters is presented that both matches the turbulent data and is well-justified by the laminar data. The model is shown to be able to predict the general behavior of hemolysis in a second turbulent case. Results suggest that wall shear may play a dominant role in most cases.

Conclusion

The ICTVSS framework of generalizing laminar power-law models to turbulent flows shows promise, but would benefit from further numerical validation and carefully designed experiments.

Introduction

The non-physiological flow patterns introduced by blood pumps are known to lead to significant blood-damage risks, including high incidences of hemolytic39 and thrombotic complications. Predicting these risks in-vitro, however, presents major time and cost commitments and large uncertainties associated with the inherent variability of blood properties between individuals, and differences in experimental protocols between labs.

Computational fluid dynamics (CFD), alternatively, promises quicker data production at a reduced cost and excellent reproducibility when using similar methodologies. However, the challenges associated with using CFD to evaluate blood damage are perhaps even greater than those of in-vitro experiments. There is a lack of consensus generally on appropriate numerical methodologies, evidenced by the wide range of fluid solvers and resulting spread in flow predictions produced in the inter-laboratory nozzle study from the U.S. Food and Drug Administration (FDA).43 The most commonly discussed method of predicting hemolysis via fluid stresses, the power-law model of Giersiepen et al.,17 is inherently phenomenological, and implementing it into a CFD solver with heterogeneous stresses is difficult due to its power-law dependence on time.14,16 Further, there is a lack of agreement on the proper method to evaluate the characteristic stress experienced by platelets and red blood cells (RBCs), or whether the reduction of the full nine-component stress tensor to a single scalar value is appropriate at all in predicting blood damage.13

A particularly vexing issue in the hemolysis research is modeling the role of turbulence. The experimental data suggest that turbulence may lead to hemolysis,24,41 though interpreting this in the context of the power law models is challenging. A common approach to incorporate turbulence is to perform Reynolds-average Navier-Stokes (RANS) simulations, and add the Reynolds shear stresses (RSS) to the mean viscous stresses to obtain a single scalar stress. However, many authors have found this questionable,18,23,26,36,38 as nearly all power-law models are fitted to experiments with constant laminar stresses. Further, Reynolds stresses are not stresses per se, but fluxes of mean momentum dominated by chaotic motions on a scale much larger than that of an RBC. Indeed, the experimental evidence shows that the necessary RSS to initiate hemolysis is an order of magnitude higher than for viscous stresses,2,15,24 suggesting that Reynolds stresses play a nuanced role in hemolysis.

This has led to an influx of novel methods of hemolysis prediction in turbulence. Goubergrits et al.18 proposed a method of adding instantaneous random noise to each timestep in a RANS simulation, and integrating viscous stresses along these stochastic streamlines. They found that simply scaling the RSS down by a factor of 20 produced similar results to the stochastic streamline method. Marom and Bluestein30 used a similar stochastic streamline method, and concluded that the details of such a method can impact the results significantly. Many authors have proposed new classes of hemolysis models based on dissipation. A correlation between dissipation and hemolysis was recognized early on by Bluestein and Mockros,4 and a theoretical link between the dissipation and the properties of the instantaneous shear stresses experienced by RBCs and platelets was presented by Morshed et al.33 Hund et al.23 further showed that there is a simple relation between viscous stresses and dissipation, and Wu et al.44 also applied a dissipation-based model to the FDA nozzle currently investigated.

With a dissipation-based model, hemolysis could in principle by predicted directly in a direct numerical simulation (DNS). However, the computational cost of DNS is often prohibitive, and it is therefore attractive to approximate the DNS results with a less computationally expensive approach. The primary goal of the model presented herein is to further justify the use of dissipation in hemolysis modeling, and introduce a closure approximation for use in LES that approximates the results of a DNS. A representative scalar stress based on dissipation that accounts for intermittency is proposed, the intermittency-corrected turbulent viscous shear stress (ICTVSS). The model is fitted using one set of laminar data and one set of turbulent data, then validated on a third turbulent dataset. The relative importance of turbulence and wall shear is discussed.

Model Formulation

The ICTVSS model presented here is based on the power-law formulation of hemolysis from Giersiepen et al.17 This model takes the form represented in Eq. 1,

$$D = A\tau ^{\alpha } t^{\beta } ,$$

(1)

where D is some measure of hemolysis, $\tau$ is a scalar representation of shear stress, t is the amount of time that RBCs have been exposed to that shear stress, and A, $\alpha$, and $\beta$ are empirical constants. At this juncture, it should be emphasized that the fluid stress is in fact a nine-component symmetric tensor. Many different stress states can therefore be mapped to any given scalar stress, and this spectrum of stress states can have significantly different impacts on an RBC.13 The aim of this work is not to resolve this issue.

Linking Scalar Stresses with Dissipation

The constitutive equation (Eq. 2) for the viscous stress in an incompressible Newtonian fluid is given as

$$\sigma _{ij}=2\mu s_{ij}=\mu \left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) ,$$

(2)

where $s_{ij}=\tfrac{1}{2}(\tfrac{\partial u_i}{\partial x_j}+\tfrac{\partial u_j}{\partial x_i})$ is the rate of strain tensor, $u_i$ is the i-th component of the velocity, and $\mu$ is the dynamic viscosity. Eq. 2 relates the full nine-component stress tensor to the state of the velocity field. By considering the conservation of total (thermal and kinetic) energy in a fluid parcel, it can be shown that when a velocity gradient acts against this stress, a one-way conversion of kinetic to thermal energy takes place. The rate at which this conversion takes place, $\varepsilon$, is called the dissipation, and is mathematically defined as in Eq. 3. Further background on the derivation and mathematics of dissipation can be found in Pope37, p. 123.

$$\varepsilon =\sigma _{ij}\frac{\partial u_i}{\partial x_j}$$

(3)

In Eq. 3, the rate of strain tensor $\frac{\partial u_i}{\partial x_j}$ may be decomposed into its symmetric ($s_{ij}$) and antisymmetric ($w_{ij}=\tfrac{1}{2}(\tfrac{\partial u_i}{\partial x_j}-\tfrac{\partial u_j}{\partial x_i})$) parts so that $\varepsilon =\sigma _{ij}(s_{ij}+w_{ij})$. Because the inner product of a symmetric tensor ($\sigma _{ij}$) with an antisymmetric tensor ($w_{ij}$) is zero, the dissipation can be rewritten as given in Eq. 4. Because $s_{ij}s_{ij}$ in Eq. 4 is the sum of squared real components, dissipation is always positive. Therefore, any hemolysis model using dissipation will result in strictly positive hemolysis.

$$\varepsilon =2\mu s_{ij}s_{ij}.$$

(4)

The von Mises scalar stress, defined in Eq. 5, comes from solid mechanics where it is used to quantify yielding in ductile materials. Its use in hemolysis modeling stems from Bludszuweit,3 and it is commonly used as the characteristic scalar stress in the power-law model for use in CFD.

$$\begin{aligned} \sigma _{vM}^2&=\frac{1}{2}[(\sigma _{11}-\sigma _{22})^2+(\sigma _{22}-\sigma _{33})^2\nonumber \\&\quad +(\sigma _{33}-\sigma _{11})^2+6(\sigma _{12}^2+\sigma _{23}^2+\sigma _{31}^2)] \end{aligned}$$

(5)

The von Mises stress may also be shown to be related to the second invariant $\text {J}^d_2=\tfrac{1}{2}\sigma ^d_{ij}\sigma ^d_{ij}$ of the stress deviator tensor given in Eq. 6,

$$\sigma ^d_{ij}=\sigma _{ij}-\tfrac{1}{3}\sigma _{kk}\delta _{ij},$$

(6)

as $\sigma _{vM}=\sqrt{3\text {J}^d_2}$. However, for an incompressible fluid, $\sigma _{kk}=2\mu \frac{\partial u_k}{\partial x_k}=0$, so that $\sigma ^d_{ij}=\sigma _{ij}$, and the invariants of the two tensors are identical (Eq. 7).

$$\begin{aligned} J^d_2=J_2=\tfrac{1}{2}\sigma _{ij}\sigma _{ij} \end{aligned}$$

(7)

At this point, the similarity between Eqs. 4 and 7 is clear, and it is trivial to show the equivalence between the von Mises stress and the dissipation (Eq. 8)

$$\begin{aligned} \sigma _{vM}=\sqrt{3J_2}=\sqrt{3\mu \varepsilon }. \end{aligned}$$

(8)

However, as noted by Faghih and Sharp,12 this does not reduce to the appropriate value in pure laminar shear flow, to which nearly all power-law models are fit. Therefore, the appropriate scalar stress $\tau$ for a fully three-dimensional flow would be different from Eq. 8 by a factor of $3^{1/2}$ (Eq. 9).

$$\begin{aligned} \tau =\sigma _{vM}/\sqrt{3}=\sqrt{\mu \varepsilon }. \end{aligned}$$

(9)

Dissipation occurs in all viscous flows, whether they are laminar or turbulent. Therefore, Eq. 9 is true regardless of the flow regime, and provides the basis for a universal turbulent/laminar hemolysis model, directly applying the empirically derived constants A, $\alpha$, and $\beta$, which are found using laminar data, to a turbulent flow. Further theoretical developments on using this model are outlined in the following subsections. A similar link between dissipation and viscous stresses was pointed out by Morshed et al.,33 Jones,26 and Wu et al.44

Hemolysis in the Turbulent Cascade

Turbulence is a cascade of motions, whereby large eddies are stretched and distorted, and impart their energy into smaller eddies in a fractal way. This cascade ends when the inertia passed down to the smallest eddies is unable to overcome viscous forces, and the energy that has been passed down the cascade is dissipated into heat. The characteristic scale at which dissipation happens is the Kolmogorov28 length scale $\eta =(\tfrac{\nu ^3}{\langle \varepsilon \rangle })^{1/4}\sim LRe^{-3/4}$, where L is a length scale characteristic of the largest eddies, $\nu$ is the kinematic viscosity, $\langle .\rangle$ indicates temporal averaging, and $Re=UL/\nu$ is the Reynolds number, where U is a characteristic velocity scale.

For a blood pump with a 12 $\text {mm}$ outlet pumping human blood at five liters per minute,9 the Reynolds number is approximately 3000. A typical Kolmogorov length scale in an implanted blood pump is then approximately 30 $\upmu$m, around four times the size of an RBC. The simplifying assumption is then made that RBCs are much smaller than the smallest turbulent scales, and the stress that they experience is characterized by these small scales.

However, it should be made clear that the Kolmogorov scale is based on the time-averaged dissipation. Dissipation is notoriously intermittent in turbulent flows, so that it is dominated actually by sub-Kolmogorov scales, and this assumption may approach the borderline of its applicability.33 Furthermore, as pointed out by Antiga and Steinman,1 there is reason to doubt that the classical small-scale characteristics of turbulence are present in blood at all, where RBCs account for around 40-45% of the volume fraction. It is therefore unlikely that turbulence can cascade in the classical sense down to the size of several RBCs.

Scalar Stress Formulation Across Reynolds Numbers in Large-Eddy Simulations

The simulations are performed using an LES approach, whereby the filtered (denoted by $\tilde{.}$) momentum (Eq. 10) and continuity (Eq. 11) equations are solved numerically.

$$\frac{\partial {\tilde{u}}}{\partial t}+{\tilde{u}}_j\frac{\partial {\tilde{u}}_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial {\tilde{p}}}{\partial x_i}+\frac{\partial }{\partial x_j}\left( \nu \left[ \frac{\partial {\tilde{u}}}{\partial x_j}+\frac{\partial {\tilde{u}}}{\partial x_j}\right] \right) +\frac{1}{\rho }\frac{\partial \tau ^{sgs}_{ij}}{\partial x_j},$$

(10)

$$\frac{\partial {\tilde{u}}_i}{\partial x_i}=0,$$

(11)

The reader is referred to Lesieur and Metais29 for the derivation of Eq. 10. In Eq. 10, $\rho$ is the density and $\nu$ is the kinematic viscosity. Equation 10 also contains the term $\tau _{ij}^{sgs}$, the sub-grid scale (SGS) stress. The SGS stress is analogous to, but not the same as, the Reynolds stress. Whereas the Reynolds stress originates from ensemble averaging being performed on the convective term in the momentum equation, the SGS stress arises from the filtering operation, and represents the impact that SGS turbulent scales have on the filtered velocity.

Similar to the Reynolds stress, $\tau ^{sgs}_{ij}$ requires a closure model. For an introductory discussion on different classes of closure models and their merits, the reader is referred to Meneveau and Katz.31 The closure model used here is the wall-adapting local eddy-viscosity (WALE) model of Nicoud and Ducros.35 The WALE model, like many SGS models, is a so-called eddy viscosity model, which models the SGS stress analogously to the viscous stress (Eq. 12),

$$\tau _{{ij}}^{{sgs}} - \tau _{{kk}}^{{sgs}} \delta _{{ij}} = 2\rho \nu _{t} \tilde{s}_{{ij}} = \rho \nu _{t} \left( {\frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \tilde{u}_{j} }}{{\partial x_{i} }}} \right),$$

(12)

where ${\tilde{s}}_{ij}$ is the filtered rate of strain tensor, and $\nu _t$ is the eddy viscosity. The WALE model is based on ${\tilde{s}}^d_{ij}$, the traceless symmetric part of the square of the velocity gradient tensor (Eq. 13),

$${\tilde{s}}^d_{ij}=\frac{1}{2}({\tilde{s}}_{ij}^2+{\tilde{s}}_{ji}^2)-\frac{1}{3}\delta _{ij}{\tilde{s}}^2_{kk},$$

(13)

where ${\tilde{s}}_{ij}^2={\tilde{s}}_{ik}{\tilde{s}}_{kj}$. The eddy viscosity $\nu _t$ is then modeled as,

$$\nu _t=(C_w{\Delta })^2\frac{\left( {\tilde{s}}_{ij}^d{\tilde{s}}_{ij}^d\right) ^{3/2}}{\left( {\tilde{s}}_{ij}{\tilde{s}}_{ij}\right) ^{5/2}+\left( {\tilde{s}}_{ij}^d{\tilde{s}}_{ij}^d\right) ^{5/4}}.$$

(14)

In Eq. 14, $C_w\simeq 0.55-0.6$ is a fitted constant, and ${\Delta }$ is the length scale of a grid cell, typically taken as the cube root of its volume. The WALE model is chosen because it correctly reduces the eddy viscosity to zero in laminar regions of the flow, particularly near walls, and has been shown to produce good results in transitionally turbulent flows. These properties are relevant to flows through blood-contacting medical devices, which may span from laminar to turbulent, or even have intermittent turbulence due to pulsatility.

By considering the energy balance of the filtered velocity field, it can be shown that energy is passed down from the resolved scales to the subgrid scales in a way that is analogous to viscous dissipation. The rate at which this happens is given in Eq. 15. While, in reality, the energy that is passed down in this manner will eventually be dissipated, that dissipation will not occur in the same location in general. However, the WALE model does not model SGS dissipation explicitly, so the simplifying assumption is made that energy passed down to the SGS turbulence is instantly dissipated in the same computational cell that that passage occurs in.

$${\Pi }=\tau ^{sgs}_{ij}\frac{\partial {\tilde{u}}_i}{\partial x_j}$$

(15)

Then, the overall dissipation in the computations has a component from both the viscous ($\varepsilon _v$) and SGS stresses, so that the scalar stress might be as given in Eq. 16.

$$\tau =\sqrt{\mu (\varepsilon _v+{\Pi })}$$

(16)

There is, however, an important issue remaining. Namely, ${\Pi }$ is only the average rate of dissipation in the computational cell. At the smallest scales, dissipation can become extremely intermittent depending on the Reynolds number of the flow, and can be dominated by sparse regions of high viscous stresses. This intermittency creates an issue with directly applying the power law. Namely, SGS hemolysis should depend on the filtered value of the SGS viscous stresses raised to the power $\alpha$, which is not the same as the filtered SGS stress (the only information available) raised to $\alpha$. That is, $\widetilde{\tau ^\alpha }\ne {\tilde{\tau }}^\alpha$.

The nature of intermittency in turbulent dissipation has enjoyed decades of theoretical research going back to the work of Kolmogorov.28 For its simplicity of application, the multifractal model of Nelkin34 is used here to correct the SGS hemolysis. The crux of the multifractal model is given in Eq. 17. The multifractal model is strictly true only for temporal averaging. However, it is applied here to filtered quantities, with the argument that intermittency is primarily a characteristic of the very small scales. This assumption is therefore asymptotically true as the ratio of the grid spacing to the Kolmogorov scale becomes large. An in-depth discussion of approximating small-scale velocity derivatives in LES is given by Johnson and Meneveau.25 Such scaling has been shown using filtering of DNS data of isotropic turbulence by Cerutti and Meneveau,7 as well as experimental data by Meneveau and O’Neil.32 Multifractal subgrid modeling has have been used to model subgrid mixing of passive scalars5,27 as well as modeling SGS stresses themselves.6

$$\frac{\langle \tau ^p\rangle }{\langle \tau ^2\rangle ^{p/2}}\sim \text {Re}_\lambda ^{x(p)}$$

(17)

In Eq. 17, $\text {Re}_\lambda =\frac{k^{1/2}\lambda }{\nu }$ is the Taylor-microscale Reynolds number, where $\lambda$ is the Taylor microscale, and k is the turbulent kinetic energy; x(p), the exponent to which $\text {Re}_\lambda$ is raised, is a function of the exponent p. As suggested by Nelkin,34 the small-exponent form as given in Eq. 18 is used here. The approximation is also made that $\text {Re}_\lambda =\sqrt{15\text {Re}}$, 10 where $\text {Re}$ is the Reynolds number of the overall flow. In the case of the FDA nozzle, where the geometry is relatively simple and the Reynolds number is easily defined, this relation is reasonable. In more complicated geometries such as a rotary blood pump, such a simple relation may not be warranted, and the Taylor microscale may need to be predicted in preliminary simulations.

$$\begin{aligned} x(p)\approx \frac{3}{64}p(p-2) \end{aligned}$$

(18)

Therefore, the ICTVSS raised to the power $\alpha$, accounting for both viscous and SGS stresses, is given in Eq. 19. Figure 1 shows the functional form of the intermittency correction across Reynolds numbers at several values of $\alpha$.

$$\begin{aligned} \widetilde{\tau ^\alpha }\approx (\mu \varepsilon _v)^{\alpha /2}+\text {Re}_\lambda ^{x(\alpha )}(\mu {\Pi })^{\alpha /2} \end{aligned}$$

(19)

Figure 1

Intermittency correction across Reynolds number for several $\alpha$ values.

Since the WALE SGS model gives a vanishing eddy viscosity in laminar flow, the second term in Eq. 19 will not contribute to hemolysis near the wall or in regions without turbulence and a laminar hemolysis simulation will be recovered.

The present simulations depend on a number of relevant parameters, which are listed in Table 1.

Table 1 Parameters used in simulations.

Simulations

Simulations are run in OpenFOAM, an open-source library of solvers and utilities for the numerical simulation of continuum mechanics problems, commonly used for CFD. Hemolysis is modeled in a custom solver based on the included pisoFoam solver, which models unsteady, transient problems and can incorporate a wide variety of turbulence models.

Hemolysis predictions are made for the FDA benchmark nozzle43 to match the experimental hemolysis data reported by Herbertson et al.22 for bovine blood. Herbertson et al.22 reported a multilaboratory study quantifying hemolysis in an in vitro flow loop. Protocols and several experimental parameters including hematocrit, temperature, blood volume, flow rate, and pressure were kept consistent between the labs. The same assays were used in all three labs to quantify hemolysis. Three test conditions are reported, with different flow rates and orientations of the nozzle model. The first is the sudden contraction orientation at 5 L/min. The second is the gradual cone orientation at 6 L/min, and the third is the sudden contraction at 6 L/min. Hemolysis values for the three cases were measured as 0.292 ± 0.249, 0.021 ± 0.128, and 1.239 ± 0.667 respectively.

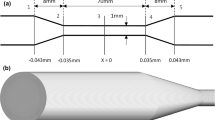
The simulated geometry is depicted in Fig. 2. Simulations are run to match the three cases reported in Herbertson et al.22 Flow from left to right is referred to as the sudden expansion (SE) orientation, while flow from right to left is referred to as the conical diffuser (CD) orientation. Flow is simulated at 6 L/min in the sudden expansion orientation (case SE6), and at both 5 and 6 L/min in the conical diffuser orientation (cases CD5 and CD6). Case CD5 has a throat Reynolds number of 6552, while cases SE6 and CD6 have a throat Reynolds number of 7863. The fluid properties reported by Herbertson et al.22 for bovine blood are used (μ = 4.21 cP, ρ = 1.04 g/mL). The grid consists of approximately 6.3 million computational cells, with near-wall refinement performed to ensure $y^+\le 2$ to properly resolve the viscous sublayer at all points near the wall. Grid spacing away from the wall was 250 μm, or approximately an order of magnitude larger than the Kolmogorov scale. The grid was generated with OpenFOAM’s snappyHexMesh utility, using the suggested grid quality constraints on properties such as grid-cell non-orthogonality, the presence of concave corners, and cell skewness. Approximately 90% of grid cells are hexahedral, 4% are prisms, and 6% are polyhedra with between 4 and 15 faces. A parabolic inlet boundary condition is used in all three simulations. In order to reduce the impact of the inlet and outlet boundary conditions, the geometry is extended 20 cm to the left of the start of the cone, and 20 cm to the right of the sudden expansion. An outlet pressure of 0 is prescribed at the outlets of all simulations, with a zero-gradient inlet pressure boundary condition. Simulations are initiated with a parabolic velocity profile throughout the domain, and are allowed to run for 0.2 seconds to achieve a fully developed turbulent flow field before hemolysis modeling begins.

Figure 2

Geometry of FDA benchmark nozzle. Scale is given in meters.

Because of the non-linear time dependence of the power-law formulation, implementing it along a pathline can lead to non-physical results such as a decrease in hemolysis in response to a reduction over time in stress levels.19 This has been addressed by Grigioni et al.20 using a time-linear dosage. A similar approach was proposed by Garon and Farinas,16 and is used herein, so that the linearized damage $\text {DI}=A^{1/\beta }\tau ^{\alpha /\beta }t$ follows the evolution equation given in Eq. 20. Hemolysis modeling is performed for 0.5 seconds after the flow is allowed to develop, and reported values are obtained via spatial averaging at the outlet. To match the MIH (modified index of hemolysis) values reported in Herbertson et al.,22 values of MIH = D × 10⁶ are reported, where $D=DI^\beta$.

$$\frac{\partial DI}{\partial t}+{\tilde{u}}_i\frac{\partial DI}{\partial x_i}=A^{1/\beta }\tau ^{\alpha /\beta }$$

(20)

To simulate the damage accumulation in bovine blood, the empirical constants $A=9.772\times 10^{-7}$, $\alpha =1.4445$, and $\beta =0.2076$ reported by Ding et al.11 are used initially, though the LES results will be used in conjunction with the data from Herbertson et al.22 to produce a new set of parameters. The goal for this new set of parameters is to analytically match the results of Ding et al.,11 and numerically match the results of Herbertson et al.22 as closely as possible.

Validation

The FDA has not provided experimental flow validation data for Reynolds numbers greater than 6500. Therefore, validation cannot be provided for the 6 L/min cases, which have a throat Reynolds number of 7863. Validation is presented here for case CD5. Several different flow statistics are made available on the FDA’s website as detailed by Stewart et al.43 In order to validate the fluid dynamic portion of the solver used, comparisons are presented between the mean centerline axial velocity (Fig. 3), mean wall pressure (Fig. 4), Reynolds stress magnitude (Fig. 5), and wall shear stress (Fig. 6). Additionally, mass conservation errors and flow asymmetry as defined in Stewart et al.42 are shown in Fig. 7.

Figure 3

Simulated vs. experimental mean centerline axial velocity u normalized by cross-sectional average velocity U for the case CD5.

Figure 4

Simulated vs. experimental mean wall pressure P normalized by average velocity and density for the case CD5.

Figure 5

Simulated vs. experimental Reynolds stress normalized by the square of the mean inlet velocity for the case CD5. Results scaled so that 0.2 mm corresponds to a normalized Reynolds stress of 1.

Figure 6

Simulated vs. experimental mean wall shear stress $\tau _w$ normalized by viscosity, average velocity, and the larger diameter D in the nozzle geometry for the case CD5.

Figure 7

Mass conservation error and flow asymmetry metric.

The mean centerline axial velocity, as depicted in Fig. 3, is close to being within the error bars throughout the domain, except in the downstream portions of the throat. The assumption of a laminar, parabolic inlet velocity slightly overestimated the velocity upstream of the throat, similar to the shear-stress transport (SST) models used in some of the simulations presented in Stewart et al.42 In contrast to the SST models, however, the velocity downstream of the conical diffuser is generally within experimental error. Stewart et al.42 contrast SST models with $k-\epsilon$ models, which broadly matched the diffuser flow well, but modestly under-predicted upstream velocity.

The wall pressure as seen in Fig. 4 is within the experimental uncertainty bounds at nearly all locations. Most CFD results presented in Stewart et al.42 agree well with the wall pressure downstream of the throat, but there is more spread upstream. This spread is perhaps due to the wide disagreement in wall shear stresses among simulations, especially at the throat. Wall shear from the LES is within experimental uncertainty except at the sudden contraction. As discussed in Stewart et al.,42 the large discrepancy at the throat may be due to the resolution of the PIV experiments. The PIV grid spacing as reported by Hariharan et al.21 ranges from 0.11 to 0.16 mm between the three laboratories that produced PIV data. In contrast, at the inlet to the throat, the LES has a grid thickness of 3 μm, between 36 and 53 times more resolved.

Reynolds stresses are well approximated in the jet. At the contraction, the LES predicts nearly zero Reynolds stress, while there is wide disagreement in values between the experimental data sets. Elsewhere in the throat, the LES lies slightly outside experimental uncertainty, particularly near the walls. Some underprediction is to be expected, as the values reported from the LES include only the resolved-scale stresses, and not subgrid stresses. Although experimental Reynolds stresses are reported on the FDA’s website, there is no discussion of CFD predictions of Reynolds stress in Stewart et al.42

Mass conservation errors in the LES have a maximum of 3.6% immediately downstream of the throat. Between 64 and 68% of simulations analyzed by Stewart et al.42 had mass conservation errors greater than 10%. The minimum asymmetry value was 0.94, where 1.0 indicates a perfectly symmetric velocity profile. There was significant disagreement in both experimental and numerical asymmetry values reported by Stewart et al.,42 with some numerical values less than zero in the diffuser, indicating net backward flow on one side. Experimental values of asymmetry in the diffuser were all greater than 0.5, as were most simulations. Unlike the RANS simulations in Stewart et al.,42 the LES presented depends on temporal averaging for the mean flow, so running the simulations longer may reduce asymmetries.

Grid independence is established for the fluid solver portion by maintaining a near-wall grid spacing of less than two wall units throughout the domain. No further refinement study is performed for the fluid dynamics portion. However, a grid-independence study is presented here for the blood damage index. For all three cases, the simulations suggest that the majority of hemolysis takes place at or near the 90° transition in the throat. The simulations are therefore run on two different grids, with refinement near the corner to ensure that shear stresses are well resolved. In the coarse grid, numerical cells within 0.4 mm of the sharp corner are split in half in all three directions. In the fine grid, numerical cells within 0.4 mm are split in four in all directions, while numerical cells between 0.4 and 0.8 mm of the corner are split in half. The two grids are depicted in Fig. 8. Grid convergence index (GCI) values as defined by Roache40 are reported. GCI values are calculated using Eq. 21, where FS = 3.0 is used as a factor of safety, $\epsilon =(MIH_f-MIH_c)/MIH_f$ is the relative change in MIH between the fine and coarse grid, $r=2$ is the ratio by which the grid spacing is refined between grids, and p=2 is the order of the finite-volume schemes used in OpenFOAM.

$$\text {GCI}=\frac{\text {FS}\epsilon }{r^p-1}$$

(21)

Fig. 8

Coarse (top) and fine (bottom) grid examined for grid independence study

Results

Figure 9

MIH values with final power-law parameters for all three cases solved on the coarse and fine grids.

MIH values with A = 2.7 × 10⁻⁹, α = 2.5, and $\beta =0.264$ (these parameters discussed shortly) for both the coarse and fine grid are shown in Fig. 9. The results of the grid independence study on MIH values indicate fractional uncertainty values as presented in Table 2. Although uncertainty could be further reduced, the reported values are small in comparison to the experimental uncertainty reported by Herbertson et al.,22 and are conservative due to the factor of safety in their calculations. The results of the fine grid are therefore accepted.

Table 2 GCI values of three simulated flow conditions.

Results using the power-law parameters presented in Ding et al.11 show a large discrepancy between simulations and experimental values of MIH. As shown in Fig. 10, hemolysis is under-predicted by about a factor of 50. This large under-prediction is attributed to the sensitivity of the numerical results to changes in the power-law parameters. Changing the value of β to 0.1 results in MIH values approximately 120 times higher than for simulations using β = 0.2076, as shown in Fig. 11.

Figure 10

Experimental vs. simulated MIH values with β = 0.2076.

Figure 11

Experimental vs. simulated MIH values with β = 0.1.

Discussion

Sensitivity of MIH Predictions to Power-Law Parameters

The impact on MIH predictions of relatively small changes to β is an important result in the context of producing reliable hemolysis predictions. As previously mentioned, the majority of the hemolysis was found to occur at the 90° corner of the nozzle geometry, particularly for the conical diffuser cases. In these cases, the exposure to high shear stress happens over a time scale of several microseconds. In this small range of exposure times, a high sensitivity to the parameter β should be expected. However, the experiments of Ding et al.11 occurred only over exposure times ranging from 0.04 to 1.5 s, strictly putting the FDA nozzle experiments outside of the fitted range of not only this set of power-law parameters, but also many others, including those of Giersiepen et al.17 whose parameters are based on experiments occurring on the order of milliseconds. These parameters are therefore untested in the stress and exposure times of the current geometry.

The fitting performed by Ding et al.11 is much less sensitive to changes in α and β than the simulations presented here. Ding et al.11 fitted their power-law parameters to a set of experimental data, and reported a correlation coefficient of 0.7162 between their fitted power law and the experimental data to show goodness of fit. However, over the range of the fitted exposure times, the time dependence does not differ substantially with β, as shown in Fig. 12. The standard deviation between the three functions shown in this figure is approximately 8% of the mean value over this range. With the assumption that the true $\beta$ value were something other than 0.2076, it is possible to find a lower bound on the correlation coefficient that would result between the altered power-law and the data of Ding et al.11 This lower bound, $\rho _{\beta ,exp}$, is given in Eq. 22.

Figure 12

Time dependence of hemolysis predictions over experimental range of Ding et al.11 with varying exponent values.

$$\rho _{\beta ,exp}\ge \cos \left[ \text {acos}(\rho _{0.2076,exp})+\text {acos}(\rho _{0.2076,2})\right]$$

(22)

In Eq. 22, $\rho _{0.2076,exp}$=0.7162 is the correlation coefficient given by Ding et al.,11 and $\rho _{0.2076,2}$ is the correlation coefficient between two power laws–one ($D_{Ding}$) using the parameters of Ding et al.,11 and one ($D_2$) using a different set of parameters. The formula for $\rho _{0.2076,2}$ is given in Eq. 23. The bounds of the integrals in this equation corresponds to the range of exposure times and shear stresses tested in the experiments of Ding et al.11

$$\rho _{0.2076,2}=\frac{\int _{.04}^{1.5}\int _{25}^{350}D_{Ding}D_2{\text{d}}t{\text{d}}\tau }{\left[ \int _{.04}^{1.5}\int _{25}^{350}D_{Ding}{\text{d}}t{\text{d}}\tau \right] ^{1/2}\left[ \int _{.04}^{1.5}\int _{25}^{350}D_2{\text{d}}t{\text{d}}\tau \right] ^{1/2}}$$

(23)

The lower bound of correlation as a function of β is shown in Fig. 13 and clearly shows that changes to β lead to only very minor differences in the goodness of fit between the power law and the data of Ding et al.11

Figure 13

Lower-bound correlation values between hypothetical power law with altered β value and experimental hemolysis values from Ding et al.11

This correlation analysis provides a way to explore changes to the entire set of parameters. Further experimentation was performed on the power-law parameters in an attempt to better match the experimental data of Herbertson et al.22 while maintaining an acceptable lower-bound correlation. Simulations were run by changing α to 2.5. When this change is made, a subsequent change in A is necessary to ensure that the hemolysis predictions maintain the same approximate magnitude in the experimental range of Ding et al.11 The A value that minimized deviations from the original power-law hemolysis results was found to be 2.7 × 10⁻⁹. Then, to match the magnitude of hemolysis predictions from the experimental data of Herbertson et al.,22 a value of β = 0.264 was found to be optimal. The standard deviation between the power law with this set of parameters and the old set is 20% of the mean value in the experimental range of Ding et al.11 The resulting MIH predictions are shown along with the experimental results of Herbertson et al.22 in Fig. 14. With these changed parameters, numerical predictions are within half a standard deviation of the experimental data of Herbertson et al.,22 and the lower-bound correlation between the power law and the experimental data of Ding et al.11 is 0.55.

Figure 14

Experimental vs. simulated MIH values with A = 2.7 × 10⁻⁹, α = 2.5, and β = 0.264.

Further refinement of the parameters could in principle lead to predictions that more closely match Herbertson et al.22 This type of parameter tuning has previously been discussed by Craven et al.,8 whose Kriging framework could be used to more closely match the experimental data. However, due to the large uncertainties in the data from Herbertson et al.,22 reporting optimized parameters with further precision is unwarranted, and won’t be pursued.

To summarize, α can be changed to alter the relative hemolysis predictions between cases, and β can be changed to alter the magnitude of the hemolysis predictions. However, A must be chosen such that deviations from the original power law of Ding et al.11 are minimized. These changes can be justified by placing a lower bound on the correlation coefficient between the new power law and the experimental hemolysis data from Ding et al.11

Applicability of ICTVSS for Hemolysis Predictions

RSS data are presented in Fig. 15 for the CD5 case along with instantaneous values of ICTVSS. Values of the ICTVSS with the previously mentioned tuned parameters are much lower than RSS values in the highly turbulent regions of the simulations (~ 100 Pascals vs. ~ 1000 Pascals).

Figure 15

Reynolds shear stress values in Pascals (top) compared with instantaneous ICTVSS values in Pascals (bottom).

Previously reported RSS thresholds for hemolysis are approximately an order of magnitude higher than for viscous stresses.24 This is consistent with the order of magnitude difference between RSS and ICTVSS, suggesting the ICTVSS may be more appropriate than RSS for hemolysis predictions. Further, using the RSS in a power law suggests that no hemolysis would occur in regions of the flow with zero mean shear. This is a problematic result, since these regions undergo significant instantaneous shear stresses. In contrast, regions of high ICTVSS are predicted throughout the turbulent jet. Ideally, this discrepancy between RSS and instantaneous stress modeling could be investigated further using direct application of the power law in a DNS. However, because the current grid spacing (250 μm) is an order of magnitude larger than the Kolmogorov scale (~ 30 μm), this would increase the computational cost over LES by several orders of magnitude, highlighting the importance of subgrid-scale modeling.

Validation in Turbulent Jet

The results presented in Fig. 14 rely on two sets of data—those of Ding et al.11 and those of Herbertson et al.22 for fitting and justifying a new set of power-law parameters (A = 2.7 × 10⁻⁹, α = 2.5, and β = 0.264). Since both sets of data were used to fit these parameters, it is not clear whether this framework can be used to predict hemolysis in other flow conditions. A large-eddy simulation is therefore presented with the goal of reproducing the results of Jhun et al.24 Jhun et al.24 measured hemolysis in bovine blood in a turbulent jet of varying Reynolds number, with a device similar to that used by Sallam and Hwang.41 In this device, a turbulent jet of phosphate-buffered saline (PBS) was injected by a nozzle with a diameter of 3 mm into a reservoir of PBS. Immediately downstream of the nozzle outlet, a beveled 17 gauge needle injected blood at a flow rate of 54 mL per minute into the jet’s shear layer. The PBS jet was run at Reynolds numbers ranging from 1000 to 117,000.

The injection of blood into PBS adds a modeling complication to the LES. In flow regions with no blood, a damage index is not meaningful as no free hemoglobin can be produced. Therefore, a modification must be made to Eq. 20 that accomplishes two goals. Firstly, production of free hemoglobin must be proportional to the local concentration of total hemoglobin. Secondly, the free hemoglobin must be normalized by local hemoglobin to recover a damage index, accounting for mixing of blood with PBS. This is resolved by adding an additional scalar species, the blood fraction $b_f$ which follows a simple advection equation.

The blood damage index D is defined as the plasma concentration of free hemoglobin fHb normalized by the total hemoglobin concentration Hb as in Eq. 24.24 To make the necessary modifications to Eq. 20, a modified damage index $D{^{\prime }}$ is defined as in Eq. 25.

$$D=\frac{fHb}{Hb}$$

(24)

$$D{^{\prime }}=\frac{fHb}{Hb_{wb}}=\frac{b_ffHb}{Hb}=b_fD=b_fA\tau ^\alpha t^\beta ,$$

(25)

In Eq. 25, $Hb_{wb}$ is the hemoglobin concentration in whole blood. Then, in a way analogous to Eq. 20, $DI{^{\prime }}=D{^{\prime }}^{1/\beta }$ follows the evolution equation given in Eq. 26.

$$\frac{\partial DI{^{\prime }}}{\partial t}+{\tilde{u}}_i\frac{\partial DI{^{\prime }}}{\partial x_i}=A^{1/\beta }b_f^{1/\beta }\tau ^{\alpha /\beta }$$

(26)

Equation 26 has the property that blood damage occurs only in regions with non-zero blood fraction, satisfying the first modeling requirement. Then, the blood damage as given in Eq. 24 is recovered by dividing $D{^{\prime }}=DI{^{\prime }}^{\beta }$ by $b_f$, so that the free hemoglobin is normalized properly by the local hemoglobin concentration. In cases such as the FDA nozzle, where the entire domain is blood ($b_f=1$), this approach reduces to the standard one.

The geometry of Jhun et al.24 is reproduced, including both the nozzle and 17 gauge needle as depicted in Fig. 16. The computational domain extends ten nozzle diameters into the nozzle to allow flow to develop before the jet outlet. The nozzle inlet uses a uniform velocity boundary condition matching the jet velocities reported in Jhun et al.,24 with random fluctuations to initiate turbulence. Not all Reynolds numbers reported in Jhun et al.24 are reproduced here; only Reynolds numbers of 32,000, 60,000, 90,000 and 117,000 are simulated. The computational domain extends similarly into the needle, with a similar velocity boundary condition. The blood fraction $b_f$ uses Dirichlet boundary conditions at the inlets, and is set to 0 at the nozzle, and 1 at the needle. Values of $DI{^{\prime }}$ and $b_f$ are sampled 6.5 nozzle diameters downstream of the nozzle tip, 1.2 nozzle radii from the center toward the needle.24 Simulations are run for 0.05 seconds to avoid startup transients, and results are averaged over another 0.05 seconds. This allows for at least 10 turnover times between the PBS inlet and the sampling location for each simulation. The resulting blood damage index $D=DI{^{\prime }}^{1/\beta }/b_f$ is reported in Fig. 17. Error bars in this figure are GCI values calculated by comparing results from two grids. Both grids used local refinement near the nozzle outlet, especially at the walls of the needle. The coarse grid contained approximately 2.9 million cells, while the fine grid contained around 6.7 million, with a grid-spacing ratio between the two grids of $r=4/3$.

Figure 16

Computational domain used to simulate the experiments of Jhun et al.24

Figure 17

Experimental hemolysis measurements from Jhun et al.24 overlaid with LES results using the proposed framework.

The results depicted in Fig. 17 suggest that the LES approach outlined is capable of at least coarsely matching the experimental trend in hemolysis over this range of Reynolds numbers despite the high sensitivity of results to the power-law parameters.

The Role of the Boundary Layer

Among the four Reynolds numbers in the Sallam and Hwang nozzle, grid convergence index values are as high as 30% and $y^+$ values at the needle wall range from 3 to 10. While further grid refinement is warranted on this basis, grid cells at the wall of the needle already have a grid spacing of approximately 12 μm, straining the assumption that hemolysis occurs at a subgrid scale as red blood cells have diameters on the range of 6–8 μm. Improving grid resolution to the point that $y^+<1$ would require a grid spacing almost an order of magnitude smaller than the diameter of an RBC. This is an issue of the flow itself, and would impact any attempt to use a power-law model in this case regardless of the assumptions made in representing the scalar stress. This issue is also present in the FDA nozzle, where grid refinement requirements necessitated a near-wall grid spacing of 3 μm.

As all cases of the Sallam and Hwang nozzle and both conical diffuser cases in the FDA nozzle experience the large majority of their hemolysis in regions with sharp geometries, it is plausible that turbulence itself has comparatively little impact on hemolysis in these cases. Rather, by increasing Reynolds number, hemolysis is increased simply by the fact that wall shear is increased. The design and experimental results of the two experiments simulated here provide further evidence of this. Despite having similar magnitudes of wall stress (5100 and 7900 Pa respectively) and Reynolds stress (3000 and 1100 Pa respectively), the Re = 60,000 case in the Sallam and Hwang nozzle has reported hemolysis values over 20,000 × higher than the CD5 case of the FDA nozzle (0.7% vs. 0.292 × 10⁻⁴% hemolysis). This is consistent with the hypothesis that wall shear dominates hemolysis in both. The design of the Sallam and Hwang apparatus, where blood is injected into a turbulent jet by a needle, subjects a higher proportion of the blood to wall stresses at the needle than the FDA nozzle, where much of the blood stays in the free-stream region when passing by the contraction.

In contrast, the SE6 FDA nozzle case does experience most of its hemolysis away from the wall in the current simulations, and experiments and simulations agree that hemolysis is much lower despite similar levels of Reynolds stresses in the SE6 and CD6 cases. However, the MIH value of 0.021 ± 0.128 reported by Herbertson et al.22 leave the predictive capability of the ICTVSS framework unclear.

Challenges for Generalized Application

Many challenges remain, and the suitability of the proposed model for general hemolysis predictions is unclear. Given the strong sensitivity of hemolysis predictions to the values of the power-law parameters, it is concerning that there is such disagreement and uncertainty in the literature on their precise values, with Ding et al.11 noting a difference of an order of magnitude between their A values and that of Giersiepen et al.,17 and β values different by nearly a factor of 3. Furthermore, the magnitudes of stress ($O(10^4)$ Pa) and exposure times (microseconds) of the FDA nozzle and Sallam and Hwang nozzle are far outside the range of any set of fitted power-law coefficients. Viscous wall shear layers on the order of microns lead to further questions on whether a continuum hemolysis model can be universally valid. The intent of the proposed ICTVSS model and both experimental nozzles is to investigate the role of turbulence in hemolysis. However, it is possible that the SE6 case is the only one with turbulence playing a dominant role, and the large experimental uncertainty in its hemolysis value leaves the situation unclear.

Conclusions

By tuning the power-law parameters from Ding et al.,11 it was possible to match the hemolysis predictions of Herbertson et al.22 to within half a standard deviation for all three cases considered. Although validation with the experimental data of Jhun et al.24 suggest this model may have generalization potential, there is plausible evidence to suggest that wall shear stresses are in fact the dominant hemolytic process for most of these cases. Further, since wall shear stresses occur at length scales on the order of microns in these cases, it is questionable whether the continuum assumption of a power-law model is always appropriate. Experiments carefully designed to investigate turbulence and strong wall shear in isolation would be valuable.