Uncertainty Quantification and Sensitivity Analysis for Computational FFR Estimation in Stable Coronary Artery Disease

Abstract

Purpose

The main objectives of this study are to validate a reduced-order model for the estimation of the fractional flow reserve (FFR) index based on blood flow simulations that incorporate clinical imaging and patient-specific characteristics, and to assess the uncertainty of FFR predictions with respect to input data on a per patient basis.

Methods

We consider 13 patients with symptoms of stable coronary artery disease for which 24 invasive FFR measurements are available. We perform an extensive sensitivity analysis on the parameters related to the construction of a reduced-order (hybrid 1D–0D) model for FFR predictions. Next we define an optimal setting by comparing reduced-order model predictions with solutions based on the 3D incompressible Navier–Stokes equations. Finally, we characterize prediction uncertainty with respect to input data and identify the most influential inputs by means of sensitivity analysis.

Results

Agreement between FFR computed by the reduced-order model and by the full 3D model was satisfactory, with a bias ($\text{FFR} _{{\text {3D}}}- \text{FFR} _{{\text {1D}}{-}{\text {0D}}}$) of $-\,0.03\,(\pm\, 0.03)$ at the 24 measured locations. Moreover, the uncertainty related to the factor by which peripheral resistance is reduced from baseline to hyperemic conditions proved to be the most influential parameter for FFR predictions, whereas uncertainty in stenosis geometry had greater effect in cases with low FFR.

Conclusion

Model errors related to solving a simplified reduced-order model rather than a full 3D problem were small compared with uncertainty related to input data. Improved measurement of coronary blood flow has the potential to reduce uncertainty in computational FFR predictions significantly.

Introduction

Ischemic heart disease is the leading cause of death globally,51 and its relevance will increase as the global population ages. In this study we consider patients with stable coronary artery disease (CAD) which, in addition to acute myocardial infarction, is the main symptomatic manifestation of CAD. In this context, fractional flow reserve (FFR) has been shown to be a reliable invasive tool to study the functional significance of coronary artery stenoses. In fact FFR is currently the gold standard for diagnosis of hemodynamic significance of coronary stenoses and is calculated as the ratio between cardiac cycle averaged pressures distal ($\bar{P}_{\text {distal}}$) and proximal ($\bar{P}_{\text {proximal}}$) to a stenosis, namely

$$\text{FFR} = \frac{\bar{P}_{\text {distal}}}{\bar{P}_{\text {proximal}}}.$$

(1)

FFR is acquired invasively by simultaneous measurement of both pressures during drug induced hyperaemia (maximum coronary flow). $\bar{P}_{\text {proximal}}$ is measured by a guiding catheter while $\bar{P}_{\text {distal}}$ is obtained with a sensor-tipped pressure wire. FFR-guided revascularization has improved event-free survival and lowered healthcare costs in randomized studies.7,33,48 Even though major clinical guidelines recommend the use of FFR, it is measured in less than 1/3 of interventions according to a study performed in the USA.15 The primary reasons reported were lack of time, unavailability of trained interventionalists and the relatively high cost of the procedure. Over the last decade many attempts have been made to predict FFR non-invasively using computational fluid dynamics and mathematical models.6 The ultimate goal of such efforts has been to provide the medical community with a readily available, cheap and non-invasive quantification of FFR.

Seeking clinical applicability, many proposed methods for non-invasive FFR prediction rely on simplified versions of the original physical problem, i.e. simplifications to the original problem are made in order to reduce computational cost and to allow for a fast calculation of FFR, for example.19,34 However, in such studies, no information on the errors made by using simplified models are provided. Two notable exceptions are found in Refs. 2 and 3, where results obtained using reduced, one-dimensional (${\text {1D}}$) blood flow models are validated by comparison to results obtained using three-dimensional (${\text {3D}}$) transient models for a synthetically generated population and for a real patient population, respectively. However, in both cases the impact of modelling assumptions chosen to simplify the problem is either only partially explored or completely ignored. We perform an extensive evaluation of the impact of model reduction choices on FFR predictions by using uncertainty quantification and sensitivity analysis (UQ&SA) tools. These tools are extremely useful in addressing such questions, as UQ&SA provide insight into which elements of the simplified model are most influential on FFR prediction and are thus ideal candidates for optimization.

A few previous studies have investigated the sensitivity of FFR predictions to various sources of uncertainty in patient-specific models of coronary flow,29,40 while others have analyzed generic models of coronary blood flow and stenoses as general investigations into the uncertainty of model predicted FFR.9,47 Sankaran et al.40 and Morris et al.29 both investigated the effects of uncertainty in computational prediction of FFR. Sankaran et al. accounted for uncertainties in lesion geometry, peripheral resistance and blood viscosity, while Morris et al. considered uncertainty about parameters for a lumped stenosis model, proximal pressure, and resistance in the coronary microvasculature.

This study extends the above mentioned previous works by considering all sources of uncertainty studied in previous works and by additionally including uncertainty in the percentage of flow to a specific coronary branch. Furthermore, by performing such a study on a population of patient-specific cases, we provide further insight into the role played by different parameters for different ranges of FFR, with particular attention to intermediate stenoses with FFR values between 0.7 and 0.9, and show how the various sources of uncertainty may impact individual cases differently.

The rest of this paper is structured as follows. In the “Materials and Methods” section we introduce a predictive model of FFR based on a reduced-order, hybrid ${\text {1D}},$ zero-dimensional (${\text {0D}}$) blood flow model. Additionally we describe the UQ&SA framework in the “Uncertainty Quantification and Sensitivity Analysis” section, with which we perform two different analyses. The first is performed as a step in the development and validation of the reduced-order model, and the second studies the effect of input parameters on FFR predictions. Next, in the “Results” section we present results for the optimal reduced-order model setup, as well as for the UQ&SA analysis performed on FFR predictions. Finally, in the “Discussion” section we discuss our findings as well as considerations on further steps to be taken in order to increase the accuracy and reduce the uncertainty in model-based FFR prediction.

Materials and Methods

Study Population

We consider a population of 13 patients that underwent invasive angiography and FFR measurement(s) after clinical and coronary computed tomography angiography (CCTA) examinations indicated stable CAD. From these patients a total of 24 FFR measurements were collected, i.e. some patients had more than one suspected stenosis. The FFR measurements had a mean of 0.77 and a standard deviation of 0.17, with a positive FFR prevalence of 41.67% for a cutoff value of $\text{FFR} <0.8.$ The patients were recruited as part of an ongoing clinical trial at St. Olavs Hospital, Trondheim, Norway.4 See Table 7 for a summary of population characteristics and Table 12 for all available data for each FFR measurement.

Recruitment

The study subjects included in the analysis had undergone CCTA due to chest pain and suspicion of stable CAD. Patients were enrolled with the findings of at least one coronary stenosis at CCTA examination and being further referred for invasive coronary angiography (ICA) with invasive FFR measurements.

Exclusion criteria included unstable CAD, previous percutaneous coronary intervention or bypass surgery, renal insufficiency (estimated glomerular filtration rate $<30$), obesity ($\text{BMI} > 40$), non diagnostic quality of the CCTA due to motion artifacts or known allergy to contrast agent or contraindications to adenosine.

Data Acquisition

Medical Data Acquisition

CCTA was performed using two CT scanners with $2 \times 128$ detector rows (Siemens dual source Definition Flash) using a standardized protocol.14

Echocardiographic imaging was performed using a GE Vivid E95 scanner (GE Vingmed Ultrasound, Horten, Norway). Cardiac output (CO) was calculated based on cross-sectional area of left ventricle outflow tract measured immediately proximal to the points of insertion of the aortic leaflets and velocity time integral derived from PW Doppler.

FFR was measured using Verrata Plus (Philips Volcano, San Diego, USA) pressure wires according to standard practice. Intra-coronary nitroglycerin (0.2 mg) was given to all patients before advancing the pressure wire into the coronary arteries and hyperemia was induced by continuous intravenous infusion of adenosine at a rate of at least $140 \,\mu {\text {g}}/{\text {kg}}/{\text {min}}.$ Pressure was measured over several cardiac cycles and FFR measurements were taken during the nadir (lowest observed value) of the $\bar{P}_{\text {distal}}/\bar{P}_{\text {proximal}}$ ratio. After measurement the interventional cardiologist removed the pressure wire back to the equalization point at the tip of the guiding catheter, to ensure that there was no drift.

Standard non-invasive diastolic/systolic pressure measurements ($P_{\text {meas}}$) were performed on both arms as part of clinical routine before ICA using an automatic, digital blood pressure device, Welch Allyn ProBP 3400.

Coronary Vessel Segmentation and Volume Meshing

Segmentation of vessels was performed using the open-source software ITK-SNAP,54 which provides a user-friendly interface for a semi-automatic active contour evolution segmentation approach. The output of ITK-SNAP is a labeled voxel volume identifying segmented vessels and a surface mesh of the segmented volume (in VTK format). Surface mesh processing, addition of flow extensions and meshing were performed using the open-source library Vascular Modeling ToolKit (VMTK).1,46 The 3D volume meshes form the basis for both the reference 3D model and the reduced-order model. For the latter, additional processing is necessary as described in the “From a 3D Domain to a 1D Network” section. For 3D simulations, the meshing refinement level was determined by a meshing algorithm parameter called edge-length factor $l_{\text {f}},$ which was set to $l_{\text {f}}=0.21$ for all simulations. A mesh independence study showed that such discretization provides mesh independent FFR predictions for a set of four patient-specific geometries.

Reduced-Order Model

In this section we present a steady state reduced-order (1D–0D) model for FFR prediction that incorporates clinical imaging and patient-specific characteristics.

Mathematical Model

1D blood flow in steady state conditions in terms of pressure and flow (P,  Q) is modeled as

$$\frac{{\partial }Q}{{\partial } x} = 0,$$

(2a)

$$\frac{\partial }{\partial x} \left( \frac{Q^{2}}{A}\right) = -\frac{A}{ \rho }\frac{{\partial }P}{{\partial } x} + \frac{f}{ \rho },$$

(2b)

where $f=-2(\zeta + 2 )\mu \pi U$ is the frictional term, $\rho =1050\,{\text {kg}}/{\text {m}}^{3}$ is the density, $\mu =0.0035$ is the viscosity of blood and $U=Q/A$ is the cross-sectional averaged velocity. The cross-sectional area A is assumed constant and equal to the area obtained from the segmentation of medical images. The velocity profile is prescribed by

$$u(x,\xi ,t) = U(x,t) \frac{\zeta + 2}{\zeta } \left[ 1 - \left( \frac{\xi }{r} \right) ^{\zeta } \right] ,$$

(3)

where r(x, t) is the lumen radius, $\xi$ is the radial coordinate and $\zeta$ is the polynomial order.

At arterial connections, conservation of mass and a coupling equation for pressure are enforced, i.e.

$$\sum _{i=1}^{N} Q_{i}=0,$$

(4a)

$$P_{1} + \lambda \frac{\rho }{2}U_{1}^{2} = P_{i}+ \lambda \frac{\rho }{2}U_{i}^{2} + \Updelta P_{i} \quad i=2,\ldots ,N,$$

(4b)

where N is the number of vessels in the connection, $\Updelta P$ is an additional pressure loss and $\lambda$ is a coefficient that can assume values between zero and one. At healthy junctions, $\Updelta P$ is set to zero and $\lambda$ is set to one, so that Eq. (4b) describes continuity of total pressure. At arterial stenoses the assumptions from which the 1D model is derived do not hold. Therefore, stenotic regions are removed from the computational domain and the coupling relation between the upstream and downstream healthy segments is modeled with Eqs. (4a)–(4b) by setting $N=2,$$\lambda =0$ and where $\Updelta P$ is obtained from the experimentally derived stenosis model presented in Ref. 53. Here we use an equivalent expression, reported in Ref. 25, namely

$$\Updelta P = \frac{K_{\text {v}} \, \mu }{A_{0} \,D_{0}}Q + \frac{K_{\text {t}} \rho }{2 \, A_{0}^{2}}\left( \frac{A_{0}}{A_{{\text {s}}}} -1\right) ^{2} Q|Q|,$$

(5)

where $A_{0}$ and $A_{{\text {s}}}$ refer to cross-sectional areas of the normal and stenotic segments, respectively. Similarly, $D_{0}$ and $D_{{\text {s}}}$ represent the normal and stenotic diameters, whereas $L_{{\text {s}}}$ is the length of the stenosis. Furthermore, $K_{\text {v}}$ and $K_{\text {t}}$ are empirical coefficients, with $K_{\text {v}} = 32(0.83\,L_{{\text {s}}} + 1.64 \,D_{{\text {s}}})\cdot (A_{0}/A_{{\text {s}}})^{2}/D_{0}$ and $K_{\text {t}}=1.52.$25

Parameters of the 1D–0D model are summarized in Table 1. Note that $\zeta$ and $K_{\text {t}}$ are studied as part of the construction of the reduced-order model (see “UQ&SA for 1D–0D Model Setting” section), whereas $\rho$ and $\mu$ are studied in the UQ&SA for $\text{FFR}$ prediction setting (see “UQ&SA for FFR Prediction Setting” section).

Table 1 Parameters of the 1D–0D model (see “Mathematical Model” section).

Numerical Solution

Integration of Eqs. (2a) and (2b) along the length of a vessel segment yields

$$Q_{\text {in}} = Q_{\text {out}},$$

(6a)

$$P_{\text {in}} + \frac{\rho }{2}\, \left( \frac{Q_{\text {in}}}{A_{\text {in}}}\right) ^{2} = P_{\text {out}} + \frac{\rho }{2}\, \left( \frac{Q_{\text {out}}}{A_{\text {out}}}\right) ^{2} + Q_{\text {in}} \, \int \limits _{0}^{l} \frac{2( \zeta + 2)\pi \mu }{A^{2}} dx,$$

(6b)

where l is the length of the 1D segment, while subscripts ${\text {in}}$ and ${\text {out}}$ denote variables at the inlet and outlet of the segment, respectively.

In this work we perform simulations considering two different settings. In the first setting, flows are prescribed at all outlets and pressure is prescribed at the network’s inlet, whereas for the second setting we consider prescribed pressure at the inlet and terminal resistances attached to each outlet. As noted below, the use of two settings is motivated by the different features of the two UQ&SA analyses described in the “Uncertainty Quantification and Sensitivity Analysis” section.

Prescribed inlet pressure and outlet flows. The solution to this problem requires traversal of the network from outlets to inlet in order to determine the flow in each vessel of the network. Subsequently, the pressure in each vessel is computed by traversing from the network’s inlet and evaluating Eqs. (6a), (6b), and coupling conditions Eqs. (4a) and (4b) for each vessel and junction. Note that the solution procedure is also valid in the limiting case of one arterial segment. We use this solution procedure in the analysis related to the construction of the reduced-order model described in the “UQ&SA for 1D–0D Model Setting” section, where the coronary networks are split into individual segments and where boundary-conditions are obtained from the 3D solutions.

Prescribed inlet pressure and resistances attached to outlets. Consider now a bifurcating network of V vessels with L outlets and N internal nodes or bifurcations. In this case, instead of prescribing flow, we attach a terminal resistance $R_{j},$ with $j=1,2,\ldots , L,$ to each outlet. The unknowns now are ${\mathbf {x}} = [Q_{{\text {out}},1}, Q_{{\text {out}},2}, \ldots , Q_{{\text {out}},{{L}}}],$ and L nonlinear equations are provided by

• The ith bifurcation with $N^ {i}_{\text {d}}$ daughters provides $N^ {i}_{\text {d}}-1$ equations like Eq. (4b), yielding $L-1$ equations. Note that two-vessel junctions and in particular vessels coupled by stenoses do not provide equations.

• The missing equation is provided by the prescribed inlet pressure: $P_{\text {in},{{k}}}-P^{\text {presc}}_{\text {in}}=0,$ where $P_{\text {in},{{k}}}$ is the pressure at the inlet of the kth vessel, and $P^{\text {presc}}_{\text {in}}$ is the prescribed pressure at the inlet of the network.

While for the case of prescribed inlet pressure and outlet flow the solution to the problem is trivial, the case of resistances attached to outlets requires solving a nonlinear problem. In fact, equations can be written as a nonlinear algebraic system of equations, ${\mathbf {f}}({\mathbf {x}})=0.$ The Python routine scipy.optimize.minimize.root22 was used to solve the nonlinear system. Note that each evaluation of ${\mathbf {f}}({\mathbf {x}})$ requires solving a problem similar to the one where flows are prescribed at outlets, but where the tree is traversed from the outlets towards the inlet and where coupling condition Eq. (4b) is only enforced between the parent vessel and one (arbitrarily chosen) daughter vessel. After convergence Eq. (4b) will be fulfilled for all vessels that share a bifurcation node. We use this solution procedure in the analysis related to UQ&SA for FFR prediction setting described in the “UQ&SA for FFR Prediction Setting” section.

From a 3D Domain to a 1D Network

The construction of a network of 1D domains from the original 3D domain involves a series of non-trivial steps that are described in detail in the following section. The methods illustrated in this section are a modification of those proposed in Ref. 2. All steps described here were performed using VMTK1 and VTK41 libraries via Python scripting.

Skeletonization of the 3D domain. In order to obtain the 1D network, centerlines of the 3D volume meshes are generated and cross-sectional areas, $A_{i},$ with normal vector aligned to centerline tangent vector at node i are calculated. Spacing between centerline nodes is approximately 0.5 mm. From $A_{i}$ we calculate the radius of the cross-sectional area, $r_{i}=\sqrt{\frac{A_{i}}{\pi }},$ while the length of each vessel segment is calculated by summing the Euclidean distance between centerline points. The intrinsic coordinate, x, is defined in a similar manner, where we have that $x_{i}=\sum _{n=1}^{i} \Updelta S_{n-1,n},$ where $S_{n-1,n}$ is the Euclidean distance between centerline point $n-1$ and n.

Masking of junctions. After centerline generation, the portions of the centerlines which coincide with arterial junctions are masked in order to exclude them from the 1D domain definition, since no reasonable 1D description of such portions of the domain can be formulated. See Appendix 1 for details.

Masking of stenotic regions. Stenotic regions are parts of the original domain where the 1D blood flow model is not valid and must be replaced by ad hoc models for the prediction of pressure drops across stenoses. Such regions are detected and quantified by comparing the observed radius, $r_{i},$ to an estimated healthy radius, ${\hat{r}}_{i},$ predicted by a weighted Gaussian kernel filtering procedure on the radius, $r_{i}.$ The healthy radius is required by the stenosis detection algorithm since a priori there is no reference radius available to characterize the stenosis degree. The methodology followed here was proposed by Shahzad et al.42

First a local average radius, $r^{\max }_{i},$ is calculated by averaging the observed radii according to a Gaussian kernel with standard deviation $\sigma _{\max },$ that is

$$r_{i}^{\max } = \frac{\sum _{i^{'}=1}^{n} \, N(i^{'} \vert i, \sigma _{\max } ) r_{i^{'}}}{\sum _{i^{'}=1}^{n} \, N(i^{'} \vert i, \sigma _{\max } )}.$$

(7)

Here and in, what follows $i^{'} \vert i$ denotes the intrinsic distance between centerline nodes with indexes i and $i^{'}.$ Based on this smoothed radius and its deviation from the local average, a weight factor is calculated for each observed radius as

$$w_{i} = N\left( r_{i} \vert r_{i}^{\max }, \sigma _{r} \right) .$$

(8)

Finally, the healthy radius is estimated by averaging the observed radii weighted by proximity, using a Gaussian kernel with standard deviation $\sigma _{x},$ and the likelihood, $w_{i},$ of each observed radius, $r_{i},$ given the local average, $r^{\max }_{i},$ i.e.

$${\hat{r}}_{i} = \frac{\sum _{i^{'}=1}^{n} \, N(i^{'} \vert i, \sigma _{x})w_{i^{'}} r_{i^{'}}}{\sum _{i^{'}=1}^{n} \, N(i^{'} \vert i, \sigma _{x})w_{i^{'}}},$$

(9)

where $N(i^{'} \vert i, \sigma ) = \frac{1}{\sigma \sqrt{2 \, \pi }}\exp {\{ {-( i^{'} - i )^{2}}/{2 \sigma ^{2}}\}}.$

A centerline node is marked as a stenosis if the stenosis degree is above a stenosis threshold, $\theta _{\text {s}}$, where stenosis degree is defined as

$${\text {SD}}_{i} = 1 -\frac{r_{i}}{{\hat{r}}_{i}}.$$

(10)

Stenotic regions are determined by traversing upstream and downstream from the centerline nodes where ${\text {SD}}_{i}>\theta _{\text {s}}$ and marking all nodes where ${\text {SD}}_{i}$ is above a certain healthy stenosis threshold, $\theta _{\text {h}}$. The radius associated with centerline points at the start (upstream, u) and end (downstream, d) are used to calculate the reference radius of the stenotic region according to $r_{0} = 0.5(r_{\text {u}} + r_{\text {d}}).$ The stenosis model [see Eq. (5)] is then parameterized by the minimum radius, $r_{{\text {s}}},$ reference radius, $r_{0}$ and stenosis length, $L_{{\text {s}}},$ computed as the distance between nodes $\text {u}$ and $\text {d}$ along the centerline, see Algorithm 1.

In the original work by Shahzad et al.42 centerline dimensions are given in millimeters, and $\sigma _{x}$, $\sigma _{r}$ and $\sigma _{\max }$ were set to 8, 0.25 and 200 mm respectively. In this work we have related the parameters to the maximum radius, $\max (r_{i}),$ of the vessel of interest such that $\sigma _{x} = \max (r_{i}) \,\sigma _{x}^{*},$$\sigma _{r} = \max (r_{i}) \, \sigma _{r}^{*}$ and $\sigma _{\max } = \max (r_{i}) \, \sigma _{\max }^{*}.$ Furthermore, $\theta _{\text {h}}$ is constrained to be less than or equal to $\theta _{\text {s}}$ by $\theta _{\text {h}} = \theta _{\text {h}} ^{*} \, \theta _{\text {s}},$ where $0 \le \theta _{\text {h}} ^{*} \le 1.$

The determination of stenotic regions is illustrated in Fig. 1. The left panel shows the original radius, r,  together with the estimated healthy radius, ${\hat{r}},$ for a 1D segment. Additionally, the calculated stenosis degree and a stenotic region based on a stenosis threshold, $\theta _{\text {s}} =0.3,$ and healthy threshold, $\theta _{\text {h}} =0.2,$ are shown. The right panel of the figure shows a 1D network extracted from a 3D volume mesh for one of the patients included in this study. The 1D segments are separated at arterial junctions, and further divided into stenotic (red) and healthy regions (blue), as described above. The segment with the most severe stenosis corresponds to the vessel shown in the left panel of the figure.

Figure 1

Original radius, r,  and estimated healthy radius, ${\hat{r}},$ together with stenosis degree, SD, and the stenotic region (shaded area) for a 1D segment is shown in the left panel. A 1D network of arteries extracted from a 3D volume mesh (transparent grey), where junctions and stenotic regions have been masked is illustrated in the right panel.

The parameters related to stenosis detection are summarized in Table 2, and all of them are studied as part of the construction of the reduced-order model (see “UQ&SA for 1D–0D Model Setting” section).

Table 2 Summary of stenosis detection parameters (see “From a 3D Domain to a 1D Network” section).

Definition of Patient-Specific Parameters for Simulations

Simulations performed in this work require the determination of parameters from patient-specific data. These parameters and the procedures for personalizing them are described in the following.

Baseline coronary flow. In this work we perform individual simulations of the left or right coronary branch depending on the site of lesion/measurement. The flow to a specific branch is based on the work of Sakamoto et al.,37 who studied coronary blood flow to the left and right branches in relation to coronary artery dominance. They report mean and standard deviation of absolute flow to each coronary branch but do not account for variability due to differences in CO or total coronary flow. Thus, the reported absolute flows and standard deviations are normalized by the population average CO, 6L/min, in order to produce the corresponding flow fractions, $\lambda _{\text {cor}},$ as given in Table 3. With this, the baseline coronary flow to a specific branch is

$$q_{\text {cor}}=\lambda _{\text {cor}}\text{CO}_{\text {meas}},$$

(11)

where measured CO, $\text{CO}_{\text {meas}},$ was available for each patient, as explained earlier in this section.

Table 3 Percentage of $\text{CO}$ to a coronary branch, $\lambda _{\text {cor}}$ as a function of branch type and dominance, adapted from Sakamoto et al.37

Mean arterial pressure. Mean arterial pressure ($\text{MAP}$) is computed via the widely used formula36

$$\text{MAP} = \frac{2}{3} \text{DBP} + \frac{1}{3} \text{SBP}.$$

(12)

Diastolic blood pressure ($\text{DBP}$) and systolic blood pressure ($\text{SBP}$) were obtained non-invasively as explained earlier in this section. $\text{MAP}$ is prescribed at the inlet of the computational domain.

Coronary resistance. Total peripheral resistance for a given branch is estimated from $\text{MAP}$ and the target branch flow in baseline conditions as

$$R_{\text {tot}} = \frac{\text{MAP}- P_{\text {d}}}{q_{\text {cor}}},$$

(13)

where $P_{\text {d}} = 5\,\hbox {mmHg}$ is the outflow/venous pressure.

The total peripheral resistance, $R_{\text {tot}}$ is distributed among outlets using Murray’s law,31 that is

$$R_{j} = \frac{\sum ^{N_{\text {out}}}_{i=1} r^{c}_{i}}{r^{c}_{j}} R_{\text {tot}},$$

(14)

where j refers to the jth outlet of the network, and c is Murray’s exponent. In order to match average branch flow, $q_{\text {cor}}$ defined in Eq. (11), total peripheral resistance is modified to account for resistance within the computational domain. Starting with the initial guess provided by Eq. (13), the reduced-order model is solved and $R_{\text {tot}}$ is updated according to

$$R_{\text {tot}}^{m+1} = R_{\text {tot}}^{m} \left( 1-\omega (q_{\text {cor}}-q_{\text {obs}})/q_{\text {cor}}\right) ,$$

(15)

where m is the iteration index, $q_{\text {obs}}$ is the observed flow at the branch inlet and $\omega =0.9$ is a relaxation parameter. Once a new value for $R_{\text {tot}}$ is available, the resistance is distributed among outlets using Eq. (14).

Coronary flow can increase significantly with respect to resting flow during hyperemic conditions. Vasodilation of peripheral vessels downstream from epicardial arteries is the most important mechanism controlling coronary flow.45 Such changes can be seen as variations in the total coronary resistance index (TCRI), $\alpha .$ We model the effect of vasodilation of peripheral coronary arteries by dividing $R_{\text {tot}}$ by such a factor

$$R_{{\text {tot}},{\text {hyp}}} = R_{\text {tot}}/\alpha .$$

(16)

The patient-specific parameters previously introduced are summarized in Table 4. Note that $\text{CO},$$\lambda _{\text {cor}},$$\text{MAP},$c and $\alpha$ are studied in the UQ&SA for $\text{FFR}$ prediction setting (see “UQ&SA for FFR Prediction Setting” section).

Table 4 Summary of patient-specific parameters discussed in the “Definition of Patient-Specific Parameters for Simulations” section.

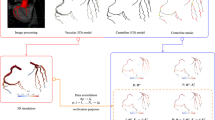
Modeling Pipeline

For a given patient-specific dataset, the pipeline for the reduced-order model FFR prediction is as follows:

• (1) Definition of 3D domain via ITK-SNAP segmentation of CCTA images.

• (2) Preparation of computational domain through meshing and centerline extraction.

• (3) Transformation of the 3D domain to a 1D network and identification of junctions and stenotic regions.

• (4) Baseline simulation using parameters defined in the “Definition of Patient-Specific Parameters for Simulations” section: total peripheral resistance $R_{\text {tot}}$ for a given branch is modified in order to match target branch flow $q_{\text {cor}}$ defined by Eq. (29).

• (5) In order to mimic hyperemic conditions, total branch resistance is reduced: $R_{{\text {tot}},{\text {hyp}}} = R_{\text {tot}}/\alpha ,$ and is subsequently distributed among outlets with criteria specified in Eq. (32).

• (6) Computational FFR is calculated based on the results of the hyperemic simulation as $P_{\text {distal}}/\text{MAP},$ where $P_{\text {distal}}$ is the pressure distal to a given stenosis.

The pipeline is illustrated schematically in Fig. 2.

Figure 2

Illustration of the modeling pipeline. (1) coronary artery segmentation, (2) preparation of computational domain, (3) transformation of the 3D domain to a 1D network and identification of junctions and stenotic regions, (4) incorporation of clinical data and performing baseline/resting simulations, (5) hyperemic simulation and (6) post-processing and extraction of computational FFR. See “Modeling Pipeline” section for additional descriptions of the different steps, and “From a 3D Domain to a 1D Network” and “Definition of Patient-Specific Parameters for Simulations” sections for detailed description of steps 3 and 4/5 respectively.

Three-Dimensional Simulations

3D simulations are used to develop and validate the reduced-order model proposed in this work in two ways. First, we perform transient and steady state 3D simulations for all 13 patients in order to verify that the steady state regime is accurate enough to model hyperemic blood flow in coronary arteries. Second, steady state solutions are used as reference results to optimize reduced-order model parameters. We use results from 3D simulations since we want to analyze to effect of modeling assumptions and corresponding errors related to the transformation of the original 3D problem into a 1D–0D problem. By using reference 3D simulations with equivalent boundary conditions we are able to isolate such errors, as would not be the case if the comparison had been made directly with invasive pressure measurements. 3D simulations are performed on segmented coronary trees treated as rigid domains with a prescribed pressure as inlet boundary condition and Windkessel models attached to each network outlet. A full description of the underlying mathematical models and their numerical treatment is provided in Appendix 2.

Uncertainty Quantification and Sensitivity Analysis

The patient-specific modelling paradigm attempts to enhance clinically measured data by predicting unmeasured physiological states through model simulations based on available data and validated modelling principles. As clinical data always has some uncertainty and unmeasured parameters may be known to vary significantly, we must characterize the uncertainty of model predictions in addition to verifying that a computational model solves the idealized mathematical model to an adequate level of accuracy. Towards this end we employ UQ&SA to assess the uncertainty present in patient-specific model predictions as well as to identify inputs that prevent greater certainty in model predictions.

In this study we perform two UQ&SA cases using Monte Carlo and polynomial chaos approaches (see Appendix 3 for an outline of the framework used in this paper, which is based on the review of Eck et al.9). First we perform an assessment of the variability of the individual pressure drop in each segment of all vessel networks considered in this study to identify which model parameters are most able to influence the resulting pressure drop, thus allowing prioritization of which parameters to estimate from the data. Subsequently, we assess the uncertainty of the final 1D–0D predictions of FFR given the uncertainties in clinical data.

First we briefly summarize notation. UQ&SA typically analyzes a model prediction $y$ as a function $M$ of inputs $\mathbf {z},$$y=M (\mathbf {z}),$ where lower case letters denote the relationship of a deterministic case where $\mathbf {z}$ is known. Uncertain inputs are denoted $\mathbf {Z}$ as they are random variables and thus $Y =M (\mathbf {Z})$ is also a random variable.

As the most commonly used measures in SA, Sobol Indices,39 is based on scalar variables, we extend the ideas of Eck et al.10 to summarize the sensitivities over all measurement locations and across patients. Eck et al.10 proposed a method to summarize sensitivities of time varying quantities by weighting the sensitivities by the uncertainty, ${\mathbb {V}}[Y],$ at each time point. This may naturally be extended to any set or region where a summary of the sensitivities is desired . First we evaluate the portion of variance of an output (k) attributable to the particular input (i):

$$V_{i}^{k}= {} {{\mathbb {V}}\left[ {\mathbb {E}}\left[ Y _{k}\mid Z_{i}\right] \right] } = S_{i} ^{k} {{\mathbb {V}}\left[ Y _{k}\right] }\,,$$

(17a)

$$V_{{T},{{i}}}^{k}= {} {\mathbb {E}}\left[ {{\mathbb {V}}\left[ Y \mid {\mathbf{Z}} _{\lnot {i}} \right] }\right] = S_{{T},i} ^{k} {{\mathbb {V}}\left[ Y _{k}\right] }\,,$$

(17b)

where the vector, Z_¬i, contains all elements of Z except Z_i, and $S_{i} ^{k}$ and $S_{{T},i} ^{k}$ are the first order and total sensitivity index of output $Y _{k}$ with respect to $Z_{i}.$ In contrast to $S_{i}$ and $S_{{T},i},$$V_{i}^{k}$ and $V_{{T},{{i}}}^{k}$ allow to perform a comparison based on the absolute amount of uncertainty due to input $Z_{i}$ for each output rather than on the normalized proportion. Finally, from $V_{i}^{k}$ and $V_{{T},{{i}}}^{k}$ the averaged first-order sensitivity indices are calculated as

$$AS_{i} = \frac{\sum _{k=1}^{n} V_{i}^{k}}{\sum _{k=1}^{n} {{\mathbb {V}}\left[ Y \right] }_{k}} = \frac{ \sum _{k=1}^{n} S_{i} ^{k}{{\mathbb {V}}\left[ Y _{k}\right] }}{\sum _{k=1}^{n} {{\mathbb {V}}\left[ Y _{k}\right] }},$$

(18)

and averaged total sensitivity indices are

$$AS_{{T},i} = \frac{\sum _{k=1}^{n} V_{i}^{k}}{\sum _{k=1}^{n} {{\mathbb {V}}\left[ Y _{k}\right] }} = \frac{\sum _{k=1}^{n} S_{{T},i} ^{k}{{\mathbb {V}}\left[ Y _{k}\right] }}{\sum _{k=1}^{n} {{\mathbb {V}}\left[ Y _{k}\right] }}.$$

(19)

These may provide useful summaries of sensitivities, particularly when the uncertainties of the various outputs of $M$ are quite different.

UQ&SA for 1D–0D Model Setting

In order to identify the most relevant parameters in the construction of the reduced-order model described in the “Reduced-Order Model” section we perform a sensitivity analysis with respect to the parameters ${\mathbf {Z}} _{\mathrm 3{{\text {D}}\rightarrow 1\text {D}}} = [ \zeta , \sigma _{\text {x}}^{*}, \sigma _{\text {r}}^{*}, \sigma _{{\max }}^{*}, \theta _{\text {s}}, \theta _{\text {h}} ^{*}, {\text {K}}_{\text {t}}].$ Parameter variability is described by using uniform distributions with limits based on the plausible ranges of each parameter (see Table 5 for exact ranges). Sensitivity analysis is performed individually for all ($N=248$) 1D segments (including three or more centerline points), and with $y =M ({\mathbf {z}}) = \Updelta {{\text {P}}}_{{\text {1D}}{-}{\text {0D}}}({\mathbf {z}} _{\mathrm {3{\text {D}}\rightarrow 1{\text {D}}}}).$ The flow rate and inlet pressure for each segment are taken from the solution obtained using the 3D modeling framework. Finally, $\Updelta {{\text {P}}}_{{\text {1D}}{-}{\text {0D}}}$ is calculated by applying the solution procedure where inlet pressure and outlet flows are prescribed, as described in the “Numerical Solution” section.

Table 5 Ranges for exploratory sensitivity analysis of the hybrid 1D–0D model (“Reduced-Order Model” section).

Measures of uncertainty and sensitivity were estimated by the Monte Carlo method as described by Saltelli,38 and the accuracy of UQ&SA results were assessed by evaluating the standard deviation of the estimates from 10 bootstrapped samples35 until the standard deviation was below 0.0033 (i.e. ${99}\%$ confident that obtained value is within $\pm \, 0.01,$ with assumptions of normality) for all sensitivity indices with an estimated value larger than 0.05. The maximum number of model evaluations was 3,121,812.

UQ&SA for FFR Prediction Setting

Conducting blood flow simulations for estimation of FFR as described in the “Reduced-Order Model” section requires the determination of parameters based on clinical imaging, patient-specific characteristics, clinical measurements and values from literature (population-based studies, physiological studies, etc.). We conduct UQ&SA to understand the effects of uncertainty in the input parameters, ${\mathbf{Z}} _{\text{FFR}} = [\text{CO}, \text{MAP}, \lambda _{\text {cor}}, {\text {c}} , \alpha , {\text {H}} , \Updelta {\text {r}}_{{\text {s}}} , \lambda _{{\text {L}}_{\text {s}}}{}]$ (see Table 6), on FFR predictions for all available (24) invasive FFR measurements. In the following we discuss the basis for the chosen distribution of $\mathbf {Z} _{\text {FFR}}$ in this UQ&SA study.

Table 6 Input uncertainties for evaluation of the effects of parametric input uncertainty on 1D–0D estimates of FFR.

A standard deviation in $\text{DBP}$ of 5.5 mmHg and a standard deviation in $\text{SBP}$ of 3.3 mmHg were reported in Ref. 17. By assuming perfect positive correlation between $\text{DBP}$ and $\text{SBP},$ a standard deviation in the estimated aortic pressure is 4.77 mmHg. By these considerations, we model the estimate of $\text{MAP}$ as a normal variable with mean given by Eq. (12) and with a standard deviation of 4.77 mmHg.

Dubin et al.8 compared echocardiographic estimates of CO to thermodilution-derived invasive estimates. The average difference between the two methods was 0.11 L/min with a standard deviation of 0.69 L/min. Thus, the uncertainty in CO based on the measurement, $\text{CO}_{\text {meas}}$, is modeled by a normally distributed random variable with mean corresponding to the PW Doppler estimate of $\text{CO}_{\text {meas}}$ and a standard deviation of 0.69 L/min.

The percent of flow to a specific coronary branch, $\lambda _{\text {cor}}$ is based on the work of Sakamoto et al.37 as explained in the “Definition of Patient-Specific Parameters for Simulations” section. Incorporating their reported values on variability we obtain the distributions of flow fractions as given in Table 6.

Blood density and viscosity are related to the hematocrit level. We adopt the relation for viscosity reported in Sankaran et al.,40 where $\mu = \frac{\mu _{\text {p}}}{(1 - H)^{2.5}},$ with viscosity of plasma $\mu _{\text {p}}= 0.001$ and hematocrit level H. With this we model H as a normal variable with a mean of 0.45 and a standard deviation of 0.031 based on average population variations.50 The density of blood can be related to the hematocrit according to $\rho = \rho _{\text {e}} H + (1 - H)\rho _{\text {p}},$ where $\rho _{\text {p}} = 1018\,{\text {kg}}/{\text {m}}^{3}$ is the density of plasma, and $\rho _{\text {e}}=1085\,{\text {kg}}/{\text {m}}^{3}$ is the density of erythrocytes.23

In our modeling framework, the total peripheral resistance is distributed among outlets using Murray’s law,31 which has a theoretical exponent of $c=3,$ derived from the principle of minimum work. More recent studies have suggested an exponent of $c=7/3,$18 and we thus consider Murray’s exponent to be a uniform variable with values between 2.0 and 3.0.

The coronary arteries are segmented semi-automatically from CT images using ITK-SNAP. The software requires one to set upper and lower thresholds for intensities (Houndsfield units) that define what is considered coronary vessel lumen. A larger lower threshold will decrease the cross-section of the segmented lumen, whereas a smaller lower threshold will have the contrary effect. Such variations in lumen cross-section are particularly important at stenotic regions. To account for this, we introduce a global parameter, $\Updelta r_{{\text {s}}},$ to be applied to all stenotic regions of a network such that the minimum radius in stenotic regions is given by $r_{{\text {s}}} = r_{{\text {s}},{\text {segmented}}} + \Updelta r_{{\text {s}}},$ where $r_{{\text {s}},{\text {segmented}}}$ is the minimum radius as obtained from the original segmentation. The minimum $r_{{\text {s}},{\text {segmented}}}$ in our population is 0.29 mm, and we model $\Updelta r_{{\text {s}}}$ as a uniform variable ranging from $-\,0.1$ to 0.1 mm. Similarly, we model the stenotic length as $L_{{\text {s}}} = (1 + \lambda _{L_{\text {s}}})L_{{\text {s}},{\text {segmented}}},$ where $\lambda _{L_{\text {s}}}$ is assumed to follow a uniform distribution between $-\,0.2$ and 0.2.

Although TCRI is difficult to measure, it is related to the coronary flow reserve (CFR),  which is the ratio of flow in hyperemic and baseline conditions. According to the meta-analysis by Johnson et al.,21 CFR is normally between 1 and 6 with an average value of 2.57 for non-ischemic vessels. The distribution is akin that of the gamma.28 From these considerations, we model the hyperemic factor $\alpha$ as a gamma distribution with shape parameter 3, scale-factor 0.75 and shifted to 1.

We perform UQ&SA for FFR predictions from the reduced-order model described in the “Reduced-Order Model” section for 24 locations where FFR was measured invasively. Parameters that are related to the process of going from a 3D problem to a ID–0D model are those deriving from the sensitivity analysis described in the “UQ&SA for 1D–0D Model Setting” section and an optimization procedure based on such analysis. The pipeline for predicting FFR is the same as outlined in the “Modeling Pipeline” section, however, now with the input parameters $\mathbf {Z} _{\text {FFR}}$ as described above and summarized in Table 6. Numerical solutions are obtained by applying the solution procedure where inlet pressure is prescribed and resistances are attached to outlets, as described in the “Numerical Solution” section.

The Python package chaospy12 was used to calculate polynomial chaos approximations of model predicted FFR. Regression was used to estimate the coefficients of the approximations for model evaluations at points sampled according to the Hammersley sequence, which allows for adaptively increasing the number of samples evaluated. The number of points used for each order of approximation was twice the number of terms in the expansion. The accuracy of the results from UQ&SA was assessed by comparing the estimates between successive orders of approximation until the difference between estimated sensitivity indices was below 0.01 for all indices with an estimated value larger than 0.05. Approximation of maximum order 7 was performed, which required 12,870 samples.

Cases that required approximation order greater than 7 were computed more efficiently in terms of computational burden by the Monte Carlo method as described by Saltelli,38 and the accuracy of UQ&SA results was assessed by evaluating the standard deviation of the indices from 10 bootstrapped samples35 until the standard deviation was below 0.0066 (i.e. $99\%$ confident that obtained value is within $\pm\,0.02,$ with assumptions of normality) for all sensitivity indices with an estimated value larger than 0.05. The maximum number of model evaluations was 1,775,970.

Results

Patient Characteristics

Table 7 provides an overview of general patient characteristics, invasive FFR measurements and quantitative coronary angiography. Full information about each patient as well as all FFR measurements used in this study are provided in Appendix 4. Moreover, Figures 13, 14 and 15 in Appendix 4 display the geometry of all coronary trees considered. These figures also include the location of distal pressure measurements used for the computation of FFR.

Table 7 Study population characteristics.

Design and Validation of the Reduced-Order Model for Coronary Blood Flow Simulations

Sensitivity Analysis

We performed sensitivity analysis as described in the “UQ&SA for 1D–0D Model Setting” section in order to identify most influential parameters, ${\mathbf {Z}} _{\mathrm {3{\text {D}}\rightarrow 1{\text {D}}}} = [ \zeta , \sigma _{{\text {x}}}^{*}, \sigma _{{\text {r}}}^{*}, \sigma _{\max }^{*}, \theta _{\text {s}}, \theta _{\text {h}} ^{*}, {\text {K}}_{\text {t}} ],$ in the construction of the reduced-order model described in the “Reduced-Order Model” section. The sensitivity analysis was performed for each of the 248 coronary vessel segments to estimate first-order ($S_{i}$) and total ($S_{{T},i}$) sensitivity indices for each case. The average sensitivities for all cases are presented in Table 8 and show that the velocity-profile parameter $\zeta$ is by far the most influential parameter for most of the cases, with an average $S_{T,\zeta }$ of 0.88. The second most influential parameter is $\theta _{\text {s}}$, which determines the marking of stenotic regions and has an average $S_{T,\theta _{\text {s}}}$ of 0.13. Moreover, aggregated sensitivities, $AS_{i}$ and $AS_{T,i},$ where the individual uncertainties, ${{\mathbb {V}}\left[ Y \right] },$ are taken into account are also shown in Table 8 and show that weighting the sensitivities with the uncertainty leads to a different ranking in terms of most influential parameters. The stenosis threshold is the parameter that contributes the most aggregate sensitivity, with $AS_{T,\theta _{\text {s}}} = 0.65.$ Second most influential is $\sigma _{x}^{*},$ followed by $\zeta$ and $\theta _{\text {h}} ^{*}.$

Table 8 Summary of sensitivities resulting from the analysis in the “UQ&SA for 1D–0D Model Setting” section.

The results from the sample based sensitivity analysis described in the “UQ&SA for 1D–0D Model Setting” section were also analyzed in terms of the residuals $res = \Updelta P_{{\text {3D}}} - \Updelta P_{{\text {1D}}{-}{\text {0D}}} (z).$ In particular, cases where no realization of $\Updelta P_{{\text {1D}}{-}{\text {0D}}} (z)$ in the broad range defined by ${\mathbf {Z}} _{\mathrm {3{\text {D}}\rightarrow 1{\text {D}}}}$ yielded residuals lower than 7.5 mmHg were inspected in detail. Such segments were either associated with a moderate to severe stenosis with non-cylindrical shape and abrupt changes in radius, i.e., calcified stenosis, or multiple mild stenoses with non-cylindrical shape.

Identification of Optimal Parameters

We performed optimization to estimate the values of the four most influential parameters (${\theta _{\text {s}}}, \sigma _{x}^{*}, \zeta$ and ${\theta _{\text {h}}}^{*}$) according to $AS_{{T},i}$. The remaining parameters were fixed: ${\sigma _{r}^{*}=1},$${\sigma _{\max }^{*}=4}$ and ${K_{\text {t}}=1.52}.$ We used the Python package scipy to perform parameter estimation. A grid search approach, scipy.optimize.brute, was chosen due to the discontinuous character of the problem in terms of stenosis identification and inability of other algorithms to provide meaningful results. In order to enhance identifiability we separated the optimization into two cohorts, one in which the parameters related to the stenosis detection were estimated, and one in which $\zeta$ was optimized. In the first cohort ($N=19$ vessel segments), all vessel segments with $V_{{T},{\theta _{\text {s}}}}^{k} > 1\,{\text {mmHg}}$ [see Eq. (17b)] were included, i.e. vessel segments where the square root of the variance due to ${\theta _{\text {s}}}$ contributed to 1 mmHg or more. In the second cohort ($N=213$ vessel segments), all vessel segments with $V_{{T},{\theta _{\text {s}}}}^{k} < 0.1\,{\text {mmHg}}$ were included and used to estimate $\zeta .$ The root mean square error was used as cost function in the parameter optimization, defined as

$$\epsilon = \sqrt{\frac{1}{N} \sum _{k=1}^{N}\left( \Updelta P_{{\text {3D}}}^{k} - \Updelta P_{{\text {1D}}{-}{\text {0D}}}^{k} \right) ^{2}}$$

(20)

with N the number of vessel segments in the optimization procedure, $\Updelta P_{{\text {3D}}}^{k}$ the pressure drop in vessel segment k obtained with the 3D model, and $\Updelta P_{{\text {1D}}{-}{\text {0D}}}^{k}$ the pressure drop obtained using the 1D–0D model. Optimized parameters are shown in Table 9, and Fig. 3 shows predicted FFR from the 1D–0D model (applying optimized parameters) vs. predicted FFR from the 3D model framework at locations where FFR was measured. Equivalent inlet (pressure) and outflow (resistance) boundary conditions were employed as defined in Appendix 2. The mean difference between $\text{FFR} _{{\text {3D}}}$ and $\text{FFR} _{{\text {1D}}{-}{\text {0D}}}$ was $-\,0.03$ and the standard deviation was 0.03. Indeed, the two worst residuals were associated with vessel segments with non-cylindrical shape and abrupt changes in radius, as identified through analysis of residuals (see previous section).

Table 9 Optimal parameters for 1D–0D model settings.

Figure 3

Comparison of ${\text{FFR}} _{{\text {1D}}{-}{\text {0D}}}$ and ${\text{FFR}} _{{\text {3D}}}.$ Scatter plot (left) and Bland–Altman plot (right). The reduced-order model had a bias of ${{\text{FFR}} _{{\text {3D}}}-{\text{FFR}} _{{\text {1D}}{-}{\text {0D}}}=-\,0.03}$ and a standard deviation of 0.03.

UQ&SA for FFR Prediction

Sensitivity Analysis

We performed UQ&SA with respect to the uncertain input parameters ${\mathbf {Z}} _{\text {FFR}} = [\text{CO},\, \text{MAP},\, \lambda _{\text {cor}},\, {\text {c}} ,\, \alpha ,\, {\text {H}} ,\, \Updelta {\text {r}}_{{\text {s}}} ,\, \lambda _{{\text {L}}_{\text {s}}}]$ at 24 locations where FFR was measured invasively, as described in the “UQ&SA for FFR Prediction Setting” section. Average first-order ($S_{i}$) and total ($S_{{T},i}$) sensitivity indices are summarized in Table 10 together with weighted first-order ($AS_{i}$) and total ($AS_{{T},i}$) sensitivity indices. Both sets of indices indicate that uncertainties due to inlet pressure, $\text{MAP},$ Murray’s exponent, c, and stenosis length , $\lambda _{L_{\text {s}}},$ have low influence on predicted FFR for the studied population, model framework, and assumed input uncertainties. Only the indices of $\alpha ,$H and $\Updelta r_{{\text {s}}}$ vary significantly between the two sets, where the sensitivity of $\Updelta r_{{\text {s}}}$ increases when the uncertainty in model output, ${{\mathbb {V}}\left[ Y \right] }$ is taken into account. The contrary is valid for H. In other words, the uncertainty in FFR is lower in the cases where H has a high influence as compared with cases where $\Updelta r_{{\text {s}}}$ has a high influence. The hyperemic factor $\alpha$ is the most influential parameter according to both sets of sensitivity indices, followed by the uncertainty in minimum radius, $\Updelta r_{{\text {s}}}.$ Sensitivity indices are also visualized in the top row of Fig. 4, where averaged sensitivity indices for all 24 locations are considered. The bottom row of the same figure shows average and weighted sensitivity indices for cases ($N=11$) where FFR was in the critical region $0.7< \text{FFR} _{\text {meas}}<0.9.$ The most significant difference is seen in sensitivity to $\Updelta r_{{\text {s}}},$ which is lower when only FFR values in this range are considered. The standard deviation of the average first-order and total sensitivity indices are also indicated through the vertical error bars in Fig. 4. As can be seen, $\alpha ,$H and $\Updelta r_{{\text {s}}}$ have particular high standard deviations, i.e. the value of these sensitivity indices varies a lot from case to case.

Table 10 Summary of sensitivities resulting from the analysis in the “UQ&SA for FFR Prediction Setting” section.

Figure 4

The average first-order ($S_{i}$) and total ($S_{{T},i}$) sensitivity indices [see Eqs. (37a) and (37b)], and the uncertainty weighted first-order ($AS_{i}$) and total ($AS_{{T},i}$) sensitivity indices are reported [see Eqs. (18) and (19)]. The top two bar-plots represent sensitivities when all 24 cases were considered, whereas in the bottom two, only cases ($N=11$) where FFR was in the critical region $0.7< {\text{FFR}} _{\text {meas}}<0.9$ were considered. The standard deviation of the first-order ($S_{i}$) and total ($S_{{T},i}$) sensitivity indices are also indicated through the vertical error bars.

The top part of Fig. 5 shows the effect of uncertainty in input parameters on predicted FFR in terms of the mean ${\mathbb {E}}\left[ Y \right]$ (blue circles) together with the $95\%$ prediction interval for all measured locations. The FFR obtained from the 3D framework and 1D–0D model with equivalent inflow and outflow boundary conditions are also shown for comparison. In the bottom part of the figure parameters CO,  $\lambda _{\text {cor}}$ and $\alpha$ are fixed at their nominal values. The horizontal lines represent ± two standard deviations (${\text {std. \; dev.}}= 0.02$) of repeated FFR measurements,20 i.e. $95\%$ probability of a FFR measurement error smaller than this under assumption of normality.

Figure 5

The mean predicted FFR, ${\mathbb {E}}\left[ Y \right] ,$ vs. invasive FFR. The vertical error bars represent the $95\%$ prediction intervals. The top part of the figure represents the impact of all input parameters with assumed uncertainties as described in the “UQ&SA for FFR Prediction Setting” section, whereas all input parameters related to flow (CO,  $\lambda _{\text {cor}}$ and $\alpha$) are fixed at their nominal values in the bottom figure. Here we also include the uncertainty in FFR (horizontal lines) represented as ± 2 standard deviations (${\text {std. \; dev.}}= 0.02$) of repeated FFR measurements.20

Discussion

Validation of the 1D–0D Modeling Framework for FFR Prediction

In this study we have presented a framework for conducting blood flow simulations for estimation of FFR based on clinical imaging and patient-specific characteristics. Furthermore, two different modeling approaches were considered. The first approach is based on the transient/steady state 3D incompressible Navier–Stokes equations in rigid domains. 3D simulations were performed to confirm that steady state simulations can accurately reproduce FFR predictions (see Appendix 2) and also used as a reference in the development of the second model considered, namely the hybrid 1D–0D model. Here, healthy segments are modeled using the 1D equations for blood in axisymmetric arteries, and stenotic regions are modeled by an experimentally derived model for stenosis.25 Fully 1D or even 1D–0D models for FFR prediction have been previously proposed in the literature.2,3 However, this study is distinct in that we consider a fast steady state version of the model and perform an extensive sensitivity analysis focusing on the model parameters that are related to the model reduction (i.e. going from a 3D to a simplified 1D–0D problem). We considered two parameters associated with necessary assumptions in the 1D–0D equations, namely the radial dependence of the velocity profile, represented by $\zeta$ in Eq. (2b) and the parameter $K_{\text {t}}$ associated with the pressure drop due to a sudden expansion. In addition, five parameters related to the detection and quantification of stenotic regions were considered. This preprocessing of the 3D domain is necessary in order to separate the coronary tree into healthy segments where the assumptions of 1D equations for blood flow are sufficiently accurate, and stenotic regions where the assumptions do no longer hold and stenoses models have to be used.

Through the SA of given input parameters ${\mathbf {Z}} _{\mathrm {{\text {3D}}\rightarrow {\text {1D}}}}$ we found that the velocity profile parameter, $\zeta ,$ was the most influential parameter. This is natural since most vessel segments were relatively smooth, and thus the stenosis detection algorithm and its associated parameters will not influence the predicted pressure drop. The other parameters under consideration will only be influential in vessels where the stenosis detection algorithm is active. Thus the smoothness of the input data is an important determinant of sensitivity. However, by weighting the sensitivities by the uncertainty according to Eqs. (18) and (19) we found that the stenosis threshold, $\theta _{\text {s}}$, is the most influential parameter with $\sigma _{x}',$$\zeta$ and $\theta _{\text {h}}$ following thereafter. These parameters were then estimated by separating vessels used in the optimization procedure into two different cohorts. The filter and stenosis detection parameters $\theta _{\text {s}}$, $\sigma _{x}'$ and $\theta _{\text {s}}$ were estimated from cases with high variance related to stenosis threshold $\theta _{\text {s}}$. The parameter $\zeta$ was estimated in a cohort of cases where $\theta _{\text {s}}$ contributed little variance. Optimal parameters were found by minimizing the difference between pressure drops calculated by using the 3D modeling framework and the 1D–0D model. Few studies have focused on estimating an appropriate velocity profile shape, $\zeta ,$ in Eq. (3) in coronary arteries by means of 3D solutions.2 Though such a profile is commonly assumed in studies focusing on pulse wave propagation, values such as $\zeta =2,$ Pouseille flow, or $\zeta =9,$ a plug-like shape,44,52 are commonly used. For the cases considered, we found that the optimal value was $\zeta = 4.31,$ which is between both values reported in the literature.

Furthermore, through the analysis of residuals between $\Updelta P_{{\text {3D}}}$ and $\Updelta P_{{\text {1D}}{-}{\text {0D}}},$ we were able to differentiate between errors resulting from poor choices of parameters in the construction of the reduced-order model, and cases where the applied models no longer hold. We acknowledge that the 1D equations are not valid at stenotic regions, and account for this by identifying and replacing such regions with stenoses models. However, the model we employed was developed based on experiments on idealized stenotic geometries,53 and as proven, has limited validity in severely calcified stenoses with non-cylindrical shape and abrupt changes in radius. Future work should focus on accounting for such 3D effects. Moreover, one can expect that the stenosis detection algorithm will not detect stenoses in the case of diffuse CAD, especially in cases where the transition from healthy to stenotic areas is smooth and the stenotic region is very long. Although one might argue that in such a case, the main contribution to the pressure drop across the stenosis will be due to viscous losses, which are included in any case in the reduced-order model, the performance of the proposed method on a population of patients with diffusive CAD is of relevance and will be addressed in future work.

FFR predictions obtained using the reduced-order 1D–0D model, employing optimized parameters, are compared with FFR predictions obtained using the 3D framework with equivalent inlet and outlet boundary conditions, see Fig. 3. General agreement was satisfactory, with a bias of $\text{FFR} _{{\text {3D}}} -\text{FFR} _{{\text {1D}}{-}{\text {0D}}} = -\,0.03$ and a standard deviation of 0.03. Moreover, it is worth noting that the mismatch between both modeling approaches is normally significantly smaller than uncertainties in FFR prediction due to FFR model setup (CO,  $\alpha ,$etc.), see Fig. 3. This suggests that even if the 1D–0D model output does not perfectly match 3D model output, it might lead to more accurate FFR predictions by allowing to explore FFR model parameters more extensively in order to design modeling setups that result in reduced uncertainty. Also predicted FFR errors with respect to measured FFR can be reduced because the lower computational cost of the 1D–0D model with respect to the 3D modeling framework might allow improved FFR modeling assumptions due to the increased capacity to explore such assumptions.

UQ&SA of Predicted FFR

We characterized FFR prediction uncertainty based on uncertainty of clinical measurements (CO,  $\text{MAP}$), and assigning conservative estimates for unmeasured inputs ($\alpha ,$$\lambda _{\text {cor}},$H,  c). Geometric uncertainty was also included in terms of variations on minimum stenosis radius $r_{{\text {s}}}$ and stenosis length $L_{{\text {s}}}.$

The hyperemic factor $\alpha$ was the most influential parameter for the assumed input uncertainties and modeling framework. $\alpha$ Represents the effect of adenosine on total coronary resistance, i.e. the factor by which peripheral resistance is reduced from baseline to hyperemic conditions. However, it is the corresponding increase of blood flow, CFR,  which is important. Figure 6 shows the predicted mean values of CFR vs. the predicted mean values of FFR. The error bars represent the ranges for the $95\%$ prediction interval. The mean value of CFR was 2.55 with a standard deviation of 0.54, in agreement with values reported in Refs. 21 and 49. It is worth mentioning that the same $\alpha$ is used for all vessels, probably increasing the sensitivity of predicted FFR to this parameter. In fact, it is expected that tissue located distal of a stenosis has a reduced vasodilatory capacity. It is also evident from Fig. 4 that the influence of $\alpha$ varies substantially from case to case. As can be seen from Fig. 6, cases with low $\text{FFR}$ values (i.e. severe stenoses) exhibit a lower increase in flow for the same value of $\alpha$. Also, since $\alpha$ reduces total resistance, flow will tend to be redirected towards regions with small epicardial resistance.

Figure 6

The mean predicted CFR vs. mean predicted FFR. The error bars represent the $95\%$ prediction intervals for CFR.

The uncertainty about stenosis segmentation, represented by $\Updelta r_{{\text {s}}}$ in this study, also plays a relevant role in terms of its contribution to overall FFR prediction uncertainty. This is especially evident when the sensitivity indices are weighted by the variance of predicted FFR. However, our results show that the influence of $\Updelta r_{{\text {s}}}$ is smaller for lesions within the critical FFR range between 0.7 and 0.9. This indicates that both the variance of predicted FFR and the influence of geometry is higher for low FFR cases, i.e. cases with severe stenoses. This is also evident when comparing the standard deviation of $\Updelta r_{{\text {s}}}$ when the full set of measurements and the subset of measurements are used. This gives promise to computational FFR as a diagnostic tool which is meant to distinguish borderline cases.

Hematocrit is a parameter that affects both density and viscosity in our model. The influence of hematocrit is non-negligible when considering averaged sensitivity indices, however, once the indices are weighted by the variance, its influence diminishes. Thus hematocrit only has a noteworthy effect in cases with low or moderate uncertainty in FFR, which indicates that literature values for hematocrit/viscosity/density are sufficiently accurate for FFR prediction.

It is worth noting that most important parameters in terms of sensitivity and uncertainty of FFR predictions are all ultimately related to the definition of flow through the coronary tree (CO,  $\lambda _{\text {cor}}$ and $\alpha$), which points to the fact that being able to model this variable correctly is of crucial importance for obtaining precise and reliable FFR predictions. Figure 5 illustrates the achievable reduction in uncertainty if flow could be measured accurately in hyperemia, with particular impact in the critical FFR range between 0.7 and 0.9. Although the velocity of blood in epicardial arteries may be estimated with transthoracic Doppler echocardiography,16 currently such an approach has not been used in the context of model-based FFR prediction, and consequently there is no evidence to determine whether it can provide useful information or not. In any case, our results show that obtaining accurate estimates for flow is an aspect on which to focus in order to reduce prediction uncertainty and increase accuracy of model-based FFR prediction. Progress in this direction has been reported in Ref. 13.

Limitations and Future Work

It must be noted that we have modeled the geometrical uncertainty in a simplified manner in terms of global parameters affecting all stenotic regions. Further assessment of the role of uncertainty in segmented geometries should consider such factors over the entire geometry and not only at stenoses, by adopting an approach similar to the one reported in Ref. 5. Focus should also be directed towards quantifying such uncertainty, e.g. by considering segmentations based on different imaging modalities and performed by different observers.

In this work we have chosen to perform the UQ&SA for the FFR prediction setting described in the “UQ&SA for FFR Prediction Setting” section on all clinically measured locations. We have chosen this despite the fact that some patients had more than one measurement. However, correlated FFR predictions are generally expected only in the case of sequential measurements in the same vessel. The only case where one might expect substantial correlation is for FFR IDs 1 and 2 (see Table 12), which are taken along the same vessel. Moreover, it might be the case that two measurements along the same vessel yield very different FFR values, since a priori one can not exclude the presence of lesions between the two locations.

Available 3D simulation results contain detailed information about velocity profiles for the coronary trees and flow regimes under examination. A natural way to proceed would have been to investigate whether one can define a velocity profile coefficient, $\zeta$ that depends on local geometric features as well as the specific flow regime under consideration. In this first work we preferred to adopt a one-fits-all approach. Such a choice was motivated because of evident practical reasons, but also by the fact that we preferred to perform such a study once more patients become available. Similarly, the parameters involved in stenosis detection were chosen with a one-size-fits-all approach as we expect that the variabilities of individual stenosis geometries to be mostly independent of individual patient characteristics.

Appendices

Appendix 1: Reduced-Order Model: from a 3D Domain to a 1D Network

After centerline generation, the portions of the centerlines which coincide with arterial junctions were masked in order to exclude them from the 1D domain definition, since no reasonable 1D description of such portions of the domain can be formulated. We used the VMTK scripts ‘vmtkbranchextractor’ and ‘vmtkcenterlinemerge’ to obtain the topology of the 1D network. The first script uses definitions on what is treated as bifurcations in order to split the centerline into segments. The second script connects centerlines at a single point at bifurcations.1 However, we did not find that these methods sufficiently split the domain into 1D segments, i.e. normally too little is considered as junction, see left part of Fig. 8. And thus additional processing was performed as described below. Points in mother (m) and daughter vessels (d) were masked based on different criteria. Points $p_{\text {d},1}$ and $p_{\text {d},2}$ in daughter vessel 1 and daughter vessel 2 were considered as part of the junction if

$$S_{\text {d}_{1}-\text {d}_{2}} \le r_{{\text {max-sphere}},\text {d}_{1}} + r_{{\text {max-sphere}},\text {d}_{2}},$$

(21)

where $S_{\text {d}_{1}-\text {d}_{2}}$ is the distance between points $p_{\text {d},1}$ and $p_{\text {d},2}$ and $r_{{\text {max-sphere}},\text {d}_{1}}$ and $r_{{\text {max-sphere}},\text {d}_{2}}$ are the maximum inscribed sphere radius at points $p_{\text {d},1}$ and $p_{\text {d},2}$ respectively. A point $p_{\text {m}}$ of the mother vessel was considered as part of the junction if

$$S_{\text {m}-\text {d}} \le 1.5 \, r_{\text {max-sphere},\text {d}_{\text {m}}} ,$$

(22)

where $S_{\text {m}-\text {d}}$ is the distance between point $p_{\text {m}}$ and a point, $p_{\text {d}}$ in a daughter vessel. The value $r_{\text {max-sphere},\text {d}_{\text {m}}}$ for a point $p_{\text {d}}$ situated n points downstream of the center of the junction is found by evaluating $r_{\text {max-sphere}}$ for all daughter vessels at the same number of points downstream the center of the junction, and taking the minimum observed value, see Fig. 7. The criteria in Eqs. (21) and (22) were designed to keep as much of the 1D–0D domain intact; however, this caused incomplete masking in some cases (particularly of centerline points in daughter vessels) as visualized in Fig. 8. In order to check for the smoothness of transition from junctions to 1D segments we calculated the ratio of the maximum inscribed sphere and radius of the cross-sectional area, $r_{i}=\sqrt{\frac{A_{i}}{\pi }}$ for successive points, i.e.

$$\gamma = \frac{\frac{r_{i}}{r_{{max-sphere}, \, i}}}{\frac{r_{i + 1}}{r_{{max-sphere}, \, i + 1}}}.$$

(23)

After the initial junction mask in step 1, $\gamma$ was calculated for the next 10 downstream centerline points in daughter vessels. If $\gamma$ exceeded a value of 1.3 for a centerline point, $i=n,$ the centerline points $1,\ldots ,n,\, n<10$ were also marked as part of the junction. $\gamma$ represents the ratio of the maximum inscribed sphere and the radius of the cross-sectional area for successive points. As noted earlier, this value is normally high in the transition from a bifurcation to an arterial segment. However this value may also be relatively high at the start/end of non cylindrical segments. Having observed values of up to approximately 1.3 in such regions, we used this value as a threshold. If we had used a lower value, non cylindrical segments could be misinterpreted as part of junctions. Figure 8 show the result before (left) and after (right) the correction.

Figure 7

Illustration of step 1 for detection of junctions. The green tubes correspond to radius obtained from cross-sectional area perpendicular to centerline, and blue tubes to the radius of the maximum inscribed sphere.

Figure 8

Illustration of the second step for masking of junctions. The left panel illustrates the result of applying junction criteria based on Eqs. (21) and (22), whereas the right panel shows the final result after correcting with criteria based on Eq. (23).

Appendix 2: 3D Modeling Framework: Model Setting and Results

Mathematical Model

We consider the domain defined by the coronary tree vessels as $\Upomega _{\text {f}} \in {\mathbb {R}}^{3}.$ Moreover, its boundary is partitioned as $\partial \Upomega _{\text {f}} :=\Upgamma _{\text {in}} \cup \Upsigma \cup \Upgamma _{\text {out}},$ where $\Upsigma$ represents the wall boundary, $\Upgamma _{\text {in}}$ is the inlet cross-section and $\Upgamma _{\text {out}} = \bigcup \nolimits _{j=1}^{N_{\text {out}}} \Upgamma _{{{out}},j}$ is the union of the $N_{\text {out}}$ outlets of the tree. Furthermore, blood flow in coronary arteries is modeled assuming that blood is an incompressible Newtonian fluid, for which the incompressible Navier–Stokes equations hold. These equations, along with boundary conditions are given by

$$\left\{ \begin{array}{l} \frac{\partial {\mathbf {u}}}{\partial t} + {\mathbf {u}} \cdot \nabla {\mathbf {u}} = - \frac{1}{\rho } \nabla p + \nu \nabla ^{2} {\mathbf {u}}\,{\text {in}}\,\;\Upomega _{\text {f}}, \\ \nabla \cdot {\mathbf {u}} = 0\,{\text {in}}\,\;\Upomega _{\text {f}},\\{\mathbf {u}} = {\mathbf {0}}\,{\text {on}}\,\;\Upsigma ,\\ p = P_{\text {in}}(t)\,{\text {on}}\,\;\Upgamma _{\text {in}},\,{\text {and}}\\ p = P_{{out},j}(t)\,{\text {on}}\,\Upgamma _{{out},j},\,\, j=1,2,\ldots ,N_{\text {out}},\\ \end{array}\right.$$

(24)

where $\rho =1.05\,{\text {g}}/{\text {cm}}^{3}$ is the blood density and $\nu$ is the kinematic viscosity, given by $\nu =\mu /\rho ,$ with blood viscosity $\mu =0.035 P.$ Furthermore, $P_{\text {in}}(t)$ is a prescribed pressure function and $P_{{out},j}(t)$ is provided by the lumped-parameter model that is coupled to the jth outlet. Coronary arteries experience increased impedance during systole due to the contraction of the myocardium and increased pressure in the left ventricle. To account for this effect each outlet is coupled to a lumped-parameter model,24 which in turn derives from the original work by Mantero et al.27 This lumped-parameter model setup is depicted in Fig. 9 and the variation of volume V of each compartment is governed by the ordinary differential equations (ODEs)

$$\left\{ \begin{array}{l} \frac{d V_{{p},j}}{dt} = Q_{{out},j} - \frac{P_{{p},j} - P_{{m},j}}{R_{{m},j}},\\ \frac{d V_{{m},j}}{dt} = \frac{P_{{p},j} - P_{{m},j}}{R_{{m},j}} - \frac{P_{{m},j} - P_{{d},j}}{R_{{d},j}}.\\ \end{array}\right.$$

(25)

Here, P and R represent pressure and resistance of different elements of the lumped model. Moreover, subscripts p, m and d stand for proximal, medial and distal, respectively. Volumes relate to pressure via compliance C by the following relation

$$\left\{ \begin{array}{l} P_{{p},j} = \frac{V_{{p},j}}{C_{{p},j}},\\ P_{{m},j} = \frac{V_{{m},j}}{C_{{m},j}} + P_{\text {LV}},\\ \end{array}\right.$$

(26)

where $P_{\text {LV}}$ is the left ventricular pressure.

Figure 9

Schematic representation of a lumped-parameter model coupled to the jth 3D domain outlet $\Upgamma ^{\text {out}}_{j},$ shown in grey, and related to Eqs. (25) and (26). Portion of the 3D domain is also shown. C is compliance, R is resistance and P is pressure. Moreover, subscripts p, m and d stand for proximal, medial and distal, respectively. $P_{\text {LV}}$ represents the time-varying left ventricular pressure.

Flow $Q_{{out},j},$ for the jth outlet, is computed as

$$Q_{{out},j} = \int \limits _{\Upgamma _{{out},j}} {\mathbf {u}} \cdot {\mathbf {n}}_{{out},j} {d}S,$$

(27)

where ${\mathbf {n}}_{{out},j}$ is the exterior unit-vector normal for $\Upgamma _{{out},j}.$ On the other hand, $P_{{out},j}$ is provided by the lumped-parameter model as

$$P_{{out},j} = P_{{p},j} + R_{{p},j} Q_{{out},j}.$$

(28)

Numerical Methods

The mathematical models presented in the “Mathematical Model” section are solved using the open-source library CBCFLOW,11 based on FEniCS.26 In particular, CBCFLOW provides a flexible problem setup, allowing to combine its highly efficient incompressible Navier–Stokes solver with typical boundary conditions and simple models used in computational hemodynamics. Here, a Python script allowed CBCFLOW to interact with lumped-parameter models and to prescribe the needed boundary conditions.

The problem defined by Eq. (24) is solved by CBCFLOW using the Incremental Pressure Correction Scheme, described in Ref. 43. The computational mesh is composed of tetrahedral elements. The velocity field is approximated using piecewise-quadratic polynomials, while linear polynomials are used for pressure. The solver implementation follows very closely the one reported in Ref. 30. Apart from spatial and temporal discretization, the only numerical parameter to be set for this scheme is a multiplicative factor for the streamline diffusion stabilization term, referred to as s in this work, see Ref. 55 for details about this term. Moreover, Eq. (25) are solved using an explicit Euler discretization. Numerical parameters are set to $\Updelta t= 1\,{\text {ms}}$ and $s=1.$ A parameter independence study has shown that such choices provide parameter independent FFR predictions for a set of patient-specific geometries.

Definition of Main Parameters from Patient-Specific Simulations

The flow to the coronary branch is based on the work of Sakamoto et al.,37 who studied the dependence of flow on coronary branch dominance. From this we calculate the relative distribution of total coronary flow, $\gamma ^{j}_{k},$ to each coronary branch j for k dominant vasculature ($j=\{{\text {right branch}},{\text {left branch}}\}$ and $k=\{{\text {left dominance}},{\text {right dominance}}\}$). Furthermore, total coronary flow was assumed to be $4.5\%$ of CO. Thus, the baseline coronary flow to a specific branch is

$$q_{\text {cor}}=0.045\cdot \gamma ^{j}_{k}\cdot \text{CO}.$$

(29)

The two flow fractions may be combined to get the fraction of CO to a branch, $\lambda _{\text {cor}}=0.045\cdot \gamma ^{j}_{k}.$

Total peripheral compliance is computed as a percentage of total arterial compliance of 1.7 mL mmHg.32 The percentage of the total arterial compliance assigned to the left/right branch is equal to the relation between flow in branch of interest over total CO,  that is

$$C_{\text {tot}} = q_{\text {cor}}/ \text{CO} \times 1.7\,{\text {mL}}\,{\text {mmHg}},$$

(30)

MAP, pulse pressure (PP) and cardiac cycle duration (T) are extracted from pressure tracings for aortic pressure acquired during invasive FFR measurement. MAP is computed by time-averaging the pressure signal over a cardiac cycle. MAP and PP are used to prescribe a scaled characteristic aortic pressure waveform at the network’s inlet and a scaled characteristic left ventricle pressure waveform (peak left ventricle pressure is 1.05 times the peak inlet pressure) for all lumped-parameter models. We chose to use a characteristic waveform as opposed to the measured waveform since the latter is not perfectly periodic and a corresponding left ventricle pressure waveform would then have to be estimated/fitted. The characteristic waveforms, taken from Ref. 24, are shown in Fig. 10. Total peripheral resistance for a given branch is estimated from MAP and the target branch flow in baseline conditions $q^{j}_{\text {cor}}$ as

$$R_{\text {tot}} = \frac{\text{MAP}- P_{\text {d}}}{q^{j}_{\text {cor}}},$$

(31)

where $P_{\text {d}} = 5\,{\text {mmHg}}$ is the outflow/venous pressure.

Figure 10

Aortic and left ventricle characteristic waveforms used for patient-specific simulations. $\tau$ and ${\tilde{p}}$ are normalized time and pressure. The waveform shapes were taken from Ref. 24.

The total peripheral resistance $R_{\text {tot}}$ and total peripheral compliance $C_{\text {tot}}$ are distributed among outlets using Murray’s law,31 that is

$$R_{j} = \frac{\sum ^{N_{\text {out}}}_{i=1} r^{3}_{i}}{r^{3}_{j}} R_{\text {tot}}$$

(32)

and

$$C_{j} = \frac{r^{3}_{j}}{\sum ^{N_{\text {out}}}_{i=1} r^{3}_{i}} C_{\text {tot}},$$

(33)

where j stands for the jth outlet of the network. $R_{j}$ and $C_{j}$ have to be subsequently distributed among the different compartments (see Fig. 9) of the lumped-parameter model attached to the jth outlet. The fractions for distributing $R_{j}$ among $R_{p,j},$$R_{m,j}$ and $R_{ d,j}$ are set to 0.01, 0.84 and 0.15, respectively. Similarly, fractions used to distribute $C_{j}$ among $C_{a,j}$ and $C_{m,j}$ are 0.025 and 0.975, respectively. Parameter distribution among components of lumped-parameter models were empirically determined to obtain diastolic coronary flow rate waveforms with appropriate pulsatility.

Modeling Pipeline

The modeling pipeline is as follows

• (1) Using parameters defined in the previous section as initial guess, total peripheral resistance $R_{\text {tot}}$ for a given branch is modified in order to match target branch flow $q_{\text {cor}}$ defined by Eq. (29). The iterative procedure is described later in this section.

• (2) We determine heart rate, MAP and PP from pressure tracings taken under hyperemic conditions. Moreover, we use $R_{\text {tot}}$ from previous step to estimate a new total peripheral resistance, now in hyperemic conditions: $R_{{\text {tot}},{\text {hyp}}} = R_{\text {tot}}/\alpha ,$ which is subsequently distributed among outlets with criteria specified in Eq. (32). The hyperemic factor, $\alpha ,$ was set to 3.

• (3) Steady state simulations are performed prescribing $\text{MAP}$ at the inlet and replacing the lumped-parameter model by a single resistance at each outlet, where such resistance is $R_{j}=R_{{p},j}+R_{{m},j}+R_{{d},j},$ as for the transient case.

Solution Monitoring and Total Resistance Estimation

As noted previously, total peripheral resistance $R_{\text {tot}}$ is modified in order to match average branch flow $q_{\text {cor}}$ defined in Eq. (29). Starting with the initial guess provided by Eq. (31), $R_{\text {tot}}$ is updated after each cardiac cycle using

$$R_{\text {tot}}^{m+1} = R_{\text {tot}}^{m} \left( 1-\omega (q_{\text {cor}}-q_{\text {obs}})/q_{\text {cor}}\right) ,$$

(34)

where m is the iteration index (which corresponds to the cardiac cycle index), $q_{\text {cor}}$ is the target coronary flow in a branch, provided by Eq. (29) and $q_{\text {obs}}$ is the observed flow at the branch inlet. $\omega$ is a relaxation parameter and was set to $\omega = 0.9.$ Once a new value for $R_{\text {tot}}$ is available, the resistance is distributed among outlets using Eq. (32).

In order to computed predicted FFR, we have to extract average pressure values form 3D solutions. To do so we first define the subdomain

$$\Upomega _{{f},k} :=\{ {\mathbf {x}} \in \Upomega _{\text {f}} : ||{\mathbf {x}}-{\mathbf {x}}_{k}|| < r_{k} \},$$

(35)

where ${\mathbf {x}}_{k}$ is the k-th node of a vessel’s centerline that corresponds to the point where the invasive FFR measurement was taken, and $r_{k}$ is the radius of the vessel at node k. Locations ${\mathbf {x}}_{k}$ were identified by inspection of angiograms and segmentation results by modelers and cardiologists. Next, average pressure (over space and time) is computed as

$$\bar{P}_k = \frac{1}{T \Upomega _{\mathrm {f},k}} \int \limits _T \int \limits _{\Upomega _{\mathrm {f},k}} p \, d\Upomega \, dt.$$

(36)

3D Simulation Results

While the primary objective of this work is to present and analyze a 1D–0D framework for model-based FFR prediction, we report here the comparison of predicted FFR values obtained using the 3D modeling framework described in B vs. invasively measured FFR values. Such values are provided in order to show that the FFR prediction modeling framework, while still under development, provides results that are aligned with many publications on model-based FFR prediction. The average error of FFR predictions was $-\,0.033$ and the standard deviation of the error was 0.119. Moreover, the correlation coefficient of predicted FFR vs. invasive FFR was 0.84. In terms of diagnostic accuracy, prediction sensitivity, specificity, positive predicted value and negative predicted value were 60,  93,  86 and $76\%,$ respectively. Figure 11 shows a scatter plot and a Bland–Altman plot for predicted FFR vs. measured FFR. More relevant for the current study are results reported in Fig. 12, that shows predicted FFR based on steady state simulations vs. predicted FFR based on transient simulations. In this case, mean error was $-\,0.004$ and standard deviation of the error was 0.003, with a correlation coefficient of 1.00.

Figure 11

Predicted FFR, ${\text{FFR}} _{{\text {3D}}},$ vs. invasive FFR, ${{ {\text{FFR}}}} _{\text {meas}}.$ Scatter plot with grey line showing the FFR cutoff value of 0.8 (left) and Bland–Altman plot with dashed lines showing ± 2 standard deviations (right).

Figure 12

Predicted FFR based on steady state simulations, ${{ {\text{FFR}}}} _{{\text {3D}},{\text {SS}}},$ vs. predicted FFR based on transient simulations, ${{ {\text{FFR}}}} _{{\text {3D}},{\text {US}}}.$ Scatter plot with grey line showing the FFR cutoff value of 0.8 (left) and Bland–Altman plot with dashed lines showing ± 2 standard deviations (right).

Appendix 3: UQ&SA Framework

We summarize the framework used by treating the patient specific model as a function $M$ that predicts $y =M (\mathbf {z})$ based on input data $\mathbf {z}.$ As the input data is uncertain it is represented as a random variable $\mathbf {Z}$ which implies that prediction $Y$ is also an uncertain random variable. We employ the nonintrusive UQ&SA methods of Monte Carlo and polynomial chaos to characterize the distribution of Y given the distribution of $\mathbf {Z}.$ This is achieved by evaluating $M$ at many samples drawn from the distribution of $\mathbf {Z},$ i.e. $y =M (\mathbf {z})$ at each sample point in $\left\{ \mathbf {z} ^{(s)}\right\} _{s=1}^{N_{\text {s}}}$. Eck et al.9 present several methods and concepts of UQ&SA within the context of cardiovascular modeling, and we refer the reader to this work for more details regarding the methods of UQ&SA used here.

The uncertainty of $Y$ is fundamentally due to the uncertainty of $\mathbf {Z}$ propagated through the model $M.$ Thus it is critical to employ a distribution of $\mathbf {Z}$ that reflects the conditions the UQ&SA is intended to analyze. To assess performance of a patient specific model the input distribution must reflect the actual uncertainties present in clinical procedures and population variation. However, UQ&SA may also be employed to analyze a model’s range of behavior and to identify parameters relevant for estimation from measured values of $y.$ In this case the distribution of $\mathbf {Z}$ should reflect the range of plausible values for the inputs. Typically, only a range of values is considered and no prior knowledge is available to prioritize certain regions, thus a uniform distribution is appropriate to investigate the model’s dependence on the parameters.

Once the approximate distribution of $Y$ is available from the UQ&SA procedure various measures of uncertainty of $Y$ are available such as statistical moments or quantiles of $Y.$. These quantities are of primary interest when assessing model performance, however, SA augments this by assessing the portion of uncertainty due to particular inputs, allowing prioritization of efforts to reduce uncertainty. In this context, Sobol sensitivity indices, first-order ($S_{i}$) and total ($S_{{T},i}$), are widely employed,39 and defined as

$$S_{i}= {} \frac{{{\mathbb {V}}\left[ {\mathbb {E}}\left[ Y \mid Z_{i}\right] \right] }}{{{\mathbb {V}}\left[ Y \right] }},$$

(37a)

$$S_{{T},i}= {} 1 - \frac{{{\mathbb {V}}\left[ {\mathbb {E}}\left[ Y \mid {\mathbf {Z}} _{\lnot {{i}}} \right] \right] }}{{{\mathbb {V}}\left[ Y \right] }},$$

(37b)

where the vector, ${\mathbf {Z}} _{\lnot {{i}}},$ contains all elements of $\mathbf {Z}$ except $Z_{i}.$ These indices partition the total ${{\mathbb {V}}\left[ Y \right] }$ into portions attributable to specific combinations of inputs. The first order indices $S_{i}$ quantify the variance due to $Z_{i}$ alone, i.e. independent of the values of the other inputs. The total sensitivity index, $S_{{T},i}$, includes effect due to interaction with other parameters and represents the reduction in variance expected to be achieved by fixing $Z_{i}$ at a particular value.

Larger values of $S_{i}$ suggest that $Z_{i}$ strongly affects $Y$ and thus may be a prime target for improved measurement or optimization in the context of parameter estimation. In the case where $S_{{T},i}$ and thus also $S_{i}$ are small, $Z_{i}$ has little influence on $Y$ and should not be prioritized for improved measurement and may not be estimated accurately in an inverse problem context. When $S_{i}$ is small but $S_{{T},i}$ is large, the effect of $Z_{i}$ depends greatly on the values of other parameters thus it may still be valuable to improve its measurement, and it may be estimated in an inverse problem though its identifiability may depend on the values of other parameters.

Appendix 4: Patient-Specific Data and Invasive Measurements

Table 11 shows patient characteristics and non-invasive measurements for all patients considered in this work. Furthermore, Table 12 shows data obtained during invasive angiography, and include stenosis location, quantitative coronary angiography (QCA), cardiac cycle averaged pressure proximal and distal to the stenosis, and heart rate. QCA is a measure of the percent diameter stenosis degree obtained by inspection of angiography images. Figures 13, 14 and 15 shows visualizations of all 3D domains for the patients considered in this work, where we have highlighted the locations of distal measurements with (magenta) spheres, and the branch inlets (orange) where proximal measurements were obtained.

Table 11 Patient-specific data for the 13 patients considered in this work.

Table 12 Data for invasive FFR measurements and quantitative coronary angiography for the 13 patients considered in this work.

Figure 13

Visualization of 3D domain for some of the patients included in the study (see figure sub-captions for details). Magenta sphere is where distal pressure $\bar{P}_{\text {distal}}$ was evaluated in 3D domains using Eq. (36). Branch inlet, where proximal pressure $\bar{P}_{\text {proximal}}$ is prescribed is highlighted in orange. The centerline used as reduced-order model domain is evidenced in blue. (a) Patient 1, left branch (b) Patient 2, left branch (c) Patient 3, left branch (d) Patient 4, right branch (e) Patient 5, left branch (f) Patient 5, right branch (g) Patient 7, left branch (h) Patient 7, right branch.

Figure 14

Visualization of 3D domain for some of the patients included in the study (see figure sub-captions for details). Magenta sphere is where distal pressure $\bar{P}_{\text {distal}}$ was evaluated in 3D domains using Eq. (36). Branch inlet, where proximal pressure $\bar{P}_{\text {proximal}}$ is prescribed is highlighted in orange. The centerline used as reduced-order model domain is evidenced in blue. (a) Patient 6, right branch (b) Patient 9, left branch (c) Patient 8, left branch (d) Patient 8, right branch (e) Patient 10, left branch (f) Patient 10, right branch (g) Patient 11, left branch (h) Patient 13, left branch.

Figure 15

Visualization of 3D domain for some of the patients included in the study (see figure sub-captions for details). Magenta sphere is where distal pressure $\bar{P}_{\text {distal}}$ was evaluated in 3D domains using Eq. (36). Branch inlet, where proximal pressure $\bar{P}_{\text {proximal}}$ is prescribed is highlighted in orange. The centerline used as reduced-order model domain is evidenced in blue. (a) Patient 12, left branch (b) Patient 12, right branch.