Introduction

Cerebral aneurysms formation is considered the result of the complex interplay among systemic effects, the biomechanical properties of the vessel wall and the continuous effect of forces exerted by blood flow on the vessels.8,19,37,39

While systemic factors influencing the development of the pathology such as genetic conditions, smoking, hypertension and familial predisposition affect the whole arterial vasculature, cerebral aneurysms tend to occur in regions with particular features such as bends and bifurcation apexes. This clinical evidence supports the hypothesis of a major involvement of hemodynamics in the aneurysms pathophysiology. However the underlying mechanisms triggering the onset of the disease still need to be identified and explained, as well as the specific factors causing some lesions to rupture. This is a particularly challenging task, given the inter-individual variability of the cerebro-vascular districts, the simultaneous presence of different relevant factors and the difficulty of collecting crucial information, in particular follow up observational studies that could provide insights into the history of unruptured aneurysms. On the other hand the accomplishment of this task would result in the definition of reliable rupture risk indexes, that would potentially provide a mean to stratify aneurysms according to their probability of bleeding and support clinicians in the critical management of unruptured lesions.38

In the last decades the focus of computational fluid dynamics (CFD) studies has mainly concentrated on the intra-aneurysmal flow features and wall shear stress (WSS) distributions on the sac dome7,9,14,37 and on the extraction of morphological indexes of aneurysm sac shape and size.10,28,42 Recently some authors have underlined the importance of the modeling and characterization of aneurysm parent vasculature. Castro et al.6 studied the influence on intra-aneurysmal flow of the portion of the upstream parent vessels included in the computational domain; Imai et al.13 and Sato et al.35 demonstrated by means of parametric studies on idealized models that different degrees of torsion of the feeding artery remarkably affect inflow patterns and flux; Hoi et al.12 parametrically studied the effect of the parent artery curvature and found that flow impingement area linearly grows with the parent artery curvature. An image-based detailed analysis of the geometric features related to the location and rupture of lateral aneurysms developing along the internal carotid artery (ICA) has been carried out by Piccinelli et al.,24 which is the observational study that has created the ground for this work.

Nevertheless, investigations on the relationship between three dimensional (3D) morphology of patient-specific vasculature and hemodynamics still have to face many challenges: primarily, real anatomies display very large variability, especially in the intracranial vasculature, and the retrieval of 3D geometric features in a robust and operator-independent way is a developing but not yet established field; secondly, a quantitative analysis of integrated datasets including geometric information and hemodynamics results is to the authors’ knowledge a rather new field that requires the application and development of ad hoc tools.

This paper aims at giving a contribution in this direction with two distinctive features, one refers to the specific subject of our investigation, the other one to the methods adopted for the data analysis.

  1. 1.

    The focus of our study is the quantitative and computational characterization of the geometry and hemodynamics of the ICA comparing features of ICAs harboring aneurysms with features of ICAs of subjects with aneurysms in a downstream location or no aneurysms at all. Vessel geometry has been recognized as a relevant factor in vascular pathologies since a long time, but a precise and quantitative analysis of the geometry of intracranial arteries as preferred sites of development of aneurysms is still insufficient.24 On the other hand, CFD studies usually focus on aneurysmal flow rather than on a characterization of the feeding arteries. The vessel geometry is here characterized by means of radius and curvature, while wall shear stress (WSS), its axial gradient and blood energy drop along the ICA path are considered as surrogate measures of hemodynamics features.

  2. 2.

    Heterogeneity and variability of the data at hand demand for sophisticated statistical methods. Our dataset comprises both geometry and fluid dynamics: these quantities are regarded as stochastic functions of an axial coordinate defined along the vessel. To extract patterns from such a complex aggregate of information we resorted to advanced statistical techniques, namely the functional principal component analysis (FPCA). These methods allow to identify the part of the data set relevant for our purposes, i.e. the detection of recurrent patterns in geometry and/or fluid dynamics that may relate to the presence of the pathology and a lesion rupture event.

The ground of this work is the integration of different types of information—from the radiological acquisition, to the 3D reconstruction of patient-specific anatomies and their geometric characterization, the CFD modeling and the statistical analysis of the comprehensive dataset—with the ultimate goal of devising rupture risk indexes with diagnostic and possibly prognostic purposes, as explained in Piccinelli et al.24,25 and Sangalli et al.31,32

The results presented here show that geometrical features such as the radius of the ICA, its curvature and the axial derivative of the WSS have a significant correlation with the rupture status of the aneurysms in our data set. As a matter of fact, the FPCA extracts from those quantities the part (or more precisely the principal component) actually related to the rupture. In particular, patients with unruptured aneurysm in the ICA or without aneurysms (up to the neuroradiological evidence) feature a double-bend siphon as opposed to patients with ruptured or distal aneurysms, presenting preferentially a single-bend siphon. Moreover, pronounced peaks of WSS are statistically related to ruptured aneurysms in the ICA. These findings provide a further justification for the pre-existing clustering of patients into two classes, \(\Upomega\) and S groups depending on the shape of the siphon. In particular, we found that patients in the group S are more protected from the development of the pathology.

We argue with statistical evidence that the different behavior in the two cases is related to the different level of energy loss in the ICA, induced by the bends.

The paper is organized as follows. In “Materials and Methods” section we describe the components of our methodological workflow: the reconstruction of 3D models and their geometric characterization, the CFD modeling and the statistical tools employed. “Results” section illustrates the results obtained after the statistical analysis. A phenomenological discussion is carried out in “Discussion” section.

Materials and Methods

The Data Set

The data set of the present study consists of 52 patients who underwent 3D-RA for cerebral aneurysm assessment following clinical routine at the Neuroradiology Division of the Niguarda Ca’Granda Hospital in Milan, Italy. At admission, patients signed a consent form for the use of their personal data according to the current Italian law. The study did not imply any change in the management of the patient, nor was any additional procedure undertaken; no further IRB procedure is currently requested for using anonymized retrospective data in Italian Hospitals.

Acquisitions were performed with an Integris Allura Unit (Philips, Best, the Netherlands) with the following parameters: C-arm rotation speed, 55 per second; matrix size 512 × 512; frame rate, 25 frames per second; 18 mL nonionic hydrosoluble contrast agent was injected prior to the acquisition at 4 mL/s. The rupture status of the patient was registered by one of the authors (EB), senior radiologist of the Hospital.

The patients were subdivided into groups according to the location and the rupture status of the lesions. Moving from the results presented in Sangalli,31 where patients with an aneurysm located at the terminal bifurcation of the ICA or distally (group U) and patients with proximal aneurysms (w.r.t. the ICA terminal bifurcation—group L) have been demonstrated to have statistically different features (U-subjects have wider, more tapered and less curved ICAs than L patients), we added to this classification the discriminant of the rupture. More precisely we considered five classes,

  • UR (Upper Ruptured) subjects with a ruptured aneurysm at or after the final bifurcation of the ICA;

  • UN (Upper Non-ruptured) subjects with a non-ruptured aneurysm at or after the final bifurcation of the ICA;

  • LR (Lower Ruptured) subjects with a ruptured aneurysm along the ICA, before its terminal bifurcation;

  • LN (Lower Non-ruptured) subjects with a non-ruptured aneurysm along the ICA, before its terminal bifurcation;

  • No (No Aneurysm).

Table 1 reports the cardinality of each group as well as details on the precise localization of the lesions within each subclass. The ICA aneurysms listed under the U group are terminal aneurysms located exactly at the bifurcation.

Table 1 Summary of the Aneurisk data set considered in the present study
Full size table

Geometric Characterization

The reconstruction of patient-specific anatomies and part of the geometric characterization of the parent vasculature were achieved by means of the Vascular Modeling Toolkit (VMTK).41 The following operations were performed for each patient.

  1. 1.

    The 3D surface model of the aneurysm and its parent vessels was reconstructed by means of a gradient-driven level-set approach2; in particular all the acquired portion of parent vasculature was included in the model.

  2. 2.

    The centerlines of the reconstructed vascular network were extracted3 as well as a centerline traveling through the aneurysm sac24; a point-wise estimate of the vessels radius was readily available from the centerline computation techniques.25

  3. 3.

    The vascular network bifurcations were automatically identified; the centerlines for each vascular branch tagged accordingly; the same subdivision was successively applied to the 3D surface model.25

  4. 4.

    A curvilinear abscissa was defined traveling along the vessel: selecting the ICA bifurcation25 as a landmark on all the models, this abscissa parameterized the ICA length in the upstream direction; by definition the abscissa was set to zero at the bifurcation point and assumed negative values moving upstream.

Figure 1 illustrates the geometric characterization performed on one of the patients of the data set, the 3D modeling, the split centerlines network and the corresponding subdivided surface.

Fig. 1
figure 1

Left: 3D surface model of ICA hosting an aneurysm; middle: split centerlines for the whole vascular network; right: split 3D surface model. Each vascular branch is associated to a different numeric label (GroupId).

Full size image

Numerical Simulations

The region investigated in the present paper is the siphon of the ICA and its main bifurcation: in the 3D model, the ICA was kept entirely while the downstream circulation was properly trimmed. Cylindrical prolongations (flow extensions) were added at each extremal section of the surface, in such a way that the geometrical model featured circular inlet and outlet sections, corresponding to the proximal and the distal boundaries respectively. The length of these cylindrical extensions was adaptively selected as 10 times the clipped section radius.

For each geometrical model we obtained a tetrahedral grid with an average element size of 0.6 mm using the Netgen Mesh Generator.36 The size of the mesh was selected as a trade-off between the accuracy and the computational time requirements. This was clearly a delicate issue, since the present research comprised the extensive CFD analysis of a large data set of patients. We verified on a smaller sample of patients that computations over finer meshes, while significantly more intensive in terms of simulation time, did not bring major improvements to the statistical results. The considered mesh size was actually capable of capturing the patterns of the WSS relevant to the FPCA.

The computational domain was assumed to be fixed, corresponding to the common hypothesis of rigid vascular walls. We further assumed that blood can be modeled as a continuous incompressible Newtonian fluid, so that the flow problem can be described by the incompressible Navier–Stokes equations.11 For each vascular geometry, three cardiac cycles were simulated, in order to reduce the effects of the initial conditions and obtain the periodic solution in the last simulated heart beat. The spatial discretization was based on the Galerkin finite element method, and was carried out with a piecewise linear approximation for both the pressure and the velocity. The numerical scheme adopted is based on an edge stabilization technique5 that allows equal order interpolation. The adopted time advancing scheme is a semi-implicit Euler method, with a time step of 10−3 s.

To estimate the WSS over the computational domain it is necessary to retrieve a suitable approximation of the velocity gradient. We used an L 2 projection method,4,43 which is proven to provide a superconvergent approximation of the gradient on linear elements.

An important issue is the prescription of the boundary conditions. Ideally, patient-specific boundary conditions should have been prescribed. Unfortunately, the current clinical protocol does not include the measurement of velocity/pressure data to be used to this aim. On the other hand, the focus of the present work is on the role of the geometry of ICA as a determinant of the flow features, so we prescribed comparable realistic hemodynamics conditions to all the geometries of the data set. More precisely, we considered the Reynolds number evaluated at the inflow section as the parameter for the description of the flow regime. A time average Reynolds number of Re = 350 is supposed to describe realistically the flow regime in the ICA.22 Accordingly, a flat axial velocity profile was prescribed at the inflow sections, the flow rate being adjusted to yield this target Reynolds number. The selection of the arbitrary velocity profile is legitimated by using cylindrical boundary extension on the inlet section. It is indeed proven that the geometrical features of the vessel have a stronger influence on the solution than the presence of secondary motion in the inlet velocity profile.18 Moreover, the effects of inlet secondary flows, even in case they are present, break down within a few diameters of the inlet,17 featuring an exponential decay from the inlet section.40 Pulsatility of the flow was forced by the classical waveform representative of the carotid arterial flow advocated in Osenberg,20 Prosi et al.,26 and Rappitsch and Perktold.30

At the outlets usual stress-free outflow conditions were prescribed. It is worth mentioning explicitly the treatment of small collateral branches. The small branches of the ICA were included in the geometrical model whenever the image resolution allowed for their reconstruction. In some cases however they were neglected, because the image quality was not sufficient to reliably determine their geometry. The effect of the presence or absence of small ICA branches on the results presented later on is however negligible. We have verified this statement in a case in which it was possible to reconstruct the ICA geometry including a small branch. The WSS profiles computed on the complete geometry and after artificially removing the collateral branch did not show significant discrepancies in view of the FPCA.

Post-processing

To integrate the analysis of the geometric and hemodynamics features, WSS field was properly post-processed and homogenized with the morphological data. The ICA was divided into a sequence of sections located at the curvilinear abscissas s k such that s k+1 − s k  = 2 mm (see Fig. 2). Each section was taken orthogonal to the centerline and was corresponded by a slice \({{\fancyscript{S}}_k}\) of the surface of the vessel (represented on the left with different colors as a function of s k ). The slices were assumed to be non overlapping, and their boundaries were defined by edges of the computational grid.

Fig. 2
figure 2

Computation of the average shear stress \(\overline{\hbox{WSS}}\) as a function of the curvilinear abscissa s. Left: the vascular surface is subdivided in slices \({{\fancyscript{S}}_k,}\) corresponding to a set of equispaced values of the curvilinear abscissas (the width of the step is 2 mm). Right: the averaged shear stress is associated to centerline points

Full size image

For each patient we computed the local average WSS over the slice \({{\fancyscript{S}}_k}\) as a function of the curvilinear abscissa s k and time,

$$ \overline{\hbox{WSS}} (s_k,t) = \left\Vert {\frac{1}{|{{\fancyscript{S}}}_k|}} \int\limits_{{{\fancyscript{S}}}_k} \hbox{WSS} (x, y, z, t) d{{\fancyscript{S}}} \right\Vert. $$

In particular we recorded the systolic peak value \(\overline{\hbox{WSS}} (s_k,t_{sys}). \) By means of spline interpolation this quantity and its axial derivative \(\frac{d\overline{\hbox{WSS}}}{d s} (s_k,t_{sys})\) were reformulated as a function of the curvilinear abscissa, as done for the radius and curvature of the vessel centerline.

The choice of the slice width of 2 mm was a trade-off between accuracy and computational effort. Computation of the average WSS on slices of 1 mm did not yield differences that affect significantly (from the statistical point of view) the results.

We also quantified the energy loss experienced by the blood stream when flowing through the ICA. Energy loss in the sac has been recently proposed as a possible index for the rupture risk quantification of cerebral aneurysms.38 In the present work it was estimated by computing the difference of the total mechanical energy of the fluid on two cross-sections of the vessel, located upstream (Section U) and downstream (Section D) the siphon (see Fig. 2). The downstream section was located at the terminal bifurcation of the ICA. The upstream section was located at the most proximal location available in all the considered geometries, after a proper alignment of the vessels centerlines to filter out systemic artifacts, as explained in the following paragraph.

Since the variation of gravitational potential energy is negligible, the total mechanical energy is defined as the sum of the kinetic and fluid energies, so that the energy loss reads

$$ {{\fancyscript{L}}}(t) = \int\limits_{{Section D}}\left(\rho \frac{{\mathbf{u}} \cdot {\mathbf{u}}}{2} (t) +p(t) \right) d s - \int\limits_{{Section U}} \left(\rho \frac{{\mathbf{u}} \cdot {\mathbf{u}}}{2} (t) + p(t) \right) d s $$

where ρ is the fluid density. In the sequel, we actually refer to the time averaged energy loss \({\overline{{\fancyscript{L}}}}\) over a heart beat.

Numerical simulations have been carried out with in-house software based on LifeV,16 an open source C++ finite element library for the solution of partial differential equations in 3D on unstructured meshes, on serial and parallel architectures. Visualization of the results has been obtained with the Paraview free software.21

Statistical Analysis

The analysis of the data reconstructed from the geometry requires three main steps. In the first one we approximated the centerlines of each ICA reconstructed by VMTK with a smooth function. Since we were interested in the curvature of the centerline, requiring the differentiation of its parametric representation, we resorted to a functional representation based on free-knots splines of order 4.32

The top left panel of Fig. 3 shows the derivatives of the three space coordinates of the estimated ICA centerlines, \(\{x^{\prime}(s), y^{\prime}(s), z^{\prime}(s)\},\) for each subject along the curvilinear abscissa. These quantities well represent the variability of our data set. The figure pinpoints a remarkable misalignment of the data. In particular we noticed a strong phase variability largely due to the different size of the body and thus of the arteries of the different patients. To filter this effect out we decoupled the phase variability among the subjects, strongly dependent on ICAs dimensions, from an amplitude variability. The latter reflects the variability in the morphological shapes of ICAs, in which we were mostly interested.31 The decoupling led to the alignment displayed in the right panel of Fig. 3, that could thus be profitably used for comparisons across subjects. The mean curve (template) resulting from the alignment of the different subjects is reported in the pictures as a black bold line. The template of the centerline first derivatives displayed in Fig. 3 still showed a large amplitude variability, especially at values of the abscissa between −5 and −2 cm, that required further investigation. Following the procedure illustrated in Sangalli et al. 34 we came up with two clusters (with two corresponding templates) as an accurate representation of the data set. The mean curves of the two clusters are reported in Fig. 4, right. The two mean centerlines identified in this way are represented in 3D in Fig. 5. A similarity analysis pinpointed that two clusters are enough for capturing the variability across the data set, a 3-groups clustering being not significantly better (Fig. 4, left).

Fig. 3
figure 3

Left: first derivatives with respect to the curvilinear abscissa of the centerlines coordinates (\(x^\prime = dx/ds, \) \(y^\prime = d y / ds, z^\prime = dz / ds\)) of the estimated ICA, reconstructed from images after the free knot estimation. The black thick curve represents the template reconstructed by the data without alignment. Right: first derivatives of centerlines after the alignment. We identified here just one cluster of data (k = 1). The template of this cluster is represented again by the black thick line

Full size image
Fig. 4
figure 4

Left: boxplots of similarity indexes between each curve and the corresponding template for original estimated centerlines and for centerlines aligned and clustered in k groups, k = 1, 2, 3. Right: After the alignment, a better clustering is obtained with two groups (k = 2), whose templates are represented by the solid thick lines

Full size image
Fig. 5
figure 5

3D image of the estimated templates of the two clusters. The dark (green) template is a prototype of \(\Upomega\)-shaped ICA (single-bend siphon), the light (orange) one is a prototype of S-shaped ICA (double-bend siphons)

Full size image

The two estimated templates identify two prototype morphological shapes of ICA that have since long time been described in medical literature.15 Namely, the dark (green) template centerline is a prototype of a so-called \(\Upomega\)-shaped ICA, whose siphon has just one main bend in its distal part; the light (orange) one is instead a prototype of a so-called S-shaped ICA, whose siphon has two main bends in the distal part.

All the data associated with the centerlines (radius, curvature, local average WSS, etc.) have been registered according to the same procedure performed for the centerlines themselves. Each variable of interest was represented therefore by a function of the registered curvilinear abscissa s along the centerline. These functions were regarded as the realization of a random process, whose features could be significantly correlated to the belonging of the subject to a specific group. The identification of such features was however made difficult by the huge complexity and variability of the data represented by these functions. FPCA pursues the goal of a reduction of the complexity of the data. Similarly to a modal or a proper orthogonal decomposition, FPCA aims at identifying a finite dimensional subspace onto which to project the functional data providing a good compromise between information loss and statistical power gain (Karhunen-Loève decomposition of the sample autocovariance operator). The identification of the most convenient basis (the set of principal components) for representing the stochastic functions at hand is data driven: FPCA actually identifies important and uncorrelated modes of variability observed in the data set i.e., eigenfunctions of the sample autocovariance operator. The coordinates of the projections of the data onto the modes in the basis are called scores. The statistical relevance of the modes in the basis can be quantified by means of the sample variance of the scores of the projected data i.e. eigenvalues of the sample autocovariance operator. Once dimensional reduction has been achieved, classical multivariate analysis of the scores of the principal components is used to investigate and verify the statistical hypothesis of interest. For an extensive introduction to these techniques we refer to Ramsay and Silverman.29 In particular, we looked for patterns that discriminate patients in different classes. Discrimination was carried out by an approach called quadratic discriminant analysis (QDA), which is a classification rule assuming, for each investigated class, a multivariate Gaussian distribution of the observed features. The basic idea is to calculate the relative proportions of the classes, their means and their covariance matrices with respect to the variables analyzed. For each possible set of features presented by a new subject, Bayes Theorem provides an estimate of his probability of belonging to each one of the groups.

Results of the combined FPCA + QDA analysis on the enriched (geometry + CFD) data set with respect to the classification presented in Table 1 are presented in the next section.

The statistical analyses have been carried out within the statistical programming environment R.27

Results

In Fig. 6, ICA radius and curvature, and the local average WSS are presented as functions of the curvilinear abscissa on the centerline. The figure shows the large variability of the data set, even after centerline alignment. It is worth noting that the length of the reconstructed centerlines has also a great variability in the data set. This figure displays, at the top of each plot, a Gaussian kernel estimate of the probability density function of the location of aneurysms along the ICA or at its terminal bifurcation. Occurrence of the aneurysms in the distal part of the ICA (where tapering is more evident), is almost null at s ≈ − 1 cm. This indirectly identifies the average position of the dural ring the ICA goes through before its terminal bifurcation. Notice that the dural ring is not detectable from images and that aneurysms distal to this position are in general more life threatening.

Fig. 6
figure 6

ICAs \(\overline{\hbox{WSS}}\) (top), radius (center) and curvature (bottom) profiles for all subjects respectively before (left) and after (right) registration. Solid black lines show mean curves, as estimated by Loess. On top of each picture is also displayed the estimate of the probability density function of the location of aneurysms along the ICA or at its terminal biforcation

Full size image

We concentrated our analysis on the distal ICA, comprising the last 5 cm before its terminal bifurcation, since this was the available tract in all considered patient’s 3D models after centerline registration.

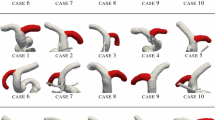
A representative subject for each class of Table 1 is presented in Figs. 7–11. On the left column we show the 3D model of the ICA, as defined after reconstruction from images and mesh generation. The magnitude of the computed WSS vector at the systolic peak is plotted on the vascular surface. On the right column we show the morphological and hemodynamical indices evaluated for each subject, expressed as functions of the curvilinear abscissa along the vessel centerline. This sequence of figures highlights the most relevant differences of ICAs in the different groups, by direct comparison.

Fig. 7
figure 7

Representative of group No: the \(\overline{\hbox{WSS}}\) at the systolic peak (left); the radius (cm), curvature (cm−1) and \(\overline{\hbox{WSS}}\) (dyn/cm2) at the systolic peak as functions of the curvilinear abscissa (right)

Full size image
Fig. 8
figure 8

Representative of group LN: the \(\overline{\hbox{WSS}}\) at the systolic peak (left); the radius (cm), curvature (cm−1) and \(\overline{\hbox{WSS}}\) (dyn/cm2) at the systolic peak as functions of the curvilinear abscissa (right)

Full size image

Notice that only the subject in the LR group presents a significant variation of the \(\overline{\hbox{WSS}}\) values along the centerline curvilinear abscissa (Fig. 9) located at the distal half of the main bend. The maximum value of the \(\overline{\hbox{WSS}}\) is larger in this case than in all the other considered cases.

Fig. 9
figure 9

Representative of group LR: the \(\overline{\hbox{WSS}}\) at the systolic peak (left); the radius (cm), curvature (cm−1) and \(\overline{\hbox{WSS}}\) (dyn/cm2) at the systolic peak as functions of the curvilinear abscissa (right)

Full size image

As shown in Figs. 10 and 11, the two subjects from the “upper” groups (UN, UR) feature relatively low values of the \(\overline{\hbox{WSS}},\) with no significant variations in the space pattern. The radius of the ICA is consistently larger in the two subjects belonging to groups UN and UR than in subjects belonging to the other groups.

Fig. 10
figure 10

Representative of group UN: the \(\overline{\hbox{WSS}}\) at the systolic peak (left); the radius (cm), curvature (cm−1) and \(\overline{\hbox{WSS}}\) (dyn/cm2) at the systolic peak as functions of the curvilinear abscissa (right)

Full size image
Fig. 11
figure 11

Representative of group UR: the \(\overline{\hbox{WSS}}\) at the systolic peak (left); the radius (cm), curvature (cm−1) and \(\overline{\hbox{WSS}}\) (dyn/cm2) at the systolic peak as functions of the curvilinear abscissa (right)

Full size image

It is also interesting to notice that the computed energy loss is significantly larger in subjects belonging to the No, LN and LR groups, while subjects in the UN and UR groups feature lower values, the p-value of the Wilcoxon test being equal to 0.0030. The difference between the two clusters is remarkable.

FPCA of radius, curvature and \(\overline{\hbox{WSS}}\) profiles along aligned ICA centerlines allowed the identification of statistical differences among the five groups of subjects with respect to the principal uncorrelated modes of variability of each quantity of interest. In the first row of Fig. 12 we report the profiles of these quantities as a function of the curvilinear abscissa. The second row of the figure displays the projections on the most significant principal components for radius, curvature and \(\overline{\hbox{WSS}}.\) Significant differences occur among the five groups of subjects, in particular emphasized by the first principal component of the radius and the curvature and the second principal component of the axial derivative of \(\overline{\hbox{WSS}}.\) The third row shows the boxplots of the scores of these principal components for the five groups of subjects. p-value in the boxplots is based on the one-sided Wilcoxon test.

Fig. 12
figure 12

First column: analysis of ICA radius profiles along aligned centerlines. Second column: analysis of curvature profiles of aligned ICA centerlines. Third column: analysis of the first derivative of the WSS profiles along aligned ICA centerlines. First row: aligned profiles. Second row: projections of subject profiles on the corresponding mode of variability. Third row: boxplots of subject scores on these principal components separated per subject group

Full size image

Discussion

From the joint morphologic-fluid dynamics analysis, we notice the following facts.

The first column of Fig. 12 shows the projections on the first principal component of the ICA radius profiles along aligned centerlines. For each subject, the component along this mode measures the average radius of the ICA; thus, changing the scores with respect to this mode we move from subjects with a narrow ICA to subjects with a wide ICA. As previously pointed out, in Sangalli et al. 31 we already highlighted the significance of the width of the ICA in discriminating among Upper and Lower group subjects. With the present analysis we can more specifically notice that UN  group subjects in particular behave differently from the other four subject groups with respect to this mode of variability, manifesting statistically wider ICAs than the other four groups (p-value: 0.016).

The second column of Fig. 12 shows the projections on the first principal component of the curvature profiles along aligned centerlines. For each subject, the component along this mode measures the prominence of the second peak of curvature of the ICA centerline; thus, changing the scores with respect to this mode we move from subjects with a non particularly evident second bend of the siphon to subjects with a very marked one. The significance of the presence/absence of the second bend of the siphon is in accordance to what emerged in Sangalli et al. 31 The current analysis refines this result, showing that, the No  and the  LN groups behave differently from the other three groups with respect to this mode of variability, being statistically associated to the presence of a double-bend siphon (p-value: ≤ 0.001).

Finally, the third column of Fig. 12 shows the projections on the second principal component of the first (axial) derivative of the WSS profiles along aligned centerlines. For each subject, the component along this mode measures the intensity of the WSS peak at the end of his ICA; thus, changing the scores with respect to this mode we move from subjects with a less pronounced WSS peak to subjects with marked WSS peak. In particular, the LR  group behaves differently from the other four, manifesting statistically more prominent WSS peaks (p-value: 0.001).

The clustering \(\Upomega\)-S, that—as we have pointed out—has been found here on the basis of a purely statistical argument and then matched with the previous literature, seems also relevant for the aneurysm pathology. As a matter of fact, our previous results showed a statistical evidence of a dependence between cluster membership and aneurysm presence and location.33 In particular the contingency table (Table 2) shows that all the subjects without aneurysms were found to display S-shaped ICAs; at the opposite, among Upper group subjects only a minority had an S-shaped ICA, whilst the majority (70%) had an \(\Upomega\)-shaped one.

Table 2 Conditional contingency table of subjects allocations to \(\Upomega\)-shaped ICAs and S-shaped ICAs clusters
Full size table

These results pinpoint on the ground of a statistical basis the presence of landmarks with a possible prognostic purpose. A slightly tapered ICA is associated with downstream aneurysms that however do not rupture. High WSS peaks are associated with the rupture of aneurysms hosted by the ICA. The analysis of the curvature suggests that the presence of more pronounced bends in the carotid siphon tends to prevent the onset (S-group) and the rupture (LN class) of the aneurysms. Based on these evidences, we formulate the conjecture that the ICA siphon has a protective effect on the intra-cranial arterial tree. In fact, most sites of aneurysm development are inside the dura mater, where arteries float in the subarachnoidal space with little or less support from the surrounding tissues, as compared to extradural locations. This could make them more sensitive to the intensity of flow-induced loads, which are dependent on viscous dissipations in the feeding arteries. Viscous dissipations are induced by flow secondary motions that have a complex dependence on the vessel geometry.1 In particular, the curvature of the bends of the ICA siphon seems to play a role on viscous dissipations. Whilst S-shaped ICAs are expected to be very effective in dissipating the flow energy, \(\Upomega\)-shaped ICAs would not be as efficient. Other features such as the vessel radius will also be relevant, since ICAs featuring larger values of the radius tend to produce less viscous dissipation.

The conjecture on the dissipative role of the siphon is supported by the computed energy loss featured by the blood stream when flowing through the ICA siphon. This value varies across different groups of subjects. Subjects in the No group behave similarly to subjects in the LN and LR groups, whose flow exhibits greater energy loss (or viscous dissipations) in the ICA siphon. The energy loss (Table 3) discriminates subjects having an aneurysm in the intra-cranial circulation versus subjects with an aneurysm on the ICA or no aneurysm at all (p-value of the one-sided Wilcoxon test 0.003). This is consistent with previous observations in Sangalli et al. 33 regarding the role of the ICA curvature. However, this result also suggests that energy losses in the ICA cannot be correctly estimated based on the vessel curvature alone.

Table 3 Energy loss computed in the representative subjects for each group. In the last row we report the average ± the standard deviation for the two macro-groups No,LR,LN and UR,UN, together with the p value of the Wilcoxon test for their statistical difference
Full size table

Limitations

There are several limitations in this study. The data set is including 52 patients and the statistical significance of the results would be greatly improved by the extension of the number of patients. We are extending the data set of patients, by including images that will undergo the same procedure described in the paper. In view of a possible cross validation of our results and hopefully to corroborate our conclusions, a web repository of the geometries considered in the present study is under construction.23 We aim at sharing our data and possibly at receiving more data for incrementing the number of cases of the present analysis.

We have focused the attention on the local average WSS and its axial gradient. These are actually advocated in the literature as principal indicator of different vascular pathologies. However, other indicators could be considered in a similar way, like the Oscillatory Shear Index or the Helicity Factor. On the other hand, it could be interesting to analyze the variation of the local maximum WSS (rather than the local average \(\overline{\hbox{WSS}}\)) as a function of the vessel curvilinear abscissa, to highlight locations that exhibit critical levels of the shear load.

One major improvement of the present study is moreover represented by an integrated analysis of the parent vessel and the sac. The joint analysis of the two regions is anticipated to provide a remarkable insight into the link between the morphology-hemodynamics and the pathology, in particular for a prognostic purpose.

Conclusions

Despite the limitations of this study, the results presented here clearly point out that the morphology of the ICA and the consequent blood dynamics is likely to play a significant role in the development (and possibly the rupture) of the aneurysm; the possible role of the siphon in protecting the downstream arterial tree deserves to be further investigated.

An attempt has been made at selecting a reduced set of indicators, able to capture the relevant features for the classification of the data set. Each indicator alone is providing only a partial characterization of the system at hand. The radius profile does not provide information regarding the shape of the cross section, which can be significantly non-circular as pointed out in Piccinelli et al. 25 The curvature profile does not provide information about the relative orientation of alternating bends in the siphon. The fluid dynamics indicator is based on arbitrary assumptions on the flow conditions at the boundary of the computational domain. However, the assumptions on the simulated flow conditions are made in order to probe different vascular geometries under the same flow regime. Fluid dynamics is here used as a proxy for morphology features which are not easy to be measured or interpreted, but affect measurable or computable flow features. Therefore, the rationale behind the joint evaluation of the three indicators is that under the proposed experimental conditions, information provided by fluid dynamics can complement the morphology characterization of subject-specific vascular structures. This eventually leads to the identification of prognostic landmarks. In particular, the results presented here suggest that a single-bend siphon, which is in general detectable from the images, is associated with a higher risk of development and rupture of the aneurysm.