Introduction

Balloon angioplasty is a minimally invasive interventional technique to restore blood flow through coronary arteries constricted by atherosclerosis. However, a subsequent re-blockage or restenosis can occur if the artery elastically recoils back to its narrowed state. Bare metal stents (BMSs) were introduced to prevent this arterial recoil but restenosis remains a significant problem with BMSs occurring in between 10 and 50% of patients treated.12 , 17 Restenosis in stented arteries is essentially caused by the excessive growth of new tissue in the stented segment of the artery, a process termed intimal hyperplasia (IH). Currently, the implantation of drug-eluting stents (DESs) has proven effective in reducing restenosis rates to below 10%.8 , 31

In a clinical study,17 stent design was found to be the second strongest risk factor, after vessel size, for restenosis at six-month follow-up angiography among 3370 patients. Stent-design-related stimuli for restenosis are arterial injury and altered hemodynamics. The influence of stent design on arterial injury has been demonstrated38 and the severity of the injury correlated to the volume of subsequent tissue growth.38 , 39 Altering the hemodynamic wall shear stress (WSS) at the artery wall through stent implantation has also been shown to influence arterial tissue growth.14 , 26 Previous works5 , 22 , 30 which have linked altered hemodynamics to stent design prompted further investigations into the hemodynamic environment of the stented artery.

Currently, state-of-the-art numerical investigations into WSS in the stented artery employ three-dimensional (3D) and transient computational fluid dynamics (CFD).3 , 4 , 6 , 10 , 11 , 15 , 21 , 23 , 25 , 37 In these studies the alteration of the WSS acting on the wall is sometimes analyzed using threshold values of the WSS (WSS < 0.5 N/m2) and WSS gradient (WSSG > 200 N/m3) as tissue growth has been found to be more prolific in areas where the WSS and WSSG are lower and higher than these thresholds, respectively.18 , 20 One such study23 examined the effect of stent foreshortening on WSS, and found that for 0, 12, and 25% foreshortening there was 71, 77, and 78% of the stented area with WSS < 0.5 N/m2 and 54, 50, and 54% of the stented area with WSSG > 200 N/m3, respectively. In a more recent study,3 CFD analyzes of four commercially available BMSs were conducted. Comparisons between two of the stents with contrasting design, the Bx-Velocity (Bx) stent (Cordis Corp., Miami, FL, USA) and the Jostent Flex (JOMED AB, Helsingborg, Sweden), showed 58 and 57% of the stented area with WSS < 0.5 N/m2 respectively. The effect of strut thickness on WSS was also examined using Jostent Flex stents with strut thicknesses of 0.05 and 0.15 mm. The thinner struts led to 61% of the stented area with WSS < 0.5 N/m2 compared with 57% for the thicker struts. Duraiswamy et al. 11 also conducted CFD analyzes of three, second-generation, commercially available BMSs: the Bx stent, the Aurora stent (Medtronic, Inc., Minneapolis, MN, USA) and the NIR stent (Boston-Scientific Corp., Natick, MA, USA). They found 59, 57, and 59% of the stented area with WSS < 0.5 N/m2 and 75, 83, and 88% of the stented area with WSSG > 200 N/m3 for the Bx, Aurora and NIR stents, respectively.

These previous studies depict only minor differences in the altered WSS between stent designs. However, numerous studies have shown that stent strut angle,26 strut thickness16 , 35 and strut configuration17 , 27 , 38 have a significant influence on the arterial response to stent implantation. In light of this, it is highly probable that using threshold values of only the WSS and WSSG variables is not sufficient to fully elucidate stent-induced alterations in arterial WSS.

In this work, a numerical prediction methodology is proposed which utilizes the two commonly used variables (i.e., WSS and WSSG) plus two additional WSS-based variables, the WSS angle gradient (WSSAG) and the oscillatory shear index (OSI). Each of these variables highlights a different type of alteration to the arterial WSS which could lead to IH. Instead of using threshold values, statistical measures of the full distribution of each of these variables are calculated for a more complete analysis. To demonstrate the methodology, it is applied to three stents with contrasting features. The stents are then ranked based on the statistical measures. Comparisons are made between the results from the analyzes and the two-variable threshold analysis described above. The proposed methodology can be used to identify areas of altered arterial WSS at the design stage of future bare metal, as well as permanent and bioabsorbable drug-eluting coronary stents.

The paper is laid out as follows: The “Materials and Methods” section describes the proposed methodology which includes the generation of the computational domain, the CFD analysis and the post-processing. The results from the application of the methodology to three stents are presented in the “Results” section, with the conclusions given in the “Discussion” section.

Materials and Methods

The methodology begins with the generation of a geometric model of the 3D lumen of the stented artery. This model is discretized and used as the computational domain for the CFD analysis. The WSS vectors are predicted on domain surfaces that represent living tissue. These vectors are then post-processed to produce the magnitudes of the four WSS-based variables: WSS, WSSG, WSSAG and OSI. The distribution of these variables is then analyzed using quantitative and qualitative statistical methods.

Generation of the Computational Domain

A 3D geometric model is first created beginning with a solid cylinder measuring the length and external diameter of the stent, from which the geometry of the complete stent is removed. This represents full strut exposure to the blood flow. The geometric model is then extended proximal and distal to the stented section by adding cylinders with lengths equal to the entrance length for fully-developed laminar flow in a circular pipe and with diameters which create a stent-to-artery deployment ratio of 1.09:1 similar to a normal in vivo value.27 This ratio is defined as the inner diameter of the deployed stent to the inner diameter of the unstented artery. Finally, a novel methodology to numerically predict tissue prolapse between stent struts32 is employed. Briefly, the prolapsing tissue creates a variable arterial radius r given by

$$ {\frac{r}{{R_{0} }}} = 1 - {\frac{x\delta }{{2R_{0} }}}\left\{ {1 + \cos {\frac{2\pi }{L}}\left( {z - \frac{L}{2}} \right)} \right\} $$
(1)

along the spatial coordinate z between two stent struts, where R 0 is the external diameter of the stent, L is the distance between the stent struts, δ is the prolapse depth and δ = CL where C is the coefficient of prolapse derived from finite element analysis (FEA) data.36 The prolapse reduction factor x is initiated at a distance of 0.5L from struts offering additional scaffolding support as shown in Fig. 1. The prolapse reduction factor linearly decreases the prolapse to zero at the stent strut providing the additional support. The prolapsing tissue is then removed from the geometric model. The geometric model thus created is discretized using an unstructured mesh topology comprising of 4-node tetrahedral elements to form the computational domain. Several simulations are performed to investigate the effect of mesh density to ensure mesh-independent results are obtained. This methodology is applied to stents closely resembling the Palmaz Schatz (PS) stent (Johnson and Johnson Interventional System, Warren, NJ, USA), the Gianturco Roubin II (GR-II) stent (Cook Inc., Bloomington, IN, USA) and the Bx stent all implanted in the left-anterior-descending (LAD) coronary artery (Fig. 2). These contrasting stent designs are chosen specifically to identify the effects of the different geometric features on the WSS. Also, the prior knowledge of the in vivo performance of these stents is useful when analyzing the results as the altered hemodynamics may have contributed to their restenosis rates.

Figure 1
figure 1

Illustration of the primary and secondary scaffolding direction of part of the PS stent. The arterial tissue protrudes a depth δ into the stented artery and is supported in the primary scaffolding direction and partially supported (shaded section) in the secondary scaffolding direction

Full size image
Figure 2
figure 2

Geometric models of the LAD arteries implanted with the PS stent (left), the GR-II stent (middle) and the Bx stent (right)

Full size image

Details of the 3D geometric models are provided in Table 1. The unstented sections of the artery are 3.2 mm in diameter and 21.3 mm in length. Mesh-independent results are achieved with 4,551,484 elements for the PS stent, 3,038,536 elements for the GR-II stent and 5,840,890 elements for the Bx stent. On the stent struts, the meshes have a maximum element edge length of 20–30 μm depending on the stent and a minimum edge length of 1 μm for all stents to allow adequate resolution of any complex geometric features. Elements in the center of the artery have a maximum edge length of 200 μm. Mesh independence is based on a less than 4% change in the RMS value of the magnitudes of WSS vectors between successive meshes along sample lines in the domain, an example of which is shown in Fig. 3a.

Table 1 Geometric characteristics of the stent models
Full size table
Figure 3
figure 3

(a) Magnitude of WSS along a sample line in the model of the LAD coronary artery implanted with a GR-II stent for three successive mesh densities and (b) average velocity applied at the inlet to simulate basal flow in the LAD coronary artery

Full size image

CFD Analysis

The general form of the governing flow equations for the conservation of mass and momentum are given in vector form in Eqs. (2) and (3), respectively:

$$ {\frac{\partial \rho }{\partial t}} + \vec{\nabla } \cdot \left( {\rho \vec{V}} \right) = 0 $$
(2)
$$ {\frac{{\partial \rho \vec{V}}}{\partial t}} + \vec{\nabla } \cdot \left( {\rho \vec{V} \otimes \vec{V}} \right) = - \vec{\nabla }p + \vec{\nabla } \cdot \left( {\vec{\vec{\tau }}_{ij} } \right) $$
(3)

where ρ is the fluid density, p is the static pressure and \( \vec{V} \) is the velocity vector. In this work, the blood flow in the stented artery is assumed time-dependent, laminar and incompressible. With these assumptions the viscous stress tensor \( \vec{\vec{\tau }}_{ij} \) is given by

$$ \vec{\vec{\tau }}_{ij} = \mu \left( {\vec{\nabla }\vec{V} + \vec{\nabla }\vec{V}^{\text{T}} } \right) $$
(4)

where μ is the fluid dynamic viscosity, which is a function of the shear rate. The governing equations are solved by the commercial software package ANSYS CFX Version 12 (Canonsburg, PA, USA) in a Cartesian coordinate system using a vertex-centered finite-volume scheme with implicit time-stepping, a scheme which is second-order accurate in both space and time.

A transient, fully-developed, laminar, axial-velocity-profile is applied at the inlet of the computational domain which corresponds to the desired blood flow conditions in the coronary artery. A fixed static pressure equal to the reference pressure of 114600 Pa is applied at the outlet of the domain. This pressure represents the mean arterial blood pressure in the LAD coronary artery. The no-slip boundary condition is applied on all surfaces representative of the artery wall and the stent struts. The blood density is assumed constant with a value of 1050 kg/m3. The non-Newtonian nature of the flow is accommodated using the Carreau model written

$$ \mu = \mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\left[ {1 + \left( {\gamma \lambda } \right)^{2} } \right]^{{\left( {{\frac{q - 1}{2}}} \right)}} $$
(5)

where γ is the shear rate calculated as the second invariant of the strain rate tensor and the constants are

$$ \begin{aligned} \mu_{0} = 0.056\,{\text{Ns/m}}^{2} \quad & \lambda = 3.31\,{\text{s}} \\ \mu_{\infty } = 0.00345\,{\text{Ns/m}}^{2} \quad & q = 0.375 \\ \end{aligned} $$
(6)

At each timestep the convergence criterion employed is a 10−5 reduction in the maximum residuals of the discretized equations. Simulations are run for three cardiac cycles to ensure periodic convergence of the results. Several simulations also are conducted to investigate the effect of the timestep so as to ensure temporal convergence is achieved.

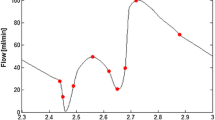
The flow rate chosen corresponds to fully-developed pulsatile basal flow conditions in the human LAD coronary artery33 and is shown in Fig. 3b. The average Reynolds number for the cycle is 111 and the average flow rate is 55 mL/min. The period of the cardiac cycle is 0.8 s, and the simulation is run for three consecutive cycles with a timestep of 12.5 ms. This timestep is sufficient to ensure temporal convergence is achieved. Computations are performed on a HP xw6400 64-bit workstation using two processors of a quad Intel (Xeon) 2 GHz CPU and 6 GB of RAM.

Post-Processing

The vertex-centered finite-volume scheme employed by ANSYS CFX calculates the variables at the vertices of the elements. All post-processing to calculate the WSS-based variables is then conducted in Tecplot 360 2008 (Bellevue, WA, USA). The WSS, WSSG, and components of the WSSAG and OSI are calculated at each timestep of the third cycle and are then time-averaged over this cycle using the trapezoidal method of numerical integration. The calculation of these variables is described below.

Wall Shear Stress

Lower than physiologic values of WSS (<1.5 N/m2) can cause dysfunction of the endothelial cells (ECs) which line the artery. Under such conditions, ECs act as a catalyst for IH through, for example, the upregulation of tissue growth factors such as PDGF-A and PDGF-B.29 , 45 Numerous studies which incorporate numerical and experimental results have correlated areas of low WSS with increased IH.26 , 43 , 46 , 47

The dot product of the unit normal vector \( \vec{l} \) to a surface and the viscous stress tensor denoted \( \vec{\vec{\tau }}_{ij} \) yields the WSS, i.e.,

$$ \vec{l} \cdot \vec{\vec{\tau }}_{ij} = \vec{\tau }_{{w_{xyz} }} = \tau_{w,x} \vec{i} + \tau_{w,y} \vec{j} + \tau_{w,z} \vec{k} $$
(7)

where τ w,x , τ w,y and τ w,z are the Cartesian components of the WSS vector in the x, y and z directions, respectively. The magnitude of the WSS vector is calculated as

$$ {\text{WSS}} = \left( {\tau_{w,x}^{2} + \tau_{w,y}^{2} + \tau_{w,z}^{2} } \right)^{1/2} $$
(8)

Wall Shear Stress Gradient

ECs which line the artery are often denuded by the stenting procedure and must be replaced to prevent IH.7 , 41 However, in vitro studies show that bovine ECs migrate away from areas of high WSSG with magnitudes above 5000 N/m3 9 and 3400 N/m3.42 As such, there are likely to be less ECs in areas of high WSSG in the stented artery. In computational studies, sites that are susceptible to IH have been correlated with sites where the WSSG has been predicted to exceed 200 N/m3 in an end to side anastomosis model20 , 34 and a rabbit iliac model.26

The WSSG is a measure of the spatial rate of change of the WSS vector and in a local coordinate system is calculated as

$$ {\text{WSSG}} = \left[ {\left( {{\frac{{\partial \tau_{w,m} }}{\partial m}}} \right)^{2} + \left( {{\frac{{\partial \tau_{w,n} }}{\partial n}}} \right)^{2} } \right]^{1/2} $$
(9)

where m is the WSS direction and n is the direction tangential to the arterial surface and normal to m. The WSSG is calculated locally at each node using least squares fitting with singular value decomposition to find the “best fit” for the gradient components from the data at the surrounding nodes.

Wall Shear Stress Angle Gradient

ECs align with the flow direction creating a selective barrier to blood borne particles such as inflammatory cells.29 Sudden directional changes in the WSS may lead to abnormal stresses on the junctions between these barrier cells resulting in increased permeability and risk of inflammation, a precursor of IH.44 The WSSAG vector has been suggested as a mesh-independent variable to quantify these directional changes.28

The magnitude of the WSSAG is calculated as

$$ {\text{WSSAG}} = \left[ {\left( {{\frac{\partial \phi }{\partial m}}} \right)^{2} + \left( {{\frac{\partial \phi }{\partial n}}} \right)^{2} } \right]^{1/2} $$
(10)

where ϕ is the angular difference between the time-averaged WSS vector at the node of interest \( \vec{\tau }_{0} \) and the corresponding vector at the neighbor node \( \vec{\tau }_{\text{r}} \) and is computed as

$$ \phi = \pm \,{ \cos }^{ - 1} \left( {{\frac{{\vec{\tau }_{0} \cdot \vec{\tau }_{\text{r}} }}{{\left| {\vec{\tau }_{0} } \right|\left| {\vec{\tau }_{\text{r}} } \right|}}}} \right),\quad - \pi < \phi \le \pi $$
(11)

for each of the neighbor nodes. At the node of interest the value of ϕ is set to zero and the WSSAG is calculated using a similar method to the WSSG calculation. The WSSAG thus calculated is mesh dependent only at points of boundary layer separation and reattachment in the flow, with values tending toward infinity as the mesh spacing reduces to zero. To prevent these flow features from affecting the WSSAG, an upper limit of 300 rad/mm is set on the variable. This approximately corresponds to the WSSAG magnitude created by the maximum angular difference between two WSS vectors (π) acting on two small (~10 μm) adjacent ECs.

Oscillatory Shear Index

Time-dependent directional changes in the WSS may also lead to endothelial dysfunction. Specifically, areas of oscillating WSS have been shown to correlate with atherosclerotic plaque location.19 Transient directional changes in WSS are quantified by the OSI. It is possible that areas of high OSI in the stented artery increase the risk of IH through endothelial dysfunction.

The OSI is calculated as

$$ {\text{OSI}} = 1 - {\frac{{\left| {\int\limits_{0}^{T} {\vec{\tau }_{w} } dt} \right|}}{{\int\limits_{0}^{T} {\left| {\vec{\tau }_{w} } \right|dt} }}} $$
(12)

where T is the period of the cardiac cycle. The range of this variable is from 0 for unidirectional flow, to a maximum of 1 in areas of highly-altered fully-oscillatory WSS.

Analysis of Results

The WSS, WSSG, WSSAG and OSI variables, initially calculated at the element vertices, are finally face-averaged for analysis. The area distribution of these face-averaged variables is visualized using histograms by displaying the amount of area contained between specific intervals of the variable value. In addition to this qualitative technique, the area-averaged mean, standard deviation and kurtosis of the distribution of each variable are also calculated for quantitative analysis. The area-averaged mean is calculated as

$$ \mu = {\frac{{\sum\limits_{j = 1}^{e} {\left( {A_{j} \times \phi_{j} } \right)} }}{{\sum\limits_{j = 1}^{e} {A_{j} } }}} $$
(13)

where ϕ j is the face-averaged variable value at the face j, A j is the surface area of the face j and the summation is over e mesh faces. A high mean is desirable for the WSS, whereas a low mean is desirable for the WSSG, WSSAG and OSI. The area-averaged standard deviation of the distribution is calculated as

$$ \sigma = \sqrt {{\frac{{\sum\limits_{j = 1}^{e} {\left[ {\left( {A_{j} } \right) \times \left( {\phi_{j} - \mu } \right)^{2} } \right]} }}{{\sum\limits_{j = 1}^{e} {A_{j} } }}}} $$
(14)

where the terms are as before. The standard deviation provides a measure of the typical difference between variable values and the mean value of the distribution. Low values of standard deviation signify that the mean is a better representation of values everywhere on the artery wall. However, the standard deviation can be heavily influenced by extreme variable values far from the mean. The kurtosis, calculated as

$$ K = {\frac{{\sum\limits_{j = 1}^{e} {\left[ {\left( {A_{j} } \right) \times \left( {\phi_{j} - \mu } \right)^{4} } \right]} }}{{\sum\limits_{j = 1}^{e} {\left( {A_{j} \times \sigma^{4} } \right)} }}} $$
(15)

provides a measure of how heavily influenced the standard deviation is by extreme values in the distribution. A mean value may still be a good representation of the variable values everywhere in the artery even though the standard deviation is high, as long as the kurtosis is also high.

For each variable, the distributions associated with each stent are compared using Cohen’s d which measures the standardized difference between the magnitudes of the distributions. Comparing stent A to stent B, Cohen’s d is calculated as

$$ d = {\frac{{\mu_{{{\text{stent}}\;{\text{B}}}} - \mu_{{{\text{stent}}\;{\text{A}}}} }}{{\sigma_{\text{pooled}} }}} $$
(16)

where

$$ \sigma_{\text{pooled}} = \sqrt {\left( {{\frac{{\sigma_{{{\text{stent}}\;{\text{A}}}} + \sigma_{{{\text{stent}}\;{\text{B}}}} }}{2}}} \right)^{2} } $$
(17)

For WSS, negative d values are produced if stent A is the better stent and conversely for WSSG, WSSAG and OSI, positive d values favor stent A. The value of d indicates the difference between the performances of the stents with regard to each variable.

Results

Results are displayed in histograms for all four WSS-based variables. Logarithmic scales are used where appropriate to display all the relevant information. The area in the histograms is normalized by the total area analyzed which is the tissue area confined within the axial limits of the stent. Contour plots of the WSS, WSSG, WSSAG and OSI are presented in Fig. 4 for visualization. Illustrations of WSS vectors and the computational mesh near a Bx strut are shown in Figs. 5a and 5b, respectively.

Figure 4
figure 4

Contour plots of the WSS, WSSG, WSSAG and OSI predicted on the artery wall after implantation of the coronary stents

Full size image
Figure 5
figure 5

(a) WSS vectors in the vicinity of an S-connector of the Bx stent and (b) a view of the surface mesh of the uneven prolapse tissue around the same S-connector

Full size image

Wall Shear Stress

The distribution of the WSS is presented in Fig. 6 for the three stents. Mean WSS values are similar for the PS and GR-II stents with values of 0.760 and 0.764 N/m2, respectively. The mean is substantially lower for the Bx stent with a value of 0.522 N/m2. These WSS values are 25–50% lower than those expected for an unstented 3.2 mm artery under similar flow conditions (~1.0 N/m2). The results therefore predict that insertion of these stents reduces the WSS on the artery wall. Figure 4 shows that WSS values are reduced below 1.0 N/m2 in large areas around all stent struts. This is a similar result to previous studies.23 , 24 The standard deviation of the WSS is slightly higher for the GR-II stent, and the relatively low kurtosis reveals this is not due to extreme values but rather a wider spread of WSS values in the artery. The 63% higher value of kurtosis for the PS stent compared to the GR-II stent indicates that the PS mean WSS value represents a larger portion of the artery compared to the similar GR-II mean value. As such, conditions are more favorable in the artery implanted with the PS stent compared to the GR-II stent, with the worst WSS values created by implantation of the Bx stent. Large areas of low WSS are visible on the proximal side of the GR-II struts in Fig. 4, due to low flow velocity in this region. The thicker struts of the Bx stent have a notable effect on the near-strut low WSS region which is considerably larger than that for the similarly shaped PS stent. Comparing the stents gives PS to Bx (d = −0.703), PS to GR-II (d = −0.010) and GR-II to Bx (d = −0.613). This puts the stents in order from best to worst as PS, GR-II and Bx.

Figure 6
figure 6

Distributions of the WSS. The bars represent the amount of normalized area with WSS values bounded by the tick marks on the abscissa. Bin widths are 0.05 N/m2

Full size image

The commonly used threshold method of analysis shows that the PS stent has 22.4% of arterial tissue exposed to WSS < 0.5 N/m2 compared with 32.3% for the GR-II stent and 49.5% for the Bx stent. In this case, through comparison with the proposed methodology, the threshold method is capable of identifying the alterations to the magnitude of the WSS after implantation of these particular stents.

Wall Shear Stress Gradient

The distribution of the WSSG is shown in Fig. 7. The GR-II stent has the highest mean value, followed by the Bx stent and finally the PS stent. Further examination of the results reveals the highest standard deviation and lowest kurtosis for the GR-II stent indicating a wider spread of WSSG values leading to more area subjected to higher magnitudes of WSSG. Comparing the PS and Bx stents, the distributions of WSSG in the artery are similar. The slightly lower mean and higher kurtosis marginally favors the PS as the stent with the best WSSG conditions. Figure 4 reveals the areas of highest WSSG at the articulation site and also proximal and distal to the struts that traverse the flow with the PS stent. High values of WSSG (>2000 N/m3) are visible along the length of the GR-II stent. The high WSSG values are located on the surfaces of the unsupported tissue that is prolapsing into the artery. Uneven prolapse near the S-connectors of the Bx stent has also produced high WSSG values. Comparing the stents gives PS to Bx (d = 0.159), PS to GR-II (d = 0.837) and GR-II to Bx (d = −0.764). This puts the stents in order from best to worst as PS, Bx and GR-II. Comparing the stents using the threshold method of analysis, the PS stent exposes 97.6% of the arterial tissue to WSSG > 200 N/m3 compared with 97.4% with the GR-II stent and 98.9% with the Bx stent. These results are very similar, and demonstrate that when analyzing the WSSG, the threshold method is unable to distinguish between the stents.

Figure 7
figure 7

Distributions of the WSSG. The bars represent the amount of normalized area with WSSG values bounded by the tick marks on the abscissa. Bin widths are 100 N/m3

Full size image

Wall Shear Stress Angle Gradient

The distribution of the WSSAG is presented in Fig. 8 using both semi-log and log–log plots to ensure firstly, that the trend of the data is identifiable and secondly, that all of the analyzed area is visible on the plot. The mean value is highest for the Bx stent indicating that implantation of this stent leads to the greatest alteration to the WSS direction. This is followed by the GR-II stent which produces the highest standard deviation and lowest kurtosis. The PS has the best result with a mean WSSAG value of 2.405 rad/mm. The log–log histograms in Fig. 8 show that all stents have a small amount of area (approximately 0.03%) in the 100–200 rad/mm histogram range and the GR-II and Bx have very small amounts of area (approximately 0.001%) in the 200–300 rad/mm range. Figure 4 shows the areas with the highest values of WSSAG located around the S-connectors of the Bx stent and also proximal and distal to the GR-II stent struts which traverse the flow. Large areas of low WSSAG are evident in between the struts of the PS stent with values peaking near the small portions of the struts that traverse the flow. Comparing the stents gives PS to Bx (d = 0.338), PS to GR-II (d = 0.213) and GR-II to Bx (d = 0.082). This puts the stents in order from best to worst as PS, GR-II and Bx.

Figure 8
figure 8

Distributions of the WSSAG. The bars represent the amount of normalized area with WSSAG values bounded by the tick marks on the abscissa. Bin widths are distributed logarithmically. Additional log–log plots are provided to display all of the arterial area analyzed

Full size image

This variable provides a new perspective on the alterations to the WSS induced by stent implantation that is not commonly analyzed. Therefore, no threshold value exists in the literature to allow for comparison of techniques.

Oscillatory Shear Index

Implantation of the Bx stent creates the greatest transient variation in the WSS direction as the mean of the OSI is 30 and 54% higher than for the GR-II and PS stents, respectively. As shown in Fig. 9, the Bx stent also has the highest standard deviation and lowest kurtosis of the three stents indicating that this stent performs the worst with regard to OSI. Comparatively the PS stent has the lowest mean and standard deviation with the highest kurtosis indicating that implantation of this stent creates the least alteration to the transient WSS direction. Since the range of the OSI is from 0 to 1, the mean values of OSI in the arteries for the three stents are very low and as such, the differences in the distributions may be viewed as insignificant. However, the OSI quantifies transient directional changes in flow direction which may only be significant for IH in specific small areas of the artery which could amplify the significance of these small differences. The log–log plot shows small areas in the 0.4–0.5 range of OSI for the PS stent and small areas in the 0.5–0.6 range for the GR-II and Bx stents. This indicates regions where there are highly transient directional changes in the WSS vector. Since the inlet flow is unidirectional, Fig. 4 shows that most of the stented artery has low values (<0.05) of OSI. The OSI is slightly elevated in the proximal region for all stents and has its peak values very close to the GR-II stent wires and in select locations near the Bx struts and S-connectors as shown in Fig. 4. Comparing the stents gives PS to Bx (d = 0.620), PS to GR-II (d = 0.315) and GR-II to Bx (d = 0.380). This puts the stents in order from best to worst as PS, GR-II and Bx.

Figure 9
figure 9

Distributions of the OSI. The bars represent the amount of normalized area with OSI values bounded by the tick marks on the abscissa. Bin widths are distributed logarithmically. Additional log–log plots are provided to display all of the arterial area analyzed

Full size image

Discussion

A new methodology is proposed to fully elucidate the alterations in arterial WSS induced by stent deployment. Four variables are employed in the methodology, each of which highlights a different type of alteration to the arterial WSS which could lead to IH development. The proposed method of analyzing the WSS-based variables provides a clear qualitative and quantitative assessment of each variable distribution making it possible to accurately assess the hemodynamic performance of a stent.

When the methodology is applied to the three stents, the results have favored the PS as the implanted stent which creates the least alteration to the WSS in the artery. The WSS, WSSG and WSSAG variables rank the PS stent the highest. The OSI also favors the PS stent; however the magnitudes of the mean OSI values are quite small for the stents. Nevertheless, the histograms and contour plots do show that the GR-II and Bx stents create higher magnitudes of OSI around the stent struts compared to the PS stent. The WSS, WSSAG and OSI variables rank the GR-II ahead of the Bx stent, with the only exception to the trend being the WSSG where the GR-II ranks the lowest. Overall, the methodology indicates the stents hemodynamically perform in the order of PS, GR-II and finally Bx.

Using the threshold method, the WSS variable identifies the PS as the best stent, followed by the GR-II and the Bx stents whereas the WSSG variable yields inconclusive results. In this case, the threshold method has managed to sufficiently distinguish between the stents using one variable, and also rank them in agreement with the proposed methodology. However, the threshold method does not quantify the complex hemodynamic disturbances that are identified in this paper. Furthermore, the threshold method has been proven unable to distinguish between stents in previous studies,3 , 11 , 23 where the proposed method may have proved more successful. An example of complex stent induced hemodynamic disturbance is shown in Fig. 5a where WSS vectors are shown to quickly change magnitude and direction due to the uneven prolapse shown in Fig. 5b. This leads to high WSSG and WSSAG in this area which may well lead to increased IH. The OSI in this area is also shown to be high. These effects are not identified by the use of the threshold method and such features could easily have been overlooked in the previous studies.

The clinical performance of these stents is available from the results of several clinical trials shown in Table 2. The most commonly used method of comparison of BMSs is angiographic restenosis rates, defined as percentage of patients with >50% renarrowing of the target vessel at follow up. The PS and GR-II stents were directly compared in a trial consisting of 755 patients with de novo lesions.27 Restenosis rates were found to be statistically significant (p < 0.001) between the two stents with values of 47.3 and 20.6% for the GR-II and PS, respectively. A possible factor in the poor GR-II result is the “clamshell” deployment which is likely to cause more arterial damage than for the slotted-tube type stents such as the PS. “Infrequent optimal GR-II size selection” was also noted in the study which would likely contribute to poor stent performance. The PS stent has also been involved in the stent equivalency trials ASCENT1 and NIRVANA2 and had restenosis rates of 22.1 and 22.4%, respectively. There were similar criteria for inclusion in these three trials such as native vessel diameter of greater than 3 mm, de novo lesions, and similar study end points. The Bx stent had a restenosis rate of 31.4% in the ISAR-STEREO-II35 which had patients with de novo and restenotic lesions, but similar vessel diameter and trial end points. The Bx stent also had a restenosis rate of 23.4% in the control arm of the RAVAL DES trial40 where inclusion criteria were a de novo lesion with native vessel diameter between 2.5 and 3.5 mm. While one must be cautious when comparing the results of different stent trials, it would appear that the PS stent has the best in vivo results, followed in turn by the Bx and GR-II stents. From the results of the current study it would appear that hemodynamics are influential in the restenosis rates associated with the PS and Bx stents. From the CFD results, the GR-II stent performed worse than the PS stent hemodynamically. However, it would have to be concluded that other influential factors were also to blame for the stents poor clinical performance as it had such a severe restenosis rate.

Table 2 Angiographic restenosis rates for the PS, GR-II and Bx stents from five clinical trials
Full size table

Limitations to the methodology employed in this paper include the assumptions of fully-developed laminar flow, a rigid stent and arterial wall, and the omission of a stenotic plaque. Whilst the depth of tissue prolapse is based on FEA data,36 the shape of the protruding tissue is a further limitation as it is idealized and based entirely on the geometry of the stent. Curvature and taper of the artery have also been omitted in the analysis for simplicity. The outlet boundary condition of a fixed pressure is a limitation creating a non-physiological transient pressure in the CFD model. However, this outlet boundary condition is the standard practice for modeling of pulsatile flow in arteries.3 – 5 , 13 , 21 , 23 , 25 , 37 With this boundary condition, the CFD software calculates the necessary inlet pressure to drive the flow. The velocity which is specified at the inlet should therefore maintain reasonable physiological accuracy in the computational domain.

The objective of this work is to introduce a more complete method of analyzing the alterations to WSS acting on the living tissue in the stented artery. As such, this method of stent assessment should assist in stent design in the future and is applicable to bare metal, drug-eluting and any future stents that alter the WSS in the artery after implantation.