Reliability modeling of a single-unit system with arbitrary distributions subject to different weather conditions

Abstract

The main concentration of the present study is on the evaluation of some important reliability measures of a single-unit system considering arbitrary distributions for the random variables associated with failure and repair times, time to change of weather conditions, inspection time and arrival time of the server. The system operates under two weather conditions-normal and abnormal. The unit fails completely via partial failure. There is a single server who takes some time to arrive at the system. Server inspects the unit at its complete failure to see the feasibility of its repair while repair of the unit at partial failure is done without inspection. The unit works as new after repair at partial failure whereas unit is assumed as degraded after repair at complete failure. Inspection of the degraded unit is also conducted at its failure to examine the feasibility of repair. The degraded unit is replaced by new one if inspection reveals that its repair is not feasible to the system. Some measures of system effectiveness are obtained using semi-Markov and regenerative point technique. Giving particular values to various parameters and costs, the numerical results for mean time to system failure, availability and profit function are obtained considering exponential and Rayleigh distributions for all random variables.

1 Introduction

The stochastic models of single-unit systems with different failure modes have been probed by the researchers at large scale due to their intrinsic reliability and common man’s affordability. The authors including Chander and Bansal (2005) and Malik (2008) studied single-unit systems under the assumptions that

• i Environmental conditions remain static.

• ii Unit has a constant failure rate.

• iii Unit works as new after repair.

• iv Server visits the system immediately when required.

But it is very difficult to keep the environmental conditions in the control which may fluctuate due to changing climate, voltage and other natural catastrophic. Also, hazard rates of many systems such as rotating shafts and valves are of linearly increased nature due to wear out under mechanical stress and so their failure times follow arbitrary distributions like Rayleigh distribution. Malik and Barak (2009) and Pawar et al. (2010) have obtained reliability measures of single-unit systems operating under different weather conditions with exponential distributions for failure and repair rates.

Further, the working capacity and efficiency of a unit after repair depend more or less on the standard of the repair mechanism exercised. If the unit is repaired by an ordinary server, it may work with reduced efficiency and so called a degraded unit. Malik et al. (2010) made cost analysis of a system with priority to repair subject to degradation. In addition to the above, it is not always possible for a server to visit the system immediately may because of his pre-occupations and in such a situation the server may take some time to arrive at the system (called arrival time).

While incorporating above ideas, in the present paper a reliability model for a single-unit system is developed considering arbitrary distributions for the random variables associated with failure and repair times, time to change of weather conditions, inspection time and arrival time of the server. The system operates under two weather conditions-normal and abnormal. The unit fails completely via partial failure. There is a single server who takes some time to arrive at the system. Server inspects the unit at its complete failure to see the feasibility of its repair while repair of the unit at partial failure is done without inspection. The unit works as new after repair at partial failure whereas unit is assumed as degraded after repair at complete failure. Inspection of the degraded unit is also conducted at its failure to examine the feasibility of repair. The degraded unit is replaced by new one if inspection reveals that its repair is not feasible to the system. Some measures of system effectiveness such as mean sojourn times, MTSF, availability, Busy period analysis of the server, expected number of visits by the server and profit function are obtained using semi-Markov and regenerative point technique. Giving particular values to various parameters and costs, the numerical results for MTSF, availability and profit function are obtained considering exponential and Rayleigh distributions for all random variables.

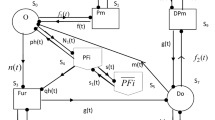
The possible transition states of the system model are shown in the following table.

S0	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13
N0	Pwr	Fwi	Pur	Pwr	Fui	Fwi	Fur	D0	Fwr	DFui	DFur	DFwi	DFwr

All states (S₀–S₁₃) are regenerative. Thus E = {S_i; 0 ≤ i ≤ 13}. The possible transition states along with transition rates for the model are shown in Fig. 1.

Fig. 1

State-transition diagram transition point, partially failed state, up state, failed state

2 Transition probabilities and mean sojourn times

It can be observed that the epoch of entry into any of the states S_i ∈ E are regenerative point. Let T ₀(≡0), T ₁, T ₂, … denote the epochs at which the system enters any state S_i ∈ E. Let X _n denote the state visited at epoch T _n +, i.e. just after transition at T _n . Then {X _n , T _n } is a Markov-renewal process with state space E and

${\text{Q}}_{\text{ij}} ({\text{t}}) = \Pr \, \{ {\text{X}}_{\text{n + 1}} = {\text{ j}},{\text{ T}}_{\text{n + 1}} - {\text{T}}_{\text{n}} \, \le {\text{ t }}|{\text{ X}}_{\text{n}} \, = {\text{ i}}\} \,$is the semi-Markov kernel over E.

The transition probability matrix of embedded Markov-chain is

${\text{p}} = ({\text{p}}_{\text{ij}} ) = ({\text{Q}}_{\text{ij}} \left( \infty \right) = {\text{Q}}(\infty ))$ with non-zero elements.

By probabilistic arguments, the non-zero elements p_ij are

$$ {\text{p}}_{ 0 1} = \int\limits_{0}^{\infty } {{\text{f}}_{1} \left( {\text{t}} \right)} \;{\text{dt}} $$

where p₀₁ means that probability of the normal unit is partially failed at time t.

All other transition probabilities can be explained in the same manner and given by

$$ \begin{aligned} {\text{p}}_{{01}} = {\text{p}}_{{25}} = {\text{p}}_{{65}} = {\text{p}}_{{8,10}} = {\text{p}}_{{97}} = {\text{p}}_{{12,10}} = {\text{p}}_{{13,11}} = 1,\quad {\text{p}}_{{12}} = \int\limits_{0}^{\infty } {{\text{f}}_{2} \left( {\text{t}} \right)} \;\overline{{\text{W}}} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{13}} = \int\limits_{0}^{\infty } {{\text{w}}\left( {\text{t}} \right)} \;\overline{{{\text{F}}_{{\text{2}}} }} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{3,0}} = \int\limits_{0}^{\infty } {{\text{g}}_{{\text{1}}} {\text{(t)}} \,\overline{{{\text{F}}_{{\text{2}}} {\text{(t)}}}} } \;\overline{{{\text{Z(t)}}}} {\text{dt}},\quad {\text{p}}_{{3,4}} = \int\limits_{0}^{\infty } {{\text{z(t)}} \,\overline{{{\text{F}}_{{\text{2}}} {\text{(t)}}}} } \;\overline{{{\text{G}}_{{\text{1}}} {\text{(t)}}}} {\text{dt}},\quad {\text{p}}_{{3,5}} = \int\limits_{0}^{\infty } {{\text{f}}_{{\text{2}}} {\text{(t)}} \,\overline{{{\text{G}}_{{\text{1}}} {\text{(t)}}}} } \;\overline{{{\text{Z(t)}}}} {\text{dt}},\quad {\text{p}}_{{4,3}} = \int\limits_{0}^{\infty } {{\text{z}}_{{\text{1}}} \left( {\text{t}} \right)} \;\overline{{{\text{F}}_{{\text{2}}} }} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{4,6}} = \int\limits_{0}^{\infty } {{\text{f}}_{{\text{2}}} \left( {\text{t}} \right)} \;\overline{{{\text{Z}}_{{\text{1}}} }} \left( {\text{t}} \right){\text{dt}},\quad \\ & {\text{p}}_{{5,0}} = \int\limits_{0}^{\infty } {{\text{qh}}_{{\text{2}}} \left( {\text{t}} \right)} \;\overline{{\text{Z}}} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{5,6}} = \int\limits_{0}^{\infty } {{\text{z}}\left( {\text{t}} \right)} \;\overline{{{\text{H}}_{{\text{2}}} }} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{5,7}} = \int\limits_{0}^{\infty } {{\text{ph}}_{{\text{2}}} \left( {\text{t}} \right)} \;\overline{{\text{Z}}} \left( {\text{t}} \right){\text{dt}},\quad \\ & {\text{p}}_{{7,8}} = \int\limits_{0}^{\infty } {{\text{g}}\left( {\text{t}} \right)} \;\overline{{\text{Z}}} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{7,9}} = \int\limits_{0}^{\infty } {{\text{z}}\left( {\text{t}} \right)} \;\overline{{\text{G}}} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{10,0}} = \int\limits_{0}^{\infty } {{\text{qh}}_{{\text{1}}} \left( {\text{t}} \right)} \;\overline{{\text{Z}}} \left( {\text{t}} \right){\text{dt}},\quad \\ & {\text{p}}_{{10,11}} = \int\limits_{0}^{\infty } {{\text{ph}}_{{\text{1}}} \left( {\text{t}} \right)} \;\overline{{\text{Z}}} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{10,12}} = \int\limits_{0}^{\infty } {{\text{z}}\left( {\text{t}} \right)} \;\overline{{{\text{H}}_{{\text{1}}} }} \left( {\text{t}} \right){\text{dt}},\quad {\text{p}}_{{11,8}} = \int\limits_{0}^{\infty } {{\text{g}}_{{\text{2}}} \left( {\text{t}} \right)} \;\overline{{\text{Z}}} \left( {\text{t}} \right){\text{dt}},\quad \\ & {\text{p}}_{{11,13}} = \int\limits_{0}^{\infty } {{\text{z}}\left( {\text{t}} \right)} \;\overline{{{\text{G}}_{{\text{2}}} }} \left( {\text{t}} \right){\text{dt}} \\ \end{aligned} $$

(1)

It can be easily verified that

$$ {\text{p}}_{01} = {\text{p}}_{25} = {\text{p}}_{65} = {\text{p}}_{97} = {\text{p}}_{8,10} = {\text{p}}_{12,10} = {\text{p}}_{13,11} = {\text{p}}_{12} + {\text{p}}_{13} = {\text{p}}_{34} + {\text{p}}_{30} + {\text{p}}_{35} = {\text{p}}_{43} + {\text{p}}_{46} = {\text{p}}_{56} + {\text{p}}_{50} + {\text{p}}_{57} = {\text{p}}_{79} + {\text{p}}_{78} = {\text{p}}_{10,0} + {\text{p}}_{10,11} + {\text{p}}_{10,12} = {\text{p}}_{11,8} + {\text{p}}_{11,13} = 1 $$

(2)

The mean sojourn times μ_i in the state S_i are given by

$$ \mu _{0} = \int\limits_{0}^{\infty } {\overline{{F_{1} (t)}} } dt,\quad \mu _{1} = \int\limits_{0}^{\infty } {\overline{{W(t)}} \overline{{\,F_{2} (t)}} } dt,\quad \mu _{2} = \int\limits_{0}^{\infty } {\overline{{W(t)}} } dt,\quad \mu _{3} = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \overline{{\,G_{1} (t)}} } \,\overline{{F_{2} (t)}} dt,\quad \mu _{4} = \int\limits_{0}^{\infty } {\overline{{Z_{1} (t)}} } \,\overline{{F_{2} (t)}} dt,\quad \mu _{5} = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \overline{{\,H_{2} (t)}} } dt,\quad \mu _{6} = \int\limits_{0}^{\infty } {\overline{{Z_{1} (t)}} } dt = \mu _{9} = \mu _{{12}} = \mu _{{13}} ,\quad \mu _{7} = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \overline{{\,G(t)}} } dt,\quad \mu _{8} = \int\limits_{0}^{\infty } {\overline{{F_{3} (t)}} } dt,\quad \mu _{{10}} = \int\limits_{0}^{\infty } {\overline{{Z(t)\,}} \overline{{H_{1} (t)}} } dt,\quad \mu _{{11}} = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \,\overline{{G_{2} (t)}} } dt $$

(3)

Also,

$$ {\text{m}}_{{01}} = \mu _{1} ,\quad {\text{m}}_{{12}} + {\text{m}}_{{13}} = \mu _{1} ,\quad {\text{m}}_{{34}} + {\text{m}}_{{35}} + {\text{m}}_{{30}} = \mu _{3} ,\quad {\text{m}}_{{43}} + {\text{m}}_{{46}} = \mu _{4} ,\quad {\text{m}}_{{50}} + {\text{m}}_{{56}} + {\text{m}}_{{57}} = \mu _{5} ,\quad {\text{m}}_{{78}} + {\text{m}}_{{79}} = \mu _{7} ,\quad {\text{m}}_{{8,10}} = \mu _{8} ,\quad {\text{m}}_{{10,0}} + {\text{m}}_{{10,11}} + {\text{m}}_{{10,12}} = \mu _{{10}} ,\quad {\text{m}}_{{11,8}} + {\text{m}}_{{11,13}} = \mu _{{13}} ,\quad {\text{m}}_{{65}} = {\text{m}}_{{97}} = {\text{m}}_{{12,10}} = {\text{m}}_{{13,11}} = \mu _{6} = \mu _{9} = \mu _{{12}} = \mu _{{13}} $$

(4)

3 Reliability and mean time to system failure

Let ϕ_i(t) be the c.d.f of first passage time from the regenerative state S_i to a failed state. Regarding the failed state as absorbing state, we have the following recursive relation for ϕ_i(t):

$$ \phi _{i} \left( t \right) = \sum\limits_{j} {Q_{{i,j}} \left( t \right)\textregistered \phi _{j} \textregistered \left( t \right)} + \sum\limits_{k} {Q_{{i,k}} \left( t \right)}$$

(5)

where S_j is an un-failed regenerative state to which the given regenerative state S_i can transit and S_k is a failed state to which the state S_i can transit directly.

Taking LST of above relations (5) and solving for $\phi _{0}^{{**}}$(s), we have

$$ {\rm{R}}^{*} \left( {\rm{s}} \right) = {{1 - {\rm{ }}\phi _{0}^{{**}} \left( {\rm{s}} \right)} \over {\rm{s}}} $$

(6)

The reliability of the system model can be obtained by taking inverse LT of (6)

MTSF is given by

$$ {\text{MTSF }} = \mathop {\lim }\limits_{{{\text{s}} \to 0}} {\text{R}}^{*} \left( {\text{s}} \right) = \frac{{{\text{N}}_{1} }}{{{\text{D}}_{1} }} $$

(7)

where N₁ = (μ₀ + μ₁)(1 − p₃₄p₄₃) + p₁₃(μ₃ + p₃₄μ₄), D₁  = 1 − p₃₄p₄₃ − p₁₃p₃₀.

4 Steady state availability

Let A_i(t) be the probability that the system is in up state at instant ‘t’ given that the system entered regenerative state S_i at t = 0. The recursive relations for A_i(t) are given as

$$ {\text{A}}_{\text{i}} \left( {\text{t}} \right) = {\text{M}}_{\text{i}} \left( {\text{t}} \right) + \sum\limits_{\text{j}} {{\text{q}}_{\text{i,j}} \left( {\text{t}} \right)\,\copyright\,{\text{A}}_{\text{j}} \left( {\text{t}} \right)} $$

(8)

where S_j is any successive regenerative state to which the regenerative state S_i can transit and M_i(t)’s obtained as

$$ M_{0} = \int\limits_{0}^{\infty } {\overline{{F_{1} (t)}} } dt,\quad M_{1} = \int\limits_{0}^{\infty } {\overline{{W(t)\,}} \overline{{F_{2} (t)}} } dt,\quad M_{3} = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \,\overline{{G_{1} (t)}} \,} \overline{{F_{2} (t)}} dt,\quad M_{4} = \int\limits_{0}^{\infty } {\overline{{Z_{1} (t)\;}} } \overline{{F_{2} (t)}} dt,\quad M_{8} = \int\limits_{0}^{\infty } {\overline{{\;F_{3} (t)}} } \;dt $$

(9)

Taking LT of relations (8) and solving for A ^*₀ (s). The steady state availability can be determined as

$$ {\text{A}}_{0} \left( \infty \right)\, = \,\mathop {\lim }\limits_{{{\text{s}} \to 0}} \,\,{\text{s}}\,{\text{A}}_{0}^{*} \left( {\text{s}} \right) = \frac{{{\text{N}}_{2} }}{{{\text{D}}_{2} }} $$

(10)

where

$$ {\text{N}}_{2} = {\text{p}}_{{78}} {\text{p}}_{{11,8}} {\text{p}}_{{10,0}} \left( {1 - {\text{p}}_{{56}} } \right)\left[ {\left( {1 - {\text{p}}_{{34}} {\text{p}}_{{43}} } \right)\left( {\mu _{0} + \mu _{1} } \right)\,+\,{\text{p}}_{{13}} \left( {\mu _{3} + {\text{p}}_{{34}} \mu _{4} } \right)} \right]\,\, + \mu _{8} {\text{p}}_{{57}} {\text{p}}_{{78}} {\text{p}}_{{11,8}} \left( {1 - {\text{p}}_{{10,12}} } \right)\left( {1 - {\text{p}}_{{34}} {\text{p}}_{{43}} - {\text{p}}_{{13}} {\text{p}}_{{30}} } \right) $$

$$ {\text{D}}_{2} = {\text{p}}_{{78}} {\text{p}}_{{11,8}} {\text{p}}_{{10,0}} \left[ {\left( {1 - {\text{p}}_{{56}} } \right)\left\{ {\left( {1 - {\text{p}}_{{34}} {\text{p}}_{{43}} } \right)\left( {\mu _{0} + \mu _{1} + {\text{p}}_{{12}} \mu _{2} } \right) + {\text{p}}_{{13}} \left( {\mu _{3} + {\text{p}}_{{34}} \left( {\mu _{4} + {\text{p}}_{{46}} \mu _{6} } \right)} \right)} \right\}} \right]\, + \left( {1 - {\text{p}}_{{34}} {\text{p}}_{{43}} - {\text{p}}_{{13}} {\text{p}}_{{30}} } \right)\left[ {{\text{p}}_{{10,0}} {\text{p}}_{{11,8}} \left\{ {{\text{p}}_{{78}} \left( {\mu _{5} + {\text{p}}_{{56}} \mu _{6} + {\text{p}}_{{57}} \mu _{8} } \right) + {\text{p}}_{{57}} \left( {\mu _{7} + {\text{p}}_{{79}} \mu _{9} } \right)} \right\}} \right.\,\left. { + \, {\text{p}}_{{57}} {\text{p}}_{{78}} \left\{ {{\text{p}}_{{11,8}} \left( {\mu _{{10}} + {\text{p}}_{{10,12}} \mu _{{12}} } \right) + {\text{p}}_{{10,11}} \left( {\mu _{{11}} + {\text{p}}_{{11,13}} \mu _{{13}} + {\text{p}}_{{11,8}} \mu _{8} } \right)} \right\}} \right] $$

5 Busy period analysis

Let B_i(t) be the probability that the server is busy in repairing the unit at an instant ‘t’ given that the system entered regenerative state S_i at t = 0. The recursive relations for B_i(t) are given as

$$ {\text{B}}_{\text{i}} \left( {\text{t}} \right) = {\text{W}}_{\text{i}} \left( {\text{t}} \right) + \sum\limits_{\text{j}} {{\text{q}}_{\text{i,j}} \left( {\text{t}} \right)\,\copyright\,{\text{B}}_{\text{j}} \left( {\text{t}} \right)} $$

(11)

where S_j is any successive regenerative state to which the regenerative state S_i can transit and W_i(t) can be obtained as

$$ W_{3} (t) = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \,\overline{{G_{1} (t)}} } \overline{{\,F_{2} (t)}} dt,\quad W_{5} (t) = \int\limits_{0}^{\infty } {\overline{{Z(t)\,}} \overline{{H_{2} (t)}} } dt,\quad W_{7} (t) = \int\limits_{0}^{\infty } {\overline{{Z(t)\,}} \overline{{G(t)}} } dt,\quad W_{{10}} (t) = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \,\overline{{H_{1} (t)}} } dt,\quad W_{{11}} (t) = \int\limits_{0}^{\infty } {\overline{{Z(t)}} \overline{{\,G_{2} (t)}} } dt $$

(12)

Taking LT of relations (11) and solving for B ^*₀ (s). The busy period of the server can be determined as.

$$ {\text{B}}_{0} = \mathop {\lim }\limits_ {{{\text{s}} \to 0}} {\text{sB}}_{0}^{*} \left( {\text{s}} \right)\, = \frac{{{\text{N}}_{3} }}{{{\text{D}}_{2} }} $$

(13)

where

$$ {\text{N}}_{3} \, = {\text{W}}_{3} {\text{p}}_{{13}} {\text{p}}_{{78}} {\text{p}}_{{11,8}} {\text{p}}_{{10,0}} \left( {1 - {\text{p}}_{{56}} } \right) + \left( {1 - {\text{p}}_{{34}} {\text{p}}_{{43}} - {\text{p}}_{{13}} {\text{p}}_{{30}} } \right) \left[ {{\text{p}}_{{10,0}} {\text{p}}_{{11,8}} \left( {{\text{W}}_{5} {\text{p}}_{{78}} + {\text{W}}_{7} {\text{p}}_{{57}} } \right)} \right. + \left. {{\text{p}}_{{57}} {\text{p}}_{{78}} {\text{p}}_{{10,11}} {\text{W}}_{{11}} } \right] $$

and D₂ has already mentioned.

6 Expected number of visits by the server

Let N_i (t) be the expected number of visits by the server in (0, t] given that the system entered the regenerative state S_i at t = 0, we have the following recurrence relations for N_i(t):

$$ {\text{N}}_{\text{i}} \left( {\text{t}} \right) = \sum\limits_{\text{j}} {{\text{Q}}_{\text{i,j}} \left( {\text{t}} \right)\textregistered \, \textregistered \left[ {\delta_{\text{j}} + {\text{N}}_{\text{j}} \left( {\text{t}} \right)} \right]^{{}} } $$

(14)

where S_j is any regenerative state to which the given regenerative state S_i transits.

$$ \delta _{{\text{j}}} = \left\{ {\begin{array}{*{20}c} 1 \hfill & {{\text{S}}_{{\text{j}}} \;{\text{is}}\;{\text{regenerative}}\;{\text{state}}} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right\} $$

Taking LST of the relation (14) and solving for $\text N_{0}^{**}$(s). The expression for expected number of visits per unit time is given by

$$ {\text{N}}_{0} \, = \,\mathop {\lim }\limits_{{{\text{s}} \to 0}} \,\,{\text{s}}\,{\text{N}}_{0}^{**} \left( {\text{s}} \right)\, = \,\,\frac{{{\text{N}}_{4} }}{{{\text{D}}_{2} }} $$

(15)

where

$$ {\text{N}}_{4}\,=\,{\text{p}}_{78} {\text{p}}_{11,8} \left[ {{\text{p}}_{10,0} \left( {1 - {\text{p}}_{56} } \right)\left( {1 - {\text{p}}_{34} {\text{p}}_{43} } \right) + {\text{p}}_{57} \left( {1 - {\text{p}}_{10,12} } \right)\left( {1 - {\text{p}}_{34} {\text{p}}_{43} - {\text{p}}_{13} {\text{p}}_{30} } \right)} \right] $$

and D₂ has already mentioned.

7 Profit analysis

Any manufacturing industry is basically a profit making organization and no organization can survive for long without minimum financial returns for its investment. There must be an optimal balance between the reliability aspect of a product and its cost. The major factors contributing to the total cost are availability, busy period of server and expected number of visits by the server. The cost of these individual items varies with reliability or mean time to system failure. In order to increase the reliability of the products, we would require a correspondingly high investment in the research and development activities. The production cost also would increase with the requirement of greater reliability.

The revenue and cost function leads to the profit function of a firm/organization, as the profit is excess of revenue over the cost of production. The profit function in time t is given by

P(t) = expected revenue in (0, t] − expected total cost in (0, t]

In general, the optimal policies can more easily be derived for an infinite time span or compared to a finite time span. The profit per unit time, in infinite time span is expressed as

$$ \mathop {\lim }\limits_{{{\text{t}} \to \infty }} \,\frac{{{\text{P}}({\text{t}})}}{\text{t}} $$

i.e. profit per unit time = total revenue per unit time − total cost per unit time. Considering the various costs, the profit equation is given as

$$ {\text{P }} = {\text{ K}}_{0} {\text{A}}_{0} - {\text{K}}_{1} {\text{B}}_{0} - {\text{K}}_{2} {\text{N}}_{0} $$

where P profit per unit time incurred to the system, K₀ revenue per unit up time of the system, A₀ total fraction of time for which the system is operative, K₁ cost per unit time for which server is busy, B₀ total fraction of time for which the server is busy, K₂ cost per visit by the server, N₀ expected number of visits per unit time for the server.

8 Results and discussion

To show the importance of results and characterize the behavior of MTSF, availability and profit of the system, here we assume that failure times of units, time of change of weather conditions, repair times of the units, inspection times and arrival time of the server as Weibull distributed with two parameters. Probability density function of Weibull distribution with two parameters is given by

$$ f(t) = \uplambda t\exp \left[ {{\raise0.7ex\hbox{${ - \uplambda t^{b + 1} }$} \!\mathord{\left/ {\vphantom {{ - \uplambda t^{b + 1} } {b + 1}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${b + 1}$}}} \right] \quad t \ge 0 \, $$

where b and λ are positive constants and are known as shape and scale parameters respectively. From the properties of Weibull distribution, If b = 0, it become the exponential distribution and when b = 1, it becomes the Rayleigh distribution.

Let

$$ {\text{f}}_{1} ({\text{t}}) = {\text{r}}_{1} \exp [ - {\text{r}}_{1} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{f}}_{2} ({\text{t}}) = {\text{r}}_{2} \exp [ - {\text{r}}_{2} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{f}}_{3} ({\text{t}}) = {\text{r}}_{3} \exp [ - {\text{r}}_{3} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{z}}({\text{t}}) = \beta \exp [ - \beta {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{z}}_{1} ({\text{t}}) = \beta {}_{1}\exp [ - \beta {}_{1}{\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{h}}_{1} ({\text{t}}) = \alpha _{1} \exp [ - \alpha _{1} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{g}}({\text{t}}) = \theta \exp [ - \theta {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{h}}_{2} ({\text{t}}) = \alpha _{2} \exp [ - \alpha _{2} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{g}}_{1} ({\text{t}}) = \theta _{1} \exp [ - \theta _{1} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{g}}_{2} ({\text{t}}) = \theta _{2} \exp [ - \theta _{2} {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1],\quad {\text{w}}({\text{t}}) = \lambda \exp [ - \lambda {\text{t}}^{{{\text{b}} + 1}} /{\text{b}} + 1] $$

For particular values to various parameters and costs, the numerical results for MTSF, availability and profit function are obtained by considering exponential and Rayleigh distributions for all random variables associated with failure, weather conditions, inspection, waiting time of the server and repair times as shown in Tables 1, 2 and 3.

Table 1 Mean time to system failure (MTSF)

Table 2 Availability

Table 3 Profit of the system

Table 1 depicts that MTSF keeps on increasing with the increase of normal weather rate (β₁) and repair rate (θ₁) of the partially failed unit. However, there is a sudden decrease in the value of MTSF with the increase of failure rate (r₂) of the partially unit and abnormal weather rate (β). From Tables 2 and 3, it is observed that availability and profit of the system increase with the increase of normal weather rate (β₁) for fixed values of other parameters including K₀ = 5,000, K₁ = 500 and K₂ = 50. And, their values decrease as failure rate (r₂) of the partially unit and abnormal weather rate (β) increase. It can also be seen that availability and profit of the system increase with the increase of repair rate (θ₁) of the partially failed unit and by interchange the values of probabilities of feasibility of repair or replacement of failed degraded unit (i.e. p₁ and q₁).

From Tables 1, 2 and 3, it is observed that the behavior for MTSF, availability and profit of the system is same for both the distributions.

9 Conclusion

The numerical results for MTSF, availability and profit function are obtained considering exponential and Rayleigh distributions for several random variables associated with failure time, repair time, change of weather conditions, inspection time and arrival time of the server as shown respectively in Tables 1, 2 and 3. It is observed that a single-unit system has more values of MTSF if random variables follow exponential distribution rather than Rayleigh distribution. But availability of such a system is more in case random variables are Rayleigh distributed. Table 3 indicates that single-unit system is more profitable with exponential distribution for random variables. However, a single-unit system will be more profitable with Rayleigh distribution if β = 0.3.