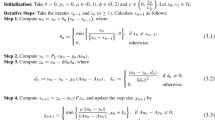1 Introduction

Throughout this paper, C is assumed to be a convex and closed nonempty set in a Hilbert space H with the inner product \(\langle \cdot , \cdot \rangle\) and the norm \(\Vert \cdot \Vert\). One gives two single-valued mappings \(A: H \rightarrow H\) and \(F: H \rightarrow H\) on H. The classical variational inequality problem (VIP) is described as follows.

$$\begin{aligned} \text {Find } y^{*} \in C \text{ such } \text{ that } \left\langle A y^{*}, z-y^{*}\right\rangle \ge 0,\quad \forall z \in C\,. \end{aligned}$$
(VIP)

One denotes by \(\mathrm {VI}(C, A)\) the set of all solutions of (VIP). In this paper, one investigates two numerical methods to find solutions of the following bilevel variational inequality problem (BVIP), which reads as follows.

$$\begin{aligned} \text {Find } x^{*} \in \mathrm {VI}(C, A) \text{ such } \text{ that } \left\langle F x^{*}, y-x^{*}\right\rangle \ge 0,\quad \forall y \in \mathrm {VI}(C, A)\,. \end{aligned}$$
(BVIP)

Bilevel variational inequality problems, which have been extensively investigated by numerical methods, cover a number of nonlinear optimization problems, such as, fixed point problems, quasi-variational inequality problems, complementary problems, saddle problems and minimum norm problems, see, e.g., [1,2,3,4,5]. It is known that (VIP) is equivalent to the fixed point problem of finding a point \(x^{*}\) in C such that \(x^{*}=P_{C}\left( x^{*}-\lambda A x^{*}\right)\), where \(\lambda\) is any positive real number and \(P_{C}\) represents the metric projection from H onto C (see the definition in Sect. 2). Recently, a number of authors proposed and analyzed various methods to solve the (VIP). Two notable methods to solve (VIP) are the regularization method and the projection method. In this paper, we focus on the second approach involving projection methods. The simplest and oldest projection method is the gradient projection method:

$$\begin{aligned} x_{n+1}=P_{C}\left( x_{n}-\lambda A x_{n}\right) \,. \end{aligned}$$
(1.1)

It is known that the iterative sequence defined by (1.1) converges to an element of \(\mathrm {VI}(C, A)\) when A is L-Lipschitz continuous and \(\alpha\)-strongly monotone and \(\lambda \in \left( 0, 2 \alpha /L^{2}\right)\). For avoiding the use of such assumptions, the extragradient method (EGM) [6] has been proposed for a monotone and L-Lipschitz continuous mapping A. The algorithm can be presented as follows:

$$\begin{aligned} \left\{ \begin{aligned}&y_{n}=P_{C}\left( x_{n}-\lambda A x_{n}\right) \,, \\&x_{n+1}=P_{C}\left( x_{n}-\lambda A y_{n}\right) \,, \end{aligned}\right. \end{aligned}$$
(1.2)

where \(\lambda \in \left( 0, 1/L\right)\). The algorithm defined by (1.2) converges to an element of \(\mathrm {VI}(C, A)\) provided that \(\mathrm {VI}(C, A)\) is nonempty.

We see that the EGM needs to compute two projections onto the feasible set C and two evaluations of operator A in each iteration. Generally, this is expensive, and when operator A and feasible set C have a complicated structure, it will affect the efficiency of the method used. To overcome one of these shortcomings, there are two notable methods in the literature. The first one is the subgradient extragradient method (SEGM) [7], which can be considered as an improvement of the EGM. The algorithm reads as follows:

$$\begin{aligned} \left\{ \begin{aligned}&y_{n}=P_{C}\left( x_{n}-\lambda A x_{n}\right) \,, \\&T_{n}=\left\{ x \in H \mid \left\langle x_{n}-\lambda A x_{n}-y_{n}, x-y_{n}\right\rangle \le 0\right\} \,, \\&x_{n+1}=P_{T_{n}}\left( x_{n}-\lambda A y_{n}\right) \,, \end{aligned}\right. \end{aligned}$$
(1.3)

where \(\lambda \in (0,1/L)\). The main advantage of SEGM is that it replaces the second projection from the closed and convex subset C to the half-space \(T_{n}\), and this projection can be calculated by an explicit formula.

The second one is called the Tseng’s extragradient method [8], which is described as follows:

$$\begin{aligned} \left\{ \begin{aligned}&y_{n}=P_{C}\left( x_{n}-\lambda A x_{n}\right) \,, \\&x_{n+1}=y_{n}-\lambda \left( A y_{n}-A x_{n}\right) \,. \end{aligned}\right. \end{aligned}$$
(1.4)

It is worth noting that the algorithm defined in (1.4) only needs to calculate one projection onto the feasible set C and two evaluations of A in each step. Since subgradient extragradient method and Tseng’s extragradient method only need to calculate once projection onto the feasible set C in each step, they have received a lot of attention and research from scientific researchers, who have improved and extended in various ways to obtain the weak and strong convergence of these methods, see [9,10,11] and the references therein. However, the subgradient extragradient method and Tseng’s extragradient method need to know the Lipschitz constant of the operator A, which limits the applicability of the algorithms. To handle the case where the Lipschitz constant of the operator A is unknown, Yang et al. [12, 13] introduced the following self-adaptive step size strategy for (1.3) and (1.4), respectively.

$$\begin{aligned}&\lambda _{n+1}=\left\{ \begin{array}{ll} \min \Big \{\dfrac{\mu \big (\left\| x_{n}-y_{n}\right\| ^{2}+\left\| x_{n+1}-y_{n}\right\| ^{2}\big )}{2\left\langle Ax_{n}-Ay_{n}, x_{n+1}-y_{n}\right\rangle }, \lambda _{n}\Big \}, &{} \text{ if } \left\langle Ax_{n}-Ay_{n}, x_{n+1}-y_{n}\right\rangle > 0; \\ \lambda _{n}, &{} \text{ otherwise }, \end{array}\right. \\&\lambda _{n+1}=\left\{ \begin{array}{ll} \min \left\{ \dfrac{\mu \left\| x_{n}-y_{n}\right\| }{\left\| Ax_{n}-Ay_{n}\right\| }, \lambda _{n}\right\} , &{} \text{ if } Ax_{n}-Ay_{n} \ne 0; \\ \lambda _{n}, &{} \text{ otherwise }, \end{array}\right. \end{aligned}$$

where \(\mu \in (0,1)\) and \(\lambda _{0}>0\).

Note that computation of the metric projection \(P_C\) onto C is not necessarily easy. In order to reduce the complexity probably caused by the projection \(P_C\), Yamada [14] introduced the following hybrid steepest descent method for solving the variational inequality \(\mathrm {VI}(C, F)\). Recall that T is nonexpansive if \(\Vert Tx - Ty\Vert \le \Vert x-y\Vert , \,\,\, \forall x, y\in H\). Let \({\text {Fix}}(T) = \{x\in H: Tx = x\}\) denote the fixed point set of T. Assume that C is the fixed point set of a nonexpansive mapping \(T: H\rightarrow H\), that is, \(C = \{x\in H : Tx = x\}\). Let F be a mapping of \(\eta\)-strongly monotone and \(\kappa\)-Lipschitzian on C. Fix a constant \(\mu \in (0, 2\eta /\kappa ^2)\) and a sequence \(\{\lambda _n\}\) of real numbers in (0, 1) satisfying the following conditions: (i) \(\lim _{n\rightarrow \infty }\lambda _n = 0\), (ii) \(\sum _{n=1}^{\infty } \lambda _n = \infty\), (iii) \(\lim _{n\rightarrow \infty } (\lambda _n - \lambda _{n+1})/ \lambda _{n+1}^2 = 0\). For any initial data \(x_0 \in H\), one can generate a sequence \(\{x_n\}\) via the following algorithm:

$$\begin{aligned} \begin{aligned} x_{n+1} = Tx_n-\lambda _{n+1} \mu F(Tx_n), \quad n\ge 0\,. \end{aligned} \end{aligned}$$

Yamada proved that \(\{x_n\}\) converges to the unique solution of the \(\mathrm {VI}(C, F)\) in norm. In recent years, there are many papers dealing with the variational inequality problems by using the steepest descent method, see [15,16,17]. Note that the methods suggested in (1.2), (1.3) and (1.4) all achieve weak convergence in infinite-dimensional spaces. Examples in CT reconstruction and machine learning tell us that strong convergence is preferable to weak convergence in an infinite-dimensional space. Therefore, a natural question is how to modify the methods (1.3) and (1.4) such that they can achieve strong convergence in infinite-dimensional spaces. Recently, based on the subgradient extragradient algorithm (1.3), the Tseng’s extragradient method (1.4) and the hybrid steepest descent method [14], Thong et al. [18] proposed two new modified extragradient algorithms with strong convergence to solve the (BVIP) in a real Hilbert space.

To accelerate the convergence rate of the algorithms, Polyak [19] considered the second-order dynamical system \(\ddot{x}(t)+\gamma {\dot{x}}(t)+\nabla f(x(t))=0\), where \(\gamma >0\), \(\nabla f\) represents the gradient of f, \({\dot{x}}(t)\) and \(\ddot{x}(t)\) denote the first and second derivatives of x at t, respectively. This dynamic system is called the Heavy Ball with Friction (HBF). Next, we consider the discretization of this dynamic system (HBF), that is,

$$\begin{aligned} \frac{x_{n+1}-2 x_{n}+x_{n-1}}{h^{2}}+\gamma \frac{x_{n}-x_{n-1}}{h}+\nabla f\left( x_{n}\right) =0, \quad \forall n \ge 0\,. \end{aligned}$$

Through a direct calculation, we can get the following form:

$$\begin{aligned} x_{n+1}=x_{n}+\tau \left( x_{n}-x_{n-1}\right) -\varphi \nabla f\left( x_{n}\right) , \quad \forall n \ge 0\,, \end{aligned}$$

where \(\tau =1-\gamma h\) and \(\varphi =h^{2}\). This can be considered as the following two-step iteration scheme:

$$\begin{aligned} \left\{ \begin{aligned}&y_{n}=x_{n}+\tau \left( x_{n}-x_{n-1}\right) \,, \\&x_{n+1}=y_{n}-\varphi \nabla f\left( x_{n}\right) , \quad \forall n \ge 0\,. \end{aligned}\right. \end{aligned}$$

This iteration is now called the inertial extrapolation algorithm, the term \(\tau \left( x_{n}-x_{n-1}\right)\) is referred to as the extrapolation point. It is known that the Nesterov accelerated gradient method [20] improves the convergence rate of the gradient method from standard \(O\left( k^{-1}\right)\) down to \(O\left( k^{-2}\right)\). However, it should be highlighted that inertial algorithms do not guarantee that the objective function is monotone. Recently, many authors constructed a large number of inertial algorithms for solving variational inequalities and optimization problems; see, e.g., [21,22,23,24] and the references therein.

Motivated and inspired by the above works, we here introduce two new inertial extragradient methods for solving (BVIP) in real Hilbert spaces. The algorithms are inspired by the inertial method, the subgradient extragradient method, the Tseng’s extragradient method and the steepest descent method. We provide a choice of inertial parameter and two new stepsize rules which allow the algorithms to work without previously knowing the Lipschitz constant of the mapping. Under some suitable conditions, we prove that the iterative sequence generated by the algorithms converges strongly to a solution of (BVIP). Some numerical experiments are carried out to support the theoretical results. Our numerical results show that the new algorithms have a better convergence speed than the existing ones presented in [18].

An outline of this paper is as follows. In Sect. 2, we recall some preliminary results and lemmas for further use. Section 3 analyzes the convergence of the proposed algorithms. In Sect. 4, some numerical examples are presented to illustrate the numerical behavior of the proposed algorithms and compare them with other ones. Finally, a brief summary is given in Sect. 5.

2 Preliminaries

The weak convergence and strong convergence of \(\left\{ x_{n}\right\} _{n=1}^{\infty }\) to x are represented by \(x_{n} \rightharpoonup x\) and \(x_{n} \rightarrow x\), respectively. For any \(x,y\in H\), the operator \(T: H \rightarrow H\) is said to be (i) L-Lipschitz continuous with \(L > 0\) if \(\Vert T x-T y\Vert \le L\Vert x-y\Vert\) (if \(L=1\), then T is called nonexpansive); (ii) \(\beta\)-strongly monotone if there exists \(\beta >0\) such that \(\langle T x-T y, x-y\rangle \ge \beta \Vert x-y\Vert ^{2}\); (iii) monotone if \(\langle T x-T y, x-y\rangle \ge ~0\); (iv) pseudomonotone if \(\langle T x, y-x\rangle \ge 0 \Longrightarrow \langle T y, y-x\rangle \ge 0\); (v) sequentially weakly continuous if for each sequence \(\left\{ x_{n}\right\}\) converges weakly to x implies \(\left\{ T x_{n}\right\}\) converges weakly to Tx. For each \(x, y \in H\), we have

$$\begin{aligned} \Vert x+y\Vert ^{2} \le \Vert x\Vert ^{2}+2\langle y, x+y\rangle \,. \end{aligned}$$
(2.1)

For every point \(x \in H\), there exists a unique nearest point in C, denoted by \(P_{C} x\), such that \(P_{C}x:= {\text {argmin}}\{\Vert x-y\Vert ,\, y \in C\}\). \(P_{C}\) is called the metric projection of H onto C. It is known that \(P_{C}\) is nonexpansive and \(P_{C} x\) has the following basic properties:

  • \(\langle x-P_{C} x, y-P_{C} x\rangle \le 0, \, \forall y \in C\);

  • \(\Vert P_{C} x-P_{C} y\Vert ^{2} \le \left\langle P_{C} x-P_{C} y, x-y\right\rangle , \,\forall y \in H\).

We give some special cases with simple analytical solutions. These give us some explicit formulas to find the projection of any point onto the half-space and the ball.

  • The Euclidean projection of \(x_{0}\) onto a halfspace \(H_{a, b}^{-}=\{x:\langle a, x\rangle \le b\}\) is given by

    $$\begin{aligned} P_{H_{a, b}^{-}}(x)=x-\max \bigg \{\frac{[\langle a, x\rangle -b]}{\Vert a\Vert ^{2}},0\bigg \} a\,. \end{aligned}$$

  • The Euclidean projection of \(x_{0}\) onto an Euclidean ball \(B[c, r]=\{x:\Vert x-c\Vert \le r\}\) is given by

    $$\begin{aligned} P_{B[c, r]}(x)=c+\frac{r}{\max \{\Vert x-c\Vert , r\}}(x-c)\,. \end{aligned}$$

It is well known that if \(F: H \rightarrow H\) is L-Lipschitz continuous and \(\beta\)-strongly monotone on H and if \(\mathrm {VI}(C, A)\) is a nonempty, convex and closed subset of H, then the (BVIP) has a unique solution (see, e.g., [25]).

The following lemmas play an important role in our proofs.

Lemma 2.1

([26]) Let \({A}: {C} \rightarrow {H}\) be a continuous and pseudomonotone operator. Then, \(x^{*}\) is a solution of \(\mathrm {VI}(C, A)\) if and only if \(\left\langle A x, x-x^{*}\right\rangle \ge 0,\, \forall x \in C\).

Lemma 2.2

([14]) Let \(\gamma >0\) and \(\alpha \in (0,1]\). Let \(F: H \rightarrow H\) be a \(\beta\)-strongly monotone and L-Lipschitz continuous mapping with \(0<\beta \le L\). Associating with a nonexpansive mapping \(T: H \rightarrow H\), define a mapping \(T^{\gamma }: H \rightarrow H\) by \(T^{\gamma } x=(I-\alpha \gamma F)(T x), \forall x \in H\). Then, \(T^{\gamma }\) is a contraction provided \(\gamma <\frac{2 \beta }{L^{2}}\), that is,

$$\begin{aligned} \Vert T^{\gamma } x-T^{\gamma } y\Vert \le (1-\alpha \eta )\Vert x-y\Vert , \quad \forall x, y \in H\,, \end{aligned}$$

where \(\eta =1-\sqrt{1-\gamma \left( 2 \beta -\gamma L^{2}\right) } \in (0,1)\).

Lemma 2.3

([27]) Let \(\left\{ a_{n}\right\}\) be a sequence of nonnegative real numbers, \(\left\{ \alpha _{n}\right\}\) be a sequence of real numbers in (0, 1) with \(\sum _{n=1}^{\infty } \alpha _{n}=\infty\), and \(\left\{ b_{n}\right\}\) be a sequence of real numbers. Assume that \(a_{n+1} \le \left( 1-\alpha _{n}\right) a_{n}+\alpha _{n} b_{n},\) \(\forall n \ge 1.\) If \(\limsup _{k \rightarrow \infty } b_{n_{k}} \le 0\) for every subsequence \(\left\{ a_{n_{k}}\right\}\) of \(\left\{ a_{n}\right\}\) satisfying \(\lim \inf _{k \rightarrow \infty }\) \(\left( a_{n_{k}+1}-a_{n_{k}}\right) \ge ~0\), then \(\lim _{n \rightarrow \infty } a_{n}=0\).

3 Main results

In this section, we introduce two new inertial extragradient methods for solving (BVIP) and analyze their convergence. First, we assume that our proposed methods satisfy the following conditions.

  1. C1

    The feasible set C is a nonempty, convex and closed set.

  2. C2

    The solution set of the (VIP) is nonempty, that is \(\mathrm {VI}(C, A) \ne \emptyset\).

  3. C3

    The mapping \(A: H \rightarrow H\) is \(L_{1}\)-Lipschitz continuous and pseudomonotone on H, and sequentially weakly continuous on C.

  4. C4

    The mapping \(F: H \rightarrow H\) is \(L_{2}\)-Lipschitz continuous and \(\beta\)-strongly monotone on H such that \(L_{2} \ge \beta\). In addition, we denote by p the unique solution of the (BVIP).

  5. C5

    Let \(\{\epsilon _{n}\}\) be a positive sequence such that \(\lim _{n \rightarrow \infty } \frac{\epsilon _{n}}{\alpha _{n}}=0\), where \(\{\alpha _{n}\}\subset (0,1)\) satisfies the following conditions: \(\sum _{n=1}^{\infty } \alpha _{n}=\infty\) and \(\lim _{n \rightarrow \infty } \alpha _{n}=0\).

Remark 3.1

Our methods are embedded with the inertial terms to ensure the strong convergence of the algorithms. Condition (C5), which is routine restriction, is easily satisfied. For example, one can take \(\alpha _{n}=1/n\) and \(\epsilon _{n}=1/n^{2}\).

3.1 The modified inertial subgradient extragradient algorithm

Now, we introduce the new modified inertial subgradient extragradient algorithm for solving (BVIP). Algorithm 3.1 reads as follows:

figure a

Remark 3.2

It follows from (3.1) that

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert =0\,. \end{aligned}$$

Indeed, we have \(\theta _{n}\Vert x_{n}-x_{n-1}\Vert \le \epsilon _{n}\) for all n, which together with \(\lim _{n \rightarrow \infty } \frac{\epsilon _{n}}{\alpha _{n}}=0\) implies that

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert \le \lim _{n \rightarrow \infty } \frac{\epsilon _{n}}{\alpha _{n}}=0\,. \end{aligned}$$

Lemma 3.1

Assume that Conditions (C1)–(C3) hold. Then, the sequence \(\{\lambda _{n}\}\) generated by (3.2) is a nonincreasing sequence and

$$\begin{aligned} \lim _{n \rightarrow \infty } \lambda _{n}=\lambda \ge \min \Big \{\lambda _{1}, \frac{\mu }{L_{1}}\Big \}\,. \end{aligned}$$

Proof

We can easily get that \(\lambda _{n+1} \le \lambda _{n}\) for all \(n \in {\mathbb {N}}\) from (3.2). Hence, \(\left\{ \lambda _{n}\right\}\) is nonincreasing. On the other hand, we have \(L_{1}\Vert w_{n}-y_{n}\Vert \ge \Vert A w_{n}-A y_{n}\Vert\), since A is \(L_{1}\)-Lipschitz continuous. Therefore, if \(\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle >0\), then

$$\begin{aligned} \mu \frac{\Vert w_{n}-y_{n}\Vert ^{2}+\Vert z_{n}-y_{n}\Vert ^{2}}{2\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle } \ge \mu \frac{\Vert w_{n}-y_{n}\Vert \Vert z_{n}-y_{n}\Vert }{\Vert A w_{n}-A y_{n}\Vert \Vert z_{n}-y_{n}\Vert }=\mu \frac{\Vert w_{n}-y_{n}\Vert }{\Vert A w_{n}-A y_{n}\Vert } \ge \frac{\mu }{L_{1}}\,, \end{aligned}$$

which together with (3.2) implies that

$$\begin{aligned} \lambda _{n} \ge \min \Big \{\lambda _{1}, \frac{\mu }{L_{1}}\Big \}\,. \end{aligned}$$

Thus, we conclude that \(\lim _{n \rightarrow \infty } \lambda _{n}\) exists since the sequence \(\left\{ \lambda _{n}\right\}\) is nonincreasing and lower bounded. \(\square\)

The following lemmas play an important role in the convergence proof of Algorithm 3.1

Lemma 3.2

Assume that Conditions (C1)–(C3) hold. Let \(\left\{ z_{n}\right\}\) be a sequence generated by Algorithm 3.1. Then, for all \(p \in \mathrm {VI}(C, A)\),

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} \le \Vert w_{n}-p\Vert ^{2}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert y_{n}-w_{n}\Vert ^{2}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert z_{n}-y_{n}\Vert ^{2}\,. \end{aligned}$$

Proof

First, from the definition of \(\left\{ \lambda _{n}\right\}\), one obtains

$$\begin{aligned} 2\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle \le \frac{\mu }{\lambda _{n+1}}\Vert w_{n}-y_{n}\Vert ^{2}+\frac{\mu }{\lambda _{n+1}}\Vert z_{n}-y_{n}\Vert ^{2}\,,\,\, \forall n\in {\mathbb {N}}\,. \end{aligned}$$
(3.3)

Indeed, if \(\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle \le 0\), then (3.3) holds. Otherwise, by (3.2) we have

$$\begin{aligned} \lambda _{n+1}=\min \bigg \{\mu \frac{\Vert w_{n}-y_{n}\Vert ^{2}+\Vert z_{n}-y_{n}\Vert ^{2}}{2\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle }, \lambda _{n}\bigg \} \le \mu \frac{\Vert w_{n}-y_{n}\Vert ^{2}+\Vert z_{n}-y_{n}\Vert ^{2}}{2\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle }\,, \end{aligned}$$

which implies that

$$\begin{aligned} 2\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle \le \frac{\mu }{\lambda _{n+1}}\Vert w_{n}-y_{n}\Vert ^{2}+\frac{\mu }{\lambda _{n+1}}\Vert z_{n}-y_{n}\Vert ^{2}\,. \end{aligned}$$

Thus, the inequality (3.3) holds. Using (3.3) and \(p \in \mathrm {VI}(C, A) \subset C \subset T_{n}\), one has

$$\begin{aligned} \begin{aligned} 2\left\| z_{n}-p\right\| ^{2}=&2\left\| P_{T_{n}}\left( w_{n}-\lambda _{n} A y_{n}\right) -P_{T_{n}} p\right\| ^{2} \le 2\left\langle z_{n}-p, w_{n}-\lambda _{n} A y_{n}-p\right\rangle \\ =&\left\| z_{n}-p\right\| ^{2}+\left\| w_{n}-\lambda _{n} A y_{n}-p\right\| ^{2}-\left\| z_{n}-w_{n}+\lambda _{n} A y_{n}\right\| ^{2} \\ =&\left\| z_{n}-p\right\| ^{2}+\left\| w_{n}-p\right\| ^{2}+ \lambda _{n}^{2}\left\| A y_{n}\right\| ^{2}-2\left\langle w_{n}-p, \lambda _{n} A y_{n}\right\rangle \\&-\left\| z_{n}-w_{n}\right\| ^{2}- \lambda _{n}^{2}\left\| A y_{n}\right\| ^{2}-2\left\langle z_{n}-w_{n}, \lambda _{n} A y_{n}\right\rangle \\ =&\left\| z_{n}-p\right\| ^{2}+\left\| w_{n}-p\right\| ^{2}-\left\| z_{n}-w_{n}\right\| ^{2}-2\left\langle z_{n}-p, \lambda _{n} A y_{n}\right\rangle \,. \end{aligned} \end{aligned}$$

This implies that

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} \le \Vert w_{n}-p\Vert ^{2}-\Vert z_{n}-w_{n}\Vert ^{2}-2\left\langle z_{n}-p, \lambda _{n} A y_{n}\right\rangle \,. \end{aligned}$$
(3.4)

Since p is the solution of (VIP), we have \(\langle A p, x-p\rangle \ge 0\) for all \(x \in C .\) By the pseudomontonicity of A on H, we get \(\langle A x, x-p\rangle \ge 0\) for all \(x \in C\). Taking \(x=y_{n} \in C\), one infers that

$$\begin{aligned} \left\langle A y_{n}, p-y_{n}\right\rangle \le 0\,. \end{aligned}$$

Consequently,

$$\begin{aligned} \left\langle A y_{n}, p-z_{n}\right\rangle =\left\langle A y_{n}, p-y_{n}\right\rangle +\left\langle A y_{n}, y_{n}-z_{n}\right\rangle \le \left\langle A y_{n}, y_{n}-z_{n}\right\rangle \,. \end{aligned}$$
(3.5)

Combining (3.4) and (3.5), one obtains

$$\begin{aligned} \begin{aligned} \Vert z_{n}-p\Vert ^{2} \le&\Vert w_{n}-p\Vert ^{2}-\Vert z_{n}-w_{n}\Vert ^{2}+2 \lambda _{n}\left\langle A y_{n}, y_{n}-z_{n}\right\rangle \\ =&\Vert w_{n}-p\Vert ^{2}-\Vert z_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-w_{n}\Vert ^{2}-2\left\langle z_{n}-y_{n}, y_{n}-w_{n}\right\rangle \\&+2 \lambda _{n}\left\langle A y_{n}, y_{n}-z_{n}\right\rangle \\ =&\Vert w_{n}-p\Vert ^{2}-\Vert z_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-w_{n}\Vert ^{2}+2\left\langle z_{n}-y_{n}, w_{n}-\lambda _{n} A y_{n}-y_{n} \right\rangle \,. \end{aligned} \end{aligned}$$
(3.6)

Since \(z_{n}=P_{T_{n}}\left( w_{n}-\lambda _{n} A y_{n}\right)\) and \(z_{n} \in T_{n}\), one has

$$\begin{aligned} \begin{aligned}&\left\langle w_{n}-\lambda _{n} A y_{n}-y_{n},z_{n}-y_{n}\right\rangle \\&=\left\langle w_{n}-\lambda _{n} A w_{n}-y_{n}, z_{n}-y_{n}\right\rangle + \lambda _{n}\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle \\&\le \lambda _{n}\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle \,, \end{aligned} \end{aligned}$$
(3.7)

which together with (3.3), we deduce that

$$\begin{aligned} 2\left\langle w_{n}-\lambda _{n} A y_{n}-y_{n}, z_{n}-y_{n}\right\rangle \le \mu \frac{\lambda _{n}}{\lambda _{n+1}}\Vert w_{n}-y_{n}\Vert ^{2}+\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Vert z_{n}-y_{n}\Vert ^{2}\,. \end{aligned}$$

From (3.6) and (3.7), we obtain

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} \le \Vert w_{n}-p\Vert ^{2}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert y_{n}-w_{n}\Vert ^{2}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert z_{n}-y_{n}\Vert ^{2}\,. \end{aligned}$$

This completes the proof of the lemma. \(\square\)

Lemma 3.3

[28, Lemma 3.3] Assume that Conditions (C1)–(C3) hold. Let \(\left\{ w_{n}\right\}\) be a sequence generated by Algorithm 3.1. If there exists a subsequence \(\left\{ w_{n_{k}}\right\}\) converges  weakly to \(z \in H\) and \(\lim _{k \rightarrow \infty }\Vert w_{n_{k}}-y_{n_{k}}\Vert =0\), then \(z \in \mathrm {VI}(C, A)\).

Theorem 3.1

Assume that Conditions (C1)–(C5) hold. Then, the sequence \(\left\{ x_{n}\right\}\) generated by Algorithm 3.1 converges to the unique solution of the (BVIP) in norm.

Proof

We divide the proof into four steps.


Setp 1. The sequence \(\left\{ x_{n}\right\}\) is bounded. Indeed, from \(\lim _{n \rightarrow \infty }\left( 1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\right) =1-\mu >0\), we know that there exists \(n_{0} \in {\mathbb {N}}\) such that

$$\begin{aligned} 1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}>0, \quad \forall n \ge n_{0}\,. \end{aligned}$$
(3.8)

Combining Lemma 3.2 and (3.8), one sees that

$$\begin{aligned} \Vert z_{n}-p\Vert \le \Vert w_{n}-p\Vert , \quad \forall n \ge n_{0}\,. \end{aligned}$$
(3.9)

On the other hand, by the definition of \(w_{n}\), we can write

$$\begin{aligned} \begin{aligned} \Vert w_{n}-p\Vert&\le \alpha _{n} \cdot \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert +\Vert x_{n}-p\Vert . \end{aligned} \end{aligned}$$
(3.10)

According to Remark 3.2 we have \(\frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert \rightarrow 0\). Therefore, there exists a constant \(M_{1}>0\) such that

$$\begin{aligned} \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert \le M_{1}, \quad \forall n \ge 1\,. \end{aligned}$$
(3.11)

Combining (3.9), (3.10) and (3.11), we obtain

$$\begin{aligned} \Vert z_{n}-p\Vert \le \Vert w_{n}-p\Vert \le \Vert x_{n}-p\Vert +\alpha _{n} M_{1},\quad \forall n \ge n_{0}\,. \end{aligned}$$
(3.12)

Using Lemma 2.2 and (3.9), it follows that

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert&=\Vert \left( I-\alpha _{n} \gamma F\right) z_{n}-\left( I-\alpha _{n} \gamma F\right) p-\alpha _{n} \gamma F p\Vert \\&\le \left( 1-\alpha _{n} \eta \right) \Vert z_{n}-p\Vert +\alpha _{n} \gamma \Vert F p\Vert \\&\le \left( 1-\alpha _{n} \eta \right) \Vert x_{n}-p\Vert +\alpha _{n}\eta \cdot \frac{M_{1}}{\eta }+\alpha _{n} \eta \cdot \frac{\gamma }{\eta }\Vert F p\Vert \\&\le \max \Big \{ \frac{M_{1}+\gamma \Vert F p\Vert }{\eta },\Vert x_{n}-p\Vert \Big \} \\&\le \cdots \le \max \Big \{\frac{M_{1}+\gamma \Vert F p\Vert }{\eta },\Vert x_{n_{0}}-p\Vert \Big \},\,\,\forall n \ge n_{0}\,, \end{aligned} \end{aligned}$$
(3.13)

where \(\eta =1-\sqrt{1-\gamma \left( 2 \beta -\gamma L_{2}^{2}\right) } \in (0,1)\). That is, this implies that \(\left\{ x_{n}\right\}\) is bounded. We get that the sequences \(\left\{ z_{n}\right\}\) and \(\left\{ w_{n}\right\}\) are also bounded.


Step 2.

$$\begin{aligned}&\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert y_{n}-w_{n}\Vert ^{2}+\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert z_{n}-y_{n}\Vert ^{2}\\&\quad \le \Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1} -p \Vert ^{2}+\alpha _{n} M_{4}, \,\, \forall n \ge n_{0} \end{aligned}$$

for some \(M_{4}>0\). Indeed, using (2.1), one has

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&=\Vert \left( I-\alpha _{n} \gamma F\right) z_{n}-\left( I-\alpha _{n} \gamma F\right) p-\alpha _{n} \gamma F p\Vert ^{2} \\&\le \left( 1-\alpha _{n} \eta \right) ^{2}\Vert z_{n}-p\Vert ^{2}+2 \alpha _{n} \gamma \left\langle F p, p-x_{n+1}\right\rangle \\&\le \Vert z_{n}-p\Vert ^{2}+\alpha _{n} M_{2} \end{aligned} \end{aligned}$$
(3.14)

for some \(M_{2}>0\). In the light of Lemma 3.2, we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2} \le \Vert w_{n}-p\Vert ^{2}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert y_{n}-w_{n}\Vert ^{2}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert z_{n}-y_{n}\Vert ^{2}+\alpha _{n}M_{2}\,. \end{aligned}$$
(3.15)

It follows from (3.12) that

$$\begin{aligned} \begin{aligned} \Vert w_{n}-p\Vert ^{2}&\le \left( \Vert x_{n}-p\Vert +\alpha _{n} M_{1}\right) ^{2} \\&=\Vert x_{n}-p\Vert ^{2}+\alpha _{n}\left( 2 M_{1}\Vert x_{n}-p\Vert +\alpha _{n} M_{1}^{2}\right) \\&\le \Vert x_{n}-p\Vert ^{2}+\alpha _{n} M_{3} \end{aligned} \end{aligned}$$
(3.16)

for some \(M_{3}>0\). Combining (3.15) and (3.16), we get

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert ^{2} \le&\Vert x_{n}-p\Vert ^{2}+\alpha _{n} M_{3}-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert w_{n}-y_{n}\Vert ^{2} \\&-\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert z_{n}-y_{n}\Vert ^{2}+\alpha _{n} M_{2}\,, \end{aligned} \end{aligned}$$

which yields

$$\begin{aligned}&\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert y_{n}-w_{n}\Vert ^{2}+\Big (1-\mu \frac{\lambda _{n}}{\lambda _{n+1}}\Big )\Vert z_{n}-y_{n}\Vert ^{2}\\&\quad \le \Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1} -p \Vert ^{2}+\alpha _{n} M_{4}\,, \end{aligned}$$

where \(M_{4}:=M_{2}+M_{3}\).


Step 3.

$$\begin{aligned}&\Vert x_{n+1}-p\Vert ^{2} \le \left( 1-\alpha _{n} \eta \right) \Vert x_{n}-p\Vert ^{2}\\&\quad +\alpha _{n} \eta \Big [\frac{2\gamma }{\eta }\left\langle F p, p-x_{n+1}\right\rangle +\frac{3M\theta _{n}}{\alpha _{n} \eta }\Vert x_{n}-x_{n-1}\Vert \Big ], \,\, \forall n \ge n_{0} \end{aligned}$$

for some \(M>0\). Indeed, we have

$$\begin{aligned} \begin{aligned} \Vert w_{n}-p\Vert ^{2} \le \Vert x_{n}-p\Vert ^{2}+2 \theta _{n}\Vert x_{n}-p\Vert \Vert x_{n}-x_{n-1}\Vert +\theta _{n}^{2}\Vert x_{n}-x_{n-1}\Vert ^{2}\,. \end{aligned} \end{aligned}$$
(3.17)

Combining (3.9) and (3.14), we get

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&\le \left( 1-\alpha _{n} \eta \right) \Vert w_{n}-p\Vert ^{2}+2 \alpha _{n} \gamma \left\langle F p, p-x_{n+1}\right\rangle , \quad \forall n \ge n_{0}\,. \end{aligned} \end{aligned}$$
(3.18)

Substituting (3.17) into (3.18), we obtain

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&\le \left( 1-\alpha _{n} \eta \right) \Vert x_{n}-p\Vert ^{2}+2 \alpha _{n} \gamma \left\langle F p, p-x_{n+1}\right\rangle \\&\quad + \theta _{n}\Vert x_{n}-x_{n-1}\Vert \left( 2\Vert x_{n}-p\Vert +\theta \Vert x_{n}-x_{n-1}\Vert \right) \\&\le \left( 1-\alpha _{n} \eta \right) \Vert x_{n}-p\Vert ^{2}\\&\quad +\alpha _{n} \eta \Big [\frac{2\gamma }{\eta }\left\langle F p, p-x_{n+1}\right\rangle +\frac{3M\theta _{n}}{\alpha _{n} \eta }\Vert x_{n}-x_{n-1}\Vert \Big ],\, \forall n\ge n_{0}\,, \end{aligned} \end{aligned}$$

where \(M:=\sup _{n \in {\mathbb {N}}}\left\{ \Vert x_{n}-p\Vert , \theta \Vert x_{n}-x_{n-1}\Vert \right\} >0\).


Step 4. \(\big \{\Vert x_{n}-p\Vert ^{2}\big \}\) converges to zero. Indeed, by Lemma 2.3, it suffices to show that \(\lim \sup _{k \rightarrow \infty }\left\langle Fp, p-x_{n_{k}+1}\right\rangle \le 0\) for every subsequence \(\left\{ \Vert x_{n_{k}}-p\Vert \right\}\) of \(\left\{ \Vert x_{n}-p\Vert \right\}\) satisfying

$$\begin{aligned} \liminf _{k \rightarrow \infty }\left( \Vert x_{n_{k}+1}-p\Vert -\Vert x_{n_{k}}-p\Vert \right) \ge 0\,. \end{aligned}$$

For this purpose, one assumes that \(\left\{ \Vert x_{n_{k}}-p\Vert \right\}\) is a subsequence of \(\left\{ \Vert x_{n}-p\Vert \right\}\) such that \(\liminf _{k \rightarrow \infty }\left( \Vert x_{n_{k}+1}-p\Vert -\Vert x_{n_{k}}-p\Vert \right) \ge 0\). By Step 2, one has

$$\begin{aligned} \begin{aligned}&\limsup _{k \rightarrow \infty }\Big [\Big (1-\mu \frac{\lambda _{n_{k}}}{\lambda _{n_{k}+1}}\Big )\Vert y_{n_{k}}-w_{n_{k}}\Vert ^{2}+\Big (1-\mu \frac{\lambda _{n_{k}}}{\lambda _{n_{k}+1}}\Big )\Vert z_{n_{k}}-y_{n_{k}}\Vert ^{2}\Big ] \\&\quad \le \limsup _{k \rightarrow \infty } \left[ \alpha _{n_{k}} M_{4}+\Vert x_{n_{k}}-p\Vert ^{2}-\Vert x_{n_{k}+1}-p\Vert ^{2}\right] \\&\quad \le \limsup _{k \rightarrow \infty }\alpha _{n_{k}} M_{4}+\limsup _{k \rightarrow \infty } \left[ \Vert x_{n_{k}}-p\Vert ^{2}-\Vert x_{n_{k}+1}-p\Vert ^{2}\right] \\&\quad =-\liminf _{k \rightarrow \infty }\left[ \Vert x_{n_{k}+1}-p\Vert ^{2}-\Vert x_{n_{k}}-p\Vert ^{2}\right] \\&\quad \le 0\,, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{k \rightarrow \infty }\Vert y_{n_{k}}-w_{n_{k}}\Vert =0 \text { and } \lim _{k \rightarrow \infty }\Vert z_{n_{k}}-y_{n_{k}}\Vert =0\,. \end{aligned}$$

Therefore

$$\begin{aligned} \lim _{k \rightarrow \infty }\Vert z_{n_{k}}-w_{n_{k}}\Vert =0\,. \end{aligned}$$
(3.19)

Moreover, we can show that

$$\begin{aligned} \Vert x_{n_{k}+1}-z_{n_{k}}\Vert =\alpha _{n_{k}}\gamma \Vert F z_{n_{k}}\Vert \rightarrow 0 \text{ as } n \rightarrow \infty \,, \end{aligned}$$
(3.20)

and

$$\begin{aligned} \Vert x_{n_{k}}-w_{n_{k}}\Vert =\theta _{n_{k}}\Vert x_{n_{k}}-x_{n_{k}-1}\Vert =\alpha _{n_{k}} \cdot \frac{\theta _{n_{k}}}{\alpha _{n_{k}}}\Vert x_{n_{k}}-x_{n_{k}-1}\Vert \rightarrow 0 \text{ as } n \rightarrow \infty \,. \end{aligned}$$
(3.21)

Combining (3.19), (3.20) and (3.21), we obtain

$$\begin{aligned} \Vert x_{n_{k}+1}-x_{n_{k}}\Vert \le \Vert x_{n_{k}+1}-z_{n_{k}}\Vert +\Vert z_{n_{k}}-w_{n_{k}}\Vert +\Vert w_{n_{k}}-x_{n_{k}}\Vert \rightarrow 0 \text{ as } n \rightarrow \infty \,. \end{aligned}$$
(3.22)

Since the sequence \(\left\{ x_{n_{k}}\right\}\) is bounded, there exists a subsequence \(\big \{x_{n_{k_{j}}}\big \}\) of \(\big \{x_{n_{k}}\big \},\) which converges weakly to some \(z \in H,\) such that

$$\begin{aligned} \limsup _{k \rightarrow \infty }\left\langle F p, p-x_{n_{k}}\right\rangle =\lim _{j \rightarrow \infty }\big \langle F p, p-x_{n_{k_{j}}}\big \rangle =\langle F p, p-z\rangle \,. \end{aligned}$$
(3.23)

By (3.21), we get \(w_{n_{k}} \rightharpoonup z\) as \(k \rightarrow \infty\). This together with \(\lim _{k \rightarrow \infty }\Vert w_{n_{k}}-y_{n_{k}}\Vert =0\) and Lemma 3.3 yields \(z \in \mathrm {VI}(C, A)\). From (3.23) and the assumption that p is the unique solution of the (BVIP), we get

$$\begin{aligned} \limsup _{k \rightarrow \infty }\left\langle F p, p-x_{n_{k}}\right\rangle =\langle F p, p-z\rangle \le 0\,. \end{aligned}$$
(3.24)

Combining (3.22) and (3.24), we obtain

$$\begin{aligned} \begin{aligned} \limsup _{k \rightarrow \infty }\left\langle F p, p-x_{n_{k}+1}\right\rangle&=\limsup _{k \rightarrow \infty } \left\langle F p, p-x_{n_{k}}\right\rangle =\langle F p, p-z\rangle \\&\le 0\,. \end{aligned} \end{aligned}$$
(3.25)

From \(\lim _{n \rightarrow \infty } \frac{\theta _{n}}{\alpha _{n}}\Vert x_{n}-x_{n-1}\Vert =0\) and (3.25), we get

$$\begin{aligned} \limsup _{k \rightarrow \infty } \Big [\frac{2\gamma }{\eta }\left\langle F p, p-x_{n_{k}+1}\right\rangle +\frac{3M\theta _{n_{k}}}{\alpha _{n_{k}} \eta }\Vert x_{n_{k}}-x_{n_{k}-1}\Vert \Big ]\le 0\,. \end{aligned}$$
(3.26)

Hence, combining Step 3, Condition (C5) and (3.26), in the light of Lemma 2.3, one concludes that \(\lim _{n \rightarrow \infty }\Vert x_{n}-p\Vert =~0\). This completes the proof. \(\square\)

Now applying Theorem 3.1 with \(F(x)=x-x_{0}\), where \(x_{0} \in H\). It is easy to check that the mapping \(F: H \rightarrow H\) is 1-Lipschitz continuous and 1-strongly monotone on H. In this case, by choosing \(\gamma =1\), the calculation of \(x_{n+1}\) in Algorithm 3.1 becomes as follows:

$$\begin{aligned} x_{n+1}=z_{n}-\alpha _{n} \gamma F z_{n}=z_{n}-\alpha _{n} (z_{n}-x_{0})=\alpha _{n} x_{0}+\left( 1-\alpha _{n}\right) z_{n}\,. \end{aligned}$$

Therefore, in this special case, the calculation of \(x_{n+1}\) does not include the mapping F. The algorithm in Corollary 3.1 only contains the variational inequality mapping A, so this algorithm can solve the variational inequality problem. A similar statement applies to Corollary 3.2.

Corollary 3.1

Let \(A: H \rightarrow H\) be \(L_{1}\)-Lipschitz continuous and pseudomonotone on H. Take \(\theta >0\), \(\lambda _{1}>0\), \(\mu \in (0,1)\). Assume that \(\left\{ \alpha _{n}\right\}\) is a real sequence in (0, 1) such that \(\lim _{n \rightarrow \infty } \alpha _{n}=0\) and \(\sum _{n=0}^{\infty } \alpha _{n}=\infty\). Let \(x_{0},x_{1} \in H\) and \(\left\{ x_{n}\right\}\) be defined by

$$\begin{aligned} \left\{ \begin{aligned}&w_{n}=x_{n}+\theta _{n}\left( x_{n}-x_{n-1}\right) \,,\\&\text {where }\theta _{n}=\left\{ \begin{array}{ll} \min \big \{\frac{\epsilon _{n}}{\Vert x_{n}-x_{n-1}\Vert }, \theta \big \}, &{} \text{ if } x_{n} \ne x_{n-1}, \\ \theta , &{} \text{ otherwise }. \end{array}\right. \\&y_{n}=P_{C}\left( w_{n}-\lambda _{n} A w_{n}\right) \,, \\&z_{n}=P_{T_{n}}\left( w_{n}-\lambda _{n} A y_{n}\right) \,, \\&\text {where } T_{n}:=\left\{ x \in H \mid \left\langle w_{n}-\lambda _{n} A w_{n}-y_{n}, x-y_{n}\right\rangle \le 0\right\} \,, \\&x_{n+1}=\alpha _{n} x_{0}+\left( 1-\alpha _{n}\right) z_{n}\,, \\&\lambda _{n+1}=\left\{ \begin{array}{ll} \min \left\{ \mu \frac{\Vert w_{n}-y_{n}\Vert ^{2}+\Vert z_{n}-y_{n}\Vert ^{2}}{2\left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle }, \lambda _{n}\right\} , &{} \text{ if } \left\langle A w_{n}-A y_{n}, z_{n}-y_{n}\right\rangle >0, \\ \lambda _{n}, &{} \text{ otherwise. } \end{array}\right. \end{aligned}\right. \end{aligned}$$
(3.27)

Then the iterative sequence \(\left\{ x_{n}\right\}\) created by (3.27) converges to \(p \in \mathrm {VI}(C, A)\) in norm, where \(p=P_{\mathrm {VI}(C, A)} x_{0}\).

3.2 The modified inertial Tseng’s extragradient algorithm

In this subsection, we introduce a new modified inertial Tseng’s extragradient algorithm for solving (BVIP). Our algorithm is described in Algorithm 3.2.

figure b

Lemma 3.4

The sequence \(\left\{ \lambda _{n}\right\}\) generated by (3.28) is a nonincreasing sequence and

$$\begin{aligned} \lim _{n \rightarrow \infty } \lambda _{n}=\lambda \ge \min \Big \{\lambda _{1}, \frac{\mu }{L_{1}}\Big \}\,. \end{aligned}$$

Proof

It follows from (3.28) that \(\lambda _{n+1} \le \lambda _{n}\) for all \(n \in {\mathbb {N}}\). Hence, \(\left\{ \lambda _{n}\right\}\) is nonincreasing. On the other hand, we get \(L_{1}\Vert w_{n}-y_{n}\Vert \ge \Vert A w_{n}-A y_{n}\Vert\) since A is \(L_{1}\)-Lipschitz continuous, consequently

$$\begin{aligned} \mu \frac{\Vert w_{n}-y_{n}\Vert }{\Vert A w_{n}-A y_{n}\Vert } \ge \frac{\mu }{L_{1}} \,\, \text{ if } \,\, A w_{n} \ne A y_{n}\,, \end{aligned}$$

which together with (3.28) implies that

$$\begin{aligned} \lambda _{n} \ge \min \Big \{\lambda _{1}, \frac{\mu }{L_{1}}\Big \}\,. \end{aligned}$$

Therefore, \(\lim _{n \rightarrow \infty } \lambda _{n}=\lambda \ge \min \big \{\lambda _{1}, \frac{\mu }{L_{1}}\big \}\) since the sequence \(\{\lambda _{n}\}\) is nonincreasing and lower bounded. \(\square\)

The following lemma is very helpful for analyzing the convergence of Algorithm 3.2.

Lemma 3.5

Assume that Conditions (C1)–(C3) hold. Let \(\left\{ z_{n}\right\}\) be a sequence generated by Algorithm 3.2. Then,

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} \le \Vert w_{n}-p\Vert ^{2}-\Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-y_{n}\Vert ^{2},\quad \forall p \in \mathrm {VI}(C, A)\,. \end{aligned}$$

Proof

First, using the definition of \(\left\{ \lambda _{n}\right\}\), one obtains

$$\begin{aligned} \Vert A w_{n}-A y_{n}\Vert \le \frac{\mu }{\lambda _{n+1}}\Vert w_{n}-y_{n}\Vert , \quad \forall n\,. \end{aligned}$$
(3.29)

Indeed, if \(A w_{n}=A y_{n}\) then (3.29) holds. Otherwise, it implies from (3.28) that

$$\begin{aligned} \lambda _{n+1}=\min \left\{ \frac{\mu \Vert w_{n}-y_{n}\Vert }{\Vert A w_{n}-A y_{n}\Vert }, \lambda _{n}\right\} \le \frac{\mu \Vert w_{n}-y_{n}\Vert }{\Vert A w_{n}-A y_{n}\Vert }\,. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert A w_{n}-A y_{n}\Vert \le \frac{\mu }{\lambda _{n+1}}\Vert w_{n}-y_{n}\Vert \,. \end{aligned}$$

Therefore, the inequality (3.29) holds when \(A w_{n}=A y_{n}\) and \(A w_{n} \ne A y_{n}\). By the definition of \(z_{n}\), one sees that

$$\begin{aligned} \begin{aligned} \Vert z_{n}-p\Vert ^{2} =&\Vert y_{n}-p\Vert ^{2}+\lambda _{n}^{2}\Vert A y_{n}-A w_{n}\Vert ^{2}-2 \lambda _{n}\left\langle y_{n}-p, A y_{n}-A w_{n}\right\rangle \\ =&\Vert w_{n}-p\Vert ^{2}+\Vert y_{n}-w_{n}\Vert ^{2}-2\left\langle y_{n}-w_{n}, y_{n}-w_{n}\right\rangle +2\left\langle y_{n}-w_{n}, y_{n}-p\right\rangle \\&+\lambda _{n}^{2}\Vert A y_{n}-A w_{n}\Vert ^{2}-2 \lambda _{n}\left\langle y_{n}-p, A y_{n}-A w_{n}\right\rangle \\ =&\Vert w_{n}-p\Vert ^{2}-\Vert y_{n}-w_{n}\Vert ^{2}+2\left\langle y_{n}-w_{n}, y_{n}-p\right\rangle \\&+\lambda _{n}^{2}\Vert A y_{n}-A w_{n}\Vert ^{2}-2 \lambda _{n}\left\langle y_{n}-p, A y_{n}-A w_{n}\right\rangle \,. \end{aligned} \end{aligned}$$
(3.30)

Since \(y_{n}=P_{C}\left( w_{n}-\lambda _{n} A w_{n}\right)\), using the property of projection, we obtain

$$\begin{aligned} \left\langle y_{n}-w_{n}+\lambda _{n} A w_{n}, y_{n}-p\right\rangle \le 0\,, \end{aligned}$$

or equivalently

$$\begin{aligned} \left\langle y_{n}-w_{n}, y_{n}-p\right\rangle \le -\lambda _{n}\left\langle A w_{n}, y_{n}-p\right\rangle \,. \end{aligned}$$
(3.31)

From (3.29), (3.30) and (3.31), we have

$$\begin{aligned} \begin{aligned} \Vert z_{n}-p\Vert ^{2} \le&\Vert w_{n}-p\Vert ^{2}-\Vert y_{n}-w_{n}\Vert ^{2}-2 \lambda _{n}\left\langle A w_{n}, y_{n}-p\right\rangle +\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Vert w_{n}-y_{n}\Vert ^{2} \\&-2 \lambda _{n}\left\langle y_{n}-p, A y_{n}-A w_{n}\right\rangle \\ \le&\Vert w_{n}-p\Vert ^{2}-\Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-y_{n}\Vert ^{2}-2 \lambda _{n}\left\langle y_{n}-p, A y_{n}\right\rangle \,. \end{aligned} \end{aligned}$$
(3.32)

Since \(p \in \mathrm {VI}(C, A),\) we have \(\left\langle A p, y_{n}-p\right\rangle \ge 0\). From the pseudomonotonicity of A, we get

$$\begin{aligned} \left\langle A y_{n}, y_{n}-p\right\rangle \ge 0\,. \end{aligned}$$
(3.33)

Combining (3.32) and (3.33), we obtain

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} \le \Vert w_{n}-p\Vert ^{2}-\Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-y_{n}\Vert ^{2}\,. \end{aligned}$$

The proof of the lemma is now complete. \(\square\)

Theorem 3.2

Assume that Conditions(C1)–(C5) hold. Then, the sequence \(\left\{ x_{n}\right\}\) generated by Algorithm 3.2 converges to the unique solution of the (BVIP) in norm.

Proof

Step 1. The sequence \(\left\{ x_{n}\right\}\) is bounded. Indeed, according to Lemma 3.4, we have \(\lim _{n \rightarrow \infty }\Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )=1-\mu ^{2}>0\). Thus, there exists \(n_{0} \in {\mathbb {N}}\) such that

$$\begin{aligned} 1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}>0,\quad \forall n \ge n_{0}\,. \end{aligned}$$
(3.34)

Combining Lemma 3.5 and (3.34), we obtain

$$\begin{aligned} \Vert z_{n}-p\Vert \le \Vert w_{n}-p\Vert , \quad \forall n \ge n_{0}\,. \end{aligned}$$

As the same as (3.10)–(3.13), we have \(\left\{ x_{n}\right\}\) is bounded. We also get \(\left\{ z_{n}\right\}\) and \(\left\{ w_{n}\right\}\) are bounded.


Step 2.

$$\begin{aligned} \Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-y_{n}\Vert ^{2} \le \Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p\Vert ^{2}+\alpha _{n} M_{4} \end{aligned}$$
(3.35)

for some \(M_4 > 0\). Indeed, from (3.14) and Lemma 3.5, we have

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&=\Vert z_{n}-\alpha _{n} \gamma F z_{n}-p\Vert ^{2} \\&\le \Vert w_{n}-p\Vert ^{2}-\Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-y_{n}\Vert ^{2}+\alpha _{n} M_{2} \end{aligned} \end{aligned}$$
(3.36)

for some \(M_{2}>0\). By (3.16), we obtain

$$\begin{aligned} \Big (1-\mu ^{2} \frac{\lambda _{n}^{2}}{\lambda _{n+1}^{2}}\Big )\Vert w_{n}-y_{n}\Vert ^{2} \le \Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p\Vert ^{2}+\alpha _{n} M_{4}\,, \end{aligned}$$
(3.37)

where \(M_{4}:=M_{2}+M_{3}\), both \(M_{2}\) and \(M_{3}\) are defined in Step 2 of Theorem 3.1.


Step 3.

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2} \le \left( 1-\alpha _{n} \eta \right) \Vert x_{n}-p\Vert ^{2}+\alpha _{n} \eta \Big [\frac{2\gamma }{\eta }\left\langle F p, p-x_{n+1}\right\rangle +\frac{3M\theta _{n}}{\alpha _{n} \eta }\Vert x_{n}-x_{n-1}\Vert \Big ] \end{aligned}$$

for some \(M>0\). Using (3.17) and (3.18), we can get the desired result immediately.


Step 4. \(\big \{\Vert x_{n}-p\Vert ^{2}\big \}\) converges to zero. According to Step 4 in Theorem 3.1, we suppose that \(\left\{ \Vert x_{n_{k}}-p\Vert \right\}\) is a subsequence of \(\left\{ \Vert x_{n}-p\Vert \right\}\) satisfying \(\liminf _{k \rightarrow \infty }\left( \Vert x_{n_{k}+1}-p\Vert -\Vert x_{n_{k}}-p\Vert \right) \ge 0\). From Step 2 and Condition (C5), one obtains

$$\begin{aligned} \begin{aligned} \limsup _{k \rightarrow \infty } \Big (1-\mu ^{2} \frac{\lambda _{n_{k}}^{2}}{\lambda _{n_{k}+1}^{2}}\Big )\Vert w_{n_{k}}-y_{n_{k}}\Vert ^{2}&\le \limsup _{k \rightarrow \infty } \{\Vert x_{n_{k}}-p\Vert ^{2}-\Vert x_{n_{k}+1}-p\Vert ^{2}+\alpha _{n_{k}} M_{4}\}\\&\le 0\,.\\ \end{aligned} \end{aligned}$$

By (3.34), it follows that \(\lim _{k \rightarrow \infty }\Vert y_{n_{k}}-w_{n_{k}}\Vert =0\). According to the definition of \(z_{n}\) in Algorithm 3.2 and (3.29), we have

$$\begin{aligned} \lim _{k \rightarrow \infty }\Vert z_{n_{k}}-y_{n_{k}}\Vert \le \lim _{k \rightarrow \infty }\lambda _{n_{k}}\Vert A y_{n_{k}}- A w_{n_{k}}\Vert \le \lim _{k \rightarrow \infty }\mu \frac{\lambda _{n_{k}}}{\lambda _{n_{k}+1}}\Vert w_{n_{k}}-y_{n_{k}}\Vert =0\,, \end{aligned}$$

which implies that \(\lim _{k \rightarrow \infty }\Vert y_{n_{k}}-z_{n_{k}}\Vert =0\). Using the same facts as (3.19)–(3.25), we obtain

$$\begin{aligned} \limsup _{k \rightarrow \infty } \Big [\frac{2\gamma }{\eta }\left\langle F p, p-x_{n_{k}+1}\right\rangle +\frac{3M\theta _{n_{k}}}{\alpha _{n_{k}} \eta }\Vert x_{n_{k}}-x_{n_{k}-1}\Vert \Big ]\le 0\,. \end{aligned}$$
(3.38)

Therefore, using Step 3, Condition (C5) and (3.38), by means of Lemma 2.3, one concludes that \(\lim _{n \rightarrow \infty }\Vert x_{n}-p\Vert =~0\). The proof is completed. \(\square\)

Now applying Theorem 3.2 with \(F(x)=x-f(x)\), where \(f: H \rightarrow H\) is a contraction mapping with constant \(\rho \in [0,1)\). It is easy to verify that the mapping \(F: H \rightarrow H\) is \((1+\rho )\)-Lipschitz continuous and \((1-\rho )\)-strongly monotone on H. In this case, by choosing \(\gamma =1\), we obtain the following result.

Corollary 3.2

Let \(A: H \rightarrow H\) be \(L_{1}\)-Lipschitz continuous and pseudomonotone on H and \(f:~{H} \rightarrow {H}\) be a \(\rho\)-contraction mapping with \(\rho \in [0, \sqrt{5}-2)\). Set \(\theta >0\), \(\lambda _{1}>0\), \(\mu \in (0,1)\). Assume that \(\left\{ \alpha _{n}\right\}\) is a real sequence in (0, 1) such that \(\lim _{n \rightarrow \infty } \alpha _{n}=0\) and \(\sum _{n=0}^{\infty } \alpha _{n}= \infty\). Let \(x_{0},x_{1} \in H\) and \(\left\{ x_{n}\right\}\) be defined by

$$\begin{aligned} \left\{ \begin{aligned}&w_{n}=x_{n}+\theta _{n}\left( x_{n}-x_{n-1}\right) \,,\\&\text {where }\theta _{n}=\left\{ \begin{array}{ll} \min \big \{\frac{\epsilon _{n}}{\Vert x_{n}-x_{n-1}\Vert }, \theta \big \}, &{} \text{ if } x_{n} \ne x_{n-1}, \\ \theta , &{} \text{ otherwise }. \end{array}\right. \\&y_{n}=P_{C}\left( w_{n}-\lambda _{n} A w_{n}\right) \,, \\&z_{n}=y_{n}-\lambda _{n}\left( A y_{n}-A w_{n}\right) \,, \\&x_{n+1}=\left( 1-\alpha _{n}\right) z_{n}+\alpha _{n} f\left( z_{n}\right) \,, \\&\lambda _{n+1}=\left\{ \begin{array}{ll} \min \left\{ \frac{\mu \Vert w_{n}-y_{n}\Vert }{\Vert A w_{n}-A y_{n}\Vert }, \lambda _{n}\right\} , &{} \text{ if } A w_{n}-A y_{n} \ne 0, \\ \lambda _{n}, &{} \text{ otherwise. } \end{array}\right. \end{aligned}\right. \end{aligned}$$
(3.39)

Then the iterative sequence \(\left\{ x_{n}\right\}\) generated by (3.39) converges to \(p \in \mathrm {VI}(C, A)\) in norm, where \(p=P_{\mathrm {VI}(C, A)} \circ f(p)\).

4 Numerical examples

In this section, we provide some numerical examples to show the numerical behavior of our proposed algorithms and compare them with Algorithm 1 and Algorithm 2 in [18]. We use the FOM Solver [29] to effectively calculate the projections onto C and \(T_{n}\). All the programs were implemented in MATLAB 2018a on a Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz computer with RAM 8.00 GB.

Example 4.1

Consider a mapping \(F: {\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{m}\,\,(m=5)\) of the form \(F(x)=M x+q\), where

$$\begin{aligned} M=B B^{\mathsf {T}}+D+K\,, \end{aligned}$$

and B is an \(m \times m\) matrix with their entries being generated in (0, 1) , D is an \(m \times m\) skew-symmetric matrix with their entries being generated in \((-1,1)\), K is an \(m \times m\) diagonal matrix, whose diagonal entries are positive in (0, 1) (so M is positive semidefinite), \(q\in {\mathbb {R}}^{m}\) is a vector with entries being generated in (0, 1) . It is clear that F is \(L_{2}\)-Lipschitz continuous and \(\beta\)-strongly monotone with \(L_{2}=\max \{{\text {eig}}(M)\}\), \(\beta =\min \{{\text {eig}}(M)\}\), where \({\text {eig}}(M)\) represents all eigenvalues of M.

Next, we consider the following fractional programming problem:

$$\begin{aligned} \begin{aligned}&\min f(x)=\frac{x^{\mathsf {T}} Q x+a^{\mathsf {T}} x+a_{0}}{b^{\mathsf {T}} x+b_{0}}\,,\\&\text{ subject } \text{ to } x \in C:=\big \{x \in {\mathbb {R}}^{5}: b^{\mathsf {T}} x+b_{0}>0\big \}\,, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} Q=\left[ \begin{array}{ccccc} 5 &{} -1 &{} 2 &{} 0 &{} 2 \\ -1 &{} 6 &{} -1 &{} 3 &{} 0 \\ 2 &{} -1 &{} 3 &{} 0 &{} 1 \\ 0 &{} 3 &{} 0 &{} 5 &{} 0 \\ 2 &{} 0 &{} 1 &{} 0 &{} 4 \end{array}\right] ,\, a=\left[ \begin{array}{c} 1 \\ 2 \\ -1 \\ -2\\ 1 \end{array}\right] , \, b=\left[ \begin{array}{c} 1 \\ 0 \\ -1 \\ 0\\ 1 \end{array}\right] , \, a_{0}=-2, b_{0}=20\,. \end{aligned}$$

It is easy to check that Q is symmetric and positive definite in \({\mathbb {R}}^{5}\) and hence f is pseudo-convex on \(C=\left\{ x \in {\mathbb {R}}^{5}: b^{\mathsf {T}} x+b_{0}>0\right\}\). Let

$$\begin{aligned} A(x):=\nabla f(x)=\frac{\left( b^{\mathsf {T}} x+b_{0}\right) (2 Q x+a)-b\left( x^{\mathsf {T}} Q x+a^{\mathsf {T}} x+a_{0}\right) }{\left( b^{\mathsf {T}} x+b_{0}\right) ^{2}}\,. \end{aligned}$$

It is known that A is pseudomonotone and Lipschitz continuous.

We compare our proposed Algorithm 3.1 and Algorithm 3.2 with Algorithm 1 and Algorithm 2 proposed by Thong et al. [18]. Our parameters are set as follows. In all algorithms, set \(\mu =0.1\), \(\alpha _{n}=1/(n+1)\), \(\gamma =1.7\beta /(L_{2}^{2})\), \(\lambda _{1}= 0.6\). Take \(\theta =0.4\), \(\epsilon _{n}=100/(n+1)^2\) in Algorithm 3.1 and Algorithm 3.2. We use \(D_{n}=\Vert x_{n}-x_{n-1}\Vert\) to measure the error of the n-th iteration since we do not know the exact solution to the problem, and the maximum iteration of 200 as the stopping criterion. Numerical results are reported in Figs. 1, 2.

Fig. 1
figure 1

Comparison of the number of iterations of all algorithms for Example 4.1

Full size image
Fig. 2
figure 2

Comparison of the elapsed time of all algorithms for Example 4.1

Full size image

Example 4.2

We consider an example that appears in the infinite dimensional Hilbert space \(H=L^{2}[0,1]\) with the inner product \(\langle x, y\rangle =\int _{0}^{1} x(t) y(t) \mathrm {d} t\) and the induced norm \(\Vert x\Vert =(\int _{0}^{1} x(t)^{2} \mathrm {d} t)^{1 / 2}\). Let r, R be two positive real numbers such that \(R/(k+1)<r/k<r<R\) for some \(k>1\). Take the feasible set \(C=\{x \in H:\Vert x\Vert \le r\}\) and the operator \(A: H \rightarrow H\) given by

$$\begin{aligned} A(x)=(R-\Vert x\Vert ) x, \quad \forall x \in H\,. \end{aligned}$$

Note that A is not monotone. Taking a particular pair \(({\tilde{x}},{\tilde{y}})=({\tilde{x}}, k{\tilde{x}})\) and choosing \({\tilde{x}} \in C\) such that \(R /(k+1)<\Vert {\tilde{x}}\Vert <r / k\), one can see that \(k\Vert {\tilde{x}}\Vert \in C\). By a straightforward computation, we have

$$\begin{aligned} \langle A({\tilde{x}})-A({\tilde{y}}), {\tilde{x}}-{\tilde{y}}\rangle =(1-k)^{2}\Vert {\tilde{x}}\Vert ^{2}(R-(1+k)\Vert {\tilde{x}}\Vert )<0\,. \end{aligned}$$

Hence, the operator A is not monotone on C. Next we show that A is pseudomonotone. Indeed, assume \(\langle A(x), y-x\rangle \ge 0\) for all \(x, y \in C\), that is, \(\langle (R-\Vert x\Vert ) x, y-x\rangle \ge 0\). Since \(\Vert x\Vert <R\), we have \(\langle x, y-x\rangle \ge 0\). Therefore,

$$\begin{aligned} \begin{aligned} \langle A(y), y-x\rangle&=\langle (R-\Vert y\Vert ) y, y-x\rangle \\&\ge (R-\Vert y\Vert )(\langle y, y-x\rangle -\langle x, y-x\rangle ) \\&=(R-\Vert y\Vert )\Vert y-x\Vert ^{2} \ge 0\,. \end{aligned} \end{aligned}$$

Let \(F: H \rightarrow H\) be an operator defined by \((F x)(t)=0.5 x(t), t \in [0,1]\). It is easy to see that F is 0.5-strongly monotone and 0.5-Lipschitz continuous. For the experiment, we choose \(R=1.5\), \(r=1\), \(k=1.1\). The solution of this problem is \(x^{*}(t)=0\). Our parameters are the same as in Example 4.1. The maximum iteration of 50 as the stopping criterion. Figs. 3, 4 show the behaviors of \(D_{n}=\left\| x_{n}(t)-x^{*}(t)\right\|\) generated by all the algorithms with the starting points \(x_{0}(t)=x_{1}(t)=t^2\). Moreover, we adjust  the inertial parameters of the proposed algorithms to \(\theta =0.2\) and keep  the other parameters the same as in Example 4.1. Figs. 5, 6 show the numerical behavior of all algorithms in this case.

Fig. 3
figure 3

Comparison of the number of iterations of all algorithms for Example 4.2 (inertial \(\theta =0.4\))

Full size image
Fig. 4
figure 4

Comparison of the elapsed time of all algorithms for Example 4.2 (inertial \(\theta =0.4\))

Full size image
Fig. 5
figure 5

Comparison of the number of iterations of all algorithms for Example 4.2 (inertial \(\theta =0.2\))

Full size image
Fig. 6
figure 6

Comparison of the elapsed time of all algorithms for Example 4.2 (inertial \(\theta =0.2\))

Full size image

Remark 4.1

We have the following comments on Examples 4.1 and 4.2.

  • As shown in Figs. 1,2, 3, 4, 5, 6, in terms of the number of iterations and execution time, we can intuitively see that our proposed Algorithm 3.1 and Algorithm 3.2 are superior to the Algorithm 1 and the Algorithm 2 proposed by Thong et al. [18], respectively. It is worth noting that, due to the large inertial parameters we choose, our algorithms have higher accuracy and there are also oscillations. How to reduce oscillation is the next issue we need to consider in the future.

  • The two algorithms proposed in this paper are semi-adaptive. That is, they can work without knowing the prior information of the Lipschitz constant of mapping A. However, in order to guarantee the strong convergence of the algorithms, we need to calculate \(x_{n+1}=z_{n}-\alpha _{n} \gamma F z_{n}\), where \(0<\gamma <\frac{2 \beta }{L_{2}^{2}}\), which requires the restriction that parameters \(\beta\) and \(L_{2}\) must be known.

5 Conclusions

In this paper, we introduced two new extragradient algorithms to solve bilevel variational inequality problems in a Hilbert space. The algorithms were constructed with the aid of the inertial technique, the subgradient extragradient method, the Tseng’s extragradient method and the steepest descent method. Only one projection onto the feasible set is needed at each iteration. Two new stepsize rules are used in our algorithms, which makes them easier to work without knowing the knowledge of the Lipschitz constant of the involved mapping. Two strong convergence theorems of the iterative sequences generated by the algorithms were proved. The theoretical results are also confirmed by some numerical examples.