Informal Mathematical Knowledge

‘Informal knowledge’, according to Baroody and Ginsburg (1986), includes the knowledge that children develop in everyday settings before entering formal schooling. Similarly, prior knowledge, according to Jonassen and Grabowski (1993) is considered as the set of knowledge background, skills or abilities that students bring to the learning process. Family life, social interactions, playgrounds, day care, and everyday experiences provide informal opportunities for the development of concepts, skills, attitudes and abilities; these, in turn, are influenced contextually and culturally, morally and emotionally, cognitively and mentally, physically and biologically, through group and/or individual engagement. During the last decades a large body of research has revealed that children at early years express informal mathematical knowledge associated with diverse notions and mechanisms such as enumeration and arithmetic problem solving (Baroody 2004; Wynn 1990), spatial reasoning and geometric knowledge (Sarama and Clements 2006; Newcombe and Huttenlocher 2000).

Seo and Ginsburg (2004) studied the types of informal mathematical activities which four- and five-year-old children express in natural settings during free play. Children demonstrated five mathematical categories; classification activities, magnitude activities, enumeration activities, dynamics and pattern and shape activities. According to Sarama and Clements (2009), children construct mathematical notions as they get actively engaged in the following sorts of play: sensorimotor or manipulative play, symbolic constructive play, symbolic dramatic play and games with rules. So, play is a means to get children involved in problem solving situations and develop their thinking on mathematical ideas and procedures.

Informal mathematical knowledge undergoes considerable development during the preschool years and provides a basis for the later acquisition of formal mathematics in the school context (Clements and Sarama 2007). In this sense, successful early childhood instruction builds on children’s informal knowledge and supports the linkage of this prior thinking to more analytical mathematical representations, while taking into account diversity in terms of language, culture, needs and interests. Children possess informal knowledge of many complex mathematical ideas, enjoy the challenges of playing with these complex ideas and, with adult or peer guidance, they can achieve greater understanding than previously expected (Ginsburg, Greenes and Balfanz 2003).

Educational Strategies Linking Informal to Formal Knowledge

The importance of prior knowledge and informal experiences on learning and perceiving the world has been stressed mainly by the theoretical approach of constructivism (Bruner 1996; Piaget 1970; Vygotsky 1986). Under this approach, learning is an active, meaningful procedure that takes place as new constructs, concepts and knowledge get absorbed through interactions with people, places, objects and ideas. Knowledge construction occurs as students use their prior informal knowledge while engaging with new experiences, mental structures, socio-cultural connections and beliefs in order to interpret the world. Young children build more advanced knowledge from prior understandings, through play, relations, explorations, games and stimulating activities (DeVries et al. 2002).

In instructional terms, the base of constructing on previous knowledge in order to conquer skills, knowledge and values occurs through scaffolding and repetition. Bruner (1996) proposed a spiral curriculum in which when teaching a subject “you begin with an intuitive account that is well within the reach of a student, and then circle back later to a more formal or highly structured account until the learner has mastered the topic or subject” (p. 119). By viewing learning as an active procedure, instruction should be designed in the direction of avoiding misunderstandings and misconceptions and acquiring deeper and longer lasting understandings (Jones and Brader-Araje 2002). Students get introduced to diverse notions at a basic level from the early years and as they grow older they deepen their understandings. In this direction, according to Ginsburg (2009), educational strategies should aim to link the spontaneous and the scientific, the everyday and the academic. For example, the child already knows, without the benefit of schooling, that while throwing a dice she/he might throw a six. This idea should be related later on to the responsive written computation and representation of probabilities, taught under the mathematics curriculum.

The informal approach encourages children to engage in rich mathematical experiences which enable them to explore their environment, either through hands-on discovery, or through computer-assisted practices, or through a combination of both. Informal knowledge encourages problem solving from simple to increasingly complex problems and develops reasoning and cognitive skills in order to make sense of the world (Carr, Peters and Young-Loveridge 1994). In general, preschool programs are to be planned on sequences of learning that elaborate on and reinforce children’s knowledge; informal in the beginning and formal later on. According to Conole (2005), these experiences should include a wide variety of activities, small-group cooperative teaching, child-oriented tasks and opportunities that encourage children to talk about and share their mathematical ideas and strategies in a responsive, reciprocal environment.

According to Greenes et al. (2004) the principles in guiding the design and implementation of a comprehensive mathematics curriculum for preschool children involve: capitalizing on children’s knowledge and interests, highlighting the mathematics in routine classroom activities, organizing instruction and sequence activities, developing complex mathematical ideas, emphasizing mathematical language development and promoting thinking like a mathematician. Clements and Stephan (2004) mention that mathematizing involves “reinventing, redescribing, reorganizing, quantifying, structuring, abstracting, and generalizing that which is first understood on an intuitive and informal level in the context of everyday activity” (p. 314). Early mathematics instruction does not mean imposing knowledge on preschoolers, drilling them with material and stimuli, or having them memorize arithmetic facts or categorize shapes. Children should get opportunities in organized activities to discover patterns and relations and invent reasoning strategies, mathematical thinking, problem solving skills and literacy (Clements and Sarama 2007; Copley 2000). Young children not only know some mathematics, but they are ready and eager to learn more of it (Greenes 1999).

The Development of Probabilistic Thinking in Preschoolers

Fischbein (1975) was amongst the first researchers to argue that although preschoolers have not reached an adequate conceptual framework, they do possess an intuitive understanding of probabilities, ratios as well as other mathematical notions. He defines intuitions as “cognitive acquisitions derived from the experience of the individual, without the need for any systematic instruction” (p. 117). In this sense, intuitions usually develop in informal settings and become ‘adjusted’ as children enter formal learning environments. Such environments are provided by educational settings in a structured, organised process with specific goals and objectives or alternatively refer to “institutionalised learning activities that are designed to lead to a learning achievement” (European Commission 2006, p. 17). Intuitions may emerge in both formal and informal contexts, but in the case of early years in terms of time intuitive thinking is mainly associated with informal knowledge. Under this perspective, young children are expected to estimate odds and unpredictability and therefore make probability judgments at a certain level, prior to formal learning.

The research on probabilistic thinking in young children is approached through two directions: on one hand there is a focus on the theoretical implications that occur and on the other hand there is a focus on the methodological practices and design that are considered as developmentally appropriate within the preschool classroom. Research is in progress and young children have been found, in terms of their cognitive and mathematical capacity, to show a minimal understanding of randomness, to identify the most/least likely event, to compare outcomes, to make use of random sampling and base rate information, to apply probabilistic evidence in order to elaborate on causal relationships, to realize part–part comparisons in order to estimate probability (Denison et al. 2006; Kushnir and Gopnik 2005; Nikiforidou and Pange 2010; Spinillo 2002). Furthermore, the design of the activities that introduce probabilities, the use of random generators, simulators and ICTs, the size, location and proportion of the sample space, the kind of stimuli used, the information given as well as other methodological features are significant in implementing probabilistic notions in the formal educational settings (Nikiforidou and Pange 2009; Pratt 2000; Skoumpourdi et al. 2009).

The aim of this study is to schematize children’s choices and prior knowledge while interacting with a spinner task. Preschoolers were asked to infer the most likely option in a one-shot probabilistic game which was designed based on the basic principles of constructivism: active engagement, play, discovery, meaningful context and oral reasoning. At a first point, it is tested whether preschoolers express informal probabilistic knowledge in estimating the probability of an event. At a second point, after an educational goal-oriented session, it is examined whether preschoolers can build on their prior knowledge in order to reach probabilistic conclusions and more complex reasoning. Theoretical, instructional and methodological issues are addressed on how the linkage of informal and formal thinking can be applied to intuitive probabilistic thinking in early years.

Methods and Materials

The study was undertaken in 2011, in 3 Greek public kindergartens selected from different geographical regions. 90 children, aged 4–6 years, participated in the test. They took part in pairs, in a separate room from their classroom after their parents’ signed letter of consent. The study was realized within 4 weeks and no previous instruction or introduction to the notion of ‘most probable’ had taken place within the classrooms.

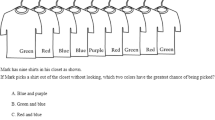
The task consisted of spinners showing fruit (oranges and apples) in Condition 1 and shapes (squares and triangles) in Condition 2; themes relevant to early years. There were 2 cases per Condition: in Case 1 the distribution of the sample space was 3:1 and in Case 2, the distribution of the sample space was 5:1. In some cases apples or triangles outnumbered, whereas in other cases oranges or squares outnumbered. The spinners were divided in equal parts, 4 in Case 1 and 6 in Case 2, with diameter 16 cm. The basis for the probabilistic game was a 40 × 40 cm board made of cork. On there the spinners and the arrows were pinned up. Children would turn around the disks by themselves in order to get motivated and actively engaged (Fig. 1).

Fig. 1
figure 1

Example of the stimulus

Full size image

As long as children were seated in pairs, they were presented with the stimulus of the game. Conditions were counterbalanced so that children would be tested either firstly on the fruit theme and then on the shape theme or the other way round. In each condition, children were asked to predict at which item they assumed the arrow would stop. They were provided with specially designed sheets in order to record their inferences as well as the actual outcome of each spin. Each case in each condition was repeated 3 times.

Between Conditions 1 and 2 an instructional session would take place, where participants would discuss and try to explain the occurrences orally. The experimenter would assist by intervening only with open-ended questions in order to encourage children’s critical thinking. Children would be stimulated to argument on what were their predictions, what was the final outcome each time and why, if any, there was difference. Apart from oral engagements children could make use of the graphical representations in order to reach conclusions. As long as a statement in the sense of “the x is more probable to win as xs are more” was reached, children would move on to the following condition. Again, children’s predictions in three spins per case were marked down and further discussed.

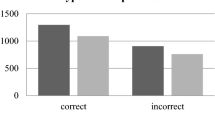
For the purposes of the current analysis two responses were recorded; the ‘MP’ (most probable) responses which corresponded to the most probable outcome and the ‘LP’ (less probable) responses which corresponded to the most unlikely outcome. Children’s choices were analyzed through decision trees (Fig 2) and the theorem of Bayes.

Fig. 2
figure 2

The decision tree through each trial

Full size image

The Bayes’ theorem relates the probability of the occurrence of an event, in our case children’s predictions of the most probable outcome in each trial, to the occurrence or non-occurrence of an associated event, which in our case was children’s choice (either MP or LP) that proceeded in the previous trials. In this way, the conditional probability of predicting the most likely outcome, each time, given children’s previous choice (MP or LP) was recorded and calculated under the rule:

$$ P(MP/N) = \frac{P(N/MP)P(MP)}{P(N)}. $$

Results

Children’s strategies and choices of MP given that they had previously selected the MP option were traced and recorded in both Conditions and every trial and case (Table 1). By comparing the impact of the Conditions (before and after the instruction), in Case 1, where the sample space was 3:1, it can be seen that there is a significant difference in selecting the MP option, t (269) = 3.59, p < 0.05. Similarly, when the sample space was 5:1, in Case 2, children gave significantly the MP answers in Condition 2 than in Condition 1; t (269) = 3.94, p < 0.05. Such findings entail that children at first have an intuitive understanding of predicting the most probable outcome; but, after justification and reasoning, they obtain a better understanding and appreciation of the likelihood of events and the notion that in problems with uneven analogies the most probable outcome is usually the outcome that associates to the most numerous set of objects.

Table 1 Results of children’s predictions of the ‘most probable’ outcome (given that they previously had selected the ‘most probable’ outcome)
Full size table

In precise, in the 1st trial of Condition 1, case 1, the percentage of the most likely predictions (MP 1) was: P (MP 1/Ν) = 70/90 = 0.77. In the 2nd trial the proportion of the correct predictions (MP 2) given that children had made a correct prediction in trial 1 (MP 1) was: P (MP 2/MP 1) = 48/70 = 0.68. Concerning the 3rd trial: given that children made correct predictions in both previous trials they gave: P (MP 3/MP 2) = 38/48 = 0.79. In Condition 1, case 2, in the 1st trial the percentage of the correct predictions (MP 1) was: P (MP 1/Ν) = 74/90 = 0.82. In the 2nd trial the percentage of the correct predictions (MP 2) given that children had made a correct prediction in trial 1 (MP 1) was: P (MP 2)/(MP 1) = 52/74 = 0.70. Respectively in the 3rd trial given that children made correct predictions in both previous trials they selected the most probable outcome by: P (MP 3/MP 2) = 46/52 = 0.88.

Respectively, in Condition 2, in Case 1, in the 1st trial the percentage of the most probable predictions (MP 1) was: P (MP 1/Ν) = 78/90 = 0.86. The 2nd time the proportion of the correct predictions (MP 2) given that children had made a most likely prediction in trial 1 (MP 1) was: P (MP 2/MP 1) = 65/78 = 0.83. Concerning the 3rd trial: given that children made correct predictions in both previous trials they gave: P (MP 3/MP 2) = 58/65 = 0.89. In Condition 2, Case 2, the first time the proportion of the correct predictions (MP 1) was: P (MP 1/Ν) = 82/90 = 0.91. In the 2nd trial the proportion of the most probable predictions (MP 2) given that children had made a correct prediction in trial 1 (MP 1) was: P (MP 2/MP 1) = 76/82 = 0.92. Concerning the 3rd trial, given that children made correct predictions in both previous trials they gave: P (MP 3/MP 2) = 68/76 = 0.89.

Results also show that children’s selection of the MP outcome given that they previously had selected the most probable outcome was found to be higher when the sample space was larger; 5:1 (case 2) rather than 3:1 (case 1). This implies that the methodological design and the number of items affect children’s responses and inferences in probabilistic games. Additionally, in terms of sequence in the 1st trial, children started with quite high percentages of MP predictions (78.5 % for Condition 1 and 88.5 % for Condition 2). In the 2nd trial they respectively gave high percentages of MP inferences (75 % in Condition 1 and 87.5 % in Condition 2). Finally, the 3rd time many children selected the most probable outcome given that they already had selected the most probable alternative twice, by 82.5 and 89 % accordingly in each Condition. Such trend implies a learning affect, although more trials would be more revealing in this direction.

Discussion and Conclusions

Overall, it can be seen that children at the age of 4 to 6 express stable informal understanding of predicting an outcome as more likely. Before any justification or exploration, children made sensible estimations about the likelihood of events; three times through both distributions of the sample space (3:1 and 5:1) and both themes of stimuli (fruit and shapes). As in previous studies (Jones et al. 1997; Nikiforidou and Pange 2010), children at these ages seem to possess prior intuitions concerning probabilistic concepts. Such findings support that preschoolers have the cognitive capacity and intuitions to access basic notions of probabilities, particularly the likelihood of events. Consequently, probabilities can be ‘mathematized’, as Clements and Stephan (2004) would outline, as the intuitive and informal understanding of probabilities can be re-directed and re-understood and in turn be inserted in formal educational setting from early years.

Another important conclusion that may be drawn relates to the importance of the linkage between informal and intuitive understanding with big maths (Greenes et al. 2004). Children’s predictions before and after the didactic sequence of discussion, observation and information processing delineated an important progress. Children gave higher responses in predicting the most probable outcome in Condition 2 rather than in Condition 1. Personal engagement, sensory experience with the manipulative, oral argument on what happens to the disks, motivation to win and experimentation intervened between the two Conditions and led young children in higher estimations about uncertain events within a contextualized problem situation.

Such constructivist aspects created a learning situation that allowed preschoolers to realize and acknowledge the probabilistic principle that within unequal proportions the most probable outcome is the one that is more numerous. The meaningful situation, presented as a game and the repetition of the events stimulated their interests, experiences and realities. Children, under the double role of ‘young scientists-players’ had the opportunity to share their opinions with their pair and the experimenter and to express their ideas verbally in an encouraging context, as proposed by Conole (2005). The structured and goal-oriented activity guided participants to take advantage of their informal knowledge and organize their personal estimations in an objective and more mathematical way.

By considering intuitions either as complementary to formal understanding (Bruner 1960), or as self-evident, subjective, holistic cognitions (Fischbein 1975), an effective educational approach on probabilities should take into consideration the probabilistic competencies young children already have. During the last decades there is a scientific orientation in this direction; in enlightening what children know or understand concerning probabilistic notions, as partly supported by the current results, and in turn how this prior knowledge and understanding may become the starting point of instruction (Langrall and Mooney 2005).

Another methodological point to be discussed refers to the influence of the nature and the structure of a particular task in probabilistic reasoning (Nikiforidou and Pange 2009; Pratt 2000; Skoumpourdi et al. 2009; Spinillo 2002). Responses and participation depend on the material, the stimuli, the design of the activity, the nature of random generators and the goal-context. In this study, children responded to the probabilistic game composed by disks depicting fruit and shapes, with alterations in the distribution of the sample space that didn’t exceed six items in total. They gave higher percentages of predicting the more probable alternative in the case where the difference in the proportion of the uneven sets was bigger. Further research could consider modifications in the size, number and arrangement of the particular stimulus, as well as changes in the theme or the scenario of the task. In addition, there are also broader methodological issues that should be taken into account related to early childhood research; such future implications relate to how and whether children’s intentions while engaging with a test could be explored accurately, or how do children’s intentions match with the objectives set up by the experimenter, or in what means can learning at these ages be measured and assessed, or which is the role of the socio-cultural influences or personality traits in learning.

Under this perspective, probabilistic thinking may be enhanced in preschool settings through what Sarama and Clements (2009) name mathematization processes: developmentally appropriate activities and instruction programs designed in order to construct on children’s prior knowledge by linking formal learning to personal experiences and understandings. Such informal experiences may be guessing games, or producing narratives and predictions about the forecast or a sports match, or elaborating on tables and graphs, or participating in board games and group games with potential winners or getting involved in problem solving situations. Learning activities and interactions may be based on representing and processing mathematical and statistical notions, creating models, engaging with, and implementing relevant realities in diverse contexts. Furthermore, while designing, organizing and assessing such activities, aspects like environment, play in all its forms, teachable moments, projects, curriculum, and intentional teaching described by Ginsburg et al. (2008) should be taken into account too.