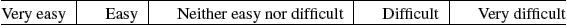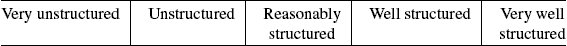Abstract
In this paper, we describe mathematical modelling activities, which deal with authentic problems. These kinds of problems have been tackled in various modelling activities, amongst others in a modelling week. After a description of the theoretical approach used, one of these authentic modelling problems is described in detail showing students’ solutions. Based on the evaluation of a modelling week with several hundred students, it is argued that these kinds of authentic problems are feasible with students from upper secondary level. Furthermore, it became apparent that most students would appreciate these kinds of examples included in school mathematics in order to promote their skills to use mathematics in their real life.
Zusammenfassung
In dem Artikel werden mathematische Modellierungsaktivitäten beschrieben, die von authentischen Problemen ausgehen. Diese Probleme wurden in verschiedenen Modellierungsaktivitäten behandelt, u.a. in Modellierungswochen. Nach einer Beschreibung des zugrundeliegenden theoretischen Ansatzes wird eines dieser authentischen Probleme im Detail mit Lösungsansätzen von Schülerinnen und Schüler beschrieben. Auf der Basis der Evaluation einer Modellierungswoche mit mehreren hundert Schülerinnen und Schüler wird argumentiert, dass diese Art von authentischen Modellierungsproblemen Schülerinnen und Schülern des oberen Sekundarbereichs zugänglich ist. Des Weiteren wird deutlich, dass die meisten Schülerinnen und Schüler der Integration solcher Beispiele in den normalen Mathematikunterricht positiv gegenüber stehen, da mit solchen Beispielen ihre Kompetenzen, Mathematik im wirklichen Leben anzuwenden, gefördert werden.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The relevance of promoting applications and mathematical modelling in schools is widely accepted. For example the PISA study emphasises developing the capacity of students to use mathematics in their present and future lives as one goal of mathematics education. It means that students should understand the relevance of mathematics in everyday life, in our environment, and for sciences.
This perception of the objectives of mathematics teaching has an impact on the structuring of mathematics lessons. It is insufficient to simply impart competencies for applying mathematics only within the framework of the school curriculum. Instead, more mathematics teaching should deal with examples from which
-
students understand the relevance of mathematics in everyday life, in our environment, and for the sciences;
-
students acquire competencies that enable them to solve real mathematics problems including problems in everyday life, in our environment, and in the sciences.
This demand for new ways of structuring mathematics teaching meets the goals for more reality-oriented mathematics education as postulated in many didactical positions since the middle or the end of the twentieth century. It has been agreed that mathematics teaching should not be reduced to just reality-based examples but that these should play a central role in education (for an overview of the historical debate, see Kaiser-Meßmer 1986, the more recent debate is reflected in Blum et al. 2007). As a consequence, it became clear that besides the application of standard mathematical procedures (such as applying well-known algorithms) in real world context and real world contexts serving as illustrations of mathematical concepts (e.g. usage of debts for the introduction of negative numbers), modelling problems as reality-based contextual examples are increasingly important. In addition, it has been discussed that students should acquire competencies which enable them to solve real mathematical problems from different extra-mathematical domains. Within the current discussion, it is stressed that it is not sufficient at all to deal with modelling examples in lessons but that the stimulation of modelling competencies through self-initiative is of central importance (see, for a comprehensive longitudinal study, Maaß 2004).
If one analyses many modelling examples discussed currently, it becomes obvious that, on the one hand different goals are connected with the introduction of modelling into mathematics lessons, while on the other hand the proposed modelling examples connected with these various goals are very different. Many of the modelling examples proposed recently are strongly reduced. Either their real world content is simplified or they are grouped around mathematical topics such as linear functions or theorem of Pythagoras (see, for example, Blum and Leiß 2006, 2007). In this paper, we want to discuss whether it is possible to treat authentic modelling examples in mathematics teaching, which are by definition neither strongly simplified nor contain easily recognisable mathematical algorithms. In order to discuss this question, we use modelling examples and evaluation results of a recent modelling activity with 350 students from the upper secondary level carried out at the University of Hamburg in March 2009.
2 Theoretical Debate on Mathematical Modelling in Mathematics Education
The question, how the different goals connected to the introduction of mathematical modelling in school influence the kind of modelling examples proposed and the ways, they are dealt with in school, has been strongly debated at the last three Congresses of the European Society for Research in Mathematics Education, i.e. CERME4, CERME5, and CERME6 in 2005, 2007, and 2009. Several classifications of the various historical and more recent modelling approaches were developed; the first proposal was published by Kaiser and Sriraman (2006) and has been modified later on by Kaiser et al. (2007). Based on these classification systems, we propose to distinguish the following theoretical approaches (see Fig. 1), which support the case for the inclusion of mathematical modelling in school and which allow us to situate our theoretical approach in the framework of the ongoing international debate on the teaching and learning of modelling.
One of the approaches distinguished in this classification relates to pragmatic-utilitarian goals, i.e. it puts the solving of real world problems, the understanding of the real world and the promotion of modelling competencies in the foreground. This approach argues for the use of authentic problems referring to a definition of authentic problems developed by Niss (1992). Niss refers to the expertise of people working in the field where the problem comes from and defines authentic problems as problems that are recognised by people working in this field as being a problem they might meet in their daily work. A central reason for the request to use authentic problems of this approach lies in the conviction that students need to experience the power of mathematical modelling for the understanding and solution of real questions meaningful to many people in order to be convinced of the usefulness of mathematics and mathematical modelling for their real life.
Coming from a more educational perspective, a similar distinction is developed by Julie and Mudaly (2007), who distinguish between modelling as vehicle in order to motivate students and provide a basis for the development of particular mathematical content and modelling as content, which aims to promote the capacity of students to address problems in the external world. According to the discussion from the ICMI Study on modelling and applications in mathematics education, various approaches can be assigned to this perspective on modelling as content (Galbraith 2007). The notion of authenticity is discussed as well within these approaches and Palm (2007) develops a framework for authenticity referring to the fact, whether the problem taken out of a situation from the real world has already occurred or might happen. He emphasises very clearly on the basis of an empirical study the positive impact of authentic problems on students’ achievement.
Another important aspect emphasised by all the perspectives on modelling described above are modelling competencies, which shall be fostered via modelling processes in mathematics teaching. It is a broad consensus that modelling competencies shall comprise a whole range of competencies connected to the phases of the modelling process (cf. the works by Blum 1996; Niss 2003; Haines et al. 2001 or Maaß 2004; Kaiser 2007). Blomhøj and Højgaard Jensen (2007) emphasise the following three aspects, which are necessary in their perspective in order to promote students’ mathematical modelling, namely the degree of coverage of the modelling process touched by the students in their work, the technical level of the mathematics used by the students in their modelling attempts, and the radius of action, i.e. the situations in which the students are able to perform modelling activities; especially, the last aspect is closely connected to the authenticity of the situations modelled in classroom; it is tempting to hypothesise that authentic problems promote the radius of action of the students in further modelling activities.
Based on extensive own empirical research (see, for example, Kaiser-Meßmer 1986), we see the necessity of treating authentic modelling problems, which promote the whole range of modelling competencies and broaden the radius of action of the students. Therefore, we assign ourselves to the perspective labelled as realistic or applied modelling approach in Fig. 1. The kind of modelling examples we argue for to include into mathematics education and the approach to mathematical modelling are strongly influenced by the ways in which applied mathematicians tackle real problems that they meet in the real world. Their main characteristics are their complexity concerning their real world context and their openness concerning the problem to be solved. Furthermore, they require extensive communicative competencies and small group activities (see Ortlieb et al. 2009). Similar proposals are developed by Haines and Crouch (2006), or already at the beginning of the modelling debate by Pollak (1969).
This theoretical approach has consequences for the design of the modelling examples to be used, as well as with how to introduce modelling activities in school. In the following, we will describe the various kinds of modelling activities we have carried out since 2000 in joint activities with applied mathematicians.
3 The Project “Mathematical Modelling in School” and Description of the Examples Used
3.1 Description of the Modelling Activities
The project ‘Mathematical modelling in school’ was established in 2000 by the Department of Mathematics (Jens Struckmeier and Claus Peter Ortlieb) in co-operation with Didactics of Mathematics at the Department of Education (Gabriele Kaiser) at the University of Hamburg (for a report of the early activities see Kaiser et al. 2004). It was originally a university course project with future teachers for upper secondary level teaching and aimed to establish a relation between university and school. Within the project, the future teachers supervised student groups from the upper secondary level (aged 16–18 years) during their modelling activities. It was intended that each group works independently on one modelling example, within the regular lessons or in separate activities. We restrict ourselves to a description of the main features of this approach, because it has already been described elsewhere; see, for example Kaiser and Schwarz (2006) and Schwarz and Kaiser (2007).
One aim of the project since its establishment is that the participating students will acquire competencies that enable them to carry out modelling examples independently, i.e. the ability to extract mathematical questions from the given problem contexts and to develop the solutions autonomously. It is not the purpose of this project to provide a comprehensive overview of relevant fields of application of mathematics. Furthermore, it is hoped that students will be enabled to work purposefully on their own in open problem situations and will experience the feelings of uncertainty and insecurity which are characteristics of real applications of mathematics in everyday life and the sciences. An overarching goal is that students’ experiences with mathematics, and their mathematical world views or mathematical beliefs are broadened. This can be described as a holistic approach, using the terminology of Blomhøj and Jensen (2003), i.e. the whole-mathematical modelling process is carried out, covering all modelling competencies described above.
The central feature of this project is the use of authentic examples. Most of the problems are suggested by applied mathematicians who work in industry who have met or tackled this problem within their working environment. The problems are only little simplified and often no solution is known, either to us as organiser of the project or to the problem poser. For example, the problem of unique identification of fingerprints is not yet solved satisfactorily; the machines do not work reliably, which creates concern at the widespread use of these machines for fingerprint identification. Quite often only a problematic situation is described and the students have to develop a question that can be solved—the development and description of the problem to be tackled is the most important and most ambitious part of a modelling process, mostly neglected in ordinary mathematics lessons. Another feature of the problems is their openness, which means that various problem definitions and solutions are possible depending on the views of the modellers.
The teaching-and-learning-process is characterised as autonomous, self-controlled learning, i.e. that the students decide their ways of tackling the problem and no fast intervention by the supervisors takes place (or should take place). The future teachers are expected to offer only essential assistance, if mathematical means are needed or if the students are heading into a cul-de-sac. With this kind of teaching approach, the students experience long phases of helplessness and insecurity which is an important aspect of modelling and a necessary phase within a modelling process.
We have used modelling activities in the following organisational forms:
-
modelling activities during ordinary mathematics lessons over three months; at the beginning of the project, we tackled two problems lasting the whole school year;
-
modelling activities within a modelling week during the school year.
Due to organisational problems caused by the introduction of central school leaving examinations in core subjects such as mathematics, in 2008, we (Gabriele Kaiser, Claus Peter Ortlieb, and Jens Struckmeier) decided to move in the direction of a modelling week, which took place the first time in March 2009. Three hundred fifty students from 19 schools from Hamburg and its surroundings participated. The students had chosen mathematics as a special subject, studying it at an advanced level (so-called “Leistungskurs”). Most of the schools had sent all the students from the mathematics course to the modelling week. In contrast to other modelling weeks (such as the ones organised by the University of Kaiserslautern or the University of Darmstadt who have already been running modelling weeks for more than a decade), we aim at working with ordinary students from upper secondary level, who have selected mathematics at an advanced level. In 2008, in Hamburg, 17.5% of the age cohort had chosen mathematics at advanced level, which means that these students are selected to a certain extent, but do not represent a special gifted group of students; they still reflect nearly a fifth of the according age cohort.Footnote 1
3.2 Overview on Modelling Examples Used So Far
Within the several modelling activities just described, we have used the following modelling problems so far:
-
Stock price forecast.
-
Premium in private health insurance.
-
Prediction of fishing quotas.
-
Optimal position of rescue helicopters in South Tyrol.
-
Radio-therapy planning for cancer patients.
-
Identification of fingerprints.
-
Pricing for Internet booking of flights.
-
Price calculation of an Internet café.
-
Traffic flow during the Soccer World Championship in 2006 in Hamburg.
-
Construction of an optimised time table of school.
-
Irrigation of a garden.
-
Development of ladybugs.
-
Chlorination of a swimming pool.
During our recent modelling week, the students dealt with the last three problems. In the following section, we will describe one of these problems in detail. We will not describe very elaborate approaches but rather concentrate on the description of approaches that were developed by the students. The modelling problem and various ways to tackle is described by Claus Peter Orlieb (see Ortlieb 2009).
3.3 Description of one Modelling Example in Detail
The problem deals with the irrigation of gardens by fixed irrigation systems and was originally developed by Martin Bracke and used in various modelling weeks at the University of Kaiserslautern. The problem was presented to the students as follows:
Planning of garden irrigation systems:
The company Gardena offers for the automatic irrigation of gardens so-called irrigation pumps (in German called a “Turbinen-Versenkregler”, in the following abbreviated TVR), which can irrigate circle sectors in an angle range between 5 and 360 degrees with the radius of 2 to 12 meters. It has to be considered in the planning that the garden area is irrigated evenly on the one hand. On the other hand, the irrigation system produces costs and, therefore, the number of devices shall be kept as low as possible.
The task consisted of finding the ideal arrangement of irrigation devices depending on the shape of the garden and on the areas that do not need to be irrigated.
This problem is highly authentic as “Gardena” even offered a software tool several years ago, which allowed customers to design the arrangement of the irrigation devices by themselves using their garden that should be irrigated. The software lead to totally unsatisfactory results and was taken out of the market, so that the customers have to develop their own ideas, how to simplify the area to be irrigated, where to place the irrigators, and how many irrigators are needed.
In the following section, some students’ approaches for this problem will be presented. The approaches were developed and presented by students during the described modelling week. Hereby an impression of the quality and complexity of real students’ approaches within the project can be given to clarify the content-related dimension of the working processes during the modelling week. Therefore, the aim of this section is not an explicit description of one complete sample solutionFootnote 2 or the description of one especially good solution developed by a group of outstanding students. The following descriptions rather refer to an approach that was chosen by two groups of students in similar forms but independently. As the students’ groups were named after famous researchers, the following depiction is based on the results of group “Kepler” (these are the students of the higher level course in mathematics from the Elsa-Brandström-Schule in Elmshorn, Schleswig-Holstein) and the group “Heinrich-Hertz” (these are the students of the higher level courses in mathematics from the Friedrich-Ebert-Gymnasium and the Emil-Krause-Gymnasium in Hamburg). Differences in the approaches of the two groups will be specified at the respective passages.
In both groups, the students generally and implicitly regarded gardens as two-dimensional areas probably also due to the phrasing of the task. Furthermore, the students in both groups decided to abstract away from the technical guidelines for the TVR and, therefore, use arbitrary angles and radii. Both assumptions were only implicitly used by the students as a basis to start from and they were never explicitly named as assumptions for the model. In order to raise the students’ awareness concerning modelling processes, the mentoring students pointed out these implicit assumptions and characterised them as modelling assumptions and, therefore, as a part of the modelling.
As they have chosen arbitrary angles and radii the general form for the area irrigated by one of the TVR for the students is a segment of a circle, the area (compare Fig. 2) of which is given by
Furthermore, the students concentrated on a sensibly chosen special case. In our case, this means that their considerations in almost all cases referred to rectangular gardens. In contrast to the previous assumptions, this restriction was explicitly named but the students did not give any reasons. One possible reason might be the easy mathematical application of square figures as well as the fact that many gardens are really almost rectangular. As one of the groups later combined different squares to get other forms, we can furthermore assume that the restriction was also based on the consideration that many gardens can be combined by using different rectangle parts.
The actual processing of the problem requires a specification of the term “ideal” in reference to the irrigation of a garden. Thus, one could couch a quality criterion that as little area of the garden as possible stays unwatered or that as little area as possible outside the garden gets watered. Alongside a solution could be regarded as being ideal when as few as possible TVR are used to water the garden in an acceptable way. In this case, the term acceptable would have to be defined as well. In all cases, it is difficult proving that a solution is ideal and within the students’ solutions this can surely not be expected in a general form. In fact, the students’ approaches are affected by a mixture of geometrical calculations as well as plausibility assumptions.
When dealing with the problem of the irrigation of a rectangular garden, the students assumed a given amount of TVR. The amount and the possible positioning of the TVR were in this case defined by the mentioned plausibility assumptions. Roughly two possibilities were dealt with to water a rectangular garden with two TVR. These are illustrated in Fig. 3.
Before the students regarded the problem in a more formal way, they tried to differentiate between different shapes of rectangles in reference to the two alternatives of irrigation by using graphical means. While the “Kepler”-group only used some sketches to compare between the two methods, the group “Heinrich-Hertz” used a computer programme to numerically calculate the ratio between the irrigated areas and the rest for different forms of rectangles and for each of the two irrigation alternatives. Some results of this process are displayed in Fig. 4.
On the basis of their respective only graphical or additionally computer based attempts, the students in both groups developed the hypothesis that the irrigation variant A is more appropriate for stretched rectangles while the irrigation variant B seems more appropriate for rectangles with four sides of nearly the same length.
Against the background of these first graphical approaches, the students began to develop a more formal approach to check their hypothesis. In order to do this, both groups again assumed a fixed number of TVR (in this case 2 TVR) and they differentiated between two different criteria to characterise the irrigation as being “optimal”. The students on the one hand developed the criterion of irrigating as much area as possible without irrigating area outside of the garden (criterion 1, the students of group “Kepler” called this “underwatering”). On the other hand, they looked at the irrigation of the whole garden while irrigating as little area as possible outside of the garden (criterion 2, the students of the “Kepler”-group called this “overwatering”).
While the group “Kepler” went on to the calculation of the ratio of irrigated areas for both irrigation methods on the basis of these qualitative descriptions of the criterions, the “Heinrich-Hertz”-group first tried to phrase the different problems that arise depending on the used criterion in a mathematically precise way. The called the area of the garden G and the irrigated area W and got to the following phrasing of the problem—with SC meaning “side condition” to the students.
Problem-phrasing when using criterion 1 (irrigating as much area as possible without irrigating area outside of the garden)
Problem-phrasing when using criterion 2 (irrigating the whole garden while irrigating as little area as possible outside of the garden):
According to the graphical approaches above, the students in both groups decided to firstly work on the first criterion. In Fig. 2, one can recognise that both methods of irrigation avoid an intersection of irrigated areas and, therefore, avoid a partial surplus of water. Therefore, the students implicitly implied that the watered areas A i shall be disjoint.
With this, the students’ aim was to find out in which cases the method of irrigation A or B (according to Fig. 3) is more appropriate if criterion 1 is taken as quality criterion.
For the further analysis in this regard, the group “Kepler” introduced the “extent of irrigation” %Footnote 3 as the ratio of the watered area in relation to the whole area of the garden. The group “Heinrich-Hertz” developed a solution without this standardisation meaning the subsequent division by the area of the garden and instead only looked at the irrigated area. In the following, the approach of the group “Kepler” will be described because the mathematical proceeding in both groups is equivalent except for the standardisation and additionally the solution of the group “Kepler” contains the procedure of the group “Heinrich-Hertz”. The question of the better variant can then be specified to the question which variant allows the higher extent of irrigation.
For all the following depiction, it is G=a⋅b and let b≤a. The collective watered area in variant A (the students called this variant “two pie slices”) is the result of adding the area of the two equal segments of a circle. With r=a and α=arctan (b/a) (compare Fig. 2) results
and, therefore, the extent of irrigation is
For variant B (the students named it “two quarter circles”), the students decided that the radius of one TVR shall be equal to b, thus a full side length. And they decided that the second segment of a circle in the opposing corner of the rectangle shall cover an area as big as possible (without overlapping). This is a further example for a plausibility assumption which was not generally proved by the students as an ideal configuration but which obviously emerged from the students’ former examinations on the square.Footnote 4 If according to criterion 1 no area outside the garden can be irrigated it follows (with the Pythagorean theorem) that the segments of the circles can only touch each other, if \(a\le b\sqrt{3}\) is true and the segments of the circle only strike each other when the radii of the segments are r 1=b and \(r_{2}=\sqrt{a^{2}+b^{2}}-b\). Let therefore \(b\le a\le b\sqrt{3}\). Then the area irrigated by the first TVR is \(A_{1}=\frac{1}{4}\pi b^{2}\), the area irrigated by the second TVR is \(A_{2}=\frac{1}{4}\pi(\sqrt{a^{2}+b^{2}}-b)^{2}\) (compare Fig. 5).
The extent of irrigation is therefore—in the original formulation of the students, which is displayed throughout the whole chapter:

It can be easily recognised that by the transformations stated above the students were able to investigate which of the two variants is more appropriate only depending on one parameter namely the ratio b/a of the side lengths of the rectangle. With reference to the solution of the problem the advantage is a higher degree of generality because different gardens with different side lengths but the same ratio of side lengths do not have to be differentiated any more but can be subsumed. With regard to dealing with the question another advantage is that the dependant value (the extent of irrigation) only depends on one variable (the ration b/a of the side lengths). The students know one-dimensional functions like these very well from their mathematics classes in the lower secondary form as well as in the upper secondary form. This enables them to deal further with the problem. On the contrary, only a few students know functions of several variables, which would include both sides of the rectangle as single variables and, therefore, such a relation would have led to further mathematical problems. For the students, these considerations about possible mathematical problems when dealing with functions of several variables were probably not very relevant for deciding on the—at least in the students’ eyes—unusual transformations which only display the extent of irrigation depending on b/a. In fact, the presentations of the groups suggest that rather the previous graphic attempts as described above and the derived hypothesis that the choice of irrigation depends more on the shape of the rectangle (and, therefore, on the ratios of the sides) than it does on the precise side lengths led to the decision to investigate the extent of irrigation depending on the ratio of the sides.
To decide which of the two variants of irrigation is to prefer, the students chose a graphical approach which for them is a familiar tool to compare graphs of different functions. For this purpose, they plotted the extent of irrigation depending on the ratio of the sides into a coordinate plane for both variants and identified the areas of b/a for which the variant A or variant B has a higher extent of irrigation (compare Fig. 6).
One can see that variant A is more appropriate if the ratio b/a is small and variant B is better for higher ratios b/a.Footnote 5 This way the students were able to confirm their hypothesis made on the basis of their graphic attempts by using a formal method as their former hypothesis was that variant A is appropriate for stretched rectangles whereas rectangles with similar lengths of sides are better watered with variant B.
After having answered their first question, both groups went on to work on the optimal irrigation of the garden concerning criterion 2. The approaches were strongly motivated by the former considerations and show a lot of parallels to the presented procedures. Furthermore, the group “Kepler” expanded the approaches concerning both criterions to a situation with an arbitrary number of TVR.
The following approach of the two groups differed. For lack of space, the further steps of the groups will only be described sketchily.
The group “Heinrich-Hertz” tried to analyse other and more complex configurations of TVR with more visually affected approaches. Here, they especially were allowing a surplus of water in some areas of the garden. Similar to the attempts carried out in the beginning with graphic analysis, different constellations of irrigation systems were visualised and compared with computer programmes. Furthermore, the ratio of areas that are watered once or more often is calculated numerically (compare Fig. 7).
In the “Kepler”-group one observed an approach which contains characteristics, which are typical for mathematical modelling in a sense that the students tried to reduce more general cases to a special case. Here, the students tried to ascribe the irrigation of a rectangular garden, which they have solved appropriately in their eyes, to the irrigation of more general forms of gardens. In order to do this, the students made up a garden, some parts of which were not to be watered (therefore, the students planned a sandbox in the middle of the garden) and some parts of which does not necessarily have to be watered (therefore, the students planned a pond and a patio in the garden). Subsequently, the students devised new different criteria for an “optimal” irrigation for this new garden configuration. And they tried to develop optimal irrigation systems depending on each of these criteria on the basis of their previous considerations and results by dividing the garden into several sub-areas.
4 Experiences—Results of the Evaluation
In the following, we will report about results of the evaluation of the modelling activities described in the last chapter. We will focus on the central question for our research, whether these kinds of complex problems are feasible for students from upper secondary level who are interested in mathematics, but not particularly selected.
We have evaluated the beliefs, the modelling competencies, and the appraisal of the participating students of several modelling activities. In the following, we will concentrate on the evaluation of the modelling week, which we have carried out recently as already mentioned. A description of the evaluation results of previous modelling activities can be found in Kaiser and Schwarz (2006) focusing on the belief part. A description of the development of modelling competencies by these modelling activities is given in Kaiser (2007).
For the recent evaluation, we used a questionnaire with four half-standardised questions on the beliefs of students about mathematics teaching and three open questions on the appraisal of modelling examples tackled in the modelling week and five closed questions to be answered on a 5-point-Likert-scale (the questionnaire is reproduced in Appendix 1). The questionnaire was filled in at the end of the modelling week from 289 students from 19 schools from Hamburg and its surrounding; originally 350 students participated, but not all of them were present at the last day or were willing to fill in the questionnaire. Based on methods of the Grounded Theory (see Strauss and Corbin 1998), we have used for the open questionnaires in-vivo-codes, i.e. codes extracted out of the text written by the students as verbatim quotation and grouped them to related quotations under a theoretical perspective. In order to finally analyse the answers of the students in the open questionnaires, we transformed the grouped in-vivo-codes into theoretical codes (the codes for two questions are displayed in Appendices 2 and 3). For quality assurance methods of consensual coding were relied on, which means that a coding team consists of two coders who conduct together simultaneously all steps described above. According to Steinke (2000), interpretations in groups are a “discursive way to create inter-subjectivity and comprehensibility by means of handling data and the respective interpretations explicitly” (p. 326, translation by Karen Stadtlander), and thus serve to assure quality.
In the following, we describe the appraisal of the modelling week restricted to a few aspects due to space limitations.
4.1 Learning Outcomes of the Modelling Week
We start with the appraisal of the modelling examples by the students. The first question dealt with the appreciation of the learning outcomes of the modelling week.
The students answered on the question, “From your point of view, what did you learn when dealing with the modelling example?” as follows: 71% of the students answered positively, only 12% did not see any learning outcomes from the modelling week. From the diagram displayed in Fig. 8, it can be seen in which area the students describe their learning results:
Particularly high learning successes have been achieved in the area of the general application of mathematics and working techniques. With regard to applying mathematics, many state that due to working on these modelling problems they understood how mathematics is applied and recognise its practical relevance, and its relevance to everyday life. Furthermore, some students say that, in fact, they are able to apply what they have learned in school. In the following, we exemplify the reasons by selected verbatim quotations of the students (in italics):
“…that mathematics not only can be applied in school, but also to specific examples in real life.” (Female student, 19 years old.)
“…that mathematics can also be applied to things in everyday life.” (Male student, 17 years old.)
With regard to working techniques, many students report that they learned about new strategies in problem solving and now understand how to approach problems that at first seem to be vague.
“…that it is possible to approach a problem in various ways, based on different assumptions.” (Female student, 17 years old.)
In addition, many respondents mention that they have improved their ability to work independently, to have more perseverance, and that they now find it easier to structure and simplify.
“…structured, co-ordinated, and deliberate planning and working.” (Male student, 19 years old.)
“I learned to compare different approaches in problem solving and to deal with a problem using quite varied methods and approaches.” (Female student, 18 years old.)
“…to solve arising problems autonomously.” (Female student, 16 years old.)
Other areas where some learning successes were achieved refer to mathematics and geometrical methods, in particular. Besides, many of the students state that they improved on deriving and constructing functions and formulae.
“…calculating sectors of a circle, combinatorics, and approximation of an area for which no specified formula existed to calculate it.” (Female student, 17 years old.)
“[…] However, what is most important is that I learned how to combine the dependencies of different parameters within a function.” (Male student, 16 years old.)
The field of mathematical understandings comprises changes in how to think about mathematics. Almost 10% of the students state that only because of this week and the intensive work on a quite open topic they realised how complex and wide-ranging mathematics is. Furthermore, they realised how many aspects are integrated in mathematics and what large variety of solutions are available.
“…that even in mathematics you do not always have to arrive at a solution in order to solve a problem.” (Male student, 18 years old.)
“…that there is not always an accurate solution to everything, even though it has to do with mathematics.” (Female student, 17 years old.)
Social aspects are emphasised as well: 10% of the students mention that during the week they not only got to know their fellow students and students of other schools, but most of all, learned something about teamwork.
“…to work well/better in groups and how important a good working atmosphere and teamwork is.” (Female student, 18 years old.)
It can be summarised that most students describe as their personal impression that they have achieved learning success during the modelling week. Furthermore, the range of aspects mentioned cover all goals connected with the inclusion of modelling problems.
4.2 Inclusion of Modelling Problems in Ordinary Mathematics Lessons
One central aspect is the question, whether the students want to have modelling examples included in their usual mathematics lessons or whether they want to keep these kinds of ambitious examples out of their usual lessons. This aspect is dealt with in the next question, where the students are asked the following question: “Should these examples be increasingly dealt with as part of regular maths classes or would you reject this?”
62% of the students make a plea to include these kinds of modelling examples in their usual mathematics teaching, 28% reject that, and 10% do not have an opinion.
An analysis of the negative answers shows the following main reasons for this answer in Fig. 9.
The most important reason for the rejection of modelling examples in ordinary mathematics lessons is the time constraint:
“To my mind this would be too time-consuming. It is more important to master the subject itself.” (Female student, 18 years old.)
“I think there would not be enough time during maths class to work on problems in such detail.” (Female student, 18 years old.)
The other reasons given by the students such as “not interesting”, “not relevant”, “too difficult”, or “imprecise” are given by similar numbers of students:
“It would not make sense to use this in class, because it has little relation to math. It is more like something you could puzzle over.” (Male student, 17 years old.)
“No, because the tasks were not narrowed down and there were too many possible solutions to choose from.” (Female student, 17 years old.)
The results clearly show the time pressure students are experiencing in upper secondary level. Furthermore, it shows that many students were simply not acquainted with independent work on open problems.
As already stated 62% of the students supported the inclusion of modelling examples in their ordinary mathematics lessons. The reasons for this decision can be separated into four distinct groups, i.e. relation to reality, advancement of working techniques, alternation, sense making. The fifth group of answers express the need for a new way of dealing with these kinds of problems before they are treated in ordinary mathematics lessons (see Fig. 10).
The following quotation describes the position of this last group:
“Yes, but the problems should be solvable concretely and more structured (problem description, support).” (Male student, 18 years old.)
Most frequently the students mentioned as reason for the inclusion of these kinds of examples their relation to the real world. Many students emphasise that only with these kinds of examples they could develop a relation between mathematics and the real world:
“I think that these examples should DEFINITELY be dealt with in maths classes. Because of these examples one will only realise what mathematics is needed for.” (Male student, 16 years old.)
“I think so, because it illustrates the importance of mathematics for everyday life.” (Male student, 16 years old.)
“These examples should be dealt with in order to establish a stronger connection between the real life and what is taught at school.” (Female student, 18 years old.)
Motivation was the second most common reason for advocating the inclusion of these kinds of examples:
“I think it would be better to introduce less theory but more practical use in class to increase the students’ motivation.” (Female student, 18 years old.)
“Yes, because this will make class more interesting.” (Female student, 17 years old.)
Many students mentioned the usefulness of these kinds of problems, being much higher than that of usual examples. Modelling examples are seen to promote complex mathematical thinking, to exercise learned topics, and to allow insight into the work of mathematicians:
“Such problems SHOULD be dealt with in class, because they will improve the so-called ‘competence in problem solving’. Furthermore, it will train the knowledge gained in previous grades.” (Male student, 19 years old.)
“I am in favour of dealing with these topics in class, because this will be good practise and they are good exercises.” (Male student, 18 years old.)
“Yes, because one automatically relates more closely to the topic and the relevant example.” (Male student, 18 years old.)
The promotion of working techniques is emphasised by 10% of the students, who say that working with modelling examples promotes perseverance, and skills for independent and group work:
“I think it would be good if such problems were dealt with in regular classes, because they support working independently and require teamwork.” (Male student, 17 years old.)
“I should think so, because with something like this you have to be very proactive and think about it yourself quite a lot.” (Male student, 17 years old.)
“Partially, because on the one hand, it really takes up a lot of time. On the other hand though, the teamwork is beneficial for the working atmosphere in class.” (Female student, 18 years old.)
Summing up, a majority of the students are in favour of the inclusion of these kinds of modelling problems. Furthermore, as reasons for that they name many of the goals also discussed in the respective didactical debate.
4.3 Appraisal of the Modelling Examples
The students were asked to rate the modelling example dealt with during the modelling week in respect of their interest in the content, the difficulty, the structuredness, and the relation to the real world of the examples. The ratings show some variance but the overall rating of all examples is highly positive. Most of the students (69%) chose the garden irrigation problem, whereas only 4% chose the chlorination of swimming pools and 27% chose the ladybug problem.
The garden irrigation problem was rated as being “interesting” by many of the students involved, but the degree of interest was lower than for the other groups working on different problems, who had worked on other problems and who decided more often that their chosen problem was “highly interesting”.
The rating of the modelling examples according to their difficulty showed some differences as well: The problem of the garden irrigation was judged more often by the students involved as being very easy or easy. About 20% of the students stated that. This judgement is in contrast to the evaluation of the ladybug problem, which was rated by many students involved as being difficult, but only a few students described that problem as too difficult.
Concerning the question, how realistic the problem dealt with is most students from each group described their problem as being realistic (see Fig. 11).
5 Conclusion
Coming back to our original question: Are these kinds of authentic problems only slightly simplified and done in a quite autonomous way, feasible for students? From our evaluation it is obvious that it is possible for ordinary students at upper secondary level to tackle these kinds of examples successfully. From the evaluation results, it is obvious that most of the students did not feel overtaxed. Although at some time during the modelling week the students had made the experience of helpless, lacking orientation, and insecurity, these impressions did not change their positive judgement of the whole modelling experience. If one looks in detail at the views of the students, it becomes clear that most of them experienced the modelling examples as difficult but not too difficult. Most of the students describe the problems as being reasonably structured. It is consensus that the problems are realistic and interesting.
Furthermore, the students describe that in their opinion they have achieved high learning outcomes, which reflect all the goals connected with modelling, ranging from psychological goals such as motivation to meta-aspects such as promoting working attitudes to pedagogical goals, namely enhancing the understanding of the world around us. The strong plea of the students for the inclusion of these kinds of examples in usual mathematics lessons supports our position that these kind of authentic complex modelling examples are not too difficult for students.
We therefore call for including these kinds of problems in ordinary mathematics lessons, clearly not everyday, but on a regular basis. The realisation of this ambitious goal to include these kinds of examples in ordinary mathematics lessons will obviously create many difficulties to the usual structuring of teaching in portions of 45 minutes. It will be necessary to carry out curricular changes, i.e. shortening of the subject-related requirements, specialised topics need to be abandoned as well as many routine algorithms and exercises. But if we really want to convince our students that mathematics is important for everyday life for everybody, we need to work with these kinds of examples on a regular basis. We can conclude that at least for students these authentic modelling problems are not too difficult.
Notes
The average number of students attending mathematics at advanced level at the Federal level of Germany is with 29.5% in 2008 remarkably higher than in Hamburg going up to 40% in parts of East Germany, such as Sachsen-Anhalt.
Such a sample solution can be found in Ortlieb (2009).
The used sign “%” was originally used by the group.
When irrigating a quadratic garden (side length a) with only one TVR, there are two equivalent ideal solutions with regard to criterion 1. Both of them have an extent of irrigation of π/4: either the TVR is placed in the middle of the garden and irrigates in a full circle with the radius r=0.5a or the TVR is placed in one corner and irrigates in a quarter circle with the radius r=a according the full side length of the square. The second configuration was probably the origin of the students’ considerations.
A numerical analysis shows that method A is to be preferred when b/a<0.77 is true.
References
Blomhøj, M., & Jensen, T. H. (2003). Developing mathematical modelling competence: conceptual clarification and educational planning. Teaching Mathematics and its Applications, 23(3), 123–139.
Blomhøj, M., & Højgaard Jensen, T. (2007). What’s all the fuss about competencies. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: the 14th ICMI study (pp. 45–56). New York: Springer.
Blum, W. (1996). Anwendungsbezüge im Mathematikunterricht – Trends und Perspektiven. In G. Kadunz, H. Kautschitsch, G. Ossimitz, & E. Schneider (Eds.), Trends und Perspektiven (pp. 15–38). Wien: Hölder-Pichler-Tempsky.
Blum, W., & Leiß, D. (2006). “Filling up”—the problem of independence preserving teacher interventions in lessons with demanding modelling tasks. In M. Bosch (Ed.), Proceedings of the fourth Congress of the European society for research in mathematics education CERME4 (pp. 1623–1633). IQS FUNDIEMI Business Institute
Blum, W., & Leiß, D. (2007). How do students and teachers deal with modelling problems? In C. P. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modelling (ICTMA 12): education, engineering and economics (pp. 222–231). Chichester: Horwood.
Blum, W., Galbraith, P.L., Henn, H.-W., & Niss, M. (Eds.), (2007). Modelling and applications in mathematics education: the 14th ICMI study. New York: Springer.
Galbraith, P. (2007). Authenticity and goals—overview. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: the 14th ICMI study (pp. 181–184). New York: Springer.
Haines, C. R., & Crouch, R. M. (2006). Getting to grips with real world contexts: developing research in mathematical modelling. In M. Bosch (Ed.), Proceedings of the fourth Congress of the European society for research in mathematics education CERME4, (pp. 1634–1644). IQS FUNDIEMI Business Institute
Haines, C. R., Crouch, R. M., & Davis, J. (2001). Understanding students’ modelling skills. In J. F. Matos, W. Blum, K. Houston, & S. P. Carreira (Eds.), Modelling and mathematics education: ICTMA9: Applications in science and technology (pp. 366–381). Chichester: Horwood.
Julie, C., & Mudaly, V. (2007). Mathematical modelling of social issues in school mathematics in South Africa. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: the 14th ICMI study (pp. 503–510). New York: Springer.
Kaiser, G. (2007). Mathematical modelling at schools—how to promote modelling competencies. In C. P. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modelling (ICTMA 12): education, engineering and economics (pp. 110–119). Chichester: Horwood.
Kaiser, G., & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. Zentralblatt für Didaktik der Mathematik, 38(3), 302–310.
Kaiser, G., & Schwarz, B. (2006). Mathematical modelling as bridge between school and university. Zentralblatt für Didaktik der Mathematik, 38(2), 196–208.
Kaiser, G. et al. (2004). Das Projekt Modellierung in der Schule. Darstellung der verwendeten Modellierungssituationen sowie ihrer Bearbeitungen, Reflexion der Modellierungsprozesse. Hamburg: Universität Hamburg. Preprint.
Kaiser, G., Sriraman, B., Blomhøj, M., & Garcia, F. J. (2007). Report from the working group modelling and applications—differentiating perspectives and delineating commonalities. In D. Pitta-Pantazi & G. Philippou (Eds.), Proceedings of the fifth congress of the European society for research in mathematics education (pp. 2035–2041). Larnaca Cyprus, ERME, 22–26 February 2007. Nicosia: University of Cyprus.
Kaiser-Meßmer, G. (1986). Anwendungen im Mathematikunterricht, Vol. 1: – Theoretische Konzeptionen, Vol. 2: – Empirische Untersuchungen. Bad Salzdetfurth: Franzbecker.
Maaß, K. (2004). Mathematisches Modellieren im Unterricht. Ergebnisse einer empirischen Studie. Hildesheim: Franzbecker.
Niss, M. (1992). Applications and modelling in school mathematics—directions for future development. Roskilde: IMFUFA Roskilde Universitetscenter.
Niss, M. (2003). Mathematical competencies and the learning of mathematics: the Danish KOM project. In A. Gagatsis & S. Papastravridis (Eds.), 3rd mediterranean conference on mathematical education (pp. 115–124). Athens: Hellenic Mathematical Society and Cyprus Mathematical Society.
Ortlieb, C. P., Dresky, V. C., Gasser, I., & Günzel, S. (2009). Mathematische Modellierung: Eine Einführung in zwölf Fallstudien. Wiesbaden: Vieweg+Teubner.
Ortlieb, C. P. (2009). Einige Überlegungen zur Modellierung der optimalen Gartenbewässerung. Unpublished manuscript.
Palm, T. (2007). Features and impact of the authenticity of applied mathematical school tasks. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: the 14th ICMI study (pp. 201–208). New York: Springer.
Pollak, H. (1969). How can we teach applications of mathematics. Educational Studies in Mathematics, 2, 393–404.
Schwarz, B., & Kaiser, G. (2007). Mathematical modelling in school—experiences from a project integrating school and university. In D. Pitta-Pantazi & G. Philippou (Eds.), Proceedings of the fifth congress of the European society for research in mathematics education (pp. 2180–2189). Larnaca, Cyprus, ERME, 22–26 February 2007. Nicosia: University of Cyprus.
Steinke, I. (2000). Gütekriterien Qualitativer Forschung. In U. Flick, E. V. Kardorff, & I. Steinke (Eds.), Qualitative Forschung – Ein Handbuch (pp. 319–331). Reinbek: Rowohlt Verlag.
Strauss, A., & Corbin, J. (1998). Basics of qualitative research. Newbury Park: Sage.
Acknowledgements
We thank Maren Hoffstall and Anna Orschulik for their extensive work within the evaluation process, Christoph Lederich for editorial support, and Hannah Heinrichs for her translational work.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Questionnaire about the Modelling Week
1.1 A.1 Questions about Mathematics
-
(1)
What is mathematics in your opinion? Describe in some sentences.
-
(2)
Are you interested in mathematics? If so, why and what are you interested in especially?
If not, why not and what are you discouraged by?
-
(3)
In your opinion, what relevance does mathematics have for this society?
1.2 A.2 Questions about Mathematics Teaching
-
(1)
Are you interested in the subject of mathematics in school? If so, why? If not, why not?
-
(2)
Describe topics, problems, and activities of mathematic classes which appeal to you. (Max. 3)
-
(3)
Describe topics, problems, and activities of mathematic classes which discourage or bore you. (Max. 3)
-
(4)
Have you been able to apply any mathematic approaches or methods which you have learned in school to everyday life or other fields of knowledge so far? If so, which ones and where?
1.3 A.3 Questions about the Modelling Example
-
(1)
Please value the modelling example that you dealt with during the modelling week:
-
(a)
How interesting was the problem that you dealt with?

-
(b)
How did you rate the difficulty of the modelling problem?
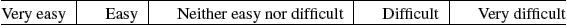
-
(c)
How highly was the problem structured?
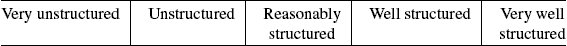
-
(d)
How realistic was the modelling example?

-
(a)
-
(2)
In your opinion, what did you learn when dealing with the subject?
-
(3)
Should these examples be increasingly dealt with as part of regular maths classes or would you reject this? Please give reasons for your position
-
(4)
Other comments that are relevant to me.
Appendix B: Codes to the Question: “From Your Point of View, What Did You Learn when Dealing with the Modelling Example?”
Application
-
General mathematical application
-
Critical questioning of techniques
-
Everyday-life reference of mathematics
-
Practical reference of mathematics
-
Geometry
Formal mathematics
-
Creating diagrams
-
Using mathematical terms
-
Developing formulae
-
Finding different approaches
-
Setting up equations
-
Stochastic
-
Calculating sectors of a circle
-
Circles in a square
-
Trigonometry
-
Geometry
-
Calculation of areas
-
Iteration
Application of the computer
-
Using mathematical programmes
-
Transforming ideas into algorithms
-
Creating algorithms
Formal work with the computer
-
Programming languages
-
Programming
-
Create graphics
-
Power Point
-
Excel
-
Matlab
Working techniques
-
Problem-solving strategies
-
Working independently
-
Gather information about unknown topics
-
Judging requirements
-
Structuring ideas
-
Recognising the variety of approaches
-
Optimism
-
Goal-oriented work
-
Organising work
-
Stamina
-
Making decisions
-
Structuring
-
Simplifying
Mathematical insights
-
Different approaches
-
Diversity of approach
-
Diversity of aspects in mathematics
-
Complexity
-
Specificity
Social aspects
-
Teamwork
-
Getting to know the fellow students
Appendix C: Codes to the Question: “Should These Examples Be Increasingly Dealt with as Part of Regular Maths Classes or Would You Reject This? Please Give Reasons for Your Position”
3.1 C.1 Yes
Reference to reality
-
Sense of mathematics
-
Recognising connections
-
Reference to reality
-
Reference to own everyday life
-
Clearness
-
Practical relevance
Improvement of working techniques
-
Working independently
-
Stamina
-
One’s own initiative
-
Group work
Variation
-
Diversified
-
Motivation
-
Interest
-
Appealing to the students
-
Fun
Requested change
-
Clearer structure
-
Simplifications
-
More support
-
Structuring of problems
-
Concreteness of problems
Sense
-
Advancement of complex thinking
-
Practise
-
Advancement of mathematical thinking
-
Simplified/“playful” learning
-
Better understanding
-
Memorising of learned things
-
No solution given
-
Puzzling
-
Good preparation/insight into the future tasks of a mathematician
3.2 C.2 No
Time problem
-
Restriction by the curriculum
-
Does not fit into the shortened time until university entrance examination
-
Too complex to be dealt with in class
-
Too extensive to be dealt with in class
Lack of interest
-
Boring
-
Uninteresting
-
Not useful for every student
Meaninglessness
-
Pointlessness
-
No connection to mathematics
-
No mediation of the foundation
-
No relevance concerning university entrance examination
Complexity
-
Complicated
-
Extensive
Inaccuracy
-
Vague formulations
-
No clear tasks
-
Variable level of difficulty
Rights and permissions
About this article
Cite this article
Kaiser, G., Schwarz, B. Authentic Modelling Problems in Mathematics Education—Examples and Experiences. J Math Didakt 31, 51–76 (2010). https://doi.org/10.1007/s13138-010-0001-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13138-010-0001-3
Keywords
- Teaching and learning of mathematical modelling
- Authentical modelling examples
- Students’ reactions on mathematical modelling