1 Introduction

1.1 Single-image super-resolution

Super-resolution is a technique for enhancing the resolution of given images. Traditionally, such methods can be categorized as multi-image super-resolution and single-image super-resolution based on the image input. Within the framework of multi-image super-resolution, a high-resolution image will be generated using multiple low images of same scene, e.g. [1,2]. Different low-resolution image contains different details related to the high-resolution image. The focus of multi-image super-resolution is locating and fusing the information of details connected with high-resolution image. Within the framework of single-image super-resolution, high-resolution image is generated with just a single low-resolution image. It is clear that the single-image super-resolution is a more challenging problem in the field of super-resolution for no enough information on high-resolution details in hand.

In order to make meaningful single-image super-resolution, prior information on high-resolution image is needed. The prior information can be presented directly or indirectly, which results in different strategies to deal with single-image super-resolution. First of all, the explicit prior information is the basis of most of single-image super-resolution. Based on the given prior information, the details missing in the low-resolution images can be estimated. The high-resolution image can be generated by combining the details with the given low-resolution image. For example, smoothing prior is extensively used in various interpolation or filtering algorithms for single-image super-resolution [3–6]. Though explicit priors are the representations of intrinsic rules behind images, it is hard to determine what and how much prior should be used in a special problem of single-image super-resolution. Therefore, such algorithms are out of main stream of study in single-resolution super-resolution recently.

Implicit prior information contains more complex information on high-resolution images than explicit prior information [7, 8]. Generally, implicit prior information is represented by a set of image pairs, which consists of low-resolution images and their corresponding high-resolution images. Various explicit prior information on high-resolution can be found in such set if the size of the set is large enough.

For super-resolving a low-resolution with implicit prior information, the key is to learn the effective rule which matches the given problem of single-image super-resolution. The rule learned from the set of image pairs unveils the relationship between the low- and high-resolution images. Based on such rule, the high-resolution image corresponding to the given low-resolution image can be well estimated.

Single-image super-resolution with implicit prior information or a set of image pairs is tightly connected with machine learning. Many achievements in machine learning, such as local linear embedding (LLE) [9] and support vector regression (SVR) [10] are the tools in learning the relationship between low- and high-resolution images. In fact, the method of super-resolution with implicit prior information is mostly named as learning-based method or example-based method [11–15]. More and more effort is devoted to such method in the field of super-resolution along with the success of machine learning in various applications.

1.2 Related work

In this section, we review some nearest neighbor-based algorithms. For more details about example-based algorithms for single-image super-resolution, we refer the readers to [11, 12, 16].

Example-based method was firstly introduced into single-image super-resolution by Freeman et al. [13, 14] in 2000. Their algorithm is designed based on the nearest neighbor-based estimation i.e. [17]. With patching technique, all given images are represented as a set of patches. For super-resolving a test low-resolution patch, a small set of low-resolution patches which consists of the k-nearest neighbors to the test low-resolution patch is chosen from the set of training set. The high-resolution patches corresponding to the chosen low-resolution patches are considered as hidden states in a Markov network model. By maximizing posterior probability, the high-resolution estimation is chosen from those high-resolution patches. Following the idea, similar nearest neighbor-based algorithms are proposed based on different probability model, e.g. [18–20].

To increase the flexibility of the nearest sample based methods, Chang et al. [15] introduced a novel nearest neighbor embedding algorithm which is motivated by the idea of LLE. Similar to the algorithm proposed by Freeman et al. [14], the k-nearest neighbor low-resolution patches are chosen. However, the high-resolution estimation is not generated by choosing from the high-resolution patches corresponding to those k-nearest neighbor low-resolution patches, but generated by combining these high-resolution patches in a linear style. The coefficients of such linear combination are defined based on the idea of LLE. On the low-resolution manifold, the local optimal linear approximation of the test patch is calculated. With the assumption on the preserving of local linear structures on low- and high-resolution manifolds, the coefficients corresponding to the optimal linear approximation of low-resolution test patch is used to the high-resolution patches. Thus, more information of training samples is used in estimating the high-resolution patch [21].

Though the performance of the nearest neighbor embedding algorithm is better than most of nearest neighbor estimation algorithms, the assumption on the preserving of local linear structures on different manifolds is always doubted. Many efforts are devoted to refine such assumption to make it more convincing. Based on those refined assumptions, different nearest neighbor embedding algorithms are proposed, such as [22–24].

1.3 Our contribution

In this paper, we introduce a local learning framework to enhance the performance of nearest neighbor-based algorithms. Similar to the nearest neighbor-based algorithms, a subset of training samples, named as local training set, is chosen for super-resolving a test low-resolution patch. Based on such local training set, a local regression function can be estimated by machine learning technique. The high-resolution estimation of the test low-resolution patch is generated by the value of the learned regression function on the test low-resolution patch.

The main merits of the local learning framework are as follows.

  • No additional assumption Traditional nearest neighbor-based algorithms are connected with the assumptions on the relationship between the low- and high-resolution patches, for example, the probability prior in nearest neighbor estimation algorithms and manifold prior in nearest neighbor embedding algorithms. As for our local learning algorithm, such relationship is directly learned from the local training samples, which make our algorithm independent on those additional priors.

  • Flexibility The local regression makes our algorithm more flexible in using the information of local training samples. Without strong prior on the relationship between low- and high-resolution patches, the more complex styles of using local training samples are available. In fact, the high-resolution estimation will be generated by some nonlinear combination of local training samples when kernel regression methods are used in local regression. It is completely different from the linear style used in traditional nearest neighbor-based algorithms.

The rest of the paper is organized as follows. In Sect. 2, the used notations are defined and the problem of single-image super-resolution is formulated strictly. In Sect. 3, a naive version of the local learning-based algorithm is presented. By comparing the performance of the local learning-based algorithm with the nearest neighbor-based algorithms, we show the merits of learning in single-image super-resolution. In Sect. 4, a refined version of the local learning-based algorithm is presented. Considering the connection between the generalization of regression algorithms and the number of training samples, the nearest neighbor training set is replaced by a larger local training set. Along with the expanding of the local range, the assumption of local linear structure is unacceptable. Therefore, the nonlinear estimation based on kernel method is adopted in local learning algorithm. In Sect. 5, various experimental results are presented to demonstrate the efficacy of the refined version of local learning-based algorithm. Finally, Sect. 6 concludes the paper.

2 Notations and problem formulation

Let \({{\mathcal{X}}}\) be a low-resolution image and \({{\mathcal{Y}}}\) its corresponding high-resolution image. Denote the magnification factor between \({{\mathcal{X}}}\) and \({{\mathcal{Y}}}\) as N.

The low-resolution image \(\mathcal{X}\) will be represented as a set of overlapping image patches, that is

$${{\mathcal{X}}}=\{x_{i}|i=1,2,\ldots,k_{{\mathcal{X}}}\}.$$

Here, x i is a l × l image patch, \({k_{\mathcal{X}}}\) is the number of patches generated from the image \({{\mathcal{X}}}.\) Similarly, the high-resolution image \({{\mathcal{Y}}}\) can be also represented as a set of small image patches \({\{y_{i}|i=1,2,\ldots,k_{\mathcal{Y}}\}}.\) If the size of y i is set to be h × h where h = N × l, \({k_{\mathcal{Y}}=k_{\mathcal{X}}}\) there is. Following image patches are treated as vectors, for example, \({x_{i}\in{\mathcal{R}}^{l^{2}}}\) and \({y_{i}\in{\mathcal{R}}^{h^{2}}}\)

Within the framework of example-based method for single-image super-resolution, a test low-resolution image \(\mathcal{X}^{{\rm test}}\) and a set of training image pairs

$$ \{({{\mathcal{X}}}^{i},{{\mathcal{Y}}}^{i})|i=1,2,\ldots,m\} $$

are available. For super-resolving the image \({{\mathcal{X}}^{{\rm test}}},\) the patching technique is always used. The test image \(\mathcal{X}^{{\rm test}}\) is blocked as a test set of patches

$$ T=\left\{x_{i}^{{\rm test}}|i=1,2,\ldots,p\right\}.$$

Meanwhile the set of training image pairs is used to generate the training set S. For ith training image pair \({({\mathcal{X}}^{i},{\mathcal{Y}}^{i})},\) a set of training patch pairs is generated, that is

$$ S^{i}=\left\{\left(x_{j}^{i},y_{j}^{i}\right)|j=1,2,\ldots,k_{i}\right\}.$$

The training set S is the union of \(S^{i},i=1,2,\ldots,m,\) that is

$$ \begin{aligned} S&=\cup_{i=1}^{m}S^{i} \\ &=\cup_{i=1}^{m}\left\{\left(x_{j}^{i},y_{j}^{i}\right)|j=1,2,\ldots,k_{i}\right\}.\end{aligned} $$

Simply, we denote below the training set as

$$ S=\{(x_{i},y_{i})|i=1,2,\ldots,n\}.$$

The focus of single-image super-resolution is to estimate the high-resolution image \({{\hat{\mathcal{Y}}}}\) corresponding to the test image \({{\mathcal{X}}^{{\rm test}}}\) with the help of the training set S.

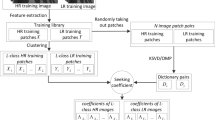
With the information in hand, there are two kinds of relationships can be estimated as showing in Fig. 1. One is low-low relation (LL-relation) which can be estimated by learning on

$$ \left\{x_{i}^{{\rm test}}|i=1,2,\ldots,p\right\}\cup \{x_{i}|i=1,2,\ldots,n\}.$$

LL-relation unveils the compatibility between the test samples and training samples. The other is low-high relation (LH-relation) which can be estimated by learning on training set S. LH-relation unveils the underlying rule of converting a low-resolution image to its corresponding high-resolution image. LL-relation helps us to collect meaningful information in super-resolution, and LH-relation helps us generalize such information to high-resolution patches and reconstructing a high-resolution image.

Fig. 1
figure 1

Two key relationships in example-based super-resolution. L-L the relationship between the low-resolution patches, and L-H the relationship between the low-resolution patches and their corresponding high-resolution patches

Full size image

It is clear that traditional nearest neighbor-based algorithms pay more attention on LL-relation. LH-relation is generally replaced by some prior. Though priors simplify the single-image super-resolution algorithms, they will also lower the performance of those algorithms. In the following sections, the machine learning method is introduced to generate sample-based LH-relation, which will enhance the performance of the nearest neighbor-based algorithms.

3 Nearest neighbor-based learning for super-resolution

In this section, we will show the power of learning in single-image super-resolution by comparing the naive local learning-based algorithm with some nearest neighbor-based algorithms.

Similar to most of the nearest neighbor-based algorithms, the local training set

$$ S_{L}^{t}=\{(x_{t_{1}},y_{t_{1}}),(x_{t_{2}},y_{t_{2}}),\ldots,(x_{t_{k}},y_{t_{k}})\}\subset S $$

corresponding to a test patch \(x_{t}^{{\rm test}}\) is generated according to the distance between training and test low-resolution patches. When local training set S t L is available, a local regression function \(f^{t}(\cdot)\) is estimated by the ridge regression. Then the high-resolution patch \({\hat{y}}_{t}\) corresponding to \(x_{t}^{{\rm test}}\) is estimated by the local regression function, that is

$$ {\hat{y}}_{t}=f^{t}\left(x_{t}^{{\rm test}}\right). $$

Consider that any manifold structure can be well approximated by a linear structure in sufficiently small range. A linear function space is used as the hypothesis space. That is

$$ {{\mathcal{H}}}=\{f(x)=Px|P\in{{\mathcal{R}}}^{h^{2}\times l^{2}},x\in {{\mathcal{R}}}^{l^{2}}\}.$$
(1)

The optimal local linear regression function is generated by minimizing the regularized empirical error, that is

$$ \begin{aligned} {\hat{f}}^{t}&=\mathop{\hbox{arg min}}\limits_{f\in{{\mathcal{H}}}} \sum_{i}{\left\Vert y_{t_{i}}-f(x_{t_{i}})\right\Vert}_{2}^{2}+ \lambda{\left\Vert f\right\Vert}_{{{\mathcal{H}}}}^{2}\\ &=\mathop{\hbox{arg min}}\limits_{P\in{{\mathcal{R}}}^{l^{2}\times h^{2}}} {\left\Vert Y-PX\right\Vert}_{2}^{2}+\lambda{\left\Vert P\right\Vert}_{F}^{2}, \end{aligned} $$
(2)

where \(X=(x_{t_{1}},x_{t_{2}},\ldots,x_{t_{k}}),\, Y=(y_{t_{1}},y_{t_{2}},\ldots,y_{t_{k}}),\lambda>0\) is a regularization parameter. Noting the necessary condition of extremum, there exits

$$ {\hat{P}}^{t}=YX^{\prime}(XX^{\prime}+\lambda I)^{-1},$$
(3)

where I is an identity matrix, which results in \({\hat{f}}^{t}(x)={\hat{P}}^{t}x.\)

The naive version of local learning-based algorithm is presented in Fig. 2. The difference between the nearest neighbor learning algorithm and the nearest neighbor-based algorithms is that the priors are replaced by a set of local regression functions which depends only on the training set. Some experimental results where five nearest neighbors are used show that the more details on high-resolution images are found by the nearest neighbor learning method. For more details, see Figs. 3 and 4.

Fig. 2
figure 2

A nearest neighbor learning-based algorithm for single-image super-resolution

Full size image
Fig. 3
figure 3

High-resolution image and the low-resolution test images are shown on the first line. The super-resolved images are shown on the second line. a Bicubic interpolation; b nearest neighbor estimation method [14]; c nearest neighbor embedding method [15]; d nearest neighbor learning (Fig. 2)

Full size image
Fig. 4
figure 4

Deviation between a super-resolved image and the original high-resolution image. a Bicubic interpolation;b nearest neighbor estimation method [14]; c nearest neighbor embedding method [15]; d nearest neighbor learning (Fig. 2)

Full size image

4 Local learning for super-resolution

In the nearest neighbor learning algorithm, each local regression function is trained on a small local training set. According to the results in learning theory [25–27], however, more training samples can lead to better generalization of estimators. Generally, better generalization will be helpful in enhancing the quality of super-resolution within the framework of learning-based method. Therefore, it is helpful to enlarge the sizes of the local training sets. With the increasing of the number of the local training samples, the local linear model maybe inappropriate to simulate the local relationship between the low- and high-resolution patches.

To benefit from the more training samples, a nonlinear model is adopted here. By enlarging the size of local training set, the local linear structure around the test patch will be destroyed. Though the linear model is unacceptable, the model learned from a local training set will be available. The kernel ridge regression (KRR) [10] is adopted to estimate the local nonlinear model for its well generalization in the small sample problem.

The hypothesis space used to define nonlinear models is a reproducing kernel Hilbert space (RKHS)

$$ {{\mathcal{H}}}_{\kappa}=\overline{\hbox{span}} \left\{f=\sum_{i}\alpha_{i}\kappa(x_{i},\cdot) |\alpha_{i}\in{\mathcal{R}},\,x_{i}\in{{\mathcal{R}}}^{l^{2}}\right\}, $$

where κ is a reproducing kernel. For the definition of reproducing kernel and RKHS, see [27] or [28].

Similar to the formulation (2), the optimal local regression function can be estimated by minimizing the regularized empirical error, that is

$$ {\hat{f}}^{t}=\mathop{\hbox{arg min}}\limits_{f\in{\mathcal{H}}_{\kappa}} \sum_{i}{\left\Vert y_{t_{i}}-f(x_{t_{i}})_{2}\right\Vert}^{2}+\lambda{\left\Vert f\right\Vert}_{{\mathcal{H}}_{\kappa}}^{2} $$
(4)

Considering the representation theory [29] or [30], the optimal local regression function can be represented as

$$ {\hat{f}}^{t}=\sum_{i}\alpha^{t}_{i}\kappa(x_{t_{i}},\cdot), $$
(5)

where \(x_{t_{i}}\in S^{t}_{L}.\) Combining the formula (4) and (5), there exists

$$ \begin{aligned} {\hat{A}}^{t}&=\mathop{\hbox{arg min}}\limits_{A\in{\mathcal{R}}^{h^{2}\times t_{k}}}{\left\Vert Y-AK\right\Vert}_{2}^{2}+\lambda {\left\Vert A\right\Vert}_{2}^{2}\\ &=YK^{\prime}(KK^{\prime}+\lambda I)^{-1} \end{aligned} $$
(6)

where \({\hat{A}}^{t}=({\hat{\alpha}}_{1}^{t}, {{\hat{\alpha}}}_{2}^{t},\ldots,{{\hat{\alpha}}}_{t_{k}}^{t}),\; K=\left(\kappa\left(x_{t_{i}},x_{t_{j}}\right)\right).\)

Combining the formulas (5) and (6), \({\hat{f}}^{t}\) can be defined as

$$ {\hat{f}}^{t}(x)={\hat{A}}^{t}(\kappa(x_{t_{i}},x))_{i=1}^{t_{k}}.$$
(7)

It should be noted that the complexity of calculating the regression function \({\hat{f}}^{t}\) is related with the number of the local training samples. Too large size of local training set will make it trouble in calculating a large kernel matrix. Thus, it is time to consider the strategy of generating local training samples. Firstly, the k-nearest neighbors \({{\mathcal{N}}=\{x_{t_{1}}^{t},x_{t_{2}}^{t},\ldots, x_{t_{k}}^{t}\}}\) of ith test patch \(x_{i}^{{\rm test}}\) are collected. Then the t j th local training sample is replaced by a set of its k-nearest neighbors \({{\mathcal{N}}_{t_{j}}=\{x_{n_{s}}^{t_{j}}|s=1,2,\ldots,k\}}.\) Finally, the local training set is generated by pooling all these k-nearest neighbor sets together, that is,

$$ S^{i}_{L}=\left(\cup_{j=1}^{k}{{\mathcal{N}}}_{t_{j}}\right) \cup{{\mathcal{N}}}.$$
(8)

Based on such strategy, more information of training samples is used to estimated the high-resolution patches meanwhile the local geometrical structure is still not too complexity.

The local learning algorithm is summarized in Fig. 5.

Fig. 5
figure 5

A local learning-based algorithm for single-image super-resolution

Full size image

5 Experiments

To validate the effectiveness of the local learning algorithm in single-image super-resolution, we compare such algorithm with other algorithms including bicubic interpolation algorithm, nearest neighbor-based estimation algorithm [14] and nearest neighbor embedding algorithm [15].

All training high-resolution images are shown on Fig. 6. The corresponding low-resolution images are generating by down-sampling and averaging. For all experiments, the magnification factor is set to be 4. The size of low-resolution patch is set to be 3 × 3 and the number of overlapping pixels is 2. The number of nearest neighbors is set to be various values including 5, 10, 50 and 100. A Gaussian kernel

$$ \kappa(x,y)=\exp\{-\sigma{\left\Vert x-y\right\Vert}^{2}\} $$
(9)

is used in all experiments. The kernel parameter σ is set to be 10−1 in all experiments, which is chosen by cross-validation. The regularized parameter λ is empirically set to be 10−3. In fact, no remarkable difference in performance there is when λ is around 10−3. However, the performance will be decrease if λ is too large or too small, such as λ > 10−2 or λ < 10−6.

Fig. 6
figure 6

All high-resolution images used in experiments. Both images on common row are used in an experiment. Left images are used to generate training samples, the right used to generate test samples

Full size image

Before super-resolving a test image, some preprocessing is needed. Consider that humans are more sensitive to the changes in luminance than to the changes in color. The YIQ color model is used in experiments. Thus all images used in experiments should be converted into the YIQ model. The super-resolution is only made for luminance values from the Y channel. The features of images are generated by uniting the first-order and second-order gradients of the luminance.

Figure 9 shows the results of applying different super-resolution algorithms to a lightning image when different numbers of nearest neighbors are considered. Figure 7 shows the curve of values of peak signal-to-noise ratio (PSNR) corresponding different super-resolution algorithms when different numbers of nearest neighbors are adopted. In the experiment, two images of lightning in Fig. 6 are used as the original images to generate training and test samples. The left one is used to generate training samples and the other one to generate test samples. Similarly, the results about flowers are shown in Figs. 8 and 10. Those experimental results show that more details are well estimated by the local learning-based algorithms than those estimated by most of nearest neighbor-based algorithms. In Figs. 7 and 8, PSNR is assessed between luminance components.

Fig. 7
figure 7

Lightning: PSNR versus number of nearest neighbors

Full size image
Fig. 8
figure 8

Flower: PSNR versus number of nearest neighbors

Full size image
Fig. 9
figure 9

Super-resolved images and deviation images for lightning, where K is the number of nearest neighbors. From left to right, the algorithms are bicubic interpolation, nearest neighbor embedding [15], nearest neighbor learning-based algorithm (Fig. 2) and local learning-based algorithm (Fig. 5)

Full size image
Fig. 10
figure 10

Super-resolved images and deviation images for flower, where K is the number of nearest neighbors. From left to right, the algorithms are bicubic interpolation, nearest neighbor embedding [15], nearest neighbor learning-based algorithm (Fig. 2) and local learning-based algorithm (Fig. 5)

Full size image

6 Conclusion

In this paper, a novel local learning-based method is introduced into the field of single-image super-resolution. The regression method is used on a local training set which is generated according to some similarity between low-resolution patches. The idea behind such method is making trade-off between generalization of estimators and the complexity of models, which is connected by the famous rule of structure empirical risk minimizing [27]. Experimental results show the effectiveness of the proposed algorithms, which also show the value of learning theory and machine learning methods in the single-image super-resolution.

Following the above idea, it is interesting to study the algorithms for super-resolution in the view of learning theory and machine learning. In the future, we will pay more attention on the theoretical analysis of example-based super-resolution methods with the help of learning theory.