1 Introduction

The single largest impurity in pig iron is carbon and is to be eliminated during the refining process. The mechanical properties of the steel are greatly affected by the amount of carbon present. High carbon content lowers the ductility and formability of the steel. In order to achieve better mechanical properties of the steel, the carbon content in it should be as low as possible.

With the increase in demand of ultra-low carbon steel (ULCS), there have been many attempts to improve the decarburization efficiency of vacuum degasser processes such as RH, DH, and tank degasser. The tank degasser is widely used because of the simplicity of its facilities and the low investment cost. However, the major drawbacks of the conventional vacuum degasser process are that the rate of decarburization in molten steel is low and operating time is longer, especially in the last stage of decarburization [1]. This impedes the productivity and economic efficiency of the process.

The reaction of oxidation of carbon practically does not take place at the slag-metal interface because of the difficulty in nucleating gas bubbles at the interface [2]. In reality, the reaction takes place at the gas-metal interface. In a steelmaking ladle, a layer of molten slag floats over the molten steel, and Argon (Ar) gas is injected through a nozzle located at the bottom of the ladle for mixing and improving the metal-slag reaction. This Ar gas forms a region uncovered by slag at the surface—the so-called plume eye [3]. The plume eye plays an important role in the reaction rates of decarburization in ultra low carbon region [4]. Although, the estimation of the gas–liquid reaction rate at the surface has been reported by many researchers [5–7], the controlling factor of the surface reaction has not been understood, fully. The decarburization rate in RH process decreases, in the low carbon region, by 20 ppm (stagnation region). To meet the demand for ultra-low carbon steel production, the improvement in the reaction rate in the stagnating regions is imperative.

It is reported that decarburization at the inner sites mainly occurs in the initial stage of the process, i.e. when the carbon concentration is high, and decarburization at the bath surface becomes dominant in the final stage of decarburization, that is, when the carbon concentration is ultra low. Recently a new decarburization process, known as revolutionary degassing activator (REDA, has been developed along with the reaction model [5]. It is claimed that using REDA process, carbon content reaches to 10 ppm in 15–20 min and further decreases to 4 ppm without any stagnation. This is significantly less time to achieve such low C content in comparison to other two processes (Tank and RH degassers). This is due to the enhancement in various reaction rates at the later stage of decarburization by using single snorkel and thus increasing the plume eye area. However, the design of REDA vessel is currently based on trial and error methods. Hardly any study is available on the fluid flow behaviour of REDA process which is necessary precursor to understand the reaction kinetics and design of the process in order to improve it further. Some preliminary work has been done in this direction by our group [8, 9]. In this paper we present a complete fluid flow and mixing study of this process considering water–air system which may help to understand and design this process better.

From numerical view point, it becomes important to study both the fluid flow and mass transfer phenomena which are occurring in the vessel simultaneously during the operation. Below, a description of the REDA process followed by numerical modeling is described in brief.

2 Process Description

REDA process differs a little from RH and tank degasser in the sense that design features of REDA were conceptualized based on logical thinking of the reaction kinetics. For example, in order to increase the decarburization efficiency at the later stage of decarburization, surface area should be increased to increase the reaction rate which means increase in snorkel area. Certainly, it works to achieve the low C content at the later stage of decarburization [5], however, proper design is not based on theoretical consideration. Therefore, it is felt that computational fluid dynamic (CFD) study would be very helpful to give better design criteria of the process in terms of mixing and fluid flow behaviour.

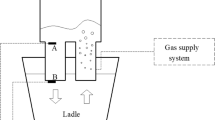
REDA process consists of one large diameter cylindrical snorkel immersed into the molten steel bath and Argon gas is purged through a nozzle into the ladle from the bottom of the ladle [5, 10, 11]. Bottom bubbling has been chosen as it reduces the perfect mixing time [11]. Porous plug is used for the gas flow and the position of the nozzle is kept away from the center of the vessel (asymmetric). In this way the activated surface area is increased which is needed at the later stage of decarburization (during the low carbon region) keeping the gas flow rate low. High gas flow rate deteriorates the vacuum pressure and contributes towards skull formation. It is found that asymmetric position gives a better bath mixing. The schematic diagram of REDA process is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of REDA process

Full size image

3 Theory

3.1 Fluid Flow Modelling

From mathematical modelling viewpoint, the REDA process is also similar to tank degasser except that it has one large snorkel. Therefore, many features of tank degasser model [12–16] can be incorporated into REDA process. Some features are common to RH process [17, 18] such as presence of snorkel. To simulate the REDA process the following assumptions have been made.

3.1.1 Assumptions

  • Two dimensional (2-D) Cartesian coordinate system is considered.

  • Isothermal condition has been considered and fluids are considered as Newtonian, and incompressible.

  • Free surfaces in the ladle and vacuum chamber are assumed to be flat.

  • To simplify the model, bubble diameter is assumed constant. Deformation of the gas bubbles is not taken into account, so the gas bubbles are assumed to be spherical and their interactions that lead to coalescence and breakup have been neglected.

  • It is assumed that the addition of tracer does not affect the flow field in the process.

Liquid and gas phase have been modeled using Eulerian–Eulerian approach. The Eulerian multiphase model is based on multiple separate, yet interacting phases tracked in an Eulerian frame of reference. In this approach, pressure and turbulence fields are shared among phases whereas phasic equations are solved for continuity and momentum equations. Each phase is described by its volume fraction such that at any space point, the sum total of all phasic volume fractions adds up to unity:

$$ \sum\limits_{i = 1}^{n} {\upalpha_{i} } = 1 $$
(1)

where n is the number of phases. The continuity equation for phase i is:

$$ \frac{\partial }{\partial t}\left( {\upalpha_{i} \uprho_{i} } \right) + \nabla \cdot \left( {\upalpha_{i} \uprho_{i} \vec{u}_{i} } \right) = 0 $$
(2)

where ρ i is the density and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{i} \) time average velocity of the ith phase.

Momentum transfer for the ith phase is:

$$ \frac{\partial }{\partial t}\left( {\uprho_{i} \upalpha_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{i} } \right) + \nabla \cdot \left( {\upalpha_{i} \uprho_{i} \vec{u}_{i} \vec{u}_{i} } \right) = - \upalpha_{i} \nabla P + K_{ij} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{j} } \right) + \upalpha_{i} \uprho_{i} \nabla g_{{}} + \nabla .\bar{\tau }_{i} $$
(3)

where \( \bar{\tau }_{i} \) is the ith phase stress–strain tensor and P is the pressure shared among the phases. The second terms in the right hand side of Eq. (3) is the momentum transfer interaction amounts between both phases (i and j) expressed through their relative velocity fields and K ij is usually known as the interphase momentum-exchange coefficient. This term can be interpreted as the drag force between the phases due to their relative movement. This coefficient is given by;

$$ K_{ij} = \frac{3}{4}C_{D} \frac{{\upalpha_{i} \uprho_{i} | {\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{j} - \overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{i} } |}}{{d_{b} }} $$
(4)

where d b is the average diameter of the bubble and C D is the drag coefficient which is given by;

$$ C_{D} = \frac{24}{\text{Re}}\left( {1 + 0.15\text{Re}^{0.687} } \right) $$
(5)

for Reynolds numbers (Re) < 1,000 and has a value of 0.44 for Re > 1,000. The Reynolds number definition in this two-phase problem is

$$ \text{Re} = \frac{{\uprho_{i} | {\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{i} - \overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{j} } |d_{b} }}{{\upmu_{i} }} $$
(6)

For modeling turbulence in multiphase mixture, k–ε turbulent model is used. The mixture turbulence model represents the first extension of the single-phase k–ε model, and it is applicable for stratified multiphase flows.

Turbulence kinetic energy (k) equation:

$$ \frac{\partial }{\partial t}\left( {\uprho_{m} k} \right) + \nabla \cdot \left( {\uprho_{m} u_{m} k} \right) = \nabla \cdot \left( {\frac{{\upmu_{t,m} }}{{\sigma_{k} }}\nabla k} \right) + G_{k} - \uprho_{m} \varepsilon $$
(7)

Turbulent rate of dissipation energy (ε) equation:

$$ \frac{\partial }{\partial t}\left( {\uprho_{m} \varepsilon } \right) + \nabla \cdot \left( {\uprho_{m} u_{m} \varepsilon } \right) = \nabla \cdot \left( {\frac{{\upmu_{t,m} }}{{\sigma_{\varepsilon } }}\nabla \varepsilon } \right) + \frac{\varepsilon }{k}\left\{ {C_{1} G_{k} } \right. - \left. {C_{2} \uprho_{m} \varepsilon } \right) $$
(8)

The mixture density (ρ m ) and the mixture velocity (u m ) are computed as:

$$ \uprho_{m} = \upalpha \uprho_{l} + \left( {1 - \upalpha } \right)\uprho_{g} $$
(9)
$$ u_{m} = \frac{{\upalpha \uprho_{l} u_{l} + \left( {1 - \upalpha } \right)\uprho_{g} u_{g} }}{{\upalpha \uprho_{l} + (1 - \upalpha )\uprho_{g} }} $$
(10)

(μ t,m ), the turbulent viscosity, is defined as

$$ \upmu_{t,m} = \uprho_{m} C_{\upmu } \frac{{k^{2} }}{\varepsilon } $$
(11)

where the production term in turbulent kinetic energy equation is given by:

$$ G_{k} = \upmu_{t,m} (\nabla \cdot u_{m} + (\nabla \cdot u_{m} )^{T}:\nabla \cdot u_{m} ) $$
(12)

The constants in the turbulence model are:

$$ C_{1} = 1. 4 4,\;C_{2} = 1. 9 2,\;C_{\upmu } = 0.0 9,\;\sigma_{k} = 1.00 \, \quad {\text{and}}\quad \sigma_{\varepsilon } = 1. 30 $$

3.2 Mass Transfer Modelling (Mixing Time)

The mass transport in REDA process is mainly due to the convection and diffusion processes along with the reaction rate, if any, which are occurring at various sites in the process. To study the mixing behaviour of REDA process, a tracer (NaCl) is introduced in the liquid (water) and its concentration with time is studied computationally by solving the mass transfer equation along with the fluid flow equations. The tracer concentration equation can be written as

$$ \frac{\partial }{\partial t}\left( {\uprho_{i} C} \right) + \nabla \cdot \left( {\uprho_{i} \vec{u}_{i} C} \right) = \Upgamma_{\it {eff}} \nabla^{2} \left( {\uprho_{i} C} \right) $$
(13)

where subscript “i” refers to the liquid phase and C is the concentration of the tracer (NaCl). Γ eff is the effective diffusion coefficient of tracer in water which includes turbulent diffusion coefficient and turbulent Schmidt number. Γ eff is defined as

$$ \Upgamma_{\it {eff}} = \frac{{\upmu_{l} }}{{S_{C} }} + \frac{{\upmu_{t} }}{{S_{Ct} }} $$
(14)

S C and S Ct are laminar and turbulent Schmidt numbers respectively. μl is laminar viscosity of the fluid. In this work, the properties of tracer are considered same as of liquid.

3.3 Boundary Conditions

  1. 1.

    Top of the ladle or vacuum chamber which is opened to atmosphere is defined as pressure out let and maintain at the vacuum chamber pressure.

  2. 2.

    Velocity inlet is defined at nozzle exit and velocity is calculated from the gas flow rate. Volume fraction is one at the inlet. Inlet velocity, turbulent kinetic energy and kinetic dissipation rate are defined as given form.

    $$ u = u_{\it{inlet}} \, {\text{and v }} = \, 0 $$
    $$ k = k_{\it{inlet}} = 1.5\left( {u_{\it{inlet}} I} \right)^{2} $$
    $$ \varepsilon = \varepsilon_{\it{inlet}} = \left( {C_{\upmu } } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}}} \left( {k_{\it{inlet}} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} /l $$

    where the turbulent length scale, l, at inlet is assumed to be the nozzle aperture or diameter). Turbulence intensity, I, is estimated using the ratio of turbulent fluctuating to mean velocity at inlet by \( I = {\raise0.7ex\hbox{${\bar{u}^{\prime}}$} \!\mathord{\left/ {\vphantom {{\bar{u}^{\prime}} {u_{\text{int}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${u_{\text{int}} }$}} \cong 0.16\left( {\text{Re} } \right)^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 8}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$8$}}}}, \)where Re is the flow Reynolds number based on the nozzle aperture and inlet velocity.

  3. 3.

    Standard wall functions [19] are employed to represent the near wall regions.

  4. 4.

    At the free surface, the normal gradients of the parallel velocity components, turbulent kinetic energy, kinetic dissipation rate and tracer concentration are set to be zero.

  5. 5.

    At the solid wall no slip condition is specified. The initial concentration of the tracer in the bath is zero.

All these boundary conditions are shown in Fig. 2.

Fig. 2
figure 2

Boundary conditions used for the REDA process

Full size image

4 Simulation Procedure

The above governing equations along with their boundary conditions were solved using the collocated variables finite volume approach. An extended SIMPLE algorithm is used for the pressure–velocity coupling in multiphase flow. To avoid bias towards a heavy phase the pressure correction is based on the conservation of the total volume. The resulting discretized form of the total volume continuity equation for incompressible fluids and the correction for the volume fluxes, derived from the coupled momentum equations are used to satisfy local mass continuity and derive pressure corrections. The coefficients of the pressure correction equation implicitly contain the whole effect of the coupling terms of the momentum equations.

Fluent® CFD software was used to solve the governing equations. Uniform grid size 25 mm is used throughout the domain. Mesh/grid was created using Gambit software (version 2.0.4). All the computations were performed on the Intel based PC with 3 GB ram. Quad-map mesh is used. The problem is solved in two-dimension. Typical CPU time, for the simulation of 2D fluid flow problem only, is about 6 h. The value of time step is 0.001 s. The CPU time for both fluid flow and mass transfer combined is about 7.5 h. All the results presented here are independent of grid size and time step. Standard values of physical properties of Ar/air gas and water are used. Diameter of the vessel is 4 m and heights of liquid in vessel and snorkel are 3.24 and 1.5 m respectively. Porous plug diameter is 5 cm. Air flow rate, location of the gas nozzle, snorkel diameter and chamber vacuum pressure are variables and their values are mentioned in the respective figures.

5 Results and Discussion

5.1 Validation

It is pre-requisite to validate any new theoretical model against the experimental data. However, there is a little information available on REDA process in the public domain and due to the scarcity of experimental data, it is difficult to compare the developed theoretical model results with the experimental data of REDA process. Because, this process resembles, to some extent, to tank and RH degassers, therefore, with little modifications in theory (mostly in the boundary conditions), models were developed for these processes also and results were compared with published computed and experimental data of these processes as they are widely studied by various investigators. Once these models were validated, model for REDA process was used for further study to see the effect of various parameters on this process. Tank degasser has symmetry along its center axis when gas is injected from center of the bottom of the vessel. However, RH and REDA processes do not have any axis of symmetry. Therefore, the governing equations were solved for the whole domain in case of REDA and RH. For tank degasser, axi-symmetry was considered and the equations were solved in cylindrical co-ordinate.

Figure 3 shows a comparison between the published theoretical [20] and our computed results for the lower vessel of RH degasser. The parameters which have been used in the published results are listed in Table 1 and the same parameters have been used in our model for the comparison sake. In the published model, vacuum chamber is not considered and fluid velocity is specified at the up and down legs. Other details can be found elsewhere [20]. From this figure one can see there is a good agreement between the published and our computed results which gives some confidence to the developed model in this study.

Fig. 3
figure 3

Comparison of published [20] computed fluid velocity (a) with present computed model results (b)

Full size image
Table 1 Numerical values of parameters used in RH and Tank degassers simulation
Full size table

Another comparison between the published experimental velocity data [21] and our computed results for tank degasser is shown in Fig. 4 at various locations. Figure compares the fluid velocity data in both radial and axial directions. The experimental conditions used to obtain the experimental fluid velocity data are given in Table 1. Same conditions have been used to simulate the computed results. More details about the experimental conditions and measurements are given [21]. Again, one can see a reasonable agreement between the published experimental and our computed results, lending a good support to our proposed model. After getting the desired confidence in our modelling and simulation, results are being presented for the REDA process below.

Fig. 4
figure 4

Comparison between computed and experimental [21] a axial velocity, and b radial velocity at different bath heights

Full size image

5.2 Effect of Gas Nozzle Position

As mentioned in Sect. 2 that the gas nozzle position in REDA process is asymmetric, therefore, the effect of nozzle position on the fluid flow has been studied. The results are shown in Fig. 5 for three nozzle positions viz. (a) centrally located, (b) 0.05 m away from the center towards the right side vessel wall and (c) 0.1 m away from the center towards the right side of vessel wall. Air flow rate and vacuum pressure in both the cases are same and they are 6.1 × 10−4 Nm3 s−1 and 0.032 atm respectively. The other parameters which have been used in simulations are mentioned in Sect. 4. From Fig. 5a, central gas injection, it is clear that only a limited number of liquid circulation zones exist and there is a large volume of the vessel is unaffected so called the dead zones. Certainly, this situation is not at all desirable in secondary steel making due to very poor liquid mixing and circulation. However, this situation improves significantly just by shifting the nozzle 0.05 m towards the right side from the center axis of the vessel, i.e. making the gas injection asymmetric (Fig. 5b). This has resulted the significant reduction in the dead zones at the expense of slight increase in gas velocity (about 10 %) at the same gas flow rate. However, one can still see some dead zones in the bath. By shifting the nozzle further 0.05 m, i.e. 0.1 m away from the center axis towards the right one can see more changes in the fluid pattern in Fig. 5c which further reduces the dead zones. From these figures it is obvious that asymmetric injections (position of nozzle) is not only beneficial in reducing the dead volume but also making the liquid bath more homoginised and thus the good mixing.

Fig. 5
figure 5

Contours of average velocity, m/s, of water a axi-symmetric condition (central nozzle), b position of nozzle is shifted 0.05 m right from the central and c position of nozzle is shifted 0.1 m right from the central with corresponding to argon flow rate of 6.1 × 10−4 Nm3/s and with vacuum pressure 0.032 atm, snorkel diameter 2.6 m and submerged depth 0.65 m

Full size image

In order to quantify further the effect of nozzle location on fluid circulation rate, which is defined as the liquid flow rate per unit time through the snorkel, was estimated in each condition. Table 2 shows the liquid circulation rate in all three conditions. It is clear from this table that liquid circulation rate is maximum for the nozzle location at 0.1 m away from the center of the vessel towards the right. It must be noted that mixing is directly proportional to the circulation rate [14, 22], therefore, a good liquid circulation is essential. However, the asymmetric position of nozzle increases the maximum liquid velocity slightly. Very high liquid velocity is not desirable as it contributes towards the erosion of refractory and thus more possibility of increase in inclusions in the steel. Therefore, in this work, for all other studies, nozzle position is kept at 0.1 m away from the center position towards the right side.

Table 2 Liquid circulation rate with nozzle position
Full size table

5.3 Effect of Gas Flow Rate

The effect of gas flow rate on liquid flow behaviour is shown in Fig. 6 in a visualized form. It is seen from this figure that as the gas flow rate increases the liquid circulation rate, and thus the mixing, is also increased when the gas injection nozzle position is 0.1 m away right side from the center axis of the vessel. The rate of liquid circulation for the gas flow rate of 2.7 × 10−4, 5.4 × 10−4 and 6.4 × 10−4 Nm3/s are 457, 592 and 652 kg/s respectively. One can get more liquid circulation rate at higher gas flow rate but at the expense of increase in liquid velocity which may have other detrimental effect to the over all process as discussed in Fig. 5. From Fig. 6 and Table 2, it is seen that at 652 kg/s liquid circulation rate, the maximum velocity is approaching very near to the snorkel wall which, if further increased, will have more detrimental effect on the refractory wall. Therefore, the gas flow rate 6.1 × 10−4 Nm3/s has been considered as the standard value for all other calculations.

Fig. 6
figure 6

Contours of average water velocity, m/s, at gas flow rate of a 2.7 × 10−4 Nm3/s, b 5.4 × 10−4 Nm3/s and c 6.4 × 10−4 Nm3/s with vacuum pressure 0.032 atm

Full size image

5.4 The Effect of Snorkel Depth

The effect of snorkel depth in the liquid bath shows quite interesting results on the liquid circulation rate as shown in Fig. 7. Initially, the liquid circulation rate is increased with the increase in snorkel depth in the liquid bath up to a point and thereafter it started decreasing with the further increase in the snorkel depth. This shows that there is an optimum depth of snorkel which should be kept in the liquid pool to achieve the optimum circulation rate beyond which it is detrimental for the liquid circulation rate and thus the mixing. The reason of decrease in liquid circulation rate is due to the resistance offered by the snorkel wall to the liquid which is in the bath (i.e. outside the snorkel region). After certain snorkel depth, its wall acts as barrier to liquid flow in entering the snorkel region from other part of the liquid bath and hence decrease in the liquid circulation rate. As the immersed depth of snorkel in the bath increases, system starts behaving more like a tank degasser (indeed, it would become tank degasser if the snorkel wall touches the bottom of the vessel).

Fig. 7
figure 7

Effect of snorkel depth in liquid bath on liquid circulation rate

Full size image

5.5 Effect of Snorkel Diameter

Figure 8 shows the effect of snorkel diameter on the liquid circulation rate. Initially, the liquid circulation rate is increased with the increase in snorkel diameter however, its gradient decreases significantly beyond 2.6 m snorkel diameter. This means beyond a certain point of snorkel diameter, there is little increment in the liquid circulation. This is because when the snorkel diameter is increased from 2.4 to 2.6 m, the liquid velocity magnitude is increased by 15 %. However, when diameter is increased from 2.6 to 3.0 m the velocity magnitude is increased by 2 % only and hence the proportion increment in the liquid circulation rate. In fact, if one keeps on increasing the snorkel diameter at one point it will become a tank degasser and will behave like it only.

Fig. 8
figure 8

Effect of snorkel diameter on liquid circulation rate

Full size image

5.6 Effect of Vacuum Pressure

Figure 9 shows the effect of vacuum pressure on liquid circulation rate. One would expect with the decrease in vacuum pressure, the rising velocity of gas bubbles would increase as the buoyancy force would increase. This will contribute towards increase in liquid velocity and thus the circulation rate. The same trend is observed in Fig. 9 between the vacuum pressure and circulation rate. Very low vacuum pressure, due to both the operational difficulty in maintaining the low vacuum and detrimental effect due to increase in liquid velocity, is not advisable. Therefore, 0.32 atm vacuum pressure has been considered for all other calculations.

Fig. 9
figure 9

Effect of vacuum pressure on liquid circulation rate

Full size image

5.7 Mixing Behaviour

Once the optimum conditions for the fluid flow behaviour in terms of liquid circulation rate are identified, the mixing behaviour of the REDA process was carried out which is described below.

After scrutinizing the various correlations which are available in the open literature [23–25] to describe the mixing behaviour of tank and RH degassers, it is found that they are not applicable directly to describe the mixing behaviour of REDA process. It is also found that these correlations have been developed for specific system and differ to each other and give considerably different results in different conditions as explained somewhere else [9]. Therefore, we restrict ourselves to compare the theoretical mixing time, obtained from the present model, for all the three systems, i.e. tank, RH and REDA degassers. Same critical parameters have been used to study the mixing behavior in all three processes like gas flow rate, total amount of liquid, etc.

Figure 10 shows a visual comparison of mixing time for all the three processes. One can see that tank degasser has the significantly higher complete mixing time than RH and REDA processes. The time required by the tracer to achieve the uniform concentration in the whole system is considered as complete mixing time. However, REDA process has the lowest complete mixing time under the same identical operating conditions. It is closely followed by RH degasser. It should be noted that mixing time is inversely related to the liquid circulation rate; therefore, the effect of various parameters (like gas flow rate, snorkel diameter & depth, etc.) on mixing time can be deduced from the results presented in the previous sub-sections.

Fig. 10
figure 10

Concentration contours of the tracer (NaCl) at different time in Tank, RH and REDA processes

Full size image

6 Implication of Results

As pointed out by Kitamura et al. [3] that inner site reaction is very important in the initial period of decarburisation. However, as the time passes, it becomes less significant and towards the end of decarburization period, bath surface reaction becomes more important along with some bubble surface reaction. Looking at it from the above viewpoint, it is clear that in the initial stage decarburization reaction can be facilitated by reducing the mixing time (this will promote inner site reaction) and by increasing the bath surface area in the later stage of decarburization.

Indeed, REDA process does reduce the complete mixing time as shown in Fig. 10 and thus promotes the inner site reaction. It also increases the bath surface area which is critical requirement to increase the decarburization efficiency especially at the final stage of it when it is controlled by bath surface reaction. In our previous work [9] it is reported that there is above 66 % increase in plume eye area in REDA process than tank degasser when the gas is injected centrally in both the cases. It is not possible to estimate the plume area correctly in asymmetric gas injection case as it interacts with the wall of the snorkel in case of REDA process. RH degasser does not have plume area so it is not considered. So, based on centrally gas injection it can be said that surface area in case of REDA will increase at least by 66 % more. This means that decarburization efficiency would be more in REDA process at the final stage of it. Therefore, it would be more efficient. Industrial results [5], though a few, available in the open literature do support it.

7 Conclusions

A new degassing process, REDA, has been simulated computationally to study the fluid flow and mixing behaviour of it along with RH and Tank degassers. For the REDA process, it is found that the mixing efficiency (liquid circulation rate) is increased with the gas flow rate and reduction in vacuum pressure in the vacuum chamber. It is also observed that for optimum mixing behaviour, there exists an optimum snorkel depth, immersed in the liquid bath, beyond which the efficiency is decreased. After a certain snorkel diameter, no significant effect on the liquid circulation rate was found. Based on the optimum fluid flow behaviour parameters, it is found that REDA process has the lowest complete mixing time than any other existing processes such as RH and Tank. It is believed that this study will help to improve the REDA process further.