Introduction

Groundwater is the primary source of domestic and agricultural water in many parts of Iran (Baghvand et al. 2010). In recent years, groundwater level has significantly plummeted in many regions of the country due to overexploitation of aquifers (Taheri Tizro and Voudouris 2008; IWRMC 2016). Overusing groundwater resources could also result in deteriorating water quality in aquifers. Understanding the spatial and temporal variations in groundwater quantity and quality is a prerequisite for properly managing the groundwater resources.

In the last two decades, there has been an extensive use of artificial intelligence for water resources modeling and management. Artificial intelligence and other data-driven techniques have been successfully used in a variety of problems in the field of surface water modeling and management, including estimating or forecasting rainfall (e.g., Hsu et al. 1997; Liu et al. 2001; Chiang et al. 2007; Chen et al. 2011; Chang et al. 2014), streamflow modeling (e.g., Moradkhani et al. 2004; Wang et al. 2009; Lin et al. 2009; Noori et al. 2011; Kasiviswanathan et al. 2016), rainfall-runoff modeling (e.g., Dibike et al. 2001; Wu and Chau 2011; Shoaib et al. 2014; Kashani et al. 2016; Nourani 2017), and water demand forecasting (e.g., Msiza et al. 2008; Adamowski et al. 2012). Some recent studies have also shown that artificial neural networks (ANNs) and support vector machines (SVMs) can provide an effective tool for modeling quantitative and qualitative parameters of groundwater resources. Khalil et al. (2005) used ANNs and SVMs to simulate groundwater nitrate concentrations in an agricultural dominated area in the Northeast US and showed the strong predictive capabilities of these learning machines. Krishna et al. (2008), using ANNs, predicted groundwater levels in a coastal aquifer in India. Adamowski and Chan (2011) combined discrete wavelet transforms and ANNs and showed the potential of their proposed method in groundwater level forecasting. Yoon et al. (2011) used ANNs and SVMs to predict groundwater level fluctuations in a coastal aquifer in South Korea. Arabgol et al. (2015) developed a SVM to predict groundwater nitrate levels in an agricultural plain in central Iran and showed the advantages of SVM in the domain of assessing groundwater quality. Modaresi and Araghinejad (2014) assessed the performance of SVMs and probabilistic neural networks in classification of groundwater qualitative samples and demonstrated that SVMs are more reliable. Nourani et al. (2016) integrated self-organizing map, an ANN that is trained using unsupervised learning, with a kriging-based method to select the most effective input data for a feed-forward neural network and to simulate groundwater salinity in an aquifer in Iran.

Guilan Province, northern Iran, is adjacent to the Caspian Sea, and its alluvial plains are highly suitable for agriculture. Following the construction of the Manjil Dam on the Sefidroud River, almost the total agricultural water in Guilan Province has been supplied by surface water since 1962, through a network of irrigation canals. Moreover, about 70% of domestic water used in Guilan Province is also supplied by surface water (WWCGP 2016). Nevertheless, in recent years, the farmer’s reliance on aquifers for irrigation is continuously growing in the region, due to an increasing scarcity of surface water resources in the Sefidroud River basin. In the case of insufficient surface water availability in dry years, water wells around the irrigation canals in Guilan Province are used by farmers to compensate the scarcity of surface water needed for irrigation. Using the water stored naturally in aquifers to reduce the bad effects of unavailability of surface water may seem a reasonable and practical solution for the problem of irrigation water scarcity in the region. However, unplanned replacing of surface water by groundwater resources may result in problems such as aquifer depletion, or seawater intrusion, both of which are often associated with deteriorating groundwater quality.

Nowadays, groundwater quality in Guilan Province, northern Iran, is a critical factor that could affect public health and agricultural productivity. So, modeling the variability of groundwater quality throughout this province using appropriate methods is necessary, now and in the future, for the proper management of this source of domestic and irrigation water. The objective of the present study is assessing the performance and analyzing the output uncertainty of ANNs and SVMs, to produce models that can be effectively used to estimate qualitative parameters of the aquifers of Guilan Province. The results of the present study can be used by the local water authorities in the region to identify the locations in the province where groundwater could be allowed to be extracted and utilized for agricultural and potable purposes, based on the knowledge of the spatial distribution of groundwater quality parameters.

Materials and methods

Study area and data

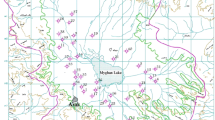
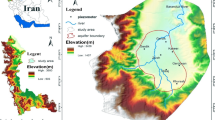
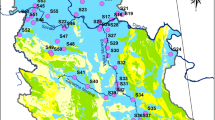
Guilan is the fourth smallest province of Iran, with an area of 14,044 km2. This coastal province is located in northern Iran and has Rasht as its capital city. It is bounded by the Caspian Sea to the north, the Alborz mountain range to the west and southeast, and Mazandaran Province to the east (Fig. 1). The climate of Guilan Province is humid subtropical with hot and humid summers and mild winters. Its average annual precipitation and average annual pan evaporation is, respectively, 1506 and 1306 mm. About 70% of the area of the province is covered by mountainous terrains. Alluvial plains, which are greatly appropriate for agriculture, account for the rest of the area of Guilan Province. Groundwater quality in the plains of the province is monitored by Guilan Regional Water Authority through a network of 140 observation wells from which water qualitative samples are collected twice each year, in March and September. All taken samples are analyzed by Guilan Regional Water Authority for pH, temperature, electrical conductivity (EC), and the concentrations of major cations and anions (Na+, K+, Ca2+, Mg2+, Cl−, SO4 2−, CO3 2−, and HCO3 −). These 140 wells, which are scattered throughout the whole province, are only used for the purpose of groundwater quality monitoring and measuring groundwater levels. Figure 2 shows the location and depth of all the existing observation wells within Guilan Province, as well as the piezometric map of the study area. The geological map of Guilan Province and the hydrogeological cross-sections illustrating the aquifer system in the study area are presented in Fig. 3.

Fig. 1
figure 1

(Source: Ashrafzadeh et al. 2016)

Map of Iran and location of Guilan Province (a), topography of Guilan Province (b)

Full size image
Fig. 2
figure 2

Location and depth of all quality observation wells in the study (top), piezometric map of the study area (bottom)

Full size image
Fig. 3
figure 3

(Source: GRWA 2016)

Geological map of Guilan Province and hydrogeological cross sections illustrating the aquifer system in the study area

Full size image

In this study, the data collected from the observation wells in March and September 2002–2014 were used to calibrate and validate ANNs and SVMs capable of estimating groundwater qualitative parameters throughout Guilan Province. All data are derived from the database of Guilan Regional Water Authority. For each sampling month (March and September), the number of analyzed qualitative samples was typically less than 140, the total number of observation wells in the groundwater monitoring network, because of some technical difficulties involved in the sampling process. The raw data set was comprised of 2954 rows. The data set was randomly partitioned into two sets, where 80% (2363 rows) was used for calibration (training) and 20% (591 rows) for validation (testing) of ANNs and SVMs. Five variables, X and Y coordinates of the observation well, distance of the observation well from the shoreline, the areal average 6-month rainfall depth (computed using the Thiessen polygon method utilizing rainfall data from 13 meteorological stations throughout the province), and groundwater level at the day of water quality sampling, were considered as primary input variables. Groundwater qualitative parameters considered for estimation using ANNs and SVMs were electrical conductivity (EC), sodium concentration (Na+), and sulfate concentration (SO4 2−). Summary statistics of the input and output variables are presented in Table 1.

Table 1 Summary statistics of raw data
Full size table

Feed-forward neural networks

ANNs are data processing systems that are inspired by biological neural information processing systems (ASCE Task Committee 2000). Although there are different types of neural networks architectures, the most popular network for hydrologic data analysis is the multilayer feed-forward type. A typical multilayer feed-forward neural network consists of a number of linear or nonlinear processing elements (PEs), also called nodes, which are interconnected through weighted connections. PEs are organized in three or more layers, an input layer, an output layer, and one or more hidden layers. Figure 4 shows the typical arrangement of a three layer feed-forward neural network. The number of PEs in input and output layers depends on the type of the problem, whereas for the hidden layers this is determined through trial and error.

Fig. 4
figure 4

A typical three layer feed-forward neural network

Full size image

The input layer receives the input variables and provides the necessary information to the PEs of the first hidden layer. The nodes in one layer are only connected to those in the next, so the information flow direction in the network is only from the input layer to the output layer. Output values of the hidden layer PEs are given by the following equation:

$$y_{j}^{{\prime }} = g\left[ {\sum\limits_{i = 1}^{{n_{\text{in}} }} {x_{i} \cdot w_{ij} } + b_{j} } \right];\quad j = 1, \ldots ,n_{\text{hid}}$$
(1)

where n in and n hid are, respectively, the number of PEs in the input layer and hidden layer; w ij is the weight of the link that connects the ith PE in the input layer and the jth PE in the hidden layer; b j is the bias for the jth PE in the hidden layer; x i is the ith component of n-dimensional input vector (the output of the ith PE in the input layer, n = n in); and g(.) is the transfer function of hidden PEs. The outputs of the network are given by:

$$y_{k} = f\left[ {\sum\limits_{j = 1}^{{n_{\text{hid}} }} {y_{j}^{{\prime }} \cdot w_{jk} } + b_{k} } \right];\quad k = 1, \ldots ,n_{\text{out}}$$
(2)

where n out is the number of PEs in the output layer (typically one); w jk is the weight of the link that connects the jth PE in the hidden layer and the kth PE in the output layer; b k is the bias for the kth PE in the output layer; and f(.) is the transfer function of the kth output PE. The transfer function determines the response of a node to the net input it receives. The most commonly used form of transfer function is the sigmoid function. The general form of this function is as follows:

$$f(x) = \frac{1}{{1 + {\text{e}}^{ - x} }}$$
(3)

The sigmoid function is a bounded, monotonic, and nondecreasing function with a nonlinear response and enables a network to simulate any nonlinear process (ASCE Task Committee 2000). A multilayer feed-forward neural network with a single hidden layer that contains finite number of nonlinear hidden PEs can approximate any function to arbitrary precision (Hornik et al. 1989). In order to generate outputs that are as close as possible to the observed or desired ones, the connection weights are successively modified during a training process. In the present study, the Levenberg–Marquardt learning algorithm, a modification to the back-propagation algorithm, is used (Fausett 1994; Hagan and Menhaj 1994). Like any model, feed-forward neural networks have certain drawbacks as well as advantages. From a theoretical point of view, probably the major drawback is that neural networks are essentially black-box type models and completely ignore the physics of the process under study. Moreover, finding the optimal architecture of a feed-forward neural network could be a time-consuming trial and error process.

Support vector machines

SVMs are supervised learning methods which were originally designed to solve pattern recognition problems (Vapnik et al. 1996). SVMs divide a set of data points (or N-dimensional vectors) into two classes by constructing a separating hyperplane between two parallel hyperplanes. The distance from the separating hyperplane to support vectors, nearest N-dimensional vectors on each side of the separating hyperplane which are located on a parallel hyperplane, is maximized through a quadratic programming problem:

$$\begin{array}{*{20}l} {\text{Minimize}} \hfill & {\varPhi ({\varvec{\upomega}},b_{v} ,\xi ) = \frac{1}{2}\left\| {\varvec{\upomega}} \right\|^{2} \,+\, C\sum\limits_{i = 1}^{m} {\xi_{i} ,} } \hfill \\ {{\text{Subject}}\,{\text{to}}} \hfill & {\left\{ \begin{aligned} y_{i} ({\varvec{\upomega}}^{\text{T}} \cdot {\mathbf{x}}_{i} + b_{v} ) \ge 1 - \xi_{i} ,\quad i = 1, \ldots ,m \hfill \\ \xi_{i} \ge 0 { } \hfill \\ \end{aligned} \right.} \hfill \\ \end{array}$$
(4)

where ω ∈ R N is the normal vector to the separating hyperplane; b v  ∈ R is the bias value; m is the number of N-dimensional vectors; x i  ∈ RN is the ith N-dimensional vector; y i  ∈ {+1, −1}; ξ i is the ith slack variable; and C > 0 is a trade-off parameter between the error of classification and the distance between parallel hyperplanes. Equation of the separating hyperplane is written as:

$${\varvec{\upomega}}^{\text{T}} \,.\,{\mathbf{x}} + b_{v} = 0$$
(5)

In order to provide the ability to handle nonlinear classification problems, kernel functions are used to map data points to a new higher dimensional feature space, where data points are linearly separable. The kernel functions most commonly used are as follows:

$$\begin{array}{*{20}l} {{\text{degree-}}d\;{\text{polynomial:}}\;\;k\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = \left( {{\mathbf{x}}_{i}^{\text{T}} .\,{\mathbf{x}}_{j} + I} \right)^{d} } \hfill \\ {{\text{radial}}\;{\text{basis}}\;{\text{function}}\;\left( {\text{RBF}} \right):\;\;k\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = \exp \left( { - \gamma \left\| {{\mathbf{x}}_{i} - {\mathbf{x}}_{j} } \right\|^{2} } \right)} \hfill \\ {{\text{hyperbolic}}\;{\text{tangent:}}\;\;k\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = \tanh \left( {\kappa {\mathbf{x}}_{i}^{\text{T}} .\,{\mathbf{x}}_{j} + c} \right)} \hfill \\ \end{array}$$
(6)

where γ > 0, κ > 0 and c < 0 are the parameters of the kernels. Besides the advantages of SVMs, there are also some practical limitations. The major drawback of SVMs is probably the selection of the best kernel function and its associated parameters. High algorithmic complexity of the required quadratic programming is also a limitation, especially for high-dimensional problems (Suykens et al. 2002).

The classical regression version of SVMs (ε-support vector regressions), proposed by Vapnik et al. (1996), is also a quadratic programming problem which can be written as follows:

$$\begin{aligned} & {\text{Minimize}}\,\,\,\varPhi ({\mathbf{w}},b,\xi ,\xi^{*} ) = \frac{1}{2}\left\| {\mathbf{w}} \right\|^{2} \,+\, C\sum\limits_{i = 1}^{m} {(\xi_{i} + \xi_{i}^{*} )} , \\ & {\text{Subject}}\,{\text{to}}\,\,\,\left\{ \begin{aligned} y_{{i({\text{out}})}} - ({\mathbf{w}}^{\text{T}} \,\cdot \,{\mathbf{x}}_{{i({\text{inp}})}} + b) \le \varepsilon + \xi_{i} ,\quad i = 1, \ldots ,m\, \hfill \\ ({\mathbf{w}}^{\text{T}} \cdot {\mathbf{x}}_{{i({\text{inp)}}}} + b) - y_{{i({\text{out}})}} \le \varepsilon + \xi_{i}^{*} ,\quad i = 1, \ldots ,m \hfill \\ \xi_{i} \ge 0,\xi_{i}^{*} \ge 0 \hfill \\ \end{aligned} \right. \\ \end{aligned}$$
(7)

where w ∈ Rn is the slope vector of the regression hyperplane; b ∈ R is the intercept; m is the number of observations; x i(inp) ∈ Rn is the ith n-dimensional input vector; y i(out) is the ith output value; ξ i and ξ *i are the ith slack variables; and C > 0 is a trade-off parameter between the slope of the regression hyperplane, and the amount up to which error values greater than ε are acceptable. In nonlinear regression analysis, the regression equation is written as follows:

$$y = \sum\limits_{i = 1}^{m} {(\alpha_{i} - \alpha_{i}^{*} )} \,k({\mathbf{x}}_{{i({\text{inp}})}} ,{\mathbf{x}}) + b$$
(8)

where α i and α i * are the Lagrange multipliers (determined after solving the quadratic programming); and k(.) is the kernel function.

Error measures

The error measures used to evaluate the accuracy of estimates were coefficient of correlation (CC), root mean square error (RMSE), and the Nash–Sutcliffe model efficiency coefficient (E). These measures are defined as follows:

$${\text{CC}} = \frac{{\sum\nolimits_{i = 1}^{n} {(y_{{i({\text{obs}})}} - \bar{y}_{\text{obs}} )} (y_{{i({\text{est}})}} - \bar{y}_{\text{est}} )}}{{s_{\text{obs}} s_{\text{est}} }}$$
(9)
$${\text{RMSE}} = \sqrt {\frac{1}{m}\sum\nolimits_{i = 1}^{m} {(y_{{i({\text{obs}})}} - y_{{i({\text{est}})}} )^{2} } }$$
(10)
$$E = 1 - \frac{{\sum\nolimits_{i = 1}^{m} {(y_{{i({\text{obs}})}} - y_{{i({\text{est}})}} )^{2} } }}{{\sum\nolimits_{i = 1}^{m} {(y_{{i({\text{obs}})}} - \bar{y}_{\text{obs}} )^{2} } }}$$
(11)

where \(\bar{y}_{\text{obs}}\) and s obs are, respectively, mean and standard deviation of all observed values; \(\bar{y}_{\text{est}}\) and s est are, respectively, mean and standard deviation of all estimated values; m is the number of observations; y i(obs) is the ith observed data; and y i(est) is the estimate of y i(obs).

Uncertainty analysis

Meaningful application of a calibrated model requires knowledge about the model output uncertainty. The output uncertainty of a model is mainly attributed to the uncertainties in the model parameters. It is obvious that single-valued parameters lead to a single model output. However, model parameters are typically uncertain. The uncertainties in model parameters are usually expressed as meaningful ranges. Propagation of these uncertainties results in an uncertainty in the model output. In the present study, p-factor and d-factor (Abbaspour et al. 2007; Yang et al. 2008) were used for evaluating the output uncertainty of ANNs and SVMs. These two factors are calculated based on the 95% prediction uncertainty (95PPU), the range from 2.5th percentile to 97.5th percentile of the model output. The p-factor is the percentage of the observed data bracketed by the 95PPU, and its ideal value is 100% (Yang et al. 2008). The d-factor is defined as follows (Abbaspour et al. 2007):

$$d{\text{-factor}} = \frac{{\frac{1}{m}\mathop \sum \nolimits_{i = 1}^{m} (X_{U} - X_{L} )_{i} }}{{s_{\text{obs}} }}$$
(12)

where m is the number of observed data, X U is the 97.5th percentile of model output, X L is the 2.5th percentile of model output, and s obs is the standard deviation of all observed data.

Results and discussion

Table 2 lists the five different combinations of the primary input variables considered for estimating the spatial variability of sulfate concentration (SO4 2−), sodium concentration (Na+), and electrical conductivity (EC), using three layer feed-forward ANNs, and SVMs. These models are designed to estimate values at unsampled intermediate locations where no observation of the desired qualitative parameters is available. So, it is essential that the variables used as input should be simple and easily measurable. The study area is a humid region which is located in proximity to the Caspian Sea. The groundwater overexploitation in the region seems to lead to saltwater intrusion and the subsequent reduction in the groundwater quality. Based on these facts, X and Y coordinates of the observation well, distance of the observation well from the shoreline, areal average 6-month rainfall depth, and groundwater level at the day of water quality sampling were considered as the primary input variables. The optimal number of nodes in the hidden layer of the ANNs was determined through a trial and error procedure by varying the number of nodes from one to 20 with an increment of one. The sigmoid function (Eq. 3) was employed as the activation function for the hidden layer nodes. The identity activation function was employed in the output layer, because this function is known to be robust for a continuous output variable (Ghorbani et al. 2016). All ANNs were trained for 100 epochs using the Levenberg–Marquardt learning algorithm with a learning rate of 0.001 and a momentum coefficient of 0.9. For the ANNs, the numerical results of the performance evaluation measures, coefficient of correlation (CC), root mean square error (RMSE), and the Nash–Sutcliffe model efficiency coefficient (E), are presented in Table 3. Both calibration (training) and validation (testing) results of the ANNs are presented in this table. Among every five calibrated ANNs for estimating each groundwater quality parameter (SO4 2−, Na+, and EC), the one with the smallest RMSE, and greatest CC and E was chosen as the best ANN. The values of CC, RMSE, and E presented in Table 3 show that the ANN with 15 nodes in the hidden layer, and with the input combination including X and Y coordinates, groundwater level, and distance from the shoreline, provides the best estimates of sulfate concentrations (the testing RMSE value of 0.93 mEq/l). The best estimates of sodium concentrations are provided by the ANN which has a (3, 16, 1) structure, i.e., three nodes in the input layer (X and Y coordinates, and distance from the shoreline), 16 nodes in the hidden layer, and one output (the testing RMSE value of 0.93 mEq/l). The ANN with the same input combination and 20 nodes in the hidden layer presents the best estimates of electrical conductivities (the testing RMSE value of 186.45 μS/cm). The RMSE and E values presented in Table 3 indicate that adding groundwater level as an input variable can improve the estimates of all three groundwater qualitative parameters (input combination 3 in comparison with input combination 1). In addition, distance of observation well from the shoreline as an input variable reduces the estimation errors of SO4 2−, Na+, and EC (input combination 2 in comparison with input combination 1, and input combination 4 in comparison with input combination 3). On the other hand, the estimation errors do not decrease when areal average 6-month rainfall depth is considered as the third input variable (input combination 5 in comparison with input combination 1).

Table 2 Input combinations used for ANNs and SVMs
Full size table
Table 3 Error measures of qualitative parameters estimates produced by ANNs
Full size table

The numerical results of CC, RMSE, and E of the SVMs, in both calibration and validation phases, are presented in Table 4. As this table suggests, the SVMs have a perfectly reasonable performance in estimation of all three qualitative parameters. The SVMs, with input combination including X and Y coordinates, groundwater level, and distance from the shoreline, provide the best estimates of all three qualitative parameters (the testing RMSE value of 0.86 mEq/l for SO4 2−, 0.87 mEq/l for Na+, and 175.74 μS/cm for EC). The RMSE and E values presented in Table 4 show that there is no significant reduction in estimation errors with increasing the number of input variables. As this table suggests, considering areal average 6-month rainfall depth as an input variable even increases the estimation errors in the validation phase. This shows the strength of SVM in estimation of qualitative parameters based on the two basic input variables, i.e., the X and Y coordinates of the observation wells.

Table 4 Error measures of qualitative parameters estimates produced by SVMs
Full size table

In conclusion, the results presented in Tables 3 and 4 indicate that both ANNs and SVMs can estimate, with reasonable accuracy, the three qualitative parameters using the X and Y coordinates as the only input variables. Furthermore, while the accuracy of the ANNs can be marginally improved by considering the distance from the shoreline as the third input variable, the SVMs work best when the only input parameters are the X and Y coordinates. So, to model the spatial variability of SO4 2−, Na+, and EC in the study area, the data of groundwater level and rainfall depth are not really helpful. The coefficients of correlation between the three qualitative parameters and the groundwater level in the study area were found to be small and negative, ranging from −0.21 to −0.17. These correlations would imply that each groundwater level value from the input set is associated with more than one qualitative parameter value from the output set. In the case of the rainfall depth in the study area, the coefficients of correlation were found to be almost zero, which means that the qualitative parameters and rainfall depth in the study area happen independently of each other. These facts could explain why the ANNs and SVMs could not find a clear and direct relation between the qualitative parameters, and the groundwater level and rainfall depth in the study area.

Generally, geostatistical interpolation techniques such as ordinary kriging and ordinary cokriging are used to estimate values of a random variable at unsampled locations where data are not available. The basic assumption of kriging-based methods is that a spatial autocorrelation exists among the measured values of the random variable under study. Geostatistical Analyst toolbox in ArcGIS 10.3 was used to create ordinary kriging and ordinary cokriging estimates of SO4 2−, Na+, and EC in the study area (Ashrafzadeh et al. 2016). Cokriging estimates were obtained treating each variable, in turn, as primary and the other two variables as auxiliary. The RMSE of the estimates produced by kriging was found to be 0.65 mEq/l for SO4 2−, 1.32 mEq/l for Na+, and 253.66 μS/cm for EC. In the case of cokriging, these values were, respectively, 0.59, 0.98, and 177.59. These values indicate that cokriging reduced the average estimation error of SO4 2−, Na+, and EC by 9.2, 25.87, and 30.0%, respectively, in comparison with kriging. Comparison of the kriging and cokriging RMSE values with the minimum testing RMSE values presented in Tables 2 and 3 implies that the both geostatistical methods produce more accurate estimates of SO4 2− than ANNs (the minimum RMSE value of 0.93) and SVMs (the minimum RMSE value of 0.86). However, in the case of Na+ and EC, the best ANNs (the RMSE value of 0.93 for Na+, and 186.45 for EC) show a similar performance to cokriging, while the best SVMs (the RMSE value of 0.87 for Na+, and 175.74 for EC) seem even more reliable than the geostatistical interpolation techniques. Some previous studies have also shown that neural networks can produce more accurate estimates of random variables such as soil water content and EC (Zheng et al. 2009), arsenic concentration of groundwater (Chowdhury et al. 2010), and total electron content of the ionosphere (Razin et al. 2016) than kriging-based techniques.

In addition to the input variables listed in Table 2, nine auxiliary input variables (pH, EC, and the concentrations of Na+, K+, Ca2+, Mg2+, Cl−, SO4 2−, and HCO3 −) were also considered and their relative influences on SO4 2−, Na+, and EC estimation were assessed through the Gamma test (Noori et al. 2010). An input combination including eight auxiliary variables was considered for estimating SO4 2−, Na+, and EC, and a Gamma value was calculated for this input combination (γ all). A set of Gamma values were also calculated using a procedure in which each input variable was individually removed from the input combination. It is expected that the input combination including all eight variables results in the minimum Gamma value. If the Gamma value obtained by omitting an input variable is smaller than γ all, then the omitted input variable has no positive effect on estimation. The calculated Gamma values are presented in Table 5. As this table suggests, the concentration of K+ can be removed from the input combination without increasing the estimate errors of SO4 2− and Na+. Also, it is observed that the input variable pH has no effect on the estimation of EC.

Table 5 Results of the Gamma test
Full size table

The Gamma test can also be used to identify the most effective input variables. For this purpose, each auxiliary variable was considered as the sole input variable and eight Gamma values were calculated. The most effective input variable has the smallest Gamma value. The results are presented in Fig. 5 in which the green columns represent the calculated Gamma values of the sole input variables. As it is observed, the Gamma values and the estimation errors of SO4 2−, Na+, and EC using a sole input variable follow an approximately similar pattern. This confirms the strength of the Gamma test in determining the relative importance of input variables.

Fig. 5
figure 5

Gamma values and the estimation errors of SO4 2− (a ANN; b SVM), Na+ (c ANN; D SVM), and EC (e ANN; f SVM)

Full size image

The final input combination for each qualitative parameter is presented in Table 6. The calibration and validation results, as well as the results of uncertainty analysis, are presented in Table 7. It is seen that considering auxiliary variables improves the estimates of all three groundwater qualitative parameters. Furthermore, comparing the testing RMSE values of these ANNs (0.22 mEq/l for SO4 2−, 0.30 mEq/l for Na+, and 33.04 μS/cm for EC) and SVMs (0.26 mEq/l for SO4 2−, 0.34 mEq/l for Na+, and 36.23 μS/cm for EC) with the cokriging RMSE values (0.59 mEq/l for SO4 2−, 0.98 mEq/l for Na+, and 177.59 μS/cm for EC) shows that the ANNs and SVMs produce more accurate estimates of SO4 2−, Na+, and EC in the study area, in comparison with kriging-based interpolation methods.

Table 6 Final input combinations for ANNs and SVMs
Full size table
Table 7 Calibration (training) and validation (testing) results and the results of uncertainty analysis of ANNs and SVMs
Full size table

RMSE and E values presented in Table 7 suggest the better performance of ANN over SVM. However, comparing the values of d-factor of both models shows that SVM has less uncertainty. As a representative example, the uncertainty of ANN and SVM in estimation of Na+ is depicted in Fig. 6. The observed and estimated values of Na+ in the validation phase, as well as the 95% prediction uncertainty (95PPU), are shown in Fig. 6. It is seen that ANN has a wider 95PPU than SVM, suggesting that the d-factor of ANN is greater than SVM. So it is concluded that the uncertainty of SVM is lower in comparison with the uncertainty of ANN. Lower uncertainty is a major criterion for selection of the best model for a given application. The results of such a model are more citable and reliable.

Fig. 6
figure 6

Uncertainty of SVM (a) and ANN (b) in estimation of Na+

Full size image

Conclusion

Knowing the spatial distribution of qualitative parameters of aquifers is necessary for proper management of water resources. The present study aimed to estimate the values of sulfate concentration, sodium concentration, and electrical conductivity of groundwater using artificial neural networks and support vector machines. Five primary input variables (X and Y coordinates of the observation well, distance of the observation well from the shoreline, the areal average 6-month rainfall depth, and groundwater level), as well as nine auxiliary input variables (pH, EC, and the concentrations of Na+, K+, Ca2+, Mg2+, Cl−, SO4 2−, and HCO3 −), were considered. The following conclusions could be drawn from the present study:

  1. 1.

    For ANNs, X and Y coordinates, and distance from the shoreline are the most important primary input variables.

  2. 2.

    SVMs provide acceptable results when X and Y coordinates are considered as the only primary input variables.

  3. 3.

    Adding auxiliary input variables improves the estimates of all three groundwater qualitative parameters.

  4. 4.

    The uncertainty of SVM is lower in comparison with the uncertainty of ANN.

Acknowledgements

The authors wish to thank Guilan Regional Water Authority for providing the data used in this study. We appreciate also the helpful comments of three reviewers.