Reactive Henry problem: effect of calcite dissolution on seawater intrusion

Abstract

Freshwater stored in a coastal aquifer is extensively extracted through pumping wells due to high water demand in coastal area (touristic, industrial, and public use). To enhance freshwater security and to avoid contamination of water reserves, seawater intrusion becomes a topic of great interest for hydrogeologists. During the last few decades, hydrogeologists have provided a deeper understanding of the prediction, processes, investigative tools, and management of such systems. The majority of the studies quantifies these hydrogeological systems using traditional density-dependent flow and transport models and does not consider the effect of the chemical reactions. Interdependence of density-dependent flow and chemical reactions and their effects on the porosity and permeability is the most important key toward a reliable modeling of these complex systems. Seawater intrusion can increase by the solid matrix dissolution processes in the saltwater–freshwater mixing zone in the case of a coastal carbonate aquifer. The dissolution of such rocks can easily induce a development of porosity and permeability as a result of the mixing processes. The increase of permeability would enhance further seawater flux to the freshwater side. In this work, a relatively complete modeling scheme is presented to quantify and predict this risk. The modeling of such a problem requires a set of highly nonlinearly coupled equations. In this regard, GEODENS code used in this work can solve these equations by a finite element procedure; it can handle density-dependent flow, transport, and geochemical reactions in porous media. Its main purpose is to represent the physicochemical processes in the subsurface system. The code is used to simulate the effect of calcite dissolution during seawater intrusion in a coastal carbonate homogeneous aquifer.

Introduction

One of the most recognized reactive transport problems is the dissolution reaction during mixing of seawater and freshwater in a coastal carbonate aquifer. An important aspect of reactive transport modeling is the appropriate evaluation of porosity and permeability development during dissolution reaction and their impact on flow and transport. In the following, two situations involving these processes are cited:

• From the beginning of the twentieth century, underground storage in salty layers is used. Currently, salty formation in deep geological layers is used for the burial of industrial long-life waste, including radioactive waste and CO₂ to counteract the greenhouse effect. Suitable and safe storage sites are searched and costly investigated in many places around the world (Ghanbari et al. 2006; Hellevang et al. 2005; Kang et al. 2010). The injection of CO₂ into the subsurface leads to a relatively rapid decrease of the water solution pH. This decrease will then be buffered by mineral reactions, such as calcite dissolution (Lagneau et al. 2005). Calcite dissolution can induce an increase in the porosity and can enhance further leakage and provide more pathways for the CO₂ (Caldeira and Rau 2000).

• Soil and groundwater salinization due to intense evapotranspiration in arid regions and/or saline water intrusion from the sea or from Chotts or Sebkhas (playas) is a limiting factor for development and food security in these areas (Tirado et al. 2010). However, the relevance of Sebkhas and Chotts in terms of mineral resources is important (Bouhlila 1999). The Tunisian territory, due to its hydroclimatic conditions, includes a large number of such depressions which contain many salts. The exploitation of these deposits cannot be done without the good knowledge of these environments, as well as of the mechanisms of formation and renewal of salts and brines (Nasri et al. 2015; Yechieli and Wood 2002).

The common feature of all these issues, and obviously many others related to salts and brines in porous media, is the coupling between geochemical processes, mainly dissolution reaction, and physical ones of density-dependent flow and multispecies reactive transport. To model these hydrogeological systems, a general model that can handle density-dependent flow and multispecies reactive transport modeling is required. The prediction of mineral interactions and water interactions using mathematical models is integral to the study of the quality and the geochemistry of natural water. Many investigations have been published in the last few years regarding the hydrogeochemical modeling, especially the issues related to calcite dissolution reaction during mixing of two different waters. The most known studies are as follows:

• Sanford and Konikow (1989) provided a quantitative estimate of the amount of calcite dissolution expected in mixing zone under typical hydrodynamic and geochemical conditions. To assess the effects of calcite dissolution on the rock matrix, the authors proposed a procedure to quantify the effect on the rock proprieties (porosity and permeability). They used the geochemical code PHREEQC (Parkhurst and Apello 1999) coupled with a finite difference model for variable density groundwater flow and solute transport.

• Rezaei et al. (2005) extended the study of Sanford and Konikow (1989) to simulate the porosity development in coastal aquifer due to calcite dissolution. The authors used RETRASO code, a finite element model (Saaltink et al. 2004) to solve simultaneously the aqueous complexation reaction, the dissolution–precipitation reaction and the flow and transport problem using a global implicit method. They found, through the simulations, two locations of maximum dissolution as obtained by Sanford and Konikow (1989): one near the aquifer bottom and another near the discharge boundary.

• Romanov and Dreybrodt (2006) used the analytical solution of Phillips (1991) to set up an alternative modeling approach to determinate the porosity change in the saltwater–freshwater mixing zone of coastal carbonate aquifers. As a first step, they solve the advection transport equation for salinity s using the finite difference code SEAWAT (Guo and Langevin 2002). The second step consists in calculating the dissolution capacity in the mixing zone by estimating the calcium equilibrium concentration that is obtained as a function of salinity using PHREEQC (Parkhurst and Apello 1999). They applied this approach for a stationary salinity distribution.

• Laabidi and Bouhlila (2015) used the analytical solution of Phillips (1991) in non-stationary step-by-step regime. At each time step, the quantity of the dissolved calcite is quantified, the change of porosity is calculated and the permeability is updated. The reaction rate which is the second derivate of the calcium equilibrium concentration in the equation is calculated using PHREEQC code (Parkhurst and Apello 1999). The authors used this result in a 2D finite element code GEODENS (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015) to calculate the initial change of the porosity after calculating the salinity gradient. For the next time step, the same protocol is used but using the updated porosity and permeability distributions.

In this paper, GEODENS code (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015) is used to predict and understand the environmental and water resources problems related to the seawater intrusion. The model tested and validated is used to simulate the effect of the calcite dissolution on the penetration length of the seawater intrusion. To provide general results, these processes are simulated using Henry problem geometry with the same hydrodynamic parameters and boundary conditions.

GEODENS code: description and governing equation

Presentation of GEODENS

GEODENS (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015) is a FORTRAN code for modeling saturated–unsaturated density-dependent flow and multispecies reactive solute transport in porous media under both local chemical equilibrium and kinetic conditions. The code is used to simulate the underground saline environments where dissolution–precipitation reactions and buoyancy convection play a key role in the spatial and temporal distribution of fluid and chemical species in the modeled domain. GEODENS (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015) is designed as a coupling of two separately built, checked and calibrated modules (1) a density-dependent flow and multispecies transport module, and (2) a geochemistry of salts and brine module. The mathematical formulation of the first module leads to a nonlinear and strongly coupled equations. The second module focuses on salts and brine geochemistry using the Pitzer model to represent the interactions between solute species in concentrated solutions (Pitzer et al. 1984). This geochemical module allows the calculation of ions and solvent activities as well as the density of the solution (Monnin 1989) and the quantities of the different salts that may precipitate or dissolve in the domain over time. The porosity change according to the quantity of precipitated or dissolved salts is evaluated by considering the pore volume filled or released. An empirical formula is used to quantify the consequences of this change on permeability. The purpose of this code is to contribute to the understanding of soil and groundwater salinization, seawater intrusion, and upwelling of deep salt water, and to quantify the hydrogeochemical mechanisms related to the genesis of evaporites in sebkhas or playas. This code can also be useful for the design of safe burial facilities for CO₂ or hazardous waste in subsurface salty media.

Governing equations

The equations governing the movement of a fluid through saturated porous medium subject to variable density conditions can be obtained from the mass and the momentum conservation principles. The following section presents briefly these governing equations (Bear 1988; Diersch and Kolditz 2002). For this study, only two-dimensional flow is considered. The fluid mass conservation equation is expressed as follows:

$$\frac{\partial }{{\partial x_{i} }}\left( {\rho q_{i} } \right) - \frac{{\partial \left( {\rho \phi } \right)}}{\partial t} + Q_{m} = 0$$

(1)

where ϕ[L³L⁻³] is the porosity, ρ[ML⁻³] is the fluid density, Q _m [ML⁻³T⁻¹] is the source/sink term (the mass flux per unit of volume), q _i is the Darcy’s velocity and t[T] is the time.

GEODENS (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015) describes two-dimensional transient convective, diffusive–dispersive and reactive transfer of specie α (α = 1, N _α ) using a sequential iteration approach of the following equation:

$$L\left( {C^{\alpha } } \right) + Q_{m} C^{\alpha } + \phi f^{\alpha } = \frac{{\partial \left( {\rho \phi C^{\alpha } } \right)}}{\partial t}$$

(2)

C ^α [MM⁻³] is the concentration of solute α, and N _α is the total number of species, Q _m is the source term, and L(C ^α) represents the transfer operator applied to C ^α including the convection and the diffusion–dispersion phenomena. L(C ^α)is expressed as follows:

$$L\left( {C^{\alpha } } \right) = \frac{\partial }{{\partial x_{i} }}\left\{ {\rho \phi D_{ij} \frac{{\partial C^{\alpha } }}{{\partial x_{j} }} - \rho \phi u_{i} C^{\alpha } } \right\} .$$

(3)

where i and j range from 1 to 2 for a two-dimensional flow and transport problem, u _i [LT⁻¹] is the effective velocity in the porous media and is related to the Darcy’s velocity q _i [LT⁻¹] by the following expression:

$$q_{i} = u_{i} \phi = - \frac{{K_{ij} }}{\mu }\left( {\frac{\partial p}{{\partial x_{j} }} - \rho g_{j} } \right) .$$

(4)

where K _ij [L²] is the intrinsic permeability, μ [ML⁻¹T⁻¹] is the fluid viscosity, p is the fluid pressure, g _j is the gravitational acceleration, and D _ij [L²T ⁻¹] is the diffusion–dispersion term and is expressed as follows:

$$D_{ij} = (d_{0} + \alpha_{T} u)\delta_{ij} + (\alpha_{L} - \alpha_{T} )\frac{{u_{i} u_{j} }}{u} .$$

(5)

where α _L [L] and α _T [L] are the longitudinal and the transversal dispersivity, respectively, d ₀ [L²T⁻¹] is the molecular diffusion coefficient, u _i [LT⁻¹] is the velocity vector component in the ith direction, u _j [LT⁻¹] is the velocity vector component in the jth direction, u [LT⁻¹] is the norm of the velocity vector, and δ _ij is the Kronecker delta function.

The f ^α term represents the geochemical mass flux of species α. If N _r is the number of reactions related to the specie α, f ^α is calculated as the sum of all the reactions which contributes to this mass flux (Bouhlila 1999), and is written as follows:

$$f^{\alpha } = \sum\limits_{r = 1}^{{N_{r} }} {\rho \left( {\frac{{\partial C^{\alpha } }}{\partial t}} \right)}_{r}$$

(6)

The geochemical flux of each species α at the time step Δt is calculated as the mass change of these species during dissolution–precipitation reactions.

Impact on porosity and permeability

The physicochemical processes are written in GEODENS (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015) at the macroscopic scale. The pore geometry is continuously modified by the dissolution–precipitation reactions of salts. The porosity at any node of the mesh and at every time step Δt is updated as follows:

$$\phi \left( {t + \Delta t} \right) = \phi \left( t \right) + \sum\limits_{js = 1}^{{N_{s} }} {r_{js} V_{js} \Delta t}$$

(7)

where V _js [L³M⁻¹] is the molar volume of the salt j, r _js [M⁻¹L⁻³T⁻¹] is the rate of the mineral precipitation (−) or dissolution (+), and N _s is the total number of salts.

Permeability enhancement due to the porosity increases is a topic of great interest in reservoir engineering. Capillary tubes or plane cracks models have been used as a relation between porosity and permeability and can give relatively simple relationships such as the Koseny–Carman formula (De Marsily 1981). Furthermore, many results have been published regarding the relation between porosity and permeability based on plotting values of porosity and permeability from large numbers of field samples. The relation presented by Sanford and Konikow (1989) is based on a data for sedimentary rocks presented by Chilingar et al. (1963), Fuchtbauer (1967), and Shenhav (1971). The fitted plot suggests an empirical relationship of porosity, ϕ, related to the logarithm of permeability, K, and is expressed as follows (Sanford and Konikow 1989):

$${\text{Log}}\left( K \right) = 20\phi + b.$$

(8)

where b is deduced from the initial known values of K and ϕ. Using the initial value of porosity (Φ = 0.35) and the intrinsic permeability (K = 1.00 × 10⁻⁹ m²), one obtains the following equation:

$${\text{Log}}\left( K \right) = 20\phi - 16.$$

(9)

Kinetics of calcite dissolution

The undersaturation of calcite in the mixture zone induces dissolution of the carbonate rocks. Many authors studied the kinetic of calcite dissolution reaction in low-temperature aqueous systems. We can find in Sanford and Konikow (1989) and in Freedman and Ibaraki (2002) a detailed description of this process. In GEODENS code (Bouhlila 1999; Bouhlila and Laabidi 2008; Laabidi and Bouhlila 2015), the kinetics of salt dissolution reactions is represented by the geochemical flux, f ^α (Eq. 6), and is written as follows:

$$\phi f^{\alpha } = \sum\limits_{r = 1}^{{N_{r} }} {\rho \phi k_{cr} } \left( {1 - \varOmega_{r} } \right) .$$

(10)

where Ω _r is the saturation index of the salt r, and k _cr [MT⁻¹] is the kinetic coefficient of the reaction.

Numerical integration

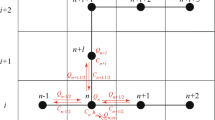
Equations 1 and 2 are solved by a finite element method based on six-node triangle. The Galerkin approximation method is applied to discretize the main field variables, p(x, y, t) and C(x, y, t). The error (residual) generated by the introduction of the nodal approximation in the governing equations needs to be minimized over the entire flow domain. In this context, the Galerkin approximations to p(x,y,t) and C(x,y,t) for each time t ≥ 0 are as follows:

$$\begin{aligned} p\left( {x,\;y,\;t} \right) = \sum\limits_{I = 1}^{n} {N^{I} \left( {x,\;y} \right)} p^{I} \left( t \right) \hfill \\ C\left( {x,\;y,\;t} \right) = \sum\limits_{I = 1}^{n} {N^{I} \left( {x,\;y} \right)} C^{I} \left( t \right). \hfill \\ \end{aligned}$$

(11)

N ^I(x, y) are the interpolation functions in node I, I = 1, n (total number of mesh nodes) and presented as a polynomial of second-order functions of the spatial coordinates x and y. These polynomials are calculated as follows (Dhatt and Touzot 1981):

$$N^{J} \left( {x^{I} ,y^{I} } \right) = \delta_{IJ} = \left\{ {\begin{array}{*{20}c} {1{\text{ I}} = J,} \\ {0{\text{ I}} \ne J.} \\ \end{array} } \right.$$

(12)

The approach used to evaluate the Darcy velocities in this work is called the discontinuity velocity approach. It consists of calculating the velocity in each element of the mesh from the pressure and concentration values by a simple application of Darcy law. Obviously, these velocities are discontinuous between elements which can generate numerical instability, especially in the cases where advection is significant (Diersch 1988). To avoid erroneous oscillations in the vertical velocity components, a consistent approach similar to that of Voss (1984) is adopted using linear ponderation functions for the concentrations used to calculate the gravity terms in the Darcy’s law (Bouhlila 1999). For this purpose, only the summit nodes are used for the linear nodal interpolations in the calculations of the fluid densities.

The integration by parts of the flow and transport equations (Eqs. 1, 2) led to a lower order integral form. By this method, a matrix algebraic system of the problem can be formulated. These systems are solved by an iterative method, at each time step an extrapolation procedure is performed to initiate the unknown variables and then to solve all the matrices and the vectors of the algebraic systems. The geochemical fluxes are calculated with the previous time step results according to an explicit procedure, and then porosity is calculated from the pore volume released or filled by mineral dissolution or precipitation in every node and each time step. The new porosity value is used to update the permeability using an empirical equation as presented in previous section. The new hydrodynamic distribution is the new inputs for the next time step to solve the problem in every nodes of the mesh.

Effect of calcite dissolution on seawater intrusion

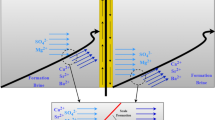
As reported by Cabral et al. (1992) and Bear and Kapuler (1981), during seawater intrusion the flow is assumed to be perpendicular to the short line, so that a two-dimensional vertical model is satisfactory to model such a problem. In this context, Bear (1979) has given some examples of real aquifers in which field data have shown that saltwater concentration is distributed in a transition zone sharply separating freshwater and saltwater. His main assumption is to neglect the transition zone compared to the aquifer dimensions. In this study, the same geometry and parameters as in Henry problem are used (Henry 1964). The Henry saltwater intrusion problem concerns a vertical slice through an isotropic, homogeneous, confined aquifer. For the flow boundary, a freshwater constant flux is applied from the inland boundary and a hydrostatic pressure is distributed on the sea boundary. As shown in Fig. 1, it is not easy to represent the transport boundary in the seaside. In this work, a mixed boundary condition in the seaside is introduced to avoid difficulties in the finite element solution near the outflow region of the aquifer (Segol et al. 1975). Segol et al. (1975) replaced the original homogeneous Dirichlet boundary by a mixed Dirichlet–Neumann boundary. The upper 20 cm was a zero concentration flux exit boundary, and the lower 80 cm remained a constant concentration Dirichlet boundary.

Fig. 1

Henry problem: domain and boundary conditions, Henry (1964)

Henry (1964) solved the governing equations in a non-dimensional form and presented a semi-analytic solution for the steady-state distribution of salt concentration and stream function. Henry problem has been widely used as a test case (benchmark) of density-dependent groundwater flow models (Abarca et al. 2007; Simpson and Clement 2003; Voss and Souza 1987). The boundary conditions of Henry problem are defined in Fig. 1. No flow occurs across the top and bottom boundaries. A freshwater flux is injected along the left vertical boundary of the domain. The prescribed pressure along the right vertical boundary is set at hydrostatic seawater pressure. A grid of 231 elements is used to simulate this problem. The soil parameters used in Henry problem are summarized in Table 1. In the original Henry problem, a pseudo-permanent regime is reached after 100 min (Bouhlila 1999; Voss 1984). If the solid matrix is calcareous, the dissolution processes are perpetual and no permanent regime is reached.

Table 1 Parameters used in Henry problem

Recently, Henry reactive problem was presented by Laabidi and Bouhlila (2015) where the authors used an alternative modeling approach to simulate the effect of calcite dissolution on the porosity and permeability. The authors showed through their simulations that porosity change due to calcite dissolution has a direct effect on the penetration length of seawater and the flux from the seaside.

The results presented by Abarca et al. (2007) and by Nick et al. (2013) showed that toe penetration of saltwater decreases with increasing transversal dispersivity, while width of the mixing zone and saltwater flux become larger.

In this simulation, the effect of calcite dissolution reaction on the behavior of saltwater intrusion during mixing is tested. During dissolution, porosity and permeability change is identified and the consequence of this latter on the flow and transport is calculated. Several simulations are carried out to get a better understanding of the effect of calcite dissolution on seawater intrusion using different kinetic coefficient values ranging from k _c  = 10⁻¹¹ mol/s to k _c  = 9 × 10⁻¹⁰ mol/s. Figures 2a, 3a, 4a, 5a, 6a, and 7a show the porosity change for different k _c values due to calcite dissolution during the mixing of the saltwater and freshwater after a simulation time of 25, 50, and 100 years. The quantity of the dissolved calcite is extremely related to the rate of calcite dissolution and to the order of the mixing (fraction of the saltwater). Maximum values are located in the mixing zone (transition zone) between seawater and freshwater. Figures 2b to 7b show the permeability change for different k _c values due to porosity change. As the porosity change, maximum values are located in the transition zone between freshwater and seawater. This new hydrodynamic distribution (porosity and permeability) controls the variation of the velocity field and the shape of the concentration repartition as shown in Figs. 2c to 7c which depict the Cl⁻ concentration (g/kgw) and velocity field after simulation time of 25, 50, and 100 years.

Fig. 2

Reactive Henry problem simulation using a kinetic coefficient k _c  = 7.0 × 10⁻¹¹ mol/s. 2D-porosity change (a), 2D-permeability change (b) and spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field (c) after 25, 50, and 100 years

Fig. 3

Reactive Henry problem simulation using a kinetic coefficient k _c  = 8.0 × 10⁻¹¹ mol/s. 2D-porosity change (a), 2D-permeability change (b) and spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field (c) after 25, 50, and 100 years

Fig. 4

Reactive Henry problem simulation using a kinetic coefficient k _c  = 9.0 × 10⁻¹¹ mol/s. 2D-porosity change (a), 2D-permeability change (b) and spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field (c) after 25, 50, and 100 years

Fig. 5

Reactive Henry problem simulation using a kinetic coefficient k _c  = 10⁻¹⁰ mol/s. 2D-porosity change (a), 2D-permeability change (b) and spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field (c) after 25, 50, and 100 years

Fig. 6

Reactive Henry problem simulation using a kinetic coefficient k _c  = 1.5 × 10⁻¹⁰ mol/s. 2D-porosity change (a), 2D-permeability change (b) and spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field (c) after 25, 50, and 100 years

Fig. 7

Reactive Henry problem simulation using a kinetic coefficient k _c  = 2.0 × 10⁻¹⁰ mol/s. 2D-porosity change (a), 2D-permeability change (b) and spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field (c) after 25, 50, and 100 years

Figure 2 displays the porosity and permeability change after 25, 50, and 100 years for k _c  = 7.0 × 10⁻¹¹ mol/s. The spatial distribution of Cl⁻ concentration and the velocity field results of the development of porosity and permeability are shown in Fig. 2c. Maximum porosity increase rate is identified in the mixing zone and is about 1.07 % after 100 years.

Figure 3 displays the porosity and permeability change after 25, 50, and 100 years for k _c  = 8.0 × 10⁻¹¹ mol/s. The spatial distribution of Cl⁻ concentration and the velocity field results of the development of porosity and permeability are shown in Fig. 3c. Maximum porosity increase rate is identified in the mixing zone and is about 1.22 % after 100 years.

For k _c  = 9 × 10⁻¹¹ mol/s, maximum porosity change is about 1.38 % and maximum permeability change is about 2.5 × 10⁻¹⁰ m² and located near to the discharge area (Fig. 4).

Figures 5, 6, and 7 display the porosity and permeability development and their effect on the flow and transport for k _c  = 10⁻¹⁰ mol/s, k _c  = 1.5 × 10⁻⁹ mol/s, and for k _c  = 2.0 × 10⁻¹⁰ mol/s, respectively. Compared to the previous simulations, for a relatively high k _c value the mixing zone is extended to the freshwater side and a displacement of the saltwater front to the freshwater side is identified. As the simulation progresses, there is a development of the spatial distribution of Cl⁻ concentration. Consequently, a movement of the saltwater front is created due to the development of the permeability in mixing zone which enhances more saltwater flux to the freshwater side and a larger mixing zone is created.

To present the effect of porosity change on the flow and transport problem, Fig. 8 depicts the Cl⁻ concentration (g/kgw) and velocity field after simulation time of 25, 50, and 100 years using a relatively high kinetic coefficient value k _c  = 5.0 × 10⁻¹⁰ mol/s.

Fig. 8

Reactive Henry problem simulation using a kinetic coefficient k _c  = 5.0 × 10⁻¹⁰ mol/s. Spatial distribution of the Cl⁻ concentration (g/kgw) and velocity field after 25 (a), 50 (b), and 100 years (c)

Results presented here provide insight on the interplay between chemistry and transport in mixing zone of coastal carbonate aquifers. As obtained by Sanford and Konikow (1989) and by Rezaei et al. (2005), two locations of maximum dissolution rate are found: one near the aquifer bottom and one near the discharge area (near the seaside boundary), with some residual dissolution occurring throughout the rest of the mixing zone. In general, dissolution tends to concentrate at the freshwater side of the mixing zone, except at the discharge area, where dissolution is maximum near the seaside.

Referring to the study of Laabidi and Bouhlila (2015) and Abarca et al. (2007), we focus in this study on the following values:

• 1. Penetration of the seawater intrusion wedge noted l _toe, as shown in Fig. 1, is calculated as the distance between the seaside boundary and the point where the 50 % mixing isoline intersects the aquifer bottom (x ^0.5C).

• 2. q _s is the seawater flux that enters the system through the seaside boundary (m³/m/s) integrated over the right boundary of the domain.

The result presented in Table 2 shows the increase of l _toe during time due to the development of velocity field during porosity and permeability change. Compared to the base case where l _toe is about 0.6 m, the l _toe in the reactive Henry problem can reach a value ranging from 0.965 to 1.881 m after 100 years for different k _c values as presented in Table 2. On the other hand, we can easily identify an increase of the seawater flux. Figure 9 depicts an increase of the seawater flux q _s compared to the base case in sampling ports at selected points on the seaside boundary (Table 3). It can be seen from Fig. 9 that the model predicts reasonably the seawater flux. Maximum value is reached in port PF4 and is about 1.51 × 10⁻⁵ m³/m/s for k _c  = 2 × 10⁻¹⁰ mol/s where the hydraulic gradient is larger than in the other part of the seaside boundary. Compared to the base case (non-reactive), the increase of saltwater flux is mainly due to the increase of permeability and the development of the velocity field that enhance more seawater penetration to the freshwater side.

Table 2 The penetration of seawater (l _toe ) for different k _c values and after simulation time of 25, 50 and 100 years

Fig. 9

Reactive Henry problem simulation: seawater flux at locations of the sampling ports for different kinetic coefficient values

Table 3 Coordinates of sampling ports used to measure the seawater flux

During simulations using different k _c values, the effect of dissolution reaction on the Ca²⁺ concentration in sampling ports is evaluated. Legend and locations of these sampling ports are given in Table 4. Figure 10 shows the transient distribution of Ca²⁺ concentration during simulation. Generally during mixing inducing dissolution of calcium carbonate, an increase of Ca²⁺ concentration is expected. This can be seen clearly by comparing the measured concentration at sampling ports to the corresponding values calculated for the base case (non-reactive). Maximum value are located in port PC3 and reach a value of 2.50 × 10⁻³ mol/kg-water for k _c  = 2.00 × 10⁻¹⁰ mol/s after a simulation time of 100 years, and is about three times greater than the corresponding value at the base case.

Table 4 Coordinates of sampling ports used to measure the Ca²⁺ concentration

Fig. 10

Reactive Henry problem simulation: total aqueous calcium concentrations at locations of the sampling ports for different kinetic coefficient values

To conclude, calcite dissolution induces an increase in the porosity which is related to the permeability. This would enhance further seawater flux and mixing in the simulated section. Chemical dissolution in such environment is another characteristic of real aquifers which the Henry problem does not account for. Calcite dissolution may affect the horizontal permeability which affects both seawater penetrations and the flux of saltwater that enters the aquifer through the seaside boundary. The shape and penetration of the saltwater intrusion wedge are controlled by the permeability which is related to the quantity of the dissolved calcite as presented above. However, it is difficult to evaluate the relative importance of this parameter. Here, we examine the results obtained when varying this parameter with respect to the base case. For this reason, several simulations were carried out to identify the role of the calcite dissolution using different k _c values. To summarize, the penetration length increases and is mainly controlled by the horizontal permeability. The amount of dissolved calcite in the mixing zone increases with time inducing an increase in porosity due to the pore volume released by calcite dissolution phenomenon. The new hydrodynamic distribution controls the variation of the velocity field and the shape of the concentration repartition as shown in Fig. 8.

Conclusion

Results presented in this work show the interplay between geochemical reaction and transport in the mixing zone in coastal carbonate aquifers. The seawater intrusion phenomenon is a real risk on the subsurface water resources in several areas around the world. This risk can be increased by the solid matrix dissolution and precipitation processes in the saltwater–freshwater mixing zone in the case of a limestone aquifer.

Calcite dissolution in the saltwater–freshwater mixing zone in coastal carbonate aquifers is described by a density-dependent flow and multispecies reactive transport model. This requires a set of highly nonlinearly coupled reaction–diffusion–advection equations. GEODENS code, used in this work, can solve these equations by a finite element procedure. To quantify this risk, a relative complete modeling scheme is presented in this work. A finite element procedure is developed to solve these coupled equations and the geochemical processes are written at each element using Pitzer model for species activities calculation. At each time step, the geochemical fluxes are calculated with the previous time step results according to an explicit procedure. The porosity is calculated from the pore volume released or filled by calcite dissolution or precipitation in every node and each time step. The new porosity value is used to update the permeability using an empirical equation. The new hydrodynamic distribution is the new input for the next time step to solve the problem in every nodes of the mesh.

Through the results of the simulations presented in this work, we have shown that the change of porosity is created in narrow regions at the freshwater side of the mixing zone. The behavior of the solution is discussed in terms of two parameters: velocity field which has a direct effect on the seawater flux, and the penetration length. An increase of the penetration length of the seawater is identified during calcite dissolution.

Sensitivity analyses were carried out to provide a clear analysis of the effect of the calcite dissolution on the flow and transport in porous media. As a first result, during calcite dissolution an increase of seawater flux is identified and is calculated in some sampling ports in the seaside boundary. Maximum seawater flux is located in region where seawater hydraulic head is larger than the other part of the seaside boundary. Compared to the seawater flux calculated in the base case (non-reactive case), the increase of seawater flux from the seaside to the freshwater side is essentially the result of the development of the velocity field during permeability increase.

Dissolution processes in the mixing zone depend on a large number of factors (mainly the differences in species concentrations, pCO₂ and ionic strength of the boundary solution). Therefore, through the simulations carried out in this work the amount of calcite dissolution and consequently the porosity development are basically sensitive to the kinetic coefficient value. On the other hand, the largest dissolution rate is found mainly in two positions: one near the aquifer bottom and the other near the discharge area (the seaside boundary) in the mixing zone.

Another important result regarding the effect of calcite dissolution on the transport is the total aqueous calcium concentrations at locations of the sampling ports for different kinetic coefficient values. Generally during calcite dissolution, an increase of Ca²⁺ concentration is expected. This can be seen clearly by comparing the measured concentration at sampling ports in the reactive simulation to the corresponding values detected for the base case (non-reactive case).

The model presented in this work is a numerical tool to predict and quantify the effect of the calcite dissolution reaction in a coastal carbonate aquifer. We essentially conclude that for a real study case of a coastal limestone aquifer, the calcite dissolution processes are important to quantify the aquifer contaminated zone wedge and also its time evolution. On the other hand, it is highly recommended to make sure that the kinetic law of calcite dissolution is written carefully in a coupled model.