Uncertain extensive game with application to resource allocation of national security

Abstract

Uncertain theory is a powerful tool for describing human uncertainty, especially in social economic studies. In this paper, we consider finite extensive games with payoffs being uncertain variables. We introduce three different criteria: the expected value criterion, the optimistic value criterion and the pessimistic value criterion to describe players’ behaviors in different decision-making situations. Accordingly, three types of uncertain equilibria and uncertain subgame perfect equilibria for the uncertain extensive game are proposed. Moreover, we provide theorems to prove the existence of uncertain equilibria and uncertain subgame perfect equilibria. Finally, the resource allocation problem for national security is formulated and analyzed using the uncertain extensive game. Results show that different decision criteria may lead to different subgame perfect equilibria, demonstrating the significance of introducing different uncertain subgame perfect equilibria.

1 Introduction

Since the seminal work of Von Neumann and Morgenstern (1944), game theory has been extensively used to study conflicting and cooperative decision-makings in economics, sociology and politics. The notion of extensive game was first introduced by Von Neumann and Morgenstern (1944), and later a more geometric definition was given by Kuhn (1950). Different from regular strategic games, extensive games mainly focus on the sequential structure of players’ actions. Nash equilibrium (1950) is a solution that no player can improve his expected payoff by changing his strategy unilaterally. Noticing Nash equilibrium ignores the sequential structure of the game, Selten (1965) proposed the concept of subgame perfect equilibrium, in which a player is required to reassess his/her plan as the game proceeds.

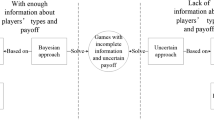
In the literature, the payoffs are generally assumed to be deterministic and can be attained by collecting and analyzing data from analogous games played before. However, as it usually occurs in practice, players lack statistics to figure out the payoff for each combination of strategies. When provided with sufficient samples, probability theory has proved its success in dealing with uncertain payoffs. Liu (2007) proposed uncertain theory to solve indeterminate problems with insufficient samples. Here we introduce uncertain theory to games to study the scenario when people do not have sufficient information to generate an accurate estimation of payoffs. Based on uncertainty theory, uncertain bimatrix game was proposed by Gao (2013), and then its Bayesian equilibria was investigated by Yang and Gao (2017). The uncertain coalitional game was also studied and various solution concepts were discussed (e.g., uncertain Shapley value by Gao et al. (2017), uncertain core by Yang and Gao (2014) and uncertain stable set by Liu and Liu (2017)). Besides, Yang and Gao (2013, 2016) initiated a spectrum of uncertain differential games. As far as we know, extensive game with uncertain payoffs has not yet been studied.

Since the tragedy of 9/11/2001, the study of game-theoretic models in the context of national security has been growing rapidly. Keohane and Zeckhauser (2003) applied game theory in security settings in order to assess the effectiveness of deterring possible attacks. Most models provide optimal budget allocations to varying targets, but fail to consider the uncertain nature of intentional attacks. Recently, game theory has been used to determine which targets to protect against intentional attacks. Bier et al. (2007) considered a sequential game between a defender and an attacker. Elisabeth et al. (2016) further developed this sequential game. In this model, the defender (she) moves first and allocates her resources among potential targets. The attacker (he) moves afterwards, using his best response function to choose a target to attack. The defender needs to predict the attacker’s action in order to successfully defend his targets.

In this paper, we consider a finite extensive game with uncertain payoffs. In an uncertain decision-making environment, different people may exhibit very different behaviors. Uncertainty theory provides three approaches to define the behaviors of different players in different decision-making situations. The expected value criterion aids risk neutral players to optimize the mean value of their uncertain objectives, the optimistic value criterion helps risk-averse players to optimize the $\alpha$-optimistic value of their uncertain objectives, and the pessimistic value criterion helps risk-seeking players to optimize the $\alpha$-pessimistic value of their uncertain objectives, where $\alpha$ is some predetermined confidence level. Correspondingly, we offer three definitions of uncertain equilibria in uncertain extensive game, i.e., expected equilibrium, $\alpha$-optimistic equilibrium and $\alpha$-pessimistic equilibrium. Then, we propose expected subgame perfect equilibrium, $\alpha$-optimistic subgame perfect equilibrium and $\alpha$-pessimistic subgame perfect equilibrium as complements to the three types of uncertain equilibria. Furthermore, we prove the existences of the uncertain equilibria and uncertain subgame perfect equilibria in the finite uncertain extensive game to ensure the significance of these new concepts. In the end, an example of a sequential game between an attacker and a defender is provided to show these new equilibria. The obvious distinction among these equilibria show the importance of introducing various equilibria to capture different human behaviors in uncertain games.

The rest of this paper is organized as follows. Section 2 reviews some basic concepts in uncertainty theory. In Sect. 3, the notion of the extensive game with uncertain payoffs is introduced. In Sect. 4, we propose three definitions of uncertain equilibria and provide theorems to show their existences. In Sect. 5, we present three concepts of uncertain subgame perfect equilibria, as well as their existence theorems. An example of resource allocation for national security is given in Sect. 6 to show the importance of these new concepts.

2 Preliminaries

Uncertainty theory, founded by Liu (2007) and refined by Liu (2009), is a branch of mathematics for modeling human uncertainty. Although the definition of the measure and the operational law are very different from those of probability theory, uncertainty theory is also based on an axiomatic system with an elegant theoretical system and a great application prospect. In the past decade, uncertainty theory was developed rapidly and has been applied to many areas such as finance (Liu 2008; Chen and Gao 2013; Liu et al. 2015; Liu and Yao 2017), control (Zhu 2010; Guo and Gao 2017) and supply chain management (Chen et al. 2017; Ke et al. 2017). In this section, we introduce some basic results in uncertainty theory.

Definition 1

(Liu 2010) Let ${\mathcal{ L }}$ be a $\sigma$-algebra on a nonempty set $\Gamma$. A set function ${\mathcal{ M }}: {\mathcal{ L }}\rightarrow [0,1]$ is called an uncertain measure if it satisfies the following axioms:

• Axiom 1: (Normality Axiom) ${\mathcal{ M }}\{\Gamma \}=1$ for the universal set $\Gamma$.

• Axiom 2: (Duality Axiom) ${\mathcal{ M }}\{\Lambda \}+{\mathcal{ M }}\{\Lambda ^{c}\}=1$ for any event $\Lambda$.

• Axiom 3: (Subadditivity Axiom) For every countable sequence of events $\Lambda _1, \Lambda _2, \ldots ,$ we have

  $$\begin{aligned} \displaystyle {\mathcal{ M }}\left\{ \bigcup _{i=1}^{\infty }\Lambda _i\right\} \le \sum _{i=1}^{\infty }{\mathcal{ M }}\{\Lambda _i\}. \end{aligned}$$

Besides, in order to provide the operational law, Liu (2010) defined the product uncertain measure on the product $\sigma$-algebra ${\mathcal{ L }}$ as follows.

• Axiom 4: (Product Axiom) Let $(\Gamma _k,{\mathcal{ L }}_k,{\mathcal{ M }}_k)$ be uncertainty spaces for $k=1, 2, \ldots .$ The product uncertain measure ${\mathcal{ M }}$ is an uncertain measure satisfying

  $$\begin{aligned} \displaystyle {\mathcal{ M }}\left\{ \prod _{k=1}^\infty \Lambda _k\right\} = \bigwedge _{k=1}^\infty {\mathcal{ M }}_k\{\Lambda _k\} \end{aligned}$$

  where $\Lambda _k$ are arbitrarily chosen events from ${\mathcal{ L }}_k$ for $k=1, 2, \ldots$, respectively.

Definition 2

(Liu 2010) An uncertain variable $\xi$ is a function from an uncertainty space $(\Gamma ,{\mathcal{ L }},{\mathcal{ M }})$ to the set of real numbers, such that, for any Borel set B of real numbers, the set

$$\begin{aligned} \{\xi \in B\} = \{\gamma \in \Gamma |\xi (\gamma )\in B\} \end{aligned}$$

is an event.

In order to describe uncertain variables in practice, the concept of uncertainty distribution was introduced.

Definition 3

(Liu 2010) The uncertainty distribution of an uncertain variable $\xi$ is defined as

$$\begin{aligned} \Phi (x)={\mathcal{ M }}\{\xi \le x\} \end{aligned}$$

for any real number x

An uncertainty distribution $\Phi (x)$ is said to be regular if its inverse function $\Phi ^{-1}(\alpha )$ exists and is unique for each $\alpha \in (0,1)$. And $\Phi ^{-1}(\alpha )$ is called the inverse uncertainty distribution of $\xi$. In this paper, we assume that all the payoffs are characterized by regular uncertain variables.

Definition 4

(Liu 2010) The uncertain variables $\xi _1, \xi _2,\ldots , \xi _m$ are said to be independent if

$$\begin{aligned} \displaystyle {\mathcal{ M }}\left\{ \bigcap _{k=1}^m\{\xi _i\in B_i\}\right\} =\bigwedge _{k=1}^m {\mathcal{ M }}\{\xi _i\in B_i\} \end{aligned}$$

for any Borel sets $B_1, B_2, \ldots , B_m$ of real numbers.

Definition 5

(Liu 2010) Let $\xi$ be an uncertain variable. Then the expected value of $\xi$ is defined by

$$\begin{aligned} \mathrm{E}[\xi ]=\int _0^{+\infty }{\mathcal{ M }}\{\xi \ge r\}\mathrm{d}r-\int _{-\infty }^0{\mathcal{ M }}\{\xi \le r\}\mathrm{d}r \end{aligned}$$

provided that at least one of the two integrals is finite.

If $\xi$ is a regular uncertain variable with uncertainty distribution $\Phi (x)$, then the expected value may be calculated by

$$\begin{aligned} \mathrm{E}[\xi ]=\int ^{+\infty }_{0}(1-\Phi (x))\mathrm{d}x-\int ^0_{-\infty }\Phi (x)\mathrm{d}x=\int ^{1}_{0}\Phi ^{-1}(\alpha )\mathrm{d}\alpha . \end{aligned}$$

An uncertain variable $\xi$ is called zigzag, denoted by $\mathcal {Z}(a,b,c)$, if it has an uncertainty distribution

$$\begin{aligned} \Phi (x)= {\left\{ \begin{array}{ll} \displaystyle 0,&{}\quad \mathrm{if}\;x< a\\ \displaystyle \frac{x-a}{2(b-a)}, &{}\quad \mathrm{if}\;a\le x\le b\\ \displaystyle \frac{x+c-2b}{2(c-b)}, &{}\quad \mathrm{if} \;b < x\le c\\ \displaystyle 1,&{}\quad \mathrm{if} \;x> c\\ \end{array}\right. } \end{aligned}$$

It is obvious that $\mathcal {Z}(a,b,c)$ is a regular uncertain variable with inverse uncertainty distribution

$$\begin{aligned} {\Phi^{-1}}(\alpha )= {\left\{ \begin{array}{ll} (1-2\alpha )a+2\alpha b, & \quad {\mathrm{if}} \;\alpha <0.5\\ (2-2\alpha )b+(2\alpha -1)c, & \quad {\mathrm{if}} \;\alpha \ge 0.5 \end{array}\right. } \end{aligned}$$

and the expected value of $\mathcal {Z}(a,b,c)$ is $(a+2b+c)/4$.

Definition 6

(Liu 2007) Let $\xi$ be an uncertain variable, and $\alpha \in (0,1]$. Then,

$$\begin{aligned} \xi _{\sup }(\alpha )=\sup \{r|{\mathcal{ M }}\{\xi \ge r\}\ge \alpha \} \end{aligned}$$

is called the $\alpha$-optimistic value to $\xi$, and

$$\begin{aligned} \xi _{\inf }(\alpha )=\inf \{r|{\mathcal{ M }}\{\xi \le r\}\ge \alpha \} \end{aligned}$$

is called the $\alpha$-pessimistic value to $\xi$.

Lemma 1

(Liu 2010) Assume that $\xi$ and $\eta$ are independent uncertain variables with finite expected values. Then for any real numbers a and b, we have

$$\begin{aligned} \mathrm{E}[a\xi +b\eta ]=a\mathrm{E}[\xi ]+b\mathrm{E}[\eta ]. \end{aligned}$$

Lemma 2

(Liu 2010) Suppose that $\xi$ and $\eta$ are independent uncertain variables, then for any $\alpha \in (0,1]$ and nonnegative real numbers a and b, we have

$$\begin{aligned} (a\xi +b\eta )_{\sup }(\alpha )=a\xi _{\sup }(\alpha )+b\eta _{\sup }(\alpha ); \end{aligned}$$

$$\begin{aligned} (a\xi +b\eta )_{\inf }(\alpha )=a\xi _{\inf }(\alpha )+b\eta _{\inf }(\alpha ). \end{aligned}$$

To define the behaviors (or rank the uncertain objectives) of decision makers, three approaches are often used. Let $\xi$ and $\eta$ be two uncertain variables. Then, we have

• 1. Expected value criterion $\xi <\eta$ if and only if $\mathrm{E}[\xi ]<\mathrm{E}[\eta ]$;

• 2. Optimistic value criterion $\xi <\eta$ if and only if $\xi _{\sup }(\alpha )<\eta _{\sup }(\alpha )$ for some predetermined confidence level $\alpha \in (0,1]$;

• 3. Pessimistic value criterion $\xi <\eta$ if and only if $\xi _{\inf }(\alpha )<\eta _{\inf }(\alpha )$ for some predetermined confidence level $\alpha \in (0,1]$.

3 Finite extensive game with uncertain payoffs

In this section, we first recall the notion of extensive game, and then introduce the finite extensive game with uncertain payoffs.

Definition 7

(Kuhn 1950) A finite extensive game with perfect information and chance moves is a tuple $\langle N,H,P,f_c,(\succeq _i)\rangle$ consisting of the following components:

• A set, N, of players.

• A set, H, of finite consequences of actions that satisfies the following two properties:

• The empty sequence ${\emptyset }$ is a member of H.

• If $(a^k)_{k=1,\ldots ,K}\in H$ and $L<K$, then $(a^k)_{k=1,\ldots ,L}\in H$.

• A function, P, that assigns to each non-terminal history a member of $N\bigcup \{c\}$. (P is the player function, with P(h) being the player who takes an action after the history h. If $P(h)=c$, then chance or nature takes the action after the history h. A history $(a^k)_{k=1,\ldots ,K}\in H$ is terminal if there is no $a^{K+1}$ such that $(a^k)_{k=1,\ldots ,K+1}\in H$.)

• A function, $f_c$, that associates with each $h \in H$ with $P(h)=c$, a probability measure on the action set of history h. Each such probability measure is assumed to be independent of every other such measure.

• For each player $i\in N$, a preference relation, $\succeq _i$, on lotteries over the set of terminal histories, Z.

The outcome O(s) of strategy profile $s=(s_i)_{i\in N}$ is defined to be the terminal history which occurs when every player follows his strategy $s_i$. Then Nash equilibrium of the extensive game is defined as follows:

Definition 8

(Kuhn 1950) A Nash equilibrium of an extensive game with perfect information and chance moves $\langle N,H,P,f_c,(\succeq _i)\rangle$ is a strategy profile $s^*$ such that for every player $i\in N$ we have

$$\begin{aligned} O(s^*_{-i},s^*_{i})\succeq _iO(s^*_{-i},s_{i}) \end{aligned}$$

for every strategy $s_i$ of player i.

Kuhn (1950) shows that a finite extensive game with complete information has a Nash equilibrium in pure strategies. However, Nash equilibrium ignores the sequential structure of the game. Selten (1965) proposed the concept of subgame perfect equilibrium, in which a player is required to reassess his plans as play proceeds. A subgame of $\langle N,H,P,f_c,(\succeq _i)\rangle$ that follows the history h is the finite extensive game $\Gamma (h)=\langle N,H|_h,P|_h,f_c,(\succeq _i|_h)\rangle,$ where $H|_h$ is the set of sequences $h'$ of actions for which $(h,h')\in H$, $P|_h$ is defined by $P|_h(h')=P(h,h')$ for each $h'\in H|_h$, and $\succeq _i|_h$ is defined by $h'\succeq _i|_h h''$ if and only if $(h,h')\succeq _i(h,h'')$.

Subgame perfect equilibrium has the characteristic that actions prescribed by each player’s strategy are optimal after any history, given all other players’ strategies. Given a strategy $s_i$ of player i and a history h in the extensive game, denote $s_i|_h$ as the strategy that $s_i$ induces in the subgame $\Gamma (h)$, i.e. $s_i|_h(h')=s_i(h,h')$ for each $h' \in H|_h$. Let $O_h(s|_h)$ be the outcome function defined on the strategy profile $s|_h=(s_i|_h)_{i \in N}$ in the subgame $\Gamma (h)$. The subgame perfect equilibrium of the extensive game is defined as follows:

Definition 9

(Selten 1965) A subgame perfect equilibrium of an extensive game with perfect information and chance moves $\langle N,H,P,f_c,(\succeq _i)\rangle$ is a strategy profile $s^{*}$ such that for every player $i\in N$ and every nonterminal history $h\in H\backslash Z$ for which $P(h)=i$ we have

$$\begin{aligned} O_h(s^*_{-i}|_h,s^*_i|_h)\succeq _i O_h(s^*_{-i}|_h,s_i|_h) \end{aligned}$$

for every strategy $s_i|_h$ of player i in the subgame $\Gamma (h)$.

By Definition 9, given a subgame perfect equilibrium $s^{*}$ and any nonterminal history h, $s^{*}|_h$ forms a Nash equilibrium to the subgame $\Gamma (h)$.

Lemma 3

(Selten 1965) Every finite extensive game with perfect information and chance moves has a subgame perfect equilibrium in pure strategies.

Traditionally, the players’ payoffs in a finite extensive game are assumed to be crisp numbers. However, Harsanyi (1995) suggested that in real-world games players may lack full information about the other players’ (or even their own) payoffs. Moreover, an extensive game consists of a large number of players with many strategies and each player has to make his decision for several rounds. Under these scenarios, it is difficult to specify the outcome corresponding to each strategy profile $s=(s_i)_{i\in N}$, thus making accurate or stochastic estimations about the payoffs almost impossible. Uncertainty theory offers an appropriate and powerful alternative to deal with incomplete information in games. With uncertainty theory, we can make use of human experiences, subjective judgements and intuitions to process the incomplete information as uncertain variables. Therefore, we introduce the finite extensive game with uncertain payoffs.

Definition 10

A finite extensive game with uncertain payoffs $\langle N,H,P,f_c,(u_i)\rangle$, abbreviated as UEG, is a finite extensive game with complete information and chance moves, where $N,H,P,f_c$ is as defined in Definition 7 and the $u_i$ is the uncertain payoff function defined on the set of terminal histories.

With the definition of finite extensive game with uncertain payoffs, we introduce three different kinds of equilibrium to characterize the behaviors of different decision makers in the next section.

4 Uncertain equilibria

People exhibit very different behaviors faced with uncertain payoffs. Risk neutral players try to maximize their expected payoff, risk averse players are reluctant to take risks and are inclined to a guaranteed minimum payoff, while risk seeking players are willing to accept greater volatility in exchange for potential higher returns. In uncertain theory, expected value criterion, optimistic value criterion and pessimistic value criterion are employed to describe the behaviors of the above mentioned players. Correspondingly, we define three uncertain Nash equilibria in the UEG.

Definition 11

An expected equilibrium of an UEG is a strategy profile $s^*$ such that for every player $i\in N$ we have

$$\begin{aligned} \mathrm{E}[u_i(s^{*}_{-i},s^{*}_i)]\ge \mathrm{E}[u_i(s^{*}_{-i},s_i)] \end{aligned}$$

for every strategy $s_i$ of player i.

Definition 12

An $\alpha$-optimistic equilibrium of an UEG is a strategy profile $s^*$ such that for every player $i\in N$ we have

$$\begin{aligned} \begin{array}{c} \sup \{r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s^*_i)\ge r\}\ge \alpha \} \\ \qquad \ge \sup \{r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s_i)\ge r\}\ge \alpha \} \end{array} \end{aligned}$$

for every strategy $s_i$ of player i and a predetermined confidence level $\alpha \in (0,1]$.

Definition 13

An $\alpha$-pessimistic equilibrium of an UEG is a strategy profile $s^*$ such that for every player $i\in N$ we have

$$\begin{aligned} \begin{array}{c} \inf \{r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s^*_i)\le r\}\ge \alpha \}\\ \qquad \ge \inf \{r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s_i)\le r\}\ge \alpha \} \end{array} \end{aligned}$$

for every strategy $s_i$ of player i and a predetermined confidence level $\alpha \in (0,1]$.

Per these definitions, a risk neutral player adopts the expected value criterion and intends to maximize his/her expected payoff. A risk averse player sets a predetermined confidence level $\alpha$ and endeavors to maximize the $\alpha$-optimistic value of his/her payoff. A risk seeking player tries to maximize the pessimistic value associated with some predetermined confidence level $\alpha$.

Next, we prove that the expected equilibrium, $\alpha$-optimistic equilibrium and $\alpha$-pessimistic equilibrium exist in the UEG. Our proofs are performed through mathematical induction. Suppose that any UEG having a maximum length of k has an equilibrium, we prove that an UEG with a length of $k+1$ also has an equilibrium. When $k=0$, the result is trivially true. Consider an UEG having a length of $k+1$. The root node of the game has a history of $\emptyset$, thus we define $P(\emptyset )$ as the function dictating who takes action at the root node. From Definition 7, we know that $P(\emptyset ) \in N\cup \{c\}$. We complete our proofs based on two different cases: when a player takes action ($P(\emptyset ) \in N$) and when the nature takes action ($P(\emptyset )=c).$ Notice that all subgames of our UEG have a maximum length of k. According to the assumption of our mathematical induction, an UEG with a maximum length of k has an equilibrium. Hence, each of the subgames has an equilibrium and we define $s^*(h)$ as the equilibrium strategy in subgame $\Gamma (h),$ where $\Gamma (h)$ has a maximum length of k. Therefore, we have

$$\begin{aligned} \mathrm{E}[u_i|_{h}(s^{*}_{-i}(h),s^{*}_i(h))]\ge \mathrm{E}[u_i|_{h}(s^{*}_{-i}(h),s_i(h))] \end{aligned}$$

for every strategy of player i in $\Gamma (h)$, denoted by $s_i(h)$. Now, we are ready to prove that an UEG has an expected equilibrium, an $\alpha$-optimistic equilibrium and an $\alpha$-pessimistic equilibrium.

Theorem 1

Every UEG has an expected equilibrium in pure strategies.

Proof

Case 1 $P(\emptyset )=c$. Suppose there are $J_c$ possible subgames after the chance move. Let $\lambda _j$ denote the probability of selecting subgame $\Gamma (h_j)$ such that $\lambda _j\ge 0$ for any $j=1,2,\cdots J_c$, and $\sum _{j=1}^{J_c} \lambda _j=1$. Let $s^*(h_j)$ be the expected equilibrium strategy in $\Gamma (h_j)$, $j=1,2,\cdots J_1$. Define a strategy profile $s^*$ of the UEG as $s^*|_{h_j}=s^*(h_j)$. We then show that $s^*$ is an expected equilibrium.

For any strategy $s_i$ of player $i\in N,$ we have

$$\begin{aligned}&\mathrm{E}[u_i(s^*_{-i},s_i^*)] \nonumber \\&\quad = \sum \limits _{j=1}^{J_c} \lambda _j \mathrm{E}[u_i|_{h_j}(s^{*}_{-i}(h_j),s_i^*(h_j))]\nonumber \\&\quad \ge \sum \limits _{j=1}^{J_c} \lambda _j \mathrm{E}[u_i|_{h_j}(s^{*}_{-i}(h_j),s_i(h_j))]\nonumber \\&\quad =\mathrm{E}[u_i(s^*_{-i},s_i)] \end{aligned}$$

(1)

where the two equalities follow from the definition of the chance move and the inequality holds since $s^*(h_j)$ is an expected equilibrium for subgame $\Gamma (h_j)$. Therefore, $s^*$ is an expected equilibrium in the UEG.

Case 2 $P(\emptyset )\in N$. Without loss of generality, we assume $P(\emptyset )= 1$, i.e. player 1 is the first to take action. Suppose player 1 has $J_1$ different actions leading to $J_1$ subgames $\Gamma (h_1),\Gamma (h_2),\ldots ,\Gamma (h_{J_1})$. Each of these $J_1$ subgames has a maximum length of k. Therefore, by our assumption, each of the $J_1$ subgames has an expected equilibrium. Suppose that action $a^*$ maximizes the expected payoff of player 1 at the beginning of the game, i.e.,

$$\begin{aligned} \mathrm{E}\left[ u_1|_{h_{a^*}}(s^*(h_{a^*}))\right] =\max \limits _{1\le j\le J_1} \mathrm{E}\left[ u_1|_{h_j}(s^*(h_j))\right] . \end{aligned}$$

Define a strategy profile $s^*$ of the UEG as $s^*_1(\emptyset )=a^*$ and $s^*|_{h_j}=s^*(h_j)$. We then prove $s^*$ is an expected equilibrium. Notice that

$$\begin{aligned}&\mathrm{E}[u_1(s^*_{-1},s_1^*)] \nonumber \\&\quad =\mathrm{E}[u_1|_{h_{a^*}}(s^{*}_{-1}(h_{a^*}),s^{*}_1(h_{a^*}))]\nonumber \\&\quad \ge \mathrm{E}[u_1|_{h_j}(s^{*}_{-1}(h_j),s^{*}_1(h_j))],\quad 1\le j\le J_1. \end{aligned}$$

(2)

For any strategy $s_1$ of player 1 with $s_1(\emptyset )=j$ and $s_1|_{h_j}=s_1(h_j)$,

$$\begin{aligned}&\mathrm{E}[u_1|_{h_j}(s^{*}_{-1}(h_j),s^{*}_1(h_j))]\nonumber \\&\quad \ge \mathrm{E}[u_1|_{h_j}(s^{*}_{-1}(h_j),s_1(h_j))]\nonumber \\&\quad = \mathrm{E}[u_1(s^*_{-1},s_1)], \end{aligned}$$

(3)

where the inequality is valid since $s^*(h_j)$ is an expected equilibrium in $\Gamma (h_j).$ Combining Eqs. (2) and (3), we have

$$\begin{aligned} \mathrm{E}[u_1(s^*_{-1},s_1^*)]\ge \mathrm{E}[u_1(s^*_{-1},s_1)] \end{aligned}$$

(4)

for any strategy $s_1$ of player 1.

In addition, for every player $i\in N,$ $i\ne 1$ and any strategy $s_i$ of player i, we have

$$\begin{aligned} \mathrm{E}[u_i(s^*_{-i},s_i^*)]= & \mathrm{E}[u_i|_{h_{a^*}}(s^{*}_{-i}(h_{a^*}), s_i^*(h_{a^*}))]\nonumber \\\ge & \mathrm{E}[u_i|_{h_{a^*}}(s^{*}_{-i}(h_{a^*}),s_i(h_{a^*}))]\nonumber \\= & \mathrm{E}[u_i(s^{*}_{-i},s_i)]. \end{aligned}$$

(5)

With Eqs. (4) and (5), we show that $s^*$ is an expected equilibrium of the UEG, which completes the proof. $\square$

Theorem 2

Every UEG has an $\alpha$ -optimistic equilibrium for any predetermined confidence level $\alpha \in [0,1]$ in pure strategies.

Proof

Case 1 $P(\emptyset )=c$. Suppose there are $J_c$ possible subgames $\Gamma (h_j)$ ($j=1,2,\cdots J_c$) after the chance move. Let $\lambda _j$ denote the probability of selecting subgame $\Gamma (h_j)$ and $s^*(h_j)$ be the $\alpha$-optimistic equilibrium of subgame $\Gamma (h_j)$. We construct a strategy profile $s^*$ of the UEG as $s^*|_{h_j}=s^*(h_j)$. We then show that $s^*$ is an $\alpha$ optimistic equilibrium. Since payoff functions are independent uncertain variables, by Lemma 2, we have

$$\begin{aligned}&\sup \left\{ r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s_i)\ge r\}\ge \alpha \right\} \\&\quad =\sup \left\{ r|{\mathcal{ M }}\left\{ \sum \limits _{j=1}^{J_c} \lambda _j u_i|_{h_j}(s_{-i}^*(h_j),s_i(h_j))\ge r\right\} \ge \alpha \right\} \\&\quad =\sum \limits _{j=1}^{J_c} \lambda _j \sup \left\{ r|{\mathcal{ M }}\{u_i|_{h_j}(s_{-i}^*(h_j),s_i(h_j))\ge r\}\ge \alpha \right\} \end{aligned}$$

Therefore,

$$\begin{aligned}&\sup \left\{ r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s_i^*)\ge r\}\ge \alpha \right\} \\&\quad =\sum \limits _{j=1}^{J_c} \lambda _j \sup \left\{ r|{\mathcal{ M }}\{u_i|_{h_j}(s_{-i}^*(h_j),s_i^*(h_j))\ge r\}\ge \alpha \right\} \\&\quad \ge \sum \limits _{j=1}^{J_c} \lambda _j \sup \left\{ r|{\mathcal{ M }}\{u_i|_{h_j}(s_{-i}^*(h_j),s_i(h_j))\ge r\}\ge \alpha \right\} \\&\quad = \sup \left\{ r|{\mathcal{ M }}\{u_i(s^{*}_{-i},s_i)\ge r\}\ge \alpha \right\} , \end{aligned}$$

where the inequality holds because $s^*(h_j)$ is the $\alpha$-optimistic equilibrium of subgame $\Gamma (h_j)$. Therefore, $s^*$ is an $\alpha$ optimistic equilibrium of the UEG.

Case 2 $P(\emptyset ) \in N$. Let $s^*(h_j)$ be the $\alpha$-optimistic equilibrium of the subgame $\Gamma (h_j)$. Similarly, we define a strategy profile $s^*$ of the UEG as $s^*_1(\emptyset )=\alpha$ and $s^*|_{h_j}=s^*(h_j)$. It can be shown that $s^*$ is the $\alpha$-optimistic equilibrium of the UEG. The prove follows exactly from the proof of Theorem 1 Case 2. $\square$

Theorem 3

Every UEG has an $\alpha$ -pessimistic equilibrium for any predetermined confidence level $\alpha \in (0,1]$ in pure strategies.

Proof

The proof is similar to Theorem 2. $\square$

5 Uncertain subgame perfect equilibria

Since uncertain equilibria in an UEG have similar disadvantages as Nash equilibrium in deterministic environment, we next give some new definitions of subgame perfect equilibrium in an UEG.

First, we use the expected value criterion to rank the uncertain payoffs and define the expected credibilistic subgame perfect equilibrium in an UEG.

Definition 14

An expected subgame perfect equilibrium of the UEG is a strategy profile $s^*$ such that for every player $i\in N$ and every nonterminal history $h\in H\backslash Z$ for which $P(h)=i$ we have

$$\begin{aligned} \mathrm{E}[u_i|_h(s^{*}_{-i}|_h,s^{*}_i|_h)]\ge \mathrm{E}[u_i|_h(s^{*}_{-i}|_h,s_i|_h)] \end{aligned}$$

for every strategy $s_i|_h$ of player i in the subgame $\Gamma (h).$

The following lemma is needed for proving the existence of pure-strategy expected subgame perfect equilibrium in the UEG.

Lemma 4

Astrategy profile $s^*$ is an expected subgame perfect equilibrium of an UEG if and only if for every player $i\in N$ and every history $h\in H$ that $P(h) = i$ we have

$$\begin{aligned} \mathrm{E}[u_i|_h(s^{*}_{-i}|_h,s^{*}_i|_h)]\ge \mathrm{E}[u_i|_h(s^{*}_{-i}|_h,s_i|_h)] \end{aligned}$$

for every strategy $s_i|_h$ for player i in the subgame $\Gamma (h)$ which differs from $s_i^*|_h$ only in the action it dictates after the initial history of $\Gamma (h).$

Proof

($\Rightarrow$) If $s^*$ is an expected subgame perfect equilibrium of the UEG, then the condition is surely satisfied.

($\Leftarrow$) Suppose the condition holds but $s^*$ is not an expected subgame perfect equilibrium, there exists some player i and a nonterminal history $h'$ with $P(h')=i$, and some strategies $s_i|_{h'}$ in $\Gamma (h')$ we have

$$\begin{aligned} \mathrm{E}[u_i|_{h'}(s^{*}_{-i}|_{h'},s^{*}_i|_{h'})] < \mathrm{E}[u_i|_{h'}(s^{*}_{-i}|_{h'},s_i|_{h'})] \end{aligned}$$

i.e., $s_i$ is more profitable for player i in subgame $\Gamma (h').$

For these $s_i|_{h'}$, there must exist some $s_i|_{h'}(h)\ne s_i^*|_{h'}(h)$ for some history $h\in H|_{h'}$ whose length is less than the length of $\Gamma (h').$ Since the game is finite, the number of h is finite and we can choose a strategy $s_i|_{h'}$ which has the least difference with $s_i^*|_{h'},$ i.e., the number of h that $s_i|_{h'}(h)\ne s_{-i}^*|_{h'}(h)$ is least. Let $h^*$ be the longest history in $H|_{h'}$ which satisfies $s_i|_{h'}(h)\ne s_i^*|_{h'}(h).$

Considering subgame $\Gamma (h^*)$, the initial history is the only history in $\Gamma (h^*)$ such that $s_i$ prescribes a different action from $s_i^*|_{h'}.$ Next, we show that $s_i|_{h^*}$ is more profitable than $s_i^*|_{h^*}.$ If not, we can modify strategy $s_i$ as $s_i|_{h^*}=s_i^*|_{h^*},$ then the revised $s_i$ is more profitable for player i in subgame $\Gamma (h')$ but there is a less number of $h\in H|_{h'}$ such that $s_i|_{h'}(h)\ne s_i^*|_{h'}(h),$ which is a contradiction. Therefore, $s_i|_{h^*}$ is more profitable and only differs from $s_i^*|_{h^*}$ in the action it dictates after the initial history of $\Gamma (h')$, which contradicts the condition. Therefore, $s^*$ is an expected subgame perfect equilibrium.

Using Lemma 5, the existence of expected subgame perfect equilibrium is demonstrated in the following theorem. Similar to the proof of Theorem 1, our proofs are conducted through mathematical induction. Suppose that any UEG having a maximum length of k has an expected subgame perfect equilibrium, we prove that an UEG with a length of $k+1$ also has an expected subgame perfect equilibrium. If $k=0$, then h is a terminal history. The result is trivial. Next, we show in our proof that for $k\ge 0$, we can find an expected subgame perfect equilibrium to any UEG with length $k+1$ if the expected subgame perfect equilibrium of an UEG with a maximum length of k exists. $\square$

Theorem 4

Every UEG has an expected subgame perfect equilibrium in pure strategies.

Proof

Consider a subgame $\Gamma (h)$ with a length of $k+1$, we complete our proof based on the following two cases:

Case 1 $P(h) = c$, i.e., P(h) is a chance move. This part can be similarly proved as Case 1 in Theorem 1.

Case 2 $P(h) \in N.$ Without loss of generality, we assume $P(h)=1$, i.e., player 1 is the first to take action in subgame $\Gamma (h)$. Suppose player 1 has $J_1$ possible actions $a_j, j=1,2,\cdots J_1$ leading to $J_1$ subgames $\Gamma (h_j)$ where $h_j=(h,a_j), j=1,2,\cdots ,J_1$. Each subgame of these $J_1$ subgames has a maximum length of k, hence we can find an expected subgame perfect equilibrium to each subgame $\Gamma (h_j)$, denoted by $s^*(h_j)$. By selecting the action $a^*$ that maximizes $\mathrm{E}[u_i|_{h_j}(s^*(h_j))]$ for player i, we construct a strategy $s^*$ in $\Gamma (h)$ where $s^*|_{h_{a^*}}=s^*(h_{a^*})$ and $s_i^*(h)=\alpha ^*.$ It follows from Lemma 5 that $s^*$ is an expected subgame perfect equilibrium. $\square$

Noticing that the concept of optimistic value also applies for the subgame perfect equilibrium, we formulate the notion of $\alpha$-optimistic subgame perfect equilibrium as follows.

Definition 15

An $\alpha$-optimistic subgame perfect equilibrium of an UEG is a strategy profile $s^*$ such that for every player $i\in N$ and every nonterminal history $h\in H\backslash Z$ for which $P(h)=i$ we have

$$\begin{aligned} \begin{array}{c} \sup \{r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s^*_i|_h)\ge r\}\ge \alpha \}\\ \qquad \ge \sup \{r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s_i|_h)\ge r\}\ge \alpha \} \end{array} \end{aligned}$$

for every strategy $s_i|_h$ of player i in the subgame $\Gamma (h)$ and a predetermined confidence level $\alpha \in (0,1].$

In order to prove the existence of $\alpha$-optimistic subgame perfect equilibrium in an UEG, we need the following lemma.

Lemma 5

A strategy profile $s^*$ is an $\alpha$ -optimistic subgame perfect equilibrium of an UEG for any predetermined confidence level $\alpha \in (0,1],$ if and only if for every player $i\in N$ and every history $h\in H$ that $P(h) = i$ we have

$$\begin{aligned} \begin{array}{c} \sup \{r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s^*_i|_h)\ge r\}\ge \alpha \}\\ \qquad \ge \sup \{r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s_i)\ge r\}\ge \alpha \} \end{array} \end{aligned}$$

for every strategy $s_i$ of player i in the subgame $\Gamma (h)$ which differs from $s^*_i|_h$ only in the action it dictates after the initial history of $\Gamma (h).$

Proof

The proof is the same as Lemma 5. $\square$

Using this deviation property of $\alpha$-optimistic subgame perfect equilibrium, we can prove that there exists an $\alpha$-optimistic subgame perfect equilibrium in the UEG.

Theorem 5

Every UEG has an $\alpha$ -optimistic subgame perfect equilibrium for any predetermined confidence level $\alpha \in (0,1]$ in pure strategies.

Proof

Using Lemma 2, the proof is similar to Theorem 2. $\square$

The pessimistic value criterion lends guidance to risk-seeking decision makers. In the following, we introduce the definition of $\alpha$-pessimistic subgame perfect equilibrium in Definition 16, present the deviation property in Lemma 6, and prove the existence of $\alpha$-pessimistic subgame perfect equilibrium in the UEG in Theorem 6.

Definition 16

An $\alpha$-pessimistic subgame perfect equilibrium of an UEG is a strategy profile $s^*$ such that for every player $i\in N$ and every nonterminal history $h\in H{\backslash } Z$ for which $P(h)=i$ we have

$$\begin{aligned} \begin{array}{c} \inf \left\{ r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s^*_i|_h)\le r\}\ge \alpha \right\} \\ \qquad \ge \inf \left\{ r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s_i|_h)\le r\}\ge \alpha \right\} \end{array} \end{aligned}$$

for every strategy $s_i|_h$ of player i in the subgame $\Gamma (h)$ and a predetermined confidence level $\alpha \in (0,1].$

Lemma 6

A strategy profile $s^*$ is an $\alpha$ -pessimistic subgame perfect equilibrium of an UEG for any predetermined confidence level $\alpha \in (0,1],$ if and only if for every player $i\in N$ and every history $h\in H$ that $P(h) = i$ we have

$$\begin{aligned} \begin{array}{c} \inf \{r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s^*_i|_h)\le r\}\ge \alpha \}\\ \qquad \ge \inf \{r|{\mathcal{ M }}\{u_i|_h(s^{*}_{-i}|_h,s_i)\le r\}\ge \alpha \} \end{array} \end{aligned}$$

for every strategy $s_i$ of player i in the subgame $\Gamma (h)$ which differs from $s^*_i|_h$ only in the action it dictates after the initial history of $\Gamma (h).$

Proof

The proof follows from Lemma 5. $\square$

Theorem 6

Every UEG has an $\alpha$ -pessimistic subgame perfect equilibrium for any predetermined confidence level $\alpha \in (0,1]$ in pure strategies.

Proof

The proof is similar to Theorem 3. $\square$

6 Resource allocation of national security

In this section, we consider a sequential uncertain game between an attacker and a defender. Following convention, we refer to the attacker as male and the defender as female. The defender can use a number of countermeasures to defend a number of targets. The attacker can choose any one of these targets to strike a number of possible threats. The defender moves first and must decide which countermeasure to use and which target to defend. The attacker moves afterwards, choosing the combination of threat and target to maximize his utility. The goal of the defender is to choose countermeasure and targets such that her utility is maximized.

We consider the payoff as an uncertain variable for each player, and each player is given a weight for each target between zero and one, where the sum over all targets is one. For each player there is a subset of targets with nonzero weight corresponding to preferences. We assume that, for each target, the defender is seeking minimization whereas the attacker is seeking maximization. For example, if the target is “a school”, the defender would be attempting minimization whereas the attacker would be seeking maximization.

We associate the following indices with the elements of the model.

• t: index for targets

• T: numbers for targets

• i: index for countermeasures

• j: index for threats

• S: the set of countermeasures, $S=\{S_1,S_2,\ldots ,S_i,\ldots \}$

• $\Omega$: the set of threats, $\Omega =\{\Omega _1,\Omega _2,\ldots ,\Omega _j,\ldots \}$

The defender and attacker place weights (not necessarily the same) on the targets, based on their relative importance to each side.

$w_{t(D)}$: the weight for defender target t, $w_{t(D)}\in [0,1]$, $\sum \limits _{t=1}^{T}w_{t(D)}=1$

$w_{t(A)}$: the weight for attacker target t, $w_{t(A)}\in [0,1]$, $\sum \limits _{t=1}^{T}w_{t(A)}=1$

Countermeasures taken by the defender can reduce the consequence of an attack. The consequences of an attack in target t are given by uncertain payoff $Q_t(S,\Omega ).$ Then we can determine the loss for the defender and gain for the attacker based on their weight vectors:

$$\begin{aligned}&L(Q(S,\Omega ),w_{(D)}) = \sum \limits _{t=1}^T Q_t(S,\Omega )*w_{t(D)},\\&U(Q(S,\Omega ),w_{(A)}) = \sum \limits _{t=1}^T Q_t(S,\Omega )*w_{t(A)}. \end{aligned}$$

Let $\Omega ^*$ be the attacker’s best response to the defender’s countermeasure. The goal for the defender is given by

$$\begin{aligned} \min \limits _{S_i} L(Q(S,\Omega ^*),w_{(D)}), \end{aligned}$$

and the best response $\Omega ^*$ for the attacker is given by

$$\begin{aligned} \Omega ^* = \arg \max \limits _{\Omega _j} U(Q(S^*,\Omega ),w_{(A)}). \end{aligned}$$

Now, we apply the three different equilibria introduced in Sect. 5 to analyze this resource allocation game of national security.

An expected subgame perfect equilibrium of the problem is a set $\{S^*,\Omega ^*\}$ such that the following conditions are met:

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{E}[U(Q(S^*,\Omega ^*),w_{(A)})] \\ \qquad \ge \mathrm{E}[U(Q(S^*,\Omega ),w_{(A)})], \,\forall \Omega ,\\ \mathrm{E}[L(Q(S^*,\Omega ^*),w_{(D)})] \\ \qquad \le \mathrm{E}[L(Q(S,\Omega ^*),w_{(D)})], \,\forall S. \end{array}\right. \end{aligned}$$

The first condition states that the attacker chooses his best response to maximize his expected payoff given the defender’s countermeasure $S^*$. The second condition states that the defender tries to minimize his expected loss given the attacker’s action $\Omega ^*$. The Nash equilibrium is achieved when no player has an incentive to from his/her strategy.

An $\alpha$-optimistic subgame perfect equilibrium of the problem is a set $\{S^*,\Omega ^*\}$ such that the following conditions are met:

$$\begin{aligned} \left\{ \begin{array}{l} \left[ U(Q(S^*,\Omega ^*),w_{(A)})\right] _{\sup }(\alpha )\\ \qquad \ge \left[ U(Q(S^*,\Omega ),w_{(A)})\right] _{\sup }(\alpha ),\, \forall \Omega ,\\ \left[ L(Q(S^*,\Omega ^*),w_{(D)})\right] _{\sup }(\alpha )\\ \qquad \le \left[ L(Q(S,\Omega ^*),w_{(D)})\right] _{\sup }(\alpha ),\quad \forall S. \end{array}\right. \end{aligned}$$

An $\alpha$-pessimistic subgame perfect equilibrium of the problem is a set $\{S^*,\Omega ^*\}$ such that the following conditions are met:

$$\begin{aligned} \left\{ \begin{array}{l} \left[ U(Q(S^*,\Omega ^*),w_{(A)})\right] _{\inf }(\alpha )\\ \qquad \ge \left[ U(Q(S^*,\Omega ),w_{(A)})\right] _{\inf }(\alpha ),\quad \forall \Omega ,\\ \left[ L(Q(S^*,\Omega ^*),w_{(D)})\right] _{\inf }(\alpha )\\ \qquad \le \left[ L(Q(S,\Omega ^*),w_{(D)})\right] _{\inf }(\alpha ),\quad \forall S. \end{array}\right. \end{aligned}$$

From our results in Sect. 4 we know that there exists an expected equilibrium, an $\alpha$-optimistic equilibrium and an $\alpha$-pessimistic equilibrium in pure strategies.

Now we provide some numerical examples to show three different equilibria.

We assume defender has two countermeasures $S_1,S_2$, attacker has two threats $\Omega _1,\Omega _2$ and the numbers of targets are two. Let $w_{1(D)}=0.4,w_{2(D)}=0.6$ and $w_{1(A)}=0.3,w_{2(A)}=0.7.$ The independent uncertain payoffs are characterized by triangular uncertain variables as follows:

$$\begin{aligned}&Q_1(S_1,\Omega _1)=\mathcal {Z}(0,5,12),&Q_2(S_1,\Omega _1)=\mathcal {Z}(1,4,7).\\&Q_1(S_1,\Omega _2)=\mathcal {Z}(3,4,7),&Q_2(S_1,\Omega _2)=\mathcal {Z}(1,5,9).\\&Q_1(S_2,\Omega _1)=\mathcal {Z}(5,6,7),&Q_2(S_2,\Omega _1)=\mathcal {Z}(4,5,6).\\&Q_1(S_2,\Omega _2)=\mathcal {Z}(3,5,9),&Q_2(S_2,\Omega _2)=\mathcal {Z}(1,6,7). \end{aligned}$$

We list the pure strategies for defender and attacker in Table 1.

Table 1 Pure strategies for defender and attacker

Expected equilibrium If defender and attacker want to optimize the mean value of their uncertain objective. By computation, we have

$$\begin{aligned}&\mathrm{E}[\mathcal {Z}(0,5,12)]=5.5,&\mathrm{E}[\mathcal {Z}(1,4,7)]=4.\\&\mathrm{E}[\mathcal {Z}(3,4,7)]=4.5,&\mathrm{E}[\mathcal {Z}(1,5,9)]=5.\\&\mathrm{E}[\mathcal {Z}(5,6,7)]=6,&\mathrm{E}[\mathcal {Z}(4,5,6)]=5.\\&\mathrm{E}[\mathcal {Z}(3,5,9)]=5.5,&\mathrm{E}[\mathcal {Z}(1,6,7)]=5. \end{aligned}$$

The payoffs of defender and attacker are given in Table 2.

Table 2 Strategic form for uncertain expected payoffs

It can be seen that the uncertain expected equilibria are $(S_1,(\Omega _2,\Omega _1))$ and $(S_1,(\Omega _2,\Omega _2))$.

The subgame perfect equilibrium can be calculated by backward induction, similar as the proof of Theorem 4. The uncertain expected subgame perfect equilibrium is $(S_1,(\Omega _2,\Omega _1))$, under which the defender chooses countermeasure $S_1$ to defend the targets and the attacker uses threat $\Omega _2$ to strike the targets.

$\alpha$-optimistic equilibrium The optimistic value criterion is widely adopted by risk-averse players who want to optimize the $\alpha$-optimistic value of their uncertain objectives. In this study, we let the confidence level be 0.8. By computation, we have

$$\begin{aligned}&(0,5,12)_{\sup }(0.8)=2,&(1,4,7)_{\sup }(0.8)=2.2.\\&(3,4,7)_{\sup }(0.8)=3.4,&(1,5,9)_{\sup }(0.8)=2.6.\\&(5,6,7)_{\sup }(0.8)=5.4,&(4,5,6)_{\sup }(0.8)=4.4.\\&(3,5,9)_{\sup }(0.8)=3.8,&(1,6,7)_{\sup }(0.8)=3. \end{aligned}$$

Payoffs of defender and attacker are given in Table 3.

Table 3 Strategic form for uncertain $\alpha$-optimistic payoffs

We find two $\alpha$-optimistic equilibria: $(S_1,(\Omega _2,\Omega _1))$ and $(S_1,(\Omega _2,\Omega _2))$. The uncertain $\alpha$-optimistic subgame perfect equilibrium is $(S_1,(\Omega _2,\Omega _1))$, under which the defender chooses countermeasure $S_1$ to defend the targets and the attacker uses threat $\Omega _2$ to strike the targets.

$\alpha$-pessimistic equilibrium The pessimistic value criterion describes a situation under which players are risk lovers and want to optimize the $\alpha$-pessimistic value of their uncertain objectives, where $\alpha$ is a predetermined confidence level. We consider the confidence level 0.6 for the $\alpha$-pessimistic equilibrium. By computation, we have

$$\begin{aligned}&(0,5,12)_{\inf }(0.6)=6.4,&(1,4,7)_{\inf }(0.6)=4.6.\\&(3,4,7)_{\inf }(0.6)=4.6,&(1,5,9)_{\inf }(0.6)=5.8.\\&(5,6,7)_{\inf }(0.6)=6.2,&(4,5,6)_{\inf }(0.6)=5.2.\\&(3,5,9)_{\inf }(0.6)=5.8,&(1,6,7)_{\inf }(0.6)=6.2. \end{aligned}$$

Payoffs of defender and attacker are given in Table 4.

Table 4 Strategic form for uncertain $\alpha$-pessimistic payoffs

There are two uncertain $\alpha$-pessimistic equilibria $(S_1,(\Omega _2,\Omega _1))$ and $(S_1,(\Omega _2,\Omega _2))$ to this game. The uncertain $\alpha$-pessimistic subgame perfect equilibrium is $(S_1,$ $(\Omega _2,\Omega _1))$.

From these examples, we find that the Nash equilibria and subgame perfect equilibria are the same under all three different criteria. Next we present a different set of examples under which the subgame perfect equilibria are different under different decision-making criteria.

We continue to assume defender has two countermeasures $S_1,S_2$, attacker has two threats $\Omega _1,\Omega _2$ and the numbers of targets are two. The weights of defender and attacker are the same: $w_{1(D)}=0.4,w_{2(D)}=0.6$ and $w_{1(A)}=0.3,w_{2(A)}=0.7$. However, independent uncertain payoffs are characterized by different triangular uncertain variables:

$$\begin{aligned}&Q_1(S_1,\Omega _1)=\mathcal {Z}(0,9,10),&Q_2(S_1,\Omega _1)=\mathcal {Z}(1,7,8).\\&Q_1(S_1,\Omega _2)=\mathcal {Z}(3,9,11),&Q_2(S_1,\Omega _2)=\mathcal {Z}(3,8,9).\\&Q_1(S_2,\Omega _1)=\mathcal {Z}(2,7,9),&Q_2(S_2,\Omega _1)=\mathcal {Z}(0,7,9).\\&Q_1(S_2,\Omega _2)=\mathcal {Z}(1,10,11),&Q_2(S_2,\Omega _2)=\mathcal {Z}(2,10,12). \end{aligned}$$

Let the confidence level be 0.8 for $\alpha$-optimistic equilibria. By computation, we have

$$\begin{aligned}&(0,9,10)_{\sup }(0.8)=3.6,&(1,7,)_{\sup }(0.8)=3.4.\\&(3,9,11)_{\sup }(0.8)=5.4,&(3,8,9)_{\sup }(0.8)=5.\\&(2,7,9)_{\sup }(0.8)=4,&(0,7,9)_{\sup }(0.8)=2.8.\\&(1,10,11)_{\sup }(0.8)=4.6,&(2,10,12)_{\sup }(0.8)=5.2. \end{aligned}$$

The payoffs of the defender and attacker are given in Table 5.

Table 5 Strategic form for uncertain $\alpha$-optimistic payoffs

It can be seen that $(s_2,(\Omega _2,\Omega _2))$ forms an uncertain $\alpha$-optimistic equilibrium. The subgame perfect equilibrium can be calculated via backward induction and we find that $(s_2,(\Omega _2,\Omega _2))$ is also an uncertain $\alpha$-optimistic subgame perfect equilibrium.

Let the confidence level be 0.8 for the $\alpha$-pessimistic equilibrium, we have

$$\begin{aligned}&(0,9,10)_{\inf }(0.8)=9.6,&(1,7,8)_{\inf }(0.8)=7.6.\\&(3,9,11)_{\inf }(0.8)=10.2,&(3,8,9)_{\inf }(0.8)=8.6.\\&(2,7,9)_{\inf }(0.8)=8.2,&(0,7,9)_{\inf }(0.8)=8.2.\\&(1,10,11)_{\inf }(0.8)=10.6,&(2,10,12)_{\inf }(0.8)=11.2. \end{aligned}$$

The payoffs of the defender and attacker are given in Table 6.

Table 6 Strategic form for uncertain $\alpha$-pessimistic payoffs

We find that the uncertain $\alpha$-pessimistic equilibrium is $(s_1,(\Omega _2,\Omega _2))$. Since the uncertain $\alpha$-pessimistic equilibrium is unique, it is not difficult to see that the uncertain $\alpha$-pessimistic equilibrium $(s_1,(\Omega _2,\Omega _2))$ also forms the $\alpha$-pessimistic subgame perfect equilibrium.

We can see that, in this example, the subgame perfect equilibria may be different under different decision-making scenarios, validating the fact decision makers with idiosyncratic character traits exhibit very different behaviors. The three different equilibria and subgame perfect equilibria we introduced provide an avenue to characterize the behaviors of decision makers with different character traits.

7 Conclusion

In this paper, we first used uncertain variables to characterize payoffs in extensive games. Then, we proposed new concepts of uncertain equilibria in UEG like Nash equilibrium in deterministic environment and correspondingly defined three versions of uncertain subgame perfect equilibria in UEG. Furthermore, we proved the existence theorems that affirm these new equilibria do exist in finite extensive game with uncertain payoffs. At the end of this paper, we gave a model in resource allocation of national security to illustrate the rationality and necessity of these new equilibria in UEG. There are numerous possible extensions and refinements to the model that could be implemented in future research. Most notably, our model assumes that the attacker can fully observe the defender’s resource allocation. In reality, the defender may well have some countermeasures that she would like to keep hidden. The model might be extended to include uncertainty in attacker preferences.