1 Introduction

Many airports suffer delays in the departure flow with, as consequence, customer dissatisfaction and an increase of the airport’s costs. The expected growth of commercial aviation and air traffic shows that, despite the current economic crisis, an increase in air service demand in the next years is expected. So if this trend will be confirmed, the systems, schemes and operative concepts of air traffic management (ATM) will be insufficient.

The realization of new infrastructures to support existing ones is subject to economic and environmental constraints and requires long times, therefore it is crucial an optimal use of existing resources. Many researchers are addressing their efforts to find new solutions to the optimization of all airport operations.

Starting from the results of (Anagnostakis et al. 2001; Anagnostakis and Clarke 2003, 2004; Bohme 2005), this work is focused on the departure management (DMAN) problem, and aims, in particular, to define a mathematical algorithm able to solve an airport multi-runway departures problem. In (Anagnostakis et al. 2001) optimal runway operations planning was faced with a "single-stage" optimization routine that takes into account all the desired objectives and constraints (air traffic control—ATC constraints), and the characteristics of each aircraft (weight class, destination, etc.).

A sequencing problem of departures with a "two stage" approach is analyzed in (Anagnostakis and Clarke 2003), considering runway crossings in the planning process of runway operations. A decomposition based algorithm was introduced and applied to the design of an heuristic for solving the runway operation problem (ROP) problem in (Anagnostakis and Clarke 2004).

The Eurocontrol/DLR DMAN is used as a tactical departure management in (Bohme 2005). Particular attention is given to the architecture and to preliminary results from real-time simulation trials RTS1 with DMAN, in the framework of the European Gate-to-Gate project at Malmoe in 2004. An algorithm for generating schedules of airport runway operations that are robust to perturbations caused by system uncertainty is presented in (Chandran and Balakrishnan 2007). This algorithm computes a tradeoff curve between runway throughput and the probability that random deviations of aircraft from the scheduling violate system constraints and require intervention from air traffic controllers. In (Atkin et al. 2007) models for evaluating schedules and determining the effects of the physical constraints are described. The authors propose a hybrid metaheuristic system applied to Heathrow airport in London. The system takes into account more aircraft than a human controller can handle, and so can aid the latter by suggesting schedules that anticipate some future problems.

Here, we propose to match a two stage algorithm, used to schedule departures for a single runway airport, with a multi-runway procedure in order to solve the departure problem for a multi-runway airport. First, we describe a model used to calculate an optimal planning of take-off operations for a single runway airport, maximizing the runway throughput and reducing delays. Then, we define a multi-runway procedure, based on the previous algorithm, which allows to find the better assignment of each independent runway (i.e., without mutual influence) to the departing flights according to airport security and safety constraints and to avoid time gaps which can compromise the airport performance.

The innovative factors are the implementation of a method to mix arrivals with departures in order to maximize the throughput of the shared runway, and the use of a very simple swapping procedure to perform the multi-runway airport, where each runway needs to optimize the departures and arrivals operations.

A prototype system has been realized, able to ensure the following potential benefits: punctuality in departures, better use of runways capacity, reduction of the air traffic controller workload, and emissions reduction (due to a queues decreasing at holding point), better services for passengers.

The prototype is based on the archetype of modular architecture to design multiple interactive stages, each of which implements an independent activity, but they are mutually connected. This choice gives to the system an open vision: other different stages can be added or an existing one should be substituted with a more performing stage. Moreover, although we perform a single objective for each stage, we are able to obtain a feasible and a near optimal solution by using the interconnection concept based on some "ad hoc" heuristic.

The paper is organized as follows. In Sect. 2 we recall the basic definitions of constraints for the airport domain; in particular, we discuss about the universally recognized restrictive classes considered to project the solving methodology. In Sect. 3 the two stage algorithm, with mathematical model for each stage and “ad hoc” heuristic to mix arrivals and departures scheduling is shown. The multi-runway procedure and its cooperation with the two stage algorithm are presented in Sect. 4. Finally, Sect. 5 reports simulations based on test-case of Milano Malpensa flight strips, dealing with two independent runways.

2 Operational context

The airport domain is subject to a set of general safety and security rules, such as safety of passengers, crew and service personnel, environment pollution gas emissions, and etc. In general these rules can be divided in two different restrictive classes:

  • Universally recognized rules, i.e., wake vortex separations, departure routes, speed group, calculated take off time (CTOT), estimated take off time (ETOT), runway occupancy separations;

  • locally recognized rules (for each airport), as status, capacity and timetable of each runway, passenger fairness, flight controller workload, priority, etc.

In what follows we deal with some typical hard constraints which will be used in the proposed algorithm.

Wake vortex separations Each aircraft is classified according to its weight class (also said wake vortex category), which is defined by maximum take-off mass (MTOM).

In fact each aircraft, in both landings and take-offs phases, generates a wake vortex caused by the wing tips, that may disrupt the operation of the next aircraft. According to wake vortex category, a time slot between two successive departures or successive departures and arrivals can be defined, to ensure that these operations are carried out safely.

Here, for simplicity only four weight classes are used:

  • light (L) with MTOM ≤7,000 Kg;

  • medium (M) with 7,000 Kg ≤ MTOM ≤ 136,000 Kg;

  • heavy (H) with MTOM ≥ 136,000 Kg;

  • super (J): Airbus A380–800.

The time slots (in seconds) between different weight classes, considering mixed operations, as arrivals and departures, are shown in Fig. 1 (these values are referred to Italy context).

Fig. 1
figure 1

Time slot between weight classes

Full size image

Departure routes Departure routes, also known as standard instrument departure (SID), are special flight procedures which allow each aircraft, after take-off, can drift away from airport in total security and reach the assigned exit point (or TMA—terminal manoeuvring area). If the same SIDis assigned to different aircraft, a separation in time has to be imposed among them, so to grant that minimum security distance is also ensured in the next en-route phase. In particular, the minimum horizontal separation, checked with radar equipment, is five miles. The Italian aeronautical information publication (API) considers as separations time slots of 1 and 2 min depending on the aircraft category.

Calculated take off time (CTOT) To ensure an efficient use of the airspace and to avoid congestions, the operative unit inside Eurocontrol, known as control flow management unit (CFMU), assigns to each aircraft a time slot, CTOT, in which the take-off is authorized. If the time slot is missed, the aircraft waits to receive a new one. CTOT is identified by a time window of 15 min, i.e., −10 min before take-off time and +5 min after the latter.

Estimated take off time (ETOT) Every flight company establishes, for each own aircraft, a take off time. The corresponding aircraft cannot start before that time.

Priority For each aircraft, a boolean value, i.e., 1 or 0, which indicates the priority to take-off, is assigned. This information is provided inside the flight plan. Observe that in the case that many aircraft have the same high priority, they will be scheduled according to other constraints.

Runway occupancy separations If a departure or arrival operation blocks the use of that specific runway, some other separations between mixed operations, as runway crossings, must be established for each runway and additional system constraints should be added.

Runway capacity Each runway can contain a maximum number of aircraft in a given time window.

Runway status In a time window one or more runway can be closed for some reasons, so the original scheduling for that runway must be re-allocated on another one.

Estimated time of arrival (ETA) It is the time computed by the flight management system (FMS) for the flight arriving at the point related to the destination airport.

3 Advanced two stages algorithm

In order to find the better assignment of each runway to the departing flights, we propose a methodology which combines a two stages algorithm for the departure management of one runway with a multi-runway procedure, considering independent runways, i.e., without mutual interference between every runway.

The two stages algorithm deals with the basic scenario of an airport with one runway, one SID and mixing of departures and arrivals operations, but the model can be generalized to more complex scenarios.

Usually the main goals of a departure management system are:

  • to maximize the runway's throughput, defined as the number of aircraft that can take off in the pre-defined time window (generally 30 or 60 min) taking into account mixing operations;

  • to minimize the aircraft delays, i.e., the planning take off time, ETOT, must be not much different from take off time target take off time (TTOT);

  • to minimize the workload of the air-traffic controllers in the runway operations management;

  • to treat all the airport users (airlines, passengers, crew, etc.) with fairness.

Since it is difficult to get a mathematical formulation of workload and fairness concepts, we reduce the algorithm objectives to the maximization of throughput and minimization of aircraft delays. Notice that, by using a tool supporting the activity of planning operation, the flight controllers workload will be surely helped and reduced, and, as consequence, the travellers would enjoy the same fairness (i.e., punctuality of own travel) due to the optimization of flight departures. As constraints we consider wake separation vortex, CTOT, ETOT and priority restrictions. Following the approach proposed in (Anagnostakis and Clarke 2003), we divide the original multi-objective problem in two sub-problems with one objective and specific constraints.

The first stage of the algorithm works to maximize throughput under wake vortex separation constraints, while in the second stage we minimize aircraft delays under CTOT, ETOT and priority constraints taking into account the output of the first stage as input in the second stage. We notice that the open character of this model gives the possibility to expand it and to insert new constraints or new elaboration stages. The data flow between the two stages is given by the high level vision presented in Fig. 2.

Fig. 2
figure 2

Two stages data flow

Full size image

As we can see, the module mixing operation system, between the two stages, allows to control the right location of each arrival in the output sequence from the first stage. Specifically, the scheduling of arrivals is pre-defined and fixed, so their time slots can never be moved inside the time window.

3.1 First stage

In order to maximize the runway's throughput, we minimize the runtime of the last authorized take off. If N D and N A denote the total number (i.e., cardinality) of take-offs and landings, respectively, the total number of mixing runway operations is given by N = N D  + N A , and the objective function is formulated as:

$$\min \max t_{i}, \quad 1\leq i\leq N_{D}+N_{A},$$

where t i is the occurrence time of the last operation.

Here we define throughput as the sum of time slots (separations) necessary to ensure that all runway operations happen safely. Introducing T a,b , the time slot between two mixed successive departing operations (a and b), since the arrival time slots are fixed, the maximization of departure throughput can be achieved as follows:

$$\max throughput =\min \sum\limits_{a,b\in N_{d}} T_{a,b}.$$
(1)

The time slots T a,b are obtained from wake vortex separation matrix shown in Table 1. The output of the first stage is a m × n matrix of class sequences, ordered from maximum to minimum throughput, where m represents the number of generated sequences and n the number of slots for each sequence. The term class sequence indicates a sequence of time slots based on weight classes of all aircraft considered in the pre-defined time window.

Table 1 Start time of each slot for the target class sequence (in seconds)
Full size table

3.1.1 Mathematical model

In order to compute the class sequence that optimizes throughput, we define a mixed integer linear programming (MILP) model, based on the archetype of asymmetric travelling salesman problem (ATSP).

An instance of these problems, belonging to the NP-hard class, can be solved with known algorithms such as branch and bound, branch and cut, when we deal with few nodes, and approximate methods and heuristics which are able to find a good solution in reasonably acceptable times for graphs with a large number of nodes. In the following steps we describe the reduction of the problem instance to an ATSP:

  • we identify the weight classes of all aircraft that take-off in the chosen time window and for each class we assign an unique label, (i.e., for the first LIGHT weight class we assign L(1));

  • each label becomes a node of the ATSP graph;

  • a directed arc connects each couple of nodes, weighted with the separation time based on wake vortex separation (in general this weight can be a function depending on several parameters);

  • we add an artificial node, labeled with Start, connected to all nodes with outgoing arcs (it represents the class of the last aircraft in the previous time window);

  • we add an artificial node, labeled with Next connected to all nodes with ingoing arcs (it represents the class of the first aircraft in the next time window).

In Fig. 3 an example of graph is reported.

Fig. 3
figure 3

Example of a first stage graph

Full size image

MILP formulation We divide the set of all take-offs in several subsets representing the flights belonging to a specific weight class:

  • \(N_{d}=\left\{ 1,\ldots,n\right\},\) the set of take-offs to schedule;

  • \(N_{L}=\left\{ 1,\ldots,l\right\},\) the set of light (L) weight classes;

  • \(N_{M}=\left\{ l+1,\ldots,m\right\},\) the set of medium (M) weight classes;

  • \(N_{H}=\left\{ m+1,\ldots,h\right\},\) the set of heavy (H) weight classes;

  • \(N_{J}=\left\{ h+1,\ldots,j\right\},\) the set of super (J) weight classes;

  • \(N_{Start}=\left\{ 1,l+1,m+1,h+1\right\},\) the set of nodes with ingoing arcs from Start node;

  • \(N_{Next}=\left\{ l,m,h,j\right\},\) the set of nodes with outgoing arcs to Next node.

We notice that N d  = N L ∪ N M ∪ N H ∪ N J . The decision variables of the problem are:

$$X_{a,b}=\left\{ \begin{array}{ll} 1 & \left\{ \begin{array}{l} \hbox{if, in the sequence, aircraft }\\ a \hbox{ follows aircraft }b \end{array}\right.\\ 0 & \hbox{otherwise} \end{array} \right.$$
$$X_{Start,a}=\left\{ \begin{array}{ll} 1 & \left\{ \begin{array}{l} \hbox{if, in the sequence, aircraft} \\ a\hbox{ follows aircraft }Start \end{array}\right.\\ 0 & \hbox{otherwise} \end{array} \right.$$
$$X_{a,Next}=\left\{ \begin{array}{ll} 1 & \left\{ \begin{array}{l} \hbox{if, in the sequence, aircraft}\\ Next \hbox{ follows aircraft }a \end{array} \right. \\ 0 & \hbox{otherwise} \end{array} \right.$$

The objective function can be formulated as

$$\min \mathop{\sum\limits_{a,b\in N_{d}}}\limits_{a\neq b} T_{a,b}X_{a,b}+\sum\limits_{a\in N_{d}} T_{a,Next}X_{a,Next}.$$

The constraints are given by

$$\begin{aligned} \sum\limits_{b\in N_{d}-N_{K}} X_{a,b}+X_{a,a+1}=1,\\ \forall a\in N_{K}-N_{Next},K=L,M,H,J, \end{aligned}$$
$$\begin{aligned} \sum\limits_{a\in Nd-N_{K}}X_{a,b}+X_{b-1,b}=1,\\ \forall b\in N_{K}-N_{Start},K=L,M,H,J, \end{aligned}$$
$$\begin{aligned} \sum\limits_{a\in N_{d}-N_{Start}-N_{K}} X_{a,b}+X_{Start,b}=1,\\ \forall b\in N_{Start},K=L,M,H,J, \end{aligned}$$
$$\begin{aligned} \sum\limits_{a\in N_{d}-N_{Next}-N_{K}} X_{a,b}+X_{b,Next}=1,\\ \forall b\in N_{Next},K=L,M,H,J, \end{aligned}$$
$$\sum\limits_{a\in N_{Start}} X_{Start,a}=1,\sum\limits_{a\in N_{Next}} X_{a,Next}=1.$$

To ensure that the computed solutions get all the aircraft of N d , we use Miller–Tucker–Zemlin formulation:

$$U_{a}-U_{b}+\left( N_{D}+1\right) X_{a,b}\leq N_{D},\quad a,b=1,\ldots,N_{D}, \qquad a\neq b, \qquad U_{a}\geq 0.$$

3.2 Mixing operation system

To obtain an admissible and optimized planning of departures, we adjust every class sequence taking into account arrivals, i.e., separations between successive arrivals and departures, in the pre-defined time window. The main steps for this operation are:

  1. 1.

    to find the right position of each arrival inside the class sequence based on ETA;

  2. 2.

    to add a new time slot for each arrival as a prohibited slot for departures, with start time equal to ETA;

  3. 3.

    to compute by means of heuristic the new start time of departure time slots.

3.2.1 Heuristic method

We indicate with \(t_{d_{j}}\) the start time of the j—departure time slot, t A the time of some arrival, \(\Updelta t\) the separation slot between departure and arrival and \(slot\left( j,j+1\right)\) the separation time between two consecutive aircraft j and j + 1. The new start time is computed as follows:

  • if \(\left\vert t_{d_{j}}-t_{A}\right\vert \leq \varDelta t,\) then \(t_{d_{j}}=t_{A}+\varDelta t, t_{d_{j+1}}=t_{d_{j}}+slot\left(j,j+1\right);\)

  • if \(\left\vert t_{d_{j}}-t_{A}\right\vert >\varDelta t,\) then t d_j  = t d_j .

3.3 Second stage

The input of the second stage is the best class sequence (called TCS—target class sequence) generated from the first stage, i.e., the sequence with the maximum runway's throughput. In order to have an aircraft scheduling, i.e., to assign each aircraft to one time slot inside the TCS, we minimize the gap between each ETOT and the start time of time slots. This stage can be presented schematically as an assignment problem (see Fig. 4).

Fig. 4
figure 4

Example of the second stage graph

Full size image

For example we consider Table 1 as input, provided from the first stage and referring to all aircraft:

In Table 2 call signs represent the identifier of aircraft, pCTOT_ETOT is a function that transforms each CTOT slot into a positional range inside TCS, bounded below by ETOT and upper by CTOT + 10, and Prt is a function that, according to the priority value indicated in the flight plan, limits the allocation time interval, forcing the aircraft with high priority to occupy the first available slot compatible with own weight class, ETOT and CTOT. The graph in Fig. 5 shows the corresponding assignment problem.

Table 2 Example of mapping between flight plan and second stage's functions
Full size table
Fig. 5
figure 5

Example of specific graph for the assignment problem

Full size image

3.3.1 Mathematical model

We indicate as TCS the set given by \(S=\left\{ s_{1},s_{2},\ldots,s_{n}\right\},\) where each s i ,  i = 1,…, n, represents one time slot \(s_{i}\in \{L,M,H,J\},\) i.e., each \(s_{i}\in S\) can be light (L), medium (M), heavy (H), super (J). The problem is formulated as follows.

We introduce the following notations:

  • \(F=\left\{ f_{1},f_{2},\ldots,f_{n}\right\}\) the set of aircraft with Identifier Code f i , i = 1,…, n, to assign to each slot;

  • \(SC_{j}=\left\{ f_{i}\in F | s_{j} is \ compatible \ with f_{i}\right\},\ \forall s_{j}\in S\) the set of each aircraft f i compatible with time slot s j ;

  • \(FC_{i}=\left\{ s_{j}\in S | f_{i} is \ compatible \ with s_{j}\right\},\ \forall f_{i}\in F\) the set of each time slot s j compatible with aircraft f i ;

  • \(ETOT\left( f_{i}\right)\) the estimated take-off time of a generic aircraft f i ;

  • \(TOff\left( s_{j}\right)\) the start time of a generic slot s j .

    Let us define the decision variables

    $$X_{f_{i},s_{j}}=\left\{ \begin{array}{ll} 1 & \left\{ \begin{array}{l} \hbox{if aircraft }f_{i}\hbox{ can be }\\ \hbox{assigned to the slot }s_{j} \end{array} \right.\\ 0 & \hbox{otherwise} \end{array} \right.;$$

    and two functions:

  • \(\max CTOT\left( f_{i}\right),\) ∀ f i  ∈ F which returns the value CTOT + 10 (in min) referred to the aircraft with identifier code f i ;

  • Prt(f i ),  ∀ f i  ∈ F which provides the allocation limit according to the specific priority value.

The objective function can be stated as

$$\min\sum_{f_{i}\in F, s_{j}\in S}\left\vert TOff(s_{j})-ETOT(f_{i})\right\vert X_{f_{i},s_{j}}$$

with constraints

$$\underset{s_{j}\in FC_{i}}{\sum}X_{f_{i},s_{j}}=1, \quad \forall f_{i}\in F,$$
$$\underset{f_{i}\in SC_{j}}{\sum} X_{f_{i},s_{j}}=1,\quad\forall s_{j}\in S,$$
$$\begin{aligned} \underset{s_{j}\in FC_{i}}{ETOT(f_{i})\leq \sum}s_{j}X_{f_{i},s_{j}}\leq \max CTOT(f_{i}),\\ \forall f_{i}\in F, \end{aligned}$$
$$\sum_{s_{j}\in FC_{i}}s_{j}X_{f_{i},s_{j}}=\Pr t\left(f_{i}\right),\quad\forall f_{i}\in F,$$

The last constraint indicates that the allocation time interval of each aircraft can be limited.

4 The multi-runway procedure

Since in most cases, airports have more runways, the problem is to find the better assignment of each departure to each runway in order to maximize the performance of the airport, i.e., to minimize the total delay, defined as the sum of each aircraft delay, in compliance with safety and security rules. Between the general allocation criteria in this context we use only:

  • runway status: ONLY ARRIVAL, ONLY DEPARTURE, BOTH, CLOSED;

  • aircraft weight class associated to the category of each runway;

  • capacity of each runway, i.e., the maximum number of operations that the runway can contain.

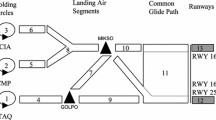
Other criteria are the wind direction, destination airport, the first fix point en route, taxi-out time, some specific airport characteristics. In Fig. 6 on the left a macroscopic vision of the multi-runway approach is shown.

Fig. 6
figure 6

Left multi-runway block schema. Right sub-module of the multi-runway procedure

Full size image

The multi-runway macroblock receives as input the departures and arrivals flight plan and the configuration parameters of each runway, i.e., status in the temporal horizon, capacity and category. The macroblock consists of three internal sub-modules (Fig. 6, right), i.e., the configuration procedure, sequencing procedure and capacity control. The second module recalls the two stage algorithm in order to control and establish if each runway current scheduling allows to get the minimum possible total departing delay, while the last module checks if the capacity of each runway is respected.

Remark In this discussion we consider independent runways, i.e., without mutual interference.

4.1 Configuration procedure

Starting from the information about the properties and characteristics of each runway, this procedure consists of several steps to locate preliminarily aircraft on the available runways:

  • Step 1: sorting of the runway considering the following order: Only Departure (or Both), Only Arrival, Closed.

  • Step 2: separations of aircraft in some configurable time windows (in minutes).

  • Step 3: alternate positioning of the separation aircraft class (found to the previous step) on each runway only departure or both.

  • Step 4: For each time window, verify if aircraft are compatible with the runway category; if not, move that specific aircraft on the compatible runway.

  • Step 5: put the arrivals inside each time window (if they exist) for the runways Both.

  • Step 6: call the sequencing procedure module.

4.2 Sequencing procedure

This module allows to reduce the total delay, using the two stage algorithm applied for each runway and successively adopting a heuristic process of swapping between the runways. First, the two stage algorithm computes the delays on each runway and a queue, formed by delayed aircraft, is created. Then, for each queue, if the compatibility between the runway category and the aircraft weight class is strictly verified, this aircraft is removed from the queue, while the more delayed one is moved on another compatible runway and using again the two stage algorithm, the new delays are computed. If the total delay, given by the sum of the delays of each runway, decreases, then the swapping is confirmed, otherwise the aircraft goes back to the original position and it is removed from the queue. This process is iteratively repeated until each queue will be empty, so that the current planning is finally accepted.

4.3 Capacity control

In order to ensure that each runway capacity is respected, starting from the final solution of sequencing procedure, an Integer linear programming problem is solved.

4.3.1 Mathematical model

We indicate with \(F=\left\{ 1,\ldots,n\right\}\) the set of the aircraft to assign, and \(R=\left\{ 1,\ldots,m\right\}\) the set of the available runways.

Let us define

  • \(E=\left\{ E_{1},E_{2},\ldots,E_{n}\right\}\) where \(E_{i}\subseteq F\) has ETOTs inside a pre-fixed time window;

  • \(U_{E}=\left\{ E_{1},\ldots,E_{t}\right\}\) such that \(E_{j}\subseteq F\) and \(\left\vert ETOT_{E_{t}}-ETOT_{E_{1}}\right\vert \leq 60\min;\)

  • \(U=\left\{ U_{E_{1}},\ldots,U_{E_{t}}\right\};\)

  • \(C_{j}=\left\{ c_{1},\ldots,c_{x}\right\}\) the capacity vector for each runway j and x time windows;

  • \(PC_{U}=\left\{ C_{1},\ldots,C_{n}\right\}.\)

The decision variable is

$$X_{i,j}=\left\{ \begin{array}{ll} 1 & \left\{ \begin{array}{l} \hbox{if aircraft }i\hbox{ can be }\\ \hbox{assigned to the runway }j \end{array} \right.\\ 0 & \hbox{otherwise} \end{array} \right.$$

Introduce a probability function \(f_{i,j}\left( \bar{D}\right)\) which gives the probability to assign each aircraft i to the runway j, where \(\bar{D}\) is the vector of assignment criteria. For example for an airport with two runway Both, the probability function is expressed as

$$f_{i,j}\left(\bar{D}\right) = \left\{ \begin{array}{ll} 1 & \left\{ \begin{array}{l} \hbox{if aircraft }i\hbox{ is assigned }\\ \hbox{to the runway }j \end{array} \right.\\ 0 & \left\{ \begin{array}{l} \hbox{if aircraft }i\hbox{ is not assigned }\\ \hbox{to the runway }j \end{array} \right.\\ 0.5 & \left\{ \begin{array}{l} \hbox{if aircraft }i\hbox{ can be assigned }\\ \hbox{to each runway }j \end{array} \right. \end{array} \right.$$

For all U E_s belonging to U the problem to compute the better aircraft planning subject to the capacity of the available runways can be formulated as

$$\max \sum_{i=1}^{n}\sum_{j=1}^{m}f_{i,j}\left( \bar{D}\right) X_{i,j},$$

with constraints

$$\underset{j=1}{\sum^{m}}X_{i,j}=1,\quad\forall i\in F,$$
$$\underset{i=1}{\sum^{n}}X_{i,j}\leq c_{j},\quad\forall j\in U_{E_{s}},\forall c_{j}\in PC_{U},$$
$$X_{i,j}\in \left\{ 0,1\right\}.$$

5 Simulations and results

The multi-runway procedure and the two stage algorithm were implemented and tested, empirically, on some real Milano Malpensa departure flight strip's sets. The airport is identified by two independent runways, 35L (left) and 35R (right) and we consider a time window in which these runways are in BOTH way. We remind that a departure and arrival flights strip, in general, is a record with some fields which identify exactly each take-off and landing. In order to solve the Integer linear programming problems associated to the algorithms, we used an Open Source Java Library named LPSolve, which allows to solve medium-low instance of this kind of problems.

We referred to a record, from 10:00 am to 11:00 am, characterized by thirteen departures and fourth arrivals (see Tables 4 and 5).

Table 3 A first example of departures flight strip
Full size table
Table 4 A first example of arrivals flight strip
Full size table
Table 5 Simulation result referred to input of Tables 4 and 5
Full size table

As we can see from Table 5, since the departures strip contains some aircraft without assigned CTOT, we have a certain free degree to locate them in the final sequence.

Considering the wake vortex separations matrix in Fig. 1, the computation of TTOT and the better departures planning obtained from the multi-runway procedure are shown in Table 5.

In the same previous conditions, we consider now departures and arrivals flight strip in Tables 6 and 7.

Table 6 A second example of departures flight strip
Full size table
Table 7 A second example of arrivals flight strip
Full size table

The corresponding planning result is shown in Table 8.

Table 8 Simulation result referred to input of Tables 6 and 7
Full size table

6 Conclusions

In this paper we implemented a new methodology to support the air controllers work in the planning operations of aircraft departures. In particular, we mixed a two stages algorithm with some heuristics to perform the best scheduling of departures in the multi-runways context, taking into account the arrivals on some shared runway. We used as test case the flight strips provided by Milano Malpensa airport using two independent runways. The obtained simulations results have been discussed and approved by the staff of the same airport. Moreover the validity of the proposed approach has been confirmed by a comparison of the results with some historical data.