First-principles calculations of structural, electronic, elastic, and thermal properties of phase M₂CdC (M = Sc, V, and Nb)

Abstract

Using the first-principle methods based on the density functional theory, in order to study structural, elastic, and electronic properties of MAX phases ${\mathrm{M}}_{2}\mathrm{CdC}$ with M = (Sc, V, and Nb). The calculated formation energies revealed that these compounds are thermodynamically stable in the hexagonal MAX phase. The stability is affirmed by the elastic constants and the conditions of the mechanical stability criterion. The calculated electron band structures and the density of states imply that the chemical bond in three compounds are a combination of covalent, ionic, and metallic nature. The main factors governing the electronic properties are the hybrid states M-d, Cd-p, and C-p, and the bond (p-d) stabilizes the structure. Fermi's surface characteristics have been studied for the first time. Based on the total energy, we conclude that as continue to increase Sc-V, Nb, the compressibility modulus decreases. At the same time, it gives a stabilization of the hexagonal structure and increases the metal support.

1 Introduction

MAX phases are the extension of Hägg phases were first studied in the 1960s. The research group led by Hans Nowotny et al. [1,2,3], their attention was focused on Hägg phases, Ti₃SiC₂, and Ti₃GeC₂ [2]. These new phases did not arouse any real enthusiasm from the scientific community of the time. It was thus necessary to wait until the 90 s for these compounds to experience a resurgence of interest with the publication of the work of Barsoum and El-Raghy [4] on the synthesis and properties of Ti₃SiC₂. These researchers have in fact noticed that the properties of these materials are a combination of those of metals and ceramics. After the discovery of Ti₄AlN₃ [5, 6], it became evident that these different phases, which shared the same basic crystallographic structure, derived similar properties from it. This family of layered ternary carbides and nitrides is represented chemically by a formula M_{n + 1}AX_n, where M is a transition metal, A is a group IIIA or IVA element, and the X atoms (C and/or N) filling the octahedral sites between the M and n layers varied from 1 to 3 [2, 3, 7]. We can see that the increase of ‘n’ plays on the number of inequivalent sites for each element. For n = 2 implies two inequivalent sites for M, and In the case where n = 3, there are two inequivalent sites for M and X [8]. The layers M and X indeed form M₂X slabs, with the stacking of the cubic face type centered [9], and the environment of the octahedral type carbon or nitrogen atoms and that of the trigonal type A element gives them a bi-dimensional layered structure [10]. The MAX phases are all interstitial compounds, where the interstitial site between the M atoms is filled with A and X atoms. The crystal lattice crystallizes in a hexagonal structure with a variable c/a ratio. Based on the value of n, this class of materials can be classified as M₂AX or 211 compounds for (n = 1) with anisotropy (c/a = 4–5), M₃AX₂ or 321 Max, (c/a = 6) for n = 2 and the compounds M₄AX₃ or 413 MAX (c/a = 8) for n = 3 respectively [11, 12]. On the other hand, there are other Max phases with the stoichiometry of X₅AX₄, X₆AX₅, and X₇AX₆ which have also been reported in the literature, especially the number of max phases and their solid solutions increase rapidly [12]. The interest in MAX phases stems from their atypical properties, which are generally described as the combination of the best properties of ceramic and metallic materials. Thus, in general, MAX phases are refractory materials with very good chemical stability, good resistance to oxidation and corrosion, high thermal and electrical conductivities, good wear resistance, and, remarkably, for ceramic material, very good machinability [13,14,15,16,17,18,19,20,21,22,23,24,25]. These remarkable properties come from the layered structure of the Max phases and the mixed metallic covalent nature of the M-X bonds, which are exceptionally strong, combined with the relatively weak M-A bonds [2, 26]. The properties of the MAX phases open up multiple applications for these materials, especially under extreme conditions: structural materials for high-temperature applications, machinable ceramics, furnace accessories, and protective materials (corrosion and wear) [26,27,28,29,30,31]. In addition, there are reports in the literature of a very interesting resistance to irradiation making MAX phases the materials of choice for nuclear applications [32,33,34]. Because of these important properties, max phases are studied experimentally and theoretically. Many researchers have been interested in studying these properties, and other properties of materials of the same family. According to research, there is no theoretical or experimental study on Sc₂CdC, V₂CdC, and Nb₂CdC Max phases. The objective of this new study is to study the structural, electronic, elastic, and mechanical properties of the Max phases. Using the first principle calculations of density functional theory calculations [35, 36] in the exchange and correlation potential of the LDA local spin density approximation [37]. This article is organized as follows: the method of calculation and the details of the calculations are described in Sect. 2, and the results are discussed in Sect. 3, and we end this work with a conclusion.

2 Calculation method

Using the WIEN2k package [38,39,40,41], we studied the structural, electronic, mechanical, and thermodynamic properties of the M2CdC MAX phase based on the density functional theory and achieved by the full-potential linearized augmented plane wave (FP-LAPW) method. LDA was used for the exchange–correlation potential [37]. The muffin-tin radii R_MT of $1.8, 1.85, 1.9, 2.4$, and 1.53 for the $\mathrm{Sc},\mathrm{ V},\mathrm{ Nb},\mathrm{ Cd}$, and $\mathrm{C}$ atoms, respectively, in such a way that the muffin–tin spheres do not overlap. The cutoff energy of − 6 Ry defined the separation between the valence and core states. Inside the muffin-tin spheres, lattice harmonics of up to ${l}_{\mathrm{max}} = 10$ were selected for the basis set. In the interstitial region, the plane wave cut-off value used was ${R}_{\mathrm{mt}}*{K}_{\mathrm{MAX}}$ =7 (where ${R}_{\mathrm{mt}}$ represents the smallest radius of muffin-tin and ${K}_{\mathrm{MAX}}$ is the cut-off of plane waves). The electronic configurations used for the ${\mathrm{M}}_{2}\mathrm{CdC}$, with (M = Sc,V, and Nb) compounds are: $\left[\mathrm{Ar}\right]4{s}^{2}4{d}^{1}$ for $\mathrm{Sc}$, $\left[\mathrm{Ar}\right]4{s}^{2}3{d}^{3}$ for $\mathrm{V}$, $\left[\mathrm{kr}\right]4{d}^{4}5{s}^{1}$ for $\mathrm{Nb}$, $\left[\mathrm{Kr}\right]4{d}^{10}5{s}^{2}$ for $\mathrm{Cd}$, and $\left[\mathrm{He}\right]2{s}^{2}2{\mathrm{P}}^{3}$ for $\mathrm{C}$. The Monkhorst–Pack special k-point scheme with 1500 special k-points in the first Brillouin zone has been used for the three compounds [42, 43]. The self-consistent convergence of the total energy was set at 0.1 mRy.

3 Results and discussion

3.1 Structural properties

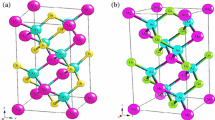
The ${\mathrm{M}}_{2}\mathrm{CdC}$ compounds ($\mathrm{M }=\mathrm{ Sc},\mathrm{ V}$, and$\mathrm{Nb}$) like most of the MAX phases are of M₂AX stoichiometry crystallize in the ${\mathrm{Cr}}_{2}\mathrm{AlC}$ crystal structure, with the space group$\mathrm{P}63 /\mathrm{ mmc }(\# 194$). Its unit cell contains two unit formulas and 8 atoms, which is a special case for the so-called 211 phases [44,45,46]. The $\mathrm{C}$ atoms are positioned at positions 2a $(\mathrm{0,0},0),$ the $\mathrm{Cd}$ atom in 2d$(\frac{1}{3},\frac{2}{3}, \frac{3}{4})$, and the ($\mathrm{M }=\mathrm{ Sc},\mathrm{ V}$, and$\mathrm{Nb}$) atoms in 4f $(\frac{1}{3},\frac{2}{3} , {Z}_{\mathrm{M}})$ [46, 47]. This structure is thus defined by two lattice parameters, a and c, and the internal structural parameter, ${Z}_{\mathrm{M}}$. For the atoms in 4f positions, the ideal value of the internal dimensionless parameter ${Z}_{\mathrm{M}}$ is $\frac{1}{12}$ for metal atom M [10]. Figure 1 presents the unit cell of${\mathrm{M}}_{2}\mathrm{CdC}$, ($\mathrm{M }=\mathrm{ Sc},\mathrm{ V}$, and$\mathrm{Nb}$) as a structural model for the crystalline structure of ${\mathrm{M}}_{2}\mathrm{AX}$ Max phases. To obtain the structural, electronic, and elastic properties, we first calculate the properties of the ground state at equilibrium, such as the total energies, the lattice constants (a and c), the free internal parameter${Z}_{\mathrm{M}}$, the volume modulus $({B}_{0}),$ and their derived pressure $({B}^{\mathrm{^{\prime}}}).$ we calculated these parameters at P = 0 GPa, by fitting the Murnaghan equation [48], which describes the total energy as a function of volume. The structural stability was obtained by minimizing the energy versus volume for each structure is plotted in Fig. 2. Our results are reported in Table 1. First, we first minimized the free internal parameters ${Z}_{\mathrm{M}}$. By taking random parameters to start our calculations because there is no indication about them. We, therefore, performed detailed structural optimizations while minimizing all energies. According to the results mentioned in Table 1 and Fig. 2 it can be said that the Nb₂CdC compound is more stable and harder than the other Sc₂CdC and Ti₂CdC compounds, due to the lower value of the equilibrium energy and the greater value of bulk modulus B (see Table 2). The bulk modulus B of a material is the measure of the compressive strength. It is defined as the ratio of the infinitesimal increase in pressure to the resulting relative decrease in volume. The ratio (c/a), and the inter free parameter are in good agreement with the ideal values (${Z}_{\mathrm{M}}$ = 1/12 = 0.0833) and the theoretical compactness ratio (c/a = 4.89) [10]. Like other ab-initio calculations for different ${\mathrm{M}}_{2}\mathrm{AX}$ compounds, Zhimei et al. [49] in their work on ${\mathrm{M}}_{2}\mathrm{AlC }(\mathrm{M}=\mathrm{Ti},\mathrm{ V},$ and $\mathrm{Cr}$), and other results of the same family for the work of Ghebouli et al. [45] for M₂SiC (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W), and the work of Denis Music, Sun et al. [50], on M₂SPb with (M = Ti, Zr, and Hf), which approved the good trend of our structural results for our three compounds. We observe that when we continue to increase$\mathrm{M}=\mathrm{ Sc}-\mathrm{ V }-\mathrm{ Nb}$, the compressibility modulus of ${\mathrm{M}}_{2}\mathrm{CdC}$ increases. (Or the compressibility modulus of ${\mathrm{M}}_{2}\mathrm{CdC}$ phases increase as the concentration of valence electrons increases (see Table 2). Based on the comparison between the compressibility modulus of the ${\mathrm{M}}_{2}\mathrm{AlC}$ phase (M = Ti, Zr, Hf …) and the compressibility modulus of the corresponding binary carbide$\mathrm{MC}$. Sun et al. [51] have shown that ${\mathrm{M}}_{2}\mathrm{AC}$ MAX phases can be divided into two groups. One group with transition metals V-B and VI-B where the mass modulus of ${\mathrm{M}}_{2}\mathrm{AC}$ is approximately the same as $\mathrm{MC}$ and the second group with transition metals IV-B where the compressibility modulus ${\mathrm{M}}_{2}\mathrm{AC}$ is significantly lower than$\mathrm{MC}$. Our calculations show that the three MAX phases studied in this report belong to the second group with their compressibility modulus significantly lower than their binary carbides [51,52,53].

Fig. 1

The crystal structure of ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }=\mathrm{ Sc},\mathrm{ V},\mathrm{ and Nb}$ (space group $P 63=mmc$)

Fig. 2

Total energy versus volume of M₂CdC (M = Sc, V, and Nb)

Table 1 The equilibrium lattice parameters (a, c and c/a), internal parameter Z(M), bulk modulus B₀ (Gpa) and its pressure derivative (B′) for ${\mathrm{M}}_{2}\mathrm{CdC}$ with M = Sc, V, and Nb

Table 2 The calculated values of the energy of formation (E_Form), bulk moduli (B), cohesive energies (Ec_oh) and the valence electron concentration (val-el) for M₂CdC, with M = Sc, V, and Nb

3.2 The formation energies and cohesive energies

To verify, and study the relative stability of the hexagonal phases, it is necessary to determine the energy of formation. The energy of formation of a given structure is defined as the difference between the total energy of the constituent atoms at an infinite separation and the total energy of that particular phase using Eq. (1) [54,55,56,57,58,59]:

$$ E_{{{\text{For}}}}^{{{\text{M}}_{2} {\text{CdC}}}} = \frac{{E_{{{\text{total}}}}^{{{\text{M}}_{2} {\text{CdC}}}} - \left[ {xE_{{{\text{bulk}}}}^{{\text{M}}} + yE_{{{\text{bulk}}}}^{{{\text{Cd}}}} + zE_{{{\text{bulk}}}}^{{\text{C}}} } \right]}}{x + y + z} $$

(1)

With x, y, and z are the numbers of M (Sc, V, Nb) Cd, and C atoms, respectively. ${E}_{\mathrm{total}}^{{\mathrm{M}}_{2}\mathrm{CdC}}$ is the total energy of the unit cell, ${E}_{\mathrm{bulk}}^{\mathrm{M}},{E}_{\mathrm{bulk}}^{\mathrm{Cd}},\mathrm{ and }{E}_{\mathrm{bulk}}^{\mathrm{C}}$ are the energies per M (Sc, V, Nb) Cd, and C atoms in the bulk states. where Sc, V, and Nb crystallize in centered cubic (space group $\mathrm{Im}\overline{3}\mathrm{m}$, prototype W) [60], and $\mathrm{Cd}$ crystallizes in the hexagonal structure (P63/mmc, prototype Mg) [60], and Carbon crystallizes in the diamond structure (space group $\mathrm{Fd}\overline{3}\mathrm{m }$), [61]. The formation energy values obtained from the three compounds ${\mathrm{Sc}}_{2}\mathrm{CdC}$, ${\mathrm{V}}_{2}\mathrm{CdC}$, and ${\mathrm{Nb}}_{2}\mathrm{CdC}$ calculated from Eq. (1), are also shown in Table 2. All values are negative, we can experimentally predict the formation of these three compounds. To confirm the structural stability, we calculated the cohesive energy which is presented in Table 2. This cohesive energy is defined as the second stability criterion. The cohesion energy is defined as the energy of the constituent atoms minus the total energy of the compound by applying Eq. (2) [62].

$$ E_{{{\text{coh}}}}^{{{\text{M}}_{2} {\text{CdC}}}} = \frac{{\left[ {xE_{{{\text{iso}}}}^{{\text{M}}} + yE_{{{\text{iso}}}}^{{{\text{Cd}}}} + zE_{{{\text{iso}}}}^{{\text{C}}} } \right] - E_{{{\text{total}}}}^{{{\text{M}}_{2} {\text{CdC}}}} }}{x + y + z} $$

(2)

where ${E}_{\mathrm{total}}^{{\mathrm{M}}_{2}\mathrm{CdC}}$ is the total equilibrium energy of the compounds ${\mathrm{M}}_{2}\mathrm{CdC }(\mathrm{M }=\mathrm{ Sc},\mathrm{ V},\mathrm{ Nb})$, and ${E}_{\mathrm{isolid}}^{\mathrm{M}},{E}_{\mathrm{isolid}}^{\mathrm{Cd}},\mathrm{and }{E}_{\mathrm{isolid}}^{\mathrm{C}}$ are the isolated atomic energies of the pure constituents. According to the cohesion energy values, which are presented in Table 2, the compound ${\mathrm{Nb}}_{2}\mathrm{CdC}$ is the most stable among the three compounds due to the lowest cohesion energy. This result is similar to the optimization part.

3.3 The electronic properties

The calculated electronic band structures of ${\mathrm{M}}_{2}\mathrm{CdC }(\mathrm{M }=\mathrm{ Sc},\mathrm{ V},$ and $\mathrm{Nb}$) at the optimal values are presented in Fig. 3. We observe the overlap between the valence bands and the conduction bands at the Fermi level, and the absence of a bandgap which clearly indicates the metallic character of these compounds. The states of lower energies below the Fermi level come from the C–2s states. The states at the Fermi level are the Sc–3d, states. The upper part of valence is formed mainly of $\mathrm{M }- 3d,\mathrm{ C }- 2p$ states, and the states of $\mathrm{Cd}$ $(s, p,d)$. This data confirms the metallicity of these three compounds. The electrical conductivity is anisotropic for these materials, ie the electrical conductivity along the c-axis is much lower than that of the basal planes [28, 52, 62].

Fig. 3

Band structure of (a) Sc₂CdC, (b) V₂CdC and (c) Nb₂CdC

3.3.1 The density of states

The total (TDOS) and partial (PDOS) density of states are calculated using the full potential augmented plane wave (FP-LAPW) method for M₂CdC (M = Sc, V, and Nb) are given in Fig. 4a–c, respectively. The details of the peak structures and the relative heights of the peaks in their DOS are quite similar, meaning similarities in chemical bonding. Analysis of Fig. 4a–c shows that there is no band gap for the three compounds and that the DOS has a large finite value at the Fermi level. This confirms that these materials have a metallic character. Another characteristic is the existence of a pseudo gap in the DOS near the Fermi level, which is an indication of stability [63, 64]. At the Fermi EF level, the DOS for Sc₂CdC, V₂CdC, and Nb₂CdC were 68.1, 40.8, and 34.2 states per unit cell per eV, respectively. It can be said that Sc₂CdC is more conductive than V₂CdC and Nb₂CdC. To see the characteristics of the atomic bond we have calculated the density of partial states ($\mathrm{PDOS}$) which are presented in Fig. 4a–c. The $(\mathrm{Sc}-d)$ electrons mainly participate in electronic conduction properties making by far the largest participation in $\mathrm{TDOS}$ at ${E}_{\mathrm{F}}$, and should be involved in conduction properties although (d) electrons are generally considered to be low-efficiency conductors. However, the electrons of carbon and Cadmium do not participate significantly at the Fermi level, due to the presence of the $(d)$ states of the $\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})-d$ atom. The covalent interaction results between the building blocks because the states degrade with respect to the position of the lattice parameter. The $\mathrm{C }-p$ and $\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})-d$ states are hybridized as well as $\mathrm{Cd}-p$, and $\mathrm{Sc}-3d$. In addition, due to the difference in electronegativity between the elements involved, certain ionic properties can be expected. The PDOS (Fig. 4b–d) presents another characteristic, the hybridization peak $\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})-d$, and $\mathrm{C}-p$ is lower in energy than that of $\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb}-3d)$, and $\mathrm{Cd }- p$. This suggests that $\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})-d,\mathrm{ C}-p$ bonds are more rigid than $\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})-d,\mathrm{ Cd }- p$ bonds. These results are in agreement with reports on MAX phases [47, 65].

Fig. 4

Total density and partial density of states for (a) Sc₂CdC, (b) V₂CdC and (c) Nb₂CdC. The Fermi level is set to zero energy and marked by a vertical dashed line

3.3.2 The charge density and Fermi surface

Figure 5a–c shows the contour of charge densities, max phases${\mathrm{Sc}}_{2}\mathrm{CdC}$,${\mathrm{ V}}_{2}\mathrm{CdC}$, and ${\mathrm{Nb}}_{2}\mathrm{CdC}$ respectively located in the basal plane$(11\overline{2}0$). The MAX phases are usually stacks of ‘hard’ M–X bonds and ‘soft’ M–A bonds along with c directions [28, 51]. The charge density distribution provides detailed information on the interaction between the different atoms, and therefore on the nature of the bonds, namely covalent, ionic, or metallic character. The covalent bonds in the phases max ${\mathrm{Sc}}_{2}\mathrm{CdC}$ can be determined from the difference in electronegativity between the elements in play. The ($p-d$) interactions between the atoms of $\mathrm{Sc}$ (electronegativity of $\mathrm{Sc }= 1.36)$ [66] and $\mathrm{C}$ (electronegativity of $\mathrm{C }= 2.55)$ [66] are covalent in nature and are quite strong. Therefore, the strong covalent nature of the $\mathrm{Sc }-\mathrm{ C}$ bond comes from the strong accumulation of charges between them of the Sc and C atoms. While the carbon atom is more electronegativity (electronegativity of $\mathrm{C }= 2.55)$ [66] than $\mathrm{Sc}$(electronegativity of$\mathrm{Sc}= 1.536$) [66], and therefore the $\mathrm{C }-\mathrm{ SC}$ bonds are ionic in nature. The ionic component results from a charge transfer of scandium to other atoms (carbon (electronegativity of$\mathrm{C }= 2.55$) [66]. The charge density is drawn from the Scandium atoms toward the two atoms of carbon and cadmium, this action is because of the difference in electronegativity, the carbon and cadmium atoms are more electronegative than Scandium. High melting points and large compressibility modulus are expected from the strong covalent and ionic bond, while good electrical conductivity and plasticity are expected from the existence of the metallic bond between manganese and silicon in the structure. So the chemical bond of these compounds is metallic covalent -ionic in nature. From Table 3, the M (Sc, V, and Nb)–C bond strength is much stronger than M (Sc, V, and Nb)–Cd. Thus, the covalent bond is due to the local Sc–d and C–p hybridization interactions, and the ionic bond is bonded to local Sc–d and Cd–p hybridization interactions. The same trend is confirmed by the results of works on certain MAX phases [44, 50]. To see and understand the information regarding the chemical bonding properties, we studied the Mulliken population [22, 67] of M₂Cd C (M = Sc, V, and Nb) as an important criterion. Mulliken bond populations explain the degree of overlap of electron clouds of two bond atoms in a solid, which are obtained from analyzes of Mulliken atomic population (MAP), effective valence charge (EVC), and the bond overlap population (BOP) [22, 68]. Therefore, at its highest and lowest values, the chemical bond achieves respectively strong covalence and strong iconicity of the chemical bond. The charge, bond, and Mulliken bond population of M₂CdC are shown in Table 3. The valence states for the Sc, V, and Nb transition metal atoms are$4{s}^{2}4{d}^{1}$,$4{s}^{2}3{d}^{3}$, and $4{d}^{4} 5{s}^{1}$, respectively. It is seen that the effective valence largely depends on the electrons of the (d) orbital of the transition metals. Its non-zero positive value is an indication of a mixed covalent and ionic nature in chemical bonds, and high values signify a high level of covalence in chemical bonds. The high values of the population band show the strong covalent bond while the low values represent the iconicity of the chemical bond. For example, C–Sc, C–V, and C–Nb bonds possess a stronger covalent bond than Cd–Sc, Cd–V, and Cd–Nb bonds in M₂CdC (M = Sc, V, and Nb). In the case of Nb₂CdC, the Nb–C bond is comparatively stronger than the Sc–Cd, Cd–V, and Cd–Nb bonds in the M₂CdC compounds (M = Sc, V, and Nb). Figure 6a–c shows the Fermi surfaces (FS) of MAX phase ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }= (\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb}),$, respectively. The three Fermi surfaces are almost quite similar. the center of the Fermi surface consists of a closed central leaf of cylindrical shape with additional leaves appearing at the corners of the Brillouin zone. We can therefore say that the Fermi surface of the MAX phase ${\mathrm{M}}_{2}\mathrm{CdC}$ is mainly composed of low dispersion bands of $[{\mathrm{Sc}}_{2}\mathrm{C}]$ blocks, responsible for conduction in the MAX phase${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }= (\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})$. This can be seen as an additional indirect component of the potential superconductivity in MAX phase ${\mathrm{M}}_{2}\mathrm{CdC },\mathrm{ M }= (\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})$ as shown in the back of Fig. 4.

Fig. 5

Charge-density contours for: (a) ${\text{Sc}}_{2} {\text{CdC}},$ (b) ${\text{V}}_{2} {\text{CdC}},$ (c) ${\text{Nb}}_{2} {\text{CdC}}$. Cuts are made in the ($11\overline{2}0$) plane

Table 3 Mulliken atomic and bond overlap population of the ${\mathrm{M}}_{2}\mathrm{CdC}$ with M = Sc, V, and Nb compounds

Fig. 6

Fermi surfaces (FS) for a ${\text{Sc}}_{2} {\text{CdC}}$, b ${\text{V}}_{2} {\text{CdC}}$, c ${\text{Nb}}_{2} {\text{CdC}}$

3.4 Elastic properties and mechanical stability

The elastic constants $({C}_{ij})$ are very important parameters and they serve as a basis for the evaluation of the mechanical performances of materials. In addition, these constants can be used to define the mechanical stability of the deformation of the crystal face. Compounds of the hexagonal structure have six different symmetry elements (${C}_{11}, {C}_{12}, {C}_{13}, {C}_{33}, {C}_{44}$ and ${\mathrm{C}}_{66}$), and only five of them are independent since ${C}_{66} = 1/2({C}_{11}-{\mathrm{C}}_{12})$. To obtain the elastic constants of these compounds, we used the numerical calculation of the first principle using the method developed by Reshak and Jamal [69] and integrated it into the WIEN2k code. For a stable hexagonal crystal, the five elastic constants must meet the well-known Born stability criteria [70, 71].

$$ C_{11} > 0,\;\left( {C_{11} - C_{12} } \right) > 0,\;C_{44} > 0\;{\text{and}}\;\left( {C_{11} + C_{12} } \right)C_{33} > 2C_{13}^{2} $$

(3)

From Table 4, we can see that our calculated elastic constants of the ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }= (\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb}$) compounds are all positive and meet the mechanical stability criterion [57, 58, 70, 71]. From our calculations, we observe that the value of the constant ${C}_{11}$ is greater than the other values of the elasticity constants for all the compounds. Thus, we can say that the resistance to change in length is greatest in compounds, with ${C}_{12}$ and ${C}_{13}$ measuring the response to a strain along a perpendicular axis, and the modulus ${C}_{44}$ is a stiffness constant that was found to be a better predictor of hardness than the other constants, and it reflects the shear strength in the $\{100\}$ plane and also demonstrates the elasticity of the shape [72, 73]. Latter shows that the compound ${\mathrm{Nb}}_{2}\mathrm{CdC}$ is harder than ${\mathrm{Sc}}_{2}\mathrm{CdC}$ and ${\mathrm{V}}_{2}\mathrm{CdC}$, due to its higher ${\mathrm{C}}_{44}$ modulus value. This result is similar to the one found in the optimization part. The elasticity constants ${C}_{11}$ and ${C}_{33}$ are greater than the elasticity constant ${C}_{44}$, this indicates that the compounds ${\mathrm{Sc}}_{2}\mathrm{CdC}$, ${\mathrm{V}}_{2}\mathrm{CdC}$, and ${\mathrm{Nb}}_{2}\mathrm{CdC}$ have very low shear strength. The $B/{C}_{44}$ values of the compounds ${\mathrm{Sc}}_{2}\mathrm{CcdC}$, ${\mathrm{V}}_{2}\mathrm{CdC}$, and ${\mathrm{Nb}}_{2}\mathrm{CdC}$ are respectively 5.97, 2.84, and 2.26. The compound ${\mathrm{Sc}}_{2}\mathrm{CdC}$ is said to be more ductile than ${\mathrm{V}}_{2}\mathrm{CcdC}$ and ${\mathrm{Nb}}_{2}\mathrm{CdC}$, i.e., ductile crystals are characterized by large values of $B/{C}_{44}$, while brittle solids are characterized by low values of $\mathrm{B }/ {\mathrm{C}}_{44}$ [46, 50]. The ductility of Sc₂CdC can be explained by its unusual structural properties, ${\mathrm{Sc}}_{2}\mathrm{CdC}$ has a small ${Z}_{\mathrm{M}}$ value, which implies a large distance between the layers for the slip planes in this material. We have used its constants ${C}_{ij}$ to determine other mechanical (elastic) quantities such as compressibility B, Young and shear moduli (Y and G), as well as Poisson’s ratio (ν) which are parameters important in technological applications and provide a fundamental description of the mechanical behavior of a material. They are obtained from Hill's approximation, this approximation is based on the approaches of Reuss and Voigt with $B=\left({B}_{\mathrm{V}}+{B}_{\mathrm{R}}\right)/2={B}_{\mathrm{H}}$ (Hill’s bulk modulus) and $G=\left({G}_{\mathrm{V}}+{G}_{\mathrm{R}}\right)/2={G}_{\mathrm{H}}$ (Hill’s shear) [70, 74]. The Young’s modulus E and the Poisson’s ratio ν can be determined, using their relationships with B and G: $E=9\mathrm{BG}/\left(3\mathrm{B}+\mathrm{G}\right)$ et $\nu =\left(3B-E\right)/6B$ [70, 74]. The compressibility modulus (B) measures a material’s resistance to volume compression under hydrostatic stress, while the shear modulus (G) measures a material’s resistance to elastic shear strain. While Young’s modulus (E) is also related to stiffness as well as thermal shock resistance. The large Young’s modulus gives high rigidity. Large Young’s modulus yields high stiffness [46, 75]. These results are listed in Table 5. ${\mathrm{Nb}}_{2}\mathrm{CdC}$ can be said to be harder than ${\mathrm{Sc}}_{2}\mathrm{CdC}$ and ${\mathrm{V}}_{2}\mathrm{CdC}$ due to its higher compressibility modulus value (B). We can see that the calculated value of the volume modulus (B) from the elastic constants is almost in the same order as found in the optimization part. The ${\mathrm{V}}_{2}\mathrm{CdC}$ material shows more high rigidity due to its higher value. The strong bond between (Sc) atom and (C) atom, and the relatively weak bond between (M = Sc, V, Nb) atoms, and Cd atom [7, 76] lead us to the behavior of elastic anisotropy of these materials. For a hexagonal system, the compounds ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }= (\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb}$) have three shear-like anisotropy factors that can be determined by [77]:

$$ A_{1} = \frac{{1/6\left( {c_{11} + c_{12} + 2c_{33} - 4c_{13} } \right)}}{{c_{44} }},\quad A_{2} = \frac{{2c_{44} }}{{c_{11} - c_{12} }},\quad A_{3} = A_{1} .A_{2} = \frac{{1/3\left( {c_{11} + c_{12} + 2c_{33} - 4c_{13} } \right)}}{{c_{11} - c_{12} }} $$

(4)

Table 4 Elastic constant $C_{ij}$ for ${\mathrm{M}}_{2}\mathrm{CdC}$ with M = Sc, V, and Nb

Table 5 The bulk modulus B, shear modulus G, Young’s modulus E (all in GPa), Poisson’s ratio ν, anisotropic factor A₁, A₂, and A₃, Vickers hardness${H}_{\mathrm{v}}$, linear compressibility ratio $f = \frac{{K_{{\text{c}}} }}{{K_{{\text{a}}} }}$ for ${\mathrm{M}}_{2}\mathrm{CdC}$ with M = Sc, V, and Nb

However, any value less than or greater than 1 indicates anisotropy, otherwise being an isotropic crystal. To assess the elastic anisotropy of ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }= (\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb}$), we calculated the ratio of the linear compressibility coefficients (kc/ka) along with the a and c axes, respectively, using the following relation [26, 78].

$$ f = \frac{{K_{{\text{c}}} }}{{K_{{\text{a}}} }} = \left( {C_{11} + C_{12} - 2C_{13} } \right)/\left( {C_{33} - C_{13} } \right) $$

(5)

From Table 5, any value equal to (1) of the compressibility modulus ratio ${k}_{\mathrm{c}} / {k}_{\mathrm{a}}$ corresponds to the isotropic compressibility, while the deviation from unity is a measure of the degree of anisotropy for linear compressibility in directions (c) and (a) [79]. Finally, if $B > G$, this involves that the parameter limiting the mechanical stability of these phases is the shear modulus [46]. From the Criterion of Pugh [46, 80], a material must behave ductile if $G/B < 0.5$, otherwise it should be fragile.

Important information about the physical processes of solids such as plastic deformation, indentation depth, indentation, and scratches can be known from the hardness of solids. The study of hardness is fundamental in the field of engineering for the design of devices. In addition, the study of the hardness parameter is beneficial for materials used as structural components such as MAX phases. To determine the hardness of our material, we used the Vickers hardness formula [81]:

$$ H_{{\text{V}}} = 0.92 \left( \frac{G}{B} \right)^{1.137} \cdot G^{0.708} $$

(6)

The calculated results are 2.66, 9.68, and 9.37 for Sc₂CdC, V₂CdC, and Nb₂CdC, respectively (see Table 5). To our knowledge, there are no theoretical or experimental values for Sc₂CdC, V₂CdC, and Nb₂CdC to compare our results, but we have compared it with close materials and the same family as Ti₂CdC [82, 83] and Zr₂CdC [52]. We may conclude that Sc2CdC is relatively soft and easily machinable compared to the other two nanolaminates. The values found are compatible with other results of the same family [84], except the compound Sc₂CdC which has a lower hardness compared to the other compounds V₂CdC, and Nb₂CdC.

3.5 Calculation of Debye temperature

After calculating the elastic constants we calculated the Debye temperature, which is an important parameter related to many materials' physical properties generally specific heat, melting temperature, thermal expansion, etc. a higher ${\theta }_{\mathrm{D}}$ implies a higher associated thermal conductivity. Knowledge of such a numerical digit is essential for the development and manufacture of electronic devices. At low temperatures, the vibratory excitation comes only from the acoustic modes. Therefore, Debye temperatures calculated from low-temperature elastic constants are the same as those determined from specific heat measurements. In order to estimate the Debye temperature amplitude, we used the simple Debye–Grüneisen model. The Debye temperature can be defined in terms of the average speed of sound and gives explicit information about lattice vibrations. It can be determined from the following equation [12]:

$$ \theta_{{\text{D}}} = \frac{h}{{K_{{\text{B}}} }}\frac{3n}{{4\pi V_{{\text{a}}} }}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \cdot V_{{\text{m}}} $$

(7)

where $h$ is Plank’s constant, ${K}_{\mathrm{B}}$ Boltzmann’s constant, $\mathrm{n}$ represents the number of atoms per formula unit, ${V}_{\mathrm{a}}$ the atomic volume, and ${V}_{\mathrm{m}}$ represents the average sound velocity is given by [12]:

$$ V_{{\text{m}}} = \left\lceil {\frac{1}{3}\left( {\frac{2}{{v^{3}_{{\text{t}}} }} + \frac{1}{{v^{3}_{{\text{l}}} }}} \right)} \right\rceil^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} $$

(8)

$$ v_{{\text{l}}} = \left( {\frac{{B + \frac{4G}{3}}}{\rho }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$

(9)

$$ v_{{\text{t}}} = \left( {\frac{G}{\rho }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$

(10)

where ${v}_{\mathrm{t}}$ and ${\nu }_{l}$ are the transverse and longitudinal sound velocities, respectively. The results concerning (The speed of sound and the Debye temperature calculated as well as the density for ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M}=(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})$ are presented in Table 6. These results show that these compounds have relatively high Debye temperature values to explain that they present a rather rigid lattice and therefore a good thermal conductivity. The gradual decrease in the mean velocities of sound in the Sc, V, and Nb series further signals the propensity to lower Debye temperatures with the same sequential order [85].

Table 6 The calculated density ($\rho$ in $\mathrm{g}/{\mathrm{cm}}^{3}$), the longitudinal, transverse and average sound velocity (${v}_{\mathrm{l}}$, ${v}_{\mathrm{l}}$, ${v}_{\mathrm{m}}$ in $\mathrm{m}/\mathrm{s}$) calculated from elastic modulus, and the Debye temperatures (${\theta }_{\mathrm{D}}$ in $\mathrm{K}$) calculated from the average sound velocity of ternary ${\mathrm{M}}_{2}\mathrm{CdC}$, $(\mathrm{ M}=\mathrm{Sc},\mathrm{V},\mathrm{and Nb})$

4 Conclusions

We studied the structural, electronic, elastic, and thermal properties of ${\mathrm{M}}_{2}\mathrm{CdC},\mathrm{ M }(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})$ MAX phase compounds using WIEN2k code. The calculated energy of formation (E_Form) per atom shows that this energy indicates that these materials can be synthesized. The calculated lattice constants are consistent with other Max 211 phase calculations. The equilibrium energy and the cohesion energy show that the compound ${\mathrm{Nb}}_{2}\mathrm{CdC}$ is more stable than the compounds ${\mathrm{Sc}}_{2}\mathrm{CdC}$, and ${\mathrm{V}}_{2}\mathrm{CcdC}$. These materials are metallic in nature and the electrons $3d-\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and nb})$, are mainly contributing to the TDOS at the ${E}_{\mathrm{F}}$. A strong covalent bond exists in compounds and the level of covalence in $\mathrm{C}-\mathrm{M }(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})$, is stronger than $\mathrm{Cd }-\mathrm{M}(\mathrm{Sc},\mathrm{ V},\mathrm{ and Nb})$. The elastic constants of these compounds are calculated according to the method developed by Reshak and Morteza. The results obtained show the compounds studied are mechanically stable. By a comparison between the compressibility modulus B and the shear modulus G, for the three compounds, we noticed that the capacity to resist the change of volume is stronger than the capacity to resist the change of shape. We distinguish the Sc₂CdC phase as having the lowest C₄₄ constant (21.37), demonstrating that it may be efficacious as a high-temperature dry lubricant. Fermi’s surface properties were studied for the first time.