Mixed convection heat and mass transfer in peristaltic flow with chemical reaction and inclined magnetic field

Abstract

A mathematical model is constructed to investigate the mixed convective heat and mass transfer effects on peristaltic flow of magnetohydrodynamic pseudoplastic fluid in a symmetric channel. An analysis has been carried out to examine the impact of an inclined magnetic field and chemical reaction in presence of heat sink/source. Mechanics of flow and heat/mass transfer described in terms of continuity, linear momentum, energy and concentration equations are predicted by using long wavelength and low Reynolds number. Expressions for stream function, temperature, concentration and pressure gradient are derived. Numerical simulation is performed for the rise in pressure per wave length. Effects of several physical parameters on the flow quantities are analyzed.

1 Introduction

Study on peristaltic transport of fluids has received a considerable attention of researchers in recent times because of its importance in swallowing food through the oesophagus, transport of urine from kidney to bladder, chyme movement in gastrointestinal tract, ovum movement in female fallopian tube, toxic liquid transport in nuclear industry, corrosive fluid transport, roller and finger pumps, sanitary fluid transport and blood circulation in small blood vessels [1–6].

Mixed convective flows are significant in applications like float glass production, cooling of electric devices, lubrication and drying technologies, flow and heat transfer in solar ponds, thermal hydraulics of nuclear reactors, dynamics of lakes, diffusion of nutrients out of blood, oxygenation and hemodialysis processes. Influence of magnetic field in such flows has pivotal role in geothermal resevoires. These problems occur in micro-electronic devices during their operations and in electronic packages. The water transport in trees is due to peristalsis and free convection. Having such applications in mind, various authors [7–16] are still engaged in the study of nonlinear problems under various aspects.

This communication aims to analyze the mixed convective heat and mass transfer effects in peristaltic transport of pseudoplastic fluid. An incompressible fluid is considered in a symmetric channel. The fluid is electrically conducting through an inclined magnetic field of uniform strength. Further the mathematical modelling is presented in presence of heat sink/source and chemical reaction. Nonlinear flow analysis is computed. Results are examined for various interesting flow parameters.

2 Mathematical modelling

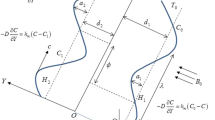
Let us examine the flow of an incompressible magnetohydrodynamic pseudoplastic fluid in a two-dimensional vertical channel of uniform thickness 2a. A sinusoidal wave (with speed c) propagates along the channel walls. $\bar{X}$ and $\bar{Y}$-axes in the rectangular coordinates $\left( \bar{X},\bar{Y}\right)$ are selected parallel and transverse to the direction of wave propagation. The fluid is electrically conducting in presence of uniform applied magnetic field B ₀. The electric field is taken as zero. Further, the contribution of induced magnetic field is neglected and subject to small magnetic Reynolds number. The geometry of wall is as follows:

$$ \bar{h}(\bar{X},\bar{t})=a+b\sin \left( \frac{2\pi }{\lambda }\left( \bar{X} -c\bar{t}\right) \right) . $$

(1)

Here λ denotes the wavelength, a is the channel half width, $\bar{t}$ is the time and b is the wave amplitude. The velocity field V can be expressed as

$$ V=[\bar{U}(\bar{X},\bar{Y},\bar{t}),\bar{V}(\bar{X},\bar{Y},\bar{t} ),0], $$

(2)

in which $\bar{U}$ and $\bar{V}$ in fixed frame designate the components along the $\bar{X}$ and $\bar{Y}$ directions respectively. Basic laws of mass, momentum, energy and concentration yield the following equations

$$ \frac{\partial \bar{U}}{\partial \bar{X}}+\frac{\partial \bar{V}}{\partial \bar{Y}}=0, $$

(3)

$$ \begin{aligned} \rho \left( \frac{\partial }{\partial \bar{t}}+\bar{U}\frac{\partial }{ \partial \bar{X}}+\bar{V}\frac{\partial }{\partial \bar{Y}}\right) \bar{U} & = - \frac{\partial \bar{P}}{\partial \bar{X}}+\frac{\partial S_{\bar{X}\bar{X }}}{\partial \bar{X}}+\frac{\partial \bar{S}_{\bar{X}\bar{Y}}}{\partial \bar{ Y}}+\rho g\beta _{t}\left( \bar{T}-T_{0}\right) +\rho g\beta _{c}\left( \bar{ C}-C_{0}\right)\\ & \quad -\sigma B_{0}^{2}\cos \beta (\bar{U}\cos \beta -\bar{V}\sin \beta ), \end{aligned} $$

(4)

$$ \rho \left( \frac{\partial }{\partial \bar{t}}+C\frac{\partial }{\partial \bar{X}}+\bar{V}\frac{\partial }{\partial \bar{Y}}\right) \bar{V} = - \frac{ \partial \bar{P}}{\partial \bar{Y}}+\frac{\partial \bar{S}_{\bar{X}\bar{Y}}}{ \partial \bar{X}}+\frac{\partial \bar{S}_{\bar{Y}\bar{Y}}}{\partial \bar{Y}} + \sigma B_{0}^{2}\sin \beta (\bar{U}\cos \beta -\bar{V}\sin \beta ), $$

(5)

$$ \rho C_{p}\left[ \frac{\partial }{\partial \bar{t}}+\bar{U}\frac{\partial }{ \partial \bar{X}}+\bar{V}\frac{\partial }{\partial \bar{Y}}\right] \bar{T} =\kappa \left[ \frac{\partial ^{2}\bar{T}}{\partial X^{2}}+\frac{\partial ^{2}\bar{T}}{\partial Y^{2}}\right] +Q_{0}, $$

(6)

and

$$ \left[ \frac{\partial }{\partial \bar{t}}+\bar{U}\frac{\partial }{\partial \bar{X}}+\bar{V}\frac{\partial }{\partial \bar{Y}}\right] \bar{C} = D\left[ \frac{\partial ^{2}\bar{C}}{\partial X^{2}} + \frac{\partial ^{2}\bar{C}}{ \partial Y^{2}}\right] + \frac{DK_{T}}{T_{m}}\left[ \frac{\partial ^{2}\bar{T} }{\partial X^{2}}+\frac{\partial ^{2}\bar{T}}{\partial Y^{2}}\right] -k_{1} \bar{C}. $$

(7)

In above equations, ρ is density, g is the acceleration due to gravity, C _p is the specific heat, T is the temperature, β is the angle of inclination of magnetic field, κ is the thermal conductivity, $\bar{P}$ is the pressure, σ is the electrical conductivity, B ₀ is the constant magnetic field, $\bar{S}_{\bar{X}\bar{X}}, \bar{S}_{\bar{X}\bar{Y}}, \bar{S}_{\bar{Y}\bar{Y}}$ are the components of extra stress tensor, D is the coefficient of mass diffusivity, Q ₀ is the heat sink source parameter, T _m is the mean temperature, k ₁ is the chemical reaction parameter, K _T is the thermal diffusion ratio, C is the concentration and and $\bar{T}$ is the temperature, T ₀ and C ₀ are the temperature and concentration at y = h respectively.

For pseudoplastic fluid the expression for extra stress tensor ${\bar{\mathbf{S}}}$ is given by Boger [17]

$$ {\bar{\mathbf{S}}}+\bar{\lambda}_{1}{\bar{\mathbf{S}}}^{\nabla }+\frac{1}{2} \left( \bar{\lambda}_{1}-\bar{\mu}_{1}\right) \left( {\bar{\mathbf{A}}}_{1} {\bar{\mathbf{S}}+{\bar{\mathbf{S}}} {\bar{\mathbf{A}}}}_{1}\right) =\mu {\bar{\mathbf{A}}}_{1}, $$

(8)

$$ {\bar{\mathbf{S}}}^{\nabla }=\frac{d{\bar{\mathbf{S}}}}{dt}-{\bar{\mathbf{S}}{\bar{\mathbf{L}}}}^{T}-{\bar{\mathbf{L}}{\bar{\mathbf{S}}}}, \quad {\bar{\mathbf{L}}}=\hbox{grad} \,\, {\bar{\mathbf{V}},} \quad {\bar{\mathbf{A}}}_{1}= {\bar{\mathbf{L}}}+{\bar{\mathbf{L}}} ^{T} $$

(9)

in which $\mu, \, {\bar{\mathbf{S}}}^{\nabla}$ and $\bar{\mu}_{1}$ and $\bar{\lambda}_{1}$ respectively denote the dynamic viscosity, upper-convected derivative and relaxation times. Denoting velocity components ($\bar{u}, \bar{v})$ and pressure $\bar{p}$ in the wave frame we define

$$ \begin{aligned} \bar{x} =&\bar{X}-c\bar{t}, \quad \bar{y}=\bar{ Y},\\ \bar{u}(\bar{x},\bar{y}) =&\bar{U}-c, \quad \bar{v}(\bar{x},\bar{y})=\bar{V}. \end{aligned} $$

(10)

We set the following dimensionless variables

$$ \begin{aligned} \lambda _{1} =&\frac{\bar{\lambda}_{1}c}{a}, \quad x=\frac{\bar{x}}{\lambda }, \quad t=\frac{c\bar{t}}{\lambda }, \quad \mu _{1}=\frac{\bar{\mu}_{1}c}{a}, \quad \gamma =\frac{\rho k_{1}}{a^{2}}, \quad c_{1}=\frac{\rho k_{1}a^{2}}{\mu }, \quad G_{t}= \frac{\rho \beta _{T}gT_{0}a^{2}}{\mu c},\\ \bar{S}_{ij} =&\frac{a\bar{S}_{ij}}{\mu c} \text{ for } (i,j =1,2,3), \quad u=\frac{\bar{u}}{c}, \quad v=\frac{\bar{v}}{c}, \quad G_{c}=\frac{\rho \beta _{c}gC_{0}a^{2}}{\mu c}, \quad M=\sqrt{\frac{\sigma }{\mu }}aB_{0}, \\ \delta =&\frac{a}{\lambda }, \quad Re=\frac{ca\rho }{\mu }, \quad \Upomega =\frac{\bar{C} -C_{0}}{C_{0}}, \quad \zeta =\frac{Q_{0}a_{1}^{2}}{\kappa T_{0}}, \quad Sr=\frac{\rho T_{0}DK_{T}}{\mu T_{m}C_{0}}, \quad Sc=\frac{\mu }{\rho D},\\ p =& \frac{a^{2}\bar{p}}{c\lambda \mu }, \quad \theta _{t}=\frac{\bar{T}-T_{0}}{ T_{0}}, \quad y=\frac{\bar{y}}{a}, \quad \Pr =\frac{\mu C_{p}}{\kappa }, \quad \alpha =\frac{b}{ a}, \end{aligned} $$

(11)

where γ , G _c , G _t , P _r , Sc, Sr, δ, Re and M are the chemical reaction parameter, mass Grashof number, local Grashof, Prandtl, Schmidt, Soret, wave, Reynolds and Hartman numbers respectively; α is the amplitude ratio, θ _t is the dimensionless temperature, $\zeta$ is the dimensionless heat sink source parameter, $\Upomega$ is the non-dimensional concentration, ψ is the stream function and λ₁ and μ₁ are the dimensionless relaxation times. The dimensionless velocity components (u, v) in terms of stream function $\Uppsi$ are related by the following relations

$$ u=\frac{\partial \Uppsi }{\partial y} , \quad v=-\delta \frac{\partial \Uppsi }{ \partial x}. $$

(12)

Now continuity of Eq. (3) is clearly satisfied and Eqs. (4)–(12) give

$$ \begin{aligned} Re\delta \left( \frac{\partial \Uppsi }{\partial y}\frac{\partial }{\partial x} -\frac{\partial \Uppsi }{\partial x}\frac{\partial }{\partial y}\right) \frac{ \partial \Uppsi }{\partial y}+\frac{\partial p}{\partial x} & = \delta \frac{ \partial S_{xx}}{\partial x}+\frac{\partial S_{xy}}{\partial y}+G_{t}\theta _{t}+G_{c}\Upomega\\ & \quad -M^{2}\cos \beta \left( \left( \frac{\partial \Uppsi }{\partial y}+1\right) \cos \beta +\delta \frac{\partial \Uppsi }{\partial x}\sin \beta \right) , \end{aligned} $$

(13)

$$ \begin{aligned} -Re\delta ^{2}\left( \frac{\partial \Uppsi }{\partial y}\frac{\partial }{ \partial x}-\frac{\partial \Uppsi }{\partial x}\frac{\partial }{\partial y} \right) \frac{\partial \Uppsi }{\partial x} &=\frac{\partial p}{\partial y} +M^{2}\delta \sin \beta \left( \left( \frac{\partial \Uppsi }{\partial y} +1\right) \cos \beta +\delta \frac{\partial \Uppsi }{\partial x}\sin \beta \right)\\ &\quad+\delta \left( \delta \frac{\partial S_{yx}}{\partial x}+\frac{\partial S_{yy}}{\partial y}\right), \end{aligned} $$

(14)

$$ \delta \Pr \hbox{Re}\left[ \frac{\partial \Uppsi }{\partial y}\frac{\partial \theta _{t}}{\partial x}-\frac{\partial \Uppsi }{\partial x}\frac{\partial \theta _{t}}{\partial y}\right] =\delta ^{2}\frac{\partial ^{2}\theta _{t}}{ \partial x^{2}}+\frac{\partial ^{2}\theta _{t}}{\partial y^{2}}+\zeta , $$

(15)

$$ \begin{aligned} \delta \hbox{Re}\left[ \frac{\partial \Uppsi }{\partial y}\frac{\partial \Upomega }{\partial x}-\frac{\partial \Uppsi }{\partial x}\frac{\partial \Upomega }{\partial y}\right] &=\frac{1}{Sc}\left[ \delta ^{2}\frac{\partial ^{2}\Upomega }{\partial x^{2}}+\frac{\partial ^{2}\Upomega }{\partial y^{2}} \right] -\gamma \Upomega -c_{1}\\ & \quad +Sr\left[ \delta ^{2}\frac{\partial ^{2}\theta _{t}}{\partial x^{2}}+\frac{ \partial ^{2}\theta _{t}}{\partial y^{2}}\right] , \end{aligned} $$

(16)

$$ \begin{aligned} 2\delta \frac{\partial ^{2}\Uppsi }{\partial y\partial x} & = S_{xx}+\lambda _{1}\left[ \left( \delta \frac{\partial \Uppsi }{\partial y}\frac{\partial }{ \partial x}+\frac{\partial \Uppsi }{\partial x}\frac{\partial }{\partial y} \right) S_{xx}-2\left( \delta \frac{\partial ^{2}\Uppsi }{\partial x\partial y} S_{xx}+\frac{\partial ^{2}\Uppsi }{\partial y^{2}}S_{xy}\right) \right]\\ & \quad +\frac{1}{2}\left( \lambda _{1}-\mu _{1}\right) \left( 4\delta S_{xx}\frac{ \partial ^{2}\Uppsi }{\partial x\partial y}+2S_{xy}\left( \frac{\partial ^{2}\Uppsi }{\partial y^{2}}-\delta ^{2}\frac{\partial ^{2}\Uppsi }{\partial x^{2}}\right) \right) , \end{aligned} $$

(17)

$$ \begin{aligned} -2\delta \frac{\partial ^{2}\Uppsi }{\partial y\partial x} &=S_{yy}+\lambda _{1}\left[ \delta \left( \frac{\partial \Uppsi }{\partial y}\frac{\partial }{ \partial x}-\frac{\partial \Uppsi }{\partial x}\frac{\partial }{\partial y} \right) S_{yy}+2\delta \left( \delta \frac{\partial ^{2}\Uppsi }{\partial x^{2} }S_{xy}+\frac{\partial ^{2}\Uppsi }{\partial x\partial y}S_{yy}\right) \right]\\ &\quad+\frac{1}{2}\left( \lambda _{1}-\mu _{1}\right) \left[ 2S_{xy}\left( \frac{ \partial ^{2}\Uppsi }{\partial y^{2}}-\delta ^{2}\frac{\partial ^{2}\Uppsi }{ \partial x^{2}}\right) -4\delta S_{yy}\frac{\partial ^{2}\Uppsi }{\partial x\partial y}\right] , \end{aligned} $$

(18)

$$ \begin{aligned} \frac{\partial ^{2}\Uppsi }{\partial y^{2}}-\delta ^{2}\frac{\partial ^{2}\Uppsi }{\partial x^{2}} &=S_{xy}+\lambda _{1}\left[ \delta \left( \frac{\partial \Uppsi }{\partial y}\frac{\partial }{\partial x}-\frac{\partial \Uppsi }{ \partial x}\frac{\partial }{\partial y}\right) S_{xy}-\left( \frac{\partial ^{2}\Uppsi }{\partial y^{2}}S_{yy}-\delta ^{2}\frac{\partial ^{2}\Uppsi }{ \partial x^{2}}S_{xx}\right) \right]\\ &\quad +\frac{1}{2}\left( \lambda _{1}-\mu _{1}\right) \left[ \left( S_{xx}+S_{yy}\right) \left( \frac{\partial ^{2}\Uppsi }{\partial y^{2}}-\delta ^{2}\frac{\partial ^{2}\Uppsi }{\partial x^{2}}\right) \right] , \end{aligned} $$

(19)

where c ₁ = k ₁ a ² C/ν (C − C ₀).

The above equations after invoking long wavelength and low Reynolds number approach [18] are reduced as follows:

$$ \frac{\partial p}{\partial x}=\frac{\partial S_{xy}}{\partial y}-M^{2}\cos ^{2}\beta \left( \frac{\partial \Uppsi }{\partial y}+1\right) +G_{t}\theta _{t}+G_{c}\Upomega , $$

(20)

$$ \frac{\partial p}{\partial y}=0, $$

(21)

$$ \frac{\partial ^{2}\theta _{t}}{\partial y^{2}}+\zeta =0, $$

(22)

$$ \frac{\partial ^{2}\Upomega }{\partial y^{2}}=Sc\left( \gamma \Upomega +c_{1}\right) -ScSr\frac{\partial ^{2}\theta _{t}}{\partial y^{2}}, $$

(23)

$$ S_{xx}=\left( \lambda _{1}+\mu _{1}\right) \frac{\partial ^{2}\Uppsi }{ \partial y^{2}}S_{xy}, $$

(24)

$$ S_{yy}=\left( -\lambda _{1}+\mu _{1}\right) S_{xy}\frac{\partial ^{2}\Uppsi }{ \partial y^{2}}, $$

(25)

$$ S_{xy}=\frac{\Uppsi _{yy}}{1+\xi \Uppsi _{yy}^{2}}, $$

(26)

with $\left( \lambda _{1}^{2}-\mu _{1}^{2}\right) =\xi$ and Eq. (21) indicates that $p\neq p\left( y\right) .$

The dimensionless boundary conditions can be put in the forms

$$ \begin{aligned} \Uppsi &=0, \quad \frac{\partial ^{2}\Uppsi }{\partial y^{2}}=0, \quad \frac{\partial \theta _{t}}{\partial y}=0, \quad \frac{\partial \Upomega }{\partial y} =0, \quad at \; y=0,\\ \Uppsi &=F, \quad \frac{\partial \Uppsi }{\partial y}=-1, \quad \theta _{t}=0, \quad \Upomega =0, \quad at \; y=h, \end{aligned} $$

(27)

where F is dimensionless time mean flow rate in the wave frame. It is related to the dimensionless time mean flow rate θ in the laboratory frame by

$$ \theta =F+1, \quad F=\int\limits_{0}^{h}\frac{\partial \Uppsi }{\partial y} dy \quad \hbox {and} \quad h=\frac{\bar{h}}{a}=1+\alpha \sin \left( 2\pi x\right) , $$

(28)

From Eqs. (20) and (26) we have

$$ \frac{\partial p}{\partial x}=\frac{\partial }{\partial y}\left[ \Uppsi _{yy}\left\{ 1-\xi \left( \frac{\partial ^{2}\Uppsi }{\partial y^{2}}\right) ^{2}\right\} \right] -M^{2}\cos ^{2}\beta \left( \frac{\partial \Uppsi }{ \partial y}+1\right) +G_{t}\theta _{t}+G_{c}\Upomega , $$

(29)

Eqs. (21) and (29) imply that

$$ \frac{\partial ^{4}\Uppsi }{\partial y^{4}}-\xi \frac{\partial ^{2}}{\partial y^{2}}\left( \frac{\partial ^{2}\Uppsi }{\partial y^{2}}\right) ^{3}-M^{2}\cos ^{2}\beta \frac{\partial ^{2}\Uppsi }{\partial y^{2}}+G_{t}\frac{\partial \theta _{t}}{\partial y}+G_{c}\frac{\partial \Upomega }{\partial y}=0. $$

(30)

3 Series solutions

Employing perturbation technique about ξ,

$$ \begin{aligned} \Uppsi &=\Uppsi _{0}+\xi \Uppsi _{1}+O\left( \xi \right) ^{2},\quad F=F_{0}+\xi F_{1}+O\left( \xi \right) ^{2},\quad p=p_{0}+\xi p_{1}+O\left( \xi \right) ^{2},\\ \theta _{t} &=\theta _{t0}+\xi \theta _{t1}+O\left( \xi \right)^{2}, \quad \Upomega =\Upomega _{0}+\xi \Upomega _{1}+O\left( \xi \right) ^{2} \end{aligned} $$

(31)

we obtain zeroth and first order systems from Eqs. (22), (23), (27) and (30). After finding the corresponding solutions of Zeroth and first order systems, we finally obtain

$$ \theta _{t} = \left. \frac{1}{2}\left( h^{2}\zeta -y^{2}\zeta \right) +\xi \lbrack 0]\right. , $$

(32)

$$ \Upomega = L_{0} \left( {c - Sr\zeta } \right)\left( {\cosh \left( {\sqrt {Scy} \sqrt \gamma } \right) - \sinh \left( {\sqrt {Scy} \sqrt \gamma } \right)} \right)L_{1} \left( y \right) + \xi \left[ 0 \right], $$

(33)

$$ \begin{aligned} \psi & = L_{3}\left( \cosh \left( M\cos \beta y\right) -\sinh \left( M\cos \beta y\right) \right) \left( 6cG_{c}hM^{2}\cos ^{2}\beta \sqrt{Sc} \sqrt{\gamma }\cosh (hM\cos \beta )\right.\\ &\quad \left.-L_{4}\left( y \right) \right) +\xi \left[ -\frac{L_{0}^{4}}{8}Sc^{2}\gamma ^{3}M^{6}\cos ^{6}\beta \left( \cosh \left( 3M\cos \beta y\right)\right.\right.\\ &\quad \left.\left.-\sinh \left( 3M\cos \beta y\right) \right) \times \sum\limits_{i=5}^{15}L_{i}(y)\right] , \end{aligned} $$

(34)

$$ \begin{aligned} \frac{dp}{dx} &= \frac{1}{2}\beta G_{t}h^{2}+\left( c-Sr\zeta \right) \left( -1+2\cosh (\sqrt{Sc}h\sqrt{\gamma })+\sinh \left( \sqrt{Sc}h\sqrt{ \gamma }\right) \right) \\ &\quad \times L_{16}\left( h\right) G_{c}+\xi \left[ -\frac{L_{3}^{3}}{4} \left( \cosh \left( 3\sqrt{Sc}h\sqrt{\gamma }\right) \right.\right.\\ &\quad \left.\left.-\sinh \left( 3\sqrt{Sc} h\sqrt{\gamma }\right) \right) G_{c}\left( c-Sr\zeta \right) M^{3}\sum\limits_{i=17}^{30}L_{i}(h) \right] , \end{aligned} $$

(35)

$$ \Updelta P_{\lambda }=\int\limits_{0}^{1}\left( \frac{dp}{dx}\right) _{y=0}, $$

(36)

where the involved L _i (i = 0, 1, 2, 3…….30) in solution expressions are computed through algebraic calculations.

4 Results and discussion

Variations of $\zeta , \beta , \gamma , \xi , Sc, Sr, G_{t}$ and G _c on the flow quantities $dp/dx, u, \Updelta P_{\lambda }, \theta _{t}$ and $\Upomega$ are shown in Figs. 1–5. Main attention is focused to the cases of grashof numbers, inclined magnetic field, chemical reaction and heat sink/source parameters.

Fig. 1

The pressure gradient dp/dx versus x (a) β = π /3, α = 0.2, ξ = 0.01, G _c  = 5, G _t  = 3, θ = 1.5, Sr = 1, Sc = 0.5, γ = 0.5, c = 1 and M = 1.2; (b) $\beta =\pi /3, \alpha =0.2, \xi =0.1, G_{c}=3 \zeta =0.5, \theta =3.5, Sr=1, Sc=0.5, \gamma =0.5, c=1.2$ and M = 1.4; (c) $\beta =\pi /3,\alpha =0.2, \xi =0.01, G_{c}=5, G_{t}=3, \theta =-1.5, Sr=1, Sc=0.5, \zeta =0.5, c=1.2$ and M = 1.4; (d) $\beta =\pi /3, \alpha =0.2, \xi =0.1, \gamma =0.2, =5, G_{t}=3, \theta =-1.5, Sr=1, Sc=0.5, \zeta =0.5, c=1.2$ and M = 1.4

Figure 1 depicts the dimensionless pressure gradient dp/dx with x. Through Fig. 1(a) and 1(d) we can see that dp/dx is an increasing function of heat sink/source parameter $\zeta$ and mass Grashof number G _c . In the wider part of channel $x\epsilon \left[ 0 ,0.2\right]$ and $x\epsilon \left[ 1.1, 1.2\right]$ the pressure gradient is comparatively small. In fact, the flow in such parts occur easily without the imposition of large pressure gradient. In the narrow part of channel $x\epsilon \left( 0.4, 1\right)$ , much larger pressure gradient is needed to maintain the flow to pass through it. Figure 1(b) and 1(c) show that pressure gradient dp/dx decreases when values of local Grashof number G _t and chemical reaction parameter γ are increased.

The pumping against the pressure rise is plotted in Fig. 2. The pressure rise $\Updelta P_{\lambda}$ is sketched against the flow rate θ (in waveframe). Pumping action divides the region into four sections: pumping region $\left( \Updelta p_{\lambda }>0, \theta >0\right)$, augmented pumping $\left( \Updelta p_{\lambda }<0, \theta >0\right)$, retrograde pumping ($\Updelta p_{\lambda }>0, \theta <0$) and free pumping $\left( \Updelta p_{\lambda }=0\right)$. Figure 2(a) shows that for certain values of flow rate the pumping curves coincide showing that there is no difference between the Newtonian and pseudoplastic fluids. However, the curves become non-linear for ξ ≠ 0. We observe that:

• (i) In the pumping region ($\Updelta p_{\lambda }>0$) the pumping rate decreases by increasing ξ.

• (ii) The free pumping rate ($\Updelta p_{\lambda }=0$) shows no effect when ξ is increased.

• (iii) In copumping ($\Updelta p_{\lambda }<0$) the pumping rate is increasing function of ξ.

Fig. 2

The pressure rise $\Updelta p_{\lambda }$ versus θ for (a) $\gamma =0.2, \beta =\pi /3, \alpha =0.2, G_{c}=2, G_{t}=5, Sr=2, Sc=2, \zeta =0.5, c=1.2$ and M = 2.5; (b) $\gamma =0.2, \alpha =0.2, \xi =0.001, \beta =\pi /6, G_{t}=5, Sr=2, Sc=1.2, \zeta =0.5, c=1.2$ and M = 1.5; (c) $\gamma =0.2, \alpha =0.2, \xi =0.01, G_{c}=2, G_{t}=5, Sr=2, Sc=2, \zeta =0.5, c=1.2$ and M = 2.5; (d) $\beta =\pi /3, \alpha =0.2, G_{c}=2, G_{t}=5, \xi =0.01, Sr=2, Sc=2, \zeta =0.5, c=1.2$ and M = 2.5; (e) $\gamma =0.2, \alpha =0.2, \xi =0.1, G_{c}=1.2, G_{t}=3, \beta =\pi /3, Sc=10, \zeta =0.5, c=1.2$ and M = 1.2; (f) $\beta =\pi /3, \alpha =0.2, G_{c}=1.2, G_{t}=5, \xi =0.01, Sr=1, \zeta =0.5, c=1.2$ and M = 2

Figure 2(b) shows the variation of $\Updelta p_{\lambda }$ with flow rate θ for various values of dimensionless mass Grashof number. It displays that all pumping regions decrease by increasing the values of G _c . Figure 2(c) reflects the influence of inclination parameter β on pressure rise $\Updelta P_{\lambda }$ against the flow rate θ. The pumping rate increases when β increases. In other words, the pressure rise per wavelength increases by increasing the angle of inclination of magnetic field. The pumping performance is better for $\Updelta p_{\lambda }>1$. For appropriate values of $\Updelta p_{\lambda }<1$, the pumping rate is decreasing function of β. The pressure field is influenced by chemical reaction parameter. Figure 2(d) shows the effects of γ on $\Updelta p_{\lambda}$. It is noticed that $\Updelta p_{\lambda}$ increases with γ. Thus, all the pumping regions increase when γ is increased. Figure 2(e) depicts that the pressure rise $\Updelta P_{\lambda}$ decreases when the values of Soret number Sr increased. The influence of Schmidt number Sc on $\Updelta p_{\lambda}$ is similar to G _c Fig. 2(f).

Figure 3 is plotted to depict the flow characteristics. Figure 3(a)–3(h) show the behaviors of $\zeta, \beta, \gamma, \xi, Sc, Sr, G_{t}$ and G _c on u versus y. These figures illustrate that the behavior of these parameters at the central narrow part of channel is quite different when compared with the wider part near the channel walls. A close look at the velocity profile in shown Fig. 3(a) and 3(b) indicate that the flow characteristics are enhanced by inclination of the applied magnetic field and heat conduction/absorption parameter. Figure 3(c) explains that as we increase the values of relaxation time $\xi \left( \xi =0.1, 0.3, 0.5 \, \hbox{and} \, 0.9\right)$, the axial velocity u is increased. The velocity at the centre of channel decreases by increasing γ, as shown in Fig. 3(d). It can be clearly seen in Fig. 3(e) and f that local and mass Grashof numbers have opposite impact on the flow distribution. At the centre of the channel, the velocity decreases by increasing the values of Soret number Sr, as shown in Fig. 3(g). Figure 3(h) clearly indicates that the influence of Sc on u is quite opposite to that shown in Fig. 3(g). Figure 4 illustrates the concentration characteristics. Figure 4(a) depicts the effects of $\zeta$ on $\Upomega$ against y. It is found that concentration profile is decreased with an increase in heat source parameter $\zeta$.

Fig. 3

The axial velocity u versus y for (a) x = 0.2, β = π /3, α = 0.2, ξ = 0.01, G _c  = 5, G _t  = 3, θ = 1.5, Sr = 1, Sc = 0.5, γ = 0.5, c = 1 and M = 1.2; (b) $x=-0.2, \alpha =0.2, \xi =0.01, \gamma =0.5, G_{t}=1, G_{c}=5, \theta =1, Sr=1, Sc=0.5, \zeta =0.25, c=1.2$ and M = 1.4; (c) x = 0.2, β = π /3, α = 0.2, G _c  = 5, G _t  = 5, θ = 1.5, Sr = 1, Sc = 3, γ = 0.5, c = 1 and M = 1.2; (d) $x=0.2, \alpha =0.2, \xi =0.01, G_{t}=5, G_{c}=3, \beta =\pi /3, \theta =1, Sr=1, Sc=0.5, \zeta =0.25, c=1.2$ and M = 1.4; (e) x = 0.2, β = π /3, α = 0.2, G _t  = 5, θ = 1.5, Sr = 1, Sc = 0.5 , ξ = 0.01, γ = 0.5, c = 1.5 and M = 1.2; (f) x = 0.2 , $\alpha =0.2, \xi =0.01, G_{c}=5, \beta =\pi /3, \theta =1.5, Sr=1 , Sc=0.5, \zeta =1, c=1.2$ and M = 1.4; (g) x = −0.2, β = π /3, α = 0.2, G _t  = 5, θ = 1.5, Sr = 1, G _c  = 0.5, ξ = 0.01, γ = 0.5, c = 1.5 and M = 1.2; (h) $x=-0.2, \alpha =0.2, \xi =0.01, G_{c}=5, \beta =\pi /3, \theta =1.5, G_{t}=5, Sc=0.5, \zeta =1, c=1.2$ and M = 1.2

Fig. 4

The concentration distribution $\Upomega$ versus y for (a) x = 0.2, α = 0.2, θ = 1.5, Sr = 1, Sc = 1, γ = 0.5 and c = 1.5; (b) $x=0.2, \alpha =0.2, \zeta =0.2, \theta =1.5, Sr=1, Sc=1$ and c = 1.5; (c) $x=0.2, \alpha =0.2, \theta =1.5, Sr=1 , \zeta =1, \gamma =0.5$ and c = 1.5; (d) $x=0.2, \alpha =0.2, \zeta =0.2, \theta =1.5, \gamma =0.5, Sc=1$ and c = 1.5

The effects of chemical reaction, Schmidt and Soret numbers on concentration profile are described in Fig. 4(b)–4(d). Obviously, the magnitude of $\Upomega$ is a decreasing function of γ , Sc and Sr. The effect of $\zeta$ on temperature distribution θ _t is depicted in Fig. 5 which indicates that the temperature profile is parabolic in nature. It is observed that the presence of a source in medium enhances temperature characteristics.

Fig. 5

The temperature profile θ _t versus y for x = 0.2 and α = 0.2

5 Conclusions

This study highlights the effects of inclined magnetic field and chemical reaction on peristaltic flow of pseudoplastic fluid. Main observations can be put into the following points:

• (i) The concentration field for pseudoplastic fluid decreases with an increase in $\zeta, \gamma, Sc$ and Sr.

• (ii) In the presence of source the temperature field increases.

• (iii) Behavior of G _c , γ and Sc is similar in pumping, copumping and augmented pumping regions.

• (iv) Effects of $\zeta$ and G _c on dp/dx are similar.

• (v) In presence of chemical reaction, the rise in pressure per wavelength is larger for viscous fluid in comparison with pseudoplastic fluid.

• (vi) The axial velocity increases with an increase in $\zeta , \beta, \xi , Sr$ and G _t while it decreases with an increase in G _c , γ and Sc.