1 Introduction

The dynamics of ion-acoustic waves has been studied for several decades both theoretically and experimentally [1–3]. The first experimental observation of ion-acoustic solitons has been made by Ikezi et al. [4]. In the limit of small amplitude approximation in the equations, one can derive some forms of nonlinear differential equations for one spatial dimension situations like Korteweg-de Vries (KdV), modified Korteweg-de Vries (m-KdV) or nonlinear Schrodinger equation, etc. Such equations have well known extended solutions, like solitary waves or solitons. A great number of authors have studied ion-acoustic solitary solutions using the reductive perturbation technique in different plasmas [5, 6]. In contrast to the usual plasmas that consist of electrons and positive ions, it has been observed that the nonlinear waves in plasmas containing additional components such as positrons have different characters [7]. The behaviour of the electron–positron–ion plasmas help us to find better knowledge about the early universe which assumes to be a kind of plasma [8, 9], describing the active galactic nuclei [10], pulsar magnetospheres [11] and also the solar atmosphere [12]. Positrons can be used to probe particle transport in tokomaks since they have sufficient lifetime. In this case, two-component (e–i) plasmas become a three-component (e–i–p) medium [13]. During the last decade, e–p–i plasmas have attracted the attention of several authors [14–17]. It is well known that the behaviour of ion acoustic solitary waves is modified when the ion velocity approaches the speed of light. In such situation, relativistic effect becomes dominant and the wave amplitude, width and its energy change. A great deal of attention has been devoted to the study of different types of collective processes in electron–positron (e–p) and electron–positron–ion (e–p–i) plasmas with relativistic ions [18–26]. Relativistic plasmas occur in a variety of situations, such as, space-plasmas [27], laser-plasma interaction [28], plasma sheet boundary layer of the earth’s magnetosphere [29], in the Van Allen radiation belts [30]. The relativistic effects may be induced by the fluid velocity of the relativistic particles which has speed near the light velocity. Also it is possible that the relativistic effects are induced by thermal effects of the particles under concern. In this case, the ratio T/mc 2 cannot be neglected. Moreover, one can consider a pair (electrons and positrons) production by relativistic ions as studied by Becker et al. [31].

It has been found that the electron and ion distributions play the crucial role in characterizing the physics of the nonlinear wave structures [32–37]. Numerous investigations of space plasmas [35–43] clearly indicate the presence of superthermal electron and ion structures as ubiquitous in a variety of astrophysical plasma environments. The latter may arise due to the effect of external forces acting on the natural space environment plasmas or to the wave-particle interaction which ultimately leads to kappa-like distributions. As a consequence, a high-energy tail appears in the distribution function of the particles. Only a few investigations have been reported on the study of ion acoustic waves in high relativistic plasmas [44, 45].

The motivation of the present paper is to study the existence of ion acoustic solitary waves in high relativistic plasmas with superthermal electrons and thermal positrons.

2 Basic equations

Consider one-dimensional, collisionless, unmagnetized high relativistic plasmas with thermal positrons and q-nonextensive electrons. Charge neutrality at equilibrium gives n 0e  = n 0p  + n 0 where n 0, n 0e and n 0p are unperturbed ion, electron and positron number densities respectively. The nonlinear dynamics of the low frequency ion-acoustic solitons in the three component plasmas are governed by the following set of equations [23]

$$ \begin{gathered} \frac{\partial n}{\partial t} + \frac{\partial (nu)}{\partial x} = 0 \hfill \\ \frac{\partial (\gamma u)}{\partial t} + u\frac{\partial (\gamma u)}{\partial x} + \frac{\partial \phi }{\partial x} = 0 \hfill \\ \frac{{\partial^{2} \phi }}{{\partial x^{2} }} = n_{e} - n - n_{p} \hfill \\ \end{gathered} $$
(1)

where n and u are ion number density and ion fluid velocity respectively. ϕ and γ are electrostatic potential and relativistic factor respectively. For high relativistic plasmas parameter γ is approximated by its expansion up to term u 4/c 4 as

$$ \gamma = \left( {1 - \frac{{u^{2} }}{{c^{2} }}} \right)^{{ - \frac{1}{2}}} \,\cong\, 1 + \frac{{u^{2} }}{{2c^{2} }} + \frac{{3u^{2} }}{{8c^{4} }} $$
(2)

Here and in the following, the subscript j = e, p stands for electrons and positrons, respectively. Considering this assumption, mj, nj and Tj are mass, density and temperature of electrons and protons. In order to modelling the effects of superthermal electrons, we use [38]

$$ n_{e} = \left( {1 - \frac{\phi }{\kappa - 1/2}} \right)^{ - \kappa - 1/2} $$
(3)

The parameter κ shapes predominantly the superthermal tail of the distribution [39] and the normalization is provided for any value of the spectral index κ > 1/2 [38]. Equation (3) reduces to the well known Maxwell- Boltzmann electron density, in the limit κ → ∞. Positrons are assumed to be in thermal equilibrium with the density of

$$ n_{p} = p\exp ( - \sigma \phi ) $$
(4)

where σ = T e /T p and p = n 0p /n 0e . The subscript “0” stands for equilibrium unperturbed quantities. In Eq. (1), the electrostatic potential, particle densities, ion velocity, space variable, and time variable are normalized by T e /e, unperturbed electron density n 0e , ion-acoustic speed c i  = (T e /m)1/2, electron Debye length \( \lambda_{D} = \left( {T_{e} /4\pi n_{0e} e^{2} } \right)^{1/2} \) and electron plasma period \( T = \left( {m_{e} /4\pi n_{0e} e^{2} } \right)^{1/2} \) respectively.

3 Derivation of the KdV equation

As mentioned before, reductive perturbation method has been used in order to investigate the behaviour of nonlinear ion acoustic waves in this plasma medium. The stretched coordinates are defined as follows [23]

$$ \xi = \varepsilon^{1/2} (x - \lambda t),\quad \tau = \varepsilon^{3/2} t $$
(5)

where ε is a small parameter which characterizes the strength of the nonlinearity and λ is the phase velocity of propagated wave. Dependent variables are expanded as follows

$$ \begin{aligned} & n = 1 + \varepsilon n_{1} + \varepsilon^{2} n_{2} + \varepsilon^{3} n_{3} + \ldots , \\ & u = u_{0} + \varepsilon u_{1} + \varepsilon^{2} u_{2} + \varepsilon^{3} u_{3} + \ldots , \\ & \phi = \varepsilon \phi_{1} + \varepsilon^{2} \phi_{2} + \varepsilon^{3} \phi_{3} + \ldots . \\ \end{aligned} $$
(6)

By substituting Eq. (6) into Eq. (1), using Eq. (5) and collecting the terms with different powers of ε, one can derive the following equations in the lowest order of ε

$$ \begin{aligned} n_{1} = \frac{(1 - p)}{{\lambda - u_{0} }}u_{1} ,\quad u_{1} = \frac{{\phi_{1} }}{{\gamma_{1} (1 - p)}}, \\ & n_{1} = \left( {\frac{2\kappa + 1}{2\kappa - 1} + p\sigma } \right)\phi_{1} \\ & \left( {\lambda - u_{0} } \right)^{2} = \frac{1 - p}{{\gamma_{1} \left( {\frac{2\kappa + 1}{2\kappa - 1} + p\sigma } \right)}}\end{aligned}$$
(7)

where \( \gamma_{1} = 1 + \frac{{3u_{0}^{2} }}{{2c^{2} }} + \frac{{15u_{0}^{4} }}{{8c^{4} }}. \) For the higher orders of ε, we have

$$ \left( { - \lambda + u_{0} } \right)\frac{{\partial n_{2} }}{\partial \xi } + \frac{{\partial n_{1} }}{\partial \tau } + \frac{{\partial \left( {n_{1} u_{1} } \right)}}{\partial \xi } + \left( {1 - p} \right)\frac{{\partial u_{2} }}{\partial \xi } = 0 $$
$$ \frac{{\partial^{2} \phi_{1} }}{{\partial \xi^{2} }} - \left( {\frac{2\kappa + 1}{2\kappa - 1} + p\sigma } \right)\phi_{2} + \left( {\frac{{p\sigma^{2} }}{2} - \frac{{\left( {2\kappa + 1} \right)\left( {2\kappa + 3} \right)}}{{2\left( {2\kappa - 1} \right)^{2} }}} \right)\phi_{1}^{2} + n_{2} = 0 $$
(8)
$$ \left[ {\gamma_{1} - \left( {\lambda - u_{0} } \right)\left( {\frac{{3u_{0} }}{{c^{2} }} + \frac{{15u_{0}^{3} }}{{2c^{4} }}} \right)} \right]u_{1} \frac{{\partial u_{1} }}{\partial \xi } - \gamma_{1} \left( {\lambda - u_{0} } \right)\frac{{\partial u_{2} }}{\partial \xi } + \gamma \frac{{\partial u_{1} }}{\partial \tau } + \frac{{\partial \phi_{2} }}{\partial \xi } = 0 $$
$$ \frac{{\partial^{2} \phi_{1} }}{{\partial \xi^{2} }} - \left( {\frac{2\kappa + 1}{2\kappa - 1} + p\sigma } \right)\phi_{2} + \left( {\frac{{p\sigma^{2} }}{2} - \frac{{\left( {2\kappa + 1} \right)\left( {2\kappa + 3} \right)}}{{2\left( {2\kappa - 1} \right)^{2} }}} \right)\phi_{1}^{2} + n_{2} = 0 $$

Finally the KdV equation is derived from Eqs. (7) and (8) as

$$ \frac{{\partial \phi_{1} }}{\partial \tau } + A\phi_{1} \frac{{\partial \phi_{1} }}{\partial \xi } + B\frac{{\partial^{3} \phi_{1} }}{{\partial \xi^{3} }} = 0 $$
(9)

where

$$ A = \frac{1}{2}\left[ {\frac{3}{{\left( {\lambda - u_{0} } \right)\gamma_{1} }} - \frac{{\gamma_{2} }}{{\gamma_{1}^{2} }} - \frac{{\gamma_{1} \left( {\lambda - u_{0} } \right)^{3} \left( {\frac{{\left( {2k + 1} \right)\left( {2k + 3} \right)}}{{\left( {2k - 1} \right)^{2} }} - p\sigma^{2} } \right)}}{{\left( {1 - p} \right)}}} \right],\quad B = \frac{{\gamma_{1} \left( {\lambda - u_{0} } \right)^{3} }}{2} $$
(10)

where \( \gamma_{1} = 1 + \frac{{3u_{0}^{2} }}{{2c^{2} }} + \frac{{15u_{0}^{4} }}{{8c^{4} }}, \) \( \gamma_{2} = \frac{{3u_{0} }}{{c^{2} }} + \frac{{15u_{0}^{3} }}{{2c^{4} }}. \)

Equation (9) is the well-known KdV equation describes the nonlinear propagation of ion acoustic solitary waves in the described media. In this equation, A and B are the nonlinear and dispersion coefficients. The stationary solution of Eq. (9) is given by

$$ \phi_{1} = \phi_{0} \sec h^{2} \frac{{\left( {\xi - U\tau } \right)}}{w} $$
(11)

in which U is constant velocity of the solitary wave. The ion acoustic wave amplitude (ϕ0) and its width (w) are given as

$$ \phi_{0} = \frac{3U}{A},\quad w = 2\sqrt \frac{B}{U} $$
(12)

Parameters A and B can be compared with the results which are published in [40] with electrons following a superthermal distribution. Note that plasma components in [40] are not relativistic.

4 Results and discussion

We have two new phenomena in the media in comparison with usual e–p–i plasmas. The first is the effect of the superthermal electrons which come into the equations through the parameter κ and the second is the relativistic ions which affect on the media through γ1 and γ2 in different terms of the equations. These effects change the soliton behaviour in complicated ways. Therefore we have to investigate these effects using some simple approximations with marginal values of these parameters for the coefficients A and B. Numerical calculations also can be employed for better clarifications. One can find from Eq. (7) that \( \left( {\lambda - u_{0} } \right) \propto \frac{1}{{\sqrt {\gamma_{1} } }} \). On the other hand Eq. (10) gives

$$ A \approx \frac{1}{2}\left[ {\frac{3}{{\left( {\lambda - u_{0} } \right)\gamma_{1} }} - \frac{{\gamma_{1} \left( {\lambda - u_{0} } \right)^{3} \left( {\frac{{\left( {2k + 1} \right)\left( {2k + 3} \right)}}{{\left( {2k - 1} \right)^{2} }} - p\sigma^{2} } \right)}}{{\left( {1 - p} \right)}}} \right] \propto \frac{1}{{\sqrt {\gamma_{1} } }},\quad B = \frac{{\gamma_{1} \left( {\lambda - u_{0} } \right)^{3} }}{2} \propto \frac{1}{{\sqrt {\gamma_{1} } }}. $$
(13)

Note that γ2/γ 21 is very small in comparison with the other terms. This means that both A and B decreases when the ion velocity u 0 increases. Therefore soliton amplitude ϕ0 increases and the soliton width w decreases when u 0 get increased. This is a new result in comparison with the other similar papers with nonrelativistic particles [40, 41].

It has been shown that only compressive solitons can be created in e–p–i solitons with Maxwell- Boltzmann distributed particles [41, 42]. For superthermal distribution Eq. (3) reduces to usual Maxwell–Boltzmann density with large values for κ. Therefore we need to investigate soliton characters in small values of κ \( \left( {\kappa \to \frac{1}{2}} \right) \). For small values of κ the term 2κ − 1 becomes very large and Eq. (10) can be approximated as

$$ A \approx \frac{1}{2}\frac{1}{{\sqrt {2\kappa - 1} }}\left[ {3\sqrt {\frac{(2\kappa + 1)}{{\gamma_{1} (1 - p)}}} - \sqrt {\frac{(1 - p)}{{\gamma_{1} (2\kappa + 1)}}} (2\kappa + 3)} \right],\quad B \approx \frac{1}{2}\sqrt {\gamma_{1} (1 - p)} \left( {\sqrt {\frac{2\kappa - 1}{2\kappa + 1}} } \right)^{3} . $$
(14)

Therefore one can find that A → ∞ and B → 0 when \( \kappa \to \frac{1}{2} \). This means that the soliton height and also its width decreases in the limit \( \kappa \to \frac{1}{2} \).

A rarefactive soliton is created if A becomes negative and from Eq. (14) the condition is

$$ 3\sqrt {\frac{(2\kappa + 1)}{{\gamma_{1} (1 - p)}}} < \sqrt {\frac{(1 - p)}{{\gamma_{1} (2\kappa + 1)}}} (2\kappa + 3). $$
(15)

Thus the condition for establishing a rarefactive soliton becomes \( \kappa < \frac{ - 3p}{4 + 2p} \) and it is impossible. Therefore a rarefactive soliton will not be created in this plasma at all.

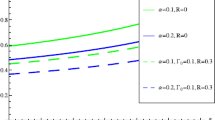
Let us look at the figures which have been plotted using Eq. (10). Figure 1 presents the soliton amplitude as a function of η0 = u 0/c with different values for the superthermal parameter κ. The other parameters have been taken as σ = 0.1, p = 0.6 and U = 0.2 in the Fig. 1. This figure shows that the soliton amplitude rapidly increases as η0 increases, specially for the large values of η0. Also Fig. 1 presents that the soliton amplitude increases with an increasing κ. Figure 2 demonstrates the soliton width as a function of η0 for different values of superthermal parameter κ. This figure clearly shows that the soliton width, a little bit decreases when η0 increases as one can find from Eq. (13) too. But soliton width increases with an increasing κ. Note that the increasing rate of the soliton width due to increasing in the superthermal parameter is very bigger than the decreasing because of the relativistic effects. This means that superthermality changes the soliton width dominantly. Figure 3 presents the soliton profiles as functions of ξ for different values of η0 and fixed values for the other parameters. This figure shows that the soliton height increases while its width decreases as η0 increases. This situation indicates that the soliton energy increases with an increasing η0. It is clear, because the relativistic particles increase the soliton energy. As soliton amplitude increases and the soliton width decreases, the soliton profile becomes spiky when relativistic effects become dominant. Soliton profiles have been sketched as functions of κ with fixed values for the other parameters in the Fig. 4. This figure clearly presents the effect of superthermal distributed electrons. This figure also shows that the soliton energy increases when κ increases. As mentioned before in the limit κ → ∞. The superthermal distribution reduces to the usual Maxwell–Boltzmann distribution. Therefore superthermal distributed electrons reduces the total energy of the soliton.

Fig. 1
figure 1

Soliton amplitude as a function of η0 with different values for the superthermal parameter κ. Other parameters are σ = 0.1, p = 0.6 and U = 0.2

Full size image
Fig. 2
figure 2

Soliton width as a function of η0 with different values for the superthermal parameter κ. The other parameters have been chosen as σ = 0.1, p = 0.6 and U = 0.2

Full size image
Fig. 3
figure 3

Soliton profiles as functions of η0 with σ = 0.1, p = 0.6, κ = 0.8 and U = 0.2

Full size image
Fig. 4
figure 4

Soliton profiles as functions of κ with σ = 0.1, p = 0.6, u0 = 0.4 and U = 0.2

Full size image

In recent years, a new statistical approach [46, 47], nonextensive statistics or Tsallis statistics, has attracted much attention. This statistics is believed to be a useful generalization of the conventional Boltzmann–Gibbs statistics, and suitable for the statistical description of long-range interaction systems, such as plasma systems [48–55]. Note that because of a lack of formal derivation, a nonextensive approach to kappa-distributions has been suggested [56]. It has been shown that distributions very close to the so-called κ (kappa)-distributions are a consequence of the generalized entropy favored by nonextensive statistics. The transformation linking q-statistics and κ-distributions was first provided by Leubner. The κ-distributions turned out as a consequence of the entropy generalization, thus providing the missing link between power-law models of suprathermal tails and fundamental physics [57, 58].

On the basis of this theoretical formulation and making use of a generalized dispersion relation and a generalized instability growth rate Liu et al. [52, 59] showed that the nonextensive parameter can be written in terms of the following relation

$$ \nabla T_{j} + \left( {1 - q_{j} } \right)Q_{j} \nabla \phi = 0 $$
(16)

where j refers to the plasma particle species, T j are the temperatures (in energy unit), q j the nonextensive parameters, Q j the charges, and ϕ the potential function (which can be any potential, Coulombian or gravitational). If q = 1, we have ∇T j  = 0, which stands for the thermal equilibrium state, where the particles are in Maxwellian distribution. If q j  = 1, we have ∇T j  = 0, which stands for the Maxwell–Boltzmann thermal equilibrium state. If q j  ≠ 1, we have ∇T j  ≠ 0, which stands for nonequilibrium stationary state. The kappa indices, k j , can be calculated directly by replacing the nonextensive parameters q in Eq. (16) with the transformation, \( k_{j} = \frac{1}{{q_{j} - 1}} \). In the limit k j  → ∞, we have ∇T j  = 0 and the thermal equilibrium state is recovered.

5 Conclusions

There exist high relativistic plasmas, because of the existence of fluid velocity of the relativistic particles or relativistic effects which are induced by thermal effects. Therefore the small amplitude ion acoustic solitary waves in plasmas consisting of high relativistic ions, superthermal electrons and thermal positrons have been investigated. It is shown that the KdV equation governs the propagation of these nonlinear waves. The marginal behaviours of the soliton amplitude and its width described using some analytical relations. It is shown that the soliton amplitude increases when the speed of relativistic ions (η0) increases. Also it decreases when superthermal parameter κ decreases. But only the compressive solitons can be created even if the superthermal effects become dominant. Therefore we would not seen critical values of the parameters for creating small amplitude solitons in this medium. The soliton width increases when κ increases, but it decreases with an increasing η0. Thus increasing η0 and κ raise the soliton energy.