1 Introduction

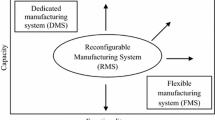
In today’s manufacturing scenario, some of the important challenges faced by manufacturers include product variety, reducing the product cost and increasing the productivity with optimum utilization of resources. Although traditional manufacturing systems like dedicated manufacturing lines (DMLs) are capable of rapidly producing identical products (mass production) but are incapable of accommodating the product variety. On the contrary, Flexible Manufacturing Systems (FMSs) are capable of accommodating the product variety but the productivity of these systems is low when compared with DMLs [19]. Further, the installation and operation of FMSs are considered to be costly and because of this, FMSs have very limited acceptability among the manufacturers [20]. A new class of manufacturing systems knows as Reconfigurable Manufacturing System (RMS) has the capability to adjust both capacity and functionality in order to cope up with product variety and production volume [4]. The RMS is having customized flexibility for a particular part family and is open ended so that it can be improved, upgraded, and reconfigured, rather than replaced [19]. Unlike the traditional systems, the focus of these RMSs is both “on part” as in case of dedicated manufacturing lines and “on machines” as for flexible manufacturing system. These RMSs focus its design and operation around a part family [10]. A part family can be defined as a group of products having some common design or manufacturing features. The literature revealed that very few RMSs are also designed around multiple part families [5, 22, 29]. In summary it can be said, RMS provides the customized functionality and capacity as and when required and its configuration can be dedicated or flexible, or in between and can be changed as required. The design and operation aspects of RMSs have been studied by various researchers in the past but some important contributions include the work carried out by Liles and Huff [16], Makino and Arai [18], Rheault et al. [23], Aranson [1], Lee [15], Koren et al. [11] and Xiaobo et al. [29–32]. The designing of an RMS begins with the classification of products into part families. All the orders belonging to a family of products can be produced on a particular configuration of RMS. After completing all of the orders of a specific family, the RMS is reconfigured for subsequent production of orders belonging to a different family. The same process of system reconfiguration is repeated till all the orders of each family are completed [5, 22, 29]. There may exist several configurations for each family [9, 14, 35]. These configurations are distinct due to different production characteristics like various costs associated with the production process and the changeover costs associated with the process of reconfiguration. An important design issue in an RMS is the optimal reconfiguration policy for distinct families of products which are to be manufactured, because different configurations have a significant impact on profits [29]. The following are some of the important researches carried out on optimal reconfiguration policies and their impact on system performance for an RMS.

Spicer et al. [26] and Yang and Hu [34] showed that with the same number of machines pure parallel configuration have better throughput and scalability performance when compared with series and mixed configurations. Koren et al. [12] demonstrated that the system configuration has a significant impact on six key system performance measures (investment cost of machines and tools, quality, throughput, capacity scalability, number of part families and system ramp up time). Maizer-Speredelozzi et al. [17] studied the effect of various configurations on systems convertibility. System performance with respect to productivity, quality, scalability and convertibility for different system configurations were studied by Zhong et al. [40]. Kimms [8] presented a mathematical model for the optimization of a flow line configuration involving multiple parts. The configuration optimization was based on minimizing the number of stages and machines in these stages. Toenshoff et al. [28] proposed an evolution based algorithm based on subjective ratings. Each of the new configurations is tested in a simulation environment and rated according to the user requirements. Only the best solutions for the required manufacturing system are used to continue with the evolution process until the ratings reach pre-defined stopping criteria. Youssef and ElMaraghy [37] coined the term “reconfiguration smoothness (RS)” that reflects the ease and smoothness of transforming the system from one configuration to the next. Youssef [36] further developed a stochastic model for evaluating the RS over a planning horizon and proposed a reconfiguration planning procedure that generates execution plans of reconfiguration. Kuo [13] and Yamada et al. [33] proposed a reconfiguration policy based on optimized equipment layout assignment for RMS with the objective of minimizing the total transportation time. The literature reviewed clearly revealed that most of the work done either focused on the cost and economic benefits during performance evaluation [6, 7, 21, 24, 29–32, 38]. Very few studies consider other system evaluation criteria like throughput [25, 27] and system availability [39]. Though, the economic aspect of these RMSs was mostly confined to systems involving single part family having one or two products. RMS involving multiple part families are very few and researches on these systems have not considered the sequence in which these part families are selected for producing orders. For a multi part family RMS sequence may also become all important for obtaining the optimal configuration. Some of the studies which take into account the reconfiguration aspect of these manufacturing systems along with their features and drawbacks are summarized in Table 1.

Table 1 Some past researches on optimal configuration selection in RMS
Full size table

The decision regarding configuration selection of the manufacturing system is very crucial and is dealt with all the possible consequences as it reflects the cost the product which is to be produced within this system. In the past several authors presented researches on optimal reconfiguration policies based on some objective functions and using various optimization techniques. Important researches include Youssef and ElMaraghy [38, 39], Dou et al. [2], Du et al. [3], Xiaobo et al. [29–32]. According to Xiaobo et al. [29], the reconfiguration selection policy determines the action of the manufacturer in the utilization period of an RMS. For example upon completing a production task, depending upon the system state the manufacturer has to decide a candidate part family and process its orders. The selection policy for the part family for a system state is an action rule by which the manufacturer selects a family. The two key issues for designing and operating an RMS include optimal configuration selection and the optimal sequence of the part families under the selected configuration. Thus, this work focuses on the following two objectives

  1. 1.

    Determining the optimal configuration based on some objective criterion for RMS dealing with multiple part families. In this work, the objective function is based on maximizing the expected benefit earned while executing orders belong to various part families on an RMS configuration.

  2. 2.

    For any configuration, it is required to find the optimal sequence of execution of orders belonging to various part families.

The motivation behind the above two objectives is based on the fact that most of the past studies done on optimum configuration selection problems are based on single part family RMSs. Also, the sequence of executions of orders is important as this consideration may have a pronounced effect on the economic profits or benefits earned during the operation of RMSs.

For the above two objectives, the model of an RMS is formulated and is applied on a numerical example which is presented in the following sections.

2 Model of an RMS

2.1 Nomenclature

PF i :

Part families for which orders are recorded, where i = 1,2,3… … … n.

λ i :

Poisson’s Arrival Rate of orders for i th part family.

M i :

Maximum limit on orders for i th part family to be accepted.

x i :

Number of orders recorded for i th part family during the recording interval.

P(x i ,λ i ):

Poisson’s probability of recording x i orders for i th part family having arrival rate of λ i .

S j  = {x 1 , x 2 … x n }:

State of orders at any time, where x 1 , x 2 … x n corresponds to number of orders of part families PF 1, PF 2 … PF i  where 0 ≤ x 1 ≤ M 1, 0 ≤ M 2, … 0 ≤ x i  ≤ M i  and 1 ≤ j ≤ {(M 1 + 1)(M 2 + 1) … (M i  + 1) … (M n  + 1) − 1}.

P(S j ):

State probability of an order mix i.e. S j .

\( C{S}_{K_i} \) :

Set of feasible configurations to process i th part family, where K i is the cardinality of the set; and \( {C}_i^k\in C{S}_{K_i} \) are its elements representing k th feasible configuration to process i th part family, where 1 ≤ k ≤ K i .

SS l :

Solution Space (combination of configurations for producing the orders for all the part families), where 1 ≤ l ≤ ∏  n i = 1 K i .

R(C k i ):

Reward associated with producing an order belonging to i th part family using its k th configuration.

P(C k p  : C z q ):

Penalty associated while switching from production of p th part family with k th configuration to the production of q th part family with its z th configuration.

E(B):

Expected Benefit.

ϑ :

Optimal configuration, where ϑ ϵ SS l .

2.2 Assumptions

  • Various products to be manufactured can be classified into distinct part families, PFi.

  • The orders for each part families follow Poisson distribution with an arrival rate, λ i .

  • The orders of various part families are recorded only for certain time duration beyond which no further order is accepted till that production run period is over.

  • There is a maximum limit M i on the number of orders that are accepted for various part families and any new order beyond this limit is rejected.

  • Simultaneous arrival of orders belonging to two or more part families is not considered.

  • Time required for changing from one configuration to another is not considered.

2.3 Operation of RMS

Consider an RMS capable of producing several part families. The state of order, S j  = {x 1, x 2 …  x n } where {x i |0 ≤ x i  ≤ M i } is defined after recording the orders of various part families over a recording period. The null state, S 0 = {0, 0 …  0} is defined as that state during which no order is recorded for any of the part family and it has been excluded from the present study i.e. S 0 ∉ S j . The probability P(x i ,λ i ) for the number of orders of any part family is calculated using Poisson distribution as follows.

$$ P\left({x}_i,{\lambda}_i\right)=\frac{\left({e}^{-{\lambda}_i}\right)\left({\lambda}^{x_i}\right)}{x!} $$
(1)

Since the events of accepting orders of different part families are independent, thus the probability of state, P(S j ) is calculated as

$$ P\left({S}_j\right)={\displaystyle \prod_{i=1}^nP\left({x}_i,{\lambda}_i\right)} $$
(2)

When an RMS completes an order of a particular part family, an expected reward R(C k i ) is earned. The expected reward so earned may differ from one selected configuration to another because of the capabilities and limitations associated with the selected system elements like reconfigurable machines tools (RMTs), controllers, AGV etc. Once all the orders of a particular family are completed, another distinct family is selected for subsequent production of its orders and the system needs to be reconfigured as per operational requirements of its various parts. Thus, some reconfiguration penalty, P(C k p  : C z q ) is incurred while changing over from one configuration to another.

Let K i be the number of configurations on which the orders of i th part family can be executed. The orders belonging to i th part family can be produced by any configuration chosen from set \( C{S}_{K_i} \)

$$ C{S}_{K_i}=\left\{\begin{array}{l}{C}_i^1\hfill \\ {}{C}_i^2\hfill \\ {}\vdots \hfill \\ {}{C}_i^{K_i}\hfill \end{array}\right\} $$
(3)

The solution space for all possible combinations of configurations can be obtained as

$$ S{S}_l={\displaystyle \underset{i=1}{\overset{n}{\cup }}\left\{C{S}_{K_i}\right\}=\left\{{C}_1^{K_1},{C}_2^{K_2},\kern0.5em \dots \kern0.5em {C}_i^{K_i}\dots, {C}_n^{K_n}\right\}} $$
(4)

For any system configuration SS l , at any observed state of orders S j , the objective is to select the orders for that family which amount to highest expected benefit, E(B) associated with its selection. This includes both the reward associated with completion of orders of that family and the penalty associated with changeover from the present configuration of the system to the new configuration selected for the production of orders of the selected family. The objective function can be formulated as

$$ Expected\kern0.5em Benifit,\kern0.5em E(B)= Maximize\left[P\left({S}_j\right){\displaystyle \sum \left\{R\left({C}_i^k\right){x}_i-P\left({C}_p^k:{C}_q^z\right)\right\}}\right] $$
(5)

For any given state of orders S j , there exists a solution space SS l which consists of all possible combinations of configurations to process orders of all the part families as listed in S j .

The objective of this algorithm is to determine the expected benefit accrued by processing all the part families as given in S j in various possible sequences. Finally, the best sequence of part families is selected which results in maximum expected benefit. This step is repeated for all for possible combinations of configurations and finally out of the total solutions which results in maximum overall benefit is selected as the optimal solution to process the part families in the selected sequence in the selected system configurations.

The following algorithm explains the step by step procedure.

  • STEP 1: List all the possible states of orders (S j ) and solution space set (SS l ).

  • STEP 2: Calculate P(x i ,λ i ) and P(S j ) for all the observed states of orders using Eqs. (1) & (2).

  • STEP 3: For a given combination of configuration within the solution space set calculate the expected benefit for all the possible sequences of the part families using objective function defined in Eq. (5).

  • STEP 4: Select the local optimal sequence as the one having maximum value of expected benefit for that particular combination of configuration within the solution space.

  • STEP 5: Repeat step-4 for all the elements of solution space set (SS l ).

  • STEP 6: Select the global optimal configuration (ϑ) as the having the highest value of maximum benefit and the global optimal sequence the one associated with this selected configuration.

3 An example

Consider an RMS that executes orders belonging to three distinct part families, PF 1, PF 2 and PF 3 with the maximum number of orders to be accepted for each family as; M 1 = 4, M 2 = 3 and M 3. Based on the maximum limit on the number of orders, the state of orders (S j ) is thus composed of 79 distinct states {(M 1 + 1)(M 2 + 1)(M 3 + 1) − 1}. The null state (S 0) is excluded from the state of orders. The various parameters used to design the RMS and the possible combinations of configurations are presented in Tables 2 and 3 respectively.

Table 2 Design and operational parameter for the RMS
Full size table
Table 3 Solution space for possible configurations
Full size table

The probabilities of arrival of orders of various part families for each observed order states (S j ) are calculated using Eqs. (1) and (2). For the solution space set SS l , under any observed state, the optimum selection of sequence of part families for completion of its orders is carried out using the objective function presented in Eq. (5). Few sample calculations are shown as below:

$$ \begin{array}{l} Say,\kern-0.1em under\kern-0.1em observed\kern-0.1em state\kern-0.1em {S}_{74}:\left\{4,2,3\right\},P\left({S}_{74}\right)=0.0037\hfill \\ {} For\kern-6em solution\kern-6em space\kern-6em {\mathrm{SS}}_1\hfill \\ {} IF\kern-0.5em sequence\kern-1em {\mathrm{PF}}_1\to {\mathrm{PF}}_2\to {\mathrm{PF}}_{3\ }\kern-1em is\kern-1em followed,\hfill \\ {} THEN\hfill \\ {}\begin{array}{c}\hfill expected\kern0.5em benifit=0.0037\left[\left(4*200\right)+\left(2*470-32\right)+\left(3*720-12\right)\right]\hfill \\ {}\hfill =14.26\hfill \end{array}\hfill \end{array} $$
$$ \begin{array}{l} IF\kern-1em sequence\kern-1em {\mathrm{PF}}_1\to {\mathrm{PF}}_3\to {\mathrm{PF}}_{2\ }\kern-1em is\kern-0.8em followed,\hfill \\ {} THEN\hfill \\ {}\begin{array}{c}\hfill expected\kern0.5em benifit=0.0037\left[\left(4*200\right)+\left(3*720-49\right)+\left(2*470-10\right)\right]\hfill \\ {}\hfill =14.21\hfill \end{array}\hfill \end{array} $$
$$ \begin{array}{l} IF\kern-1em sequence\kern-1em {\mathrm{PF}}_2\to {\mathrm{PF}}_1\to {\mathrm{PF}}_{3\kern-0.5em } is\kern-1em followed,\hfill \\ {} THEN\hfill \\ {}\begin{array}{c}\hfill expected\kern0.5em benifit=0.0037\left[\left(2*470\right)+\left(4*200-51\right)+\left(3*720-49\right)\right]\hfill \\ {}\hfill =14.06\hfill \end{array}\hfill \end{array} $$
$$ \begin{array}{l} IF\kern-1em sequence\kern-1.2em {\mathrm{PF}}_2\to {\mathrm{PF}}_3\to {\mathrm{PF}}_{1\kern-5em } is\kern-1em followed,\hfill \\ {} THEN\hfill \\ {}\begin{array}{c}\hfill expected\kern0.5em benifit=0.0037\left[\left(2*470\right)+\left(3*720-12\right)+\left(4*200-38\right)\right]\hfill \\ {}\hfill =14.24\hfill \end{array}\hfill \end{array} $$
$$ \begin{array}{l} IF\kern-1em sequence\kern-1em {\mathrm{PF}}_3\to {\mathrm{PF}}_1\to {\mathrm{PF}}_{2\ }\kern-1.5em is\kern-1em followed,\hfill \\ {} THEN\hfill \\ {}\begin{array}{c}\hfill expected\kern0.5em benifit=0.0037\left[\left(3*720\right)+\left(4*200-38\right)+\left(2*470-32\right)\right]\hfill \\ {}\hfill =14.17\hfill \end{array}\hfill \end{array} $$
$$ \begin{array}{l} IF\kern0.5em sequence\kern0.5em P{F}_3\to P{F}_2\to P{F}_{1\ }\kern0.5em is\kern0.5em followed,\hfill \\ {} THEN\kern-5em expected\kern-5em benifit\hfill \\ {}\kern3.72em =0.0037\left[\left(3*720\right)+\left(2*470-10\right)+\left(4*200-51\right)\right]\hfill \\ {}\kern3.72em =14.20\hfill \end{array} $$
$$ \begin{array}{l} Thus,\kern0.5em the\kern0.5em local\kern0.5em optimal\kern0.5em sequence\hfill \\ {} is\kern0.75em P{F}_1\to P{F}_2\to P{F}_{3\ } with\kern0.5em maximum\kern0.5em benifit\kern0.5em as\kern0.75em 14.26\hfill \end{array} $$
$$ \begin{array}{l} Similary,\hfill \\ {} For\kern-5.5em {\mathrm{SS}}_2,\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.75em P{F}_1\to P{F}_2\to P{F}_{3\ }\kern0.5em with\hfill \\ {} maximum\kern-3.5em benfit\kern-3.5em as\kern-3.5em 12.4\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_3,\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.5em P{F}_3\to P{F}_1\to P{F}_{2\ }\kern0.5em with\hfill \\ {} maximum\kern-3.5em benfit\kern-3.5em as\kern-3.5em 12.9\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_4,\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.5em P{F}_2\to P{F}_1\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern-3.5em benfit\kern-3.5em as\kern-3.5em 11.3\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_5,\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.75em P{F}_3\to P{F}_2\to P{F}_{1\ }\ with\hfill \\ {} maximum\kern-3.5em benfit\kern-3.5em as\kern-3.5em 15.29\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_6,\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.5em P{F}_2\to P{F}_1\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern-3.5em benfit\kern-3.5em as\kern-3.5em 13.49\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_7,\hfill \\ {}\kern0.5em local\ optimal\ sequence\ is\kern0.5em P{F}_1\to P{F}_2\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern-3em benfit\kern-3em as\kern-3em 13.94\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.25em S{S}_8,\hfill \\ {} local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.5em P{F}_1\to P{F}_2\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern-3em benfit\kern-3em as\kern-3em 12.29\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5em S{S}_9,\hfill \\ {}\kern0.5em local\ optimal\ sequence\ is\kern0.5em P{F}_1\to P{F}_2\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern-3em benfit\kern-3em as\kern-3em 10.71\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em S{S}_{10},\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.5em P{F}_2\to P{F}_1\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern-3.2em benfit\kern-3.2em as\kern-3.2em 11.71\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_{11},\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.75em P{F}_1\to P{F}_2\to P{F}_{3\ }\ with\hfill \\ {} maximum\kern0.5em benfit\ as\ 12.19\hfill \end{array} $$
$$ \begin{array}{l} For\kern-5.5em {\mathrm{SS}}_2,\hfill \\ {}\kern0.5em local\kern0.5em optimal\kern0.5em sequence\kern0.5em is\kern0.5em P{F}_1\to P{F}_3\to P{F}_{2\ }\ with\hfill \\ {} maximum\kern-3em benfit\kern-3em as\kern-3em 10.58\hfill \end{array} $$
$$ \begin{array}{l} Thus,\hfill \\ {} The\kern-5em global\kern-5em optimal\kern-5em sequence\kern-5em obatined\hfill \\ {} is\kern0.75em P{F}_3\to P{F}_2\to P{F}_{1\ } for\kern0.5em S{S}_5:\left\{\begin{array}{ccc}\hfill {C}_1^2\hfill & \hfill {C}_2^1\hfill & \hfill {C}_3^1\hfill \end{array}\right\} with\kern0.5em maximum\kern0.5em benfit\kern0.5em as\kern0.5em 15.29\hfill \end{array} $$

The objective is to identify a configuration (ϑ) from the solution space set, SS l and the corresponding sequence of execution of orders of part families which gives maximum expected benefit based on the algorithm presented above. The optimal configuration(s), optimal sequence and expected benefit obtained for various order states are shown in Table 4.

Table 4 Optimal configuration and corresponding sequence of part families for execution of orders
Full size table

The results obtained for optimal configuration and the corresponding sequence of execution of orders belonging to the part families along with the expected benefit for all the order states are presented in Table 4. The results for the numerical data used in the example showed for the order states of the form {x 1,0,0}, configurations SS 5, SS 6, SS 7 and SS 8 are the optimum configuration for executing orders belonging to part family PF 1. It is important to note here that among all these configurations only C 21 (marked in bold) is relevant as this individual element within these combination of configuration is responsible for producing orders belonging to part family PF 1 as there are no recoded orders for the other two part families viz PF 2 and PF 3. Similarly, for order state of the form {0,x 2,0}, optimum configurations obtained are SS 1, SS 2, SS 5, SS 6, SS 9, and SS 10. Within these optimum configurations the relevant individual configuration for producing orders of part family PF 2 is C 12 (marked in bold). For order states of the form {0,x 2,0}, optimum configuration obtained are SS 1, SS 3, SS 5, SS 7, SS 9, and SS 11 with common relevant individual configuration C 13 for producing orders of part family PF 3. In all these three forms of order states the sequence of execution of orders is immaterial as orders recoded belongs to only single individual part families. For order states of the form {x 1,x 2,0}, {x 1,0,x 3} and {0,x 2,x 3} the optimal configurations obtained are SS 5, SS 6; SS 5, SS 7 and SS 1, SS 5, SS 7 respectively. The two individual relevant configurations for these three from of state orders have been marked bold in Table 4. For these forms of order states under each optimum configuration the corresponding sequence of execution of orders of the two part families obtained are PF 2 → PF 1, PF 1 → PF 3 and PF 1 → PF 3. If the state of order is of the form {x 1,x 2,x 3}, where there are some recorded orders of each part family the optimum configuration obtained is SS 5 with the corresponding optimum sequence of part families as PF 3 → PF 2 → PF 1. It has been found that irrespective of the form of order states configuration SS 5 is a common optimum configuration ϑ.

4 Conclusion and scope for future research

The proposed solution to the problem gives an important insight regarding various types of costs to be taken into account while carrying out reconfiguration planning. The optimally selected configuration maximizes the expected benefit earned by the manufacturer. Though, the problem has been solved as an NP hard problem but some optimization techniques may also be used to obtain the solution which will reduce the computational efforts. Since, most of the earlier models for optimum selection of configurations available in literature focus on a single part family because of which the order of selection of part families became non application. Thus, the present methodology also suggests the sequence of part families orders which is to be followed for various configuration so that the expected benefit is maximized. The problem can be further extended to calculate the service level for distinct part families under consideration and the optimal configurations can be selected based on the criterion of service level for each part family.