1 Introduction

In a distributed space system, satellites operate collectively to achieve a common task. The rising interest for missions based on formation flying (Prisma [1], Grace [2], Tandem-X [3]) is mainly due to the high degree of flexibility offered by distributed space architecture. The possibility of substituting obsolete or damaged components for mission lifetime increase and the exploitation of multiple payloads for realization of sensors not conceivable with monolithic spacecraft are only few of the possibilities offered by these systems. Furthermore, the advanced miniaturization of single components is paving the way for distributed mission concepts based on small satellites [4], whose synergetic exploitation would in future allow reaching performance comparable to those of standard platforms.

The formation-flying potential is high especially in the field of remote sensing [5, 6]. Tandem-X is the most tangible result of this technology. In this case, the proper utilization of data collected by two spaceborne synthetic aperture radar (SAR) orbiting the Earth in a close formation enables the generation of digital elevation models of the whole Earth. The evolution of bistatic radar concept is that of multistatic SAR, where the antennas are distributed on several platforms. Such a system is capable of multiple acquisitions of the same target area in a single orbital pass. Moreover, both the availability of data acquired by physically separated devices and the possibility to implement different working modes permit various applications to be realized (3D imaging, moving target indication, high resolution-wide swath imaging, etc.).

If on the one hand the innovation offered by a fractionated SAR is high in terms of achievable products, on the other hand it entails novel aspects to be tackled from the system point of view. Among these, advanced Guidance Navigation and Control (GN&C) schemes are required to guarantee an autonomous formation flying, especially in the presence of short satellite separations. A leading role is played by formation keeping [7] and maintenance [8] algorithms that control the platform relative motion and ensure a periodic repetition of the desired spatial pattern [9]. Cluster re-configurability [10] is another relevant feature of fractionated space systems, with path-planning procedures enabling the satellites to adapt their arrangement according to various mission tasks [11, 12]. In the case of a distributed SAR, this entails a variation of the acquisition geometry, hence of achievable radar performance.

The cluster maneuverability necessitates both interacting satellites for satisfaction of safe requirements and advanced GN&C algorithms for real-time generation of transfer orbits. In this sense, the major research efforts are dedicated to the development of procedures relying on reduced communication and computation capabilities [13,14,15]. In this way, the reconfiguration can be easily run on smaller and less expensive platforms. Concerning the algorithm architecture, it can be centralized [16] or decentralized [17]. In the first case, a single unit manages the calculations entirely, while in the other, the computational load is split among the component satellites. This could be a benefit for the entire system that is not depending on a single spacecraft anymore. The cost to pay is an increased complexity of the procedure.

The contribution of this paper is in the development of a method for path planning and guidance of a spaceborne fractionated SAR system during the reconfiguration maneuver. The proposed strategy allows the spatial arrangement to be changed according to remote sensing requirements, such as geometric resolution or application type. To give an example, let us consider the sparse radar needs to be modified so that the combined antenna pattern could satisfy a particular mission objective. In this case, the proposed strategy would allow each satellite to

  • determine the formation target state,

  • define its role during the maneuver recurring to a task-assignment process,

  • compute a guidance trajectory enabling a safe transition from the initial to the final state (if required by task-assignment).

The procedure relies on a distributed architecture. Therefore, the satellites are supposed to be interconnected on a local network, but each platform is considered to manage autonomously its tasks and to elaborate on-board the transfer orbit.

Moving from SAR-interferometry typical requirements, this paper combines methods of astrodynamics trajectory optimization, task assignment and formation flying to delineate a strategy able to support the reconfiguration of a radar antenna distributed on small satellites. The paper content is organized as follows. Section 2 introduces the mathematical model for reconfiguring a satellite formation. Section 3 describes the derived approach, with emphasis on the main parts composing the algorithm. Simulation results are included in Sect. 4 to demonstrate the viability of the proposed method. Finally, the concluding remarks are given in Sect. 5.

2 Formation reconfiguration problem

A reconfiguration maneuver for a spacecraft formation is generally approached as a constrained optimization problem. In this case, the control law \(({\varvec{u}})\), hence the orbit transferring a generic satellite from an initial state \(({{\varvec{x}}}^{0})\) to a final one \(({{\varvec{x}}}^{f})\), is estimated by means of a procedure that optimizes a cost function \((C)\) with respect to some variables \(({\varvec{Z}})\) in the presence of several constraints.

The cost function can be defined to minimize the total propellant consumption (propellant-optimal reconfiguration) or the time \((t)\) required for the whole cluster to reach the target state (time-optimal reconfiguration). In both the cases, the mathematical formulation of the problem is

$$\mathrm{min}\;C\left({\varvec{Z}}\left({\varvec{t}}\right)\right),$$

subject to

$$\begin{gathered} {\text{system dynamics}}: \dot{\user2{x}}\left( t \right) = {\varvec{Ax}}\left( t \right) + {\varvec{Bu}}\left( t \right) + {\varvec{C}} \hfill \\ {\text{collision avoidance}}:f\left( {{\varvec{x}}\left( t \right),{\varvec{x}}_{l} \left( t \right)} \right) \ge R_{{{\text{col}}}} ,\quad t \in \left[ {0,t_{r} } \right] \hfill \\ {\text{maximum avalaible thrust}}: g\left( {{\varvec{u}}\left( t \right)} \right) \le T_{{\max}} , \quad t \in \left[ {0,t_{r} } \right] \hfill \\ {\text{initial state}}: {\varvec{x}}\left( 0 \right) = {\varvec{x}}^{0} \hfill \\ {\text{final state}}: {\varvec{x}}\left( {t_{r} } \right) = {\varvec{x}}^{f} \hfill \\ \end{gathered}$$
(1)

where \({\varvec{A}}\), \({\varvec{B}}\) and \({\varvec{C}}\) are the matrices modeling the system dynamics, \(f\) is the function guaranteeing the separation between the considered platform and the others \(\left({{\varvec{x}}}_{l}\right)\) is higher than a minimum value \(\left({R}_{\mathrm{c}\mathrm{o}\mathrm{l}}\right)\) during the reconfiguration time \(\left({t}_{r}\right)\), and \(g\) is the law setting a constraint on the maximum specific thrust \(\left({T}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\).

The final state for each unit of the cluster is identified by assignment routines that guarantee a propellant-optimal or time-optimal reconfiguration. In other words, the decisional process leading the satellite to reach the state \({{\varvec{x}}}^{f}\) is defined by means of a strategy that has a common objective with that defined by the trajectory optimization.

In conclusion, the satellite formation reconfiguration problem can be subdivided into three different phases.

The first is the definition of the final state, hence the formulation of terminal constraints.

Once the target pattern for the cluster reconfiguration is known, an assignment strategy manages the transition toward the desired configuration. More specifically, this routine aims at identifying for each platform the tasks which optimize the behavior of the whole formation during the maneuver.

With all the constraints being defined in the previous steps, the optimal trajectories for maneuvering each satellite are computed. The numerical resolution of the continuous non-linear problem in Eq. (1) requires two further steps. At first, all the equations are reformulated in a discrete temporal domain. Then, some approximations are introduced to reduce the non-linearity. The adopted approach is making the optimization convex [15]. Such a methodology not only allows a global minimum solution to be found, but it also enables a faster convergence of the solver by exploiting ad hoc algorithms.

3 Autonomous reconfiguration of a distributed SAR

The guidance algorithm proposed in this paper is conceived for the autonomous reconfiguration of a fractionated SAR.

The antenna is distributed on small satellites orbiting the Earth in a close formation. The assumed scenario consists of a single transmitting spacecraft that is mounted on the platform at the center of the formation and of several passive devices that collect the backscattered signal from the illuminated area (Fig. 1). Thus, the reconfiguration involves the receiving-only satellites that orbit around the transmitter to generate a new acquisition geometry. These platforms are assumed to be equipped with a propulsion system for a low-thrust reconfiguration of the cluster.

Fig. 1
figure 1

Flow diagram of the logic behind the guidance algorithm. In the final configuration, the red boxes represent the satellites that are going to be reconfigured, while the blue boxes are those that are not involved in the maneuver

Full size image

The proposed approach is developed as a decentralized architecture, with the component satellites capable of data processing. Furthermore, all the spacecraft are assumed to be connected on a local network for data sharing in which every platform would be able to determine and broadcast its state, and hence to evaluate that of the entire formation. Potential limitations to a situation where all the sensors transmit and receive (such as radio-frequency interference) may be overcome resorting to disciplined data-sharing strategies for the space segment. As an example, information can be shared circularly so that all the data about the cluster state return to the same platform after one round trip. Possible enhancements can be obtained by including the ground segment in the loop. This also serves as a backup solution in case of failures in the spaceborne broadcasting system. In this instance, the formation state can be periodically uplinked from the ground to one of the satellites of the cluster, which acts as the chief and broadcasts the information to the remaining spacecraft. In this way, the maneuver can be managed autonomously by each platform once the remote sensing requirements are known.

The algorithm is described in the following sections with reference to the three phases defined in Sect. 2. A preliminary overview of the proposed strategy is shown in the diagram of Fig. 1 that basically summarizes the main steps leading to the final computation of transfer orbits.

Hereinafter, the state vector \({{\varvec{x}}}_{j} = {\left[{x}_{j},{y}_{j}, {z}_{j}, {\dot{x}}_{j},{\dot{y}}_{j},{\dot{z}}_{j}\right]}^{T}\) will define the position and velocity of the jth deputy satellite in the Hill reference frame of the transmitter—i.e., the origin is the instantaneous position of this chief satellite, with the x-axis in the radial direction, the z-axis along the angular momentum vector and the z completing the right-handed reference system. Similarly, the control vector \({{\varvec{u}}}_{j} = {\left[{u}_{j}^{x},{u}_{j}^{y},{u}_{j}^{z}\right]}^{T}\) will represent the specific thrust in the same reference frame. Moreover, all the parameters without the subscript j will refer to the transmitter.

3.1 Final state design

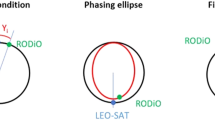
The target configuration is designed according to mission requirements. More specifically, a scenario is considered with a low Earth orbit SAR covering specific target regions for interferometric applications (InSAR). The acquisition geometry and hence the relative distances (or baselines) among the satellites are defined once the InSAR typology is specified. If cross-track interferometry (XTI) [3] is required for 3D imaging, the main parameter triggering the formation design is the cross-track baseline \(\left({b}_{c}\right)\), depicted in green in Fig. 2. On the other hand, a properly configured along-track baseline (\({b}_{a}\), which is depicted in red in Fig. 2) allows the distributed SAR to detect moving targets within the sensed scene by means of processing techniques based on along-track interferometry (ATI) [19].

Fig. 2
figure 2

Acquisition geometry in the Hill reference frame of the chief satellite. The transmitting SAR points toward the \(\widehat{\varvec{p}}\) direction with an off-nadir angle equal to \(\theta\). The deputy is identified by the purple vector, while along-track \(\left(b_a\right)\) and cross-track \(\left(b_c\right)\) baselines are depicted with dashed red and green lines, respectively

Full size image

Assuming \({b}_{c}\) and \({b}_{a}\) are selected according to remote sensing requirements (as an example, \({b}_{c}\) is chosen according to the maximum altitude to be measured, while \({b}_{a}\) is chosen according to the maximum velocity to be sensed), the final configuration is identified in terms of total number of constituent satellites \((N)\) and the state of each platform \(\left({{\varvec{x}}}_{j}^{f}, j=1, 2, ..., N\right)\) is defined by a set of relative orbital parameters\((ro{e}_{j})\). The design approach relies on a first-order approximation that describes the relative dynamics [20],

$${{\varvec{x}}}_{j}^{f}=\left[\begin{array}{c}{x}_{off}+{A}_{x}\mathrm{sin}\left[{M}_{j}+{\varphi }_{x}\right]\\ {y}_{off}+2{A}_{x}\mathrm{cos}\left({M}_{j}+{\varphi }_{x}\right)\\ {A}_{z}\mathrm{sin}\left({M}_{j}+{\omega }_{j}+{\varphi }_{z}\right)\\ {A}_{x}{\dot{M}}_{j}\mathrm{cos}\left({M}_{j}+{\varphi }_{x}\right)\\ -2{A}_{x}{\dot{M}}_{j}\mathrm{sin}\left({M}_{j}+{\varphi }_{x}\right)\\ {A}_{z}\left({{\dot{M}}_{j}+\dot{\omega }}_{j}\right)\mathrm{cos}\left({M}_{j}+{\omega }_{j}+{\varphi }_{z}\right)\end{array}\right],$$
(2)

with

$$\begin{gathered} x_{off} = da_{j} \hfill \\ A_{x} = a\sqrt {\left[ {de_{j} + 2e\sin^{2} \left( {\frac{{dM_{j} }}{2}} \right)} \right]^{2} + \left[ {e\sin \left( {dM_{j} } \right)} \right]^{2} } \hfill \\ \varphi_{x} = \tan^{ - 1} \left( { - \frac{{de_{j} + 2e\sin^{2} \left( {\frac{{dM_{j} }}{2}} \right)}}{{e_{j} \sin \left( {dM_{j} } \right)}}} \right) \hfill \\ y_{off} = a\left( {d\omega_{j} + dM_{j} + d{\Omega }_{j} \cos i} \right) \hfill \\ A_{z} = a\sqrt {di_{j}^{2} + \left( {d{\Omega }_{j} \sin i} \right)^{2} } \hfill \\ \varphi_{z} = \tan^{ - 1} \left( { - \frac{{d{\Omega }_{j} \sin i}}{{di_{j} }}} \right) \hfill \\ \end{gathered}$$
(3)

and \(d\) referring to the difference between elements of the classic orbit set \(\left[{a}_{j},{e}_{j}, {i}_{j}, {\Omega }_{j}, {\omega }_{j}, {M}_{j}\right]\).

Equation (2) is used to find bounded formations, i.e., configurations characterized by closed relative trajectories. Therefore, the differences of semi-major axes \((a)\) and of inclination \((i)\) between the platforms are set equal to zero. The remaining relative orbital elements (relative eccentricity \(de\), relative right ascension of the ascending node \(d\Omega\), relative argument of perigee \(d\omega\), relative mean anomaly \(dM\)) are determined to accomplish the desired acquisition geometry and to guarantee that the separations between consecutive satellites is never below the \({R}_{col}\) minimum value, whatever is the desired formation \(\left(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\_\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\right)\). Those formations selected for remote sensing applications are cartwheel, pendulum, or helix [21] configurations.

The final design in terms of relative orbit elements is summarized in Table 1.

Table 1 Relative orbit elements characterizing formation geometries for XTI and ATI InSAR applications. \(L\) is the integer number that varies in the range \(\left[\begin{array}{c}-\lceil\frac{N}{2}\rceil,-1,1,\dots \end{array}\lceil\frac{N}{2}\rceil\right]\)
Full size table

Formulas are derived from Eq. (2)Footnote 1 according to the geometry shown in Fig. 2, where

$$\begin{array}{c}{b}_{c}=\sqrt{{\Vert {{\varvec{r}}}_{xz}\Vert }^{2}-{\left({{\varvec{r}}}_{xz}\cdot \widehat{{\varvec{p}}}\right)}^{2}}=\sqrt{{x}^{2}+{z}^{2}-{\left(z\mathrm{sin}\theta -x\mathrm{cos}\theta \right)}^{2}}\\ {b}_{a}=y\end{array}.$$
(4)

with \(\theta\) identifying the off-nadir angle of the transmitting SAR, \({{\varvec{r}}}_{xz}\) the xz-projection of spacecraft’s relative separation, and \(\widehat{{\varvec{p}}}\) the unit vector along the SAR-to-target line of sight.

The output of the design process is the final state \({{\varvec{X}}}^{f}=\left[{{\varvec{x}}}_{1}^{f}, \dots {{\varvec{x}}}_{j}^{f}, \dots {{\varvec{x}}}_{N}^{f}\right]\) of a formation characterized by a synthetic aperture not exceeding the effective baseline imposed by InSAR requirements.

3.2 Task assignment

Once the target pattern has been defined, the best reconfiguration strategy for maneuvering the satellites from the initial state \({{\varvec{X}}}^{0}=\left[{{\varvec{x}}}_{1}^{0}, \dots {{\varvec{x}}}_{j}^{0}, \dots {{\varvec{x}}}_{N}^{0}\right]\) to \({{\varvec{X}}}^{f}\) has to be identified. The task-assignment procedure, considered in the following example, is extensively described in [14]. In detail, an algorithm selects, among the M satellites composed of initial formation, the N platforms that have to be maneuvered toward the final state by preserving the total propellant consumption. The cost function \({C}_{j}\) for a propellant-optimal orbit transfer moving a satellite from \({{\varvec{x}}}_{j}^{0}\) to \({{\varvec{x}}}_{j}^{f}\) in \({t}_{r}\)

$${C}_{j}=\underset{0}{\overset{{t}_{r}}{\int }}\left({{u}_{j}^{x}}^{2}+{{u}_{j}^{y}}^{2}+{{u}_{j}^{z}}^{2}\right)dt$$
(5)

is analytically resolved in [14] using the theory of calculus of variation. This approach assumes that the relative dynamics are governed by the Hill–Clohessy–Wiltshire (HCW) equations and the satellites to be equipped with an electric propulsion system supplying a continuous thrust. Hence, the best reconfiguration plan is defined by means of a numerical routine based on dynamic programming [14] that is formulated to minimize the cost function,

$$C=\sum_{j=1}^{N}{C}_{j}$$
(6)

that is the propellant cost to re-shape the whole formation.

The outputs of the task assignment are two vectors: a go–no-go vector \({\varvec{a}}\) and a decisional vector \({\varvec{d}}\).

The first one is an Mx1 vector and the jth component is either 1 or 0 depending on whether or not the satellite j takes part in the maneuver. The second parameter d is an Nx1 vector, whose jth component indicates the satellite in the initial configuration which is occupying the jth position in the final formation.

With reference to the procedure described in [14], the determination of a and d would require a continuous exchange of data among the satellites, which may complicate the functioning of a dedicated communication system. Indeed, the related issues (synchronization, interference, etc.) could be limited if only an initial data transmission is considered in the current approach. In detail, in a situation where each satellite could autonomously determine its own orbital set and broadcast it to the remaining elements of the formation, a generic platform may average all the received data to derive the orbital set of the transmitter and thus the initial state of the entire formation \({{\varvec{X}}}^{0}\). Relying on this information, it can carry out autonomously both the procedure of formation design and task assignment. The conceptual scheme proposed in Fig. 3 is meant to clarify how the proposed approach may work.

Fig. 3
figure 3

Task assignment: logical flow for formulation of terminal constraints in a decentralized reconfiguration

Full size image

3.3 Trajectory generation and collision avoidance

The previous two phases of formation design and task assignment define the constraints required for the resolution of the trajectory optimization problem.

It is worth noting that, depending on the desired observation scenario, the number of spacecraft that have to be reconfigured (N) could be lower than that of the initial formation (M). In this case, it is assumed that the M–N satellites not involved in the reconfiguration evolve along their initial orbits. Indeed, the N platforms specified by \({\varvec{a}}\) have to be rearranged through the optimized trajectories according to the sequence in \({\varvec{d}}\).

A propellant-optimal reconfiguration in a specific time \({t}_{r}\) requires to minimize Eq. (6) subject to the same constraints that are defined in Eq. (1).

To solve this problem by means of convex optimization [22], the temporal range \(\left[0, {t}_{r}\right]\) is first reduced to a mesh of K discrete time instants. This transforms Eq. (6) into

$$C=\sum_{j=1}^{N}\left[\sum_{k=1}^{K}\left({{{u}_{j}^{x}}^{k}}^{2}+{{{u}_{j}^{y}}^{k}}^{2}+{{{u}_{j}^{z}}^{k}}^{2}\right)\right],$$
(7)

where the superscript k indicates the corresponding parameter is evaluated at the k time instant.

The discretization of the entire problem entails a reformulation of all the continuous constraints specified in Eq. (1). In this case, a collocation method is used [23] which approximates the state and control by piecewise continuous cubic functions such that the value at each point of the temporal grid is equal to the state/control value.

System dynamics is approximated through a zero-order-hold approach, that is, the temporal derivatives are approximated resorting to Euler-based finite difference schemes. Therefore, the relative motion between the satellites, which is assumed to be described by a modified version of the HCW equations that accounts for the presence of the thruster, is expressed as

$${{\varvec{x}}}_{j}^{k+1}=\left({\varvec{I}}+dt {\varvec{A}}\right){{\varvec{x}}}_{j}^{k}+dt {\varvec{B}} {{\varvec{u}}}_{j}^{k}, \; k=1,\dots K,$$
(8)

where I is a 6 × 6 identity matrix, \(dt={t}_{k+1}-{t}_{k}\), \({\varvec{A}} =\left[\begin{array}{c}0\\ 0\\ 0\\ 3{n}^{2}\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ -{n}^{2}\end{array}\begin{array}{c}1\\ 0\\ 0\\ 0\\ -2n\\ 0\end{array}\begin{array}{c}0\\ 1\\ 0\\ 2n\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right]\), \({\varvec{B}}=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 1\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\end{array}\right]\) and n is the angular rate.

In the proposed approach, it is assumed that a thruster is available in every direction, leading to

$${{u}_{j}^{x}}^{k}\le {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}, {{u}_{j}^{y}}^{k}\le {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}, {{u}_{j}^{z}}^{k}\le {T}_{\mathrm{m}\mathrm{a}\mathrm{x}} , k=1,\dots K-1.$$
(9)

In consideration of the algorithm distributed architecture, the following approach is considered to express collision avoidance constraints: the jth platform computes its maneuvering trajectory by evaluating analytically the evolution of the other satellites. In other words, the relative motion of the outstanding platforms is determined as in the task assignment routine and the collision avoidance constraints are expressed as [15]

$${{\varvec{D}}}_{jl}^{k}{{\varvec{x}}}_{j}^{k}\ge {{\varvec{D}}}_{jl}^{k}{\stackrel{\sim }{{\varvec{x}}}}_{l}^{k}+{R}_{col}\Vert {\varvec{G}}\left({\stackrel{\sim }{{\varvec{x}}}}_{j}^{k}-{\stackrel{\sim }{{\varvec{x}}}}_{l}^{k}\right)\Vert , \; \left\{\begin{array}{c}k=1,\dots K\\ l=1,\dots , N\\ l\ne j\end{array}\right.,$$
(10)

where \({{\varvec{D}}}_{jl}^{k}={\left({\stackrel{\sim }{{\varvec{x}}}}_{j}^{k}-{\stackrel{\sim }{{\varvec{x}}}}_{l}^{k}\right)}^{T}{{\varvec{G}}}^{T}{\varvec{G}}\), \({\varvec{G}}=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\begin{array}{c}0\\ 1\\ 0\end{array}\begin{array}{c}0\\ 0\\ 1\end{array}\begin{array}{c}0\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\end{array}\right]\) and \({\stackrel{\sim }{{\varvec{x}}}}_{j/l}^{k}\) is the analytical state of the jth/lth platform computed at the discrete time k.

It is worth noting that \({\stackrel{\sim }{{\varvec{x}}}}_{j}^{k}\) and \({\stackrel{\sim }{{\varvec{x}}}}_{l}^{k}\) only approximate the real evolution of the formation: these trajectories do not account for thruster technology and collision avoidance. This entails the \({\stackrel{\sim }{{\varvec{x}}}}^{k}\) trajectory is particularly suitable for implementation on a distributed architecture, but could be slightly different from the optimized one (i.e., \({{\varvec{x}}}^{k}\)). In the considered scenarios, this does not represent a real issue. Indeed, the reconfiguration is between passively safe configurations and the transfer from a formation to the other entails the minimum distance between the satellites \(\left({R}_{\mathrm{c}\mathrm{o}\mathrm{l}}\right)\) is reached in the initial or final phases of the maneuver. Therefore, the chance of collisions is very low.

The constraint set is completely defined by the initial condition

$${{\varvec{G}}{\varvec{x}}}_{j}^{1}={{\varvec{G}}{\varvec{x}}}_{j}^{0}$$
(11)

and by that on the final state

$${{\varvec{x}}}_{j}^{K}={{\varvec{x}}}_{j}^{f}.$$
(12)

Once all the constraints are specified, the optimization can be run autonomously by each platform \(\left(j=1, \dots , N\right)\). The decisional vector

$${{\varvec{Z}}}_{j}=\left[{{\varvec{X}}}_{j};{{\varvec{U}}}_{j}\right] , \; j=1,\dots N$$
(13)

where \({{\varvec{X}}}_{j}=[{{\varvec{x}}}_{j}^{1};\dots {{\varvec{x}}}_{j}^{k};\dots {{\varvec{x}}}_{j}^{K}]\) and \({{\varvec{U}}}_{j}=[{{\varvec{u}}}_{j}^{1};\dots {{\varvec{u}}}_{j}^{k};\dots {{\varvec{u}}}_{j}^{K-1}]\), is thus evaluated by optimizing Eq. (7) subject to Eq. (8)–(12), that is,

$$\min \mathop \sum \limits_{{j = 1}}^{N} \left[ {\mathop \sum \limits_{{k = 1}}^{K} \left( {u_{j}^{{x} ^{{k} ^{2}}} + u_{j}^{{y} ^{{k} ^{2}}} + u_{j}^{{z} ^{{k} ^{2}}} } \right)} \right]$$

subject to

$$\begin{aligned} &{\bf{x}}_{j}^{{k + 1}} = \left( {{\bf{I}} + dt\ \bf{A}} \right){\bf{x}}_{j}^{k} + dt \ {\bf{B}} \ {\bf{u}}_{j}^{k} , \; k = 1, \ldots K \hfill \\ &u_{j}^{{x}^{k}} \le T_{{max}} , u_{j}^{{y}^{k}} \le T_{{max}} , u_{j}^{{z}^{k}} \le T_{{max}} , \; k = 1, \ldots K - 1 \hfill \\ &{\bf{D}}_{{jl}}^{k} {\bf{x}}_{j}^{k} \ge {\bf{D}}_{{jl}}^{k} {\tilde{\bf{x}}}_{l}^{k} + R_{{col}} \| {\bf{G}}\left( {\tilde{\bf{x}}_{j}^{k} - {\tilde{\bf{x}}}_{l}^{k} } \right)\|, \; \left\{ {\begin{array}{l} {k = 1, \ldots K} \hfill \\ {l = 1, \ldots ,\ N} \hfill \\ {l \ne j} \hfill \\ \end{array} } \right. \hfill \\ &{\bf{Gx}}_{j}^{1} = {\bf{Gx}}_{j}^{0} \hfill \\ &{\bf{x}}_{j}^{K} = {\bf{x}}_{j}^{f} \hfill \\ \end{aligned}$$
(14)

In conclusion, the problem described in Eq. (1) is reduced to a form where the cost function and the inequality constraints are expressed as convex functions, and the equality constraints as affine functions. This ensures that the solution to the problem in Eq. (14)—if feasible—is a global minimum. As for the resolution strategy, it is entrusted to dedicated routines tailored to this class of problems. The one selected in this paper is CVX [18], a MATLAB-based modeling tool for convex optimization. Despite that, it is worth noting that the quality of the optimization further depends on the constraints considered for modeling the reconfiguration problem, on the discretization procedure (as an example, on the numerical schemes used for description of system dynamics) and on the density of the mesh representing the discrete time instants.

4 Simulation results

This section presents the low-thrust reconfiguration maneuvers as computed by the algorithm. It is worth noting that the main scope of the following simulations is to prove the viability of the devised strategy for autonomous path planning and guidance of multiple space systems. Indeed, radar applications have tight constraints in terms of requirements on relative position accuracy between the different deployed sensors. These are needed for avoiding distortion in the distributed antenna pattern and are a function of the radar wavelength (generally a fraction of it). Therefore, after generation of the transfer orbits according to the methodology proposed in this paper, a relative navigation and control strategy would be required to finally achieve the target state.

A specific mission scenario is considered, with an X-band fractionated radar in a Sun synchronous orbit at an altitude of 700 km. The antenna is distributed on 100 kg microsatellites and every platform is assumed to be equipped with an electric propulsion system supplying a 50 mN thrust.

The chief’s initial conditions are specified in Table 2.

Table 2 Chief’s classical orbit elements at the beginning of the reconfiguration
Full size table

Initial and final acquisition geometries are set from remote sensing requirements. More specifically, simulations are run presuming the parameters \(\left(\theta , \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\_\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}, {{b}_{c}, {b}_{a}, {R}_{\mathrm{c}\mathrm{o}\mathrm{l}},t}_{r}\right)\) are transmitted from the ground to the cluster, which is then able to process the received data and to autonomously determine the best reconfiguration strategy. Concerning the reconfiguration time \({t}_{r}\), this is selected to be consistent with orbital maneuvering constraints. As an example, the reconfiguration from and to the helix and pendulum formations entails non-coplanar transfers (Table 1 indicates for these geometries a change in the right ascension of the ascending nodes). In these cases, \({t}_{r}\) is selected so that it includes at least one passage through the poles, where the initial and final orbits of spacecraft belonging to helix or pendulum formations intersect each other. Whatever the conditions, the feasibility of the problem in Eq. (14) (and consistency of \({t}_{r}\) with all the remaining constraints) is supposed to be verified before triggering the reconfiguration from the ground.

In the following simulations, the radar antenna is assumed to be distributed on five orbiting platforms (M = 5): the spacecraft at the center acts like the illuminator, while the other satellites can be rearranged around it to give the fractionated antenna the required shape. Moreover, a safety requirement \({R}_{\mathrm{c}\mathrm{o}\mathrm{l}}\)=200 m is considered.

Figure 4 shows the trajectories reconfiguring an XTI-cartwheel formation that senses a target scene with an off-nadir angle of 20° and with a cross-track baseline equal to 2 km, in an XTI-helix formation designed to realize acquisitions with \(\theta =45^\circ\) and \({b}_{c}=3\) km. The reconfiguration time is set to one orbital period \(\left({t}_{r} = 2\pi /n\right)\) and the control laws enabling the transfers shown in Fig. 4 are presented in Fig. 5-left. Also, Fig. 5-right demonstrates that no collisions are possible.

Fig. 4
figure 4

XTI-cartwheel to XTI-helix reconfiguration as seen from the transmitter (black dot): \(t_r = 2\pi/n\), \(\theta^0 = 20^\circ\), \(b_c^0 = 2\,km\), \(\theta^f = 45^\circ\), \(b_c^f = 3 \, km\)

Full size image
Fig. 5
figure 5

XTI-cartwheel to XTI-helix reconfiguration: \({t}_{r} = 2\pi /n\), \({\theta }^{0}=20^\circ\), \({b}_{c}^{0}=2 \, km\), \({\theta }^{f}=45^\circ\), \({b}_{c}^{f}=3 \, km\). Control law (left) and satellite separations (right) during the maneuver

Full size image

The strategy to reshape an XTI-helix formation in an XTI-pendulum SAR distributed on three spacecraft is illustrated in Fig. 6. In this case, the reconfiguration partially involves the initial cluster \(\left(N=3\right)\) and the task assignment routine identifies the inner spacecraft as the one to be maneuvered to save the propellant. The satellites that are excluded by reconfiguration naturally evolve on their orbits. In this scenario, the off-nadir angles and the cross-track baselines are assumed to be the same before and after the maneuver \(\left({\theta }^{0}={\theta }^{f}=45^\circ , {b}_{c}^{0}={b}_{c}^{f}=1 \, km\right)\), while \({t}_{r}\) is set to 3π/(2n). The thrust components and the relative baselines between the satellites are shown in Fig. 7-left, and –right, respectively.

Fig. 6
figure 6

XTI-helix to XTI-pendulum reconfiguration as seen from the transmitter (black dot): \(t_r = 3\pi/2n\), \(\theta^0 = \theta^f = 45^\circ\), \(b_c^0=b_c^f=1\,km\). Blue dashed trajectories indicate the evolution of satellites not involved in the reconfiguration

Full size image
Fig. 7
figure 7

XTI-helix to XTI-pendulum reconfiguration: \(t_r = 3\pi/2n\), \(\theta^0 = \theta^f = 45^\circ\), \(b_c^0=b_c^f=1\,km\). Control law (left) and satellite separations (right) during the maneuver

Full size image

Finally, a path-planning strategy is proposed to reconfigure a SAR operating in XTI mode toward a configuration enabling ATI applications. The maneuver is aimed at reshaping the distributed antenna to generate an along-track baseline of 2 km. Spacecraft are initially arranged in a pendulum-like formation characterized by a cross-track baseline of 1.5 km. The reconfiguration time is assumed to be equal to π/n, while the off-nadir angle is kept constant and equal to 30°. The optimized trajectories, the control laws, and the platform separations are illustrated in Figs. 8, 9-left, right.

Fig. 8
figure 8

XTI-pendulum to ATI-helix reconfiguration as seen from the transmitter (black dot): \(t_r = \pi/n\), \(b_c^0 = 1.5\,km\), \(b_a^f = 2\,km,\;\theta^0=\theta^f=30^\circ\)

Full size image
Fig. 9
figure 9

XTI-pendulum to ATI-helix reconfiguration: \(t_r = \pi/n\), \(b_c^0 = 1.5\,km\), \(b_a^f = 2\,km,\;\theta^0=\theta^f=30^\circ\). Control law (left) and satellite separations (right) during the maneuver

Full size image

To have a sense on how strategy performances scale as a function of the number of sensors involved in the reconfiguration, several simulations are performed with reference to the above presented scenarios. The final results are summarized in Table 3 in terms of delta-v consumption and time required to compute the reconfiguration trajectories. It is worth noting that, when required, the minimum safety distance for collision avoidance has been modified to make the reconfiguration feasible under the same conditions presented above.

Table 3 Algorithm performance as a function of the number of satellites of the formation. Reference scenarios (in terms of \(b_c\), \(b_a\), \(\theta\) and \(t_r\)) are those described in Figs. 4, 6 and 8, respectively
Full size table

5 Conclusions

In this paper, an algorithm for the autonomous reconfiguration of a SAR distributed on a small-sat formation is presented.

The approach is developed assuming the fractionated radar in an Earth observation mission for InSAR applications. Therefore, a pattern variation may be required according to various mission tasks (3D imaging or Moving Target Indication), or to implement the acquisition geometry that maximizes the performance expected from the final products. The algorithm is conceived so that once the terminal specifics are known in terms of \(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\_\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}, \, \theta , \, {b}_{c}, \, {b}_{a}\) and \({t}_{r}\), every platform is able to vary its configuration with respect to the transmitter to minimize the total propellant consumption.

The proposed strategy is described with reference to the main phases of the algorithm: definition of the final state, task assignment, and trajectory optimization. Hence, the cluster is able to determine autonomously the acquisition geometry that better fits mission requirements and to manage the transition toward the final state. The transfer orbits are calculated taking into account collision avoidance constraints.

Simulations are performed under the simplified assumptions of Keplerian dynamics and small satellite separations, with perfect communications. The results assess the viability of the approach in the management of the reconfiguration when considering formations made of several units.