A Likelihood-Based Qualitative Flexible Approach with Hesitant Fuzzy Linguistic Information

Abstract

The qualitative flexible multiple criteria method (QUALIFLEX) is a useful outranking method for multi-criteria decision analysis due to its flexibility in regard to cardinal and ordinal information. This paper puts forward an extended QUALIFLEX approach with a new likelihood-based comparison method to address multi-criteria decision-making problems in a hesitant fuzzy linguistic environment. The rankings produced by our new comparison method are more convincing than those obtained by existing methods, such as likelihood, distance measures, and the score function of hesitant fuzzy linguistic term sets or hesitant fuzzy linguistic elements. The proposed QUALIFLEX model, which is based on the likelihood-based comparison method, can measure the level of concordance or discordance of the complete preference order for tackling multi-criteria decision-making problems. Finally, two cases are presented as a comparative analysis between the proposed approach and other related methods. This example demonstrates the effectiveness and flexibility of the proposed methodology in the context of hesitant fuzzy linguistic information.

Introduction

Every day people are challenged with multiple acts of decision making. An increasing amount of research is being conducted on the use of cognitive information during the decision-making process [1, 8, 26, 51]. Because of the fuzziness and uncertainty involved in decision-making problems, specific numerical ratings do not always accurately reflect the behavior and opinions of decision makers. Natural language is the appropriate expression of decision makers. Over recent years, various studies have been conducted regarding linguistic multi-criteria decision-making (MCDM) problems [10–12, 24, 25, 33, 35, 36, 49]. However, experts may hesitate when choosing linguistic terms to accurately evaluate alternatives in some fuzzy linguistic decision contexts, making it difficult to reach a consensus. An increasing number of linguistic proposals have been introduced to enrich linguistic expressions rather than using a single linguistic term. One of the popular proposals is intuitionistic linguistic sets (ILSs) [23] and their extensions [22, 44]. Hesitant fuzzy linguistic sets (HFLSs) [20, 45] and linguistic hesitant fuzzy sets (LHFSs) [28, 52, 56] have also been proposed. Furthermore, there are various schemes for handling linguistic variables: representing linguistic information using fuzzy membership functions [4, 9, 40], relying on the 2-tuple linguistic representation model [13, 39, 42], and using the cloud model to depict the uncertainty of a qualitative concept [41, 53].

Although the proposals for generating linguistic expressions have been justified and applied in real-life decision-making problems, decision makers and experts may prefer to depict evaluation information using multiple linguistic terms. Rodríguez et al. [32] defined hesitant fuzzy linguistic term sets (HFLTSs), which have been used to address situations where experts hesitate when choosing among several linguistic terms. Zhang and Wu [55] defined HFLSs, in which the linguistic terms contained in the hesitant fuzzy linguistic elements (HFLEs) are not consecutive. Wei et al. [48] developed a hesitant fuzzy linguistic weighted average (HLWA) operator and a hesitant fuzzy linguistic ordered weighted average (HLOWA) operator based on the Round operation. Moreover, Wei et al. [47] extended the TODIM (Tomada de decisao interativa e multicritévio, a Portuguese acronym for interactive and MCDM) method for solving MCDM problems with HFLTSs. Chen and Hong [3] presented a hesitant fuzzy linguistic MCDM method that considers the pessimistic and optimistic attitudes of decision makers. Liu and Rodríguez [21] developed a representation of HFLTSs by means of the fuzzy envelope. Liao et al. [18, 19] presented a family of distance and similarity measures of HFLTSs. Li et al. [17] proposed a distance-based method for determining the decision makers’ weights and a weighted aggregation operator for obtaining the criterion weights. Lee and Chen [16] developed a likelihood-based comparison relation and proposed a family of hesitant fuzzy linguistic aggregation operators. Wang et al. [38, 43] proposed an outranking method for HFLTSs, which involves systematic comparisons of assessment values with respect to each criterion. The above methods are effective when managing hesitant fuzzy MCDM problems with HFLTs or HFLEs. However, they have various drawbacks as outlined below.

• 1. Some methods, including the hesitant fuzzy linguistic distance measure [43], the possibility degree [32, 48], and the likelihood-based comparison relation [16], depend partly on HFLTS envelopes. In these methods, the linguistic terms are converted into intervals. However, such designs ignore the fact that the linguistic term set is not a simple array with equal distances between neighbors.

• 2. Numerous distance measures [17–19, 47] have been developed, creating a need for normalization of HFLTSs. In this process, any two HFLTSs should be the same length. This normalization relies on the subjectivity of decision makers, but the determination of risk preference is an intractable task.

• 3. When aggregation operators [32, 55] are applied to process linguistic values, the final results do not always have syntax or semantics assigned. Moreover, a Round operation [48] has often been used to confine the results to the initial expression domain, which may lead to an indistinguishable order of alternatives.

To overcome these limitations, this paper focuses on the development of a new likelihood-based comparison method that uses the closeness coefficients from the technique for order of preference by similarity to ideal solution (TOPSIS) [15, 37, 57]. The proposed comparison method can effectively deal with HFLTSs by conducting systematic comparisons of every linguistic term in two HFLTSs. It does not adopt the calculations involving intervals and normalization. This allows for the original information to be maintained and used fully. The likelihood-based comparison method was further integrated with the outranking approach, QUALIFLEX, as this eliminates numerous aggregation operators and score functions.

The QUALIFLEX method, proposed by Paelinck [29–31], is one of the most effective outranking methods [14], and several useful extensions have recently been developed to enrich the methodology. For instance, Alinezhad and Esfandiari [2] conducted a sensitivity analysis of the QUALIFLEX and VIKOR (vlsekriterijumska optimizacija i kompromisno resenje) methods. Moreover, Chen and Tsui [5] proposed a QUALIFLEX method for relating optimism and pessimism in an intuitionistic fuzzy environment. Chen [6] also developed a QUALIFLEX approach with interval-valued intuitionistic fuzzy sets (IVIFSs). Based on a signed distance comparison approach, Chen et al. [4] extended the QUALIFLEX method for tackling medical decision-making problems with interval type-2 fuzzy sets (IT2FSs). Zhang and Xu [54] extended the QUALIFLEX method for managing green supplier selection under the hesitant fuzzy environment. Likelihood-based comparison methods used with QUALIFLEX have also been presented. Chen [7] proposed an interval intuitionistic fuzzy QUALIFLEX method with a likelihood-based comparison approach, and Wang et al. [40] developed a likelihood-based QUALIFLEX approach with IT2FSs.

Although the QUALIFLEX method has been extended to address MCDM problems within the context of IVIFSs, IT2FSs, and hesitant fuzzy sets (HFSs), it has not yet been extended to address HFLTSs. The objective of this work is to develop a hesitant fuzzy linguistic QUALIFLEX approach with a new likelihood-based comparison method. The proposed approach can flexibly manage MCDM problems in the context of HFLTSs and HFLEs.

The rest of the paper is organized as follows. Section “Preliminaries” briefly reviews the concepts of linguistic term sets, including HFLTSs and HFLSs. Section “Likelihood of Fuzzy Preference Relations Between HFLTSs” presents the development of a new likelihood-based comparison relation for HFLTSs. Section “The QUALIFLEX Approach Based on HFLTSs” proposes a hesitant fuzzy linguistic QUALIFLEX approach using the likelihood-based comparison from section “Likelihood of Fuzzy Preference Relations Between HFLTSs.” Section “Illustrative Example” gives an illustrative example to demonstrate the feasibility and applicability of the proposed approach. In addition, two comparative analyses are carried out between the proposed approach and existing methods in the context of HFLTSs and HFLEs. Section “Conclusions” presents the conclusions of the study.

Preliminaries

This section briefly reviews the relevant definitions and operations on HFLTSs and HFLSs that will be used in the later analysis. It also discusses the effectiveness of some existing methods that use HFLTSs.

Let $S = \left\{ {s_{i} \left| {i = 0,1,2, \ldots ,2g,\;\quad g \in N} \right.} \right\}$ be a finite ordered discrete term set, where s _i represents a possible value for a linguistic variable. We require that s _i and s _j satisfy the following conditions [11, 12]:

• 1. The set is ordered: if i < j, $s_{i} < s_{j}$;

• 2. Negation operator: $\text{neg}(s_{i} ) = h_{(2g - i)}$; and

• 3. If $s_{i} < s_{j}$, then $\hbox{max} \{ s_{i} ,s_{j} \} = s_{j}$ and $\hbox{min} \{ s_{i} ,s_{j} \} = s_{i}$.

Hesitant Fuzzy Linguistic Term Sets

Definition 1

[32] Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set. The HFLTS H _s is an ordered finite subset of the consecutive linguistic terms of S.

Rodríguez et al. [32] defined a context-free grammar G _H that generates simple but rich linguistic expressions and can be easily represented by HFLTSs.

Definition 2

[32] Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set, and let E _GH be a function that transforms the linguistic expression II, obtained by a context-free grammar G _H , into a HFLTS H _s :

$$ E_{{G_{H} }} :II \to H_{S} $$

Various expressions generated by production rules are then used to transform the linguistic expressions, into HFLTSs:

• 1. $E_{{G_{H} }} (s_{i} ) = \left\{ {s_{i} \left| {s_{i} \in S} \right.} \right\}$;

• 2. $E_{{G_{H} }} ({\text{less than }}s_{i} ) = \left\{ {s_{j} \left| {s_{j} \in S{\text{ and }}s_{j} \le s_{i} } \right.} \right\}$;

• 3. $E_{{G_{H} }} ({\text{greater than }}s_{i} ) = \left\{ {s_{j} \left| {s_{j} \in S{\text{ and }}s_{j} \ge s_{i} } \right.} \right\}$; and

• 4. $E_{{G_{H} }} ({\text{between }}s_{i} {\text{ and }}s_{j} ) = \left\{ {s_{k} \left| {s_{k} \in S{\text{ and }}s_{i} \le s_{k} \le s_{j} } \right.} \right\}$.

Definition 3

[43] Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set. The function of the position index i for the element s _i in S can then defined by

$$ I:S \to Z\quad {\text{and}}\quad s_{i} \to i, $$

where Z is the set containing the position index i for the element s _i in S.

Definition 4

[32] The envelope of an HFLTS H _S , denoted by env(H _S ), is a linguistic interval $[H_{S}^{ - } ,H_{S}^{ + } ]$, where $H_{S}^{ - }$ and $H_{S}^{ + }$ are the lower and upper bounds of H _S , respectively.

Rodríguez et al. [32] provided a method for comparing two HFLTSs, $H_{S}^{a}$ and $H_{S}^{b}$, which uses the envelope of an HFLTS:

• 1. $H_{S}^{a} > H_{S}^{b}$ if and only if $env(H_{S}^{a} ) > env(H_{S}^{b} )$; ands

• 2. $H_{S}^{a} = H_{S}^{b}$ if and only if $env(H_{S}^{a} ) = env(H_{S}^{b} )$.

Rodríguez et al. [32] revised the preference relation of linguistic intervals to compare two HFLTSs, which is similar to the method for comparing numerical intervals in [34, 46].

However, if two HFLTSs have common elements but different envelopes then neither can be defined as absolutely superior to the other based on Definition 4.

Example 1

Let $H_{S}^{1} = \{ s_{4} ,s_{5} ,s_{6} \}$, $H_{S}^{2} = \{ s_{3} ,s_{4} \}$, and $H_{S}^{3} = \{ s_{2} ,s_{3} \}$ be three HFLTSs. According to Definition 4, $env(H_{S}^{1} ) = [s_{4} ,s_{6} ]$, $env(H_{S}^{2} ) = [s_{3} ,s_{4} ]$, and $env(H_{S}^{3} ) = [s_{2} ,s_{3} ]$.

Moreover, the following results can be calculated from the preference relation between two numerical intervals [46]:

• 1. $P([s_{4} ,s_{6} ] > [s_{3} ,s_{4} ]){ = }1$, so $H_{S}^{1} > H_{S}^{2}$;

• 2. $P([s_{4} ,s_{6} ] > [s_{2} ,s_{3} ]){ = }1$, so $H_{S}^{1} > H_{S}^{3}$; and

• 3. $P([s_{3} ,s_{4} ] > [s_{2} ,s_{3} ]){ = }1$, so $H_{S}^{2} > H_{S}^{3}$.

It is evident that $H_{S}^{1} > H_{S}^{3}$ is acceptable. However, both $H_{S}^{1} > H_{S}^{2}$ and $H_{S}^{2} > H_{S}^{3}$ must be discussed further, as these two pairs contain a common element. According to the definition of HFLTSs, each element in an HFLTS represents one possible choice for an expert to express their opinion. Both s ₅ and s ₆ in $H_{S}^{1}$ are greater than any element in $H_{S}^{2}$, but s ₄ is a common element of $H_{S}^{1}$ and $H_{S}^{2}$. Thus, it is unreasonable to say that $H_{S}^{1}$ is absolutely superior to $H_{S}^{2}$. The comparison between $H_{S}^{2}$ and $H_{S}^{3}$ is similar.

A similar limitation appears when using the likelihood-based comparison relations proposed by Lee and Chen [16], which are constructed based on intervals for HFLTSs. Because each HFLTS consists of finite consecutive linguistic terms but not continuous linguistic values, HFLTSs cannot be transformed into intervals and compared using methods applicable to numerical values.

Furthermore, Wei et al. [48] developed a new comparison method constructed from the indices of the related HFLTS envelopes.

Assume that $H_{S}^{1}$, $H_{S}^{2}$, and $H_{S}^{3}$ are the same as in Example 1. According to the concrete formula for the possibility degree [48], $PF(H_{S}^{1} \ge H_{S}^{2} ) = 0.9167$, $H_{S}^{1} \mathop > \limits^{0.9167} H_{S}^{2}$; $PF(H_{S}^{1} \ge H_{S}^{3} ){ = }1$, $H_{S}^{1} \mathop > \limits^{1} H_{S}^{3}$; and $PF(H_{S}^{2} \ge H_{S}^{3} ){ = }0.875$, $H_{S}^{2} \mathop > \limits^{0.875} H_{S}^{3}$.

The results calculated from the possibility degree method seem to be more acceptable in comparison with the results obtained by the methods in [16, 32]. Using the concrete formula, the possibility degree that $H_{S}^{1}$ is superior to $H_{S}^{2}$ is 0.9167, but not 1.

The proposals developed in [16, 32, 48] are generally incapable of handling situations where the linguistic terms in HFLTSs are not consecutive. For example, three experts are required to assess the “safety” of two cars a ₁ and a ₂. Suppose that one of the experts provides an assessment of “fair” for a ₁, and the other two experts provide an assessment of “good” for a ₁, and assume that they cannot persuade one another to change their opinions. The evaluation values for a ₁ can be expressed as $H_{S}^{{a_{1} }} = \{ s_{3} ,s_{5} \}$ by deleting the repeated values. Assume that the collective opinions of a ₂ are $H_{S}^{{a_{2} }} = \{ s_{3} ,s_{4} ,s_{5} \}$. The methods presented in [16, 32, 48] cannot distinguish between a ₁ and a ₂. This calls for a new comparison method that maintains the simplicity of HFLTSs.

Hesitant Fuzzy Linguistic Sets

Xu [49] extended the discrete term set S to a continuous linguistic term set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} { = }\left\{ {s_{i} \left| {s_{0} \le s_{i} \le s_{2g} ,\;i \in [0,2g]} \right.} \right\}$ to preserve all of the given information. If $s_{i} \in S$, then s _i is called an original linguistic term; otherwise, s _i is called a virtual linguistic term.

Definition 5

[55]. Let X be a reference set and let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} { = }\left\{ {s_{i} \left| {s_{0} \le s_{i} \le s_{2g} ,\;i \in [0,2g]} \right.} \right\}$ be a continuous linguistic term set. An HFLS H _LS on X is defined in terms of a function h _LS that returns a subset of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}$:

$$ H_{LS} = \left\{ {\left\langle {x,\;h_{LS} (x)} \right\rangle \left| {x \in X} \right.} \right\}, $$

(1)

where $h_{LS} (x)$ is a set of linguistic terms in $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}$ denoting the possible membership degrees of the elements $x \in X$ to the set H _LS .

For convenience, $h_{LS} (x)$ is called a hesitant fuzzy linguistic element (HFLE), and H _LS is the set of all HFLEs. It is obvious that an HFLTS is an HFLE, whereas it uncertain whether an HFLE is an HFLTS.

Definition 6

[55]. For an HFLE h _LS , the score function can be defined as:

$$ S(h_{LS} ) = \frac{{\sum\nolimits_{{s_{\alpha } \in h_{LS} }} {\left( {\frac{\alpha }{2g}} \right)} }}{{\# h_{LS} }}, $$

(2)

where $\# h_{LS}$ is the number of elements in h _LS . If $S(h_{LS}^{a} ) > S(h_{LS}^{b} )$ for two HFLEs $h_{LS}^{a}$ and $h_{LS}^{b}$, then $h_{LS}^{a} > h_{LS}^{b}$; if $S(h_{LS}^{a} ) = S(h_{LS}^{b} )$, then $h_{LS}^{a} = h_{LS}^{b}$.

The score function presented in [55] has some evident flaws that arise in situations where HFLEs are indistinguishable as a result of the linguistic variables having the same average value.

Example 2

Assume that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} { = }\left\{ {s_{i} \left| {s_{0} \le s_{i} \le s_{6} ,\;i \in [0,6]} \right.} \right\}$ is a continuous linguistic term set and that $h_{LS}^{1} = \{ s_{3} ,s_{4} ,s_{5} \}$ and $h_{LS}^{2} = \{ s_{3} ,s_{5} \}$ are two HFLEs on $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}$. According to Definition 6, $S(h_{LS}^{1} ) = S(h_{LS}^{2} ) = \frac{2}{3}$, and $h_{LS}^{1} = h_{LS}^{2}$. This result is unreasonable, because $h_{LS}^{1}$ and $h_{LS}^{2}$ have different linguistic terms.

Likelihood of Fuzzy Preference Relations Between HFLTSs

This section defines the likelihood of fuzzy preference relations with HFLTSs to determine the binary relation between two HFLTSs.

Likelihood of Fuzzy Preference Relation Between Two HFLTSs

Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set, and let $H_{S}^{a}$ and $H_{S}^{b}$ on S be two arbitrary HFLTSs. $H_{S}^{a}$ and $H_{S}^{b}$ denote the evaluation values of the alternatives a and b, respectively.

Let the event “a ≥ b” express “the alternative a is not inferior to b.” To measure the possibility of the event a ≥ b, the hesitant fuzzy linguistic preference relation $H_{S}^{a} \ge H_{S}^{b}$ is used. The preference relation $H_{S}^{a} \ge H_{S}^{b}$ is constructed based on the closeness coefficients from TOPSIS. In the following study, $L(H_{S}^{a} \ge H_{S}^{b} )$ denotes the likelihood of the fuzzy preference relation $H_{S}^{a} \ge H_{S}^{b}$ on the HFLTSs.

Definition 7

Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set, and let $H_{S}^{a} = \left\{ {a_{i} \left| {a_{i} \in S,\;i = 1,2, \ldots ,l_{a} } \right.} \right\}$ and $H_{S}^{b} = \left\{ {b_{j} \left| {b_{j} \in S,\;j = 1,2, \ldots ,l_{b} } \right.} \right\}$ be two arbitrary HFLTSs on S, where l _a and l _b are the numbers of elements in $H_{S}^{a}$ and $H_{S}^{b}$, respectively. Assume that the elements in both $H_{S}^{a}$ and $H_{S}^{b}$ are arranged in ascending order. The likelihood $L(H_{S}^{a} \ge H_{S}^{b} )$ of a fuzzy preference relation $H_{S}^{a} \ge H_{S}^{b}$ on HFLTSs is defined as

$$ L(H_{S}^{a} \ge H_{S}^{b} ) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {H_{S}^{a + } < H_{S}^{b - } } \hfill \\ {\frac{1}{{l_{a} l_{b} }}\left( {\sum\limits_{i = 2}^{{l_{a} }} {\sum\limits_{j = 1}^{{l_{b} }} {\frac{{I(a_{i} )}}{{I(a_{i} ) + I(b_{j} )}} + \frac{1}{2}} } } \right),} \hfill & {H_{S}^{a - } \le H_{S}^{b + } ,\;H_{S}^{b - } \le H_{S}^{a + } \;{\text{and}}\;H_{S}^{a - } = H_{S}^{b - } = s_{0} } \hfill \\ {\frac{1}{{l_{a} l_{b} }}\sum\limits_{i = 1}^{{l_{a} }} {\sum\limits_{j = 1}^{{l_{b} }} {\frac{{I(a_{i} )}}{{I(a_{i} ) + I(b_{j} )}}} } ,} \hfill & {H_{S}^{a - } \le H_{S}^{b + } ,\;H_{S}^{b - } \le H_{S}^{a + } \;{\text{and}}\;H_{S}^{a - } \ne s_{0} \;{\text{or}}\;H_{S}^{b - } \ne s_{0} } \hfill \\ {1,} \hfill & {H_{S}^{b + } < H_{S}^{a - } } \hfill \\ \end{array} } \right. $$

(3)

Property 1

Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set, and let $H_{S}^{a} = \left\{ {a_{i} \left| {a_{i} \in S,\;i = 1,2, \ldots ,l_{a} } \right.} \right\}$, $H_{S}^{b} = \left\{ {b_{j} \left| {b_{j} \in S,\;j = 1,2, \ldots ,l_{b} } \right.} \right\}$, and $H_{S}^{c} = \left\{ {c_{k} \left| {c_{k} \in S,\;k = 1,2, \ldots ,l_{c} } \right.} \right\}$ be three arbitrary HFLTSs on S, where l _a , l _b , and l _c are the numbers of elements in $H_{S}^{a}$, $H_{S}^{b}$, and $H_{S}^{c}$, respectively. The likelihood of a fuzzy preference relation on HFLTSs satisfies the following properties:

• 1. $0 \le L(H_{S}^{a} \ge H_{S}^{b} ) \le 1$;

• 2. If $a_{{l_{a} }} < b_{1}$, then $L(H_{S}^{a} \ge H_{S}^{b} ) = 0$;

• 3. If $a_{1} > b_{{l_{b} }}$, then $L(H_{S}^{a} \ge H_{S}^{b} ) = 1$;

• 4. $L(H_{S}^{a} \ge H_{S}^{b} ) + L(H_{S}^{a} \le H_{S}^{b} ) = 1$;

• 5. If $L(H_{S}^{a} \ge H_{S}^{b} ) = L(H_{S}^{a} \le H_{S}^{b} )$, then $L(H_{S}^{a} \ge H_{S}^{b} ) = L(H_{S}^{a} \le H_{S}^{b} ) = 0.5$; and

• 6. If $L(H_{S}^{a} \ge H_{S}^{c} ) \ge 0.5$ and $L(H_{S}^{c} \ge H_{S}^{b} ) \ge 0.5$, then $L(H_{S}^{a} \ge H_{S}^{b} ) \ge 0.5$.

The proof of Property 1 is shown in the Appendix.

Definition 8

Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set, and let $H_{S}^{a} = \left\{ {a_{i} \left| {a_{i} \in S,\;i = 1,2, \ldots ,l_{a} } \right.} \right\}$ and $H_{S}^{b} = \left\{ {b_{j} \left| {b_{j} \in S,\;j = 1,2, \ldots ,l_{b} } \right.} \right\}$ be two HFLTSs on S, where l _a and l _b are the numbers of elements in $H_{S}^{a}$ and $H_{S}^{b}$, respectively. We define the following fuzzy preference relations:

• 1. If $L(H_{S}^{a} \ge H_{S}^{b} ) > 0.5$, then $H_{S}^{a}$ is superior to $H_{S}^{b}$, denoted by $H_{S}^{a} > H_{S}^{b}$;

• 2. If $L(H_{S}^{a} \ge H_{S}^{b} ) < 0.5$, then $H_{S}^{a}$ is inferior to $H_{S}^{b}$, denoted by $H_{S}^{a} < H_{S}^{b}$; and

• 3. If $L(H_{S}^{a} \ge H_{S}^{b} ) = 0.5$, then $H_{S}^{a}$ is indifferent to $H_{S}^{b}$, denoted by $H_{S}^{a} = H_{S}^{b}$.

Assume that $H_{S}^{1}$, $H_{S}^{2}$, and $H_{S}^{3}$ are the same as in Example 1. According to Eq. (3), $L(H_{S}^{1} \ge H_{S}^{2} ){ = 0} . 5 8 6 4 { > 0} . 5$. Thus, $H_{S}^{1}$ is superior to $H_{S}^{2}$, or $H_{S}^{1} > H_{S}^{2}$ to the degree of 0.5864. Similarly, $H_{S}^{2} > H_{S}^{3}$ to the degree of 0.5845, and $H_{S}^{1} > H_{S}^{3}$ to the degree of 1. This demonstrates that the proposed likelihood-based comparison method can effectively differentiate between HFLTSs with common linguistic elements in some cases, overcoming the defects of methods presented in [16, 32].

Moreover, for the aforementioned example regarding evaluating the “safety” of two cars, we find $L(H_{S}^{{a_{1} }} \ge H_{S}^{{a_{2} }} ){ = 0} . 4 9 7 4$, and $H_{S}^{{a_{1} }} < H_{S}^{{a_{2} }}$. Hence a ₁ is inferior to a ₂ with respect to the criterion “safety.” For Example 2, we find $L(h_{LS}^{1} \ge h_{LS}^{2} ){ = 0} . 5 0 2 6$, and $h_{LS}^{1} > h_{LS}^{2}$; hence, $h_{LS}^{1}$ is superior to $h_{LS}^{2}$. Thus, the proposed method can be extended to deal with HFLEs. It overcomes the limitations of the score function in [55] and handles situations where two HFLEs have the same linguistic average values.

Likelihood of Fuzzy Preference Relations Between Two Collections of HFLTSs

In some real-life decision-making processes, alternatives are assessed against different criteria. Thus, assessment information regarding all aspects must be considered. When the assessment information of alternatives for different criteria is denoted by several collections of HFLTSs, it is necessary to calculate the likelihood of the fuzzy preference relations between these collections.

Definition 9

Let $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ be a linguistic term set. Two collections of HFLTSs, $H_{S}^{A} { = }\left\{ {H_{s}^{{a_{1} }} ,H_{s}^{{a_{2} }} , \ldots ,H_{s}^{{a_{n} }} } \right\}$ and $H_{S}^{B} { = }\left\{ {H_{s}^{{b_{1} }} ,H_{s}^{{b_{2} }} , \ldots ,H_{s}^{{b_{n} }} } \right\}$, have the associated weighting vector $\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} )$, where $\omega_{j} \in [0,1]$ and $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. The weighted likelihood of fuzzy preference relation between $H_{S}^{A}$ and $H_{S}^{B}$ can be defined as:

$$ L_{w} \left( {H_{S}^{A} \ge H_{S}^{B} } \right) = \sum\limits_{j = 1}^{n} {\omega_{j} L(H_{S}^{{a_{j} }} \ge H_{S}^{{b_{j} }} )} . $$

(4)

Motivated by the generalization idea of Yager [50], we define a generalized weighted likelihood of fuzzy preference relation between $H_{S}^{A}$ and $H_{S}^{B}$ as

$$ L_{gw} \left( {H_{S}^{A} \ge H_{S}^{B} } \right) = \left( {\sum\limits_{j = 1}^{n} {\omega_{j} \left( {L(H_{S}^{{a_{j} }} \ge H_{S}^{{b_{j} }} )} \right)^{\lambda } } } \right)^{{\frac{1}{\lambda }}} , $$

(5)

where λ > 0. If λ = 1, then Eq. (5) reduces to Eq. (4).

The QUALIFLEX Approach Based on HFLTSs

The section proposes a new hesitant fuzzy linguistic likelihood-based QUALIFLEX approach.

Consider an MCDM problem within the hesitant fuzzy linguistic context. Let $A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{m} } \right\}$ be a discrete set consisting of m alternatives, and let $C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\}$ be a set consisting of n criteria. Assume that the weight of criterion $c_{j} \;(j = 1,2, \ldots ,n)$ is ω _j , where $\omega_{j} \in [0,1]$ and $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. The weight vector of criteria can be expressed as $\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} )$.

In this decision-making problem, one linguistic term set $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{2g} \}$ together with a context-free grammar G _H is used. The grammar G _H is used to produce linguistic expressions $II(a_{i} ,c_{j} )\;(i = 1,2, \ldots ,m;j = 1,2, \ldots ,n)$ based on comparative linguistic terms. The linguistic expressions provided by experts are then transformed into HFLTSs using the transformation function E _GH . The hesitant fuzzy linguistic value of a _i under c _j is denoted by h _ij in the form of HFLTSs. The MCDM problem with transformed linguistic expressions can be concisely expressed as the following matrix:

$$ H = \left[ {h_{ij} } \right]_{m \times n} = \left[ {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & \cdots & {h_{1n} } \\ {h_{21} } & {h_{22} } & \cdots & {h_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {h_{m1} } & {h_{m2} } & \cdots & {h_{mn} } \\ \end{array} } \right]. $$

The Proposed Approach

The proposed approach starts with the computation of the concordance/discordance index based on successive permutations of all possible rankings of alternatives. A set of alternatives is given by A, and it is assumed that m! permutations of the ranking of alternatives exist. Let P _l denote the l-th permutation:

$$ P_{l} = ( \ldots ,a_{\alpha } , \ldots ,a_{\beta } , \ldots ),{\text{ for }}l = 1,2, \ldots ,m!;\quad \alpha \ne \beta , $$

(6)

where $a_{\alpha } ,a_{\beta } \in A$, and the alternative a _α is ranked higher than or equal to a _β . If a _α and a _β are ranked in the same order within two pre-orders, then concordance exists. If they have the same rank, then ex aequo exists. If they are counter-ranked, then discordance exists.

Recall that HFLTSs h _αj and h _βj are the transformed assessments of the alternatives a _α and a _β , respectively, with respect to each criterion $c_{j} \in C$. The likelihood of fuzzy preference relation $L(h_{\alpha j} \ge h_{\beta j} )$ can be used to obtain a ranking of the given HFLTSs. This likelihood-based comparison approach can also be used to identify the concordance/discordance index.

The likelihood $L(h_{\alpha j} \ge h_{\beta j} )$ of each pair of alternatives $(a_{\alpha } ,a_{\beta } )$ must be calculated to conduct a comparison between h _αj and h _βj . According to Property 1, if $L(h_{\alpha j} \ge h_{\beta j} ) = L(h_{\alpha j} \le h_{\beta j} )$, then $L(h_{\alpha j} \ge h_{\beta j} ) = L(h_{\alpha j} \le h_{\beta j} ) = 0.5$. Therefore, the likelihood $L(h_{\alpha j} \ge h_{\beta j} )$ can be used to define the concordance/discordance index $I_{j}^{l} (a_{\alpha } ,a_{\beta } )$ for each pair of alternatives (a _α , a _β ) at the level of pre-order with respect to the criterion $c_{j} \in C$. The ranking corresponding to the permutation P _l is given as follows:

$$ I_{j}^{l} (a_{\alpha } ,a_{\beta } ) = L(h_{\alpha j} \ge h_{\beta j} ) - 0.5, $$

(7)

where $I_{j}^{l} (a_{\alpha } ,a_{\beta } ) \in [ - 0.5,0.5]$. If $I_{j}^{l} (a_{\alpha } ,a_{\beta } ) > 0$, meaning that $L(h_{\alpha j} \ge h_{\beta j} ) > 0.5$, then a _α ranks higher than a _β under c _j . Thus, concordance exists between the likelihood-based ranking and the pre-order of a _α and a _β in P _l . If $I_{j}^{l} (a_{\alpha } ,a_{\beta } ) = 0$, meaning that $L(h_{\alpha j} \ge h_{\beta j} ) = 0.5$, then both a _α and a _β have the same ranking under c _j . Thus, ex aequo exists between the likelihood-based ranking and the pre-order of a _α and a _β in P _l . If $I_{j}^{l} (a_{\alpha } ,a_{\beta } ) < 0$, meaning that $L(h_{\alpha j} \ge h_{\beta j} ) < 0.5$, then a _α is ranked over by a _β under c _j . Thus, discordance exists between the likelihood-based ranking and the pre-order of a _α and a _β in P _l .

The concordance/discordance index $I_{j}^{l} (a_{\alpha } ,a_{\beta } )$ can be re-written as follows:

$$ I_{j}^{l} (a_{\alpha } ,a_{\beta } ) = \left\{ {\begin{array}{*{20}l} {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5 > 0 \Leftrightarrow \;{\text{concordance exists}}} \hfill \\ {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5 = 0 \Leftrightarrow \;{\text{ex aequo exists}}} \hfill \\ {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5 < 0 \Leftrightarrow \;{\text{discordance exists}}} \hfill \\ \end{array} } \right.. $$

(8)

According to the criterion c _j and the ranking that corresponds to the permutation P _l , the concordance/discordance index $I_{j}^{l}$ of the pre-order can be calculated using Eq. (7) to give the following:

$$ I_{j}^{l} = \sum\limits_{{a_{\alpha } ,a_{\beta } \in A}} {I_{j}^{l} (a_{\alpha } ,a_{\beta } )} = \sum\limits_{{a_{\alpha } ,a_{\beta } \in A}} {\left( {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5} \right)} . $$

(9)

The index $I_{j}^{l} (a_{\alpha } ,a_{\beta } )$ is an assessment value of (a _α , a _β ) in the permutation P _l with respect to the criterion c _j . It is not objective to assign equal importance to each criterion in practice. Considering the importance weight ω _j of c _j , Eqs. (3) and (7) can be used to derive both the weighted concordance/discordance index $I^{l} (a_{\alpha } ,a_{\beta } )$ at the level of pre-order and the ranking corresponding to the permutation P _l :

$$ I^{l} (a_{\alpha } ,a_{\beta } ) = \sum\limits_{j = 1}^{n} {I_{j}^{l} (a_{\alpha } ,a_{\beta } )\omega_{j} } = \sum\limits_{j = 1}^{n} {\left( {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5} \right)\omega_{j} } . $$

(10)

The comprehensive concordance/discordance index I ^l for the permutation P _l can be obtained by integrating Eqs. (9) and (10), which gives the following:

$$ I^{l} = \sum\limits_{j = 1}^{n} {\sum\limits_{{a_{\alpha } ,a_{\beta } \in A}} {I_{j}^{l} (a_{\alpha } ,a_{\beta } )\omega_{j} } } = \sum\limits_{j = 1}^{n} {\sum\limits_{{a_{\alpha } ,a_{\beta } \in A}} {\left( {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5} \right)\omega_{j} } } . $$

(11)

Based on Eqs. (5) and (11), the generalized comprehensive concordance/discordance index can be presented as:

$$ I_{g}^{l} = \left( {\sum\limits_{j = 1}^{n} {\frac{{2\omega_{j} }}{m(m - 1)}\sum\limits_{{a_{\alpha } ,a_{\beta } \in A}} {\left( {I_{j}^{l} (a_{\alpha } ,a_{\beta } )} \right)^{\lambda } } } } \right)^{{\frac{1}{\lambda }}} = \left( {\sum\limits_{j = 1}^{n} {\frac{{2\omega_{j} }}{m(m - 1)}\sum\limits_{{a_{\alpha } ,a_{\beta } \in A}} {\left( {L(h_{\alpha j} \ge h_{\beta j} ) - 0.5} \right)^{\lambda } } } } \right)^{{\frac{1}{\lambda }}} , $$

(12)

where λ > 0. If λ = 1, then, $I_{g}^{l} = {{2I^{l} } \mathord{\left/ {\vphantom {{2I^{l} } {(m(m - 1))}}} \right. \kern-0pt} {(m(m - 1))}}$.

According to the likelihood-based comparison approach for HFLTSs, the credibility of the final ranking results of alternatives increases with increasing $I_{g}^{l}$. Therefore, the best ranking of alternatives P* can be identified by comparing the values of $I_{g}^{l}$ for each permutation:

$$ I_{g}^{ * } = \mathop {\hbox{max} }\limits_{l = 1}^{m!} \left\{ {I_{g}^{l} } \right\}. $$

(13)

The Proposed Algorithm

Based on the above analysis, the hesitant fuzzy linguistic MCDM approach with likelihood-based QUALIFLEX method can be summarized as follows.

Step 1 :

Transform the linguistic expressions into HFLTSs, and construct the decision matrix

Transform the linguistic expressions into HFLTSs according to Definition 2. Then construct and normalize the HFLTS decision matrix $H = \left[ {h_{ij} } \right]_{m \times n}$. For the maximizing criterion c _j , there is no need to conduct operations on h _ij ; for the minimizing criterion c _j , the negation operator must be used to normalize all elements of h _ij .

Step 2 :

List all possible permutations.

List all possible m! permutations of m alternatives that must be tested in the following steps. Let $P_{l} \;(l = 1,2, \cdots ,m!)$ denote the l-th permutation.

Step 3 :

Calculate the generalized comprehensive concordance/discordance indices.

Calculate the likelihood $L(h_{\alpha j} \ge h_{\beta j} )$ for each pair of alternatives $(a_{\alpha } ,a_{\beta } )$ with respect to the criterion c _j , and use Eqs. (3), (7), and (12) to derive the generalized comprehensive concordance/discordance index $I_{g}^{l}$ for each permutation P _l .

Step 4 :

Rank $I_{g}^{l}$, and determine the optimal ranking of all alternatives.

Use Eq. (13) to determine the ranking, and select the optimal alternative(s).

Illustrative Example

This section presents an evaluation problem for choosing an appropriate enterprise resource planning (ERP) system. The illustrative example demonstrates the application, validity, and effectiveness of the proposed decision-making approach.

China’s economy has improved dramatically following economic reformation and market opening. A large volume of machinery has been applied to facilitate the construction of infrastructure, which helps to improve the investment environment. Consequently, an increasing number of enterprises both at home and abroad participate actively in a fiercely competitive market. Numerous companies plan to implement ERP projects to improve operational efficiency and to lower costs. The feasibility study selected when using ERP systems may involve MCDM more than once, because various factors need be taken into consideration to guarantee the proper functioning of certain systems.

ABC Machinery Manufacturing Co., Ltd. is a famous equipment enterprise whose main business is developing and producing construction machinery transporters in China. The top managers for ABC plan to an ERP system to enhance their competitiveness. After thorough investigation, three ERP systems, denoted by {a ₁, a ₂, a ₃}, were taken into consideration. There are many criteria that reflect the performance of an ERP system; four criteria were chosen based on the experience of the chief information officer (CIO). These criteria include: function and technology (c ₁), strategic fitness (c ₂), vendor’s ability (c ₃), and vendor’s reputation (c ₄). The weight vector of the criteria is ω = (0.3, 0.2, 0.4, 0.1).

The decision makers, including the CIO and executive managers from different departments, gathered to determine the evaluation information. The linguistic term set $S = \{ s_{0} = {\text{very poor}},\;s_{1} = {\text{poor}},\;s_{2} = {\text{medium}}\;{\text{poor}},\;s_{3} = {\text{fair}},\;s_{4} = {\text{medium good}},\;s_{5} = {\text{good}},\;s_{6} = {\text{very good}}\}$ is used herein. The evaluation information provided by experts is shown in Table 1.

Table 1 Evaluation information from the decision makers

Illustration of the Proposed Approach

We follow the procedure outlined in section “The Proposed Algorithm” to obtain the best ranking of alternatives.

Step 1 :

Transform the linguistic expressions into HFLTSs and construct the decision matrix.

Transform the linguistic expressions into HFLTSs referring to Definition 2. Because all criteria are maximizing criteria, the HFLTS decision matrix H is

$$ H = \left[ {h_{ij} } \right]_{3 \times 4} = \left[ {\begin{array}{*{20}l} {\{ s_{2} ,s_{3} \} } \hfill & {\{ s_{4} ,s_{5} ,s_{6} \} } \hfill & {\{ s_{0} ,s_{1} ,s_{2} \} } \hfill & {\{ s_{4} ,s_{5} \} } \hfill \\ {\{ s_{3} \} } \hfill & {\{ s_{2} ,s_{3} ,s_{4} \} } \hfill & {\{ s_{2} ,s_{3} \} } \hfill & {\{ s_{6} \} } \hfill \\ {\{ s_{3} ,s_{4} \} } \hfill & {\{ s_{3} ,s_{4} \} } \hfill & {\{ s_{4} \} } \hfill & {\{ s_{0} ,s_{1} ,s_{2} ,s_{3} \} } \hfill \\ \end{array} } \right]. $$

Step 2 :

List all possible permutations.

List all ${\kern 1pt} 6( = 3!)$ permutations of the three alternatives that are to be tested. Let $P_{l} \;(l = 1,2, \ldots ,6)$ denote the l-th permutation.

$$ \begin{aligned} P_{1} \; & = (a_{1} ,a_{2} ,a_{3} ),\;P_{2} \; = (a_{1} ,a_{3} ,a_{2} ),\;P_{3} \; = (a_{2} ,a_{1} ,a_{3} ), \\ P_{4} \; & = (a_{2} ,a_{3} ,a_{1} ),\;P_{5} \; = (a_{3} ,a_{1} ,a_{2} ),\;{\text{and}}\;P_{6} \; = (a_{3} ,a_{2} ,a_{1} ). \\ \end{aligned} $$

Step 3 :

Calculate the generalized comprehensive concordance/discordance indices, and let $\lambda = 1$.

Use Eqs. (3), (7), and (12) to calculate the likelihood $L(h_{\alpha j} \ge h_{\beta j} )$ for each criterion c _j . Then derive the generalized comprehensive concordance/discordance index $I_{g}^{1}$ for each permutation of P _l . The results are shown in Tables 2 and 3.

Table 2 Likelihood of fuzzy preference relations

Table 3 Concordance/discordance indices of all permutations

Consider the index $I_{g}^{1}$ for the permutation $P_{1} \; = (a_{1} ,a_{2} ,a_{3} )$. According to Eq. (12),

$$ \begin{aligned} I_{g}^{1} & = \sum\limits_{j = 1}^{4} {\frac{{2\omega_{j} }}{3(3 - 1)}\sum\limits_{{a_{\alpha } ,a_{\beta} \in A}} {I_{j}^{l} (a_{\alpha } ,a_{\beta } )} } \\ & = \frac{1}{3}\left( {0.3 \times ( - 0.05 - 0.0845 - 0.0357) + 0.2 \times (0.1277 + 0.0864 - 0.0444)} \right. \\ & \quad \left. + 0.4 \times ( - 0.2528 - 0.5 - 0.5) + 0.1 \times ( - 0.5 + 0.5 + 0.5) \right) \\ & = - 0.1561. \\ \end{aligned} $$

The values of $I_{g}^{2}$, $I_{g}^{3}$, $I_{g}^{4}$, $I_{g}^{5}$, and $I_{g}^{6}$ can be derived similarly:

$I_{g}^{2} = - 0.0430,\;I_{g}^{3} = - 0.0624,\;I_{g}^{4} = 0.0430,\;I_{g}^{5} = 0.0624\;{\text{and}}\;I_{\text{g}}^{6} = 0.1561.$

Step 4 :

Rank $I_{g}^{l}$, and determine the optimal ranking of all alternatives.

Use Eq. (13) to determine the ranking of all alternatives:

$$ I_{g}^{ * } = \mathop {\hbox{max} }\limits_{l = 1}^{6} \left\{ {I_{g}^{l} } \right\} = I_{\text{g}}^{6} = 0.1561\; {\text{and}}\;P * = P_{6} = (a_{3} ,a_{2} ,a_{1} ). $$

The ranking of alternatives is a ₃ > a ₂ > a ₁. Thus, the optimal ERP system is a ₃.

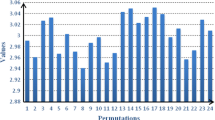
To investigate the effect of the parameter λ, different values of λ were taken into consideration. The result is shown in Fig. 1.

Fig. 1

Generalized comprehensive concordance/discordance indices for varying λ

The values of the generalized comprehensive concordance/discordance indices vary as λ changes. However, the ranking of the generalized comprehensive concordance/discordance indices remains the same. The ranking of alternatives is always a ₃ > a ₂ > a ₁, with the best alternative always being a ₃. This conclusion is drawn directly from Fig. 1, where $I_{g}^{6}$ is always at the top of the figure. The analysis results indicate that the ranking of alternatives remains the same as λ changes, and that the proposed approach accurately ranks all alternatives for $\lambda { = 1,3}, \ldots , 9$.

Comparative Analysis and Discussion

This section presents two comparative studies to validate the flexibility and feasibility of the proposed approach. These studies use different methods to solve the same MCDM problem in the context of HFLTSs and HFLEs.

Case 1 :

Comparative analysis in the context of HFLTSs

Wei et al.’s method [48] used the HLWA and HLOWA operators to aggregate evaluation information, which involved convex combinations of linguistic terms based on the usual Round operation. The possibility degree method was then used to determine the ranking of alternatives.

Lee and Chen’s method [16] defined the 1-cut of an HFLTS, and constructed likelihood-based comparison relations to compare the obtained linguistic intervals. In this method, four operators were used to derive the comprehensive values. They are the hesitant fuzzy linguistic weighted average (HFLWA) operator, the hesitant fuzzy linguistic weighted geometric (HFLWG) operator, the hesitant fuzzy linguistic ordered weighted average (HFLOWA) operator, and the hesitant fuzzy linguistic ordered weighted geometric (HFLOWG) operator.

Liao et al.’s method [18] developed a family of distance measure for HFLTSs, and constructed a fuzzy TOPSIS model to determine the ranking of alternatives. In the comparison analysis, they assume that the risk preference parameter is $\theta { = 0} . 5$ and the parameter of the generalized distance measure is $\lambda { = 1}$.

Wang et al. [43] defined dominance relations and established an outranking method with the Euclidean distance measure to rank the alternatives.

The ranking results obtained by these different methods are summarized in Table 4.

Table 4 Ranking results of different approaches in the context of HFLTSs

The following observations can be drawn from Table 4:

• 1. The MCDM method based on the HLWA and HLOWA operators [48] may only yield partial orders of alternatives. The results from this method show that a ₃ is better than a ₂ in terms of criteria c ₁, c ₂, and c ₃. Although a ₃ is inferior to a ₂ for c ₄, the weight of c ₄ is 0.1, which is not be sufficient to change the superiority of a ₃. A similar relationship exists between a ₁ and a ₃. Moreover, both the HLWA and HLOWA operators are based on the Round operation, which may lead to information loss in the process of approximation. Thus, the results obtained using HLWA and HLOWA are not convincing.

• 2. The results obtained by Lee and Chen’s method [16] are not consistent with those yielded by the proposed approach, except when using the HFLWG operator. Because a ₃ is predicted to be superior to a ₂, as discussed in (1), the results obtained using the HFLWA, HFLOWA, and HFLOWG operators are also unacceptable. In addition, the process in [16] relies on likelihood-based comparison relations, which are established using intervals constructed from the indices of the related HFLTS envelopes. It seems unreasonable to judge one HFLTS as being absolutely superior to another if they contain common elements. The limitations of transforming HFLTSs into intervals have been discussed in section “Hesitant Fuzzy Linguistic Term Sets.” Moreover, the transformation from linguistic terms to intervals is by nature inappropriate because HFLTSs have finite elements. The hesitance among linguistic values is replaced directly with a range, which is applicable to both discrete and continuous values. This range may cause information distortion. Therefore, the ranking results are not always reliable.

• 3. Liao et al.’s method [18] is based on generalized distance measures that are constructed by artificially adding linguistic values and allowing HFLTSs to have the same length. This is unreasonable and distorts the original evaluation information. Although the ranking results obtained when using the generalized distance measures with $\lambda { = 1}$ are in agreement with the results derived using the proposed approach, they are different otherwise. However, the ranking results obtained using the proposed approach remain the same when the parameter λ changes as discussed in section “Illustration of the Proposed Approach.” Varying the value of λ affects the results of these distance-based methods, which could justify the robustness of the proposed method to some extent.

• 4. The proposed QUALIFLEX approach yields the same ranking results as the outranking method ELECTRE [43]. This outranking method constructs the distance measure by acquiring only the upper and lower bounds on an HFLTS, which discards some linguistic terms and may cause information distortion. In addition, the computation process is complex. The proposed approach retains the original evaluation information and does not require complicated computations for each $P^{l}$. This is demonstrated in the illustrative example of selecting an optimal ERP system.

  Case 2 :

  Comparative analysis in the context of HFLEs

In this case, the proposed approach is extended to accommodate an MCDM problem where the criteria values are HFLEs with non-consecutive linguistic terms. Furthermore, a method based on the generalized hesitant fuzzy linguistic weighted average (GHFLWA) operator associated with the score function in [55] is used to solve the same problem. A comparative analysis is conducted between the two methods.

Three experts were called to evaluate the ERP systems for the example in section “Illustration of the Proposed Approach.” The evaluation information was given in the form of HFLEs, and the weight information remained the same. For instance, the three experts were asked to assess system a ₁ in terms of criterion c ₂, “strategic fitness”; with two experts providing the assessment “medium good” and the other providing the assessment “very good.” We assume that they cannot persuade each other to change their opinions. The evaluation values can be expressed as $h_{12}^{{\prime }} = \left\{ {s_{4} , s_{6} } \right\}$ by deleting the repeated values. The decision matrix can then be constructed as follows:

$$ H^{\prime} = \left[ {h^{\prime}_{ij} } \right]_{3 \times 4} = \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}c} {\{ s_{2} ,s_{3} \} } & {\{ s_{4} ,s_{6} \} } & {\{ s_{0} ,s_{2} \} } & {\{ s_{4} ,s_{6} \} } \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} {\{ s_{3} ,s_{5} \} } & {\{ s_{2} ,s_{4} \} } & {\{ s_{2} ,s_{3} \} } & {\;\;\{ s_{6} \} } \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} {\{ s_{3} ,s_{4} \} } & {\{ s_{3} ,s_{5} \} } & {\;\;\{ s_{4} \} } & {\{ s_{0} ,s_{2} ,s_{3} \} } \\ \end{array} } \hfill \\ \end{array} } \right]. $$

Equations (3), (7), and (12) can then be used to obtain the generalized comprehensive concordance/discordance indices with varying λ. The calculation steps are the same as those in section “Illustration of the Proposed Approach.” Additionally, the GHFLWA operator from Zhang et al.’s method [55] can be used to calculate the ranking results. The results of the different approaches are shown in Table 5.

Table 5 Ranking results of different approaches in the context of HFLEs

The method based on the GHFLWA operator [55] is not always effective, as the results vary when the value of λ changes. This may be caused by the defect of the score function. Additionally, each aggregation process is complex, and the number of operations relies heavily on the numbers of elements in each HFLE. For example, there are 3 × 2 = 6 elements in $h_{LS}^{1} \oplus h_{LS}^{2}$. The operation results will increase exponentially if a large number of HFLEs are involved in the operation. This deterioration resulting from the complexity may restrict the application of hesitant fuzzy linguistic aggregation operators. The proposed approach, however, is capable of obtaining acceptable results with varying λ and has a relatively simple process. Furthermore, the proposed likelihood-based comparison method effectively overcomes the disadvantages of the hesitant fuzzy linguistic score function discussed in sections “Hesitant Fuzzy Linguistic Sets” and “Likelihood of Fuzzy Preference Relation Between Two HFLTSs.”

According to the comparison analysis, the approach proposed in this paper has the following advantages over the other methods.

• 1. The calculations required for the proposed approach are relatively straightforward. The burden of computation can be significantly decreased with the assistance of the proven properties.

• 2. The developed likelihood-based comparison method does not require the transformation of HFLTSs into linguistic intervals or the addition of linguistic values. The fuzziness of the original information can be maintained and used fully. Thus, compared with other existing measures, such as likelihood, distance measures, and the score function for HFLTSs or HFLEs, the results obtained using the proposed approach are more reliable in some sense.

• 3. The proposed QUALIFLEX approach uses a new likelihood-based comparison method. It can handle not only HFLTSs, but also deals effectively with HFLEs with non-consecutive linguistic terms. Therefore, the proposed method is more flexible and competent in hesitant fuzzy linguistic MCDM than other methods.

An evident limitation of the proposed approach compared with existing methods is the tedious calculations required to address an MCDM with a large number of alternatives. The proposed approach is flexible and applicable to complex MCDM problems with many criteria but a limited number of alternatives. Furthermore, with the assistance of programming software, the amount of computation can be reduced sharply.

Conclusions

Hesitant fuzzy linguistic term sets are valuable for quantifying the ambiguous and hesitant nature of subjective judgments in a method developed for MCDM problems. We propose a useful QUALIFLEX approach, which uses a new likelihood-based comparison method, for managing MCDM problems with criterion values that are HFLTSs and have unknown weights. This paper develops a new likelihood-based comparison relation to measure the possibility that one HFLTS is superior to another. Furthermore, a comprehensive index is used to measure the levels of concordance and discordance. Finally, the feasibility and applicability of the proposed approach is validated by the practical problem of selecting a suitable ERP system in the contexts of both HFLTSs and HFLEs.

This study makes several significant contributions to the existing literature on solving MCDM problems with HFLTSs. First, the rankings produced by the proposed likelihood-based comparison method are more convincing than those obtained using existing measures, such as likelihood, distance measures, and the score function for HFLTSs or HFLEs. Second, this paper proposes an innovative way to incorporate the developed comparison method into QUALIFLEX. Third, the proposed approach extends the traditional QUALIFLEX methodology, making it flexible and applicable to complex MCDM problems with many criteria but a limited number of alternatives in a hesitant fuzzy linguistic environment. Future studies will focus on extending the proposed method to the hesitant fuzzy environment where the elements in hesitant fuzzy sets are repeated.

Appendix

Proof of Property 1.

Proof

Only (4) of Property 1 will be proven; the proofs of the other properties are omitted.

• a. If $H_{S}^{a + } < H_{S}^{b - }$ or $H_{S}^{b + } < H_{S}^{a - }$, then Definition 7 reveals that $L(H_{S}^{a} \ge H_{S}^{b} ) + L(H_{S}^{a} \le H_{S}^{b} ) = 1$.

• b. If $H_{S}^{a - } \le H_{S}^{b + } ,\;H_{S}^{b - } \le H_{S}^{a + } \;{\text{and}}\;H_{S}^{a - } = H_{S}^{b - } = s_{0}$, then Definition 7 reveals the following:

  $$ \begin{aligned} L(H_{S}^{a} \ge H_{S}^{b} ) & = \frac{1}{{l_{a} l_{b} }}\left( {\sum\limits_{i = 2}^{{l_{a} }} {\sum\limits_{j = 1}^{{l_{b} }} {\frac{{I(a_{i} )}}{{I(a_{i} ) + I(b_{j} )}} + \frac{1}{2}} } } \right) \\ & = \frac{1}{{l_{a} l_{b} }}\left( {\frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{1} )}} + \frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{2} )}} + \cdots + \frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{{l_{b} }} )}}} \right. \\ & \quad + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{1} )}} + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{2} )}} + \cdots + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{{l_{b} }} )}} + \cdots \\ & \quad + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{1} )}} + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{2} )}} + \cdots + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{{l_{b} }} )}} + \left. {\frac{1}{2}} \right). \\ \end{aligned} $$

  (14)
  $$ \begin{aligned} L(H_{S}^{a} \le H_{S}^{b} ) & = L(H_{S}^{b} \ge H_{S}^{a} ) = \frac{1}{{l_{a} l_{b} }}\left( {\sum\limits_{j = 2}^{{l_{b} }} {\sum\limits_{i = 1}^{{l_{a} }} {\frac{{I(b_{j} )}}{{I(b_{j} ) + I(a_{i} )}} + \frac{1}{2}} } } \right) \\ & = \frac{1}{{l_{a} l_{b} }}\left( {\frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{1} )}} + \frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{2} )}} + \cdots + \frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{{l_{a} }} )}}} \right. \\ & \quad + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{1} )}} + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{2} )}} + \cdots + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{{l_{a} }} )}} + \cdots \\ & \quad + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{1} )}} + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{2} )}} + \cdots + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{{l_{a} }} )}} + \left. {\frac{1}{2}} \right). \\ \end{aligned} $$

  (15)

By combining Eqs. (14) and (15), Eq. (16) can be obtained:

$$ \begin{aligned} & L(H_{S}^{a} \ge H_{S}^{b} ) + L(H_{S}^{a} \le H_{S}^{b} ) \\ & \quad = \frac{1}{{l_{a} l_{b} }}\left( {\frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{2} )}} + \frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{2} )}} + \frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{3} )}} + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{2} )}} + \cdots } \right. \\ & \quad \quad + \frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{{l_{b} }} )}} + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{2} )}} \\ & \quad \quad + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{2} )}} + \frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{3} )}} + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{3} )}} + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{3} )}} + \cdots \\ & \quad \quad + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{{l_{b} }} )}} + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{3} )}} + \cdots \\ & \quad \quad + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{2} )}} + \frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{{l_{a} }} )}} + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{3} )}} + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{{l_{a} }} )}} + \cdots \\ & \quad \quad + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{{l_{b} }} )}} + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{{l_{a} }} )}} \\ & \quad \quad + \frac{{I(a_{2} )}}{{I(a_{2} ) + I(b_{1} )}} + \frac{{I(a_{3} )}}{{I(a_{3} ) + I(b_{1} )}} + \cdots + \frac{{I(a_{{l_{a} }} )}}{{I(a_{{l_{a} }} ) + I(b_{1} )}} \\ & \quad \quad + \frac{{I(b_{2} )}}{{I(b_{2} ) + I(a_{1} )}} + \frac{{I(b_{3} )}}{{I(b_{3} ) + I(a_{1} )}} + \cdots + \frac{{I(b_{{l_{b} }} )}}{{I(b_{{l_{b} }} ) + I(a_{1} )}} + \left. {\frac{1}{2} + \frac{1}{2}} \right) & \\ & \quad = \frac{1}{{l_{a} l_{b} }}\left( {(l_{a} - 1)(l_{b} - 1) + (l_{a} - 1) + (l_{b} - 1) + 1} \right) = 1. \\ \end{aligned} $$

(16)

• c. If $H_{S}^{a - } \le H_{S}^{b + } ,\;H_{S}^{b - } \le H_{S}^{a + } \;{\text{and}}\;H_{S}^{a - } \ne s_{0} \;{\text{or}}\;H_{S}^{b - } \ne s_{0}$, then, similar to Eqs. (14) and (15):

  $$ L(H_{S}^{a} \ge H_{S}^{b} ) + L(H_{S}^{a} \le H_{S}^{b} ) = \frac{1}{{l_{a} l_{b} }}(l_{a} l_{b} ) = 1. $$

  (17)

Therefore, $L(H_{S}^{a} \ge H_{S}^{b} ) + L(H_{S}^{a} \le H_{S}^{b} ) = 1$.

The proof is now complete.