Analogical Mapping with Sparse Distributed Memory: A Simple Model that Learns to Generalize from Examples

Abstract

We present a computational model for the analogical mapping of compositional structures that combines two existing ideas known as holistic mapping vectors and sparse distributed memory. The model enables integration of structural and semantic constraints when learning mappings of the type $x_i \rightarrow y_i$ and computing analogies $x_j \rightarrow y_j$ for novel inputs x _j . The model has a one-shot learning process, is randomly initialized, and has three exogenous parameters: the dimensionality $\mathcal{D}$ of representations, the memory size S, and the probability χ for activation of the memory. After learning three examples, the model generalizes correctly to novel examples. We find minima in the probability of generalization error for certain values of χ, S, and the number of different mapping examples learned. These results indicate that the optimal size of the memory scales with the number of different mapping examples learned and that the sparseness of the memory is important. The optimal dimensionality of binary representations is of the order 10⁴, which is consistent with a known analytical estimate and the synapse count for most cortical neurons. We demonstrate that the model can learn analogical mappings of generic two-place relationships, and we calculate the error probabilities for recall and generalization.

Introduction

Computers have excellent quantitative information processing mechanisms, which can be programmed to execute algorithms on numbers at a high rate. Technology is less evolved in terms of qualitative reasoning and learning by experience. In that context, biology excels. Intelligent systems that interact with humans and the environment need to deal with imprecise information and learn from examples. A key function is analogy [1–6], the process of using knowledge from similar experiences in the past to solve a new problem without a known solution. Analogy-making is a high-level cognitive function that is well developed in humans [5, 7]. More formally, analogical mapping is the process of mapping relations and objects from one situation (a source), x, to another (a target), $y; M : x \rightarrow y$ [7, 8]. The source is familiar or known, whereas the target is a novel composition of relations or objects that is not among the learned examples.

Present theories of analogy-making usually divide this process into three or four stages. In this work, we follow [7] and describe analogy-making as a three-step process consisting of: retrieval, mapping, and application. As in the previous computational models of analogy-making, see section “Related Work”, this paper focuses mainly on the challenging mapping stage. We present a model that is based on a well-known mechanism for analogical mapping with high-dimensional vectors, which are commonly referred to as mapping vectors. By integrating this mechanism with a model of associative memory, known as sparse distributed memory (SDM), we obtain an improved model that can learn multiple mapping vectors. The proposed model can learn mappings $x_{k,z} \rightarrow y_{k,z}$, where k denotes different examples of one particular relationship z. If x _k,z is in the training set, the model retrieves a mapping vector that transforms x _k,z to an approximation of the learned y _k,z , otherwise x _k,z is transformed to an approximate generalization (an analog), y _k,z , of learned examples corresponding to the relationship z. The mechanism that enables the possibility to learn multiple mapping vectors that can be used for analogy-making is the major contribution of this paper.

An SDM operates on high-dimensional binary vectors so that associative and episodic mappings can be learned and retrieved [9–13]. Such high-dimensional vectors are useful representations of compositional structures [14–18]. For further details and references, see [19–22]. With an appropriate choice of operators, it is possible to create, combine, and extract compositional structures represented by such vectors. It is also possible to create mapping vectors that transform one compositional structure into another compositional structure [14, 17, 18]. Such mapping vectors can generalize to structures composed of novel elements [14, 17] and to structures of higher complexity than those in the training set [18]. The idea of holistic mapping vectors and the results referenced above are interesting because they describe a simple mechanism that enables computers to integrate the structural and semantic constraints that are required to perform analogical mapping. In this paper, we integrate the idea of holistic mapping vectors with the SDM model of associative memory into one “analogical mapping unit (AMU), which enables learning and application of mappings in a simple way. The ability to learn unrelated mapping examples with an associative memory is a novel feature of the AMU model. The AMU also provides an abstraction that, in principle, enables visualization of the higher-level cognitive system architecture.

In the following subsection, we briefly summarize the related work on analogical mapping. In section “Background,” we introduce the theoretical background and key references needed to understand and implement the AMU model. The AMU model is presented in section “Model”. In section “Simulation Experiments,” we present numerical results that characterize some properties of the AMU model. Finally, we discuss our results in the context of the related work and raise some questions for further research.

Related Work

Research on computational modeling of analogy-making traces back to the classical works in the 60s by Evans [23] and Reitman [24] and since then many approaches have been developed. In this section, we introduce some models that either have been influential or are closely related to the work presented here. For comprehensive surveys see [25, 26], where computational models of analogy are categorized as symbolic, connectionist, or symbolic-connectionist hybrids.

A well-known symbolic model is the Structure Mapping Engine (SME) [27], which implements a well-known theory of analogy-making called Structure Mapping Theory (SMT) [1]. With SMT, the emphasis in analogy-making shifted from attributes to structural similarity between the source and target domains. The AMU, like most present models, incorporates the two major principles underlying SMT: relation-matching and systematicity (see section “Simulation Experiments”). However, in contrast to SMT and other symbolic models, the AMU satisfies semantic constraints, thereby allowing the model to handle the problem of similar but not identical compositional structures. Satisfying semantic constraints reduces the number of potential correspondence mappings significantly, to a level that is psychologically more plausible [7, 28] and computationally feasible [26].

Connectionist models of analogy-making include the Analogical Constraint Mapping Engine (ACME) [4] and Learning and Inference with Schemas and Analogies (LISA) [29]. The Distributed Representation Analogy MApper (Drama) [7] is a more recent connectionist model that is based on holographic reduced representations (HRR). This makes Drama similar to the AMU in terms of the theoretical basis. A detailed comparison between ACME, LISA, and Drama in terms of performance and neural and psychological plausibility is made by [7]. Here, we briefly summarize results in [7], add some points that were not mentioned in that work, and comment on the differences between the AMU and Drama.

ACME is sometimes referred to as a connectionist model, but it is more similar to symbolic models. Like the SME, it uses localist representations, while the search mechanism for mappings is based on a connectionist approach. In ACME, semantics is considered after structural constraints have been satisfied. In contrast to ACME, the AMU and Drama implement semantic and structural constraints in parallel, thereby allowing both aspects to influence the mapping process. In comparison with the previous models, Drama integrates structure and semantics to a degree that is more in accordance with human cognition [7]. Semantics are not decomposable in ACME. For example, ACME would be unable to determine whether the "Dollar of Sweden" (Krona) is similar to the “Dollar of Mexico" (Peso), whereas that is possible with the AMU and Drama because the distributed representations allow compositional concepts to be encoded and decomposed [7, 14, 17, 18, 20, 22]. LISA is a connectionist model that is based on distributed representations and dynamic binding to associate relevant structures. Like the AMU and Drama, LISA is semantically driven, stochastic, and designed with connectionist principles. However, LISA has a complex architecture that represents propositions in working memory by dynamically binding roles to their fillers and encoding those bindings in long-term memory. It is unclear whether this model scales well and is able to handle complex analogies [7, 26, 30].

The third category of computational models for analogy-making is the “hybrid approach”, where both symbolic and connectionist parts are incorporated [25, 26]. Well-known examples of such models include Copycat [31], Tabletop [32], Metacat [33], and AMBR [34].

Other related work that should be mentioned here includes models based on Recursive Auto-Associative Memory (RAAM) [35] and models based on HRR [19]. RAAM is a connectionist network architecture that uses backpropagation to learn representations of compositional structures in a fixed-length vector. HRR is a convolution-based distributed representation scheme for compositional structures. In [35], a RAAM network that maps simple propositions like (LOVED X Y) to (LOVE Y X) in a holistic way (without decomposition of the representations) is presented. In [36], a feed-forward neural network that maps reduced representations of simple passive sentences to reduced representations of active sentences using a RAAM network is presented. In [37], a feed-forward network is trained to perform inference on logical relationships, for example, the mapping of reduced representations of expressions of the form $(x \rightarrow y)$ to corresponding reduced representations of the form $(\lnot x \lor y)$. Similar tasks have been solved with HRR [18, 19]. In particular, Neumann replicates the results by Niklasson and van Gelder using HRR and she demonstrates that HRR mappings generalize to novel compositional structures that are more complex than those in the training set. The significance of relation-matching in human evaluation of similarity is demonstrated in [38] by asking people to evaluate the relative similarity of pairs of geometric shapes. In [19], distributed representations (HRR) for each of these pairs of geometric shapes are constructed, and it is found that the similarity of the representations is consistent with the judgement by human test subjects.

From our point of view, there are two issues that have limited the further development of these analogical mapping techniques. One is the “encoding problem”, see for example [39, 40]. In this particular context, it is the problem of how to encode compositional structures from low-level (sensor) information without the mediation of an external interpreter. This problem includes the extraction of elementary representations of objects and events, and the construction of representations of invariant features of object and event categories. Examples demonstrating some specific technique are typically based on hand-constructed structures, which makes the step to real-world applications non-trivial, because it is not known whether the success of the technique is due to the hand-crafting of the representations and there is no demonstration of the feasibility of mechanically generating the representations. The second issue is that mapping vectors are explicitly created and that there is no framework to learn and organize multiple analogical mappings. The construction of an explicit vector for each analogical mapping in former studies is excellent for the purpose of demonstrating the properties of such mappings. However, in practical applications, the method needs to be generalized so that a system can learn and use multiple mappings in a simple way.

Learning of multiple mappings from examples is made possible with the AMU model that is presented in this paper. The proposed model automates the process of creating, storing, and retrieving mapping vectors. The basic idea is that mapping examples are fed to an SDM so that mapping vectors are formed successively in the storage locations of the SDM. After learning one or two examples, the system is able to recall, but it typically cannot generalize. With additional related mapping examples stored in the SDM, the ability of the AMU to generalize to novel inputs increases, which means that the probability of generalization error decreases with the number of examples learned.

Background

This section introduces the theoretical background and key references needed to understand and implement the AMU model, which is presented in section “Model”.

Vector Symbolic Architectures

The AMU is an example of a vector symbolic architecture (VSA) [41], or perhaps more appropriately named a VSA “component” in the spirit of component-based software design. In general, a VSA is based on a set of operators on high-dimensional vectors of fixed dimensionality, so-called reduced descriptions/representations of a full concept [42]. The fixed length of vectors for all representations implies that new compositional structures can be formed from simpler structures without increasing the size of the representations, at the cost of increasing the noise level. In a VSA, all representations of conceptual entities such as ontological roles, fillers, and relations have the same fixed dimensionality. These vectors are sometimes referred to as holistic vectors [16] and operations on them are a form of holistic processing [18, 43]. Reduced representations in cognitive models are essentially manipulated with two operators, named binding and bundling. Binding is similar to the idea of neural binding in that it creates a representation of the structural combination of component representations. It combines two vectors into a new vector, which is indifferent (approximately orthogonal) to the two original vectors. The defining property of the binding operation is that given the bound representation and one of the component representations, it is possible to recover the other component representation. The implementation of the binding operator and the assumptions about the nature of the vector elements are model specific. The bundling operator is analogous to superposition in that it creates a representation of the simultaneous presence of multiple component representations without them being structurally combined. It typically is the algebraic sum of vectors, which may or may not be normalized. Bundling and binding are used to create compositional structures and mapping vectors. Well-known examples of VSAs are the Holographic Reduced Representation (HRR) [14, 19, 20] and the Binary Spatter Code (BSC) [15–17]. The term “holographic” in this context refers to a convolution-based binding operator, which resembles the mathematics of holography. Historical developments in this direction include the early holography-inspired models of associative memory [44–47]. Note that the BSC is mathematically related to frequency-domain HRR [48], because the convolution-style operators of HRR are equivalent to element-wise operations in frequency space.

The work in VSA has been inspired by cognitive behavior in humans and the approximate structure of certain brain circuits in the cerebellum and cortex, but these models are not intended to be accurate models of neurobiology. In particular, these VSA models typically discard the temporal dynamics of neural systems and instead use sequential processing of high-dimensional representations. The recent implementation of HRR in a network of integrate-and-fire neurons [49] is, however, one example of how these cognitive models eventually may be unified with more realistic dynamical models of neural circuits.

In the following description of the AMU we use the Binary Spatter Code (BSC), because it is straightforward to store BSC representations in an SDM and it is more simple than the HRR which is based on real- or complex-valued vectors. It is not clear how to construct an associative memory that enables a similar approach with HRR, but we see no reason why that should be impossible. In a BSC, roles, fillers, relations, and compositional structures are represented by a binary vector, x _k , of dimensionality ${{\mathcal{D}}}$

$$ x_k \in B^{{\mathcal{D}}},\,x_k=(x_{k,1}, x_{k,2}, x_{k,3},{\ldots}, x_{k,{{\mathcal{D}}}}). $$

(1)

The binding operator, ⊗, is defined as the element-wise binary XOR operation. Bundling of multiple vectors x _k is defined as an element-wise binary average

$$ \left\langle \sum_{k=1}^n x_{k,i}\right\rangle = \Uptheta\left(\frac{1}{n}\sum_{k=1}^n x_{k,i}\right), $$

(2)

where $\Uptheta(x)$ is a binary threshold function

$$ \Theta (x) = \left\{ {\begin{array}{*{20}c} 1 \hfill & {{\text{for}}\quad x > 0.5,} \hfill \\ 0 \hfill & {{\text{for}}\quad x < 0.5,} \hfill \\ {{\text{random}}} \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right. $$

(3)

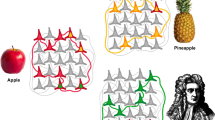
This is an element-wise majority rule. When an even number of vectors are bundled, there may be ties. These elements are populated randomly with an equal probability of zeros and ones. Structures are typically constructed from randomly generated names, roles, and fillers by applying the binding and bundling operators. For example, the concept in Fig. 1 can be encoded by the two-place relation $\langle a + a_1 \otimes \bullet + a_2 \otimes \blacksquare \rangle$, where a is the relation name (“above”), a ₁ and a ₂ are roles of the relation, and the geometric shapes are fillers indicating what is related.

Fig. 1

The circle is above the square. This implies that the square is below the circle. The analogical mapping unit (AMU) can learn this simple “above–below” relation from examples and successfully apply it to novel representations, see sections “Model” and “Simulation Experiments”

All terms and factors in this representation are high-dimensional binary vectors, as defined in (1). Vectors are typically initialized randomly, or they may be compositions of other random vectors. In a full-featured VSA application, this encoding step is to be automated with other methods, for example, by feature extraction using deep learning networks or receptive fields in combination with randomized fan-out projections and superpositions of patterns. A key thing to realize in this context is that the AMU, and VSAs in general, operate on high-dimensional random distributed representations. This makes the VSA approach robust to noise, and in principle and practice, it enables operation with approximate compositional structures.

Holistic Mapping Vectors

The starting point for the development of the AMU is the idea of holistic mapping vectors, see [17–19]. In [17], a BSC mapping of the form “X is the mother of Y” $\rightarrow$ “X is the parent of Y” is presented. This mapping is mathematically similar to the above–below relation illustrated in Fig. 1, with the exception that the mother–parent mapping is unidirectional because a parent is not necessarily a mother. The above–below relationship is bidirectional because a mapping between “the circle is above the square” and “the square is below the circle” is true in both directions. We think that the geometric example illustrated here is somewhat simpler to explain and we therefore use that. The key idea presented in [17] is that a mapping vector, M, can be constructed so that it performs a mapping of the type: “If the circle is above the square, then the square is below the circle”. If the mapping vector is defined in this way

$$ M = \bullet_\uparrow \blacksquare_\downarrow \otimes \blacksquare_\downarrow \bullet_\uparrow, $$

(4)

then it follows that

$$ M\otimes \bullet_\uparrow \blacksquare_\downarrow = \blacksquare_\downarrow \bullet_\uparrow, $$

(5)

because the XOR-based binding operator is an involuntary (self-inverse) function. The representations of these particular descriptions are illustrated in Table 1 and are chosen to be mathematically identical to the mother-parent representations in [17].

Table 1 Two different representations of the geometric composition presented in Fig. 1

Making Analogies with Mapping Vectors

A more remarkable property appears when bundling several mapping examples

$$ M = \langle \bullet_\uparrow \blacksquare_\downarrow \otimes \blacksquare_\downarrow \bullet_\uparrow + \blacksquare_\uparrow \blacktriangle_\downarrow \otimes \blacktriangle_\downarrow \blacksquare_\uparrow + \cdots \rangle, $$

(6)

because in this case the mapping vector generalizes correctly to novel representations

$$ M\otimes \bigstar_\uparrow \blacklozenge_\downarrow \approx \blacklozenge_\downarrow \bigstar_\uparrow. $$

(7)

The symbols $\bigstar$ and ⧫ have not been involved in the construction of M, but the mapping results in an analogically correct compositional structure. This is an example of analogy-making because the information about above–below relations can be applied to novel representations.

The left- and right-hand side of (7) are similar compositional structures, but they are not identical. The result is correct in the sense that it is close to the expected result, for example, in terms of the Hamming distance or correlation between the actual output vector and expected result, see [17] for details. In real-world applications, the expected mapping results could well be unknown. It is still possible to interpret the result of an analogical mapping if parts of the resulting compositional structure are known. For example, the interpretation of an analogical mapping result can be made using a VSA operation called probing, which extracts known parts of a compositional structure (which by themselves may be compositional structures). This process can be realized with a “clean-up memory”, see [p. 102, 14]. A mapping result that does not contain any previously known structure is interpreted as noise.

Observe that the analogical mapping (7) is not simply a matter of reordering the vectors representing the five-pointed star and diamond symbols. The source and target of this mapping are two nearly uncorrelated vectors, with different but analogical interpretations. In principle, this mechanism can also generalize to compositional structures of higher complexity than those in the training set, see [18] for examples. These interesting results motivated the development of the AMU.

Making Inferences with Mapping Vectors

Note that (4) is symmetric in the sense that the mapping is bidirectional. It can perform the two mappings M ⊗ ●_↑ ■_↓ = ■_↓ ●_↑ and M ⊗ ■ _↓ ●_↑ = ●_↑ ■_↓ equally well. This is a consequence of the commutative property of the binding operator. In this particular example that does not pose a problem, because both mappings are true. In the parent–mother example in [17], it implies that “parent” is mapped to “mother”, which is not necessarily a good thing. A more severe problem with bidirectional mappings appears in the context of inference and learning of sequences, which requires strictly unidirectional mappings. To enable robust analogical mapping, and inference in general, the mapping direction of BSC mapping vectors must be controlled. This problem is solved by the integration of an associative memory in the AMU model, see section “Learning Circuit”.

Sparse Distributed Memory

To make practical use of mapping vectors, we need a method to create, store, and query them. In particular, this involves the difficulty of knowing how to bundle new mapping vectors with the historical record. How should the system keep the examples organized without involving a homunculus (which could just as well do the mappings for us)? Fortunately, a suitable framework has already been developed for another purpose. The development presented here rests on the idea that an SDM used in an appropriate way is a suitable memory for storage of analogical mapping vectors, which automatically bundles similar mapping examples into well-organized mapping vectors. The SDM model of associative and episodic memory is well described in the seminal book by Kanerva. Various modifications of the SDM model have been proposed [50–54] but here we use the original SDM model [9].

Architecture and Initialization

An SDM essentially consists of two parts, which can be thought of as two matrices: a binary address matrix, A, and an integer content matrix, C. These two matrices are initialized as follows: The matrix A is populated randomly with zeros and ones (equiprobably), and the matrix C is initialized with zeros. The rows of the matrix A are so-called address vectors, and the rows of the matrix C are counter vectors. There is a one-to-one link between address vectors and counter vectors, so that an activated address vector is always accompanied by one particular activated counter vector. The address and counter vectors have dimensionality $\mathcal{D}$. The number of address vectors and counter vectors defines the size of the memory, S.

The SDM can be described algebraically as follows. If the address and counter vectors have dimensionality $\mathcal{D}$, the address matrix, A, can be defined as

$$ A = \left[ \begin{array}{llll} a_{11} &a_{12} & \ldots & a_{1{\mathcal{D}}} \\ a_{21} & a_{22} & \ldots & a_{2{\mathcal{D}}} \\ \ldots \\ a_{S1} & a_{S2} & \ldots & a_{S{\mathcal{D}}} \\ \end{array} \right], $$

(8)

where $a_{i,j} \in \{i=1, 2, \ldots, S, j=1,2, \ldots, \mathcal{D}\}$ are random bits (short for binary digits) with equal probability for the two states. The content matrix, C, is defined as

$$ C = \left[ \begin{array}{llll} c_{11} &c_{12} & \ldots & c_{1{\mathcal{D}}} \\ c_{21} & c_{22} & \ldots & c_{2{\mathcal{D}}} \\ \ldots \\ c_{S1} & c_{S2} & \ldots & c_{S{\mathcal{D}}} \\ \end{array} \right], $$

(9)

where $a_{i,j} \in \{i=1, 2, \ldots, S,\,j=1,2, \ldots, \mathcal{D}\}$ are integer numbers that are initialized to zero in an empty memory.

Storage Operation

When a vector is stored in the SDM, the content matrix C is updated, but the address matrix A is static. It is typically sufficient to have six or seven bits of precision in the elements of the content matrix [9]. The random nature of the compositional structures makes saturation of counter vectors unlikely with that precision.

Two input vectors are needed to store a new vector in the SDM: a query vector, ${x = (x_1, x_2 \ldots , x_{\mathcal{D}})}$, and a data vector, ${d = \{d_1, d_2 \ldots , d_{\mathcal{D}}\}}$. The query vector, x, is compared with all address vectors, a _i , using the Hamming distance, δ. The Hamming distance between two binary vectors x and a is defined as

$$ \delta(x,a) = \sum_{i=1}^{{\mathcal{D}}} I(x_i, a_i) $$

(10)

where I is a bit-wise XOR operation

$$ I(x_i, a_i) = \left\{ \begin{array}{ll} 1, &x_i \neq a_i \\ 0, &x_i = a_i. \end{array} \right. $$

(11)

The Hamming distance between two vectors is related to the Pearson correlation coefficient, ρ, by ρ = 1 − 2δ [16]. A predefined threshold value, T, is used to calculate a new vector $s = \{s_1, s_2 \ldots , s_S\}$ so that

$$ s_i = \left\{ \begin{array}{ll} 1, &\delta(s, a_i) < T\\ 0, &\delta(s, a_i) \geq T. \end{array} \right. $$

(12)

The non-zero elements of s are used to activate a sparse subset of the counter vectors in C. In other words, the indices of non-zero elements in s are the row-indices of activated counter vectors in the matrix C. With this definition of s, the activated counter vectors correspond to address vectors that are close to the query vector, x.

In a writing operation, the activated counter vectors are updated using the data vector, d. For every bit that is 1 in the data vector, the corresponding elements in the activated counter vectors are increased by one, and for every bit that is 0, the corresponding counters are decreased by one. This means that the elements, c _i,j , of the matrix C are updated so that

$$ c_{i,j} \leftarrow \left\{ \begin{array}{lll} c_{i,j}+1 & s_{i}=1, &d_{j}=1\\ c_{i,j}-1 & s_{i}=0, &d_{j}=1\\ c_{i,j} & s_{i}=0 \end{array} \right. $$

(13)

The details of why this is a reasonable storage operation in a binary model of associative memory are well described in [9].

Various modifications of the SDM model have been presented in the literature that address the problem of storing non-random patterns and localist representations in an SDM without saturating the counter vectors. In our perspective, low-level structured inputs from sensors need to be preprocessed with other methods, such as methods for invariant feature extraction. There are good reasons to operate with random representations at the higher cognitive level [9, 55], and this is a typical prerequisite of VSAs.

Retrieval Operation

In a retrieval operation, the SDM functions in a way that is similar to the storage operation except that an approximate data vector, d, is retrieved from the SDM rather than supplied to it as input. For a given query vector, ${x = (x_1, x_2 \ldots , x_{\mathcal{D}})}$, the Hamming distances, δ(x, a _i ), between x and all address vectors, a _i , are calculated. A threshold condition (12) is used to activate counter vectors in C with addresses that are sufficiently close to the query vector. The activated counter vectors in C are summed,

$$ h_j = \sum_{i=1}^S s_i c_{ij}, $$

(14)

and the resulting integer vector, h _j , is converted to a binary output vector, d, with the rule

$$ d_j = \left\{ \begin{array}{ll} 1, & h_j>0\\ 0, & h_j<0\\ \hbox {random} & \hbox{otherwise}. \\ \end{array} \right. $$

(15)

In this paper, we use the term recall for the process of retrieving a data vector from the SDM that previously has been stored. An SDM retrieval operation is analogous to bundling (2) of all vectors stored with an address vector that is similar to the query vector.

Implementation

An SDM can be visualized as suggested in Fig. 2, with two inputs and one output. The open circle denotes the query vector, which is supplied both when storing and retrieving information. The open square denotes the input data vector, which is supplied when storing information in the SDM. The solid square denotes the output data vector, which is generated when retrieving information. For software simulation purposes, for example in Matlab, the VSA operators and the SDM can be implemented in an alternative way if binary vectors are replaced with bipolar vectors according to the mapping $\{0 \rightarrow 1, 1 \rightarrow -1\}$. In that case, the XOR binding operator is replaced with element-wise multiplication.

Fig. 2

Schematic illustration of a sparse distributed memory (SDM), which is an associative memory for random high-dimensional binary vectors [9]

The number of counter vectors that are activated during one storage or retrieval operation depends on the threshold value, T. In this work, we choose to calculate this parameter so that a given fraction, χ, of the storage locations of the SDM is activated. Therefore, χ is the average probability of activating a row in the matrices A and C, which we also refer to as one storage location of the SDM. The number of activated locations in each storage or retrieval operation is exactly χ S. When storing multiple mapping vectors in an SDM, it is possible that a subset of the counter vectors are updated with several mapping vectors, which can correspond to different mapping examples. On average, the probability for overlap of two different mapping vectors in a location of the SDM is of the order χ².

Next, we present the AMU model, which incorporates an SDM for the storage and retrieval of analogical mapping vectors.

Model

The AMU consists of one SDM with an additional input–output circuit. First, we introduce the learning and mapping parts of this circuit, and then, we combine these parts into a complete circuit that represents the AMU.

Learning Circuit

The AMU stores vectors in a process that is similar to the bundling of examples in (6), provided that the addresses of the mapping examples are similar. If the addresses are uncorrelated, the individual mapping examples will be stored in different locations of the SDM and no bundling takes place, which prevents generalization and analogical mapping. A simple approach is therefore to define the query vector of a mapping, $x_k\rightarrow y_k$, as the variable x _k . This implies that mappings with similar x _k are, qualitatively speaking, bundled together within the SDM. The mapping vector x _k  ⊗ y _k is the data vector supplied to the SDM, and it is bundled in counter vectors with addresses that are close to x _k . A schematic diagram illustrating this learning circuit is shown in Fig. 3.

Fig. 3

Schematic diagram of learning circuit for mappings of type $x_k\rightarrow y_k$. Learning can be supervised or unsupervised, for example, in the form of coincidence (Hebbian) learning

This circuit avoids the problem of bidirectionality discussed in section “Making Inferences with Mapping Vectors” because the SDM locations that are activated by the query vector x _k are different from the locations that are activated by the query vector y _k of the reversed mapping. The forward and reversed mappings are therefore stored in different SDM locations. Therefore, the output of a query with y _k is nonsense (noise) if the reversed mapping is not explicitly stored in the SDM. In other words, the reversed mapping $y_k\rightarrow x_k$ is not implicitly learned.

Note that different types of mappings have different x _k . Queries with different x _k activate different locations in the SDM. Therefore, given a sufficiently large memory, it is possible to store multiple types of mappings in one SDM. This is illustrated with simulations in section “Simulation Experiments”.

Mapping Circuit

The learning mechanism in combination with the basic idea of analogical mapping (7) suggests that the mapping circuit should be defined as illustrated in Fig. 4. This circuit binds the input, x _k , with the bundled mapping vector of similar mapping examples that is stored in the SDM. The result is an output vector y′ _k . If the mapping $x_k\rightarrow y_k$ is stored in the SDM, then y′ _k ≈ y _k .

Fig. 4

Schematic diagram of circuit for mappings of type $x_k\rightarrow y^{\prime}_k$. Here, y′ _k ≈ y _k when $x_k\rightarrow y_k$ is in the training set. Otherwise y ^′ _k is an approximate analogical mapping of x _k , or noise if x _k is unrelated to the learned mappings

When a number of similar mapping examples are stored in the SDM, this circuit can generalize correctly to novel compositional structures. In such cases, y _k ′ is an approximate analogical mapping of x _k . This is illustrated with simulations in the next section.

The Analogical Mapping Unit

The AMU includes one SDM and a combination of the learning and mapping circuits that are presented in the former two subsections, see Fig. 5. It is a computational unit for the mapping of distributed representations of compositional structures that takes two binary input vectors and provides one binary output vector, much like the SDM does, but with a different result and interpretation. If the input to the AMU is x _k the corresponding output vector y′ _k is calculated (mapping mode). With two input vectors, x _k and y _k , the AMU stores the corresponding mapping vector in the SDM (learning mode). In total, the AMU has three exogenous parameters: S, χ, and the dimensionality $\mathcal{D}$ of the VSA, see Table 2. In principle, the SDM of the AMU can be shared with other VSA components, provided that the mappings are encoded in a suitable way. Next, we present simulation results that characterize some important and interesting properties of the AMU.

Fig. 5

The analogical mapping unit (AMU), which includes the learning and mapping circuits introduced above. This unit learns mappings of the type $x_k\rightarrow y_k$ from examples and uses bundled mapping vectors stored in the SDM to calculate the output vector y′ _k

Table 2 Summary of exogenous parameters of the AMU

Simulation Experiments

An important measure for the quality of an intelligent system is its ability to generalize with the acquired knowledge [56]. To test this aspect, we generate previously unseen examples of the “above–below relation using the sequence shown in Fig. 6. The relations between the items in this sequence are encoded in a similar way to those outlined in Table 1, with the only difference being that the fillers are different, see Table 3.

Fig. 6

A sequence of novel “above–below” relations that is used to test the ability of the AMU to generalize

Table 3 Representation of “above–below” relations between novel structures

Comparison with Other Results

Our mapping approach is similar to that in [17], but differs from that in three ways. First, mapping examples are fed to an SDM so that multiple mapping vectors are stored in the SDM, instead of defining explicit mapping vectors for each mapping. Second, the model uses binary spatter codes to represent mappings, which means that the mapping vectors generated by the AMU are binary vectors and not integer vectors. Third, the dimensionality ${{\mathcal{D}}}$ is set to a somewhat low value of 1,000 in most simulations presented here, and we illustrate the effect of higher dimensionality at the end of this section. We adopt the method in [17] to calculate the similarity between the output of the AMU and alternative mappings with the correlation coefficient, ρ, see section “Storage Operation”. Randomly selected structures, such as: $a, b, a_{1}, a_{2}, b_{1}, b_{2}, \bullet, \blacksquare \dots$ A, B are uncorrelated, ρ ≈ 0. That is true also for x _i and y _i , such as: ●_↑ ■_↓ and ■_↓ ●_↑. However, ●_↑ ■_↓ and A_↑ B_↓ include the same relation name, a, in the composition, and these vectors are therefore correlated, ρ ≈ 0.25.

The AMU learns mappings between compositional structures according to the circuit shown in Fig. 3, and the output y′ _k of the AMU is determined according to Fig. 4 and related text. The output, y′ _k , is compared with a set of alternative mapping results in terms of the correlation coefficient, ρ, both for recall and generalization. The number of training examples is denoted with N _e . To estimate the average performance of the AMU, we repeat each simulation 5000 times with independently initialized AMUs. This is sufficient to estimate the correlation coefficients with a relative error of about ± 10⁻².

In order to compare our model with [17], we first set the parameters of the AMU to ${S = 1, {\mathcal{D}} = 1,000}$ and χ = 1. This implies that the AMU has one location that is activated in each storage and retrieval operation. The result of this simulation is presented in Fig. 7. Figure 7a shows the average correlation between the output y′ _k resulting from the input, x _k  = ●_↑ ■_↓, which is in the training set, and four alternative compositional structures. Figure 7b shows the average correlation between four alternative compositional structures and the AMU output resulting from a novel input, x _k  = A_↑B_↓. The alternative with the highest correlation is selected as the correct answer. With more training examples, the ability of the AMU to generalize increases, because the correlations with wrong alternatives decrease with increasing N _e . The alternative with the highest correlation always corresponds to the correct result in this simulation, even in the case of generalization from three training examples only.

Fig. 7

The correlation, ρ, between the output of the analogical mapping unit (AMU) and alternative compositional structures versus the number of training examples, N _e , for a recall of learned mappings; b generalization from novel inputs. The parameters of the AMU are S = 1, χ = 1 and ${{\mathcal{D}} = 1,000}$

These results demonstrate that the number of training examples affects the ability of the AMU to generalize. This conclusion is consistent with the results (see Fig. 1) and the related discussion in [17]. The constant correlation with the correct mapping alternative in Fig. 7b is one quantitative difference between our result and the result in [17]. In our model, the correlation of the correct generalization alternative does not increase with N _e , but the correlations with incorrect alternatives decrease with increasing N _e . This difference is caused by the use of binary mapping vectors within the AMU, instead of integer mapping vectors. If we use the integer mapping vectors (14) that are generated within the SDM of the AMU, we reproduce the quantitative results obtained in [17]. Integer mapping vectors can be implemented in our model by modifying the normalization condition (15). The correlation with correct mappings can be improved in some cases with the use of integer mapping vectors, but the use of binary representations of both compositional structures and mapping vectors is more simple, and it makes it possible to use an ordinary SDM for the AMU. By explicitly calculating the probability of error from the simulation results, we conclude that the use of binary mapping vectors is sufficient. (We return to this point below.)

In principle, there are many other “wrong” mapping alternatives that are highly correlated with the AMU output, y′ _k , in addition to the four alternatives that are considered above. However, the probability that such incorrect alternatives or interpretations would emerge spontaneously is practically zero due to the high dimensionality and random nature of the compositional structures [9]. This is a key feature and design principle of VSAs.

Storage of Mapping Vectors in a Sparse Distributed Memory

Next, we increase the size of the SDM to S = 100, which implies that there are one hundred storage locations. The possibility to have S > 1 is a novel feature of the AMU model, which was not considered in former studies [14, 17, 18, 20, 22]. We investigate the effect of different values of χ and present results for χ = 0.05 and χ = 0.25. That is, when the AMU activates 5% and 25% of the SDM to learn each mapping vector. Figure 8 shows that the effect of increasing χ is similar to training with more examples, in the sense that it improves generalization and reduces the accuracy of recall. This figure is analogous to Fig. 7, with the only difference being that here the AMU parameters are S = 100 and χ = 0.05 or χ = 0.25. Figure 8a, c show the average correlation between the output y′ _k resulting from the input, x _k  = ●_↑ ■_↓, which is in the training set, and four alternative compositional structures for, respectively, χ = 0.05 and χ = 0.25. Figure 8b, d shows the average correlation between four alternative compositional structures and the AMU output resulting from a novel input, x _k  = A_↑B_↓. When retrieving learned examples for χ = 0.05 and χ = 0.25, the alternative with the highest correlation always corresponds to the correct result in this simulation experiment. See Fig. 7 and related text for details of how the average correlations are calculated. A high value of χ enables generalization with fewer training examples, but there is a trade-off with the number of different two-place relations that are learned by the AMU. We return to that below.

Fig. 8

Correlations between alternative compositional structures and the output of an AMU versus the number of examples in the training set, N _e , for a recall with χ = 0.05; b Generalization with χ = 0.05; c Recall with χ = 0.25; d Generalization with χ = 0.25. The size of the SDM is S = 100 in all four cases

Probability of Error

The correlations between the output of the AMU and the alternative compositional structures varies from one simulation experiment to the next because the AMU is randomly initialized. The distribution functions for these variations have a non-trivial structure. It is difficult to translate average correlation coefficients and variances into tail probabilities of error. Therefore, we estimate the probability of error numerically from the error rate in the simulation experiments. An error occurs when the output of the AMU has the highest correlation with a compositional structure that represents an incorrect mapping. The probability of error is defined as the number of errors divided by the total number of simulated mappings, N _e N _r N _s , where N _e is the number of training examples for each particular two-place relation, N _r is the number of different two-place relations (unrelated sets of mapping examples), and N _s  = 5,000 is the number of simulation experiments performed with independent AMUs. We test all N _e mappings of each two-place relation in the training set, and we test equally many generalization mappings in each simulation experiment. This is why the factors N _e and N _r enter the expression for the total number of simulated mappings. The N _e different x _k and y _k are generated in the same way for the training and generalization sets, by using a common set of names and roles but different fillers for the training and generalization sets. Different two-place relations are generated by different sets of names and roles, see section “Storing Multiple Relations”.

When the probability of error is low, we have verified the estimate of the probability by increasing the number of simulation experiments, N _s . For example, this is sometimes the case when estimating the probability of error for mappings that are in the training set. As mentioned in section “Comparison with Other Results,” this is why we choose a suboptimal and low value for the dimensionality of the representations, $\mathcal{D}$. The probability of error is lower with high-dimensional representations, which is good for applications of the model but makes estimation of the probability of error costly. Figure 9 presents an interesting and expected effect of the probability of error during generalization versus the number of training examples. The probability of activating a storage location, χ, affects the probability of generalization error significantly. For χ = 0.25 and N _e = 30, the AMU provides more than 99.9% correct mappings. Therefore, that point has poor precision and is excluded from the figure.

Fig. 9

The probability of generalization error versus the number of training examples, N _e , for χ = 0.05 and χ = 0.25

In Fig. 7, all mapping vectors are bundled in one single storage location, while Fig. 9 is generated with AMUs that have an SDM of size S = 100 so that each mapping vector is stored in multiple locations. Figures 8 and 9 are complementary because the parameters of the AMUs used to generate these figures are identical. For χ = 0.25 the AMU generalizes correctly with fewer training examples compared to the results for the lower value of χ = 0.05. This result is consistent with Fig. 8, which suggests that the AMU with χ = 0.25 generalizes with fewer training examples. The rationale of this result is that a higher value of χ gives more overlap between different mapping vectors stored in the AMU, and multiple overlapping (bundled) mapping vectors are required for generalization, see (7). This effect is visible also in Fig. 7, where the AMU provides the correct generalization after learning three examples.

Storing Multiple Relations

Since mapping vectors are bundled in a fraction of the storage locations of the SDM, it is reasonable to expect that the AMU can store additional mapping vectors, which could be something else than “above–below” relations. To test this idea, we introduce a number, N _r , of different two-place relations. The above–below relation considered above is one example of such a two-place relation, see Tables 1, 3. In general, names and roles can be generated randomly for each particular two-place relation, see Table 4, in the same way as the names and roles are generated for the above–below relations. For each two-place relation, we generate N _e training examples and N _e test (generalization) examples, see the discussion in section “Probability of Error” for further details. This way we can simulate the effect of storing multiple two-place relations in one AMU.

Table 4 Representation of generic two-place relations, labeled by z, between two compositional structures represented by the fillers f _1,k,z and f _2,k,z

An interesting effect appears when varying the number of two-place relations, N _r , and the size of the SDM, see Fig. 10a. The size of the SDM, S, and the average probability of activating a storage location, χ, affect the probability of generalization error. Provided that the SDM is sufficiently large and that N _e is not too high, there is a minimum in the probability of error for some value of N _r . A minimum appears at N _r  = 3 − 4 for χ = 0.05 and S = 1,000 in Fig. 10a. Figure 10b has a minimum at N _r  = 2 for chi = 0.25 and S = 100. Generalization with few examples requires that the number of storage locations is matched to the number of two-place relations that are learned. The existence of a minimum in the probability of error can be interpreted qualitatively in the following way. The results in Figs. 7, 8, 9 illustrate that a low probability of generalization error requires that many mapping vectors are bundled. The probability of error decreases with increasing N _e because the correlation between the AMU output and the incorrect compositional structures decreases with N _e . This is not so for the correlation between the output and the correct compositional structure, which is constant. This suggests that one effect of bundling additional mapping vectors, which adds noise to any particular mapping vector that has been stored in the AMU, is a reduction of the correlation between the AMU output and incorrect compositional structures. A similar effect apparently exists when bundling mapping vectors of unrelated two-place relations. The noise introduced mainly reduces the correlation between the AMU output and compositional structures representing incorrect alternatives.

Fig. 10

The probability of generalization error versus the number of different two-place relations, N _r , for a S = 100 and S = 1,000 when χ = 0.05; b χ = 0.05 and χ = 0.25 when S = 100. Other parameters are ${{\mathcal{D}} = 1,000}$ and N _e  = 10

Another minimum in the probability of error appears when we vary the average probability of activating a storage location, χ, see Fig. 11. In this figure, we illustrate the worst-case scenario in Fig. 10, S = 100 and N _e  = N _r  = 10, for different values of χ. A minimum appears in the probability of error for χ≈ 0.2. This result shows that the (partial) bundling of mapping vectors, including bundling of unrelated mapping vectors, can reduce the probability of generalization error.

Fig. 11

The probability of error of the AMU versus the average probability of activating a storage location, χ, for recall and generalization

The interpretation of these results in a neural-network perspective on SDM and binary VSAs is that the sparseness of the neural codes for analogical mapping is important. In particular, the sparseness of the activated address decoder neurons in the SDM [9] is important for the probability of generalization error. A similar effect is visible in Fig. 9, where χ = 0.25 gives a lower probability of error than χ = 0.05.

Effect of Dimensionality

All simulations that are summarized above are based on a low dimensionality of compositional structures, ${{\mathcal{D}} = 1,000}$, which is one order of magnitude lower than the preferred value. A higher dimensionality results in a lower probability of error. Therefore, it would be a tedious task to estimate the probability of error with simulations for higher values of $\mathcal{D}$. We illustrate the effect of varying dimensionality in Fig. 12. By choosing a dimensionality of order 10⁴, the probabilities of errors reported in this work can be lowered significantly, but that would make the task to estimate the probability of error for different values of the parameters S, χ, N _e , and N _r more tedious. The analytical results obtained by [9, 17, 22] suggest that the optimal choice for the dimensionality of binary vector symbolic representations is of order 10⁴, and this conclusion remains true for the AMU model. A slightly higher dimensionality than 10⁴ may be motivated, but 10⁵ is too much because it does not improve the probability of error much and requires more storage space and computation. Kanerva derived this result from basic statistical properties of hyperdimensional binary spaces, which is an interesting result in a cognitive computation context because that number matches the number of excitatory synapses observed on pyramidal cells in cortex.

Fig. 12

The probability of generalization error versus the dimensionality of binary compositional structures, ${{\mathcal{D}}}$. Other parameters are S = 100, χ = 0.05, N _e  = 10 and N _r  = 10. The optimal dimensionality is of the order ${{\mathcal{D}}=10^4}$

Discussion

Earlier work on analogical mapping of compositional structures deals with isolated mapping vectors that are hand-coded or learned from examples [7, 14, 17, 18, 20, 22]. The aim of this work is to investigate whether such mapping vectors can be stored in an associative memory so that multiple mappings can be learnt from examples and applied to novel inputs, which in principle can be unlabeled. We show that this is possible and demonstrate the solution using compositional structures that are similar to those considered by others. The proposed model integrates two existing ideas into one novel computational unit, which we call the Analogical Mapping Unit (AMU). The AMU integrates a model of associative memory known as sparse distributed memory (SDM) [9] with the idea of holistic mapping vectors [17–19] for binary compositional structures that generalize to novel inputs. By extending the original SDM model with a novel input–output circuit, the AMU can store multiple mapping vectors obtained from similar and unrelated training examples. The AMU is designed to separate the mapping vectors of unrelated mappings into different storage locations of the SDM.

The AMU has a one-shot learning process and it is able to recall mappings that are in the training set. After learning many mapping examples, no specific mapping is recalled and the AMU provides the correct mapping by analogy. The ability of the AMU to recall specific mappings increases with the size of the SDM. We find that the ability of the AMU to generalize does not increase monotonically with the size of the memory; It is optimal when the number of storage locations is matched to the number of different mappings learnt. The relative number of storage locations that are activated when one mapping is stored or retrieved is also important for the ability of the AMU to generalize. This can be understood qualitatively by a thought experiment: If the SDM is too small, there is much interference between the mapping vectors, and the output of the AMU is essentially noise. If the SDM is infinitely large, each mapping vector is stored in a unique subset of storage locations and the retrieved mapping vectors are exact copies of those learnt from the training examples. Generalization is possible when related mapping vectors are combined into new (bundled) mapping vectors, which integrate structural and semantic constraints from similar mapping examples (7). In other words, there can be no generalization when the retrieved mapping vectors are exact copies of examples learnt. Bundling of too many unrelated mapping vectors is also undesirable because it leads to a high level of noise in the output, which prevents application of the result. Therefore, a balance between the probability of activating and allocating storage locations is required to obtain a minimum probability of error when the AMU generalizes.

The probability of activating storage locations of the AMU, χ, is related to the “sparseness of the representation of mapping vectors. A qualitative interpretation of this parameter in terms of the sparseness of neural coding is discussed in [9]. We find that when the representations are too sparse the AMU makes perfect recall of known mappings but is unable to generalize. A less sparse representation results in more interference between the stored mapping vectors. This enables generalization and has a negative effect on recall. We find that the optimal sparseness for generalization depends in a non-trivial way on other parameters and details, such as the size of the SDM, the number of unrelated mappings learnt, and the dimensionality of the representations. The optimal parameters for the AMU also depend on the complexity of the compositional structures, which is related to the encoding and grounding of compositional structures. This is an open problem that needs further research.

A final note concerns the representation of mapping vectors in former work versus the mapping vectors stored by an AMU. In [17], integer mapping vectors for binary compositional structures are used to improve the correlation between mapping results and the expected answers. An identical approach is possible with the AMU if the normalization in (15) is omitted. However, by calculating the probability of error in the simulation experiments, we conclude that it is sufficient to use binary mapping vectors. This is appealing because it enables us to represent mapping vectors in the same form as other compositional structures. Kanervas estimate that the optimal dimensionality for the compositional structures is of order 10⁴ remains true for the AMU. The probability of errors made by the AMU decreases with increasing dimensionality up to that order and remains practically constant at higher dimensionality.

There is much that remains to understand concerning binary vector symbolic models, for example, whether these discrete models are compatible with cortical networks and to what extent they can describe cognitive function in the brain. At a more pragmatic level, the problem of how to encode and ground compositional structures automatically needs further work, for example, in the form of receptive fields and deep learning networks. Given an encoding unit for binary compositional structures the AMU is ready to be used in applications. Therefore, this paper is a small but potentially important step toward a future generation of digital devices that compute with qualitative relationships and adapt to the environment with minimal assistance from humans.