Introduction

Analytical ultracentrifugation (AUC) underwent a renaissance in the 1990s that reflected a shift from classical applications in biochemistry and molecular biology, such as determining the size of a macromolecule, towards the emerging wide-spread interest in protein interactions, a development that has continued and intensified in the last two decades. This renaissance was fueled by the introduction of (at the time) modern instrumentation that greatly facilitated data acquisition, as well as by the emerging recombinant protein expression technology that enabled the production of suitable samples to address a myriad of questions about specific protein interactions in biochemistry, molecular biology, immunology, etc. (Schachman 1989). Coincident with these developments, desktop computers became ubiquitously available in laboratories and increasingly powerful. One example of the application of computers was, for the first time, the routine calculation of solutions to the Lamm equation, which is the fundamental partial differential equation underlying the evolution of macromolecular concentration profiles in the centrifugal field (Lamm 1929). This, in turn, stimulated significant progress in the theory of sedimentation of interacting macromolecules, accompanied by the development of new computational data analysis approaches, feeding back to improved experimental designs and new questions that can be addressed by AUC. Thus, in only two decades the theory, practice, and applications of AUC underwent dramatic evolution. Currently, AUC is widely and increasingly used in a diverse number of fields, including biochemistry, immunology, virology, molecular biology, polymer chemistry, supramolecular chemistry, nanoparticles, biomaterials, protein pharmaceuticals in biotechnology industry, and others.

Several virtues make AUC a uniquely useful tool for studying protein interactions. First, in contrast to spectroscopic approaches that provide a superposition of signals from all species, in AUC a size-dependent migration of complexes takes place that can allow the hydrodynamic separation and identification of different species by size. Yet, different from chromatographic approaches, the migration takes place in free solution, allowing for the rigorous quantification based on first principles, and it is usually conducted in a way that allows complexes to remain at all times in a bath of their constituent species, and for exchange between all species to proceed in a way that reflects the kinetic and equilibrium properties of the interacting system. While sedimentation velocity (SV) experiments are focused on the temporal evolution of concentration distributions, in sedimentation equilibrium (SE), the final thermodynamic equilibrium between different states is probed. Beyond the spatial and temporal domain of the experiment, different optical signals that can be measured from the sedimenting species add a spectroscopic dimension to the AUC data that is particularly useful for the study of multi-component interactions. Expanding the flexibility of AUC even more, density contrast experiments allow one to probe protein–solvent or co-solvent interactions. Finally, AUC is fully compatible and offers rich set of tools for the study of solubilized membrane proteins.

The purpose of the present work is to provide a comprehensive overview of the current state of the art in AUC for the study of protein interactions and multi-protein complexes, especially highlighting some of the most important areas that have seen significant expansion of the methodology during the last two decades. Applications and methods of AUC are highly diverse, such that, unfortunately, an inclusive review of all new developments is beyond the scope of the present work. Acknowledging the unavoidable bias of selection, the goal is to cover the most important techniques and those most commonly applied to solve practical questions of protein interactions. Best practices to conduct the experiments will not be discussed; instead the reader is referred to introductory and more detailed practical protocols (Lebowitz et al. 2002; Balbo et al. 2007; Brown et al. 2008; Schuck et al. 2010; Zhao et al. 2013).

Sedimentation equilibrium

As reviewed recently by Rivas and Minton (2011), the thermodynamic equilibrium of a species i in the centrifugal field can be described as

$$ {\mu_i}(r)-{\mu_i}\left( {{r_0}} \right)=RT\,\mathrm{In}\frac{{{a_i}(r)}}{{{a_i}\left( {{r_0}} \right)}}=M_i^{*}\frac{{{\omega^2}}}{2}\left( {{r^2}-r_0^{{^2}}} \right) $$
(1)

where μ(r) and a(r) are the chemical potential and activity, respectively, as a function of the distance from the center of rotation r, with r 0 a reference radius, and ω the angular velocity, R the gas constant, and T the absolute temperature. On the right-hand-side, the mechanical potential energy in the centrifugal field is governed by ω and the buoyant molar mass

$$ M_i^{*}={M_i}{{\left( {{{{d\rho }} \left/ {{d{w_i}}} \right.}} \right)}_{\mu }} $$
(2)

, where M i is the species molar mass and \( {{\left( {{{{d\rho }} \left/ {{d{w_i}}} \right.}} \right)}_{\mu }} \) is the density increment at constant chemical potential of all other species. In aqueous solvents and in the absence of preferential solvation, the latter is often approximated as the buoyancy term \( \left( {1-\overline{v}\rho } \right) \), with \( \overline{v} \) denoting the protein partial specific volume and ρ the solvent density.

Dependent on the strength and type of the interaction to be studied and, correspondingly, the macromolecular concentration range used in the SE experiment, the description branches into that of (1) thermodynamically ideal sedimentation at low concentrations, typically applied to study species molecular weights and specific biochemical interactions in a traditional analytical ultracentrifuge with real-time optical detection, and (2) non-ideal sedimentation at high concentrations, typically applied to study weakly attractive or repulsive interactions and conducted in analytical ultracentrifugation experiments with post-centrifugal fractionation and quantitation.

SE at high concentrations: repulsive and weakly attractive interactions

The study of SE at high concentrations of macromolecules of interest can reveal both attractive interactions from weak self-association or hetero-association as well as repulsive interactions from steric or electrostatic forces. In view of mimicking the intracellular environment or other milieus crowded by a high concentration of unrelated molecules, which can have profound effects on the thermodynamics of protein interactions (Zhou et al. 2008), SE may also be conducted in the presence of a high concentration of unrelated macromolecules that produce a solution with a background of volume-excluding but otherwise inert macromolecules, as pioneered by Minton and coworkers (Rivas et al. 1999).

In both cases, due to the potential of optical aberrations caused by refractive index gradients (González et al. 2003), experiments at very high total macromolecular concentrations are often conducted in a preparative ultracentrifuge followed by post-centrifugal fractionation and protein quantitation by various methods (Darawshe and Minton 1994). Commensurate with the radial resolution of this approach, it is convenient to phrase this type of SE in terms of apparent molar mass, M* i,app , which can be measured from the slope and curvature of the concentration gradient,

$$ M_{{i,\,app}}^{*}\left( {\left\{ c \right\}} \right)=\frac{2RT }{{{\omega^2}}}\times \frac{{d\,\mathrm{In}\,{c_i}(r)}}{{d{r^2}}} $$
(3)

, where {c} highlights its dependency on the total loading concentrations, which is typically varied in a series of experiments.Footnote 1 Using the relationship a = γc between concentration, chemical activity, and the activity coefficient γ, and expanding the differential \( {{{d\,\mathrm{ln}\,{a_i}}} \left/ {{d{r^2}}} \right.} \) to take into account interactions between different components, we obtain for the true buoyant molar mass

$$ M_i^{*}=M_{i,app}^{*}+\sum\limits_j {{c_j}\frac{{\partial\,\mathrm{ln}{\gamma_i}}}{{\partial {c_j}}}} M_{{j,\,app}}^{*} $$
(4)

(Rivas and Minton 2011).

The interaction free energy ln γ may be expanded into a power series

$$ \mathrm{In}\,{\gamma_i}=\sum\limits_j {{B_{ij }}{c_j}+\sum\limits_{jk } {{B_{kjk }}{c_j}{c_k}+\ldots } } $$
(5)

with virial coefficients B ij for two-body interactions, B ijk for three-body interactions, etc. (Zimmerman and Minton 1993; Hall and Minton 2003). If the solution is sufficiently dilute such that only two-body interactions are significant, then the second virial coefficient may be extracted from experimental data and interpreted, for example, in the context of effective rigid particles with hard-particle potential (Zimmerman and Minton 1993). Alternatively, in the absence of significant long-range electrostatic interactions, the interaction free energy may be calculated following the effective hard particle method, where macromolecules are treated as a fluid mixture of hard convex particles. This allows the description of ln γ and its composition dependence only with variables for the specific volume of the effective hard particle of each species, for example, in scaled particle theory (Minton 1998; Rivas and Minton 2011). Examples for the application of this approach are studies of weak self-association of fibrinogen and tubulin (Rivas et al. 1999) and FtsZ (Rivas et al. 2001).

In a regime of only moderately high protein concentrations (∼10 mg/ml) a direct analysis of the concentration profiles measured in real-time during standard analytical ultracentrifugation is possible. As observed by Rowe (2005, 2011), the transcendental form of the radial-dependence of protein concentration c(r) implied by Eq. 3 can be eliminated by inversion of the sedimentation equilibrium expression to the form r(c), and determination of equilibrium constants of dimerization and second and third virial coefficients is possible (Ang and Rowe 2010). In the ‘close-to-dilute’ regime, the approximation to account for only nearest-neighbor interactions may be sufficient (Wills et al. 2012).

SE in dilute solutions: moderate to strong specific protein interactions

In sufficiently dilute solutions for thermodynamic non-ideality to be negligible, the radial-dependent signal a(r) of each species i in SE will follow Boltzmann exponentials

$$ {a_i}(r)={c_i}\left( {{r_0}} \right){\varepsilon_i}d\,\exp \left\{ {{M_i}\left( {1-\overline{{{v_i}}}\rho } \right)\frac{{{\omega^2}}}{2RT}\left( {{r^2}-r_0^2} \right)} \right\} $$
(6)

, where d denotes the optical path length, c i (r 0 ) denotes the species concentration at a reference radius r 0 , ε i denotes its molar extinction coefficient, and \( {M_i}\left( {1-\overline{{{v_i}}}\rho } \right) \) denotes its buoyant molar mass. For convenience, the buoyant molar mass is often expressed as \( {M_{i,app }}\left( {1-\overline{v}^*\rho } \right) \) with an apparent molar mass M app on the arbitrary buoyancy scale of \( \overline{v}^*; \) either M app can often be easily determined from SE on a single species, or \( \overline{v}^* \) may be determined by SE if M app is taken to be a known molar mass, for example, from mass spectrometry or amino acid composition. For interacting systems of components A and B, the mass action law for chemical equilibrium can be fulfilled simultaneously at all radii,

$$ {c_{ij }}(r)={K_{ij }}{c_{10 }}{(r)^i}{c_{10 }}{(r)^j} $$
(7)

, with an equilibrium constant K ij for the formation of the complex with stoichiometry of iA:jB from free species A at a concentration c 10 and B at a concentration c 01 (and with K 10  = K 01  = 1). In the absence of pressure-dependence, and in the absence of hyper- or hypochromatic changes upon complex formation, this leads to the total signal profile

$$ a(r)=\sum\limits_{i,j } {{c_{ij }}\left( {{r_0}} \right)\left( {i{\varepsilon_A}+j{\varepsilon_B}} \right)d\,\exp \left\{ {\left( {i{M_{A,app }}+j{M_{B,app }}} \right)\left( {1-\overline{v}^*\rho } \right)\frac{{{\omega^2}}}{2RT}\left( {{r^2}-r_0^2} \right)} \right\}} $$
(8)

, i.e., a superposition of Boltzmann exponentials of all free and complex species. As a direct consequence of Eq. 8 it is not possible to establish from a single SE profile whether different species are stable or in chemical equilibrium.

A major advance of SE in the last decades is that a large number of SE signal profiles are now routinely obtained from side-by-side experiments with different loading concentrations, and sequentially acquired at different rotor speeds. Due to the ubiquitously available computational resources, they can be fit simultaneously in a global analysis. This can not only establish chemical conversion, but also significantly improve the confidence in the interaction model and the derived binding constants. Furthermore, for multi-component systems, the inclusion of SE data acquired with different optical systems and/or at different absorption wavelengths (Hsu and Minton 1991; Lewis et al. 1993; Schuck 1994; Noy et al. 2005; Zhao et al. 2013) has become routine, either exploiting intrinsic differences in the UV extinction of proteins due to their different content of aromatic amino acids or exploiting extrinsic or intrinsic chromophores in the visible spectrum.

A central problem arising in the global analysis is the high number of fitting parameters to be adjusted, which arise from the unknown free species’ concentrations at the reference radius of each solution column and at each rotor speed. These lead to a very complex error surface of minimization with local minima and near-correlated parameters. The latter problem is greatly exacerbated when studying proteins of very similar (MA/MB < 2) or very dissimilar (MA/MB > 10) size, where the Boltzmann exponentials of free species, or of the larger free species and the complex, respectively, will become too similar for a well-posed analysis of binding constants (which requires all species to be independently quantifiable). Multi-signal detection can break the ensuing parameter correlation to some degree, if components have distinguishable signal contributions.

A powerful strategy to address this problem is the addition of constraints to the analysis. In particular, it is reasonable to expect that the total mass of macromolecules of each component in the closed solution column be conserved during the SE experiment. However, this introduces the difficulties of knowing both the exact loading concentrations and the exact solution geometry. Especially the ‘bottom’ position at the highest radius is essential for the mass balance, as the concentration profiles are exponentially increasing and most of the material will accumulate close the bottom. Neglect of this region in ‘signal conservation’ approaches will therefore lead to erroneous constraints. [This is of no consequence if the constraint is used operationally only to stabilize non-linear regression in its initial phases but finally eliminated (Philo 2000).]

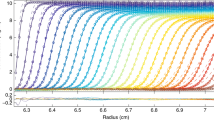
This problem can be solved in the ‘implicit mass conservation’ approach, where the solution columns are brought to sedimentation equilibrium sequentially at multiple rotor speeds, such that both the ‘effective’ loading concentration (as the soluble material measured in SE at the first rotor speed, not necessarily equaling the measured concentration prior to the experiment) as well as the bottom position can be treated as parameters to be adjusted in the data analysis (Vistica et al. 2004; Ghirlando 2011) (Fig. 1). This provides opportunities for the introduction of additional constraints, for example, for the bottom position applied to data sets from the same solution column but acquired at different wavelengths, and for effective loading concentrations of components across different cells that were loaded systematically in titration or dilution series (Vistica et al. 2004; Ghirlando 2011; Zhao et al. 2013). In this way, a stable, unbiased analysis of SE with significantly more precise estimates for the binding constants is possible (Fig. 1).

Fig. 1
figure 1

Example for the change of equilibrium profile as a function of rotor speed in a multi-speed sedimentation equilibrium (SE) experiment and the benefit from implicit mass conservation constraints. A set of three samples in a dilution series of mixtures of a natural killer cell receptor fragment and its binding partner, the major histocompatibility complex class I protein (Dam et al. 2006) were brought to SE sequentially at rotor speeds of 15,000, 20,000, and 25,000 rpm and scanned at 280 and 250 nm. Shown are representative radial absorbance profiles of one sample acquired at 250 nm (symbols) and best-fit distributions (solid lines). Global fitting parameters were the macroscopic binding constants and the loading molar ratio of components common to all samples; local fitting parameters for each cell were the dilution factors of each sample and the best-fit bottom position (meniscus and bottom are represented in the plot as the limits of the abscissa). In the global analysis of three cells, the implicit mass conservation (Vistica et al. 2004) reduced the number of fitting parameters reflecting unknown protein concentrations from 18 to 4

Full size image

Implicit mass conservation can also ensure a well-conditioned analysis even in the absence of spectral resolution of components. This relationship between multi-signal analysis and mass conservation analysis in SE is observed again in SV (see below). A large number of applications of the ‘implicit mass conservation’ approach have confirmed that mass conservation is fulfilled in the overwhelming majority of systems of interacting proteins, and binding constants ranging from ∼10 nM (Zhao et al. 2012) to ∼1 mM (Chaudhry et al. 2009) have been determined.

Sedimentation velocity

In the last two decades, SV has surpassed SE as the first method of choice for most AUC studies. Although SE is firmly rooted directly in equilibrium thermodynamics and can therefore be applied to non-ideal solution conditions, correlation between exponential (or close to exponential) terms can lead to ambiguity between interpretations based on different models, and to susceptibility to unexpected sample imperfections, a concern especially due to the long time-course of the SE experiment (Gilbert and Gilbert 1980a; Zhao et al. 2012). SV experiments are much faster and capable of achieving a significantly higher size-dependent resolution, and they can therefore serve as a very effective quality control for samples. In addition, many strategies have been developed for the analysis of interacting systems based on SV, complementary to those of SE. With some exceptions, these SV techniques are limited, however, to the study of dilute macromolecular solutions where thermodynamic non-ideality as well as hydrodynamic interactions can be largely neglected (e.g., macromolecular concentrations below a few milligrams per milliliter for compact globular particles, in the absence of long-range electrostatic interactions); these conditions are assumed to be fulfilled in the following unless mentioned otherwise.

Direct SV analysis with solutions to the Lamm equation

As presented first by Lamm (1929), the fundamental equation of SV is based on local mass balance between sedimentation, diffusion, and chemical reaction fluxes:

$$ \frac{{\partial {c_k}}}{{\partial t}}+\frac{1}{r}\frac{\partial }{{\partial r}}\left[ {{c_k}{s_k}{\omega^2}{r^2}-{D_k}\frac{{\partial {c_k}}}{\partial }r} \right]={q_k} $$
(9)

where c k (r,t) is the temporal evolution of radial concentration distributions of species k, s k and D k are this species’ sedimentation and diffusion coefficients, respectively, and q k is the chemical reaction flux (Fujita 1975). Boundary conditions are reflective at the meniscus and bottom of the solution column, and usually there is initially a uniform radial distribution for all species, which are in chemical equilibrium prior to the SV experiment. The lack of analytical or otherwise readily available solutions to this equation presented a significant hurdle to the development of SV until the mid-1990s. While the foundation for numerical solutions had been laid several decades earlier (Dishon et al. 1966; Cox 1965; Claverie et al. 1975; Cann 1994), more readily available laboratory computers invigorated research in this topic (Holladay 1979; Urbanke et al. 1980; Philo 1996; Schuck 1998; Schuck et al. 1998; Demeler et al. 2000; Stafford and Sherwood 2004; Dam et al. 2005). Currently, rigorous criteria for precision and modern algorithms for efficient solutions are available (Brown and Schuck 2007; Schuck 2009), and refinements to account for experimental factors, such as finite rotor acceleration (Schuck et al. 2001), dynamic density gradients from sedimenting co-solvents (Schuck 2004a), solvent compressibility (Schuck 2004b), and the finite time of data acquisition (Brown et al. 2009) have been made.

In practice, a second essential ingredient for the modeling of experimental SV data is the description of their peculiar noise-structure, where the signals from the sedimenting solutes are offset by stochastic time-dependent and radial-independent offsets [‘RI-noise’, β(t), in interferometric detection resulting from the lack of an absolute reference of the periodic fringe shift data, as well as mechanical oscillations in the optical system], and stochastic time-independent but radial-dependent baseline profiles [‘TI-noise’, b(r), occurring due to constant imperfections in the optical system of absorbance and interference detectors]. Both are largely uncorrelated with signals from the sedimentation process that changes simultaneously in time and space. Since both types of baselines produce only additive offsets, although comprising a large number of unknowns, they can both be easily explicitly accounted for in the model for the data to be analyzed (Schuck and Demeler 1999; Schuck 2010a). More complex baseline contributions arise from signals of sedimenting solvent components, which can be further complicated if they are present in both sample and solvent reference compartments with possibly different solution geometries. Such signals can (and often must) also be explicitly considered in SV analysis of sedimenting proteins (Zhao et al. 2010). The ability to model these static and dynamic baseline offsets greatly expands the potential for the application of SV, especially SV with interference optical detection, by significantly lowering the required macromolecular signals needed for the analysis and by relaxing or eliminating the requirement for precise optical matches of the reference solution that necessitated dialysis steps prior to SV.

The long-standing goal in the field of AUC was that SV data from interacting systems can be modeled directly with solutions of the coupled Lamm equations (Eq. 9) (Gilbert and Gilbert 1980a), which has now been fully implemented for global analysis of samples at different loading concentrations (Stafford and Sherwood 2004; Dam et al. 2005). This method and its applications have been recently reviewed (Correia and Stafford 2009; Brautigam 2011). A pre-requisite for this approach is that the samples are of sufficient purity to be described as discrete, free, and complex species. Unfortunately, this requirement is of concern due to the well-known fact that SV is exquisitely sensitive to sample heterogeneity (Gilbert and Gilbert 1980b; Cann 1986; Dam et al. 2005). In fact, even single-species Lamm equation models to putative single component samples frequently fail to produce adequate fits close to the level of noise in the data acquisition (a test that should be conducted to prior to the interaction analysis of heterogeneous systems).

This is exacerbated by the fact that not all parameters required in Eq. 9 may be well-determined by the experimental data, even when probing a wide concentration range. This is true, in particular, for kinetic rate constants that govern the chemical fluxes in Eq. 9. While multiple kinetic steps are generally not resolvable, systems with a single kinetic rate constant are usually well-determined in SV only when the rate constant falls into the narrow range of ∼10−3–10−4/s (Dam et al. 2005)—i.e., when the chemical conversion takes place on the characteristic time-scale of sedimentation. This motivates the classification of interacting systems to be either fast or slow on the time-scale of sedimentation, a simplification that holds in practice for most systems, with few intermediate cases.

Accordingly, different methods have been developed for the more robust study of interacting systems in the limit of fast reactions and slow reactions on the centrifugal time-scale. They are based on a hierarchical interpretation of the SV data, first in terms of sedimentation coefficient distributions, followed by a second-stage interpretation of the boundary structure as a function of loading composition.

Sedimentation coefficient distributions

As indicated above, SV data of single components can only be fitted well in cases of samples with exceptional purity (Dam and Schuck 2004). For example, the high statistical accuracy of detected slopes in solution and of solvent plateaus of single species makes it possible to detect reliably trace amounts of <1 % of oligomeric contaminants, which has led to the wide-spread application of SV in the characterization of protein pharmaceuticals in the biotechnology industry [e.g., see the review Gabrielson and Arthur (2011) and references cited therein]. Similarly, microheterogeneity and contaminants close in size to the molecule of interest lead to excess boundary spread, which in a naïve data interpretation of a single species model would imply an excessively large apparent diffusion flux and an underestimate of the molar mass. Finally, many important classes of macromolecules are intrinsically heterogeneous in size or shape, such as glycoproteins, carbohydrates or synthetic polymers.

Thus, it is usually essential to account for sample heterogeneity. This can be accomplished very effectively by considering the measured sedimentation signal as a superposition of independently sedimenting species, each described by a Lamm equation solution, in a two-dimensional size-and-shape distribution

$$ a\left( {r,t} \right)=\iint {\chi \left( {s,D,r,t} \right)c\left( {s,D} \right)dsdD+b(r)+\beta (t)} $$
(10)

(Brown and Schuck 2006), or by taking advantage of a hydrodynamic scaling laws D = D(s)

$$ a\left( {r,t} \right)=\iint {\chi \left( {s,D(s)r,t} \right)c(s)dsdD+b(r)+\beta (t)} $$
(11)

(Schuck 2000), with χ(s,D,r,t) denoting Lamm equation solutions of non-interacting species at unit concentration. The precise form of the scaling law can be selected depending on the macromolecules under study: for example, for compact particles it is advantageous to use the traditional s∼M 2/3 relationship with a common frictional ratio being an adjustable parameter (Schuck et al. 2002) (which may be extended to a multi-segmented approach with multiple frictional ratios for describing multiple boundaries). This takes advantage of the fact that most folded proteins have shape asymmetries that fall into a very narrow range of numerical values for translational frictional ratios, even though they may exhibit very different actual three-dimensional structures. Other options include models for worm-like chains, or a general scaling law with adjustable or user-defined scaling parameters (Harding et al. 2011). Extending Eq. 11 to the global analysis of experiments with solvent density contrast it is possible to determine effective partial-specific volumes of the sedimenting particles, which can report, for example, on protein–solvent or protein–detergent interactions (Brown et al. 2011).

Computationally, while empirical algorithms have been proposed ad hoc and without proof (Brookes et al. 2010), Eqs. 10 and 11 can in fact be solved in the rigorous mathematical framework established for similar image deconvolution problems (Schuck 2009), with Tikhonov, maximum entropy, or Bayesian regularization being an essential technique to avoid over-interpretation of the data and to incorporate available prior knowledge (Brown et al. 2007; Schuck 2009). The selection of the regularization method is an opportunity to import specific knowledge on the system under study. For example, while maximum entropy performs best for samples with a few discrete species, Tikhonov regularization is advantageous for samples with broad quasi-continuous size distributions. An example of the resulting sedimentation coefficient from the standard c(s) approach using maximum entropy regularization (Eq. 11) is shown in Fig. 2.

Fig. 2
figure 2

Sedimentation velocity data of a sample of bovine serum albumin and c(s) analysis. a Interference optical fringe profiles (every 5th scan and every 10th data point shown) at different point in time as indicated by color temperature. Solid lines are the best-fit model from c(s) analysis with maximum entropy regularization on a confidence level of P = 0.95, producing residuals as shown in b. c The corresponding c(s) distribution (blue) and, for comparison, the best-fit distribution ls-g*(s) (Schuck and Rossmanith 2000) without diffusional deconvolution (gray)

Full size image

In the context of the study of interacting systems, the representation of the SV data through their c(s) distributions offers several highly useful tools. Obviously, taking advantage of the high size-dependent resolution in conjunction with the diffusionally deconvoluted sedimentation coefficient distribution allows one to discriminate species (or pseudo-species, see below) reflecting the interacting molecules of interest from those that constitute impurities and degradation products. The latter can be excluded from further consideration.

It is very useful to superimpose c(s) distributions from experiments with different loading concentrations. If peaks remain invariant at the same s-value at all loading concentrations, then the kinetics of the interaction is slow on the time-scale of sedimentation. If the c(s) peaks exhibit a non-trivial concentration-dependence, this is a signature of an interaction with chemical conversion on the time-scale of sedimentation or faster, which will be discussed in further detail below.

For slow systems, peaks in c(s) directly reflect the sedimentation of different hydrodynamically separated species, and the number and s-value of peaks can reveal the number and size of complexes, from which we can derive important information about the reaction scheme of the interaction. In heterogeneous systems this can often be significantly enhanced by multi-signal SV, which additionally can reveal the component composition of complexes (see below). For evaluating binding constants, in slow systems the relative population of all peaks directly reflects the species populations, and as such can be directly interpreted in the context of mass action law, for example, by fitting isotherms of species populations as a function of solution composition with mass action law models. This can be combined, in a global analysis, with isotherms of the weighted average sedimentation coefficient as a function of solution composition (see below).

Multi-signal sedimentation coefficient distributions

Just as in SE, the ability to acquire simultaneously multiple signals a λ (r,t) in real-time from the same sedimentation experiment greatly enhances the opportunity to study heterogeneous protein interactions. Direct global modeling of multi-signal SV (MSSV) boundaries can be achieved in terms of component sedimentation coefficient distributions c k (s), defined as

$$ {a_{\lambda }}\left( {r,t} \right)\cong \sum\limits_{k=1}^K {{\varepsilon_{{k\lambda }}}d} \int\limits_{{{s_{\min}}}}^{{{s_{\max }}}} {{c_k}(s)\chi \left( {s,D(s),r,t} \right)ds+b_\lambda(r)+\beta _\lambda(t)} $$
(12)

, where ε kλ is the extinction coefficient (or interference molar signal increment) of species k at wavelength λ (Balbo et al. 2005). For non-singular matrices ε kλ , i.e., for components that are spectrally distinguishable but may have overlapping spectral contributions, the MSSV approach permits the simultaneous spectral and hydrodynamic resolution of species (Balbo et al. 2005). MSSV greatly helps to define the association mode in heterogeneous interactions, by simultaneously displaying the number, s-value, and, from the peak area ratio of c k (s) of the different components, the composition of all species and complexes. For example, MSSV allows the study of ternary systems with formation of multiple binary and ternary complexes. An example of a MSSV analysis and resulting component sedimentation coefficient distributions c k (s) is shown in Fig. 3. Principles and applications have been reviewed by Brautigam and colleagues (Padrick et al. 2010; Padrick and Brautigam 2011).

Fig. 3
figure 3

Example of the multi-signal c k (s) analysis of a triple protein mixture of a viral glycoprotein (green), its cognate receptor (blue), and a heterogeneous antigen–recognition receptor fragment (red). The content of each protein component in the different s-ranges is obtained from the global analysis of sedimentation data acquired with the interference optics and with the absorbance system at two different wavelengths (data not shown), using two chromophorically labeled proteins and one unlabeled protein. Solid lines show the c k (s) analysis of the triple mixture. The analogous distributions of each protein alone are shown as dashed lines. The formation of two coexisting binary complexes at ∼5 S and ∼7 S and a ternary complex with 1:1:1 stoichiometry at ∼8.5 S can be discerned. Figure reproduced from Schuck et al. (2010)

Full size image

The requirements for spectral discrimination are not very high. Criteria for the prediction of successful MSSV analyses have been established on the basis of ε kλ (Padrick and Brautigam 2011). Often different contents of aromatic amino acids of proteins are sufficient to allow spectral discrimination in two- or even three-component mixtures, as demonstrated experimentally (Balbo et al. 2005). To further enhance the discrimination of species without the need for extrinsic labeling, it is possible to combine Eq. 12 with constraints on c k (s) that embed approximate mass conservation requirements and/or the knowledge that a certain component is a priori confined to a certain s-range (Brautigam et al., submitted). It can be shown theoretically, that, similar to the case of SE, this can substitute for spectral discrimination of components. Different from SE, the loading concentrations cannot be estimated from the SV data themselves, but need to be entered as prior knowledge. However, effective loading concentrations can be assessed from independent experiments carried out side-by-side with the interacting mixture, from which the extinction coefficients ε kλ can also be determined (Brautigam et al., submitted).

Weighted-average sedimentation coefficients

The weighted-average sedimentation coefficient s w provides a measure of the average overall transport in the system, which reflects on the species populations due to the fact that complexes usually sediment faster than their free building blocks, thereby leading to overall faster sedimentation when complexes are of higher relative abundance. Theoretically s w is deeply rooted in the second moment method and reflects the chemical composition in the plateau region of the cell, essentially independent of boundary shape and any reaction kinetics (Goldberg 1953; Schachman 1959; Schuck 2003). Since it relies on the balance

$$ {s_w}\equiv -\frac{{{\omega^2}r_p^2}}{{{a_p}}}\frac{d}{dt}\int\limits_{{{r_m}}}^{{{r_p}}} {a\left( {r,t} \right)rdr} $$
(13)

(with r p and a p denoting the radius and corresponding signal concentration in the plateau region, and r m the meniscus radius), it follows that s w is naturally weighted by each species’ signal contribution. Furthermore, it follows from the definition Eq. 13 that any boundary fit that describes the experimental data a(r,t) to within the noise of data acquisition will lead to the correct s w value. It should be noted that this is true independent of the physical motivation underlying the boundary model (Schuck 2003). This relationship is uncertain for s-values from historically used data transformation approaches, such as the apparent sedimentation coefficient distributions g(s*) (Stafford 1992) or the integral distribution G(s) (Demeler and Van Holde 2004) [although both can be back-projected into the original data space to examine the faithfulness of the description of the original data (Schuck and Rossmanith 2000; Schuck et al. 2002)]. However, faithful modeling of the boundary data can be ensured for any of the new direct boundary models, provided they fit the data well. This offers the opportunity to derive rigorous s w -values from integrals of c(s) (Schuck 2003).

To the extent that s w reflects the signal-weighted contributions to transport of all species, the measured isotherm of s w as a function of solution composition can be modeled as

$$ {s_w}\left( {{c_{tot,A }},{c_{tot,B }}} \right)=\frac{{\sum\limits_{i,j } {{K_{ij }}{c_A}{(r)^i}{c_B}{(r)^j}\left( {i{\varepsilon_A}+j{\varepsilon_B}} \right){s_{ij }}} }}{{{c_{tot,A }}{\varepsilon_A}+{c_{tot,B }}{\varepsilon_B}}} $$
(14)

for a two-component system, where, in analogy to Eqs. 5 and 6, the indexes i and j enumerate complexes with composition iA:jB (and K 10  = K 01  = 1). For not too complex interactions, this allows binding constants and complex species’ sedimentation coefficients to be determined. The complex sedimentation coefficients may not always be well-determined on the basis of s w data alone, as for s w to be close to the largest complex the latter has to be the near-exclusive species in solution. Therefore, it is useful to add additional information: for rapidly reversible systems this information may come from the isotherm of the reaction boundary s-value in a global model (see below); for slow systems independent knowledge on the peak s-values may be available. Alternatively, complex s-values may be estimated by hydrodynamic modeling of available molecular structures (García De La Torre et al. 2000; Aragon 2011).

For very weak associations concentrations have to be raised above the limits mentioned above for ideally sedimenting macromolecules, and into the range where hydrodynamic interactions become relevant. In this case, the concentration-dependence of the sedimentation coefficient can, in a first-order correction, be accounted for by the relationship s(c) = s0(1 − k s c), superimposed to the concentration-dependent increase in s w due to association (Patel et al. 2007).

Sedimentation of systems with rapidly reversible interactions: effective particle theory

Interacting systems where the chemical conversion is fast on the time-scale of sedimentation exhibit a complex behavior. It is easy to see that two-component systems that fulfill mass action law locally at all times can only exhibit two boundaries: one fast ‘reaction boundary’ containing a mixture of all free and complex species, and one ‘undisturbed boundary’ consisting of one of the free species. The reaction boundary exhibits an amplitude and s-value (‘s A⋯B ’) that depends on the loading concentration, all species’ sedimentation coefficients, and the equilibrium constant. It has long been considered counter-intuitive, however, that its composition, (‘R A⋯B ’), does not reflect the stoichiometry of the complex and that the s A⋯B -value along a titration series does by no means always increase with increasing loading concentrations. Furthermore, the undisturbed boundary is not necessarily the species in overall molar excess over the reaction stoichiometry, and its amplitude is variable and can take zero values at loading concentrations that do not reflect the stoichiometry of the complex. When it does vanish, there will be only one reaction boundary, sedimenting at an s A⋯B -value unequal to that of any of the chemical species.

This seemingly confusing behavior remained unexplained throughout the 20th century and has therefore significantly hampered the quantitative analysis of reacting systems, despite the fact that the bimodal boundary patterns are very easy to observe and very robust to quantify with regard to the boundary s-values, amplitudes, and composition (Fig. 4a). While the phenomenology is predicted accurately by Eq. 9, and was confirmed early by Gilbert and Jenkins who pursued the numerical solution of a diffusion-free analogue of Eq. 9 to predict boundary patterns in the limit of infinite time (Gilbert and Jenkins 1956), the physical basis of the observed phenomenology remained largely obscure and this topic remained poorly explored. This left direct Lamm equation modeling, or where application of this is not possible, sw({ctot}) isotherm analysis, as the only analytical approach.

Fig. 4
figure 4

Sedimentation of rapidly reversible heterogeneous interactions. a Typical bimodal boundary pattern. Profiles are calculated using Lamm equation solutions, Eq. 6, for the sedimentation of a 40-kDa protein binding a 60-kDa protein with a kinetic off-rate constant of 0.1/s, at loading concentrations at a ratio 2:1:K D . Sedimentation was simulated at 50,000 rpm, and total absorbance profiles (assuming equal weight-based extinction coefficients of both components) are shown in 10-min intervals. b Cartoon of the effective particle A⋯B (encircled in red). Indicated is the fractional time thatA (green) and B (blue) spend free or in complex (grayed time intervals). A spends a smaller fraction of time free than B, resulting in a match of their time-average velocities. An animated cartoon can be downloaded from https://sedfitsedphat.nibib.nih.gov/tools/Reaction%20Boundary%20Movies/Movies%20S1%20-%20S3.pdf, or created in the software SEDPHAT faithfully reflecting user-defined binding parameters and sedimentation coefficients. c Velocity of the reaction boundary A⋯B as a function of the total loading concentration of a and b, calculated by effective particle theory. For more details, including tools for using these isotherms in the data analysis and experimental design, see Schuck (2010b)

Full size image

This problem has very recently been addressed by the effective particle theory (EPT), which derives a simple physical picture of the coupled sedimentation process of rapidly reversible multi-component systems (Schuck 2010b, c) and results in robust models for the analysis of the information-rich sedimentation patterns of interacting systems (Zhao et al. 2011). EPT follows a similar concept as outlined by Goldberg (Goldberg 1953) to determine the second-moment boundary positions, by considering the equivalent step-function boundary that equals the boundary areas and mass balance, but now extended to both the undisturbed and the reaction boundary. This establishes a relationship between the so determined sedimentation boundaries with integrals over c(s) differential sedimentation coefficient distributions (see above). Furthermore, this motivates the use of superpositions of Heaviside step-functions to solve a diffusion-free analogue of Eq. 9 (Schuck 2010b), which allows the differential equation system to be reduced to simple algebraic equations. For example, for a two-component system of A and B having s-values s A and s B and forming a 1:1 complex with equilibrium constant K and sedimenting with s AB , this results for the reaction boundary s-value in

$$ {s_{{A\cdots B}}}=\left\{ {\begin{array}{*{20}c} {{{{\left( {{c_A}{s_A}+{c_A}{c_B}K{s_{AB }}} \right)}} \left/ {{\left( {{c_A}+{c_A}{c_B}K} \right)\quad for\quad {c_{Btot }} > c_{Btot}^{*}\left( {{c_{Atot }}} \right)}} \right.}} \\ {{{{\left( {{c_B}{s_B}+{c_A}{c_B}K{s_{AB }}} \right)}} \left/ {{\left( {{c_B}+{c_A}{c_B}K} \right)\quad \mathrm{else}}} \right.}} \\ \end{array}} \right. $$
(15a)

and for the molar ratio A/B in the reaction boundary in

$$ {R_{{A\cdots B}}}=\left\{ {\begin{array}{*{20}c} {{{{1-\left( {{s_B}-{s_A}} \right)}} \left/ {{K{c_B}\left( {{s_{AB }}-{s_B}} \right)}} \right.}\quad \mathrm{for}\quad {c_{BtOt }} > c_{Btot}^{*}\left( {{c_{Atot }}} \right)} \\ {1-{{{\left( {1+K{c_A}\left( {{{{{s_{AB }}-{s_A}}} \left/ {{{s_B}-{s_A}}} \right.}} \right)} \right)}}^{-1 }}\quad \mathrm{else}} \\ \end{array}} \right. $$
(15b)

(Schuck 2010b). More general expressions for multi-site interactions are given in (Schuck 2010b). There is a previously undiscovered transition in the parameter space of loading concentration, akin to a second-order phase transition, at

$$ c_{Btot}^{*}\left( {{c_{Atot }}} \right)={c_{Atot }}+\frac{{\left( {{s_B}-{s_A}} \right)}}{{2K\left( {{s_{AB }}-{s_B}} \right)}}\left( {1+\sqrt{{1+\sqrt{{\frac{{4{c_{Atot }}K\left( {{s_{AB }}-{s_B}} \right)}}{{\left( {{s_{AB }}-{s_A}} \right)}}}}}}} \right) $$
(15c)

which is a line along which the undisturbed boundary vanishes (dotted line Fig. 4c).

Importantly, Eq. 15a, b, c could have been derived solely and independently based on the physical principle of ergodicity in the reaction boundary, and the requirement that the time-average s-value experienced by all molecules taking part in the reaction boundary is identical. An illustration of the mechanism of propagation is shown in Fig. 4b: the entire phenomenology can be reduced to the fact that molecules of the faster sedimenting species B take turns in temporarily recombining with the slower sedimenting molecules A to help those catching up with the reaction boundary while sedimenting in the fastest species AB. Since the free species B do not fall behind as quickly as free species A, free species B can remain free for a longer time and is therefore more populated than free species A in the reaction boundary. The phase transition line arises as the condition that the entire solution loading composition can satisfy the relationships in the reaction boundary. Outside the phase transition line, the component in excess of the requirement for a reaction boundary will constitute the undisturbed boundary. The latter can be composed of species B only when the complex state is sufficiently populated such that the time-average velocity of all species A in the reaction boundary exceeds that of free species B.

The benefit of the EPT framework is several-fold. First, the simple physical picture allows, for the first time, intuitive access to the mechanism of coupled migration in rapidly reversible systems. Second, the expressions of Eq. 15a, b, c can be used directly to model isotherms of s-values, amplitudes, and the composition of the boundary pattern that arises in heterogeneous interacting systems (Zhao et al. 2011). This modeling can be combined in a global analysis with the s w isotherm. Notably, the s A⋯B -values are close to the complex s-values whenever one component is in significant molar excess and can therefore greatly add to the information content of the data. Third, the simple nature of the algebraic equations allows us to predict the entire concentration-dependent behavior of the reaction boundaries at once (e.g., Fig. 4c for the s A⋯B values), which can serve as a highly effective tool to predict informative experimental conditions (Zhao et al. 2011).

Finally, in an extension of EPT considering the concentration gradients arising in the reaction boundary, it was shown that the reaction boundary exhibits diffusional broadening approximately like that of real physical species (Schuck 2010c). This provides an explanation for the wide-spread observation that deconvolution of diffusion from reaction boundaries by c(s) is possible for reacting systems just like it is for non-interacting systems, despite the fact that c(s) is based on superpositions of non-interacting Lamm equation solutions. The normalcy of diffusion, along with the relationship between c(s) and the second moment analysis, justifies the application of c(s) for the analysis of reacting systems. It can naturally account for the polydispersity of the reaction boundary s-value predicted in the limit of infinite time by the Gilbert–Jenkins theory (Gilbert and Jenkins 1956), which arises from the concentration gradients within the reaction boundary. However, it was found that this polydispersity is actually close to negligible throughout most of the parameter space, and significant only in some regions close to the phase transition line (Schuck 2010c). Going further, based on the apparent diffusion coefficient and Svedberg equation (Svedberg and Pedersen 1940), the effective particle of EPT can be assigned an apparent molar mass, M A⋯B , which is between that of the complex and the weight-average molar mass in the loading mixture (Schuck 2010c). While not exploited quantitatively, this relationship may be useful to build a hypothesis for the complex size in an unknown reaction scheme.Footnote 2

Conclusions

This review highlights the significant change in theory and practice of AUC during the last two decades. Due to its limited scope, the presentation does not come close to completely describing these changes. For example, the power of SE and SV can be further increased by global analysis of the two techniques (Chou et al. 2006), or in the context of global multi-method analysis (Zhi et al. 2010; Zhao and Schuck 2012). In addition, considerable progress has been made in many applications of AUC to protein interactions, which are not covered here; this includes new techniques for studying membrane proteins, where, for example, the laboratory of Christine Ebel has significantly extended the work of Tanford and Reynolds (Tanford and Reynolds 1976), leveraging the new high-resolution and multi-signal SV techniques for the study of membrane proteins in detergent solutions (Ebel 2011), and where, for example, several laboratories have established the use of nanodiscs in AUC for studying membrane protein interactions in lipid environment (Alami et al. 2007; Hernández-Rocamora et al. 2012; Inagaki et al. 2012).

Considering the advances of the recent decades, although most are fueled or facilitated by computational advances, many approaches have appeared that were previously not anticipated, and some of those were even rather fundamental. Therefore, despite its almost century-long history, one can argue that AUC is still a young technique with respect to protein interactions, likely with many new approaches and applications still to come.