1 Introduction

The use of continuous welded rail (CWR) has increased at a high rate due to the widespread popularity of high-speed trains such as the Korea Train eXpress (KTX). CWR is manufactured by welding rails of 50–200 m in length into a single rail of several kilometers. CWR is suitable for high-speed trains due to the lower noise and vibration allowed by its longer rails [1, 2].

However, CWR suffers a critical vulnerability to buckling compared with rails of 50–200 m in length due to the absence of gaps, which were removed by welding [1, 2].

The buckling of the rail, caused by its excessive deformation from prolonged exposure to high-temperature environments, may cause trains to derail. Although such accidents are infrequent, they cause catastrophic loss of human lives and property. Therefore, the development of the technology to prevent buckling is an important issue in the field of railway safety [1,2,3].

CWRs are periodically reset to prevent buckling, thereby eliminating the accumulation of excessive axial load. CWRs are tightly fastened to the sleepers using a rail-fastening device. Resetting is the process of loosening all rail-fastening devices, freeing the new rail, and, then, tightening them again.

Since resetting requires a great deal of time and effort, therefore, it is performed only occasionally, and the regulation of train speeds according to rail temperature is used as an underlying measure to prevent train derailment. For example, KTX has a speed limit of 230 kmph when the rail temperature is at 55–60 °C and a speed limit of 70 kmph when the rail temperature is at 60–64 °C. Other jurisdictions such as the USA, UK, Australia, and Europe have similar standards for speed limits based on rail temperature [3,4,5].

However, it is difficult to determine the local rail temperature for the entire track. To solve this problem, various rail-temperature-prediction models using weather data have been developed [6,7,8,9,10].

These models can be classified into two categories: statistical-method models and thermodynamic-method models.

Among the statistical methods, the simplest rail-temperature-prediction model only uses the air temperature, a model developed by Hunt and Esveld [6, 7]. In this model, the rail temperature is expressed as a linear equation of the air temperature, such that it can be predicted using air temperature alone.

Another statistical model is the rail-temperature-prediction model based on multivariate regression analysis, as performed by Wu et al. [8]. This model predicts the rail temperatures using 24 weather variable, including surface temperature, cloudiness, sea-level pressure, and air temperature.

The thermodynamic models for rail-temperature prediction were proposed by Chapman and Zhang et al. Chapman’s model calculates the rail temperature by balancing the energy delivered to the head and web of the rail. Zhang’s model calculates the rail temperature by balancing the energy delivered to the rail after considering the rail as a mass [9,10,11].

Chapman also conducted sensitivity tests on the parameters that could affect the rail temperature [9]. According to this sensitivity test, the temperatures of rails installed on a south–north axis differed from those installed along a north–east/south–west axis. In particular, as the installed rail’s latitude increased, the daily maximum rail temperature did so as well. Whittingham’s study also mentioned that the rail temperature shows a different pattern depending upon its installation direction [11]. This means that the position of the sun affects the rail’s temperature. However, previous rail-temperature-prediction models have failed to consider the relative positional relationship between the sun and the rail.

In this study, we propose a novel rail-temperature-prediction model considering the position of the sun. This model calculates the rail-surface area directly affected by the sun at a given position, which changes with time of day. The rail temperature is calculated using energy-balance equations that take into account the radiation, considering the rail-surface area directly affected by the sun, as well as convection.

2 Methods

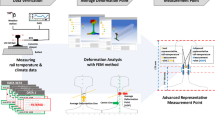
Rails are placed in environments where they are exposed to a combination of conduction, radiation, convection, and other effects (Fig. 1). In this study, various parameters affecting the rail temperature were directly measured by the measurement system and the measurement data was used to develop a rail-temperature-prediction model.

Fig. 1
figure 1

External environmental factors affecting the rail temperature

Full size image

2.1 Measurement of Rail Temperatue and Weather Data

Measuring the rail temperature with trains running may lead to safety problems. In this study, the rail temperature and local weather data were measured using a measurement system similar to the real rail environment at Chungnam National University (CNU), Daejeon, Korea (Fig. 2).

Fig. 2
figure 2

Actual measurement system

Full size image

The measurement system was designed to match the thermal environment of an actual rail. The rail was installed on ballast and concrete sleepers just like the actual track, and the location of the experimental area was selected to minimize the influence of shadows.

The measured environmental data were acquired every 10 min from August 2016 to May 2017.

A 50-kgN rail was installed on the measuring system with a south–north orientation after being cut into a 500-mm piece in the longitudinal direction. The rail temperature was measured using 16 K-type thermocouples to obtain the surface/internal rail-temperature data.

The rail temperature at different measurement points may vary by as much as 7 °C [12, 13]. In this study, the internal rail temperature at a 70-mm height above its bottom (where the average deformation of the rail occurs) was used as the representative temperature of the rail [14].

The Weather Station (Vantage Pro2, Davis) was used to measure the weather data. The data included wind speed, wind direction, solar radiation, air temperature, humidity, and rainfall.

2.2 Reflectance of the Rail

Reflectance is the ratio of reflected to incident light, which expresses the influence of the sun. Since the sun is a major heat source to the rail, the accurate measurement of the rail’s reflectance is essential for developing a rail-temperature-prediction model.

The surface of the rail in actual operation is usually corroded and abraded by a combination of factors such as rain, wind, and contact stress from the wheels of the train. Thus, the rail surface is discolored and rusted, bringing about changes in the reflectance.

In this study, 1.5 cm × 1.5 cm × 1 cm specimens were prepared using an unused rail and an used (10-year-old) rail (Fig. 3). A diffuse-reflectance UV–VIS–NIR spectrophotometer (SolidSpec-3700, SHIMADZU) was used to measure the reflectance of the prepared specimens.

Fig. 3
figure 3

a Used rail specimen (1.5 cm × 1.5 cm × 1 cm) that has been used for more than 10 years, b unused rail specimen (1.5 cm ×  1.5 cm  × 1 cm)

Full size image

Energy absorption vary depending on the energy intensity of the sun and the reflectance of each wavelength. Thus, we define as ‘standard reflectance’. The standard reflectance was calculated by multiplying the solar energy intensity by the reflectance of the wavelength at 400–1100 nm, which is the range of spectral response in our solar radiation sensor.

2.3 Calculating the Orbit of the Sun

In the horizontal coordinate system, the position of the sun can be expressed in terms of azimuth and altitude (Fig. 4). The azimuth (Φsun) is the angle between the projected vector and the north (N) vector. The altitude (αsun) is the angle between a vector of sunlight and the projected vector. Using azimuth and altitude, we can simply express the position of the sun [15].

Fig. 4
figure 4

Definitions of azimuth and altitude on a horizontal coordinate system

Full size image

The surface area of the rail, which is directly affected by the sun, depends upon the position of the sun (Fig. 5). Since the actual rail extends infinitely in the longitudinal direction, this area was normalized by dividing into the length. We called this factor as the ‘normalized solar-incident area (\(S_{{sun}}^{\prime }\))’.

Fig. 5
figure 5

The surface area of the rail directly affected by sunlight

Full size image

When the azimuth and the altitude were 121° and 59° respectively, \(S_{{sun}}^{\prime }\) was 0.4206 m2/m. However, when they were 180° and 47° respectively, \(S_{{sun}}^{\prime }\) was 0.1678 m2/m. Under the same conditions (atmospheric temperature, solar altitude), the rate of temperature rise can vary greatly depending on the exposed area, \(S_{{sun}}^{\prime }\).

In this study, Michalsky’s method was used to calculate azimuth and altitude of the sun [16]. This method computes the ecliptic coordinates, uses them to calculate the equatorial coordinates, and finally computes the horizontal coordinates. The reliability of this method is guaranteed for dates between 1950 and 2050.

The main feature of this method is that the position of the sun (azimuth, altitude) can be calculated based on latitude, longitude, and time (year, month, day, hour, minute)

The ecliptic-coordinate system is based on the ecliptic, which is the path of the sun on the celestial sphere (Fig. 6). The ecliptic coordinates represent the position of a celestial body using the ecliptic longitude (I) and the ecliptic latitude (β). In this study, we calculated the obliquity of the ecliptic (ep) and the ecliptic longitude using the proposed equation, because we focused upon calculating the position of the sun. The equations used for calculating this orbit are as follows:

Fig. 6
figure 6

Definition of ecliptic longitude, ecliptic latitude, and obliquity of the ecliptic in the ecliptic-coordinate system

Full size image
$$delta = year - 1949 ;$$
(1a)
$$leap = integer\; portion \;of \left( {\frac{delta}{4}} \right);$$
(1b)
$$Jd = 2432916.5 + delta \times 360 + leap + day + \frac{hour}{24};$$
(1c)
$$L = 280.46 + 0.9856474 \times n;$$
(1d)
$$g = 357.528 + 0.9856003 \times n;$$
(1e)
$$I = L + 1.915 \times \sin (g) + 0.02 \times \sin (2 \times g);$$
(1f)
$$ep = 23.439 - 0.0000004 \times (Jd - 2451545).$$
(1g)

The equatorial-coordinate system is based on the celestial equator, which is the plane projected from Earth’s equator (Fig. 7). The coordinates of the sun are indicated by right ascension (ra) and declination (dec). The equatorial coordinates are calculated as follows:

Fig. 7
figure 7

Definition of right ascension and declination on the equatorial-coordinate system

Full size image
$$ra = a\tan \left( {\frac{\cos (ep) \times \sin (I)}{\cos (I)}} \right);$$
(2a)
$$dec = a\sin \left( {\frac{\sin (ep)}{\sin (I)}} \right).$$
(2b)

Finally, the horizontal coordinate system is based on the position of an observer on the surface of the Earth. In this system, the coordinates of a celestial body are measured from the plane on which an observer stands (Fig. 4). The horizontal coordinates (azimuth, altitude) are calculated as follows:

$$gmst = 6.697375 + 0.0657098242 \times n + hour;$$
(3a)
$$lmst = gmst + \frac{lte}{15};$$
(3b)
$$ha = lmst - \frac{ra}{15};$$
(3c)
$$\alpha_{sun} = a\sin (\sin (dec) \times \sin (lat) + \cos (dec) \times \cos (lat) \times \cos (ha));$$
(3d)
$$\emptyset_{sun} = a\sin \left( {\frac{{ - \cos \left( {dec} \right) \times \sin \left( {ha} \right)}}{{\cos \left( {\alpha_{sun} } \right)}}} \right)$$
(3e)

2.4 Calculating the Position-Varying Solar-Incidence Area

Since it is difficult to directly apply the position of the sun into the thermodynamic model, the solar-incidence area (Ssun) is calculated from the shadow area of the rail (Sshadow) caused by the movement of the sun.

We need to know the coordinates of rail model’s vertices to calculate the shadow area. However, since the rail consists of curved surfaces, it is very difficult to calculate these coordinates (Fig. 8a). Therefore, the model of the rail was simplified (Fig. 8b) to consist of 28 vertices. Then, the simplified model was placed on the imaginary XY plane. The south–north inclination of the rail model was fixed to the X-axis, such that it was the same as the actual measurement environment. Finally, we calculated the coordinates of 28 vertices using the center of the rail’s bottom as the origin (O).

Fig. 8
figure 8

Rail-modeling images (50kgN rail) a original rail model; b coordinates given to simplified rail model (28 points)

Full size image

Using Eq. (3), the position of the sun can be calculated in terms of azimuth and altitude using time (year, month, day, hour) and the coordinates (latitude, longitude) of the measurement system. Using the calculated azimuth and altitude, the coordinates of the sun ((X, Y, Z)sun) in the XYZ-coordinate system can be expressed as follows:

$$\left( {X, Y, Z} \right)_{sun} = \left( {L_{sun} \times \cos \left( {\alpha_{sun} } \right) \times \sin \left( {\emptyset_{sun} } \right),\;L_{sun} \times \cos \left( {\alpha_{sun} } \right) \times \cos \left( {\emptyset_{sun} } \right), L_{sun} \times \sin \left( {\alpha_{sun} } \right)} \right).$$
(4)

The vector of the origin (O) from the position of the sun is expressed as follows. This vector is the direction of the solar energy that directly affects the rail:

$$\overrightarrow {Sun} = \left( {L_{sun} \times \cos \left( {\alpha_{sun} } \right) \times \sin \left( {\emptyset_{sun} } \right),\;L_{sun} \times \cos \left( {\alpha_{sun} } \right) \times \cos \left( {\emptyset_{sun} } \right), L_{sun} \times \sin \left( {\alpha_{sun} } \right)} \right).$$
(5)

Applying this vector to the linear equation, it is possible to project the vertex of the rail onto the XY plane, as Fig. 9a shows. If the vertices of the rail are represented by An(xn, yn, zn), the linear equation can be expressed as Eq. (6):

$$\begin{aligned} \frac{{x - x_{n} }}{{\cos \left( {\alpha_{sun} } \right) \times \sin \left( {\emptyset_{sun} } \right)}} & = \frac{{y - y_{n} }}{{ \cos \left( {\alpha_{sun} } \right) \times \cos \left( {\emptyset_{sun} } \right)}} \\ & = \frac{{z - z_{n} }}{{\sin \left( {\alpha_{sun} } \right)}}. \\ \end{aligned}$$
(6)

when the vertex An(xn, yn, zn) is projected onto the XY plane using a linear equation, it can be expressed as A′n(x′n, y′n, 0). x′n and y′n are simplified as follows:

Fig. 9
figure 9

a Method of projecting a cube onto a plane. b A shadow area on the XY plane

Full size image
$$x_{n}^{\prime } = - \frac{{\sin \left( {\emptyset_{sun} } \right)}}{{\tan \left( {\alpha_{sun} } \right)}}z_{n} + x_{n} ;$$
(7a)
$$y_{n}^{\prime } = - \frac{{\cos (\emptyset_{sun} )}}{{\tan \left( {\alpha_{sun} } \right)}}z_{n} + y_{n} .$$
(7b)

Using the proposed equation, it is possible to project all the 28 vertices of the rail model onto the XY plane. A polygon can be drawn using the vertices of the rail projected on the XY plane, as is shown in Fig. 9b. The area of this polygon is equivalent to the area of the shadow (Sshadow) and changes with the movement of the Sun. To calculate the area of this polygon, we use Eq. (8). The proposed equation computes the area using adjacent coordinates:

$$S_{shadow} = \frac{1}{2}\mathop \sum \limits_{i = 1}^{n} (x_{i} + x_{i + 1} )(y_{i} - y_{i + 1} ).$$
(8)

Using the calculated shadow area (Sshadow), it is possible to calculate the solar-incidence area (Ssun) (Fig. 10); this is the surface area of the rail directly affected by the sun. Just as the shadow area changes with the sun’s position, the solar-incidence area also changes. The equation for calculating the solar-incidence area from the area of the shadow can be expressed as follows:

Fig. 10
figure 10

Method of calculating the solar-incidence area (Ssun) using shadow area (Sshadow)

Full size image
$$S_{sun} = S_{shadow} \times \sin (\alpha_{sun} ).$$
(9)

2.5 Rail-Temperature-Prediction Model Using Energy-Equilibrium Equation

Zhang et al. [10, 11]proposed an energy-equilibrium equation as a rail-temperature-prediction model. In this study, we modify their model to reflect the position of the sun with time. The developed model calculates the rail temperature by drawing the balance of the energy from the sun to the rail and the heat loss due to convection and radiation. The energy-equilibrium equation developed is expressed as follows:

$$SA \times SR \times {A_s} \times \sin \left( {{\alpha_{sun}}} \right) - \left[ {{h_{conv}} \times {A_c} \times ({T_r} - {T_i}) + {\epsilon_r} \times \sigma \times {A_r} \times ({T_r}^4 - {T_{sky}}^4)} \right] = {\rho_r}{c_r}{V_r}\frac{{d{T_r}}}{dt}$$
(10)

The convection coefficient can be calculated using Eq. (11), by which the convection coefficient is calculated using the windspeed [11].

$$h_{conv} = \left\{ {\begin{array}{*{20}c} {5.6 + 4 \times v_{wind} ,} & {for\; v_{wind} \le 5 \;{\text{m}}/{\text{s}}} \\ {7.2 \times \left( {v_{wind} } \right)^{0.78} ,} & {for \;v_{wind} > 5\;{\text{m}}/{\text{s}}} \\ \end{array} } \right. .$$
(11)

2.6 Rail-Temperature-Prediction Program for Evaluation of the Novel Model

The model proposed in this study predicts the rail temperature using the mathematical algorithm for calculating the solar-incidence area and the energy-equilibrium equation. To quickly apply this algorithm, which is more complicated than the conventional one, we developed a rail-temperature-prediction program based on LabVIEW and used it to evaluate this model.

3 Results and Discussions

3.1 Measurement of the Reflectance of a Rail

As shown in the Fig. 11, rail specimens were analyzed using a diffuse-reflectance spectrophotometer. This figure shows reflectance according to wavelength.

Fig. 11
figure 11

Results of reflectance analysis using a diffuse-reflectance spectrophotometer

Full size image

The standard reflectance considering energy intensity was 1.6% for the unused rail specimen and 18.9% for the (10-years) used rail specimen. The standard reflectance difference of the specimen was caused by wear on the rail surface and paint erosion. As shown in the Fig. 3, the (10-years) used rail was installed in constructed measurement station. So we used 18.9% standard reflectance for constructing a rail-temperature-prediction model.

3.2 Rail-Temperature-Prediction Program and Algorithm for Evaluation

We developed a rail-temperature-prediction program based on LabVIEW to evaluate our proposed model (Fig. 12). This program can use the weather data to predict rail temperature in real time (Fig. 12a).

Fig. 12
figure 12

Rail-temperature-prediction program based on LabVIEW. a LabVIEW VI, b program algorithm

Full size image

Figure 12b shows the program’s algorithm. The measured data (time, air temperature, wind speed) and location information (latitude and longitude) of the measurement point were treated as the input values in this program. The input data were converted into a recognizable form by preprocessing. Then, the position of the Sun was calculated based on the measurement point and the measured time. The normalized solar-incidence area (Ssun) was calculated from the position of the Sun. Finally, the energy-equilibrium equation was used to predict the rail temperature. This equation was solved using a MATLAB ordinary differential equation (ODE) solver such as ODE45.

3.3 Comparison of Fixed- and Non-Fixed-Solar-Incidence-Area Models

The solar-incidence area, which changes along with the position of the sun, is the biggest difference between our model and the previous one.

We compared rail-temperature predictions made with a fixed solar-incidence area to those with an area that changed with time. For a fixed solar-incidence-area model, a fixed area constant of 0.1 m2, which is the average solar-incident area was used to perform the evaluation.

35,325 data sets (time, air temperature, solar radiation, and wind speed) measured from August 2016 to May 2017 are used to evaluate this model.

The CNU model 1 uses a fixed solar-incident area; CNU model 2 considers changes in the solar-incidence area; and Hunt 1 and 2 are linear models using air temperature. Table 1 shows that the CNU model 2 has a higher R-squared value and lower root-mean-square error (RMSE) than the other models. Box plots in Fig. 13 show the error distributions of four models. In the box-plot, the interquartile range of CNU models were narrower than that of Hunt models. Moreover, the medians of CNU models were closed at zero line. These mean that our models exhibit higher accuracy than the previous models.

Table 1 Comparisons between measured and predicted rail temperatures
Full size table
Fig. 13
figure 13

Boxplot of error for Hunt 1, Hunt 2, CNU model 1 and CNU model 2. Error: difference of measured and predicted rail temperature

Full size image

Figure 14 shows the predicted rail temperature compared with measured rail-temperature for 3-days. Our predicted rail temperature and measured temperature trends were almost similar. In the maximum rail temperature points, max error was 4 degrees for CNU model 1 and 1 degree for CNU model 2.

Fig. 14
figure 14

Comparison of the predicted rail temperature and the measured data graphs in September 2016

Full size image

In the CNU model 2, it is important to note that the position of the sun (azimuth, altitude) can be calculated using only the latitude, longitude and time, without any additional measurements.

3.4 Limitations and Directions for Improvement

In this study, we measured the temperature of a 500-mm-long piece of rail mounted on the measurement system. The cut section of the rail was exposed to the sun as it was being measured. However, the difference between the reflectivity of the cross section of the rail and that of its normal surface was not taken into consideration in the rail-temperature-prediction model, which may have compromised its accuracy.

In addition, since our model is constructed using only the weather data at the measurement system in CNU, problems may occur when it is applied to other measurement environments. To solve this problem, it is necessary to construct a new measurement system at different latitudes, longitudes, and road environments, and to perform additional verification experiments.

4 Conclusion

In this study, a novel rail-temperature-prediction model was developed using the measured data concerning meteorological phenomena including the position of the sun. The following conclusions were drawn.

  1. 1.

    The rail temperature can be calculated by balancing the solar energy from the sun to the rail and the heat loss due to convection and radiation using the energy-equilibrium equation. 

  2. 2.

    The azimuth and altitude representing the position of the sun at the measurement point can be calculated using only the time, latitude, and longitude without additional measurement.

  3. 3.

    The novel rail-temperature-prediction model using the position of the sun exhibits a higher accuracy than that exhibited by a model that does not consider the position of the sun.