1 Introduction

High-entropy alloys (HEAs) have become the most popular metallic alloy concept in recent days [1,2,3]. They form face-centered cubic or body-centered cubic single-phase solid solution with mixing five or more elements. Many material engineers and scientists are investigating this concept for developing new alloys and understanding the work hardening mechanism during deformation because of its attractive mechanical properties. In particular, their superior mechanical properties are obtained from mechanical twinning, dislocation accumulation, and/or transformation-induced plasticity, as well as solid solution strengthening, depending on stacking fault energy [4] under operating temperatures.

Especially, the most well-known CoCrFeMnNi alloy (generally called Cantor alloy) has been studied by many scientists because of their excellent mechanical properties with over 2 GPa strength and 60% elongation at 77 K [5,6,7,8]. The reasons for the enhanced mechanical properties can be obtained from the relation between the evolution of twinning and dislocation mobility. Therefore, an appropriate modeling parameter is required to compare different deformation behaviors at various temperatures.

A deformation twinning behavior with dislocation glide modeling has been developed from the discovery of twinning–induced plasticity (TWIP) steels [9]. The previous model on TWIP steels has used either critical twinning strain [10,11,12] or critical twinning stress [13] for indicating the twinning initiation point for accumulation of the twin volume fraction. In TWIP steel models, a saturation of the twin volume fraction and the critical twinning strain have been widely used as modeling parameters. The TWIP steel model has also been recently used for HEAs modeling with critical twining strain [14, 15]. However, the evolution of twinning is generally known as stress-driven rather than strain-driven [16]. Therefore, the critical twinning stress is required when describing the initiation of deformation twinning rather than critical twinning strain.

In this work, a constitutive model is constructed based on experimental tensile test results at 77 K and 293 K. These models are developed to investigate the temperature effects on the twinning and dislocation glide in HEAs. To obtain a precise twinning initiation point, the critical twining stress of CoCrFeMnNi HEA is employed in the model. Also, the dislocation behavior affected by the shortening of the mean free path of dislocation during deformation and the amount of annihilation of dislocations due to temperature effects is well defined by the estimated dislocation density from the simulation results. The objective of this work is to introduce an enhanced twinning kinetics model with the critical twining stress and to perform quantitative analysis of the temperature effect on twinning and dislocation glide by using the ABAQUS software for finite element method (FEM).

2 Experiment

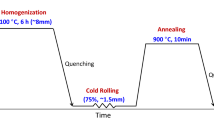
An equimolar CoCrFeMnNi HEA ingot was produced using vacuum induction melting. The homogenization annealing of the ingot was carried out at 1100 °C/6 h in an argon atmosphere/water quenching. These homogenized ingots were cold-rolled to reduce the thickness from 7.8 to 1.5 mm. The cold-rolled strips were subsequently annealed at 800 °C/1 h in an argon atmosphere/water quenching. Dog bone-shape tensile test specimens with a gauge length of 5 mm, gauge width of 2.5 mm, and thickness of 1.5 mm was extracted using electric discharge machining. The tensile tests were conducted on a universal tensile testing machine (Instron 1361, Instron Corp, USA) at a strain rate of 10–3 s−1 strain rate. A digital image correlation technique (DIC: ARAMIS v6.1, GOM Optical Tech., Germany) with black and white speckles on the surface of the tensile specimens was used to determine the tensile strain at 293 K. However, the tensile strain measurement at 77 K was performed using a micro-extensometer as mentioned in Ref. [17].

Electron backscatter diffraction (EBSD) analysis was conducted using a field emission scanning electron microscope (FE-SEM) with a step size of 50 nm (Model: Quanta 3D FEG, FEI Company, USA). The EBSD samples were prepared by mechanical polishing of samples with SiC paper up to 1200 grit, followed by diamond (3 μm and 1 μm pastes), and then finished with colloidal silica polishing (0.04 μm). Orientation imaging microscopy analysis software (TSL OIM analysis 7) was used to analyze the EBSD data. In addition, the average grain size of the annealed sample was estimated using EBSD data by considering high angle grain boundaries without considering annealing twin boundaries (Σ3, TBs).

3 Constitutive Model

3.1 Dislocation and Twin Strains

The principal operation slip system in FCC metals is <110> {111}. As the perfect dislocation splits into two Shockley partial dislocations, the burger’s vector of each Shockley partial determines whether twinning or slip will occur [18, 19]. Like this, the competitive relation between twinning and dislocation glide affects deformation mechanisms. When twinning occurs, the twin boundaries act as barriers to the dislocation motion and suppresses slip. It delays necking onset and helps to reach high work hardening rates. Therefore, the total plastic shear strain should take into account both twinning and shear strain of dislocation contribution. The strain can be decomposed into dislocation contribution and twin contribution as follows [10]:

$$d\varepsilon = \left( {1 - F} \right) \cdot d\varepsilon_{dis} + \varepsilon_{tw} \cdot dF,$$
(1)

where \(d\varepsilon_{dis}\) is the increment of shear strain in the untwined matrix undergoing slip and \(F\) is twin volume fraction at that deformation point. Here, \({\varepsilon }_{tw}\) is the twinning strain that is equal to \({1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}\) along {112} <111> [20]. The shear strain is related to the macroscopic strain as γ = Mε, where M is the Taylor factor considering the average texture depending on crystal structure in the isotropic model. Thus, Eq. (1) can be represented by Eq. (2):

$$\frac{{d\varepsilon_{dis} }}{d\varepsilon } = \frac{1}{1 - F}\left( {1 - \frac{1}{\sqrt 2 M}\frac{dF}{{d\varepsilon }}} \right).$$
(2)

3.2 Twinning Model

In general, the occurrence of twinning during deformation can be recognized from the apparent slope change of the work hardening rate curve. As can be seen from Fig. 1, a clear slop change is evident in the 77 K tested sample, indicating the formation of twins during work hardening. To analyze the twinning behavior at 77 K quantitatively, the twin volume fraction, twin thickness, and mean twin spacing are to be measured at certain strain levels. In the present model, the twin volume fraction is represented as:

$$\frac{dF}{{d\varepsilon }} = \left( {F_{max} - F} \right)NV_{tw} ,$$
(3)
Fig. 1
figure 1

Experimental tensile stress–strain (σ–ε) curves and the strain hardening rates (θ = dσ/dε) of CoCrFeMnNi HEA at a 77 K and b 293 K

Full size image

where \(F_{max}\) is the max twin volume fraction, N is the number of twin nuclei per unit volume, and Vtw is the twin volume with newly-formed twin thickness at the deformation point. When the flow stress reaches the critical twinning stress, the increment of the twin volume fraction is activated. The critical twinning stress value used here was calculated by using Eq. (4) [21]:

$$\sigma_{crit} = \frac{{M\gamma_{SFE} }}{{b_{p} }} + \frac{{K_{tw}^{H - P} }}{\sqrt d }.$$
(4)

In the previous models of critical twinning stress, it was difficult to obtain the saturation value of the twin volume fraction [22, 23]. To overcome this limitation, the maximum twin volume fraction \(\left( {F_{max} } \right)\) is adopted in Eq. (3). As a result, F can be smoothly increased up to \(F_{max}\) in the overall deformation region.

$${\text{N}} = { }N_{0} {\exp}\left[ { - \left( {\frac{{\sigma_{crit} }}{\sigma }} \right)^{s} } \right],$$
(5)

where N0 is the initial number of twin nucleation, and s is a parameter determining the sharpness of the transition from non-twinning to the twinning domain during deformation. During the plastic flow, the probability of successful nucleation decreases gradually as exponential terms. The twin nucleus is assumed to be growing into a disc-like twin immediately. The twin volume (Vtw) is calculated by increasing twin thickness and constant diameter which is the same as the average grain size.

$$V_{tw} = \frac{1}{4}\pi ed^{2} .$$
(6)

3.3 Dislocation Evolution

The relationship between dislocation density and flow stress, is given by the Taylor equation, expressed as:

$$\sigma = \sigma_{0} + \alpha MGb\sqrt \rho ,$$
(7)

where σ0 is friction stress to activate dislocation glide, α related to the interaction strength between dislocations, G is the shear modulus, b is the magnitude of the Burgers vector, and ρ is the total dislocation density. The dislocation density evolves with strain by dislocation glide, as follows:

$$\frac{d\rho }{{d\varepsilon_{dis} }} = M\left( {\frac{1}{bL} + \frac{k}{b}\sqrt \rho - f\rho } \right),$$
(8)
$$\frac{d\rho }{{d\varepsilon_{dis} }}\frac{{d\varepsilon_{dis} }}{d\varepsilon } = M\left( {\frac{1}{bL} + \frac{k}{b}\sqrt \rho - f\rho } \right)\frac{1}{1 - F}\left( {1 - \frac{1}{\sqrt 2 M}\frac{dF}{{d\varepsilon }}} \right),$$
(9)

where L is dislocation mean free path or obstacle spacing, k is the rate of athermal storage coefficient, and f is the dynamic recovery parameter for dislocation annihilation. From Eq. (8), the increase of dislocation density depends on the amount of dislocation glide shear strain and dislocation movement is affected by temperature effect with k and f coefficients.

The obstacle spacing (L) is determined by the average grain size (d) and the mean twin spacing (t).

$$\frac{1}{L} = \frac{1}{d} + \frac{1}{t} .$$
(10)

The mean twin spacing (t) is obtained by twin thickness and twin volume fraction at the deformation state.

$$t = {\text{ 2e}}\frac{1 - F}{F}.$$
(11)

Furthermore, the evolution of twinning leads to the formation of sub-grain structure inside grains with a reduction of mean twin spacing, creating smaller grain size environment and disturbs hindering dislocation glide. This phenomenon is called “dynamic Hall–Petch” behavior: twinning plays a role as a dislocation’s obstacles and twin boundaries behave as grain boundaries [24, 25]. As a result, dislocation mean free path L suddenly drops with decreased mean free twin space and the dislocation movement is suppressed.

3.4 Back Stress Model

Dislocation at the coherent matrix/twin boundary in the grain creates additional internal stress fields for the further slip. In other words, the back stress needs to be considered with the available distance of dislocation movement against the grain and twin boundaries. When twinning is not considered, the back stress is expressed as \(\sigma_{b} = M{\text{G}}b{\text{n }}(1/d)\) [26], where n is the number of accumulated dislocations arriving at interfaces per slip plane (Fig. 2).

Fig. 2
figure 2

Schematic representation of the strain-hardening mechanism of CoCrFeMnNi HEA a {112} <111> twins form at the onset of critical twinning stress and leads to the formation of sub-grain structures with twin boundaries. b For further deformation, the dislocation mean free path is decreased by dynamic grain refinement with higher twin volume fraction and wider twin thickness

Full size image

In the recent TWIP steel report [27], this is formulated as:

$$\sigma_{b} = MGb\left( {\frac{1}{d} + \frac{1}{t}} \right)n.$$
(12)
$$\frac{dn}{{d\varepsilon_{dis} }} = M\frac{\lambda }{b}\left( {1 - \frac{n}{{n^{*} }}} \right),$$
(13)

where λ is the mean spacing between slip plane and n* is the maximum number of dislocations that can pile-up at interfaces on a given slip plane. Then, Eq. (9) becomes Eq. (14):

$$\frac{d\rho }{{d\varepsilon_{dis} }}\frac{{d\varepsilon_{dis} }}{d\varepsilon } = M\frac{\lambda }{b}\left( {1 - \frac{n}{{n^{*} }}} \right)\frac{1}{1 - F}\left( {1 - \frac{1}{\sqrt 2 M}\frac{dF}{{d\varepsilon }}} \right).$$
(14)

4 Results and Discussion

4.1 Model Validation of One Element

Based on the above the equations, the strength formula is expressed as:

$$\sigma = \sigma_{0} + \alpha MGb\sqrt \rho + MGb\left( {\frac{1}{d} + \frac{1}{t}} \right)n.$$
(15)

On the right-hand side, the first term is friction stress, the second term is dislocation forest hardening, and the last term is back stress hardening. In other words, we consider isotropic kinematic hardening to represent the plastic deformation behavior of twinning and dislocation glides. The modeling parameter values in Tables 1 and 2 are used by tuning to the experimental results at 77 K and 293 K.

Table 1 Modeling parameter values compared with experimental data for CoCrFeMnNi HEA
Full size table
Table 2 Depending on the different temperature, appropriated modeling parameter values were used, respectively
Full size table

Generally, critical stress values for twinning are suggested to be approximately insensitive to the temperature although stacking fault energies are generally temperature-dependent [30]. Hence, the critical twinning stresses at 77 K and 293 K in the present study are assumed to have the value 712 MPa by ignoring their negligible difference [16, 21].

Figure 3 shows the evolutions of the twin variables (mean twin spacing, thickness, and volume fraction) comparing the experiment and modeling values. The modeling and experimental results match closely with each other. In the initial deformation stage at 77 K, because the slip stress is much higher than twinning stress, the relatively low strain generates high stress reaching critical twinning stress and causes the initiation of twinning [16]. At 77 K, the dominant twinning mechanism is observed from the work hardening rate curve according to Fig. 1a. The twin volume fraction at 77 K in Fig. 3a represents smoothly increased behavior and saturated behavior at the end of the strain region. The increasing density of the twin boundary brings the dynamic Hall–Petch effect. Also, with further straining, the mean twin spacing is rapidly fall off with increasing twin volume fraction in grain. It leads to a further reduction in the dislocation mean free path and a gradual decrease in the work hardening rate. In particular, when calculating the mean twin spacing in this model, unlike other papers, the average value of the twin thickness is not used. Through the transmission electron microscopy (TEM) analysis reported in Ref. [17], the twin thickness is increased with an increase in the applied strain. Also, the formation of nano-twins is found at 77 K, and the twin thickness is suggested to be increased linearly with strain as shown in Fig. 3c.

Fig. 3
figure 3

The experimental results are adopted from Ref.[17]

Above the critical twinning stress (712 MPa), the twin volume fraction start increasing. a, b experimental and model-predicted plots of twin volume fraction versus true strain plot at 77 K and 293 K, respectively; c Increased twin width during deformation; d Inter twin spacing with strain.

Full size image

At 293 K, however, no twinning transition is observed in the work hardening rate curve as shown in Fig. 1b. Hence, instead of conducting TEM analysis, the twin volume fraction of CoCrFeMnNi is taken into account from the previous paper [14], which obtains about 0.008 as a maximum twin volume fraction with 52 µm grain size. Since twinning occurs more easily with larger grain size, with 13 µm grain size in this paper, a slightly lower twin volume fraction is obtained than in Ref. [14], as shown in Fig. 3b.

Figure 4a shows the EBSD inverse pole figure map of the sample annealed at 800 °C for 1 h. The as-annealed microstructure consists of equiaxed grains with the average size of 13 μm and a high fraction of annealing twins. The strain distributions map of the tensile specimen which is tested at 293 K is illustrated in Fig. 4b. The EBSD analysis performed at different strain levels are presented at Fig. 4c–j. The EBSD inverse pole figure (IPF) maps of regions with different strain levels presents that the grains are elongated in the direction of uniaxial tensile test. Also, the boundary maps of the corresponding regions shown in Fig. 4g–j represent the evolution of high-angle and annealing twin boundaries during the plastic deformation. The EBSD results indicate that the plastic deformation at 293 K is mainly governed by dislocation activity, and twinning activity is limited. However, there are several reports that the dominant deformation temperature at 77 K is mechanical twinning in the present CoCrFeMnNi HEA [16, 17, 21].

Fig. 4
figure 4

a EBSD IPF map of the as-annealed sample, b Effective strain distribution map along the tensile specimen obtained experimentally by using the digital image correlation (DIC) technique; EBSD IPF maps of the tensile specimen at different strain regions of about c 15%, d 22%, e 35%, and f 52% elongations; and corresponding grain boundary maps of the tensile specimen at different strain regions of about g 15%, h 22%, i 35%, and j 52% elongations. The black and red lines represented in the boundary maps correspond to the high-angle grain boundaries and annealing twin boundaries, respectively. (Color figure online)

Full size image

During the plastic deformation, dislocation activities can lead to local misorientation due to the grain’s rotation toward the slip direction. To analyze the evolution of local misorientation at different strain levels in the tensile specimen tested at 293 K, Kernel average misorientation (KAM) was used. The KAM maps from the corresponding regions presented in Fig. 4c–f are shown in Fig. 5a–d. Also, the quantitative average KAM values of the corresponding strains are plotted in Fig. 6a. The KAM values were obtained by considering the third nearest neighbor kernel with a maximum misorientation of 5°.

Fig. 5
figure 5

Kernel average misorientation (KAM) maps a–d and Geometrically necessary dislocation (GND) maps e–h of the tensile specimens at different strain regions of a, e 15%, b, f 22%, c, g 35%, and d, h 52% elongations. White color in the GND maps represents high average GND density regions which cannot be indexed

Full size image
Fig. 6
figure 6

a Average KAM and GND values versus effective strain at different strain levels obtained from the EBSD analysis of the tensile specimen tested at 293 K, b Strain dependence of the dislocation density predicted using the proposed model at 77 K and 293 K

Full size image

In addition, the strain distribution based on the dislocation density can be studied using geometrically necessary dislocation (GND) by measuring the changes in the local orientation. The GNDs are generally induced at the interface boundaries to accommodate the strain incompatibility between two grains during the plastic deformation. The average value of GND density at a certain area can be considered as an approximation of the total dislocation density at that region [31, 32]. Thus, in the present study, the evolution of average GND density is considered as the change in local dislocation density to validate the trend of the modeling results. The GND maps of the regions with different strain levels are illustrated in Fig. 5e–h and the average GND densities versus effective local strain is plotted in Fig. 6a. As clearly can be seen in Fig. 5, the KAM and GND density increased with an increase in the applied strain.

The correlation between temperature and dislocation density evolution behavior is investigated by dividing the curve into the early, middle and late strain stages as shown in Fig. 6b. At the early strain stage, the dislocation accumulation rate is much higher at 77 K compared to at 293 K. Because the flow stress during initial deformation reaches the critical twinning stress, the twin mechanism can be dominantly activated and the obstacle spacing (L) in Eq. (8) is steeply decreased. Experimental observation has discovered that a twin boundary can act as a source for dislocation nucleation [33]. When dislocation encounters nano-twin boundaries during plastic deformation, dislocation cannot penetrate the twin obstacles. While some of the accumulated dislocations at the twin boundary will undergo slip in another favorable slip plane, some dislocations remain at the twin boundary (twinning partial dislocations). In other words, along the nano-twin boundaries, dislocations continuously accumulate until the twin spacing is sufficiently small, leading to a more uniform plastic deformation [33,34,35].

From the middle and late strain stages, temperature-dependent dislocation behavior can be explained. The coefficient of athermal dislocation storage is set to be 0.018 regardless of temperature. The activation volume for dislocation glide and the dynamic recovery by dislocation annihilation is highly dependent on the temperature [36]. Therefore, it can be predicted that the low dynamic recovery coefficient is required to have low activation volume at 77 K [37].

The high dislocation density of twinning partial dislocations at small twin spacing causes an enhanced work hardening with ductility against necking. It can be confirmed from Fig. 1, that a larger amount of twin volume fraction at 77 K has greatly helped in achieving higher uniform elongation than at 293 K. the strength of dislocation interactions can be obtained from the α value given in Table 2. For determining α value, we need to understand the dislocation distribution and characteristics with work hardening mechanisms. The uniformly distributed dislocation and low dislocation reaction have a low \(\alpha\) value [38]. Because of the formation of twin boundaries, dislocations are uniformly distributed and forest dislocations interact less with the twinning partial dislocations. Therefore, the lower α is applied at 77 K.

The close inspection of dislocation density evolution versus strain at 293 K shown in Fig. 6b presents a similar trend of increment in the average KAM and GND values illustrated in Fig. 6a. Although the GND density is the lower bound of the total dislocation density, their similar evolution trend versus strain can be considered as an approximation to validate the modeling results.

When a leading dislocation encounters a grain boundary, it cannot move further, resulting in a dislocation pile-up behind the leading dislocation. This phenomenon requires an additional stress field for the slip to occur. The more dislocation pile-up in front of the grain boundaries, the higher is the back stress [39]. The saturated back stress could be attained by limiting the maximum number of piled up dislocations inside a grain.

In addition, considering twinning, the effect of hindering dislocation glide becomes greater in twin boundary than grain boundary. The formation of sub-grain structures inside the grain results in an exponential decrease in the mean free path of dislocations. Therefore, the back stress of the material where the twinning occurs is significantly influenced by twin boundaries rather than grain boundaries. As a result, higher back stress of ~ 130 MPa is obtained at 77 K as compared with ~ 4 MPa at 293 K due to the difference in twin volume fraction and mean twin spacing. By considering twin volume fraction, dislocation density and back stress, the predicted stress–strain of modeling results in Fig. 7 show a good agreement with experimental results.

Fig. 7
figure 7

Tensile stress–strain curves with experimental data and FEM simulations of 1 element at a 77 K and b 293 K

Full size image

4.2 Model Validation of 3D Tensile Specimen

Tensile testing simulations are compared with the experimental test results. The geometry and the loading condition are kept similar to the experimental condition. The input modeling parameter values are the same as the values in Tables 1 and 2. The specimen is discretized using a fully integrated 8-node brick element (C3D8) with a mesh size of 0.2 mm in the gauge length region.

The stress–strain results obtained from the 3D tensile simulation (navy-line) and experiments (red-dot) in Fig. 8. The FEM simulation results show a relatively lower strength behavior than the experimental results. In particular, the differences in strength between experiment and modeling is more noticeable at 77 K than that at 293 K. From these results, it can be concluded that twinning has a significant influence on the plastic deformation behavior. Especially, it might be expected that the actual specimen could contain slightly higher dislocation density than that of simulation results as shown in Fig. 8.

Fig. 8
figure 8

Tensile stress–strain curves with experimental data and FEM simulations of multi-element at a 77 K and b 293 K

Full size image

In Fig. 9, the twinning mechanism is highly activated with plastic deformation from the center of the gauge region at 77 K. Even though the evolution of twins also occurred at 293 K, the formation of twinning is hardly observed in tensile tested specimen at 293 K. This result shows good agreement with the experimental data in Fig. 3

Fig. 9
figure 9

Distributions of twin volume fraction in about 50% elongated 5 mm tensile test specimens at a 77 K and b 293 K

Full size image

5 Conclusions

In summary, the plastic deformation behavior of the equiatomic CoCrFeMnNi HEA at different temperatures was analyzed using the constitutive model based on the twin volume fraction and dislocation density. This developed model was validated by experimental data obtained for the CoCrFeMnNi HEA alloy. In particular, twinning behavior was determined by experimentally obtained twin thickness and twin volume fraction. The critical twinning stress was used to indicate the specific twinning initiation point. The dislocation density-based phenomenological constitutive model was used to investigate dislocation behavior for different temperatures. The result demonstrates that the twin volume fraction influences the plastic deformation behavior directly by forming twinning partial dislocation and dynamic Hall–Petch effect. The model makes an accurate prediction of the plastic deformation behavior and microstructure evolution of CoCrFeMnNi HEA, which is considered to be a combination of twinning kinetics and isotropic kinematic dislocation hardening with the appropriate modeling parameter values. For further study, a dynamic model needs to be constructed for the CoCrFeMnNi HEA, considering both twinning and slip that are highly affected by the thermal effect in the high-temperature region.