First-Principles Studies on Twinnability of Magnesium Alloys: Effects of Yttrium and Lithium on $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ Compression Twinning Deformation Processes

Abstract

We investigate the energetics involved in the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation processes in magnesium via first-principles studies. Through identification of structural changes associated with each deformation process, we study the energetics of each deformation process and the local instability in the twin boundary region. We observe that the energy barrier in the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation pathway is higher than that in the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation pathway, even though the $\left( {10\bar{1}1} \right)$ compression twin boundary is more stable than the $\left( {10\bar{1}2} \right)$ tension twin boundary. We extend our study to examine the effects of Y and Li as alloying elements on each twinning deformation process. Our calculations predict that the addition of Y causes a reduction in the probability of fracture by an order of magnitude when the twinning deformation occurs and weakening of the resistivity to twinning deformation. However, the effect of Li addition on the twinning deformations is weaker than that of Y addition.

1 Introduction

Magnesium and its alloys are among the lightest metallic materials and are about only 30% heavier than most of the commonly used plastics [1, 2]. Owing to their high fatigue resistance, good recyclability, low density, and high stretch-to-weight ratio, Mg and its alloys are believed to be potential engineering materials with applicability in the aircraft and automobile industries [1, 3, 4]. However, the use of pure Mg is limited owing to its low ductility at room temperature, and improvement of its ductility at room temperature is considered to be one of the most important problems in industries that require engineering materials [3, 5, 6].

From a crystallographic viewpoint, the poor ductility of pure Mg at room temperature is due to the fact that the hexagonal close-packed (hcp) crystal structure of Mg is more limited in terms of the variety of independent deformation modes that can be activated at room temperature than are the cubic crystal structures of other metals. According to the von Mises criterion for general grain deformation compatibility, at least five independent deformation modes are necessary for the occurrence of arbitrary and homogeneous deformations in a given polycrystalline material [7,8,9]. In pure Mg, only three independent deformation modes can be activated at room temperature: two originate from the $\langle \varvec{a}\rangle$ basal slip mode and the remaining one originates from the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning mode. Many experimental studies have revealed these deformation modes through a texture analysis of wrought Mg [10,11,12]. Other possible deformation modes in the hcp crystal structure, such as the $\langle \varvec{c} + \varvec{a}\rangle$ pyramidal slip modes and the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning mode, cannot be activated easily because they have very high critical resolved shear stress (CRSS) at room temperature [10, 11, 13]. In particular, the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning mode can be observed only when a material is in a highly strained state, and the material fractures easily owing to the strain energy piled up at the $\left( {10\bar{1}1} \right)$ compression twin boundaries [12, 14]. Therefore, the activation of such deformation modes at room temperature and control of the material texture are some of the important tasks for the design of a Mg-based alloy with high ductility at room temperature. The effects of various alloying elements on the texture of Mg have been extensively studied through experiments [3, 10, 12, 15,16,17,18,19,20,21,22,23,24,25]. The ultimate goal of these experiments was to reveal the mechanism by which these alloying elements enhance the ductility of Mg.

Mg alloys with added non-rare-earth elements, including the commonly available AZ31 alloys, show improved ductility owing to activation of the $\langle \varvec{c} + \varvec{a}\rangle$ pyramidal slip modes. In particular, the effects of Li—which is lighter than Mg and highly soluble in it—on the texture and ductility of Mg have been extensively studied both experimentally and theoretically. It is well known that in Mg–Li alloys, with a decrease in the $c/a$ ratio, the energy barrier associated with the formation of the non-basal planar fault decreases, and this causes activation of the $\langle \varvec{c} + \varvec{a}\rangle$ pyramidal slip mode [10, 15,16,17,18]. Other series of Mg-based alloys, such as WE43 alloys, are those with added rare-earth elements [3]. Experiments have shown that the addition of rare-earth elements such as Y, Ce, and Nd to the Mg alloys improves both ductility and strength [10, 12, 20,21,22,23,24]. Recent studies have shown that both $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries, as well as $\langle \varvec{c} + \varvec{a}\rangle$ pyramidal slips, are frequently observed in deformed Mg–Y alloy [12, 22, 23]. On the basis of these results, these studies tried to explain why the ductility of Mg–Y improves at room temperature, as follows. Formation of the $\left( {10\bar{1}1} \right)$ compression twin boundary, which is rarely activated in pure Mg, forces the texture to randomize, and this improves the ductility of the Mg–Y alloy at room temperature. The actual mechanism of ductility improvement by the addition of rare-earth elements, however, is still in debate.

Although much evidence is available for the activation of both slip modes and twinning modes causing the texture changes of Mg alloys, experimental study of the energy profiles accompanying a deformation process involving the slip and twinning modes remains a challenging task. This is due to the small amount of energy changes occurring with the formation of stacking faults and twin boundaries, which are the coherent planar defects closely related to slip and twinning, respectively [26, 27]. Nowadays, advancements in computer technology have enabled the use of first-principles calculations based on the density-functional theory to investigate the interfacial energy of such coherent planar defects within systems of reasonable sizes. In fact, many first-principles studies of Mg have focused on the calculation of generalized stacking-fault energy (GSFE) curves of Mg alloys in order to analyze the activation of slip modes and the effects of alloying elements on it [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Furthermore, until recently, the stability of twin boundaries, twinning dislocation structures, and the segregation behavior of alloying elements at the twin boundaries have been studied theoretically [27, 43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. However, first-principles studies of the twinning deformation process and the effects of alloying elements on the process have rarely been conducted owing to the complicated atomic movements involved in these deformation processes. In the present study, we investigated the energy profiles accompanying two major twinning deformation processes, known as the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation process and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation process, via first-principles calculations. On the basis of identification of the deformation pathways and associated structural changes, we examined twinnability in a more quantitative way. That is, we estimated the probability of a structure becoming a twinned structure as well as the probability of occurrence of fracture. We further investigated the effects of addition of rare-earth element Y on the two twinning deformation processes and compared it with the effects of addition of Li—which is a non-rare-earth alloying element—on the two twinning deformation processes.

2 Methods

2.1 Prototype Models for $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ Deformation Twinning of Mg

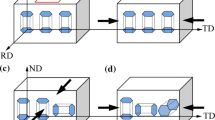
In this study, we focus on $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning, which are the two major twinning processes in the plastic deformation of Mg-based alloys. Wang et al. [49] proposed a simple procedure for modeling twin boundary structures of Mg: Starting with the perfect hcp structure, a twin boundary structure can be constructed by removing the atoms on one side of the interfacial plane and subsequently performing a mirror reflection operation on the remaining structure with respect to the interfacial plane. Our task is to understand the energy profiles that accompany the twinning deformation processes, as well as the structures and stabilities of the twin boundaries themselves. Therefore, we need to know detailed atomic movements and the energy changes that lead to the conversion from a perfect hcp structure to a twinned structure. Classically, deformation twinning is referred to as the process in which a region of a crystal undergoes a homogeneous shear deformation that transforms the lattice points into the original crystal structure with a new orientation. In a crystal with a many-atom basis, however, the situation is rather complicated because of the displacement caused by the shuffling motion of the basis atoms in the transformation process. Wang et al. [47, 51] conducted topological studies of the dichromatic patterns of the twin boundaries in hcp crystal and proposed the minimal Burgers vectors and atomic shuffling movements involved in the twin dislocations of two crystallographic layer units. We adopted the atomic displacements originating from the twin dislocations, and on the basis of these displacements, we designed atomistic models of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation processes. Figure 1 shows the initial and final structures of the two twinning deformation processes that occur when 20 layers of perfect hcp crystal are deformed by shearing deformation. The structure of the supercell used in the simulation is composed of a total of 160 atoms constituting 40 atomic layers, where each layer consists of 4 atoms with $\left( {10\bar{1}2} \right)$ or $\left( {10\bar{1}1} \right)$ crystallographic planes. All simulations were performed under the periodic boundary condition.

Fig. 1

Initial (perfect hcp) and final (20-layer twinned) structures for a $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and b $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformations of Mg. The vivid-colored atoms are those contained in the supercell, whose boundary is indicated by black solid lines, and the pale-colored atoms are their periodic images. The blue dotted lines represent the c-axis of primitive hcp crystal. (Color figure online)

Figure 1a shows the initial and final structures for the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation. When $2n$ $\left( {10\bar{1}2} \right)$ atomic layers are twinned, the total shearing displacement accompanying the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation is given as

$$\varvec{d}_{{\left( {10\bar{1}2} \right)}}^{\text{S}} = n\varvec{b}_{{\left( {10\bar{1}2} \right)}}^{\text{tw}}$$

(1)

where

$$\varvec{b}_{{\left( {10\bar{1}2} \right)}}^{\text{tw}} = \frac{{3 - \kappa^{2} }}{{3 + \kappa^{2} }}\left[ {\bar{1}011} \right]$$

(2)

is the Burgers vector for the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning dislocation ($\kappa$ is the $c/a$ ratio of Mg) [47]. Further, when $2n$ $\left( {10\bar{1}1} \right)$ atomic layers are twinned (see Fig. 1b), the total shearing displacement accompanying the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation can be written as

$$\varvec{d}_{{\left( {10\bar{1}1} \right)}}^{\text{S}} = \left\{ {\begin{array}{*{20}l} {\frac{n}{2}\left( {\varvec{b}_{{\left( {10\bar{1}1} \right)}}^{{{\text{tw}}, + }} + \varvec{b}_{{\left( {10\bar{1}1} \right)}}^{{{\text{tw}}, - }} } \right),\quad \text{if }n \text{ is even number}} \\ {\frac{{\left( {n + 1} \right)}}{2}\varvec{b}_{{\left( {10\bar{1}1} \right)}}^{{{\text{tw}}, + }} + \frac{{\left( {n - 1} \right)}}{2}\varvec{b}_{{\left( {10\bar{1}1} \right)}}^{{{\text{tw}}, - }} ,\quad \text{if }n \text{ is odd number}} \\ \end{array} } \right.$$

(3)

where

$$\varvec{b}_{{\left( {10\bar{1}1} \right)}}^{{{\text{tw}}, \pm }} = \frac{1}{2}\frac{{9 - 4\kappa^{2} }}{{3 + \kappa^{2} }}\left[ {\bar{1}012} \right] \pm \frac{1}{6}\left[ {1\bar{2}10} \right]$$

(4)

is the Burgers vector for the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning dislocation [51]. In Eq. (4), the first and second terms represent the edge and screw components, respectively, of the Burgers vector. In the case of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning dislocation, we can express the Burgers vector corresponding to the experimentally observed shearing displacement by using only the edge component that is along the $\left[ {\bar{1}011} \right]$ direction. However, in the case of the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning dislocation, if the Burgers vector is expressed using only the edge component that is along the $\left[ {\bar{1}012} \right]$ direction, then the shearing displacement expressed by the Burgers vector is too large compared to the experimentally observed shearing displacement, and the screw component provided in Eq. (4) is required to express the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning dislocation by using the Burgers vector [51]. In a real system, the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is described by the superposition of the screw components in two opposite directions (positive- and negative-$\left[ {1\bar{2}10} \right]$ directions), and therefore, the shearing displacement is observed only in the $\left[ {\bar{1}012} \right]$ direction [61,62,63]. The Burgers vector for the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning dislocation, which contains both the edge and the screw components, is known as the synchroshear model, and it is considered as a more realistic model than the one with only the edge component. For Mg ($\kappa = 1.623$), the direction of shearing displacement of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation is along the $\left[ {\bar{1}011} \right]$ direction, whereas that of the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is along the $\left[ {10\bar{1}\bar{2}} \right]$ direction (positive and negative x-directions in Fig. 1a and b, respectively). The initial structures of the supercell with the $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries with a thickness of $2n$ layers ($n = 1\sim10$) were designed using Eqs. (1) and (3) and subsequently performing full geometry optimization for the structure corresponding to each $n$, and finally, when $n = 10$, calculation of the energy profiles along the deformation pathways were performed for both the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformations. For each twinning deformation pathway, initial structures of nine intermediate structures were designed by linear interpolation between the perfect hcp structure and the twin boundary structure, and for each of these intermediate structures, constrained geometry optimization was performed along the y-direction only. We extended our study to understand the effects of Y/Li on the stabilities of twin boundaries and on the changes in the energy barriers in the twinning deformation processes. Figure 2 shows the Voronoi volume of each site atom as a function of the y-coordinates for the case of 20-layered $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries of pure Mg. The Voronoi volume of a given site atom is defined as the volume of a polyhedron whose sides are the planes composed of perpendicular bisectors between a particle and its neighbors; this volume provides a quantitative measure of the effective volume of each atom in a reasonable way [64]. There are two different types of sites at the twin boundary layers for the $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries: one has a larger volume and the other has a smaller volume than the Voronoi volume of a single atom in hcp Mg. These sites have already been demonstrated by Nie et al. [27]. through transmission electron microscopy (TEM) analysis, and they are termed extended and contracted sites, respectively. Recently, J. Zhang et al. studied the segregation energies of various alloying elements at the $\left( {10\bar{1}2} \right)$ tension twin boundary by the first-principles method [43]. Their results showed that Y, which is larger than Mg, prefers the extended site for substitution, whereas Li, which is smaller than Mg, prefers the contracted site for substitution.

Fig. 2

Atomic Voronoi volume profiles for a $\left( {10\bar{1}2} \right)$ tension twin boundary and b $\left( {10\bar{1}1} \right)$ compression twin boundary of pure Mg as a function of y-coordinates of atom position in a given layer measured relative to the first twin boundary layer (denoted as TB1 in Fig. 1). The dotted magenta lines represent the atomic Voronoi volume of Mg with a perfect hcp crystal structure

2.2 Calculation Details

All the calculations in this study were performed using the first-principles density-functional theory implemented in the SIESTA code [73]. The generalized-gradient approximation published by Perdew, Burke, and Ernzerhof was used as the exchange–correlation functional [74]. Numerical atomic orbitals (NAOs) [75] were used for the basis functions of the valence electrons, and the interactions between the valence electrons and the core electrons were treated using norm-conserving scalar-relativistic pseudopotentials, including nonlinear partial-core corrections [76]. For accurate atomistic description of the twin boundary structures, two s orbitals plus one p-polarization orbital and one d-polarization orbital, two s orbitals plus one p-polarization orbital, and two s and two d orbitals plus one p-polarization orbital were employed as the minimal NAO basis sets for the Mg, Li, and Y atoms, respectively. We optimized these basis functions to fit the bulk properties of each hcp-Mg, hcp-Y, and bcc-Li. Test results of our basis set show good agreement with the results reported in other literatures, as shown in Table 1. In all the electronic structure calculations, the real-space mesh grid was determined using the maximum kinetic energy of the plane wave, which was 200 Ry. For Brillouin-zone sampling, uniform Monkhorst–Pack meshes of $4 \times 1 \times 20$ and $6 \times 1 \times 20$ were chosen for the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning systems, respectively. Electronic iterations were continued until the element from among those in the density matrix that showed the largest difference from the value in the previous step became smaller than $10^{ - 5}$. Geometry optimization was performed until the maximum atomic force became smaller than 0.01 eV/Å.

Table 1 Crystal structures and bulk properties of Mg, Y, and Li

3 Results and Discussion

3.1 Stability of $\left( {10\bar{1}2} \right)$ Tension and $\left( {10\bar{1}1} \right)$ Compression Twin Boundaries

Figure 3 shows the energies of the $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries for pure Mg, Mg–Y, and Mg–Li as a function of the thickness of the twinned region. For each composition $i$ ($i =$ Mg, Mg–Y, Mg–Li), the twin boundary energy $\Delta E_{\text{TB}} \left( i \right)$ is obtained from the following relation:

Fig. 3

Twin boundary energies as a function of thickness of twinned region. The filled points are the energies of the $\left( {10\bar{1}2} \right)$ tension twin boundaries, and the hollow points are those of the $\left( {10\bar{1}1} \right)$ compression twin boundaries. Black, red, and green colors represent the twin boundary energies of the pure Mg, Mg–Y, and Mg–Li compositions, respectively. The dotted magenta lines are the reference density-functional theory data for the twin boundaries of pure Mg, which were obtained by Wang et al. [49]. (Color figure online)

$$\Delta E_{\text{TB}} \left( i \right) = \frac{{E_{\text{TB}}^{\text{tot}} \left( i \right) - E_{hcp}^{\text{tot}} \left( i \right)}}{2A}, i = {\text{Mg}}, {\text{Mg}} - {\text{Y}}, {\text{and Mg}} - {\text{Li }}$$

(5)

where $E_{\text{TB}}^{\text{tot}} \left( i \right)$ and $E_{hcp}^{\text{tot}} \left( i \right)$ are the total energy of a supercell with twin boundary structures of composition $i$ and that of a supercell with perfect hcp structures of composition $i$, respectively, and $A$ is the area of the xz-plane of the supercell. The multiplication factor of 2 is adopted given the fact that there are two twin boundaries associated with area $A$ in the supercell when twinning occurs. The energy of the $\left( {10\bar{1}2} \right)$ tension twin boundary shows smoothly decreasing behavior and converges to 118 mJ/m² [11, 47, 49]. Twin boundaries for thicknesses of 2 and 4 layers show exceptional stability close to zero. This occurs because the geometry optimization causes transformation of the supercell system with the twin boundary structure to that with the original hcp structure. Therefore, the twin boundary structures with thicknesses of 2 and 4 layers do not exist as thermodynamically stable structures. The overall behavior of the energy of the $\left( {10\bar{1}2} \right)$ tension twin boundary as a function of the thickness of the twinned region is in good agreement with the results of J. Wang et al. [47]. The behavior of the twin boundary deformation energy reveals that the dependence of the $\left( {10\bar{1}1} \right)$ compression twin boundary on the thickness of the twinned region exhibits different behavior from that of the $\left( {10\bar{1}2} \right)$ tension twin boundary on the thickness. The energy for the case of the $\left( {10\bar{1}1} \right)$ twin boundary rapidly converges to the limiting value, i.e., 86 mJ/m², after a thickness of more than 6 layers, whereas that for the $\left( {10\bar{1}2} \right)$ twin boundary shows slow convergence to a limiting value [11, 49]. Therefore, the instability energy associated with the formation of the twin boundaries is considered as a sum of the interfacial interaction energy at the twin boundary layer and the instability energy accumulated in the twinned region between the two twin boundaries. Furthermore, in the case of the $\left( {10\bar{1}1} \right)$ twin boundary, the energy accumulated in the twinned region relaxes rapidly as the thickness of the twinned region increases, whereas in the case of the $\left( {10\bar{1}2} \right)$ twin boundary, the relaxation occurs slowly. One interesting point to note pertains to the energy of the $\left( {10\bar{1}1} \right)$ compression twin boundary at the thickness of 2 layers. Because of the repulsive character of the $\left( {10\bar{1}1} \right)$ compression twin boundary, the energy of the $\left( {10\bar{1}1} \right)$ compression twin boundary with a thickness of 2 layers is expected to be higher than that with a thickness of 4 layers. However, the opposite result is observed in Fig. 3. The Voronoi volume profile in Fig. 2b indicates that the two layers adjacent to the twin boundary layer have noticeable deviation from the volume of perfect hcp Mg. This means that the local strain energy is accumulated in these layers, as well as at the twin boundary layer. For the $\left( {10\bar{1}1} \right)$ compression boundary with thickness of 4 layers or higher, the number of nearest neighboring layers of each twin boundary is two and a total of four nearest neighboring layers of the twin boundary layers exist in the supercell. When the thickness is 2 layers, on the other hand, the two twin boundary layers share an adjacent layer and only three nearest neighboring layers exist. This fact explains the exceptional behavior of the energy of the $\left( {10\bar{1}1} \right)$ compression twin boundary with a thickness of 2 layers.

The effects of alloying elements Y and Li are also shown in Fig. 3. In the present study, one Y/Li atom is substituted for an Mg atom at the twin boundary (0.6 at.% for both alloying elements for the supercell with 160 atoms). The concentration of Y in the supercell is 2.24 wt%, and it is within the maximum solubility limit of Y in Mg [77]. Although both Y and Li stabilize the $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries, the stabilization effect of Y is stronger than that of Li. J. Zhang et al. studied the segregation behavior of various alloying elements at the $\left( {10\bar{1}2} \right)$ tension twin boundary of Mg [43]. They showed that the segregation energy of Y is larger than that of Li, and their result is consistent with our energy calculation result. For both the twin boundaries, however, the qualitative behavior of the twin boundary energy curve remains nearly the same as that of the energy curves of pure Mg.

3.2 Energetics Accompanying Twinning Deformation Processes

Figure 3 reveals that the $\left( {10\bar{1}1} \right)$ compression twin boundary is more stable than the $\left( {10\bar{1}2} \right)$ tension twin boundary for all the compositions, i.e., pure Mg, Mg–Y, and Mg–Li. However, experimental observations reveal contradictory results: the texture of the $\left( {10\bar{1}2} \right)$ tension twin boundary is strongly observed in pure Mg at low temperature. In this section, therefore, we investigated the deformation pathways of $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning for a twinned region thickness of 20 layers and identified the intermediate structures and the energy profile associated with each corresponding transformation. We also extended our investigation to the effects of Y/Li on the energetics of each twinning deformation. Figure 4 shows the energy profiles of the pure Mg, Mg–Y, and Mg–Li compositions along the twinning deformation pathways. To quantify the advancement of twinning deformation, we employed the magnitude of shearing displacement, $\left| {{\varvec{d}}^{\text{S}} } \right|$, defined in Eqs. (1) and (3), as the extent of the advancement. Although the $\left( {10\bar{1}1} \right)$ compression twin boundary is more stable than the $\left( {10\bar{1}2} \right)$ tension twin boundary, it can be seen from Fig. 4 that the energy barrier of the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is twice that of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation (255 and 518 mJ/m² for the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformations, respectively.). The difference in the energy barrier between the two deformation processes implies that the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is more difficult to activate than is the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation in the case of pure Mg at room temperature, and the texture of the $\left( {10\bar{1}1} \right)$ compression twins can be observed only in a highly strained state. The addition of Y reduces the energy barriers of both the twinning deformations: according to our calculations, for the Mg–Y composition, the energy barrier of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation is 232 mJ/m² ($\sim$ 8% reduction) and that of the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is 491 mJ/m² ($\sim$ 5% reduction). Recently, Sandlöbes et al. [12] showed via cold-rolling experiments that the addition of 3 wt% Y to Mg improves the low-temperature ductility. On the basis of a texture analysis of cold-rolled Mg–Y alloys, they suggested that formation of compression twin boundaries—which can be easily observed in a wide range of samples even in low strain states—is a key mechanism of ductility improvement. Our result in Fig. 4 well reflects their experimental results. However, the addition of Li atoms does not significantly reduce the barriers of both the twinning deformations.

Fig. 4

Potential energy profiles of $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension (solid lines) and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning (dashed lines) deformations as functions of magnitude of shearing displacement, $\left| {\varvec{d}^{\text{S}} } \right|$, which is defined in Eqs. ( 1 ) and ( 3 ). The black, red, and green lines represent the pure Mg, Mg–Y, and Mg–Li compositions, respectively

The issue with twinning deformation in Mg-based alloys, especially with the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation, is that large amounts of strain energy are required to activate the twinning deformations and that the strain energy piled up around $\left( {10\bar{1}1} \right)$ twin boundaries during the deformation causes the system to break easily. Therefore, estimation of the probability of fracture during the twinning deformation process and how to lower it are important problems that need to be resolved. By calculating the bonding energy between two adjacent layers, we can estimate the cleavage energy, and this cleavage energy may be regarded as a reasonable estimate of the energy required for fracture to occur at that layer. The cleavage energy between two adjacent layers, denoted as $\Delta E_{\text{c}}$, can be obtained from the following relationship:

$$\Delta E_{\text{c}} = \frac{{E_{\text{tot}}^{\text{slab}} - E_{\text{tot}}^{\text{bulk}} }}{2A}$$

(6)

where $E_{\text{tot}}^{\text{slab}}$ is the total energy of the slab structure in which the two target layers are infinitely separated and $E_{\text{tot}}^{\text{bulk}}$ is the total energy of the supercell in which the two neighboring layers are in a bonded state. The cleavage energy between given two adjacent layers refers to the energy required to separate the solid in the bulk state into two parts. In obtaining the net energy required to break the bonding between the two adjacent layers, we did not allow relaxation of the slab structures. Table 2 lists the cleavage energies on the $\left( {10\bar{1}2} \right)$ and $\left( {10\bar{1}1} \right)$ planes for each case of the hcp structures of the pure Mg, Mg–Y, and Mg–Li compositions. In the case of pure Mg, the cleavage energies are 899.5 mJ/m² and 796.4 mJ/m² for the $\left( {10\bar{1}2} \right)$ and $\left( {10\bar{1}1} \right)$ planes, respectively. The smaller cleavage energy of the $\left( {10\bar{1}1} \right)$ plane means that this plane can fracture more easily than the $\left( {10\bar{1}2} \right)$ plane during twinning, even though the final $\left( {10\bar{1}1} \right)$ compression twin boundary is more stable than the $\left( {10\bar{1}2} \right)$ tension twin boundary. The cleavage energies of pure Mg obtained in this study are in good agreement with the unrelaxed surface energies obtained by Tang et al. [78]. Substitution of Y or Li has opposite effects on the cleavage energies of the hcp structure: For both types of planes, substitution of Y causes an increase in the magnitude of the cleavage energy whereas substitution of Li decreases it. Effects of Y/Li on the cleavage energy can be explained by the use of the relative difference in the number of valence electrons of Mg, Y, and Li. Y, which has more valence electrons than Mg, has a greater strengthening effect on the metallic bond with the adjacent Mg atoms than does Mg, whereas Li, which has fewer valence electrons than Mg, has a smaller strengthening effect on the metallic bond with the adjacent Mg atoms than does Mg, and this property is well reflected in the cleavage energy, as can be seen in Table 2.

Table 2 Cleavage energies of $\left( {10\bar{1}2} \right)$ and $\left( {10\bar{1}1} \right)$ planes in hcp Mg, Mg–Y, Mg–Li alloys

We further investigated the behavior of the interfacial bonding energy along the tension and compression twinning deformation pathways. For this purpose, we introduced $\Delta \Delta E_{\text{c}}^{ + }$ ($\Delta \Delta E_{\text{c}}^{ - }$), which is defined as the cleavage energy between a twin boundary layer (see TB1 in Fig. 1) and its upper (lower) adjacent layer, measured from that between corresponding layers in hcp structure, for each individual intermediate structure in a given transition pathway. Then, a negative or positive value of $\Delta \Delta E_{\text{c}}^{ + }$ ($\Delta \Delta E_{\text{c}}^{ - }$) of a given intermediate structure indicates that the bonding between the twin boundary layer and its upper (lower) adjacent layer is weaker or stronger, respectively, than the bonding between two adjacent layers in an hcp structure. Figure 5 shows the $\Delta \Delta E_{\text{c}}^{ - }$ and $\Delta \Delta E_{\text{c}}^{ + }$ values for the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformations for the pure Mg, Mg–Y, and Mg–Li compositions. As illustrated in Fig. 1, the atomic motions on each side of the layer that forms the twin boundary are different, because the crystal orientation of only one side of the two sides changes. As shown in Fig. 1a, b, owing to the change in crystal orientation, only the upper adjacent layer from TB1 shows a large displacement to form a twin structure. The different behaviors of $\Delta \Delta E_{\text{c}}^{ - }$ and $\Delta \Delta E_{\text{c}}^{ + }$ shown in Fig. 5a, b clearly reflect the asymmetric behavior of the atomic movements. Even though such asymmetric behavior is preserved, the cleavage energy decreases gradually during the processes of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformations in pure Mg. When Y or Li is added, the change in cleavage energy between TB1 and its lower adjacent layer shows similar behavior to that in the case of pure Mg, the only difference being that there is some change in its magnitude. The patterns of $\Delta \Delta E_{\text{c}}^{ - }$ for the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation shown in Fig. 5a indicate that the extent of weakening of interfacial bonding in Mg–Y and Mg–Li alloys is smaller than that in pure Mg. Similar behaviors are observed for the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation of the Mg–Y alloy. However, the bonding between the layers weakens in the case of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation of the Mg–Li alloy. The effect of Y or Li on the two twinning deformations is more clearly reflected in the changes in $\Delta \Delta E_{\text{c}}^{ + }$, as shown in Fig. 5b. In the case of Li addition, the situation is similar to the results shown in Fig. 5a; that is, the extent of weakening of the bonding energy between the two layers is just smaller than that in the case of pure Mg. However, it is interesting to note that when Y is added, the change in the cleavage energy becomes positive as the twinning deformation proceeds. This means that the addition of Y to Mg reduces the resistivity to the shearing deformation as the twinning deformation proceeds. Furthermore, since $\Delta \Delta E_{\text{c}}^{ + }$ is a larger positive value in the case of the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation process than in the case of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation process, the resistivity should be larger in the former case.

Fig. 5

Changes in a ${\Delta \Delta }E_{c}^{-}$ and b ${\Delta \Delta }E_{c}^{ + }$ as functions of shearing displacement for $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension (solid lines) and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression (dashed lines) twinning deformations. The black, red, and green curves represent profiles of ${\Delta \Delta }E_{c}^{ - }$ (${\Delta \Delta }E_{c}^{ + }$) for Mg, Mg–Y, and Mg–Li, respectively. The interfacial plane where cleavage occurs for each case is indicated by the dotted blue lines in the inset of each figure. (Color figure online)

Finally, another point to be mentioned pertains to the probability of occurrence of fracture during the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation processes at room temperature. We obtained the energy barrier of each twinning deformation process and the cleavage energies for the structure corresponding to the maximum point of the energy barrier. Using these data, we can estimate the ratio between the probability of fracture of the structure, $P_{\text{f}}$, to the probability of twinning, $P_{\text{t}}$, at temperature $T$ as follows:

$$\frac{{P_{\text{f}} }}{{P_{\text{t}} }} = e^{{ - \left( {\Delta \varepsilon_{\text{c}} - \Delta \varepsilon_{\text{b}} } \right)/kT}}$$

(7)

where $\Delta \varepsilon_{\text{b}}$ and $\Delta \varepsilon_{\text{c}}$ are the energy barrier of twinning deformation and the cleavage energy of the structure corresponding to the top of the barrier, respectively, normalized by the number of interfacial atoms in the supercell, i.e., 8 in our case. The ratio of these two probabilities refers to the conditional probability that the material will fracture during twinning deformation. Table 3 lists the energy barriers of the two twinning deformations, the cleavage energies in the barrier structures, and the values of $P_{\text{f}} /P_{\text{t}}$ at 300 K for the Mg, Mg–Y, and Mg–Li compositions. In the case of the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation, the conditional probabilities are extremely small regardless of the composition, owing to the fact that the cleavage energies are much larger than the energy barriers of the twinning deformation process. On the other hand, the conditional probabilities of fracture for the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation have comparably larger values on the order of 10$^{ - 3}$, since the difference between the energy barrier of twinning and the cleavage energy is significantly reduced. In view of the alloy compositions, it can be seen that the addition of Y causes the conditional probability of fracture during the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation process to reduce to one-tenth the probability for pure Mg, whereas this probability does not change in the case of addition of Li. The reduction in the probability of fracture is caused by the increase in cleavage energy, as well as by the reduction in the energy barrier of the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation. Our theoretical interpretation of the role of Y is consistent with a previous experimental result that Mg alloy with an added rare-earth element such as Y shows higher strength as well as higher ductility at room temperature than pure Mg [12].

Table 3 Energy barriers, cleavage energies at the barrier structure, and ratio of fracture probability to probability of occurrence of twinning ($P_{\text{f}} / P_{\text{t}}$) at 300 K for $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension and $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformations for Mg, Mg–Y, and Mg–Li compositions

4 Conclusion

In summary, we performed first-principles studies of the stabilities of the $\left( {10\bar{1}2} \right)$ tension and $\left( {10\bar{1}1} \right)$ compression twin boundaries of a Mg system with and without segregation of Y/Li solutes and observed the energetics accompanying each twinning deformation process. We demonstrated that the stabilities of the two twin boundaries as a function of the thickness of the twinned region show characteristic differences: the change in the energy of the $\left( {10\bar{1}2} \right)$ tension twin boundary with an increase in the thickness of the twinned region shows slower convergence than that of the $\left( {10\bar{1}1} \right)$ compression twin boundary with the increase in thickness. This behavior seems to be attributable to the fact that the atomic structural relaxation in the twinned region is more limited in the $\left( {10\bar{1}2} \right)$ tension twin than in the $\left( {10\bar{1}1} \right)$ compression twin. The substitution of Y or Li at the twin boundaries stabilizes both the twin boundary structures, but Y stabilizes both the twin boundaries more effectively than does Li after the segregation. Although the $\left( {10\bar{1}1} \right)$ compression twin boundary itself is more stable than the $\left( {10\bar{1}2} \right)$ tension twin boundary, we observed that the energy barrier associated with the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is much higher than that associated with the $\left( {10\bar{1}2} \right)\left[ {\bar{1}011} \right]$ tension twinning deformation. Furthermore, the energy barrier associated with the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is comparable to the cleavage energy at the $\left( {10\bar{1}1} \right)$ planes in pure Mg. This implies that the probability of fracture during the $\left( {10\bar{1}1} \right)\left[ {\bar{1}012} \right]$ compression twinning deformation is quite high. In the Mg–Y composition, however, the probability of fracture is lowered owing to two reasons: the addition of Y (1) reduces the energy barriers of the twinning deformations and (2) increases the cleavage energy at the corresponding crystallographic planes. Our results supports the experimental results obtained by S. Sandlöbes et al. [12]. The addition of Li does not cause any visible change in the probability of fracture, since the barrier of the twinning deformation and the cleavage energy are reduced simultaneously. We also found that the addition of Y causes strengthening of the bonding between TB1 and its upper adjacent layer as the twinning deformation proceeds. This implies that Y plays the role of reducing the resistivity to twinning deformation. However, we did not observe such behavior for pure Mg and Mg–Li systems.