Introduction

In cities, the considerable population density is exerting tremendous pressure on urban traffic. The subway has the characteristics of high transportation efficiency and is not affected by other means of transportation. Therefore, the subway is widely used in urban transportation, and this has dramatically alleviated the traffic pressure in cities. Currently, subway tunnels are typically constructed using the shield method, but the shield machine disturbs the surrounding environment during the tunneling process(Bouayad et al. 2015; Zhang et al. 2013). However, the urban underground space is limited, and the distribution of various living and transportation pipelines is complex. The additional stress generated by the shield machine during tunneling may cause deformation or even damage to the pipeline, which affects the normal use of existing pipelines(Wang et al. 2011). Therefore, it is very important to clarify the mechanism by which an existing tunnel deforms owing to shield machine excavation. The deformation of existing pipelines caused by shield tunnel construction is a popular research topic(Shirlaw 2019; Zhang and Huang 2012). The theoretical analysis method(Klar and Marshall 2008, 2015), numerical simulation method(Jian et al. 2013; Liu and Liu 2010), and laboratory test method have been used to investigate the shield machine’s disturbance to the surrounding environment during the tunneling process. However, existing studies have generally only considered the case wherein the existing pipeline is orthogonal or parallel to the tunneling axis of the shield machine, or the case wherein the oblique intersection of the existing pipeline and the tunneling axis is ignored. In actual engineering, the situation of the shield machine tunneling obliquely crossing existing pipelines is common, but relevant research is scarce.

Compared with the numerical simulation method and indoor test method, the theoretical analysis method has high efficiency and strong applicability, and can thus provide a more reasonable assessment basis for designers and construction personnel within a very short time(Deng et al. 2022a). Therefore, a reasonable theoretical analytical solution is indispensable in engineering. Based on the research background of a shield tunnel obliquely crossing existing pipelines, the influence of the additional thrust on the cutter head, shield shell friction, additional grouting pressure at the shield tail, and ground loss were considered, and the change of the surrounding displacement field caused by the shield tunneling was deduced based on the Loganathan equation and Mindlin solution. The existing pipeline was simplified as an Euler–Bernoulli beam placed on the Pasternak foundation beam. The deformation equation of the existing pipeline caused by the shield machine excavation was deduced. Then, based on the FoShan-DongGuan intercity railway project, the corresponding FDM model was constructed to analyze the existing pipeline deformation, and the applicability of the equation and FDM model was verified by comparison to field monitoring data. Finally, the influence of the angle between the pipeline and the shield tunnel axis, pipeline stiffness, and distance between the pipeline and the shield tunnel on the deformation of the existing pipeline was analyzed.

Theoretical basis

Assumptions

In the theoretical calculation, many actual construction factors need to be simplified to meet the application scope of the theoretical formula. The most considerable controversy is that the soil is regarded as an elastic body while an elastic–plastic body is in the actual situation. However, in shield tunnel engineering, scholars usually ignore the plastic deformation of the soil in the preliminary design and regard the soil as an elastic body to make a rough prediction. Existing studies have proved that the elastic prediction solution can meet the accuracy of construction prediction(Xue et al. 2018). According to the calculation theory adopted in this article, the following assumptions need to be satisfied (Deng et al. 2022b):

  • The soil is assumed to be isotropic and homogeneous, and the calculation area is linear elastic semi-infinite space without considering the influence of soil drainage and consolidation during construction in this paper. Shield machine tunneling is only a change in spatial position, without considering the time effect.

  • The friction force between the shield shell and the soil is evenly distributed. The excavation surface of the shield machine is the acting surface of additional thrust, and the additional thrust load is circular and uniformly distributed.

  • The influence range of shield tail grouting is the width of the two ring tunnel segments behind the shield tail. Synchronous grouting liquid can quickly spread and fill the construction gap in a short time, so the influence of the gap on the grouting load can be ignored. So, the additional grouting load is usually regarded as evenly distributed along the radial direction of the tunnel segment circumference.

Mindlin solution

Mindlin (1936) proposed an equation for calculating the settlement w1 and w2 of another point (x, y, z) in elastic semi-infinite space; the settlement is caused by the horizontal concentrated force Ph and vertical concentrated force Pv at a certain point (x0, y0, z0).

The equations for calculating w1 caused by the concentrated horizontal force and w2 caused by the concentrated vertical force are expressed as follows:

$${w}_{1}=\frac{{P}_{\mathrm{h}}\left(x-{x}_{0}\right)}{16\pi G\left(1-\mu \right)}\times \left[\frac{z-{z}_{0}}{{{R}_{1}}^{3}}+\frac{\left(3-4\mu \right)\left(z-{z}_{0}\right)}{{{R}_{2}}^{3}}\right.\left.-\frac{6{zz}_{0}\left(z+{z}_{0}\right)}{{{R}_{2}}^{5}}+\frac{4\left(1-\mu \right)\left(1-2\mu \right)}{{R}_{2}\left({R}_{2}+z+{z}_{0}\right)}\right]$$
(1)
$${w}_{2}=\frac{{P}_{\mathrm{v}}}{16\pi G\left(1-\mu \right)}\times \left[\frac{3-4\mu }{{R}_{1}}+\frac{{\left(z-{z}_{0}\right)}^{2}}{{{R}_{1}}^{3}}+\frac{6{zz}_{0}{\left(z+{z}_{0}\right)}^{2}}{{{R}_{2}}^{5}}\right.+\left.\frac{8{\left(1-\mu \right)}^{2}-\left(3-4\mu \right)}{{R}_{2}}+\frac{\left(3-4\mu \right){\left(z+{z}_{0}\right)}^{2}-2{zz}_{0}}{{{R}_{2}}^{3}}\right]$$
(2)

where μ is Poisson’s ratio of the soil; G is the shear modulus of the soil, and G = Et/(2(1 + μ)); Et is the elastic modulus of the soil (MPa); R1 = ((x-x0)2 + (y-y0)2 + (z-z0)2)1/2 and R2 = ((x-x0)2 + (y-y0)2 + (z + z0)2)1/2.

Owing to its simple mechanical model and fewer parameters, the Mindlin equation is widely used to analyze the disturbance caused by shield tunneling to the surrounding environment. In this study, the Mindlin equation was also used to analyze the variation of the surrounding displacement field caused by the additional thrust on the cutter head, friction of the shield shell, and grouting pressure at the shield tail.

Loganathan equation

Loganathan (1998) considered the uneven distribution of ground loss caused by tunnel excavation and proposed a calculation model for the surrounding ground settlement w3 caused by the ground loss. The calculation equation of settlement w3 caused by an uneven distribution of ground loss is expressed as follows:

$${w}_{3}=2\left(1-\mu \right)\left(Rg-{g}^{2}/4\right)\times \frac{\left(z-H\right)}{{\left(x-{x}_{0}\right)}^{2}+{\left(z-H\right)}^{2}}\times exp\left[-\frac{1.38{\left(x-{x}_{0}\right)}^{2}}{{\left(H+R\right)}^{2}}\right]\times \left(1-\frac{\left(x-{x}_{0}\right)}{\sqrt{{\left(y-{y}_{0}\right)}^{2}+{\left(x-{x}_{0}\right)}^{2}+{\left(z-H\right)}^{2}}}\right)$$
(3)

where R is the tunnel excavation radius, (m); g is the soil loss parameter, and the values of g are based on empirical parameters(Lee et al., 1992), (mm); H is the buried depth of the center point of the cutter head (m); (x, y, z) are the coordinates of the calculated point; (x0, y0, H) are the coordinates of the cutter head center point.

Analysis of settlement caused by construction factors

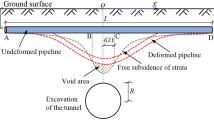
The main factors that cause disturbance to the surrounding soil layer during shield tunneling are the ground loss, additional thrust load on the face of the tunnel, friction load on the shield shell, and the additional grouting pressure load on the shield tail; the influence of other construction factors can be ignored(Liang et al. 2021; Zhang et al. 2015). Figure 1 shows the distribution of the construction factors considered in this study and the spatial position relationship between the existing pipelines and the construction tunnels.

Fig. 1
figure 1

Distribution of construction factors and spatial position relationship

Full size image

It is assumed that the pipeline axis and shield tunneling axis intersect at the cutter head (x = 0 m). According to the spatial position relationship between the shield tunnel and the existing pipeline shown in Fig. 1, the coordinate expression of any point (x, y, z) on the existing pipeline can be determined as follows:

$$\left\{\begin{array}{c}x=D+dsin\beta \\ y=dcos\beta \\ z=h\end{array}\right.$$
(4)

where D is the distance from the intersection of the pipeline axis with tunneling axis to the position of the cutter head (m); d is the distance from the point on the pipeline to the intersection of the tunnel axis and pipeline axis (m); β is the angle between the pipeline axis and the shield tunneling axis (°); h is the buried depth of the pipeline (m); H is the buried depth of the cutter head center point (m).

Calculation of settlement caused by thrust load of the cutter head

The acting position of the thrust load is located on the cutter head of the shield machine, and its calculation diagram is shown in Fig. 2.

Fig. 2
figure 2

Calculation diagram of thrust load of the cutter head

Full size image

In Fig. 2, r is the distance from the micro-element area to the center point of the cutter head; P1 is the thrust load (kPa); θ is the angle between the micro-element body and the y-axis (°); dA is the micro-element area subjected to the load at the cutter head, and dA=r·dr·dθ; the magnitude of the load acting on the micro-element body is F1=r·dr·dθ·P1. By substituting the size and coordinates of the load into Eq. (1) and integrating the entire cutter head range, the calculation equation for the settlement change of the corresponding pipe depth caused by the thrust load of the cutter head can be obtained as follows:

$${w}_{q}=\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{R}{\int }}\frac{{F}_{1}\left(D+sin\beta -{x}_{0}\right)}{16\pi G\left(1-\mu \right)}\times \left[\frac{h-H}{{{R}_{q1}}^{3}}+\frac{\left(3-4\mu \right)\left(h-H\right)}{{{R}_{q2}}^{3}}-\frac{6hH\left(h+H\right)}{{{R}_{q2}}^{5}}+\frac{4\left(1-\mu \right)\left(1-2\mu \right)}{{R}_{q2}\left({R}_{q2}+h+H\right)}\right]drd\theta$$
(5)

where Rq1 = ((D + dsinβ-x0)2 + (dcosβ-y0)2 + (h–H)2)1/2; Rq2 = ((D + dsinβ-x0)2 + (dcosβ-y0)2 + (h + H)2)1/2.

Calculation of settlement induced by shield shell friction load

The acting area of the shield shell friction load is the shield shell of the shield machine. The calculation diagram is shown in Fig. 3.

Fig. 3
figure 3

Calculation diagram of shield shell friction load

Full size image

In Fig. 3,s is the distance from the micro-element area to the cutter head (m); dA is the micro-element area on the shield shell, and dA=R·ds·dθ; the friction per unit area on the shield is Ff=R·ds·dθ·Pf; where Pf is the friction load between the shield shell and the surrounding soil. The load Pfdepends on the pressure of the surrounding stratum on the shield shell and the friction coefficient between the shield shell and the surrounding soil. Alonso et al. (1984) and Potyondy (1961) proposed the following equation for calculating the friction load of the shield shell:

$${P}_{f}={\beta }_{s}\sigma tan\alpha$$
(6)

where βs denotes the softening coefficient; σ is the normal radial stress acting on the shield, and σ=σvsin2φ+σhcos2φ;σv is the vertical earth pressure, and σv=γH-γRsinθ;σh is the horizontal earth pressure, andσh=Kσv;K=1-sinφ, where φ is the soil friction angle; α is the angle of shin friction.

By substituting the size and coordinates of the shield shell friction into Eq. (1) and integrating the entire shield shell, the equation for calculating the settlement change caused by the shield shell friction load at a pipeline location can be obtained as follows:

$${w}_{f}=\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\int }}\frac{{F}_{f}\left(D+sin\beta -{x}_{0}-s\right)}{16\pi G\left(1-\mu \right)}\times \left[\frac{h-H}{{{R}_{f1}}^{3}}+\frac{\left(3-4\mu \right)\left(h-H\right)}{{{R}_{f2}}^{3}}-\frac{6hH\left(h+H\right)}{{{R}_{f2}}^{5}}+\frac{4\left(1-\mu \right)\left(1-2\mu \right)}{{R}_{f2}\left({R}_{f2}+h+H\right)}\right]Rdsd\theta$$
(7)

where Rq1=((D+dsinβ-x0)2+(dcosβ-y0)2+(h–H)2)1/2; Rq2=((D+dsinβ-x0)2+(dcosβ-y0)2+(h+H)2)1/2.

Calculation of settlement induced by grouting pressure load

In existing research, the acting area of the grouting pressure load is generally considered as the width of 1–2 ring segments behind the shield tail. The grouting pressure acts along the normal direction of the segments. The calculation diagram is shown in Fig. 4.

Fig. 4
figure 4

Calculation diagram of grouting pressure load

Full size image

In Fig. 4, a is the distance from the micro-element area to the tail of the shield (m); l is the range of the grouting pressure load (m); P2 is the grouting pressure load (kPa); dA is the area of the micro-element within the range of the grouting pressure load, and dA = R da dθ. The force on the area of the micro-element at this time is F2 = P2 R da dθ; the action direction of F2 is along the normal outer direction of the segment, and can be decomposed into the horizontal force Fh = F2sinθ and vertical force Fv = F2cosθ. By substituting Fh and Fv into Eqs. (1) and (2), respectively, the equation for calculating the settlement change caused by the grouting pressure at the corresponding position of the pipeline depth can be calculated as follows:

$$w_p=\int\limits_0^{2\pi}\int\limits_0^l\left(\frac{F_h\left(D+sin\beta-x_0-L-s\right)}{16\pi G\left(1-\mu\right)}\times\left[\frac{h-H}{R_{p1}^3}+\frac{\left(3-4\mu\right)\left(h-H\right)}{R_{p2}^3}-\frac{6hH\left(h+H\right)}{R_{p2}^5}+\frac{4\left(1-\mu\right)\left(1-2\mu\right)}{R_{p2}\left(R_{p2}+h+H\right)}\right]\frac{F_v}{16\pi G\left(1-\mu\right)}\times\left[\frac{3-4\mu}{R_{p1}}+\frac{\left(h-H\right)^2}{R_{p1}^3}+\frac{6hH\left(h+H\right)^2}{R_{p2}^5}+\frac{8\left(1-\mu\right)^2-\left(3-4\mu\right)}{R_{p2}}+\frac{\left(3-4\mu\right)\left(h+H\right)^2-2hH}{R_{p2}^3}\right]\right)Rdad\theta$$
(8)

where Rp1 = ((D + dsinβ-x0-L-s)2 + (dcosβ-y0)2 + (h–H)2)1/2;

Rp2 = ((D + dsinβ-x0-L-s)2 + (dcosβ-y0)2 + (h + H)2)1/2.

Calculation of settlement induced by ground loss

The Loganathan equation does not consider that part of the ground loss is located at the tail of the shield machine. Therefore, the coordinates in the Loganathan equation must be transformed accordingly. The transformed equation is expressed as follows:

$$\begin{array}{c}{w}_{3}=2\left(1-\mu \right)\left(Rg-{g}^{2}/4\right)\times \frac{\left(h-H\right)}{{\left(D+dsin\beta -L-{x}_{0}\right)}^{2}+{\left(h-H\right)}^{2}}\times \\ exp\left[-\frac{1.38{\left(D+dsin\beta -L-{x}_{0}\right)}^{2}}{{\left(H+R\right)}^{2}}\right]\times \left(1-\frac{\left(D+dsin\beta -L-{x}_{0}\right)}{\sqrt{{\left(dcos\beta -{y}_{0}\right)}^{2}+{\left(D+dsin\beta -L-{x}_{0}\right)}^{2}+{\left(h-H\right)}^{2}}}\right)\end{array}$$
(9)

By superimposing Eqs. (5), (7), (8), and (9), the calculation equation for the settlement change at the corresponding position of the pipeline depth caused by the shield machine tunneling process can be calculated as follows:

$$w={w}_{q}+{w}_{f}+{w}_{p}+{w}_{3}$$
(10)

Calculation of existing pipeline deformation

In the calculation of the disturbance caused by the surrounding disturbance to the existing pipeline, the existing pipeline is typically considered as an Euler Bernoulli beam model placed on a foundation beam(Marshall et al. 2010; Zhang et al. 2019). By establishing the displacement coordination relationship between the existing pipeline and the soil, the equation for calculating the deformation of the existing pipeline caused by the surrounding disturbance can finally be determined. The Pasternak foundation beam model(Pasternak 1954) considers the shear relationship between the pipe and the soil. The calculation model is more in line with the actual situation, and is thus widely used. The basic assumptions of the model are as follows: (a) regardless of the axis of the pipeline deformation, the existing pipeline is considered as a circular beam with a width e and stiffness EI. (b) the pipeline is closely connected to the surrounding soil and the pipeline displacements are equal to the displacements at the pile-soil contacting surface. (c) the shear force caused by the additional load can be transmitted between the springs.

Pasternak foundation beam model

The Pasternak foundation beam model is shown in Fig. 5.

Fig. 5
figure 5

Pasternak foundation beam model

Full size image

According to the model shown in Fig. 5, the Pasternak two-parameter foundation deflection differential equation can be expressed as follows:

$$q\left(z\right)={kw}_{g}\left(z\right)-{G}_{c}\frac{{\partial }^{2}{w}_{g}\left(z\right)}{\partial {y}^{2}}+\frac{EI}{e}\frac{{\partial }^{4}{w}_{g}\left(z\right)}{\partial {y}^{4}}$$
(11)

where wg(z) is the settlement deformation of the existing pipeline; q(z) is the additional load on the existing pipeline, andq(z)=kw;w is the vertical deformation of the soil at the corresponding pipeline position and is calculated using Eq.(10);e and EI are the width and bending stiffness of the existing pipeline, respectively;k is the stiffness of the springs(Vorster et al. 2005), G is the stiffness of the shear layer, and they can be calculated as follows(Tanahashi 2004):

$$k=\frac{0.65{E}_{t}}{e\left(1-{\mu }^{2}\right)}\sqrt[12]{\frac{{E}_{t}{e}^{4}}{EI}}$$
(12)
$${G}_{c}=\frac{{E}_{t}{h}_{t}}{6\left(1+\mu \right)}$$
(13)

where Et and μ are the elastic modulus and Poisson’s ratio of the soil, respectively; ht is the thickness of the shear layer related to the soil characteristics, and ht is typically considered to be 2.5 times equal to the pipe diameter.

Calculation of pipeline deformation

Equation (11) is a high-order differential equation, which is difficult to analyze using conventional calculation methods. Marshall et al. (2010) and Warming and Hyett (1974) proposed the use of the finite difference method to solve high-order differential equations. The pipeline is discretized into N+5 elements in the calculation range B, and the length of each element is denoted as b.

According to the central difference criterion, the difference scheme of the higher-order differential term in Eq. (11) can be expressed as follows:

$$\left\{\begin{array}{c}\frac{{\partial }^{4}{w}_{gi}\left(z\right)}{\partial {y}^{4}}=\frac{6{w}_{gi}\left(z\right)-4\left({w}_{gi+1}\left(z\right)+{w}_{gi-1}\left(z\right)\right)+\left({w}_{gi+2}\left(z\right)+{w}_{gi-2}\left(z\right)\right)}{{b}^{4}}\\ \frac{{\partial }^{2}{w}_{gi}\left(z\right)}{\partial {y}^{2}}=\frac{{w}_{gi+1}\left(z\right)-2{w}_{gi}\left(z\right)+{w}_{gi-1}\left(z\right)}{{b}^{2}}\end{array}\right.$$
(14)

It is assumed that the pipeline outside of the calculation range is not affected by the excavation. Therefore, the displacement of the elements numbered -2, -1, N+1, and N+2 is zero. The corresponding displacement equation can be transformed as follows:

$$\left\{\begin{array}{c}{w}_{-2}=4{w}_{0}-4{w}_{1}+{w}_{2}\\ {w}_{-1}=2{w}_{0}-{w}_{1}\\ {w}_{N+1}=2{w}_{N}-{w}_{N-1}\\ {w}_{N+2}=4{w}_{N}-4{w}_{N-1}+{w}_{N-2}\end{array}\right.$$
(15)

By substituting the boundary condition expressed by Eq. (15) and the reduction Eq. (14) into Eq. (11), the higher-order differential equation corresponding to N + 5 nodes after discretization can be transformed into a continuous equation that can be solved by constructing the corresponding matrix. The loading matrix, displacement matrix, and stiffness matrix of the pipeline element can be expressed as follows:

$$\left[q\left(z\right)\right]=\left\{\left[k\right]-\left[G\right]+\left[K\right]\right\}\left[{w}_{\mathrm{g}}\left(z\right)\right]$$
(16)

where [q(z)]is the additional load matrix acting on the nodes; [k] is the coefficient matrix of the soil foundation bed; [G] is the shear layer stiffness matrix; [K] is the pipe stiffness matrix; [wg(z)] is the deformation matrix of all nodes in the pipeline(Deng et al. 2021).

$$\left[k\right]=k{\left[\begin{array}{cccc}1& & & 0\\ & \ddots & & \\ & & \ddots & \\ 0& & & 1\end{array}\right]}_{n\times n}$$
(17)
$$\left[G\right]=\frac{{G}_{c}}{{e}^{2}}{\left[\begin{array}{cccccc}-2& 2& & & & \\ 1& -2& 1& & & \\ & \ddots & \ddots & \ddots & & \\ & & \ddots & \ddots & \ddots & \\ & & & 1& -2& 1\\ & & & & 2& -2\end{array}\right]}_{n\times n}$$
(18)
$$\left[K\right]=\frac{EI}{{de}^{4}}{\left[\begin{array}{ccccccccc}6& -8& 2& & & & & & \\ -4& 7& -4& 1& & & & & \\ 1& -4& 6& -4& 1& & & & \\ & \ddots & \ddots & \ddots & \ddots & \ddots & & & \\ & & \ddots & \ddots & \ddots & \ddots & \ddots & & \\ & & & & 1& -4& 6& -4& 1\\ & & & & & 1& -4& 7& -4\\ & & & & & & 2& -8& 6\\ & & & & & & & & \end{array}\right]}_{n\times n}$$
(19)

The settlement displacement at the location of the pipeline caused by the shield machine tunneling process can be determined using Eq. (10). The deformation of the existing pipeline caused by the shield tunneling can be obtained by substituting the calculated settlement displacement into Eq. (16).

Comparative analysis of numerical simulation

The Foshan-Dongguan Intercity Railway is a critical construction project in Guangdong Province. The project is located in PanYu District, Guangzhou, which has considerable population density and complicated underground pipeline distribution. The shield tunnel is constructed with a tunnel radius R of 6.55 m, segment thickness of 0.55 m, shield shell length L of 11.0 m, and average buried depth H of 16.0 m. The shield tunneling through the ground is dominated by mixed fill, gravel soil, and argillaceous sandstone. Based on this project, a corresponding FDM was constructed to analyze the disturbance of the shield machine to the environment surrounding the tunneling excavation.

FDM model and boundary conditions

Figure 6 shows the 3D FDM model established for this case study. The model with the dimensions of 100 m × 110 m × 42 m had 794,839 nodes and 580,647 elements, and each soil layer was assumed to be homogeneous and equal in thickness, regardless of the layer variation(Liu et al. 2020). Regarding the boundary conditions of this model, the bottom surface of the model was set to a fixed constraint to limit the horizontal and vertical displacement at the bottom; the top surface of the model was set as a free surface, regardless of the influence outside of the model boundary, and only the normal displacement of the side surface of the model was limited.

Fig. 6
figure 6

Finite difference model

Full size image

In the FDM model, three pipelines were constructed. The diameter and thickness of the existing pipeline were 0.5 m and 0.05 m, respectively. The angle between the pipeline axis and the tunneling axis of the shield machine was 60°. The three pipeline axes intersected with the shield tunnel axis at 11 m in front of the cutter head (x = 11 m, Pipeline 1), at the cutter head (x = 0 m, Pipeline 2), and at 11 m behind the cutter head (x = -11 m, Pipeline 3), respectively.

In the FDM model, the soil parameters adopt the Mohr–Coulomb constitutive model, and the soil’s mechanical parameters were mainly obtained by field and laboratory tests. The specific parameters are shown in Fig. 6. The pipe, cutter head, and shield shell parameters were mainly obtained from the design drawings. The longitudinal and circumferential joints of the segments were not considered in the FDM model. The shield tunnel joints’ influence on the stiffness of the tunnel can be considered through stiffness reduction. According to the equivalent continuity model and stiffness calculation equation of the shield tunnel proposed by Zhang et al. (2015) and Zhou et al. (2020), the reduction factor of the shield tunnel segment was calculated as 0.88. The segments were made of C30 grade concrete, and the elastic modulus E, Poisson’s ratio, and gravity were 25.9 GPa, 0.2, and 25 kN/m3, respectively. After the stiffness was reduced, the elastic modulus of the segment was 22.8 GPa. Notably, owing to the presence of the cutter-head and the chamber, the shell shield elements had a stiffness that was 100 times higher than the elastic modulus of the segment, and the deformations were ignored. Because the grout material’s elastic modulus is time-dependent, an initial elastic modulus of 40 MPa was assigned to the unsolidified area of the grout to simulate the mechanical properties of fresh grout. However, an elastic modulus of 500 MPa was assigned to the grout solidification area(Meng et al. 2018; Zhang et al. 2020).

Cast iron is one of the main materials used in urban pipelines. The elastic modulus of cast iron materials is 60 GPa, and their Poisson’s ratio is 0.22. Fewer pipeline bolts and particular welding measures are typically required at the pipe joints, which have higher strength. Therefore, for the stiffness reduction, it was assumed that the reduction factor is 0.9 and the elastic modulus after reduction is 54 GPa.

Modelling of construction loadings

Face pressure loading

The thrust load of the tunnel face is related to the formation pressure. It is assumed that the EPB-TBM shield’s pressure on the excavation face varies linearly with the elevation and ground density. The following equation can be used to calculate the pressure load on the tunnel face:

$$p=\gamma {H}_{g}K$$
(20)

where γ is the weight of the soil (kN/m3); Hg is the depth of the node (m); K is the coefficient of earth pressure at rest, and K = 1- sinφ; φ is the friction angle of the soil.

Accordingly, to increase the speed of shield tunneling, an additional thrust loading (approximately 120 kPa) was applied to the tunnel face during actual construction. The additional thrust load mainly determines the formation of deformation caused by the thrust load at the cutter head.

In the FDM model, the coordinates of all nodes at the cutter head were extracted, and the static earth pressure at the corresponding position was calculated. The corresponding static earth pressure and additional thrust load were applied to the cutter head to realize the thrust load on the face.

Friction force loading

As expressed by Eq. (6), the shield shell’s friction resistance is related to the surrounding earth pressure, which changes with the depth; the distribution of the friction force loading is very complicated. The coordinate information of all nodes in the shield shell element is extracted. Then, the corresponding load is applied to the corresponding node through the load calculation statement to realize the application of the shield shell friction load.

Modelling grouting pressure loading

Ninic and Meschke (2017) proposed that the grouting pressure load is related to the buried depth of the tunnel, and the following equation can be used to calculate the grouting pressure:

$$q=1.2\gamma {H}_{g}$$
(21)

The grouting pressure offsets the surrounding formation pressure. The remaining grouting pressure is called the additional grouting pressure, and squeezes the formation to control the continuous settlement of the soil. The additional grouting pressure mainly determines the formation deformation caused by the grouting pressure.

The theoretical calculation and numerical simulation parameters are listed in Table 1. In the theoretical calculation, the soil parameters are the weighted average of all soil parameters.

Table 1 Calculation parameters
Full size table

FDM calculation steps

The numerical simulation model considers many factors, and constructing a dynamic tunneling model is highly complicated. Yin et al. (2018) proposed that the tunneling process can be simulated by building multiple static models. The following steps are carried out in the simulation:

  • Each soil layer was assigned material properties according to the corresponding depth, then the initial stress field and initial displacement field were calculated. At last, the initial displacement field was reset to zero, and the initial stress field was retained.

  • First, the soil units in the shield shell (x = -11 m ~ x = 0 m) and IGST were removed. The cutter head units, shield shell units, and tunnel segment units were given corresponding material properties. Then, the related calculation loads were applied on the cutter head, shield shell, and grouting area according to chapter 5.2. The above operation includes all factors considered in the theoretical calculation during the tunneling process, which can achieve static simulating the shield machine tunneling.

Comparative analysis of calculation results

According to the FDM calculation results, the settlement of the section at 11 m in front of the cutter head, section at the cutter head, and section at 11 m behind the cutter head was extracted, respectively. The comparison of the FDM calculation results, field monitoring data, and theoretical calculation results is presented in Fig. 7.

Fig. 7
figure 7

Comparison of surface subsidence. a Surface subsidence the along y-direction. b Surface subsidence along the x-direction

Full size image

  • The error among the FDM model calculation results, theoretical calculation results, and field monitoring results is small, which validates the FDM model and proposed equation.

  • The surface subsidence was distributed along the horizontal direction in a “V” shape, and the maximum subsidence position was at the center of the cutter head. By comparing the data of the three cross-sections, it can be seen that the surface deformation of the cross-section at the tail of the shield is more significant than the surface deformation of the cross-section at the cutter head and at 11 m in front of the cutter head. This rule holds because the ground loss is mainly distributed at the tail of the shield. As the distance from the ground loss increases, the settlement effect caused by the ground loss becomes smaller.

  • The distribution of the surface settlement has an “S” shape along the longitudinal direction, and the maximum settlement position is 24 m behind the cutter head. The ground loss is the main factor causing surface settlement, followed by the shield shell friction. The additional thrust and grouting pressure load only have a minor effect on the surface deformation.

  • The FDM calculation results are more consistent with the on-site monitoring data. The layered nature of the soil and the grouting slurry’s solidification process was considered in the FDM model according to the on-site construction situation. However, these factors were not considered in the theoretical calculation.

Figure 8 shows the pipeline deformation in the FDM model. Within the scope of the calculation, the shield tunnel excavation can cause the settlement deformation of the existing pipeline. There were significant differences in the size and distribution of the pipeline settlement at different locations.

Fig. 8
figure 8

Existing pipeline deformation

Full size image

The settlement data of three pipelines were extracted, and the comparison between the FDM simulation results and the theoretical analysis results is presented in Fig. 9.

Fig. 9
figure 9

Settlement curve of existing pipeline. a Settlement curve of pipeline 1. b Settlement curve of pipeline 2. c Settlement curve of pipeline 3

Full size image

From Fig. 9, the following conclusions can be drawn:

  • The error between the theoretical calculation results and the FDM calculation results is small, which validates the proposed method. By considering the existing pipelines as Euler–Bernoulli beams placed on the Pasternak foundation beam model, the disturbance of the existing pipelines caused by the shield machine excavation can be effectively analyzed.

  • The settlement curve of the existing pipeline caused by tunnel excavation exhibits a “V” shape, which is inconsistent with the law that is in effect when the shield tunnel crosses the existing pipeline orthogonally. When the existing pipeline crosses the shield tunnel obliquely, the uneven settlement rate of the pipeline is more significant and the settlement law is more complicated.

  • There existed a considerable gap between the pipeline settlement deformation at different positions. When the pipeline axis intersected the tunneling axis at 11 m in front of the cutter head, the distance from the maximum deformation position to the intersection of the pipeline axis with the tunnel axis was 11 m, and the maximum settlement was 4.5%. When the intersection of the pipeline axis with the tunnel excavation axis was 11 m behind the cutter head, the distance from the maximum deformation position of the pipeline to the intersection of the pipeline axis and the tunnel axis was 3 m, and the maximum settlement was 34 mm, which is approximately 7.5 times equal to the former.

  • The ground loss and shield shell friction are the main factors causing pipeline deformation, while the thrust load of the tunnel face and the grouting load only have a minor effect on the pipeline, which is consistent with the influencing factors of surface settlement. When the calculation point on the pipeline was located in front of the cutter head, the shield shell friction caused a slight bulge in the pipeline.

The maximum settlement value of the ground surface and the maximum settlement value of the existing pipeline obtained by the three calculation methods are respectively extracted. The comparison of the three calculation results is shown in Table 2. It can be seen that the calculation errors of the three calculation results are small, which verifies the correctness of the theoretical calculation formula.

Table 2 Maximum settlement value comparison
Full size table

Analysis of Sensitivity Factors

Different included angle β

Based on the previous investigation, the influence of the different included angles between the axis of the pipeline and the axis of the shield on the deformation of the pipeline was analyzed. The angle β between the axis of the pipeline and the axis of the shield tunnel was 75°, 60°, 45°, and 15°, respectively. Take pipeline 3 as the research object. The settlement curves of the pipe at different positions with different angle β are shown in Fig. 10.

Fig. 10
figure 10

Settlement curve of pipeline 3 with different angle β

Full size image

The following laws can be inferred from Fig. 10:

  • When the position of the pipeline is the same, the maximum deformation of the pipeline decreases with the increase of the angle between the pipeline axis and the tunnel axis. As the angle decreases, the maximum settlement of the pipeline is farther from the intersection of the pipeline axis with the tunnel axis.

  • As the angle between the pipeline axis and the shield tunnel decreases, the pipeline settlement curve gradually changes from a “V” type to an “S” type, and the settlement of the pipeline also increases. This suggests that when the existing pipeline axis is parallel to the shield tunnel axis, the shield tunneling causes the most remarkable disturbance to the pipeline. In contrast, when the existing pipeline axis is orthogonal to the shield tunnel axis, the tunneling of the shield machine causes the minimum disturbance to the pipeline.

The existing pipelines are prone to misalignment when they are subjected to shearing stress, which will cause pipe joints to break in severe cases. Therefore, it is important to clarify the shearing stress of the pipeline to ensure the normal use of the pipeline. Figure 11 shows the shear stress on the pipeline when the angle between the pipeline axis and the shield tunneling axis is different under different working conditions.

Fig. 11
figure 11

Shearing stress of pipeline 3 with different angle β

Full size image

From the Fig. 11, the maximum shear stress on the pipeline is about 340 kPa. If the pipeline is connected by steel bolts (maximum shear strength is 140 MPa), the shear stress that causes pipeline deformation will not damage the joint. If the pipeline is connected by concrete (the maximum shear strength is 2.2 MPa), the joint is also in the safe range of force. Which verifies that the pipeline will not be damaged due to shear stress.

Different elastic modulus of pipeline E

In cities, concrete, steel, and cast iron are typically used in underground pipelines; the corresponding elastic moduli are 23 GPa, 60 GPa, and 230 GPa, respectively. Hence, based on the previous investigation, it is concluded that the most significant disturbance to the pipeline during the shield tunneling project occurs when the pipeline axis and tunnel axis intersect at the tail of the shield (x =—11 m). Therefore, the following discussion mainly considers the case wherein the pipeline axis and tunnel axis intersect at the tail of the shield (x =—11 m). The strength property of the existing pipeline was changed. The settlement of the pipeline and shear stress of the pipeline observed when the angle β between the pipeline axis and the tunnel axis was 75°, 45°, and 15°, respectively, was compared as shown in Fig. 12.

Fig. 12
figure 12

Settlement and shear stress of pipeline with different elastic modulus E. a Settlement of the pipeline. b Shear stress of the pipeline

Full size image

As can be seen in Fig. 12, the material strength has a significant influence on the deformation of the pipeline. When the angle between the pipeline axis and the shield tunneling axis was 15°, the maximum settlement value of the concrete pipeline was 80.6 mm. The maximum settlement value of the steel pipeline was 6.4 mm, and the maximum settlement value of the cast iron pipeline was 26.9 mm. The disturbance to the steel pipeline during the shield tunneling was the smallest, followed by the cast-iron pipeline, which caused the most remarkable disturbance to the concrete pipeline. The change of the material strength did not affect the pipeline’s maximum settlement position, and angle β is the main factor determining the maximum settlement position of the pipeline. As β decreases, the pipeline’s maximum settlement position gradually deviates from the intersection of the pipeline axis and excavation direction axis. When the pipeline material is concrete, the change of the angle β has a great influence on the shear stress of the pipeline. When the angle β = 15°, the maximum shear stress of the concrete pipeline is 810 kPa. At this time, the safety reserve of the pipeline is smaller, which means the pipeline needs to strengthen observation.

Conclusion

Based on the Mindlin solution and the Loganathan equation, this study deduced an equation for calculating the deformation of existing pipelines caused by shield machine tunneling. The corresponding FDM calculation model was established based on an actual engineering case. The disturbance of the shield machine to the existing pipeline during tunneling was analyzed, and the conclusions drawn from this study are as follows:

  • The error among the results obtained using the proposed equation, the calculation results obtained using the FDM, and the actual monitoring data is small, which confirms the applicability of the proposed equation. The two-stage method is reliable for analyzing the pipeline deformation caused by shield tunnel construction.

  • In the process of shield tunneling, the main factors causing disturbance to the surface and pipeline are the shield shell friction and ground loss, while the additional thrust and additional grouting pressure only cause minor disturbance to the surrounding environment.

  • The maximum deformation of the pipeline decreases with the angle between the pipeline axis and the tunnel axis. The maximum settlement position deviates from the tunnel axis. The deformation curve of the pipeline changes from a “V” shape to an “S” shape as the angle between the pipeline axis and the tunnel axis decreases. When the pipeline is parallel to the shield tunnel, the shield tunneling causes the most remarkable disturbance to the pipeline.

  • The strength of the pipeline has a significant influence on the settlement of the pipeline. The shield tunnel causes great disturbance to the concrete material pipeline during tunneling. However, steel pipelines and cas-iron pipelines are less disturbed during the shield tunneling process. The pipeline’s maximum settlement position is determined by the angle β between the pipeline axis and the tunnel axis.

  • The shear stress distribution law of the existing pipeline is the same as the settlement law of the existing pipeline, but the shear stress is more susceptible to changes in other factors. When the existing pipeline is made of concrete and the joint strength of the pipeline is relatively low, it is more attention should be paid to the pipeline joints.