Introduction

The anisotropy of rock is one of the important properties of a natural rock mass. Especially for layered rock mass, its anisotropy directly affects the stress distribution and deformation characteristics of rock mass (Watson et al. 2015). With the development of rock mechanics theory and mechanical constitutive theory, the anisotropic characteristics of rock have gradually received the attention of scholars, which is one of the research focus and hotspots in the field of rock mechanics and engineering geology (Barton and Quadros 2015).

The anisotropy of rock mass usually refers to the structural characteristics, mechanical parameters, and stress-strain relationship of rock and soil materials with different differences in different directions. The causes and forms of anisotropy of different rock masses are different, which can be divided into primary anisotropy (also called intrinsic anisotropy) and secondary anisotropy (also called induced anisotropy). Primary anisotropy refers to the difference in the arrangement of mineral particles in different directions during the formation of rock and soil materials, which leads to the difference in structural properties and mechanical parameters of rocks in different directions. Secondary anisotropy refers to when the stress state changes, the deformation characteristics of the rock and soil materials in different stress directions are different. Therefore, the original anisotropy and secondary anisotropy are essentially different (Tomac and Sauter 2018). The primary anisotropy is mainly a description of the natural intrinsic properties of the rock and soil materials and is a physics property parameter, while the secondary anisotropy describes the stress. The mechanical parameters caused by the state change; the deformation law caused by the state change of the stress in different directions is different. The study of anisotropy mainly focuses on primary anisotropy (Sangode et al. 2017). In 1963, the elastic theory equation of anisotropic materials based on the generalized Hooke’s law of continuum was deduced, which is the theoretical support for the subsequent study of anisotropy. Anisotropic bodies can be classified into transverse anisotropy, single joint anisotropy, and extreme anisotropy and orthorhombic, depending on the symmetry plane of the physics parameters. Extreme anisotropy refers to the fact that the object exhibits different mechanical properties in any two different directions at any point. However, according to the elastic symmetry relationship, it can be transformed into an isotropic body through multi-step degeneration of extreme anisotropy. Transverse anisotropy is produced by the development of rock shale (Geng et al. 2016) or bedding (Wenning et al. 2018), which is symmetrical about the axis of rotation perpendicular to the isotropic plane.

Because it is very difficult to study the anisotropy of rock mass in a general sense, the current research fields mainly focus on the anisotropic rock mass under orthorhombic and transverse isotropic conditions. These two models have basically met the needs of solving most anisotropic engineering problems. However, due to the complexity of rock anisotropy, the research on the anisotropic yield criterion and constitutive relation of rock mass is still in the theoretical research stage, and it is seldom applied in actual rock mass engineering and geology engineering. The main reasons are as follows: (1) The anisotropic yield criterion and its constitutive relation are very complicated, with many parameters, and it is very difficult to get the values of parameters; (2) The orthorhombic or transverse isotropic yield criterion and the constitutive relationship cannot be expressed by explicit mathematical formulas, but can only be calculated by numerical methods. The calculation process is complicated and the calculation amount is huge.

Studying the anisotropic characteristics of layered rock mass requires theoretical analysis, laboratory test, field test, and numerical analysis (Yan et al. 2020a), and then the corresponding anisotropic deformation and strength properties, failure criterion, and elastoplastic constitutive relation of rock are obtained.

Theory of anisotropic media

Isotropic self-consistency theory

Self-consistent approximation (SCA) is a typical theory of inclusion equivalent medium. The theory was first proposed by Norris. The basic idea of the theory is to treat each mineral component and pore of the complex medium that needs to be simulated as a single phase independent of each other. The multi-phase medium is placed in a background medium with adjustable elastic parameters, and the background medium is infinite. SCA model is a high-frequency model suitable for laboratory measurement, which means that pore pressure does not have enough relaxation time to reach equilibrium. A dry rock skeleton based on SCA theory was constructed, and then the Gassmann equation was used to obtain the equivalent elastic modulus of saturated fluid.

The equivalent sketch of SCA is shown in Fig. 1. The gray and blue ellipsoids are different mineral phases, the black flat ellipsoids are porous, and the gray background medium is imaginary equivalent medium. By adjusting the elastic parameters of the gray background medium, the parameters of the background medium keep approaching the multi-phase medium until a plane wave incident, the multi-phase medium does not scatter, and the elastic modulus of the background medium is equal to the elastic modulus of the multi-phase medium. The self-consistent approximation formula for N-phase mixtures proposed by Berryman is the most widely used as follows:

$$ \left\{\begin{array}{c}{\sum}_{j=1}^n{f}_j\left({K}_j-{K}_{SC}^{\ast}\right){P}^{\ast j}=0\\ {}{\sum}_{j=1}^n{f}_j\left({\mu}_j-{\mu}_{SC}^{\ast}\right){Q}^{\ast j}=0\end{array}\right. $$
(1)

where fj, Kj, and μj refer to the volume percentage, bulk modulus, and shear modulus of the ith phase inclusion body, respectively. P∗j and Q∗j are the same as P and Q in the KT model.

Fig. 1
figure 1

SCA effective theory

Full size image

In recent years, the SCA model has been widely used in shale model construction (Kanitpanyacharoen et al. 2015). However, many research results indicate that when the porosity exceeds 60%, the equivalent results of SCA will coincide with the lower limit of HS boundary when the equivalent fluid phase and solid phase are used in the SCA model. At this time, the rock is in a “particle suspension” state; that is, the pore fluid phase completely encapsulates the solid phase. At this point, solid particles are not connected with each other because SCA is a symmetric model. Therefore, when the porosity is equal to 40–60%, the two-phase materials can maintain mutual connectivity.

Introduction of anisotropy theory

Seismic anisotropy (Okaya et al. 2018) is that seismic attributes change with direction (seismic velocity, travel time, amplitude, polarity, etc.). Thomsen defines anisotropy as seismic wave velocity varying with angle. The angle can be an incident angle, azimuth angle, etc. The velocity can be ray velocity, wavefront velocity, group velocity and phase velocity, interlayer velocity, NMO velocity, or RMS velocity.

Based on the generalized Hooke’s law, the elastic wave theory of seismic wave describes the anisotropic elastic tensor by the expression of stress and strain.

$$ {\sigma}_{ij}={c}_{ij kl}{\varepsilon}_{kl} $$
(2)

In the formula, cijkl is a fourth-order elastic stiffness matrix. Because of the symmetry of stress and strain, the stiffness matrix has the following relations:

$$ {c}_{ijkl}={c}_{jikl}={c}_{ijlk}={c}_{jilk} $$
(3)

Strain energy density is a positive definite quadratic function of strain, so there is the following relationship:

$$ {c}_{ijlk}={c}_{klij} $$
(4)

Anisotropic media are usually classified as triclinic anisotropy, monoclinic anisotropy, orthorhombic anisotropy (Pan et al. 2018), trigonal anisotropy, tetragonal anisotropy, hexagonal anisotropy, and cubic anisotropy and isotropy in physics. The independent constants describing them decrease in turn. For geophysics, scholars are interested in triclinia anisotropy, monoclinic anisotropy, orthorhombic anisotropy, hexagonal anisotropy, and isotropic media.

Triclinal anisotropic medium

Twenty-one independent parameters are required to describe the triclinic anisotropic medium. It is difficult to identify such media by current seismic exploration techniques.

$$ {C}^{TRI}=\left(\begin{array}{cc}\begin{array}{ccc}{C}_{11}& {C}_{12}& {C}_{13}\\ {}{C}_{12}& {C}_{22}& {C}_{23}\\ {}{C}_{13}& {C}_{23}& {C}_{33}\end{array}& \begin{array}{ccc}{C}_{14}& {C}_{15}& {C}_{16}\\ {}{C}_{24}& {C}_{25}& {C}_{26}\\ {}{C}_{34}& {C}_{35}& {C}_{36}\end{array}\\ {}\begin{array}{ccc}{C}_{14}& {C}_{24}& {C}_{34}\\ {}{C}_{15}& {C}_{25}& {C}_{35}\\ {}{C}_{16}& {C}_{26}& {C}_{36}\end{array}& \begin{array}{ccc}{C}_{44}& {C}_{45}& {C}_{46}\\ {}{C}_{45}& {C}_{55}& {C}_{56}\\ {}{C}_{46}& {C}_{56}& {C}_{66}\end{array}\end{array}\right) $$
(5)

Monoclinic anisotropic medium

The geophysics model may be a layered deposition medium containing two sets of non-orthogonal strain cracks. Although its independent parameters have been reduced to 13, the current seismic data is still unable to study this.

$$ {C}^{MON}=\left(\begin{array}{cc}\begin{array}{ccc}{C}_{11}& {C}_{12}& {C}_{13}\\ {}{C}_{12}& {C}_{22}& {C}_{23}\\ {}{C}_{13}& {C}_{23}& {C}_{33}\end{array}& \begin{array}{ccc}0\ & 0\ & {C}_{16}\\ {}0\ & 0\ & {C}_{26}\\ {}0\ & 0\ & {C}_{36}\end{array}\\ {}\begin{array}{ccc}0& 0& 0\\ {}0& 0& 0\\ {}{C}_{16}& {C}_{26}& {C}_{36}\end{array}& \begin{array}{ccc}{C}_{44}& {C}_{45}& 0\\ {}{C}_{45}& {C}_{55}& 0\\ {}0& 0& {C}_{66}\end{array}\end{array}\right) $$
(6)

Orthorhombic anisotropic medium

Orthorhombic anisotropic medium contains three mutually orthogonal symmetry planes and nine independent parameters, which can be used to describe horizontally layered media with vertical cracks, or isotropic media with two sets of mutually perpendicular cracks.

$$ {C}^{ORT}=\left(\begin{array}{cc}\begin{array}{ccc}{C}_{11}& {C}_{12}& {C}_{13}\\ {}{C}_{12}& {C}_{22}& {C}_{23}\\ {}{C}_{13}& {C}_{23}& {C}_{33}\end{array}& \begin{array}{ccc}\ 0\ &\ 0\ &\ 0\ \\ {}\ 0\ &\ 0\ &\ 0\ \\ {}\ 0\ &\ 0\ &\ 0\ \end{array}\\ {}\begin{array}{ccc}0& 0& 0\\ {}0& 0& 0\\ {}0& 0& 0\end{array}& \begin{array}{ccc}{C}_{44}& 0&\ 0\\ {}0& {C}_{55}&\ 0\\ {}0& 0& {C}_{66}\end{array}\end{array}\right) $$
(7)

Hexagonal anisotropic medium

Hexagonal anisotropic (Sun et al. 2017) medium belongs to a transversely isotropic medium. The substance contains a symmetrical axis in a single direction and can be described by 5 elastic parameters. There are two TI media models: transverse isotropy with a vertical axis of symmetry (VTI) and transverse isotropy with a horizontal axis of symmetry (HTI). In addition, TTI (transverse isotropy with a tilted axis of symmetry) media appears when the symmetric axis is tilted, as shown in Fig. 2.

Fig. 2
figure 2

TI model

Full size image

For VTI media, if the X3 direction is set to the symmetry axis direction, the stiffness matrix can be expressed as:

$$ {C}^{VTI}=\left(\begin{array}{cc}\begin{array}{ccc}{C}_{11}& {C}_{11}-2{C}_{66}& {C}_{13}\\ {}{C}_{11}-2{C}_{66}& {C}_{11}& {C}_{13}\\ {}{C}_{13}& {C}_{13}& {C}_{33}\end{array}& \begin{array}{ccc}0\kern0.5em & 0& \kern0.5em 0\ \\ {}0\kern0.5em & 0& \kern0.5em 0\ \\ {}0\kern0.5em & 0& \kern0.5em 0\ \end{array}\\ {}\begin{array}{ccc}\kern1em 0\kern0.5em & \kern1.25em 0\ & \kern1em 0\kern0.5em \\ {}\kern0.5em 0& \kern1em 0& \kern0.5em 0\\ {}\kern0.5em 0& \kern1em 0& \kern0.5em 0\end{array}& \begin{array}{ccc}{C}_{44}& 0\ & 0\\ {}0\ & {C}_{44}& 0\\ {}0\ & 0\ & {C}_{66}\end{array}\end{array}\right) $$
(8)

The HTI model can be obtained by bond transformation of the VTI model and rotation of X1 as symmetrical axis direction by 90° (Xu and Arson 2015). HTI medium presents azimuthal anisotropy, which is commonly used to represent vertical cracks. Its stiffness matrix is as follows:

$$ {C}^{HTI}=\left(\begin{array}{cc}\begin{array}{ccc}{C}_{11}& {C}_{13}& {C}_{13}\\ {}{C}_{13}& {C}_{33}& {C}_{33}-2{C}_{44}\\ {}{C}_{13}& {C}_{33}-2{C}_{44}& {C}_{33}\end{array}& \begin{array}{ccc}0\kern0.5em & 0& \kern0.5em 0\ \\ {}0\kern0.5em & 0& \kern0.5em 0\ \\ {}0\kern0.5em & 0& \kern0.5em 0\ \end{array}\\ {}\begin{array}{ccc}\kern1em 0\kern0.5em & \kern1.25em 0\ & \kern1em 0\kern0.5em \\ {}\kern0.5em 0& \kern1em 0& \kern0.5em 0\\ {}\kern0.5em 0& \kern1em 0& \kern0.5em 0\end{array}& \begin{array}{ccc}{C}_{44}& 0\ & 0\\ {}0\ & {C}_{66}& 0\\ {}0\ & 0\ & {C}_{66}\end{array}\end{array}\right) $$
(9)

Isotropic medium

Isotropic is a special anisotropic medium with no physics changes in all directions. The Lame constant can be used to describe isotropic media. The P wave velocity and S wave velocity can also be calculated by using the Lame constant. The equation is as follows:

$$ \left\{\begin{array}{c}{V}_P=\sqrt{\frac{\lambda +2\mu }{\rho }}\\ {}{V}_S=\sqrt{\frac{\mu }{\rho }}\end{array}\right. $$
(10)

The stiffness matrix of isotropic media is:

$$ {C}^{TRI}=\left(\begin{array}{cc}\begin{array}{ccc}\lambda +2\mu & \lambda & \lambda \\ {}\lambda & \lambda +2\mu & \lambda \\ {}\lambda & \lambda & \lambda +2\mu \end{array}& \begin{array}{ccc}0& 0& 0\\ {}0& 0& 0\\ {}0& 0& 0\end{array}\\ {}\begin{array}{ccc}\kern0.5em 0\kern0.5em & \kern0.5em 0\ & \kern1em 0\kern0.5em \\ {}0&\ 0& \kern0.5em 0\\ {}0&\ 0& \kern0.5em 0\end{array}& \begin{array}{ccc}\mu & 0& 0\\ {}0& \mu & 0\\ {}0& 0& \mu \end{array}\end{array}\right) $$
(11)

Thomsen found that most of the underground rocks exhibit weak anisotropy through a large number of experiments and analyses and put forward anisotropic parameters with clear physics meaning. The specific expressions are as follows:

$$ \left\{\begin{array}{c}\varepsilon =\frac{c_{11}-{c}_{33}}{2{c}_{33}}\\ {}\gamma =\frac{c_{66}-{c}_{44}}{2{c}_{44}}\\ {}{\delta}^{\ast }=\frac{1}{2{c}_{33}^2}\left[2{\left({c}_{13}+{c}_{44}\right)}^2-\left({c}_{33}+{c}_{44}\right)\left({c}_{11}+{c}_{33}-{c}_{44}\right)\right]\end{array}\right. $$
(12)

All three Thomsen parameters are dimensionless. ε is very close to the decimal difference of P wave velocity in the vertical and parallel directions of the symmetry axis, so it is defined as “P wave anisotropy parameter.” Similarly, parameter γ represents the difference degree of SH waves perpendicular to the parallel direction, which is called “shear wave anisotropy parameter” (Li and Peng 2017). The definition of δ is not only intuitive like ε and γ but it also has a clear meaning: it controls the change of P wave velocity outside the symmetric axis, and it also affects the change of SV wave velocity.

Experimental research on anisotropic characteristics of rock mass

The mechanical properties of engineering rock mass anisotropy are a very complex project. How to use effective theoretical methods, experimental methods, and numerical analysis software to study the basic physics properties, mechanical parameters, and strength of anisotropic rock mechanics problems such as theory are important for understanding and understanding the anisotropy of engineering rock masses.

Conventional test methods for anisotropic rocks

Uniaxial compression test

Uniaxial compression test is the simplest and commonly used method to determine the strength and deformation characteristics of isotropic rock materials (Zhang et al. 2016a, b), so this method has been used to study the anisotropic characteristics of rock (Chang et al. 2019). As shown in Fig. 3, transversely isotropic rock samples with three different dip angles only exert vertical stress in the Y direction. Assuming that the internal stress and strain distribution of the rock sample are uniform, then:

$$ \left\{\begin{array}{c}{\varepsilon}_x={K}_{12}{\sigma}_y\\ {}\begin{array}{c}{\varepsilon}_y={K}_{22}{\sigma}_y\\ {}{\varepsilon}_z={K}_{23}{\sigma}_y\\ {}{\gamma}_{xy}={K}_{26}{\sigma}_y\end{array}\\ {}{\gamma}_{yz}={\gamma}_{xz}=0\end{array}\right. $$
(13)
Fig. 3
figure 3

Uniaxial compression tests of three transverse anisotropic rock samples with different dips

Full size image

Triaxial compression test

For most rock materials, elastic constants are often related to the stress level, which is a function of the stress level, not a fixed value. In order to study the variation of elastic constants with the increase of stress level, the elastic parameters of rock samples under different confining pressures are usually measured by triaxial compression tests in the laboratory (Wu et al. 2016).

For transversely isotropic (Park and Min 2015) rock samples with different dips shown in Fig. 4, confining pressure is applied first, and then the axial load is applied until the rock samples are destroyed. The strain values in different directions under different confining pressures can be obtained by pasting the strain gauge on the side surface (Liu et al. 2015a).

Fig. 4
figure 4

Triaxial confining pressure test of transversely anisotropic rock samples

Full size image

Brazilian splitting tensile test

Because the direct tensile test is difficult, the Brazilian splitting method (Kundu et al. 2018) is one of the most commonly used indirect test methods for determining the tensile strength of rock. Figure 5 is a schematic diagram of the Brazilian disk radial splitting test. Affected by the concentrated force P in the radial direction, the two different loading modes only change the stress distribution near the contact point, but have no effect on the stress distribution near the center (Wang et al. 2018).

Fig. 5
figure 5

Diagram of Brazilian disc radial splitting test

Full size image

Tensile test of pure bending beam

The research group led by Academician Liu B.C. has proposed a new method for testing the anisotropic elastic constant through the experimental study of a large number of anisotropic rock materials—the pure curved beam method.

The anisotropic rectangular beam shown in Fig. 6 shows that under the action of bending moment M, the upper-end surface is in a compressed state, the lower end surface is in a tensile state, the denaturing characteristics are linear elasticity, and the compression elastic modes are Ea and Eb, respectively. The arbitrary cross-section of the pure curved part of the beam is always flat during the playing process, and the neutral surface is kept parallel with the upper and lower end faces. According to the equilibrium condition, the internal force and bending moment of the cross-section of the beam satisfy the following relationship:

$$ \left\{\begin{array}{c}\int {\sigma}_{xa}d{A}_a+\int {\sigma}_{xb}d{A}_b=0\\ {}\int {\sigma}_{xa} yd{A}_a+\int {\sigma}_{xb} yd{A}_b=M\end{array}\right. $$
(14)
Fig. 6
figure 6

Diagram of force acting on pure bending beam

Full size image

From this, the formulas of compressive stress and tensile stress on the upper and lower ends of rectangular beams can be deduced.

$$ \left\{\begin{array}{c}{\sigma}_a=-\frac{3M}{b{h}^2}\frac{\varepsilon_a{\varepsilon}_b}{\varepsilon_a}\ \\ {}{\sigma}_b=+\frac{3M}{b{h}^2}\frac{\varepsilon_a{\varepsilon}_b}{\varepsilon_a}\end{array}\right. $$
(15)

Through the force analysis of pure bending beams, it can be seen that the XY plane of rectangular beams under bending moment M does not produce shear deformation (Stierle et al. 2016), which makes the upper and lower ends in unidirectional compression and unidirectional tension, and reduces many complex factors brought about by the test method itself.

Experimental research on meso-fabric characteristics

The intrinsic anisotropy of rock material is directly related to its fabric characteristics. Polarizing microscopy and X-ray diffraction techniques are used to analyze the microstructure of sandstone (Gehne and Benson 2017) in order to understand the anisotropy characteristics of rock material more comprehensively.

Microscopic analysis of optical thin sheets of sandstone

The study of rock fabrics includes analysis of all macroscopic and microscopic structural units at various scales (Douma et al. 2017). For sedimentary rocks, the bedding is the most obvious scale in a major sedimentary structure (Song et al. 2018). The dominant orientation of macro-bedding can be clearly seen through macro-pictures of vertical sandstone bedding direction. In order to study the performance of material anisotropy in micro-structure, the single polarization photographs of sandstone abrasives in vertical and parallel directions are usually used under a polarizing microscope (Ge et al. 2015).

X-ray diffraction test of sandstone materials

Through the x-ray diffraction test (Kim et al. 2016) and physics property analysis of sandstone samples, the maximum dry density of sandstone is 2.00–2.259/cm3, and the main chemical components are quartz, calcite, feldspar (Biedermann et al. 2016), chlorite, and illite. The content of quartz is generally 40–60%, the content of calcite is 20~40%, the content of feldspar is 10~25%, the content of mica mineral is 10~20%, and the content of clay mineral is generally 5~15%. The results of the X-ray diffraction analysis are shown in Fig. 7.

Fig. 7
figure 7

X-ray diffraction analysis of sandstone samples

Full size image

Ultrasound testing

Dynamic deformation parameters of rocks are parameters reflecting the deformation properties of rocks under dynamic loads. The common dynamic deformation parameters are the following: dynamic Young’s modulus (Lusakowska et al. 2017), dynamic Poisson’s ratio, dynamic shear modulus, and dynamic bulk modulus. The indoor method for determining the dynamic deformation parameters of rock is the acoustic wave test method (Zhao et al. 2019). The basic principle is to measure the P wave and S wave propagation velocity values of the acoustic wave on the same line in the rock specimen, and then according to the longitudinal wave, the transverse wave velocity and the rock and deformation (Almqvist and Mainprice 2017). The relationship between the parameters, the dynamic elastic modulus, the dynamic Poisson’s ratio, and the dynamic shear modulus (Ong et al. 2016) is also measured.

Scholars proposed different experimental methods, and the most common ones are shown in Fig. 8. They are measured on a cylinder core, on a sphere sample or on the sidewall of a cylinder core, and on a hexagonal core sample. The most common method to measure the core of a cylinder is shown Fig. 8a. Three cylinder cores are usually drilled from rock samples along three different directions, and then two parallel ends are obtained by cutting the two ends. Finally, the ultrasonic exciter and the receiver are respectively placed at both ends of the rock sample, and the wave velocity value is calculated by measuring the time elapsed during the transmission of the ultrasonic pulse signal in the rock (Bo et al. 2016).

Fig. 8
figure 8

Different experimental methods for measuring transversely isotropic rocks. a Measurements on three pillar cores. b Measurement on the sidewall of a spherical sample or core. c Measurement on a hexagonal prism

Full size image

Figure 8 b and c show two more common measurement methods, i.e., on the sidewall of a sphere and on a hexagonal prism. Compared with this method, it has the advantage that all wave velocity measurements are carried out simultaneously on the same sample, and the effect of rock heterogeneity can be reduced (Lahmira et al. 2016). These methods are based on the ultrasonic transmission method, so no matter which method is used, the experimental measurement is affected by the accuracy of the ultrasonic transmission method. In anisotropic media, the ultrasonic beam generated by the ultrasonic exciter will have the phenomenon of beam offset and diffraction, which will affect the measured ultrasonic velocity.

High-frequency ultrasonic waves decay faster than low-frequency seismic waves. Therefore, in laboratory measurements, an excitation source with a certain size is usually used to excite high-energy ultrasonic waves instead of point source excitation (Huang et al. 2018). These exciters are typically larger than one wave field of the ultrasonic wave and are referred to as finite-size transducers.

The ultrasonic measurement is convenient (Lokajíček and Svitek 2015), and the rock mass can be subjected to a wide range of non-destructive testing. Therefore, understanding the relationship between the ultrasonic velocity and the rock mass strength or deformation parameters has theoretical significance and high engineering application value (Zhan et al. 2016).

Numerical analysis theory

The theoretical analysis can only be used for simple or more regular crack arrangements, and the test cannot consider all the cases (Freire-Lista and Fort 2017). At the same time, the loading conditions in the test have a great influence on the experimental results (Yan et al. 2020b). On the contrary, the numerical simulation method is not restricted by this restriction and can not only reproduce the typical experimental phenomena but also achieve the ideal. Loading conditions can also be used to study the process which cannot be achieved by experiment and theory. Therefore, the numerical simulation method has become a development trend in recent years.

With the rapid development of numerical analysis theory and computer technology, numerical analysis methods such as finite difference method, discrete element method (Duan and Kwok 2016), finite element method, boundary element method, and interface element method have been widely used in the stability analysis of underground engineering. The numerical simulation of the three-dimensional jointed rock mass as a transversely isotropic material was carried out by the stochastic finite element method (Yang et al. 2015). Considering the randomness of elastic modulus, joint spacing, joint orientation, joint stiffness coefficient, and resistance parameters of jointed rock mass (Chen et al. 2016), the Rosenbluth method is used to determine the statistic of elastic parameters, and the corresponding three-dimensional stochastic finite element and reliability calculation formula are derived. Considering the characteristics of the interface element method, spring and slider elements which can simulate the elastic and plastic deformation of materials are introduced at the interface of the element. The interfacial element method solves the elastic-plastic analysis of materials without any additional sandwich elements. The ATEZD program of rock test and analysis system is used to study the control degree of rock deformation and failure by pore and fissure layers, thus revealing the control effect of various layers of rock mass defects on rock deformation and instability. The evolutionary finite element method and parallel evolutionary neural network finite element method can be used to analyze the stability of large underground caverns. Three-dimensional nonlinear layered anisotropic elastic-plastic damage finite element method can be used to analyze the stability of surrounding rock of underground caverns in steep dip rock mass (Zeng et al. 2018). It can better reflect the excavation failure characteristics of underground caverns in the steep dip rock mass and provide an effective calculation method for the stability analysis of surrounding rock mass of complex rock masses (Angus et al. 2016). Through the lithologic combination of layered rock mass characteristics, weak interlayer, distribution of fissures, and structural characteristics of rock mass are analyzed, studied, and partitioned, and corresponding sample units are established. The numerical analysis method is used to simulate the “sample unit method” of large-scale field test, which is obtained according to the mechanical parameters of rock mass (the mechanical parameters of the fractured rock mass in Ren et al. 2015).

Flagstone software is used to simulate the effect of joint dip on the peak strength of anisotropic rock samples. The results show that the peak strength of intact rock samples is the highest, the shear strain of jointed rock samples (Wang et al. 2017) is concentrated on joints or new shear bands, and the peak strength varies with joint inclination. The boundary element method can be used to study the effect of elastic anisotropy (transverse isotropy) on the convergence of tunnel section (Chan and Schmitt 2015). According to whether the transverse isotropic plane is parallel to the tunnel axis or not, the problem is divided into two situations, and the applicability of the convergence formula used to evaluate the tunnel surrounding the rock section is discussed. The research shows that the isotropic formula applied to uniform stress only applies when the transverse isotropic plane is parallel to the tunnel axis. When the isotropic plane is not parallel to the tunnel axis, three-dimensional stress analysis must be carried out. The finite element calculation model of layered surrounding rock with weak interlayers is established. It is proposed that the layered rock mass and weak interlayers are transversely isotropic, and the interlayer contact surface is simulated by the Goodman contact surface element with rotational freedom. By comparing the engineering measured data and the elastoplastic nonlinear finite element calculation results, it is proved to be reasonable. Using the RFPA2D numerical simulation software developed on the basis of meso-damage mechanics, two different rock materials were used to form seven transversely isotropic rock specimens with different dip angles. The uniaxial loading numerical simulation test was used to simulate the horizontal and the entire process of progressive rupture of isotropic rocks.

In recent years, numerical simulation methods made significant progress in describing the failure process of rock materials by numerical simulation methods, such as the fast Fourier transform method, discrete element method, finite/discrete element method (F/DEM), RFPA method, bond cell model, cellular automata method, and improved rigid spring method. The basic idea of these methods is to simulate the whole process of the generation, propagation, and penetration of micro-cracks (Sesetty and Ghassemi 2018) by using simple constitutive relation on the meso-scale on the basis of fine simulation of the meso-structure of rock materials. Finally, the macro-stress-strain curves and failure modes of rocks are obtained. Numerical simulation can overcome the difficulties of field test and model experiments and has obvious advantages in some aspects. Therefore, it is necessary to make full use of numerical simulation methods (Chang et al. 2019).

Anisotropic failure criterion and constitutive theory of rock mass

The Mohr-Coulomb criterion and the Drucker-Prager criterion commonly used in geotechnical engineering make up for the deficiency of classical plastic mechanics only for metals and other materials and are widely used in the plastic analysis of geomaterials. However, the above criteria apply only to the analysis of isotropic geotechnical problems. In order to describe the strength and deformation characteristics of anisotropic rock mass materials, scholars have proposed various anisotropic failure criteria, as shown in Table 1 (Duveau et al. 1998).

Table 1 Classification of anisotropic strength criterion
Full size table

According to the assumptions and reasoning methods of anisotropic failure criterion, it can be classified into two categories: continuous failure criterion and discontinuous piecewise failure criterion. Continuous medium failure criterion can also be classified into mathematical and empirical ones. The following is a further review and summary of the research progress related to the anisotropic strength criterion of geomaterials.

Failure criterion for mathematical continuum

Mathematical continuous failure criterion is established on the basis of tensor function and other mathematical theories (Chen et al. 2017). Von Mists criterion showed the earlier mathematical anisotropic failure criterion, i.e., generalized anisotropic Mises criterion. The Von Mises criterion was modified to describe the orthorhombic anisotropy of timber disciplines in a more concise form in 1950. But this criterion does not take into account the intensities of the tensile strength of the material and the water pressure (Bobet 2016). In order to consider the influence of the tensile and compressive strength of the geomaterials and the water pressure, the Hill criterion was modified to be the generalized Hill criterion.

A strength criterion for true triaxial stress state was proposed in view of the defect that most failure criteria only consider the traditional triaxial stress state. An anisotropic failure criterion was derived by extending the isotropic Stassi criterion and using tensor function theory (Cossette et al. 2016). The isotropic Mises-Schleicher criterion was generalized and the anisotropic Mists-Schleicher criterion was established under three-dimensional stress state. The concept of microstructure tensor was proposed, and a new anisotropic failure criterion was established by a second-order tensor. Pietruszezak, Lydzba, and Shao verified the microstructural tensor failure criterion based on the anisotropy test results of sedimentary rocks (Roy et al. 2017). Based on the concept of a critical plane, the damage tensor was introduced into linear and nonlinear Mohr-Coulomb criteria and the failure criterion was established for describing anisotropic damage of rock materials. The Mohr-Coulomb criterion for orthorhombic damage correction is proposed by introducing the damage tensor into the Mohr-Coulomb condition through the homogenization treatment (Hackston and Rutter 2016).

The mathematical continuum criterion mentioned above assumes that the material is a continuum medium and that the change of strength is also continuous (Ai et al. 2016). Its characteristics are based on the symmetry of materials. Generally, the anisotropic characteristics of strength are described by mathematical reasoning methods such as tensor functions of different orders reflecting the anisotropy of materials, which have a strict theoretical system.

Empirical failure criterion for continuous media

In order to simplify the characterization of strength anisotropy, some scholars regard the parameters in the isotropic strength criterion as a function of plane dip angle and use the method of fitting test data to find the variation law of anisotropic strength parameters (Liu et al. 2015b). The representative empirical continuum failure criterion is the variable cohesion theory proposed by Jaeger, which generalizes the Mohr-Coulomb criterion. Jaeger regards the internal cohesive force in the Mohr-Coulomb criterion as a function of plane inclination angle θ, while the internal friction force is still regarded as a constant. The theory of variable bond strength was improved on the basis of the analysis of test results. Both internal friction coefficient and internal bond force were regarded as functions of plane inclination angle.

McLamore and Gray’s empirical failure criteria were revised by using nonlinear damage envelopes in Mohr plane. Zhou Dagan proposed a five-point empirical formula through the fitting of the test results. An empirical expression of shear strength C was proposed and varying with direction of layered rock mass.

These criteria are representative empirical continuum criteria, most of which are supplements and amendments to the Jaeger criterion. The basic idea is to regard some parameters in the isotropic damage criterion as a function of the plane inclination angle θ and determine the variation law of anisotropic strength. The disadvantage of this kind of model is that each parameter has no clear physics and mathematical background, and the parameters require a large amount of experimental data to be determined (Nourani et al. 2017).

Failure criterion for discontinuous media

Unlike the two types of criteria described above, the discontinuous medium criterion is developed based on the discontinuous weak surface theory (Farhadian et al. 2016). The criterion emphasizes the description of physics mechanism in the process of failure. According to the different failure modes of the rock sample during the test, the following basic assumptions are proposed: (1) there are two different modes of the destruction of the anisotropic body; one is along the material. The slippage of the bedding plane is caused by another, and the other is caused by the fracture of the rock skeleton (the matrix between adjacent bedding planes); (2) the two fracture modes are described by two different criteria. The most representative non-continuous criterion is Jaeger’s single plane of the weakness theory (Ma et al. 2017).

Hoek regards the parameters m and s in the Hoek-Brown criterion as functions of plane dip angle θ and proposes an empirical criterion for describing anisotropic characteristics. Walsh and Brace considered weak planes as directed Griffith cracks (Ramos et al. 2017) and established anisotropic Griffith failure criteria based on the Griffith strength criteria revised by McClintock and Walsh. A modified single weak plane theory was established based on Barton criterion for the strength nonlinearity of anisotropic rock materials. A discontinuous failure criterion with seven parameters was proposed based on maximum strain theory and single weak surface theory. After the coefficient transformation, the criterion can be degenerated into a single weak surface criterion and a generalized Jaeger criterion.

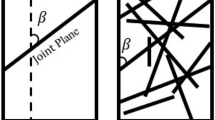
The Hoek-Brown criterion is often used to evaluate the anisotropy of rocks by using the results of uniaxial and triaxial tests of rock samples. The stress pattern of the unit in the sample is shown in Fig. 9. The intermediate stress is ignored in the conventional triaxial test, so the confining pressure σ2 = σ3, and σ1 is the axial stress. The bedding angle (β) of the rock sample is defined as the angle between the normal direction of the discontinuous interface and the direction of the applied maximum principal stress (σ1), that is, the angle between the discontinuous interface and the X-axis in Fig. 9. When β = 0°, the applied σ1 is perpendicular to the discontinuous interface; when β = 90°, the applied σ1 is parallel to the discontinuous interface.

Fig. 9
figure 9

Bedding angle (β) of anisotropic rocks and stress diagram of internal elements

Full size image

Rock masses with discontinuous or weak surfaces are mainly classified into three categories (Fig. 10): a single weak rock mass, a weak rock mass, and two weak rock masses. For rock mass with a single weak plane, the axial peak strength characteristic curve has a characteristic of one side concave and two straight ends when the β changes from 0° to 90° (Fig. 10 I). The point of the lowest value is generally located near β = 30°. When rock mass contains a group of weak planes, its strength characteristic curve often presents U-shape (Fig. 10 II). The lowest point of strength generally appears near the point of β = 30°, and the highest point of strength generally appears near the point of β = 0° or β = 90°. When rock mass contains two groups of weak planes, its strength characteristic curve often presents W-shape (Fig. 10 III). The lowest point of strength generally appears near the point of. For this study, without a special explanation, it means that there is a group of weak rock mass, i. e., type 10-II.

Fig. 10
figure 10

Anisotropic strength characteristic curves of rock mass with different discontinuous interfaces (weak surfaces)

Full size image

The advantage of the discontinuous failure criterion is that each parameter has a clear physics meaning and is easy to be determined by experiment. The defect of this criterion is that different strength criteria are used to describe the failure mode of rock materials, which makes the failure criterion a piecewise function and makes the application inconvenient (Zhang 2017a, 2017b).

Anisotropic constitutive theory of rock materials

With the study of mechanical properties of jointed and layered rock masses, many constitutive models for rock conditions have been proposed by rock mechanics workers, such as equivalent anisotropic constitutive model, Cosserat constitutive model of layered rock masses, and anchored layered rock mass constitutive model.

The most commonly used joint constitutive model is the Goodman joint constitutive model. The successful application of the Goodman joint constitutive model in jointed rock masses has greatly promoted the study of joint constitutive models. In the study of the equivalent constitutive model of layered rock mass, the equivalent elastoplastic constitutive relation of layered rock mass under different combinations of rock thickness and layer mechanical properties is studied. The anisotropy of underground caverns is analyzed by the boundary element method, and a quasi-continuous anisotropic model considering equivalent modulus is established (equivalent elastic-plastic constitutive model for strength anisotropy of layered rock mass in Vishnu et al. 2018).

Based on the analysis of the structure and mechanical properties of the layered rock mass, the sandwiched rock mass is regarded as a mechanical system, and the mechanical model of the composite system with interlayer rock mass is established, which reveals the damage and instability of the rock mass containing the interlayer. The mechanism and the determination of the stability index of the interlayer rock mass provide a basis for the control of the stability of the layered rock mass.

The Cosserat medium theory is a continuum theory that studies the deformation and failure of a medium with a certain characteristic structure under external loads. Because it considers the couple stress and is more suitable for the case of bending deformation, the scholars studied the Cosserat elastic or elastoplastic constitutive model and analyzed the bending deformation failure of the layered rock mass (Guayacan-Carrillo et al. 2017). In order to consider the reinforcement effect of the anchor in the layered rock mass (Hatzor et al. 2015), many scholars have discussed this. There are two treatment methods: one is to treat the anchor as an anchor element and the other is to homogenize the action of bolt into rock mass. In the rock mass, the constraint effect of the anchor is considered by increasing the mechanical parameters of the anchored rock mass.

Because of the complexity of rock anisotropy, the research on yield criterion and constitutive relation of rock anisotropy is still in the stage of theoretical research, and it is seldom applied in actual rock engineering. The main reasons are as follows: (1) the yield criterion and its constitutive relation are very complex, there are many parameters, and it is very difficult to get the value; (2) the yield criterion of rock anisotropy and its constitutive relation are very complex. The anisotropic constitutive relation cannot be expressed by explicit mathematical formulas. It can only be calculated by numerical method. The calculation process is complex and the amount of calculation is huge.

Rock physics model of anisotropic media

The physics model of rock has an important influence on the study of the anisotropic characteristics of rock (Guo et al. 2016). Therefore, the establishment of an appropriate rock physics model has a direct impact on the accurate determination of rock anisotropy parameters and P-S wave velocity. Therefore, the effects of rock bulk modulus, shear modulus and fracture density, and fracture porosity and aspect ratio on anisotropic parameters in different physics models are analyzed, and the applicability of rock physics models is obtained (Liu et al. 2017).

Modulus inversion of matrix minerals

Depth, density, P wave velocity, S wave velocity, and water saturation and porosity are known (Bobet 2016). The volume modulus of fluid is obtained using the Wood formula. The bulk modulus of dry rock can be obtained by solving the following Gassmann-Boit-Geertsma equation.

$$ \left(Y-1\right){\beta}^2+\left[ Y\varphi \left(\frac{K_0}{K_{fl}}-1\right)-Y+\frac{M}{K_0}\right]\beta -\varphi \left(Y-\frac{M}{K_0}\right)\left(\frac{K_0}{K_{fl}}-1\right)=0 $$
(16)

where γ is the coefficient related to Poisson’s ratio, β is the Biot coefficient, φ is the porosity, M is the longitudinal wave modulus, and K0 and Kfl are the rock matrix mineral bulk modulus and fluid bulk modulus, respectively.

Combined with the Poisson ratio of dry rock, Russell fluid factor, and Gassmann fluid factor, according to the relative relationship between Krief empirical relationship and bulk modulus, the interval of matrix mineral modulus is determined and calculated (Mainprice 2015). The upper and lower limits of the interval are substituted into the above formula. If the absolute value of the difference between the two fluid factors is less than the initial value, the modulus corresponding to the small initial value can be selected to determine the matrix mineral modulus parameters (rock matrix bulk modulus, shear modulus, and Poisson’s ratio to dry rock).

A set of parameters was proposed to characterize the elastic properties (Chekhonin et al. 2018) of TI media, which are defined as follows:

$$ \left\{\begin{array}{c}\varepsilon =\frac{c_{11}-{c}_{33}}{2{c}_{33}}\\ {}\gamma =\frac{c_{66}-{c}_{44}}{2{c}_{44}}\\ {}\delta =\frac{{\left({c}_{13}-{c}_{44}\right)}^2-{\left({c}_{33}-{c}_{44}\right)}^2}{2{c}_{33}\left({c}_{33}-{c}_{44}\right)}\end{array}\right. $$
(17)

In practical application, the elastic matrix and anisotropic parameters can be obtained by using different models.

Rock physics model

Xu-White model

The bulk modulus of the rock matrix is known, and the Xu-White model is substituted to invert the equivalent rock aspect ratio, P wave velocity, and S wave velocity. This paper studies based on the crack model, that is, only considers the case where the aspect ratio is less than one. When the absolute value of the difference between P wave velocity and measured value of saturated rock is the smallest, the corresponding equivalent rock aspect ratio is obtained (Mallick et al. 2017).

Hudson model

The results of the first two steps are substituted into the Hudson cracked model. According to the conversion relationship between elastic constants in linear elastic anisotropic media summarized by Birch, it can be seen that Lame constant can be converted to bulk modulus and shear modulus. Thus, the background modulus, the first-order correction, and the second-order correction can be calculated. From the equivalent modulus of elasticity, the anisotropic elastic parameters of Thomsen can be obtained (Togashi et al. 2018). Among them, ε describes the difference of P wave velocity in horizontal and vertical directions, γ describes the difference of SH wave velocity and SV wave velocity in a horizontal direction, and δ is a comprehensive reflection of P wave and S wave velocity (Price et al. 2017).

Hudson model

The Hudson model is based on the analysis of the diffusion principle of effective waves in a thin coin elliptical elastic solid medium (Zhang 2019). The effective elastic modulus is given by the following formula:

$$ {c}_{ij}^{eff}={c}_{ij}^0+{c}_{ij}^1+{c}_{ij}^2 $$
(18)

where \( {c}_{ij}^0 \) represents the same background modulus, \( {c}_{ij}^1 \) is the first-order correction which is the correction term generated by the independent action of each crack, and \( {c}_{ij}^2 \) is the second-order correction which is the correction term generated by the mutual coupling of the cracks. The model assumes that the fracture shape is a thin coin shape and its application range is the fracture density e < 0.1.

Eshelby-Cheng model

The equivalent modulus model of transversely isotropic jointed rock is given. It is based on the static solution of internal strain in isotropic solid minerals with ellipsoidal inclusions (Zhang et al. 2016a, b). For an ellipsoidal fracture filled with liquid along three axes in the vertical direction of a fracture, the equivalent modulus of rock is as follows:

$$ {c}_{ij}^{eff}={c}_{ij}^0+\varphi {c}_{ij}^1 $$
(19)

where φ is the porosity, \( {c}_{ij}^0 \) is the same as the background modulus, and \( \varphi {c}_{ij}^1 \) is the correction term.

Schoenberg model

Schoenberg linear sliding model is proposed based on the Backus average. The elastic matrix of the model is:

$$ C=\left(\begin{array}{cc}\begin{array}{ccc}{M}_b\left(1-{\Delta }_N\right)& {\lambda}_b\left(1-{\Delta }_N\right)& {\lambda}_b\left(1-{\Delta }_N\right)\\ {}{\lambda}_b\left(1-{\Delta }_N\right)& {M}_b\left(1-{\Delta }_N\right)& {\lambda}_b\left(1-{\Delta }_{\mathrm{N}}\right)\\ {}{\lambda}_b\left(1-{\Delta }_N\right)& {\lambda}_b\left(1-{\Delta }_N\right)& {M}_b\left(1-{\Delta }_N\right)\end{array}& \begin{array}{ccc}\kern0.5em 0\kern1.25em & 0\kern2em &\ 0\kern1.25em \\ {}0\kern0.75em & 0\kern2em &\ 0\kern1.25em \\ {}0\kern0.75em & 0\kern2em &\ 0\kern1.25em \end{array}\\ {}\begin{array}{ccc}\kern0.5em 0\kern0.5em & \kern0.5em 0\ & \kern1em 0\kern0.5em \\ {}0&\ 0& \kern0.5em 0\\ {}0&\ 0& \kern0.5em 0\end{array}& \begin{array}{ccc}{\mu}_b& 0& \kern0.5em 0\\ {}0& {\mu}_b\left(1-{\Delta }_T\right)& \kern0.5em 0\\ {}0& 0& {\mu}_b\left(1-{\Delta }_T\right)\end{array}\end{array}\right) $$
(20)

where Mb = λb + 2μb, rb = λb / Mb; Schoenberg gives the relationship between the linear sliding model and Hudson:

$$ \left\{\begin{array}{c}{\Delta }_N=\frac{\lambda +2\mu }{\mu }{U}_3\varepsilon \\ {}{\Delta }_T={U}_1\varepsilon \end{array}\right. $$
(21)

Hornby model

The Hornby model is established by the combination of self-consistent approximation (SCA) model and differential effective medium (limn, DEM) model. It mainly compares the anisotropic elastic relationship between mineral components in solid rocks. Both the SCA model and the DEM model are typical isotropic effective medium models: SCA model takes into account the influence of pore shape and porosity. If multi-phase medium does not disperse, it can be said that the background value of elastic modulus is equal to that of an effective elastic modulus. The two-phase medium in the DEM model is usually different. The effective modulus of elasticity can be determined by calculating the effective modulus of elasticity, using the first phase as the matrix and another mineral as an isolated inclusion (Zhang 2017a, b).

Brown-Korringa model

The Brown-Korringa model is a commonly used model for dry anisotropic media, focusing on the relationship between effective elastic tensors in rocks, mainly referring to anisotropic dry rocks and fluid-saturated rocks, which are related to the compressibility of pore fluids and minerals and porosity of rocks. The relationships are as follows: (1) the effective elastic tensor of the dry rock; (2) the effective elastic tensor of the rock saturated pore fluid; (3) the effective elastic tensor of the rock mineral; (4) the compressibility of the pore fluid; (5) the compressibility of minerals.

The Brown-Korringa model is a typical fluid replacement model that describes the properties of an anisotropic fluid and the saturation of the fluid, and the effect of the fluid on the effective elastic tensor can also be reflected by the model (Brownlee et al. 2017).

Conclusion and prospect

Since it is very difficult to study the anisotropy of rock mass in the general sense, the current research scope mainly focuses on anisotropic rock mass problems under orthorhombic and transverse isotropic conditions. These two models have basically met the needs of solving most anisotropic engineering problems. However, due to the complexity of rock anisotropy, the research on yield criterion and the constitutive relationship of rock anisotropy is still in the stage of theoretical research and is seldom applied in actual rock engineering. This is because the anisotropic yield criterion and its constitutive relationship are very complex, and there are many parameters, so it is very difficult to get the values of parameters. Orthorhombic or transverse isotropic yield criteria and constitutive relations cannot be expressed by explicit mathematical formulas and can only be calculated by numerical methods. The calculation process is complex and the amount of calculation is huge.

Therefore, in the future research, we can focus on the following aspects of research:

  • The mechanical properties of engineering rock mass anisotropy are a very complex project. How to adopt effective theoretical methods, experimental means, and numerical analysis software to study the basic physics properties, mechanical parameters, and strength theory of anisotropic rock mechanics is of great importance to understand and grasp the anisotropy of engineering rock mass.

  • In the diagenesis process and the crustal movement after diagenesis, the rock can form layers such as bedding, joints, and faults. The existence of these planar structures will inevitably lead to the anisotropy of rock strength. The rock failure envelope sometimes exhibits obvious nonlinear properties. Many data indicate that the failure envelope of soil is close to a straight line, the soft rock is parabolic, and the hard rock can be regarded as hyperbola or cycloid. In addition, due to the uneven distribution of material composition and the uneven arrangement of structure, the mechanical properties of rocks show heterogeneity. In the non-uniform temperature field, rock strength is also affected. Combining the above properties, it is necessary to establish a heterogeneous nonlinear anisotropic rock failure, which will have certain theoretical and practical significance for solving engineering problems in complex rock masses.

  • The selection of rock physics model should be specific to the geological conditions. The influence of crack density and crack shape aspect ratio on crack normal and tangential compliance can be used to characterize the relevant characteristics of the reservoir, which is of great significance for inversion of fracture parameters.

  • On the basis of the preliminary experimental study, a series of systematic experimental studies have been carried out considering the loading modes closer to the anisotropic failure process of rock mass (such as earthquake incubation process), such as elastic deformation stage, non-fixed rate, and stress repeated loading mode. The resistivity in the process of rock anisotropy research should be discussed in depth. The variation rule of an image can be used to judge whether it can be used as an anomalous possibility of seismic resistivity.