Introduction

The method of curve number (CN) for estimation of direct runoff in a catchment from storm rainfall is becoming a fundamental technique in flood impact analyses, design of hydraulic structures, and hydrological engineering studies (Ponce 1996). The technique was developed by the Soil Conservation Service (SCS) in 1954 (Rallison 1980), and was described in NRCS National Engineering Handbook Section 4 (NEH-4) (USDA-SCS 1985). The Soil Conservation Service (SCS) name has been changed in 1994 to Natural Resources Conservation Service (NRCS). The NRCS-CN method is based on the principle of the mass conservation law and two essential hypotheses given by Mishra and Singh (2002). The first hypothesis says that the ratio of direct runoff, Q, to potential maximum runoff (P-Ia), where Ia is the initial abstraction, is identical to the ratio of infiltration, F, to potential maximum retention, S. The second hypothesis says that Ia is proportional to the potential maximum retention, S (i.e., Ia = λ S). The NRCS-CN method equations which are introduced by the USDA-SCS (1985) and USDA-NRCS (2004) are given by:

$$ Q=\left\{\begin{array}{c}\frac{{\left(P-\lambda S\right)}^2}{P+\left(1-\lambda \right)S},\kern0.5em P>\lambda S\\ {}0,\kern0.5em P\le \lambda S\end{array}\right. $$
(1)

Where P is the rainfall depth, Q is the direct runoff depth (effective rainfall), λ is the initial abstraction ratio, and S is the potential maximum retention of the catchment.

There is no specific approach to estimate NRCS-CN from rainfall-runoff events. Through the review of literature, it has been shown that many formulas are presented, e.g., USDA-SCS (1972); Rallison and Cronshey (1979); Hjelmfelt (1980); Rallison and Miller (1982); Hawkins et al. (1985); Zevenbergen (1985); Hawkins (1993). These formalisms show different ways in handling measured precipitation (P) and runoff (Q) data for 24-h rainfall duration. However, in arid regions, most storms have short durations which are less than 24 h with intense rainfall. These storms are considered in the analysis.

Several studies have been conducted to describe the variability of the curve number (CN). Most of these studies, if not all, are performed in climate conditions that are not arid or semi-arid like Saudi Arabia. Moreover, the catchments that have been considered in most of these studies are agriculture catchments; therefore, the tables of the NRCS-CN method are mainly estimated based on these types of catchments, e.g., Rallison (1980); Rallison and Miller (1982); McCuen (1982); Hjelmfelt (1991); Rawls and Maidment (1993); Pilgrim and Cordery (1993); Hawkins (1993); Banasik et al. (1994); Ponce (1996); Schneider and McCuen (2005); Soulis and Dercas (2007); Soulis and Valiantzas (2012, 2013); and Banasik et al. (2014).

Many studies have dealt with NRCS-CN method to find out a theory behind the method and applications in different regions in the world under various climate conditions. Rallison and Cronshey (1979) presented a document where data from daily precipitation and runoff for yearly flood events were used in the original Soil Conservation Service handbook. A validation technique of the CN procedure was presented in the Soil Conservation Service handbook USDA-SCS (1972) which compared the frequency distributions of the synthesized and measured runoff volumes. Hjelmfelt (1980) estimated CNs from measured data of P and Q pairs by the use of frequency distributions, a CN transformation model, and by fitting techniques. Bonta (1997) used derived frequency distributions as a technique to determine curve numbers from field data, treating rainfall and runoff measurements as discrete distributions. He concluded that the derived distribution method had a potential for determining curve numbers when rainfall and runoff data are limited. According to McCuen (2002) the CN was treated based on the theory of random variables. A general technique is presented to estimate CN for making confidence intervals. Since CN is a value between 0 and 100, it was found that its distribution is negatively skewed. However, common probability distribution are positively skewed; therefore, the use of 100-CN shows positively skewed distributions and consequently is considered in the study. The amount “100-CN” was fitted by the gamma distribution, and therefore, CN confidence intervals were estimated for the range of CN between 65 to 95 of his data.

NRCS-CN adopted the standard value of the initial abstraction ratio, λ (the ratio between initial abstraction, Ia, and the maximum retention potential, S), equals 0.2. The validity and applicability of λ = 0.2 has been questioned by many researchers like Ponce (1996); Hawkins et al. (2001); Jiang (2001); and Baltas et al. (2007). Woodward et al. (2003) stated that the effect of using λ equal to 0.05 in place of 0.20 leads either to lower CNs or lower rainfall depths. However, the values documented in the literature were varying in the range of (0.0 up to 0.3) in a number of studies that include different geographic locations in the US and many countries e.g. Cazier and Hawkins (1984); Ramasastri and Seth (1985); Bosznay (1989); Woodward et al. (2003); Mishra and Singh (2004); and Mishra and Singh (2013). Yuan et al. (2014) stated that the estimation of direct runoff from rainfall using curve number (CN) for semiarid catchments can be inaccurate. The inaccuracy was due to the customary NRCS value of λ equals 0.2. They had shown that runoff estimation is sensitive to the initial abstraction ratio, in case of relatively low rainfall depth and for basins covered by coarse soil conditions that are dominant in many semiarid basins in the world. For Walnut Gulch catchments, optimal values of λ ranging from 0.01 to 0.53 improved runoff estimation. It was concluded that the effect of λ on runoff estimation increases with decreasing the value of CN.

From the aforementioned review of literature on the topic, and to the best of the authors’ knowledge, there is no extensive research work on CN from measurements of rainfall and runoff on arid basins especially in Saudi Arabia except the work by Alagha et al. (2016). They studied the relationship between CN and morphometric parameters of some sub-basins in Saudi Arabia and deduced some empirical equations to estimate CN from the wadi morphology. However, in their study, there was no detailed statistical analysis on the CN values. They considered only a single catchment which made the study not sufficient for a reliable statistical analysis.

The objective of this research is to perform a detailed study on NRCS-CN in arid and semi-arid basins that cover the following items: (1) determining the range of values of the curve number CN and λ under arid conditions in the study region from field measurements of rainfall and runoff events, (2) derivation of the best probability distribution of precipitation, P, runoff, Q, and curve number CN values, and (3) estimation of the confidence intervals of CN values for arid and semi-arid basins. The expected results would improve the flood predictions in arid and semi-arid regions especially in Saudi Arabia and consequently would come up with reliable parameters for the design of the flood protection schemes in the region.

Material and methods

Study area

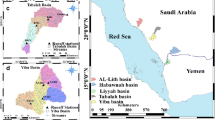
The study basins are located in the southwestern part of Saudi Arabia. The region is located in the eastern Asir escarpment with elevations of up to 3000 m which runs towards the west to the Red Sea coast. Saudi Arabian Dames and Moore (1988) developed a detailed study of five selected basins with their sub-basins (19 sub-basins) which include: Al-Lith, Yiba, Habawnah, Liyyah, and Tabalah basins. Al-Lith, Yiba, and Liyyah basins drain towards the Red Sea. However, Habawnah and Tabalah basins drain from the mountains to the interior, towards the Rub al Khali. Figure 1a shows the geographic location of the study area and the locations of the five basins. Each of these basins is divided into sub-basins with runoff stations at the outlet of the each sub-basin. Figure 1b shows the locations of the runoff basin in each of the five basins. Table 1 summarizes the information for the basins and sub-basins.

Fig. 1
figure 1figure 1

(a) Location of the studied basins in the southwestern part of Saudi Arabia. (b) The studied basins and locations of the runoff stations

Full size image
Table 1 Summary of the basins and the sub-basins data
Full size table

Data collection

The data has been measured by Saudi Arabian Dames and Moore (1988). They installed an extensive measuring network. In arid region in general and in Saudi Arabia in particular, runoff measurements are often rare. The only limited detailed runoff measurements are found in the period 1984–1987. The company that made such measurements had a contract with the ministry for 4 years. During these 4 years, there were 161 storms recorded in the study area which are considered statistically acceptable. In the current study, the climate change is out of the scope of this study and could be considered in the future if there would be extra measurements. Figure 2 shows a sample of rainfall and runoff events (27 April 1985) on station N-404 in Habawnah basin, in the south-west of Saudi Arabia.

Fig. 2
figure 2

Sample of rainfall and runoff events at station N-404 in wadi Habawnah, South-West Saudi Arabia (event date 27 April 1985), Saudi Arabian Dames and Moore (1988)

Full size image

Estimation of the CN and λ

Since P and Q data are available for the study catchments, P and Q pairs are used directly to estimate the maximum potential retention, S, characterizing the catchment as (Chen 1982),

$$ \mathrm{S}=\frac{\mathrm{P}}{\uplambda}+\frac{\left(1-\uplambda \right)\mathrm{Q}-\sqrt{{\left(1-\uplambda \right)}^2{\mathrm{Q}}^2+4\lambda \mathrm{PQ}}}{2\ {\uplambda}^2} $$
(2)

Assuming λ = 0.2 (the common value), Eq. (2) becomes the common quadratic formula for S (Hawkins 1973) as,

$$ \mathrm{S}=5\left[\left(P+2\mathrm{Q}\right)-\sqrt{Q\left(4\mathrm{Q}+5\mathrm{P}\right)}\right] $$
(3)

and,

$$ \mathrm{CN}=\frac{25400}{\mathrm{S}+254} $$
(4)

In the current analysis, three different ways of the estimation of CN and λ are suggested as follows:

  1. Method 1:

    estimation of CN and λ from all events on the sub-basins of each basin to obtain the best values. The obtained values are called λbest and CNbest.

  2. Method 2:

    estimation of CN at λ = 0.2 (the common value) from all events on the sub-basins for each basin to obtain the value for CN at λ = 0.2. This is called CN(λ = 0.2), and.

  3. Method 3:

    estimation of CN and λ from each event on the sub-basins of the basin to obtain the best values per event and averaging over the number of events. The obtained values are called \( {\overline{\lambda}}_{\mathbf{best}} \), and \( {\overline{\mathbf{CN}}}_{\mathbf{best}} \).

Figure 3 shows a flowchart of the procedure used to estimate CN for every storm at each sub-basin based on inverse modeling technique. The details of the procedure is presented in the following section.

Fig. 3
figure 3

Flowchart illustrates the estimation of CN from rainfall and runoff data

Full size image

The Least Squares Method

The LSM for CN estimation was introduced by Hawkins et al. (2002) and Hawkins et al. (2008). The method determinates the parameters λ and CN of the well-known runoff equation. The LSM is a minimization of the sum of squared differences between the observed direct runoff (Q) and the estimated runoff \( \left(\hat{Q}\right) \). It gives the best estimation, of the parameters. In the current study, the application of the least square method is made by using Excel solver in Microsoft Excel. The implementation of the optimized procedure in Excel solver provides λbest and CNbest, where λbest and CNbest are the best values of λ and CN for each rainfall-runoff event. Also, the same procedure is used for estimation of λbest and CNbest for each sub-basin as a representative value from the recoded storms on the sub-basin. The mathematical formulation of the optimization problem is given below. The estimated runoff \( \hat{Q} \) equation is obtained by Mishra and Singh (2013),

$$ \hat{Q}=\frac{{\left[P-254\lambda \left(\frac{100}{\mathrm{CN}}-1\right)\right]}^2}{P+254\left(1-\lambda \right)\ \left(\frac{100}{\mathrm{CN}}-1\right)} $$
(5)

The minimization problem is formulated by the objective function as Hawkins et al. (2008),

$$ \mathrm{f}\left(\mathrm{CN},\lambda \right)=\min \sum \limits_{\mathrm{i}=1}^{\mathrm{n}}{\left({Q}_{\mathrm{i}}-{\hat{Q}}_{\mathrm{i}}\right)}^2 $$
(6)

Where: Qi is the observed runoff (mm), \( {\hat{Q}}_i \) is the estimated runoff (mm), and n is the no. of observations.

Testing of distribution for rainfall, runoff and CN using Kolmogorov-Smirnov test (K-S test)

The K-S test (Hamed and Rao 1999) was used to test the hypothesis based on the following:

$$ {H}_{{}^{\circ}}:\mathrm{z}\ \mathrm{distributed}\ \mathrm{as}\kern0.5em \mathrm{the}\ \mathrm{specified}\ \mathrm{distribution}. $$
$$ {H}_1:\mathrm{z}\ \mathrm{is}\ \mathrm{not}\ \mathrm{distributed}\ \mathrm{as}\ \mathrm{the}\ \mathrm{specified}\ \mathrm{distribution}. $$

Where, Ho is the null hypothesis, H1 is the alternative hypothesis, and z is the parameter under consideration, i.e., rainfall, runoff, CN, or 100-CN. This test compares the cumulative distribution function of a specified distribution, and the empirical cumulative distribution function for a sample size n. The K-S test (Hamed and Rao 1999) looks at the max difference as given by,

$$ \mathrm{K}-\mathrm{S}={\max}_{\mathrm{i}=1,\dots, \mathrm{n}}\left|G\left({z}_i,\theta \right)-{G}_n\left({z}_i\right)\right| $$
(7)

Where, G(zi, θ) is the assumed cumulative distribution function with parameters θ, and Gn(zi) is the empirical cumulative distribution functions.

If the calculated value of the K-S test is greater than the tabulated value, the null hypothesis can be rejected at the level of significance α.

Many distributions can represent the data, however, to find out the best out of these distributions, the Akaike Information Criterion (AIC) is computed as given by Laio et al. (2009),

$$ \mathrm{AIC}=-2\sum \limits_{i=1}^n\mathit{\ln}\ g\left({z}_i\right)+2N $$
(8)

Where, g(zi) is the probability density function of the theoretical model evaluated at zi and N is the number of parameters of the theoretical model. The minimum value of the AIC provides the best distribution to represent the data.

Estimation of confidence intervals

The confidence interval is widely used in statistical analysis. It describes the variability and accuracy of the parameter under study. In this paper, the confidence intervals were computed for CN. Since the CN shows gamma distribution at λ = 0.2 and to make values comparable with the antecedent moisture condition (AMC-CN) tables, therefore, the confidence equations of the gamma distribution are given herein. The confidence intervals for the gamma distribution are expressed mathematically as (Kite 1977; and Hamed and Rao 1999),

$$ CL=\overline{\mathrm{CN}} \pm \left[\left(\frac{\upchi^2\upgamma}{4}\right)-\left(\frac{2}{\upgamma}\right)\right]\upsigma $$
(9)
$$ {\upchi}^2=\upnu {\left[1-\left(\frac{2}{9\upnu}\right)+\mathrm{u}\sqrt{\frac{2}{9\upnu}\ }\ \right]}^3 $$
(10)
$$ \upnu =\frac{8}{\ {\upgamma}^2} $$
(11)

where: CL is the confidence intervals, \( \overline{\mathrm{CN}\ } \) is the average curve number (CN), χ2 is the chi-square value at probability, p, γ is the skewness coefficient, σ is the standard deviation, ν is the degrees of freedom, and u is the standard normal variate for the p value (0.9,…, and 0.995).

Results and discussions

Analysis of CN and λ

Table 2 summarizes the estimated values of CN and λ based on the estimation methods described in “Estimation of the CN and λ” It is obvious from the table (the second and third columns) that λbest and CNbest provide the lowest estimation values which may account for unrealistically high transmission losses in the basins. The table shows λ = 0 in three basin out of five. This also explains the reason why low CN values are obtained since most of the losses are due to infiltration and no abstraction losses which it seems unrealistic. Figure 4 shows a conceptual model for the relationship between losses in the SCS-CN method. There are two kinds of losses namely: the abstraction losses described by λ and the infiltration losses described by the CN. The high value of λ leads to high values of CN and vise-versa for a given rainfall and runoff. In arid regions where transmission losses, due to high infiltration in a dry bed, are the main feature in arid and semi-arid regions would lead to having a low CN values and consequently low value of λ. In the case of CN(λ = 0.2), which appears in the fifth and sixth columns in the table, the values of CN are the highest. The value of λ = 0.2 does not reflect the behavior of an arid basin (i.e., incorporating transmission losses in the CN). This result is also confirmed by the work presented by Yuan et al. (2014). The third estimation method, which appears in the eighth and ninth columns in the table, shows the case of \( {\overline{\boldsymbol{\uplambda}}}_{\mathbf{best}} \) and \( {\overline{\mathrm{CN}}}_{\mathbf{best}} \). The estimated values fall in between the two above cases. This is because it is an averaging over the results of every event. The third estimation method seems to provide more realistic values for arid basins with realistic transmission losses since λ does not equal to zero and therefore the values of CN are not too low. It is also obvious from Table 2 that average values of λ and CN for all wadis are 0 and 34 for estimation method 1, 0.2, and 68.69 for estimation Method 2, and 0.0105 and 51.99 for estimation Method 3 respectively. The average correlation coefficient between estimated and observed effective rainfall is moderate (0.61) for both estimation Methods 1 and 3 while it is low for estimation Method 2 (0.36). This confirms that λ = 0.2 is not suited for such wadis and the appropriate values of λ lies between 0 and 0.0105. However, the value of λ = 0.0105 seems to be more realistic since the corresponding CN of 52 is within the acceptable field data in SCS-CN table (National Engineering Handbook Section 4 (NEH-4) USDA-SCS (1985). The last row in Table 2 shows the results of the three estimation methods considering all the wadis. The results show that the estimation Methods 1 and 3 provides the highest correlation of 0.86, while, the second estimation method provides a correlation of 0.75.

Table 2 Summary of the Statistical Analysis of CN and λ
Full size table
Fig. 4
figure 4

Conceptual model of the relationship between the losses in NRCS-CN method: Abstraction losses (λ) and infiltration losses (CN)

Full size image

Figure 5 shows scatter plots between estimated and observed effective rainfall based on the three estimation methods for wadi Yiba (left column) as a sample and for all wadi (right column). The corresponding correlation coefficient for each estimation method is presented in Table 2 for each wadi and for all wadis. Wadi Al-Lith and Yiba show the highest correlation coefficients amongst the wadis for the three estimation methods. Wadi Tabalah and Liyyah provide moderate correlation for estimation Methods 1 and 3, while poor correlation of estimation Method 2. Wadi Habawnah shows poor correlation for the three estimation methods. The worst correlation is for Method 2. The results of such analysis confirm that λ =0.2 is not a good choice for flood modeling in such area that covers the western part of Saudi Arabia.

Fig. 5
figure 5

Scatter plot for the observed and estimated effective rainfall based the different estimation methods for wadi Yiba as an example and all wadis: First row is Method 1 at (λbest and CNbest), second row is Method 2 at CN(λ = 0.2) and third row is Method 3 at \( {\overline{\lambda}}_{\mathrm{best}} \) and \( {\overline{\mathrm{CN}}}_{\mathrm{best}} \)

Full size image

Figure 6 shows a relationship between CN and λ. The relation confirms the conceptual model of SCS-CN loss model presented in Fig. 4. The figure shows a coefficient of determination, R2, equals to 0.45 which is relatively moderate relationship between CN and λ. This relationship helps in estimating a meaningful value of λ based on CN in the basin and not relying on the customary value of 0.2.

Fig. 6
figure 6

Relationship between initial abstraction ratio λ and curve number CN for the averaging over the events (i.e., \( {\overline{\lambda}}_{\mathrm{best}} \) and \( {\overline{\mathrm{CN}}}_{\mathrm{best}} \))

Full size image

General descriptive statistics and probability distribution of P, Q, and CN

An Excel sheet is designed to calculate the descriptive statistics for grouped and ungrouped data and also to perform hypothesis testing for fitting theoretical a probability distribution function to the data. The main statistical measures of the data are presented in Table 3. These statistics provide the arithmetic mean, standard deviation, SD, skewness coefficient,γ, kurtosis coefficient, median and coefficient of variation, CV, respectively as sorted in the table. The CV for rainfall is 1.13 that shows relatively high degree of variability which is common in arid regions. However, for the runoff the CV is 2.51 which shows much more variability than in rainfall. It is clear from the table that the rainfall and runoff data are highly skewed since the coefficient of skewness is ranging between 3.28 and 6.79 respectively that is far from zero and it is negatively skewed. This observation reflects the relatively high frequency of low values of rainfall and runoff. For CNbest, the CV is relatively higher than CV for CN(λ = 0.2). However, both show relatively low coefficient of variation when compared with rainfall and runoff. This reflects that the variability in CN is less than the variability in rainfall and runoff. The coefficient of variation shows low degree of variability for CNbest while negligible variability is observed for CN(λ = 0.2). The skewness coefficient for CN is less than zero (i.e., it is positively skewed). This means the large values of CN has high frequency than the low CN values. This result is on the contrary of the skewness of rainfall and runoff.

Table 3 Summary of the statistical analysis
Full size table

The kurtosis indicates peaked distribution w.r.t. the normal distribution in both rainfall and runoff, since the values are larger than three, which is called leptokurtic. The minus sign in the table for the kurtosis is due to the subtraction of 3 to make it comparable with the normal distribution. The runoff distribution is extremely peaked when compared with the rainfall distribution since the kurtosis is 54.24 and 13.8 respectively. Sometimes, researchers prefer to use 100-CN instead of CN to perform statistical analysis, e.g., McCuen (2002). Therefore, in the current study both CN and 100-CN are considered. The mean for 100-CN is different from the mean of CN however, the SD is the same for both. The100-CN is negatively skewed. The kurtosis is the same as for CN. The coefficient of variation, CV, of 100-CN is higher than CV for CN. For CN(λ = 0.2) and 100-CN(λ = 0.2) the kurtosis is 1.37 which is low peaked, while in the cases of CNbest, and 100-CNbest, the kurtosis is less than three that is called platykurtic.

Several probability distribution functions (e.g., Gaussian, log-normal, exponential, gamma, beta, and Gumbel) are used to test the data. Tables 4, 5, and 6 display the results of the Kolmogorov-Smirnov (K-S) test. The results show that the K-S test accepts some distributions. According to Table 4, most cases give more than one distribution. The suitable distribution can be selected by comparing K-S sample values and K-S critical value. The lower value of the K-S sample than the K-S critical, the best is the distribution.

Table 4 Summary of the hypothesis testing results at significant level (α = 0.05)
Full size table
Table 5 K-S test values compared with critical values
Full size table
Table 6 AIC for K-S test
Full size table

Figure 7 (first row) presents the cumulative distribution of the rainfall and runoff depths from all wadis and fitting of different theoretical distribution functions. According to the K-S test at 5% significant level, the log-normal distribution seems to fit well the data for both rainfall and runoff depths (see Tables 4 and 5). However, exponential distribution seems to fit also the rainfall depth. According the AIC criterion, the log-normal is the best as shown in Table 6.

Fig. 7
figure 7

Fitting probability distribution function: First row, rainfall depth (left) and runoff (right), second row, CN at λ = 0.2 (left) and CNbest (right), and third row, 100-CN at λ = 0.2 (left) and 100-CNbest (right)

Full size image

Figure 7 (second row) and Fig. 8 (first row) present the cumulative distribution form the data and the frequency histogram of CN(λ = 0.2) and CNbest respectively. The K-S test at 5% significant level (Table 4) shows that Gaussian, gamma, and beta distribution can be accepted for CNbest; however, beta distribution is accepted for CN(λ = 0.2). The AIC criterion shows that Beta distribution is the best for both (Table 6).

Fig. 8
figure 8

Frequency histogram of CN and 100-CN compared with different theoretical frequency distribution (CN is presented in the top row and 100-CN is presented in the bottom row) for λ = 0.2 (left) and CNbest (right)

Full size image

Figure 7 (third row) and Fig. 8 (second row) presents the cumulative distribution for the data and the frequency histogram of 100-CN(λ = 0.2) and 100-CNbest respectively. Table 4 shows the results of the K-S at 5% significant level. Gaussian and beta can be accepted for 100-CNbest, However, for 100-CN(λ = 0.2) Lognormal, gamma and beta can be accepted. The AIC criterion presented in Table 6 confirms that beta distribution is the best. It is worse mentioning that the acceptance of gamma distribution for 100-CN(λ = 0.2) is in agreement with earlier results of (McCuen 2002) for agricultural catchments in USA. However, beta seems to be the best for the study wadis in Saudi Arabia.

Confidence intervals of CN

The confidence bounds are presented in Table 7 for CNs ranging from 45 to 85, which is the approximate range for the sample values of CN from the five basins in SA. Limits for probabilities (1-α) of 0.90, 0.95, 0.975, 0.99, and 0.995 were obtained from the cumulative distribution. Figure 9 shows limits of curve number and relationship between \( \overline{\mathrm{CN}\ } \) average curve number, CNU upper limit of CN at confidence level (1-α) and CNL lower limit of CN at confidence level (1-α). Figure 10 shows relationship between AMC CNs from National Engineering Handbook USDA-SCS (1963) at dry (AMCI) and wet (AMCIII) and the upper and lower bounds of CN at different confidence levels of 0.90, 0.95, 0.975, 0.99, and 0.995 calculated in this study. Form the analysis, it is found out that the AMC I and III bounds are wider than by as much as 9 CNs at confidence level 0.90. Table 8 shows the maximum difference between AMC bounds and the confidence Limits obtain in this study based on different confidence levels. Maximum at 0.90 and minimum at confidence level 0.975, 0.99, and 0.995.

Table 7 Confidence limits for selected levels of confidence and runoff curve number
Full size table
Fig. 9
figure 9

Limits of the curve number: \( \overline{\mathrm{CN}\ } \) average curve number, CNU is the upper limit of CN at confidence level (1-α) and CNL is the lower limit of CN at confidence level (1-α)

Full size image
Fig. 10
figure 10

Comparison between CN confidence limits and AMCI and AMCIII. The Source for AMCI and AMCIII is the National Engineering Handbook USDA-SCS, (1963), AMCI: antecedent moisture condition I and AMCIII: antecedent moisture condition III

Full size image
Table 8 Max different between AMC CNs and CNU and CNL
Full size table

Conclusions

The current study leads to the following conclusions. From the statistical analysis of the data, it was found out that CN is event dependent. Therefore, the range of CN varied between 45 and 85 from the studied basins which deviates from the rural basins studied by McCuen (2002) that varied between 65 to 95. The reason is due to the transmission losses in the arid basins which provides lower CN values. The descriptive statistics showed a positively skewed distribution and kurtosis was leptokurtic for both rainfall and runoff. The statistical tests for rainfall and runoff exhibited log-normal distribution. The average initial abstraction ratio \( \overline{\lambda} \)best was found to be 0.0105. This value is falling within the limits of the common range available in the literature (0.0–0.3). Since the average correlation coefficient between estimated and observed runoff is 0.61 at λ = 0.0105 (based on average) and 0.86 at λ = 0.0091 (based on all wadis) while it is 0.36 at λ = 0.2 (based on average) and 0.75 at λ = 0.2 (based on all wadis), therefore, the value of λ ≈ 0.01 seems to best represent the runoff in the study area. The value of λ = 0.01 is more suited to arid region rather than the common value of 0.2, since it leads to low value of CN that accounts for the transmission losses in the wadi. The statistical tests for (100-CN) at λ = 0.2 showed that the gamma and beta distributions are the best for describing the variability of (100-CN). These results are in agreement with the results of McCuen (2002) for the gamma distribution. The analysis for CN showed that the beta distribution is the best at λ = 0.2 and \( \overline{\lambda} \)best = 0.01. In this study, the confidence intervals for CN have been estimated and tabulated in Table 7 for different confidence levels ranging from 0.9 up to 0.995. These values are recommended to be used in the design of hydraulic structures in arid regions for risk-based analysis under uncertainty.