Introduction

Mean sea level change is a considerable interest variable in the climate change studies. The measurement of changes in sea level can provide an important corroboration of predictions by climate models of global warming. For the past century, global mean sea level rise has occurred at a mean rate of 1.8 mm/year (Douglas 1997; Church and White 2006) and more recently, during the satellite era of sea level measurement, at rates estimated near 2.8 ± 0.4 mm/year (Chambers et al. 2003) to 3.1 ± 0.7 mm/year (Bindoff et al. 2007) (1993–2003). AVISO Altimetry (2011) estimated a rate of 3.20 mm/year during the period 1993 to mid-2011.

This sea level rise is due significantly to global warming (Bindoff et al. 2007), which will increase the sea level over the coming century and longer periods (Meehl et al. 2007). Increasing temperatures result in sea level rise by the thermal expansion of water and through the addition of water to the oceans from the melting of mountain glaciers, ice caps, and ice sheets. At the end of the twentieth century, thermal expansion and melting of land ice contributed roughly equally to sea level rise, while thermal expansion is expected to contribute more than half of the rise in the upcoming century (Bindoff et al. 2007).

In 2007, the Intergovernmental Panel on Climate Change's Fourth Assessment Report (AR4) predicted that by 2100, global warming will lead to a sea level rise between 180 and 590 mm (IPCC 2007a), depending on which of six possible world scenarios comes to pass and barring rapid dynamical changes in ice flow (IPCC 2007b). More recent research, which has observed rapid declines in ice mass balance from both Greenland and Antarctica, finds that sea level rise by 2100 is likely to be at least twice as large as that presented by IPCC AR4, with an upper limit of about 2 m (Allison et al. 2009). Based on the projected increases in global sea level, the IPCC-TAR WG II report notes that current and future climate change would be expected to have a number of impacts, particularly on coastal systems (IPCC 2001).

Although the global trend indicates a rise in the mean level of the oceans, there are marked regional differences that vary between −10 and 10 mm/year (AVISO Altimetry 2011). There are several “suspects” which may be responsible for the nonuniformity in regional trends: regional changes in thermal expansion, water mass adding to the oceans, and melting of continental ice which leads to the significant geographic variations in the sea level change (Jevrejeva et al. 2006).

In this paper, we analyze 18 monthly sea level time series from satellite altimeters to determine the variability of different large ocean regions using an automatic approach of trend extraction within the framework of the singular spectrum analysis (SSA) technique. The used approach has been first proposed in Alexandrov and Golyandina (2005) and was studied in detail in the author's unpublished Ph.D. thesis (Alexandrov 2006) available only in Russian in AutoSSA (2005). This method is easy to use, facilitates the batch processing, does not need specification of models of time series and trend, and allows to extract trend in the presence of oscillations and noise.

The remainder of the paper is organized as follows. “Altimetry data used” introduces the geometric principle of altimetry and describes the altimetry time series datasets used in this study. The SSA method, briefly explained in “Methodology,” is a data-adaptive tool allowing signal decomposition and a precise quantification of trend, low-frequency components, and seasonal cycles. Furthermore, the related method used for automatic trend extraction is elucidated in this section. Following this description, the results are presented in “Empirical analysis.” Finally, the conclusions are provided.

Altimetry data used

Radar altimeters permanently transmit signals to Earth and receive the reflected echo from the sea surface. The satellite orbit has to be accurately tracked, and its position is determined relative to a reference surface (an ellipsoid). The sea surface height (SSH) is calculated by subtracting the measured distance between the satellite–sea surface from the precise orbit of the satellite. The sea surface height anomalies (SSHA), defined as variations of the SSH with respect to a priori mean sea surface, are generally used as a precious and main indicator for development of scientific applications which aims to study the ocean variability (mesoscale circulation, seasonal variation, El Niño,…).

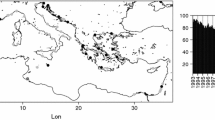
In our research, we investigate 18 SSHA times series from TOPEX, Jason-1, and Jason-2 altimeters. These time series are defined as the area averaged of SSHA at different scales: global scale, Atlantic Ocean, Indian Ocean, Pacific Ocean and Adriatic Sea, Andaman Sea, Arabian Sea, Bay of Bengal, Bering Sea, Caribbean Sea, Gulf of Alaska, Gulf of Mexico, Indonesian Throughflow, Mediterranean Sea, Sea of Japan/East Sea, South China Sea, Yellow Sea, and Maldives. Figure 1 (from the University of Colorado) shows the localization of the sea regions.

Fig. 1
figure 1

Map of the sea regions

Full size image

These data sets were obtained from the University of Colorado at Boulder and are available under the KNMI Climate Explorer website (KNMI Climate Explorer 2012). These datasets cover the period from January 1993 to the end of 2010, with a sampling rate of 1 month. The main input data for these time series processing are the Geophysical Data Records produced by NASA and CNES (TOPEX, Jason-1, Jason-2), which are therefore of the highest quality, notably in orbit determination. All of the standard corrections to the altimeter range were applied to the SSH including removal of ocean tides and an inverted barometer correction. Table 1 describes the parameters and corrections used by the University of Colorado in the computing of sea level time series.

Table 1 Altimetry data processing parameters and corrections
Full size table

Methodology

The SSA technique decomposes the original time series into a sum of a small number of interpretable components such as slowly varying trend, oscillatory components, and noise. The basic SSA method consists of two complementary stages: decomposition and reconstruction; each stage includes two separate steps. At the first stage, we decompose the series, and at the second stage, we reconstruct the noise free series (for more information, see Golyandina et al. 2001 and Hassani 2010). Furthermore, several book chapters, papers, and software about the SSA technique are available in SSAwiki (2012). Note that the possible application areas of the SSA technique are diverse: from mathematics and physics to economics and financial mathematics, from meteorology and oceanology to social sciences and market research. For a variety of applications of SSA, see Hassani (2007, 2009, 2010), Hassani and Thomakos (2010), Hassani and Zhigljavsky (2009), Hassani et al. (2009a, b; 2010a, b; 2011), Ghodsi et al. (2009, 2010), and Patterson et al. (2011) and references therein.

Within the framework of SSA, the trend is defined as a smooth component containing information about time series global change. A simple approach to trend extraction in SSA is to reconstruct a trend from several first SVD components (by visual examination of singular values and vectors). However, this approach fails when the values of a trend are small enough as compared with other components (oscillations and noise), or when a trend has a complicated structure and is characterized by many (not only by the first ones) SVD components (Alexandrov et al. 2008). Here, we present the used approach for automatic identification of slowly varying eigenvectors (trend). Although the basic components of this method are reviewed here, readers are referred to Alexandrov (2009) for more details.

Let us consider the periodogram I Y (ω) of a vector \( Y\in {{\mathbb{R}}^M} \), \( Y={{\left( {{y_0},\ldots,{y_{M-1 }}} \right)}^T} \):

$$ {I_y}\left( {{k \left/ {M} \right.}} \right)=\left( {{1 \left/ {M} \right.}} \right){{\left| {\sum\nolimits_{n=0}^{M-1 } {{e^{{{-i2nnk \left/ {{{M_{{{y_n}}}}}} \right.}}}}} } \right|}^2},k=0,\ldots,\left\lfloor {{M \left/ {2} \right.}} \right\rfloor $$
(1)

which can be interpreted as the contribution of the frequency k/M. The cumulative contribution is evaluated as:

$$ {n_Y}\left( \omega \right)=\sum\nolimits_{{{{{k:0\leqslant k}} \left/ {{M\leqslant \omega }} \right.}}} {{I_Y}\left( {{k \left/ {M} \right.}} \right)}, \omega \in \left[ {0,0.5} \right] $$
(2)

For ω 0 ∊ (0, 0.5), the contribution of low frequencies to \( Y\in {{\mathbb{R}}^M} \) is defined as:

$$ C\left( {Y,{\omega_0}} \right)={{{{n_Y}\left( {{\omega_0}} \right)}} \left/ {{{n_Y}\left( {0.5} \right)}} \right.} $$
(3)

Let us consider eigenvectors U j . Then, given ω 0 ∊ (0, 0.5) and C 0 ∊ [0, 1], we select SVD components with eigenvectors satisfying \( C\left( {{U_j},{\omega_0}} \right)\geqslant {C_0} \). One may interpret this method as a selection of SVD components characterized mostly by low-frequency fluctuations.

The low-frequency boundary ω 0 manages the scale of the extracted trend; the lower ω 0 is, the slower the trend varies. The parameter C 0 regulates an acceptable share of higher frequencies in the extracted component and is selected as summarized below.

Let us have a time series F and denote its trend extracted with the method with parameters ω 0, C 0 as T(ω 0, C 0). The normalized contribution of low-frequency oscillations in the residual F − T(ω 0, C 0) is defined as (Alexandrov 2009):

$$ {R_{{F,{\omega_0}}}}\left( {{C_0}} \right)=C\left( {F-T\left( {{\omega_0},{C_0}} \right),{\omega_0}} \right)C{{\left( {F,{\omega_0}} \right)}^{-1 }} $$
(4)

The elementary reconstructed components corresponding to a trend have large contribution of low frequencies. Thus, the maximum values of C 0 which lead to selection of trend-corresponding SVD components should generate jumps of \( {{\mathcal{R}}_{{F,{\omega_0}}}}\left( {{C_0}} \right) \). Exploiting this idea, the choice of C 0 follows this criterion:

$$ C_0^R=\min \left\{ {{C_0}\in \left[ {0,1} \right]:{R_{{F,{\omega_0}}}}\left( {{C_0}+\varDelta C} \right)-{R_{{F{\omega_0}}}}\left( {{C_0}} \right)\geqslant \varDelta R} \right\} $$
(5)

where ΔC is a search step and \( \varDelta \mathcal{R} \) is the given threshold. The step ΔC is to be chosen as small as possible to discriminate identifications occurring at different values of C 0. We commonly take \( \varDelta C\geqslant 0.01 \) to reduce computational time and \( 0.05\leqslant \varDelta \mathcal{R}\leqslant 0.1 \).

Empirical analysis

The single parameter of the embedding stage is the window length L. Selection of the proper window length depends on the studied problem and on the preliminary information on the time series. Nonetheless, theoretical results tell us that L should be large enough but not greater than N/2 (Golyandina et al. 2001). Furthermore, if we know that the time series may have a periodic component with an integer period (for example, if this component is a seasonal component), then to get better separability of this periodic component, it is advisable to take the window length proportional to that period (Hassani 2010). In our case, all sea level time series have the same length: N = 216, they contain monthly data, and each time series has evident annual seasonal component (T = 12). So, using the lasts recommendations, we have selected the SSA window length \( L=N/2=108 \).

As described in Alexandrov (2009), in order to include the seasonal component in the trend, we select \( {\omega_0}=0.08<1/T \). The search for C 0 was performed in the interval \( \left[ {{C_{{0\min }}}=0.5,\ {C_{{0\max }}}=1} \right] \). The ΔC is to be chosen as small as possible to discriminate identifications occurring at different values of C 0. To reduce computational time, we take a default value of \( \varDelta C=0.01 \) with a threshold of \( \varDelta \mathcal{R}=0.05 \). The first L/2 = 54 eigentriples will be examined to search the trend components.

Using these parameters, we analyze separately each sea level time series to determine its trend. Here, we present first in detail the results of global sea level time series analysis, and then, a summary is given for all sea level time series analysis.

Note that the calculations were made in Matlab using the software package AutoSSA of Dr. Theodore Alexandrov, Center for Industrial Mathematics of the University of Bremen, available in AutoSSA (2005). This program presents a collection of parametric methods for solution of trend/periodic components extraction and signal forecasting.

Global sea level time series analysis

Based on this window length and on the SVD of the trajectory matrix (108 × 108), we have 108 eigentriples for each time series. Fig. 2 presents the plot of logarithms of the 108 singular values obtained from SVD of the global sea level time series.

Fig. 2
figure 2

Logarithms of the 108 eigenvalues

Full size image

The first L/2 = 54 eigentriples are examined to search the trend components. From Fig. 3, the values of \( {{\mathcal{R}}_{{F,{\omega_0}}}}\left( {{C_0}+\varDelta C} \right)-{{\mathcal{R}}_{{F,{\omega_0}}}}\left( {{C_0}} \right) \) used for the choice of C 0 resulted in a value \( C_0^{\mathcal{R}}=0.94 \). The eigenvectors satisfying \( C\left( {{U_j},{\omega_0}} \right)\geqslant {C_0} \) are: 1, 2, 10, 11, 12, 13, 14, 15, and 17.

Fig. 3
figure 3

Eigenvectors satisfying \( C\left( {{U_j},{\omega_0}} \right)\geqslant {C_0} \)

Full size image

Figure 4 presents the trend eigenvectors (1, 2, 10, 11, 12, 13, 14, 15, and 17) ordered by their contribution in the SVD. The selected eigenvectors present slow variations, confirming that it represents only the trend components (no seasonal components). The contribution of the trend eigenvectors in the original series in percent are: 1 (86.600 %), 2 (7.827 %), 10 (0.134 %), 11 (0.083 %), 12 (0.073 %), 13 (0.065 %), 14(0.053 %), 15(0.053 %), and 17(0.040 %). Thus, the trend represents 94.928 % of the original global sea level time series.

Fig. 4
figure 4

Trend eigenvector graphs and their contributions

Full size image

The reconstruction of the global sea level trend is done in Fig. 5 from these eigenvectors. It can be seen from Fig. 5a that the global sea level trend is subject to significant rise, from −18 to 35 mm during the period 1993–2010. The reconstructed trend of global sea level change clearly follows the main tendency in the original global time series. Applying a least squares linear regression analysis to the extracted global sea level trend gives a rate of 3.19 ± 0.03 mm/year between 1993 and 2010. This obtained rate agrees with the recent study of AVISO Altimetry (2011), which suggested a rate of sea level rise of 3.20 mm/year over 1993 to mid-2011. Figure 5b presents the residuals as differences between the original global sea level time series and the extracted trend. The amplitude of the residual signal is about 15 cm. These residuals represent mainly the existing seasonal components in the global sea level time series (Haddad et al. 2011a).

Fig. 5
figure 5

Global sea level time series analysis. a Original global sea level time series (blue line) and the extracted trend (red line) with L = 108, \( \varDelta C=0.01 \), \( \varDelta \mathcal{R}=0.05 \), and ω 0 = 0.08. b Residuals

Full size image

Summary of trend extraction results

Table 2 gives the summary of obtained trend extraction results for the 18 sea level time series. The columns of this table indicate: sea level region, estimated low-frequency threshold C 0, identified trend eigentriples, contribution of the trend in the original time series in percentage, trend rate, and their standard error in millimeters per year. Note that the trend rate for each time series is estimated for the period from the beginning of 1993 to the end of 2010 by least squares linear regression of the related extracted trend.

Table 2 Trend extraction results for the all sea level time series
Full size table

By comparing the contribution of obtained trends for the different seas (Table 2), the Mediterranean Sea presents the lowest trend contribution value (2.249%). The Mediterranean Sea case presents the performance and the advantage of the use of automatic trend extraction approach when the trend contribution is small enough as compared with other components. In fact, the Mediterranean Sea variability is more known for its strong annual frequency signal which represents about 72.38 % of the total variability (or original sea level time series), while its amplitude is about 144 mm (Haddad et al. 2011b).

Figure 6 presents the original 18 sea level time series and their extracted trends (in millimeters): from the top to the bottom and from the left to the right: global sea level, Atlantic Ocean, Indian Ocean, Pacific Ocean, Adriatic Sea, Andaman Sea, Arabian Sea, Bay of Bengal, Bering Sea, Caribbean Sea, Gulf of Alaska, Gulf of Mexico, Indonesian Throughflow, Mediterranean Sea, Sea of Japan/East Sea, South China Sea, Yellow Sea, and Maldives.

Fig. 6
figure 6

Original sea level time series (blue line) and extracted trend (red line)

Full size image

Conclusions

In this paper, an approach of automatic trend extraction using singular spectrum analysis has been used to extract trends of 18 sea level time series from TOPEX, Jason-1, and Jason-2 altimeters that extend back to 1993. The global sea level time series analysis indicates that the global mean sea level is characterized by its strong trend, which represents about 95 % of the original sea level signal. Applying a least squares linear regression analysis to the global sea level trend gives a rate of 3.19 ± 0.03 mm/year between 1993 and 2010.

Although the global trend indicates a rise in the mean sea level, our results show that sea level trends of oceans are nonuniform: the Atlantic Ocean, Indian Ocean and Pacific Ocean exhibit a rate of 2.46 ± 0.05, 3.78 ± 0.08, and 2.57 ± 0.07 mm/year, respectively. Also, the results show that the level behavior of seas is far from uniform. As an extremity, while in Indonesian Throughflow, the sea level has indeed risen during the period 1993–2010 by up to 6.78 ± 0.62 mm/year, the level of the Bering Sea has fallen with a rate of −0.94 ± 0.32 mm/year.