Resilient network design of two supply chains under price competition: game theoretic and decomposition algorithm approach

Abstract

This paper utilizes a Stackelberg game approach for designing resilient supply chains under price competition and facilities disruption. The impact of using resilience strategies, namely holding extra inventory at distribution centers and considering reliable distribution centers, was investigated on the supply chains competition. A two-phase bi-level mixed integer programming approach is utilized to model the assumed problem, and a decomposition-based approach is utilized to solve the resultant model. Then, the performance of the presented model and solution approach is examined through numerical experiments. Finally, some discussions are presented with a number of examples, and managerial insights are suggested for the conditions similar to the assumed problem. Our analysis focuses on exploring the advantages of considering resilience strategies in the competitive supply chain netwrok design problems.

1 Introduction

The last few years has witnessed the rise of supply chains (SCs) complexity while the severity and frequency of disruptions seem to be increasing. Most of the SCs components are dispersed across national boundaries. Although the globalization of SCs improves the allocation of scarce resources such as labor and materials, it makes the SCs more vulnerable to disaster risks (Fahimnia et al. 2015; Sabouhi et al. 2018a). Since it is impossible to prevent disasters from happening, considering resiliency can provide opportunities for SCs to reduce the negative impacts and respond to significant disruptions. Resilience is mostly described as the SC power to recognize its core function and return to its normal condition after being disrupted (Tukamuhabwa et al. 2015). Designing a resilient SC avoids exacerbating disruption effects. Although the injection of resiliency to SCs is costly, it will reduce both possible rewards and the adverse effects of disruption risks as a competitive advantage. From a risk management perspective, essential concerns to supply chains are caused by natural (i.e., earthquake and so on) and human-made (i.e., political unrest, war, and so on) disruptions. Both of these disasters result in simultaneous widespread crisis and endanger the performance of logistics providers, suppliers, manufacturers, and other SC’ beneficiaries for maintaining the normal continuity of businesses (Fahimnia et al. 2017; Snyder et al. 2006).

Besides raising the frequency of disruptions, intense competition leads the managers to consider possible risks in the strategic and operational planning of SCs (Baghalian et al. 2013). They should be aware that a small crash or disruptive event can impress the performance of total SC and cause harmful effects. In a competitive environment, disruptions can reduce the market share of affected SC while the rivals may benefit from this condition. Organizational managers have to deal with not only disasters that may come 1 day, but also a global competition that industrial sites have to face with every day. For example, if a company holds extra inventory for the fear of the next major earthquake, it may lose its global competitiveness and not see the next earthquake. To avoid unexpected irreparable damages and driven costs, increasing the resilience of SCs seems to be essential for all involved entities. Also, designing a resilient SC subjected to disruption risks will reduce costs, and increase reliability, competitiveness, and responsiveness (Rezapour et al. 2017).

Accordingly, disruptions and the manner that SCs are coping with them can be a challenge in a highly competitive environment. It clearly affects the performance of SCs and the competition among them to achieve more market share. As an instance, a disaster in Japan in March 2011 made the automobile plant stop production; however, what occurred for Nisan (an automobile manufacturer) was different from what happened to other companies at the country. Surprisingly, production at Nisan increased by 9.3% after the disaster since appropriate resilience strategies were contrived by the company (Rezapour et al. 2017). In another real-world example, labor lockout caused cargo ships blocking in the United States west coast ports in December 2002, leading to paralyzing several global SCs. Remarkably, Dell Inc. (a leading multinational technology corporation) recovered quickly as some effective resilience strategies, including collaboration with other backup suppliers and using airways for transporting goods, were considered for such a disastrous situation. Therefore, Dell turned the incident into an opportunity, unlike its competitors.¹

SCs are assumed to perform exclusively while the existence of the rivals and their effects are ignored in most studies concerning supply chain network design (SCND) problems (Farahani et al. 2014). Although considering resilient strategies for strengthening SCs under competition helps organizations and companies to perform more confident in a competitive environment, disruption and competition have rarely been considered simultaneously in the literature of SC design. Therefore, this study highlights the simultaneous consideration of disruption risks, resilient strategies, and competition among SCs in the area of network design problem. This paper contributes to investigating how the competition among the SCs is affected by disruptions and how SCs can benefit from considering resilient strategies in the presence of possible disruptions in the competitive markets. This research aims to consider resiliency in designing two competing SCs by developing a two-phase model. In the first phase, a Stackelberg game is designed to determine price between two competing SCs under disruption risk, and in the second phase, decisions are determined related to the SCND. In the first phase, the Stackelberg game is utilized for modeling the proposed problem, and then, bi-level programming is proposed to design the competitive SCs.

The remainder of the current paper is stuctured as follows. The relevant literature are reviewed on resilient SCND and competition among the SCs. The assumed problem is stated and modeled in Sects. 3 and 4, respectively. Thereafter, the presented model is solved in Sect. 5, and numerical results are utilized to examine the presented model and solution approach in Sect. 6. Finally, conclusions and future research directions are suggested in Sect. 7.

2 Literature review

The primary contribution of the current paper is to design a resilient network of two SCs under price competition. The literature of designing resilient SCs network is reviewed in this section, followed by examining the literature of competition among supply chains. Finally, the contribution of the current paper compared with the reviewed researches.

2.1 Modeling SC resilience

Considering operational and disruption risks helps SCs and related companies to improve their responsiveness and competitiveness. Recently, excessive studies have considered uncertainties and disruption risks in SCND models. As a strategic decision in SCND models, appropriate location of facilities can reduce the impact of disruptions and empower the SCs to be reliable enough against disruption risks. The majority of research assumes that disruption in the facilities of SC (suppliers, manufacturers, distribution centers, etc.) makes them entirely or partially inaccessible or unreachable (Lee 2001; Snyder et al. 2006; Berman et al. 2009; Aryanezhad and Jabbarzadeh 2009; Liu et al. 2010; Diabat et al. 2019; Ghavamifar and Sabouhi 2018; Jabbarzadeh et al. 2018b; Peng et al. 2011). Most of researchers consider uncertainty in supply side (Shen and Daskin 2005; You and Grossmann 2008; Cardona-Valdés et al. 2011; Rezaee et al. 2015; Cardoso et al. 2015) whereas others assume it in demand side (Jabbarzadeh et al. 2015; Bode and Wagner 2015; Makui and Ghavamifar 2016). Designing a resilient SC and considering resilience strategies (i.e., holding extra inventory, establishing the backup facility, and fortification of the facility) are an area on which researchers and academic centers have focused recently. In a review paper, Tukamuhabwa et al. (2015) provided a broad review of resilient SCs. A systematic review on recent studies has defined the concept of SC resilience in various studies. Also, more than 20 strategies have been introduced for increasing the resiliency of SCs. After that, recent studies have been assessed from four viewpoints of the strategy and methodology of research. Finally, a broad research gap for future research is suggested by the authors.

Gong et al. (2014) presented disruption impacts of infrastructures on the SCs’ performance. Another network model is proposed for capturing the interdependency among civil infrastructures and the SC. SC is then modeled by using graph theory and some therapeutic strategies have been proposed for increasing the SC resiliency after occurring disruption and failure of infrastructures. A resilient retail SCND was studied by Sadghiani et al. (2015) in which they considered backup facilities for enhancing the SC resiliency and developed a novel scenario generation method for disruption scenarios. Hasani and Khosrojerdi (2016) considered six strategies for mitigating disruption effects in an international SCND by considering disruption risks based on the region of occurrence.

Moreover, disruptions are assumed to be correlated, in other words, it is assumed that disruption in each facility leads to disrupted performance of other facilities. Ivanov et al. (2016) developed a linear programming and system dynamic model for reconfiguration of a SC where the flow of materials is determined in a linear model, and recovery planning due to disruptions is modeled by using system dynamic approach. For recovery planning, they compared some resilience approaches for two optimistic and pessimistic scenarios. In another research, Paul et al. (2016) developed a reactive mitigation approach at the recovery phase after occurring a disruption. They designed a recovery plan for reducing the unexpected effects of disruption on SCs performance. A simulation-based model along with a linear programming approach was provided for modeling iterative disruptions in supply side that might occur in recovery phases.

Fahimnia and Jabbarzadeh (2016) proposed a sustainable model for designing a resilient SC. They investigated the disruption effects on the sustainability of the SC and analyzed the relationships between these two factors. In another study, a hybrid robust model was proposed by Jabbarzadeh et al. 2016) for designing a resilient SC subjected to supply and demand uncertainties while disruption in facilities is possible. They considered that disruptions depend on the investments for establishing the facilities. Then, the Monte Carlo simulation was implemented to examine the described model. In a latest work, Zahiri et al. (2017) have analyzed a pharmaceutical SC network under operational uncertainties and disruption risks. An integrated resilient-sustainable SC has been designed and a novel approach has been developed to mitigate uncertainties. Fattahi et al. (2017) presented a stochastic model for designing a responsive, resilient SC where the facilities’ capacities are randomly varied due to possible disruptions. They analyzed the benefits of contingency and mitigation strategies on the SC’s resiliency. Also, Vahidi et al. (2018) have recently formulated a stochastic model for a resilient supplier selection problem. To cope with risks of disruption and uncertainty, they have proposed a possibilistic–stochastic model. In a more recent study, Jabbarzadeh et al. (2018a) have presented a hybrid approach to design a resilient and sustainable supply chain in the face of disruption risks at suppliers and production facilities. They have developed a stochastic bi-objective optimization model that uses a clustering method to evaluate the sustainability performance of the suppliers. In another recent study, Sabouhi et al. (2018b) have proposed a two-phase methodology based on data envelopment analysis and mathematical programming method for the design of a resilient supply chain under disruption and operational risks. Their model incorporates quantity discount for the procurement of raw materials and proactive strategies to improve the resiliency level of supply chain.

2.2 Modeling competition among SCs

As claimed by Farahani et al. (2014), there are few studies investigating the SC competition between different SCs in the last decades (Boyaci and Gallego 2004; Zhang 2006; Xiao and Yang 2008). The most recent studies in the area of SCs competition are reviewed in this section. Rezapour and Farahani (2010) investigated the competition between two chains with an identical or highly substitutable product to determine the equilibrium conditions. Also, the impacts of a strategic decision making model were investigated on tactical and operational level problems. Rezapour et al. (2011) presented a novel model network for newcomer SCs that provide similar products in a market. Static competition was assumed to be between a new entrant SC and existing SCs. They then examined the presented model for a real industrial case. In another study, Rezapour et al. (2014) proposed a novel bi-level competitive model for determining the strategic facility location along with flows decisions. The customers’ demand was considered to be elastic with regard to price and distance. Apart from an exact algorithm, a metaheuristic algorithm was also applied for solving the presented model.

Rezapour et al. (2015) designed a new model to investigate the competition between an existent SC and a new rival SC, the latter assumed to supply remanufactured products. In order to distribute the remanufactured products, the rival SC should determine the strategic facility locations of the closed loop supply chain network. A modified projection solution strategy is implemented to solve the proposed bi-level problem. Fallah et al. (2015) developed a game theoretical approach for two competing closed-loop SC under uncertainty. A Stackelberg game was designed to explore the impact of competition on the primary goal of two closed-loop SCs. The study of Ghavamifar et al. (2018) can be considered as the most recent research in the area of competition and disruption risk management. They have considered disruption risks in designing a competitive supply chain network design. The competition is considered among the main producer and resellers of the company while determining the strategic decisions of the supply chain. They used bi-level programming to model the competition between the resellers and the main producer, and then a hybrid approach is utilized to solve the model. In a recent study, Amiri et al. (2018) developed a bi-level model for a chain-to-chain competition by using an iterative approach to solve the proposed model in which the follower reaction to the leader problem is considered by adding new constraints as a cut. Finally, Nobari et al. (2019) have developed a multi-objective model for an integrated network design of two SCs competing on environmental and social concerns. A two-stage approach, including game theory approach and the pareto-based multi-objective meta-heuristic algorithm, is utilized to solve the model. The major purpose of our study is to contribute to the literature by utilizing the concept of the game theory in designing of two SCs under price competition and disruption risks. In addition, a novel iterative exact approach is developed to solve the proposed bi-level model which can be used in similar studies. The proposed model can be employed in the competitive business environment in the existence of possible disruptions and scarce resources.

2.3 Research gap: design of resilient competing SC networks

Exploring the literature demonstrates that, although attention to SCND and competitive supply chain network design (CSCND) under risks of disruption is gaining ground by the practitioners and researchers, there is a handful of mathematical modeling paper in CSCND that considered disruptions in facilities. Therefore, more accommodation with the real-life condition seems to be necessary. Perhaps the studies of Zhang et al. (2016) and Rezapour et al. (2017) are among the ones most related to a resilient and competitive SC network modeling. Zhang et al. (2016) incorporated service competition in a facility location problem by considering disruption risks and developed a bi-level model to formulate the problem. Moreover, a hybrid approach, combining variable neighborhood search algorithm and a decomposition approach, was developed to solve the model. However, their study focused on the facility location decisions only while ignoring other decisions related to SCND problem. In another study, Rezapour et al. (2017) investigated a competitive model by assuming disruption. For this purpose, a model was formulated in bi-level form considering disruption and competition. The application of their developed model was demonstrated using the automotive industry as a case study. Also, their work explored the benefit of concurrent consideration of resiliency and competition in an intra-SC competition, not competition between two distinctive SCs.

To cover the research gap found based on the literature review, our study contributes to (1) considering disruption risks in a competitive environment including two competing SCs, (2) developing resilient strategies and investigating how it can affect the competing SCs’ costs, (3) developing a two-phase model including pricing model and bi-level model to formulate the competition among SCs, (4) solving the proposed bi-level model by developing a decomposition algorithm, and (5) designing several experiments to highlight the performance of our model and solution approach to be used in a similar instance in the real-life conditions. Here, a two-phase model is examined for two SCs competing on the price and the location of their distribution centers (DCs) to increase their market share. Two SCs simultaneously want to enter the same market and determine the strategic, operational, and tactical decisions of their SCs. It is assumed that disruption risks influence their competition. Therefore, each of the SCs considers resilience strategies in order to reduce unexpected arisen costs. The leader SC is assumed to have more resilience strategies versus the rival SC. In the considered network of two competing SC motivated by a real case, a private partner company exists to manufacture the products of the SCs. The problem was formulated using path-based modeling to deliver the products of manufacturers to markets. Moreover, the developed model is solved by an iterative technique, depending on a decomposition algorithm proposed for finding the optimal value of model variables. The ultimate aim is to design different experiments for evaluating both the developed model and the solution approach.

3 Problem description

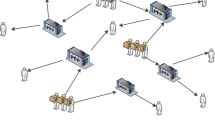
In this section, Stackelberg game is utilized for modeling the competition among two SCs where their goal is to obtain more profit. In light of this, two SCs (including manufacturer, DCs, and retailers) want to determine their optimal decisions in the competition. The assumed SC network structure is depicted in Fig. 1. The SCs produce identical products to fulfill customer’s demand, which are categorized into normal and luxury products. The former is produced at manufacture site while the latter is manufactured by the coordination of the manufacturer and the private partner company (PPC) site. In order to do some specific operations for the production of luxury products, normal products at each SC should be transferred to PPC site before stocking at DCs. After being produced at the manufacture and PPC sites, both normal and luxury products are delivered to DCs, and then be transferred into markets to satisfy customer’s demand. The DCs in both the SCs and PPC are assumed to be subjected to disruption risks. Therefore, it is suggested that each SC considers resilience strategies against possible disruptions for which the resilience strategies in this paper include holding extra inventory at DCs and establishment of reliable DCs. Also, it is assumed that the first SC (leader) considers a proactive resilience strategy for possible disruption of PPC while the other SC (follower) has no resilience strategy for such a situation. Therefore, occurring a disruption at PPC leads to the fulfillment of all the demands for luxury products by the first SC. Therefore, the market turns into a monopoly market for luxury products if the PPC is exposed to disruption.

Fig. 1

The structure of two competing SCs

The SCs compete to determine the amounts of products that should be manufactured and provided to the markets, the competitive price, utilized capacity level of PPC, and location of DCs. The main assumptions made in the current paper can be organized as follows:

• The structure of two SCs is assumed to be similar to each other.

• The potential locations to establish new DCs are known.

• The production and storage capacities in production plants and DCs are considered definite and limited.

• The potential locations to establish DCs are shared between SCs, and they compete for establishing their DCs in the best points with regard to disruption risks and SC costs.

• SCs compete for gaining the production capacity of PPC.

• Disruption in DCs is taken partially into consideration while complete disruption is assumed in the PPC.

• A specified percentage of normal products are wasted in the PPC site for producing luxury products.

The above SCs compete to achieve more profit in a competitive market. As mentioned above, DCs and PPC are subjected to disruption risks. A set of scenarios is developed and two-stage stochastic model is utilized to cope with disruption risks and uncertainty. Therefore, the SCs should determine the optima of following decisions subjected to disruption risks:

• Number and location of their DCs.

• Competitive price of each product at each market.

• Resilience strategies for SC.

• The flow of products in SC.

• The amount of extra holding inventory at each established DCs.

Our proposed novel model includes two independent models consisting of the SCND problem and competitive pricing model utilizing a Stackelberg game model. The interactions between the two phases are as follows:

• Outputs of the network design model Location, capacity, and resilience strategies are determined by the SCND problem, and then these decisions are used in the Stackelberg model.

• Outputs of the Stackelberg model Retail price and market share of each SC are determined in this model and used as inputs in the network design model.

In this paper, the benefit of using resilience strategies is investigated to improve the competitiveness of SCs under disruption risks. In the next section, a two-phase model is proposed using a Stackelberg game model and bi-level mixed integer programming.

4 Modeling formulation

First, the nomenclatures are defined used for the formulation of the developed model.

Sets and indices
$I$	Set of SCs, $i \in \left\{ {I,J} \right\}$
$N$	Set of candidate locations to establish unreliable DCs, $n \in \left\{ {1,2, \ldots ,N} \right\}$
$L$	Set of potential locations to establish reliable DCs, $l \in \left\{ {1,2, \ldots ,L} \right\}$
$K$	Set of candidate locations to establish DCs $K = N \cup L$, $k \in \left\{ {1,2, \ldots ,K} \right\}$
$M$	Set of market, $m \in \left\{ {1,2, \ldots ,M} \right\}$
$P$	Set of types of product, $P \in \left\{ {P_{1} ,P_{2} } \right\}$
$S$	Set of scenarios, $s \in \left\{ {1,2, \ldots ,S} \right\}$
Parameters
$Pcap^{i}$	The production capacity of the manufacturer of SC i
$Dcap_{k}^{i}$	The capacity of distribution center k in SC i
$tcap$	The production capacity of PPC
$oc^{i}$	The unit operational cost of the manufacturer at SC i for the production of normal products
$toc$	The unit operational cost at PPC for the production of luxury products
$tc_{k}^{i}$	Transportation cost among the manufacturer of SC i and kth DC
$ttc^{i}$	Transportation cost among the manufacturer of SC i and PPC
$tdc_{k}^{i}$	Transportation cost between PPC and DC k in SC i
$td_{km}^{i}$	Transportation cost between DC k and market m in SC i
$ttoc_{{p_{2} }}$	The purchasing cost of luxury products from the PPC at the beginning of each period
$h_{n}$	The average holding cost at DC n
$\delta$	The wastage percentage of normal products at PPC for the production of luxury products
$\lambda_{s}$	Equal to 1 if PPC is disrupted under scenario s; otherwise 0.
$\xi_{n}^{s}$	Rate of reduction in the unreliable DC n capacity under scenario s
Positive decision variables
$Y_{kp}^{is}$	The amount of product p sent from manufacturer to DC k in SC i under scenario s
$W_{p}^{is}$	The amount of product p sent from manufacturer to PPC in SC i under scenario s
$O_{{lp_{2} }}^{is}$	The amount of luxury product p purchased from PPC at the beginning of the period and delivered to DC l in SC i under scenario s
$Z_{{kp_{2} }}^{is}$	The amount of luxury product p transferred from PPC to DC k in SC i under scenario s
$Q_{kmp}^{is}$	The amount product p transferred from DC k to market m in the SC i under scenario s
$p_{mp}^{is}$	The price of product p at the market m in SC i under scenario s
$q_{mp}^{is}$	The market share of SC i for product p at market m under scenario s
Binary decision variables
$x_{kmp}^{is}$	1, if product p is transferred from the DC k to market m in the SC i under scenario s; otherwise 0
$X_{k}^{i} \,$	1, if a DC (reliable or unreliable) is established at potential location k in the SC i; otherwise 0

4.1 Phase 1: developing a Stackelberg game model

The first SC is assumed to have more power and budget for designing its SC. Therefore, the first SC is considered as the leader of the Stackelberg game model and the other one is considered as the follower of the game. Demand function of products is assumed as a descending function of the SC’s price and increasing function of the price offered by the rival in that market. Therefore, demand function of SCs (I and J) for normal products are introduced bellow (Tsay and Agrawal 2000):

$$ q_{{mp_{1} }}^{is} = \alpha_{i} - \beta_{i} p_{{mp_{1} }}^{is} + \eta \left( {p_{{mp_{1} }}^{js} - p_{{mp_{1} }}^{is} } \right) $$

(1)

The above equation is for the demand of normal products ($\alpha_{i}$, $\beta_{i}$, and $\eta$ are positive parameters) as explained in Sect. 3. A disruption at PPC turns the market into a monopoly market for luxury products. Hence, the following demand functions are presented for luxury products:

$$ q_{{mp_{2} }}^{is} = \alpha_{i} - \beta_{i} p_{{mp_{2} }}^{is} + \left( {1 - \lambda_{s} } \right)\left( {p_{{ms_{2} }}^{js} - p_{{mp_{2} }}^{is} } \right) $$

(2)

$$ q_{{mp_{2} }}^{js} = \left( {1 - \lambda_{s} } \right)\left[ {\alpha_{j} - \beta p_{{mp_{2} }}^{js} + \eta \left( {p_{{mp_{2} }}^{is} - p_{{mp_{2} }}^{js} } \right)} \right] $$

(3)

It should be mentioned that disruptions are assumed to disrupt the PPC production capacity completely. Accordingly, only the SC that considered resilience strategies could continue supplying luxury products in the market if disruptions occur in the PPC.

The following is the profit function of normal products for each rival:

$$ \pi_{i}^{s} = \left( {p_{{mp_{1} }}^{is} - c_{{kmp_{1} }}^{i} x_{{mp_{1} n_{t} }}^{is} } \right)q_{{mp_{1} }}^{is} = \left( {p_{{mp_{1} }}^{is} - c_{{nmp_{1} }}^{i} x_{{mn_{t} }}^{is} } \right)\left[ {\alpha_{i} - \beta_{i} p_{{mp_{1} }}^{is} + \eta \left( {p_{{mp_{1} }}^{js} - p_{{mp_{1} }}^{is} } \right)} \right] $$

(4)

The profit functions is differentiated over retailer price for the follower to determine the optimal Stackelberg equilibrium.

$$ \begin{aligned} & \frac{{\partial \pi_{j} }}{{p_{{mp_{1} }}^{js} }} = 0 \Rightarrow \left[ {\alpha_{j} - \beta_{j} p_{{mp_{1} }}^{js} + \eta \left( {p_{{mp_{1} }}^{is} - p_{{mp_{1} }}^{js} } \right)} \right] + \left( { - \beta_{j} - \eta } \right)\left( {p_{{mp_{1} }}^{js} - c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} } \right) = 0 \Rightarrow \\ & \quad \quad \quad - 2\left( {\beta_{j} + \eta } \right)p_{{mp_{1} }}^{js} + (\beta_{j} + \eta )c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \eta p_{{mp_{1} }}^{is} + \alpha_{j} = 0 \Rightarrow p_{{mp_{1} }}^{js\,\,\,*} = \frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \eta p_{{mp_{1} }}^{is} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} \\ \end{aligned} $$

(5)

It is evident that $p_{{mp_{1} }}^{js\,\,\,*}$ is positive because all the elements are positive and no subtraction exists in the equation. The optimal retailer price of the follower is determined by setting the first derivate function equal to zero. In addition, the second order condition indicates the concave status of the follower profit function.

$$ \frac{{\partial^{2} \pi_{j} }}{{\partial^{2} p_{ms}^{j} }} = - 2\left( {\beta_{j} + \eta } \right) \le 0 $$

(6)

By substituting the $p_{{mp_{1} }}^{js\,\,\,*}$ in the leader function into Eq. (1):

$$ \pi_{i}^{s} = \left( {p_{{mp_{1} }}^{is} - c_{{kmp_{1} }}^{i} x_{{kmp_{1} }}^{is} } \right)\left[ {\alpha_{i} - \beta_{i} p_{{mp_{1} }}^{is} + \eta \left( {\frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \eta p_{{mp_{1} }}^{is} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} - p_{{mp_{1} }}^{is} } \right)} \right] $$

(7)

Now, the optimal retailer price of the leader at each market is obtained by using Eq. (8). Afterward, the flower quantities of products are determined by the substitution of $p_{{mp_{1} }}^{is\,\,\,*}$ and $p_{{mp_{1} }}^{js\,\,\,*}$ into Eq. (1). Both the leader and follower market prices and, therefore, the market share of them are achieved according to the binary variables $x_{kmp}^{js}$ and $x_{kmp}^{is}$ obtaining as the inputs from the resilient supply chain network design phase.

$$ \begin{aligned} & \frac{{\partial \pi_{i} }}{{\partial p_{{mp_{1} }}^{is} }} = 0 \Rightarrow \left[ {\alpha_{i} - \beta_{i} p_{{mp_{1} }}^{is} + \eta \left( {\frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \eta p_{{mp_{1} }}^{is} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} - p_{{mp_{1} }}^{is} } \right)} \right] + \left( { - \beta_{i} - \eta + \frac{{\eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)\left( {p_{{mp_{1} }}^{is} - c_{{kmp_{1} }}^{i} x_{{kmp_{1} }}^{is} } \right) = 0 \\ & \quad \quad \quad \Rightarrow \,2\left( { - \beta_{i} - \eta + \frac{{\eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)p_{{mp_{1} }}^{is} - \left( { - \beta_{i} - \eta + \frac{{\eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)c_{{kmp_{1} }}^{i} x_{{kmp_{1} }}^{is} + \eta \frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} + \alpha_{i} = 0 \\ & \quad \quad \quad \Rightarrow 2\left( {\beta_{i} + \eta - \frac{{\eta^{2} }}{{2(\beta_{j} + \eta )}}} \right)p_{{mp_{1} }}^{is} = \eta \frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} + \alpha_{i} + \left( {\beta_{i} + \eta - \frac{{\eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)c_{{kmp_{1} }}^{i} x_{{kmp_{1} }}^{is} \\ & \quad \quad \quad \Rightarrow \,p_{{mp_{1} }}^{is\,\,\,*} = \frac{{\eta \frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{1} }}^{j} x_{{kmp_{1} }}^{js} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} + \alpha_{i} + \left( {\beta_{i} + \eta - \frac{{\eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)c_{{kmp_{1} }}^{i} x_{{kmp_{1} }}^{is} }}{{2\left( {\beta_{i} + \eta - \frac{{\eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)}} \\ \end{aligned} $$

(8)

In addition, the second order condition indicates the concave status of the leader profit function [Eq. (7), as proved in Eq. (9)]:

$$ \frac{{\partial^{2} \pi_{i} }}{{\partial^{2} p_{{mp_{1} }}^{is} }} = \frac{{ - 2\beta_{j}^{2} - 3\beta_{j} \eta - \eta - \beta_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} \le 0 $$

(9)

The same as normal products, the market price of luxury products is determined for each SC, the final results of which are given in Eqs. (10) and (11):

$$ p_{{mp_{2} }}^{js\,\,\,*} = \left( {1 - \lambda_{s} } \right)\frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{2} }}^{j} x_{{kmp_{2} }}^{js} + \eta p_{mp2}^{is} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} $$

(10)

Then, the leader price for luxury products is achieved by substituting the $p_{{mp_{2} }}^{js\,\,\,*}$ in Eq. (2) and then differentiating over the $p_{{mp_{1} }}^{is}$.

$$ p_{{mp_{2} }}^{is\,\,\,*} = \frac{{\eta \left( {1 - \lambda_{s} } \right)^{2} \frac{{\left( {\beta_{j} + \eta } \right)c_{{kmp_{2} }}^{j} x_{{kmp_{2} }}^{js} + \alpha_{j} }}{{2\left( {\beta_{j} + \eta } \right)}} + \alpha_{i} + \left( {\beta_{i} + \eta (1 - \lambda_{s} } \right) - \frac{{\left( {1 - \lambda_{s} } \right)^{2} \eta^{2} }}{{2\left( {\beta_{j} + \eta } \right)}})c_{{kmp_{2} }}^{i} x_{{kmp_{2} }}^{is} }}{{2\left( {\beta_{i} + \eta \left( {1 - \lambda_{s} } \right) - \frac{{\eta^{2} \left( {1 - \lambda_{s} } \right)^{2} }}{{2\left( {\beta_{j} + \eta } \right)}}} \right)}} $$

(11)

This section offers the calculated market price and market share of each SC. In the next section, a mixed integer programming (MIP) bi-level model is presented to design SCs by considering competition.

4.2 Phase 2: resilient supply chain network design

After determining the retailer prices and market share of each SC at the markets, a bi-level programming approach is utilized to design the SC networks. A single-period CSCND problem is considered here in which each manager of SC should decide about the location, number, and capacity of DCs along with determining the flow of products in SC. Unlike the common methods for modeling SCND problem (e.g., defining the flow variables between multiple echelons), a path-based approach is introduced in this paper. As such, different paths are defined in the SC to deliver the products to markets, including the following paths:

• 1. Starts from a manufacturer site, crosses the established DC (reliable or unreliable), and ends at the market. In this case, the total costs of delivering a unit of normal product to the market consist of operational costs of producing a product, transportation costs, and average holding costs at DC.

  $$ c_{{nmp_{1} }}^{i} = oc^{i} + tc_{n}^{i} + \frac{{h_{n} }}{2} + td_{nm}^{i} $$

  (12)

• 2. Starts from a manufacturer site, crosses PPC site and the established DC, and ends at the market. In this case, the total costs of delivering a unit of luxury product to the market are gained as follows:

  $$ c_{{nmp_{2} }}^{i} = oc^{i} + ttc^{i} + toc + tdc_{n}^{i} + \frac{{h_{n} }}{2} + td_{nm}^{i} $$

  (13)

• 3. Starts from a reliable DC and ends at the market. In this case, it is assumed that at the early of the period, the manager of SCs orders extra inventory of products (normal and luxury products), which are stocked at reliable DCs to compensate the lost capacities. In this case, total costs are calculated for both luxury and normal products by Eqs. (14) and (15), respectively.

  $$ c_{{lmp_{1} }}^{i} = oc^{i} + tc_{l}^{i} + \frac{{h_{l} }}{2} + td_{lm}^{i} $$

  (14)
  $$ c_{{lmp_{2} }}^{i} = ttoc_{{p_{2} }} + tdc_{l}^{i} + \frac{{h_{l} }}{2} + td_{lm}^{i} $$

  (15)

Equation (14) is calculated similar to Eq. (12) for holding extra inventory of normal products at reliable DCs, but different assumptions are considered for luxury products. PPC is assumed to be capable of supplying limited amounts of luxury products itself in the normal business condition (no disruption occurs). Therefore, the leader SC can buy luxury products form PPC with higher costs and then stock them in a reliable DC. The last alternatives can be utilized in the condition that the SCs have considered resilience strategies such as holding extra inventory at reliable DCs.

Utilization of potential paths concept for modeling the SCs under competition enables us to consider different disruptions and uncertainties simultaneously; it also has a significant effect on the reduction of computational efforts. In the following, a bi-level MIP model is proposed for designing assumed SCs.

4.2.1 Leader’s problem

$$ {\varvec{Leader}{:}}\;\;Max\,Z_{i} = \sum\limits_{s} {pr_{s} } \sum\limits_{m} {\sum\limits_{k} {\sum\limits_{p} {\left( {p_{mp}^{is} - c_{kmp}^{i} } \right)x_{kmp}^{is} q_{mp}^{is} } } } - \sum\limits_{n} {f_{n} X_{n}^{i} } - \sum\limits_{l} {f_{l} X_{l}^{i} } $$

(16)

The gained profit of leader is maximized in Eq. (16). The first term is the income of selling products (normal or luxury products). The second and the third terms imply the fixed cost of opening DCs (reliable or unreliable) at each supply chain.

$$ \begin{aligned} & {\mathbf{S}}{\mathbf{.t}}{\mathbf{.}} \\ & q_{mp}^{is} \le M\sum\limits_{k} {x_{kmp}^{is} } \quad \forall m,p,s \\ \end{aligned} $$

(17)

Equation (17) states that each market demand should be satisfied through a potential path.

$$ \sum\limits_{k} {x_{kmp}^{is} } \, \le 1\quad \forall m,p,s $$

(18)

Equation (18) expresses that demand of markets is satisfied only by a maximum of one path, in other word, the problem is assumed to be a single allocation problem.

$$ x_{kmp}^{is} \, \le X_{k}^{i} \quad \forall m,p,s $$

(19)

Constraint (19) indicates that the products could be delivered to markets from DC if it has been established (either normal or reliable DCs).

$$ Y_{{np_{1} }}^{is} + Z_{{np_{2} }}^{is} \le Dcap_{n}^{i} (1 - \xi_{n}^{s} )X_{n}^{i} \quad \forall n,p,s $$

(20)

$$ Y_{{lp_{1} }}^{is} + Z_{{lp_{2} }}^{is} + O_{{lp_{2} }}^{is} \le Dcap_{l}^{i} X_{l}^{i} \quad \forall l,p,s $$

(21)

Constraint (20) and (21) consider the capacity of unreliable and reliable DCs, respectively.

$$ \sum\limits_{k} {Y_{{kp_{1} }}^{is} } + W_{{p_{1} }}^{is} \le Pcap^{i} \quad \forall p,s $$

(22)

Constraint (22) considers the production capacity of the manufacturer in the leader SC.

$$ \sum\limits_{k} {Z_{{kp_{2} }}^{is} } \le \delta W_{{p_{1} }}^{is} \quad \forall p,s $$

(23)

$$ \sum\limits_{l} {O_{{lp_{2} }}^{is} } \le B\quad \forall p,s $$

(24)

Constraints (23) and (24) determine the amounts of luxury products supplied by the PPC.

$$ \sum\limits_{m} {Q_{{kmp_{1} }}^{is} } \le Y_{{kp_{1} }}^{is} \quad \forall k,p,s $$

(25)

$$ \sum\limits_{m} {Q_{{kmp_{2} }}^{is} } \le Z_{{kp_{2} }}^{is} + O_{{kp_{2} }}^{i} \quad \forall k,p,s $$

(26)

Constraints (25) and (26) consider the flow of products between DCs and markets.

$$ Q_{kmp}^{is} \le q_{mp}^{is} x_{kmp}^{is} \quad \forall k,m,p,s $$

(27)

$$ \sum\limits_{k} {Q_{kmp}^{is} } = q_{mp}^{is} \quad \forall m,p,s $$

(28)

Constraints (27) and (28) consider the demand of markets satisfied by each SC.

4.2.2 Follower’s problem

In the follower’s mathematical model, only constraint (21) is replaced by constraint (30), and constraint (24) is removed from the model. Finally, constraints (32)–(35) are added to the model. Therefore, the follower’s problem is formulated as follow:

$$ {\varvec{Follower}{:}}\;\;Max\,Z_{j} = \sum\limits_{s} {pr_{s} } \sum\limits_{m} {\sum\limits_{k} {\sum\limits_{s} {\left( {p_{mp}^{js} - c_{kmp}^{j} } \right)x_{kmp}^{js} q_{mp}^{js} } } } - \sum\limits_{n} {f_{n} X_{n}^{j} } - \sum\limits_{l} {f_{l} X_{l}^{j} } $$

(29)

$$ \begin{aligned} & {\mathbf{S}}{\mathbf{.t}}{\mathbf{.}} \\ & Y_{{lp_{1} }}^{js} + Z_{{lp_{2} }}^{js} \le Dcap_{l}^{j} X_{l}^{j} \quad \forall l,p,s \\ \end{aligned} $$

(30)

$$ \sum\limits_{m} {Q_{{kmp_{2} }}^{is} } \le Z_{{kp_{2} }}^{is} \quad \forall k,p,s $$

(31)

$$ W_{{p_{1} }}^{is} + W_{{p_{1} }}^{js} \le \lambda_{s} tcap\quad \forall p,s $$

(32)

$$ X_{n}^{i} + X_{n}^{j} \le 1\quad \forall n $$

(33)

$$ X_{k}^{i} ,x_{kmp}^{is} \in \left\{ {0,1} \right\} $$

(34)

$$ Y_{np}^{is} ,Z_{np}^{is} ,O_{lp}^{i} ,W_{p}^{is} ,Q_{kmp}^{is} \ge 0\quad X_{k}^{i} ,x_{kmp}^{is} \in \left\{ {0,1} \right\} $$

(35)

Moreover, constraints (17)–(20), (22)–(23), and (25)–(28) should be rewritten for the follower SC.

The same as the leader objective, the follower objective function in Eq. (29) maximizes the follower’s profit. Constraint (30) considers the capacity of reliable DCs and constraint (31) accounts the flow of products between DCs and markets in the follower SC. Constraint (32) takes the capacity of PPC into consideration, and constraint (33) indicates that only one of the SCs can establish DC at each candidate location. At last, constraints (34) and (35) determine the sign and kind of each variable.

5 Problem solution

A decomposition-based algorithm for the MIP model is proposed to solve the presented model. There are binary variables at both levels in our model. Therefore, it is impossible to utilize Karush–Kuhn–Tucker (KKT) reformulation technique. As Ben-Ayed et al. (1988) claimed, even a simple bi-level problem can become NP-hard. Also, bi-level models may be non-convex despite the convexity of the both upper and lower level problems. In light of this, a decomposition-based algorithm is utilized for the reformulation of the bi-level model. In our model, both the leader and follower are allowed to have binary variables (opening reliable and unreliable DCs and the selected path for satisfying the demand of customers) along with continuous variables (production amount, transportation quantity, and extra holding inventory). For ease of exposition, the continuous and discrete decision variables are defined by ($x^{L} ,y^{L}$) for the leader and as ($x^{F} ,y^{F}$) for the follower. The reformulation approach implemented in this paper is suggested by Yue and You (2016), to which the interested reader can refer for more information about the proposed approach. In the following, the application of the mentioned approach is explained to solve our model.

Later on, the proposed bi-level model is considered to be in the following form (BP). Also, it is considered that the leader and the follower strive to maximize their profits.

$$ \begin{array}{*{20}l} {({\mathbf{BP}})} \hfill & {U(0)\;\;Max\;Q\left( {x^{L} ,\,y^{L} ,x^{F} ,y^{F} } \right)\,} \hfill \\ \end{array} $$

(36)

$$ \begin{array}{*{20}l} {{\mathbf{S}}{\mathbf{.t}}{\mathbf{.}}} \hfill & {H_{i} \left( {x^{L} ,\,y^{L} ,x^{F} ,y^{F} } \right)\,\, \le 0} \hfill \\ \end{array} $$

(37)

$$ L\left( 0 \right)\;\;\;Max\,q\,(x^{L} ,\,y^{L} ,x^{F} ,y^{F} ) $$

(38)

$$ \begin{array}{*{20}l} {{\mathbf{S}}{\mathbf{.t}}{\mathbf{.}}} \hfill & {h_{j} \,\left( {x^{L} ,\,y^{L} ,x^{F} ,y^{F} } \right)\,\, \le 0} \hfill \\ \end{array} $$

(39)

In the master level, the leader wants to maximize its profit in Eq. (36) subjected to the constraint (37) expecting that the follower selects the best decisions to maximize its objective. Therefore, given the leader decisions, the follower will determine the optima of its decisions subjected to constraint (39) to maximize its objective (38). As explained above, it is impossible to use KKT optimality condition for solving the bi-level programming when binary variables exist in the slave problem objective function. One general solution can be the enumeration of all possible binary variables in the lower-level and coversion of the lower-level model to a LP problem. After that, it is possible to use KKT optimality conditions for converting the bi-level model. This approach has fundamental challenges. First of all, enumeration of all feasible solutions is nearly impossible for problems in large sizes because increasing the number of binary variables leads to increasingly growing of the model complexity. Secondly, a number of decision variables for the follower probably make the leader problem infeasible owing to the fact that these decisions are obtained by ignoring the leader constraints. In here, the finite set of all combination of follower’s binary variable is introduced by the index $l$ and then form the follower problem (FP).

$$ \begin{array}{*{20}l} {({\mathbf{FP}})} \hfill & {Max\,\,Q\left( {x^{L} ,\,y^{L} ,x^{F0} ,y^{F0} } \right)} \hfill \\ \end{array} $$

(40)

$$ \begin{aligned} & {\mathbf{S}}{\mathbf{.t}}{\mathbf{.}} \\ & H_{i} \left( {x^{L} ,\,y^{L} ,x^{F0} ,y^{F0} } \right)\,\, \le 0 \\ \end{aligned} $$

(41)

$$ h_{j} \,\,\left( {x^{L} ,\,y^{L} ,x^{F0} ,y^{F0} } \right) \le 0 $$

(42)

$$ q\,\,(x^{L} ,\,y^{L} ,x^{F0} ,y^{F0} ) \ge q\,\,(x^{L} ,\,y^{L} ,x_{l}^{F} ,y_{l}^{F} )\quad l = 1,2, \ldots ,n $$

(43)

$$ \sum\limits_{j} {u_{jl} \frac{{\partial h_{j} }}{{\partial x_{l}^{F} }}} = \frac{\partial q}{{\partial x_{l}^{F} }}\quad l = 1,2, \ldots ,n $$

(44)

$$ h_{j} \,\left( {x^{L} ,\,y^{L} ,x_{l}^{F} ,y_{l}^{F} } \right)\,\, \le 0\quad l = 1,2, \ldots ,n $$

(45)

$$ u_{jl} .h_{j} \,\left( {x^{L} ,\,y^{L} ,x_{l}^{F} ,y_{l}^{F} } \right) = 0\quad j = 1, \ldots ,m;\quad l = 1, \ldots ,n $$

(46)

$$ u_{jl} \ge 0\quad l = 1, \ldots ,n $$

(47)

In the above model, it should be mentioned that $y_{l}^{F}$ is a predetermined combination of binary variables of follower’s problem and ($x^{F0} ,y^{F0}$) is a duplication of ($x^{F} ,y^{F}$). Constraints (41) and (42) are the same as constraints (37) and (39) with new variables ($x^{F0} ,y^{F0}$). Constraints (44)–(46) indicate the KKT optimality condition including stationary and complementary conditions. Also, constraint (43) will be used as optimality cut in the next section.

Consequently, (FP) is equivalent to bi-level problem (BP), because (BP) is converted to a single-level form by examining all combinations of the binary decision variables in the slave problem and KKT conditions. Since the enumeration of all mixtures of follower’s binary variables is impossible, the following approach is applied proposed by Yue and You (2016). Three sub-problems are needed to be introduced for decomposition of the problem in the following steps:

• Step 1 Instead of all combinations of binary variables for follower’s problem, a subset of them is considered at each iteration. In other words, a subset of $y_{l}^{F}$ is assumed to be equal to one at each iteration. After this assumption, the master problem (MP) is obtained by replacing $y_{l}^{F}$ in constraints (43)–(47) and then ($x^{L*} ,y^{L*}$) can be obtained by solving MP. This step provides us with the upper-bound of the algorithm because it is obtained by considering a subset of constraints of the BP. This upper bound is denoted as $UB\left( {x^{L*} ,y^{L*} } \right)$.

• Step 2 After fixing ($x^{L} ,y^{L}$) at ($x^{L*} ,y^{L*}$), the second sub-problem (SP1) is introduced in the forms of (38) and (39), followed by determining the follower’s optimal objective value and its optimal decision variables. The objective value of this sub-problem is denoted as $FLB\left( {x^{L*} ,y^{L*} } \right)$.

• Step 3 The follower’s optimal decision obtained in previous section might be infeasible, or SP1 might have multiple optimal solutions, all of which might not be a favorable solution for the upper-level. Therefore, another sub-problem is posed to solve this challenge denoted as SP2 including constraints (36)–(37) and (39) along with ($x^{L} ,y^{L}$) fixed at ($x^{L*} ,y^{L*}$).The optimal decisions for objective of SP2 are addressed as $SLB\left( {x^{L*} ,y^{L*} } \right)$.

If SP2 is feasible at ($x^{L*} ,y^{L*}$), then $SLB\left( {x^{L*} ,y^{L*} } \right)$ is considered as the lower-bound of the algorithm and an optimality cut in the form of constraint (43) is added up to the master problem to tighten the relaxation. Additionally, $y_{l + 1}^{F}$ is obtained from the optimal value of the SP2. If SP2 is infeasible, $y_{l + 1}^{F}$ is gained from the optimal value of SP1. Convergence and also the flowchart for the implementation of the proposed algorithm have been demonstrated by Yue and You (2016). The algorithm is implemented on the proposed bi-level model till the gap between the master and lower bounds is less than a pre-defined quantity. At last, the algorithm flowchart is illustrated in Fig. 2.

Fig. 2

Flowchart of the solution algorithm

It should be mentioned that as our model includes two phases, and needs to develop an algorithm that can solve two models iteratively at each running iteration. At each iteration, the method of Yue and You (2016) is used to solve the bi-level model in the second phase. The obtained binary variables are introduced to the Stackelberg game model as the first-phase inputs to solve the Stackelberg model. The algorithm continues until the convergence of price and quantity is obtained in the Stackelberg game model.

6 Computational results

Different sets of experiments were generated for evaluating the proposed solution procedure, investigate the impact of considering resilience strategies, realize the tradeoff between resiliency and competition in the SCs, and finally examine the benefit of decentralizing versus centralizing decision making in the SCs. Nine random data sets were generated in different sizes as defined in Table 1. Then, the presented model is solved by GAMS software-version 24.1 and all the experiments are performed by a laptop with 12 GB RAM and Core i7 CPU 2.6 GHz. The results and parametric data analyses are provided in the next section. Additionally, managerial insights are addressed to improve the present situation of the SCs.

Table 1 The size of the generated experiments

6.1 The initial numerical results

In this section, the upper-bounds and lower-bounds are obtained from the decomposition algorithm, iteration number, and running times are reported for all the experiments. The percentage of the difference between upper and lower bounds is defined as the Gap. The defined gaps are calculated from $((UB - LB) /UB) \times 100$, and upper and lower bounds are introduced as the UB and LB of the proposed solution algorithm, respectively. Also, the leader and follower objectives are reported in Table 2. The presented solution approach was able to reach the optimal decisions in a reasonable length of time for the negligible gap. However, the solution quality can be improved within a longer runtime, but as can be seen, the obtained solutions are close-to-optimal for all the generated experiments.

Table 2 Computational results for the different data sets

Herein, the obtained solution is analyzed for small size data sets. Since the illustration of small size experiments is more understandable for the reader, the solutions are reported in this size. Figures 3, 4, 5 illustrate the structure of two SCs in the small sizes. The Fig. 3 states that with the utilization of resilience strategies, leader SC uses extra inventory and establishes reliable DC while unreliable DC is established in the follower SC. For dataset 2, the utilized resilience strategy is also similar to the results of dataset 1 (Fig. 4). For dataset 3, however, reliable DCs are established in both of the SCs, while leader SC utilizes extra inventory for luxury products along with establishing reliable DC as well. The consequent results are presented in Fig. 5. It is noteworthy to conclude that leader SC is more prone to consider all the resilience strategies leading to its increased profit in comparison with the follower SC.

Fig. 3

The structure of competing SCs for dataset 1

Fig. 4

The structure of competing SCs for dataset 2

Fig. 5

The structure of competing SCs for data set 3

For more clarification, we have investigated the SCs illustrated in Fig. 3 as a small example. In this dataset, two possible scenarios are considered (with the same probability) which affect the capacity of the unreliable DCs and PPC in two SCs. In the first scenario, the capacity of unreliable DCs is considered to be disrupted while in the second scenario, the capacity of PPC is considered to be depleted regarding the disruption scenario. As it can be seen in Fig. 3, after solving the model, in the leader SC, one unreliable and one reliable DC are established and no flow of product to the PCC is observed while the extra inventory of PPC is used to meet the demand of market 1, which is covered by the SC1. In addition, we should indicate that the price of normal products is equal to 23.8 and 24.3 at the first and second scenarios, respectively while the price of luxury products at scenario1 and scenario 2 are equal to 29.02 and 36.92, which are calculated by the proposed iterative approach. In the other SC, only one unreliable DC is established while the flow of product to the PPC is observed in the follower SC, unlike the leader SC. In addition, the price of normal products is equal to 23.9 and 25.4 at the first and second scenarios, respectively while the price of the luxury products is just calculated in the first scenario which is equal to 29.02. It should be mentioned that regarding the disruption of PPC in the second scenario, only the SC1 can supply the demand for luxury products due to the considered resilience strategy.

6.2 Effect of changes in the final product price coefficient

As it is evident in Fig. 6, the total profit will increase consequently by increasing the leader’s final product price coefficient because the effect of increasing the leader price in the objective function is more than that of decreasing the demand. Therefore, the objective value grows gradually by increasing its retail price coefficient to about 0.6. After that, the demand will decrease in an exponential form, and the effect of increasing the leader price coefficient cannot overcome the demand reduction.

Fig. 6

Effect of increasing the price coefficient on total profit (leader)

So, increasing the price coefficient by more than 0.6 is not profitable since the market share declines enormously. The same trend can be described for the follower as the consequence of using the concept of competition in defining a price-dependent demand function for each SC in the current market.

6.3 Impact of considering resilience strategies on SCs competition

In this section, the obtained results of all the experiments are defined in Table 3. The results indicate that the selected resilience strategies by each SC are affected by the number of markets covered by them, which are determined in the first phase of our proposed model. Also, it is obvious that considering more resilience strategies will increase the profit of SC, which is clear according to the results gained from Table 2. Table 2 represents the quantities of both leader and follower objective functions. By exploring Tables 2 and 3 simultaneously, therefore, it can be concluded that more resilience strategies will improve the performance of SCs under disruption risks. As more resilience strategies are considered for leader SC in this paper, it is obvious that the profit achieved by the leader is more than the followers in all experiments.

Table 3 The results of experiments by using random datasets

6.4 Impact of changes in capacity on the SC’s total costs

Capacity limitations considerably affect the CSCND owing to the possibility of producing products. The SCs performance trend on the production capacities changes is studied in this section. As shown in Fig. 7, the capacity of facilities has a significant role in reducing costs. Therefore, focusing on amplifying the capacity of these facilities is highly suggested to the SCs. It should be mentioned that the increasing of facilities’ capacity more than 160% does not affect the SCs’ costs, therefore the range of optimality can be considered more than 160% while by increasing of the capacity no infeasible solution is observed. However, the model is feasible by 38% decreasing of capacity. In Table 4, the optimality and feasibility percentages of decreasing and increasing of facilities’ capacity, holding cost, and transportation costs are given.

Fig. 7

Effects of changes in capacity on the SC’s total costs

Table 4 The feasibility and optimality range of parameters

6.5 Impact of disruptions on SCs

Figure 8 depicts the impacts of considering disruption at the planning phase in the CSCND problem and after the planning time. It should be noted that considering disruption on the planning time is much more efficient than a corporation fails to consider disruption besides the other planning decisions. It also shows that both the customer satisfaction and the supply chain profit will increase by considering disruption risks, which represents the improvements made in the proposed supply chain.

Fig. 8

Effects of considering disruption

As mentioned before, considering disruption risks along with competition in the SCs are among the main contributions of the current paper. In this regard, some experiments are designed for evaluating the disruption effects in the following conditions:

• Experiment 1 The SCs competition with no disruptions in facilities, DCs, or PPC.

• Experiment 2 The SCs competitions under disruptions in the DCs, not in PPC, and the SCs have not considered the resilience strategies.

• Experiment 3 The SCs competitions under disruptions in the DCs, not in PPC, and the SCs have considered the resilience strategies.

• Experiment 4 The SCs competitions under disruptions in DCs and PPC, and the SCs have not considered the resilience strategies.

• Experiment 5 The SCs competitions under disruptions in the DCs and PPC, and the SCs have considered resilience strategies.

To avoid infeasibility in experiment 2 and experiment 4, a random unit cost is consider for increasing the capacity, and the results are illustrated in Figs. 9 and 10, respectively.

Fig. 9

Leader’s SC profit in the different designed experiments

Fig. 10

Follower’s SC profit in the different designed experiments

Investigation of the results indicates that both the leader and follower’s SCs have the uppermost profit in experiment 1 where no disruption occurs. However, a remarkable point is that minimum profits for the leader and follower’s SCs occur at experiment 2 and experiment 4, respectively. As mentioned in Sect. 3, when disruption occurs at PPC, the leader SC is an exclusive SC existing in the market and responsible for supplying luxury products. Therefore, the unavailability of PPC and considering no resilience strategy for this condition is more harmful to the leader SC while disruption of DCs is more harmful to follower’s SC.

6.6 Competition on the production capacity of private partner company

As discussed in Sect. 3, the SCs in the assumed problem compete to obtain more production capacity of PPC by serving both the SCs simultaneously. In this problem, competition on the production capacity of the PPC is more dependent on the transportation costs between the manufacturer of the SCs and the PPC site, as well as on the transportation costs between the PPC site and the reliable or unreliable DCs of the SCs. In this numerical study, the influences of these costs are investigated on the competitiveness of each SC and its profitability. The flow of luxury products from the PPC site to the reliable and unreliable DCs of each SC for five different amounts of wastage is reported in Table 5. The results are for the scenarios in which the PPC is not disrupted.

Table 5 Competition on the production capacity of PPC

Table 5 indicates that TCMP is more dependent on $\delta$ (the wastage percentage of products at the PPC) while TCDP is almost constant in the experiments due to the constant demand for luxury products. It can, therefore, be concluded that the lower transportation costs between manufacturer, PPC, and DCs lead to more production capacity achievement of PPC by the SCs. As obviously shown in the datasets 6 and 9, (Table 5), the summation of TCMP and TCPD for the leader SC is less than that of follower SCs, resulting in more production capacity achievement of the PPC. As a result, the transportation costs have a high impact on the competition among the SCs to obtain PPC’s production capacity. Also, selling more luxury products to the market can boost the benefit of each SCs due to higher market price.

6.7 Decentralization against centralization

In this section, two centralized models are compared with the proposed decentralized model. In problem (P2), the emphasis is on the leader objective function while in problem (P3), equal importance degrees are assigned to each objective function. Two defined problem are introduced as follows:

$$ \begin{aligned} & {P2{:}}\;Max\,\,\,\,Z_{i} + \varepsilon \,Z_{j} \quad \varepsilon \cong 10^{ - 9} \\ & {\text{Subject}}\;{\text{to:}}\;\;All\;the\;constraints\;of\;leader\;and\;follower\;problems. \\ \end{aligned} $$

(48)

$$ \begin{aligned} & {P3{:}}\;Max\,\,\,\,Z_{i} + Z_{j} \\ & {\text{Subject}}\;{\text{to:}}\;\;All\;the\;constraints\;of\;leader\;and\;follower\;problems. \\ \end{aligned} $$

(49)

After solving the above-mentioned problem, the optimal solution in the centralized model is better than the decentralized model (Table 6). In the decentralized model, the favorable decisions should generally change to adapt with the bi-level decision making. In the centralized model, a decision maker could actually determine the optimal decisions in a cooperative environment while more than one decision maker compete with each other to obtain more profit in the majority of real-world problems. In other words, the follower in the centralized model (P2 and P3) is forced to agree with the leader decisions while they could not be favorable for him/her while he/she can reject uneconomical decisions in the bi-level model. Therefore, the game theory tools utilized in this paper can be employed in such a competitive environment in the area of supply chains competition.

Table 6 The optimal solution of centralized and decentralized models

6.8 Evaluation of the proposed decomposition algorithm

In this section, ten test problems have been designed to explore the performance of the proposed solution approach. The needed input parameters are generated randomly in the domain of input parameters of numerical examples. As mentioned in Sect. 5, the bi-level model cannot be directly solved by the commercial solvers and a common approach for solving such a problem is enumeration method (EM). In this method, all the binary variables are examined for obtaining the optimal solution. As seen in Table 7, our proposed method is capable of solving the bi-level model in all the examined sizes while the EM has failed to solve the model in the larger sizes. In addition, the model is solved in a reasonable length of time, indicating that the proposed decomposition algorithm is suitable for solving such a bi-level problem. It should be mentioned that the presented model is solved for the larger sizes (|I| = 2, |N| = 48, |L| = 20, |K| = 48, |M| = 20, |P| = 2, |S = 25|) in less than 48 h. In order to find the computational limits of the proposed solution approach, the model has been tested in the larger sizes to find out whether it could be solved in a reasonable length of time or not. It is observed that the running time depends more on the number of scenarios and number of markets. It should be indicated that the model could not be solved less than 48 h by 21 number of scenario and 42 number of market. However, the largest size that the model can be solved by the proposed algorithm is for |I| = 2, |N| = 26, |L| = 25, |K| = 51, |M| = 42, |P| = 2,|S| = 21. However, we have indicated that it depends more on the number of scenarios and markets. In other word, the model can be solved in the larger sizes for |N| ≥ 26, |L|  ≥ 25, and |K|  ≥ 51 while |S| ≤ 21 and |M| ≤ 42.

Table 7 Comparative results between the proposed decomposition algorithm and EM

7 Conclusion

The prevailing trends in the business market lead to intractable complexities in both supply chains. In addition, global SCs have become more sensitive to disruptions or disasters, operational failure, and terrorist attacks. Operational and disruption risks are the most determining factors influencing SC responsibility. Moreover, the competitiveness of the SC is affected by the disruption risks. Hence, it is more critical to design a profitable, competitive, and responsive SC in comparison to that in the past. In this regard, a two-phase model was developed to investigate how disruptions affect the performance and profitability of the SCs in this paper. The role of considering resilience strategy was highlighted to empower the SCs against disruption risks to provide them with excellent performance in the competitive market. Two kinds of disruptions, including disruption of the internal facility (DCs) and disruption of the facility outside the SCs (PPC), are considered in the assumed problem. A resilience strategy is offered for each kind of disruption, and the improvements of SCs are explored after using the resilience strategies. The results indicate the effect of disruptions on the leader and follower’s profit functions, and show which kind of the disruption has more impacts on each rival of the competition. This analysis highlights that the strategic decision makers of the SCs should be aware of proactive resilient measures to lower the side effects of disruption risks. A decomposition-based algorithm was developed as an exact algorithm to solve the presented model in bi-level form, and to investigate the proposed solution approach efficiency.

The presented model may be extended by developing a stochastic optimization or robust programming approach for handling the uncertainty. Also, considering other parts of the SCs, such as suppliers, and considering their disruptions make the problem closer to real life conditions. As this paper has proposed one of the first-ever contributions to the area of CSCND under the risk of disruptions, further research and extending the literature on this area seem to be critical in the author’s opinion.