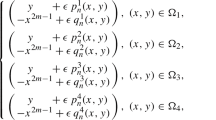Weak-Foci of High Order and Cyclicity

Abstract

A particular version of the 16th Hilbert’s problem is to estimate the number, M(n),  of limit cycles bifurcating from a singularity of center-focus type. This paper is devoted to finding lower bounds for M(n) for some concrete n by studying the cyclicity of different weak-foci. Since a weak-focus with high order is the most current way to produce high cyclicity, we search for systems with the highest possible weak-focus order. For even n, the studied polynomial system of degree n was the one obtained by Qiu and Yang (J Differ Equ 246:3361–3379, 2009) where the highest weak-focus order is $n^2+n-2$ for $n=4,6,\ldots , 18$. Moreover, we provide a system which has a weak-focus with order $(n-1)^2$ for $n\le 100$. We show that Christopher’s approach (Differ Equ Symb Comput Trends Math 30:23–35, 2006), aiming to study the cyclicity of centers, can be applied also to the weak-focus case. We also show by concrete examples that, in some families, this approach is so powerful and the cyclicity can be obtained in a simple computational way.

1 Introduction and Statement of the Main Results

The second part of the 16th Hilbert’s problem is concerned with the maximal number [denoted by H(n)] and relative positions of the limit cycles of planar polynomial systems of degree n

$$\begin{aligned} (\dot{x}, \dot{y})= (P_n(x,y), Q_n(x,y)). \end{aligned}$$

(1)

This problem remains unsolved even for quadratic systems. There have been a lot of attempts to make progress in this problem, see the survey articles of Ilyashenko and Li [13, 15]. Many results have been obtained for lower bounds of H(n). For example, $H(2)\ge 4$, $H(3)\ge 13$, $H(4)\ge 22$, $H(5)\ge 28$, and $H(6)\ge 35.$ Recently, Johnson [14] show numerically that $H(4)\ge 26$. Han and Li detail other lower bounds in [12]. In particular, developing the method used in [7] and introducing some new perturbation techniques, they improve all the existing results for $n\ge 7$ and prove that H(n) grows at least as fast as $(n+2)^2\log (n+2)/\log 4$, see also [12].

We note that the standard technique to obtain a high number of limit cycles for a polynomial differential system is the perturbation of symmetric polynomial systems or systems with many centers or weak-foci. But there are relative few results concerning on the maximum number of limit cycles surrounding only one singularity. In the first paragraph of his paper [29], Zoladek said “The particular version of this (Hilbert’s 16th) problem is to estimate the number M(n) of small amplitude limit cycles bifurcating from an elementary center or an elementary focus. The ...problem is ...still complicated”. Clearly $M(n)\le H(n).$

Bautin [3, 4] proved that $M(2)=3$. For cubic systems without quadratic terms, Sibirskii [25] proved that no more than five limit cycles could be bifurcated from one critical point. Zoladek found an example where 11 limit cycles could be bifurcated from a single critical point of a cubic system, see [29, 30]. Christopher [6] gave a simpler proof of Zoladek’s result perturbing a Darboux cubic center. The same lower bound was also done with a different Darboux cubic center by Bondar and Sadovskii [5]. By perturbations of a family of Darboux quartic (resp. quintic) systems inside the general quartic (resp. quintic) systems, Giné [11] proved that $M(4)\ge 21$ [resp. $M(5)\ge 26$]. It was also shown in [11] that $M(6)\ge 11$, $M(8)\ge 13,$ and $M(9)\ge 16$. These result were obtained by studying polynomial differential systems whose nonlinear terms are homogeneous. Recently in [16] it is showed that $M(n)\ge n^2+n-2$ for $4\le n\le 13$ perturbing holomorphic centers.

The cyclicity results in all the cited papers are done providing the existence of weak-foci of a given order bifurcating from a center. In all cases the limit cycles appear from a generic unfolding inside the polynomial class of a given degree. We are interested in finding explicit polynomial systems, instead of the previous existential ones, with a weak-focus of high order. In particular such systems with prescribed weak-foci should provide, if it is possible, as many limit cycles as its order.

The first result of this paper shows the systems with high cyclicity from a weak-focus of high order for $n=4,6,7$ and 8. Here system (1) is transformed to complex coordinates using the change $z=x+iy.$ The systems for even degree were done in [21] and the odd degree system is new.

Theorem 1.1

• (a) The cyclicity of the weak-focus of the quartic system

  $$\begin{aligned} \dot{z}=iz-2z^4+z\bar{z}^{3}+ i\sqrt{\frac{52278}{20723}}\ \bar{z}^4 \end{aligned}$$

  (2)

  is 18 under the general quartic polynomial perturbations.

• (b) There are at least 39 limit cycles bifurcating from the weak-focus of the system

  $$\begin{aligned} \dot{z}=iz-\frac{3}{2}z^6+z\bar{z}^{5}+i \sqrt{\frac{963010778697180}{958721342366881}}\ \bar{z}^6, \end{aligned}$$

  (3)

  under general polynomial perturbations of degree 6.

• (c) There are at least 34 limit cycles bifurcating from the weak-focus of the system

  $$\begin{aligned} \dot{z}=iz+z\bar{z}^{6}+z^7, \end{aligned}$$

  (4)

  under general polynomial perturbations of degree 7.

• (d) There are at least 63 limit cycles bifurcating from the weak-focus of the system

  $$\begin{aligned} \dot{z}=iz-\frac{4}{3}z^8+z\bar{z}^{7}+i \tau _8 \bar{z}^8, \end{aligned}$$

  (5)

  where $\tau _8=\sqrt{\dfrac{8923642104029923643215704392751836}{14723617165367560603816000942842897}},$ under general polynomial perturbations of degree 8.

A direct consequence of the above result is the next corollary.

Corollary 1.2

For polynomial differential systems of degree n, we have that $M(6)\ge 39$, $M(7)\ge 34$ and $M(8)\ge 63$.

We remark that Wang and Yu [28], perturb a $Z_2$-equivariant Hamiltonian system inside the class of polynomials of degree 6 in order to obtain $H(6)\ge 35.$ Hence the limit cycles emerge from several foci. But the above result provides 39 limit cycles emerging from only one singularity.

The method to produce limit cycles from a singular point is based on the study of the Poincaré return map, see [18–20]. In this paper we assume that system (1) has an elementary monodromic singularity at the origin, i.e., the origin is an elementary center or an elementary focus. Therefore, without loss of generality, system (1) can be written using $z=x+iy$ as the complex equation

$$\begin{aligned} \dot{z}=(i+\lambda _1)z+ p_n(z,\bar{z}, \varvec{\lambda }^*), \end{aligned}$$

(6)

where $\varvec{\lambda }^*=(\lambda _2, \lambda _3, \ldots , \lambda _m)$, $n, m\in {\mathbb {N}}^+$ and $m\ge 2, n\ge 2.$ Here $p_n\in {\mathbb {C}}[z,\bar{z}, \lambda _2, \ldots , \lambda _m]$ and $p_n(z,\bar{z},\mathbf {0})$ is a polynomial of degree n with only nonlinear terms. We also assume that $p_n(0,0,\varvec{\lambda }^*)=\frac{\partial }{\partial z}p_n(0,0,\varvec{\lambda }^*)=\frac{\partial }{\partial \bar{z}}p_n(0,0,\varvec{\lambda }^*)=0$.

Clearly when $\lambda _1\ne 0$ Eq. (6) has a strong focus at the origin. When $\lambda _1=0$, to distinguish a center from a focus is one of the most classical problems in qualitative theory of planar ordinary differential equations, and was theoretically solved by Poincaré and Lyapunov, see [18–20]. It is the so-called center-focus problem.

The main method to deal with the center-focus problem, as well as the problem of producing limit cycles from a monodromic singularity, is the computation of Poincaré return map $\Pi :\Sigma \rightarrow {\mathbb {R}},$ where $\Sigma$ is a transversal section at the origin. Moreover, for analytic differential equations, the return map is analytic. Hence we can expand the return map associated to Eq. (6) as a Taylor series:

$$\begin{aligned} \Pi (h)=h+\sum _{j=1}^{\infty }\alpha _j h^j. \end{aligned}$$

(7)

The function $d(h):=\Pi (h)-h$ is the so-called displacement function. Therefore the periodic orbits of (6) correspond to fixed points of (7) or, equivalently, to zeros of its displacement function. If all $\alpha _j=\alpha _j(\varvec{\lambda })\ (\varvec{\lambda }=(\lambda _1,\ldots ,\lambda _m))$ vanish, then we have a center at the origin. Otherwise, we have a weak-focus. Detailed calculations show that $\alpha _1={\text {e}}^{2\pi \lambda _1}-1$. Moreover, when $\lambda _1=0$, all $\alpha _j(\varvec{\lambda })=\alpha _j(\varvec{\lambda }^*)$ are polynomials in the ring ${\mathbb {C}}[\lambda _2,\ldots ,\lambda _m].$ Let $\beta _1=2\pi \lambda _1$ and $\beta _k$ is defined from $\alpha _k$ modulo $\beta _1, \ldots , \beta _{k-1}$. It is known that since $\beta _{2k}$ always lies in the ideal generated by the previous $\beta _j$ in the ring ${\mathbb {C}}[\lambda _2,\ldots ,\lambda _m]$, the only important $\beta _{j}$ are the ones with odd subscript, see [1, p. 243]. We call the function $\beta _{2j+1}$ the j -Lyapunov quantity and we denote it by L(j).

The so-called Bautin ideal, generated by all L(j) is Noetherian and hence, by the Hilbert’s basis theorem, it is finitely generated. Hence, theoretically the center-focus problem can be solved in a finite number of steps. The main two difficulties are the number of required steps, that it is not known a priori, and the explicit calculation of the Lyapunov quantities, L(j). The second one is really a hard problem to attack, even for $n=3,$ because of the huge size of the Lyapunov quantities. Although, for a given family these quantities can be obtained, the solution of the system of equations necessary to characterize the centers, for example, is also very difficult to find.

If L(k) is the first nonzero Lyapunov quantity, then we say that the origin is a weak-focus of order k. The focus order, k,  plays an important role in the qualitative behavior of the system. In fact, according to Roussarie [22] at most k limit cycles can arise from a weak-focus of order k,  under analytic perturbations. These limit cycles are called small-amplitude limit cycles. Therefore to obtain the maximum number of them, in a concrete family, one can try to find the maximum possible focus order inside it. These families can be found solving the polynomial systems of equations defined by the Lyapunov quantities. But the necessary number of that quantities to solve the center problem is not directly related with the maximum order of a weak-focus. In that direction, Gasull and Giné [8] show a family for which only one Lyapunov quantity is necessary to solve the center problem but from the weak-focus can bifurcate k limit cycles under analytic perturbations. This is due to the nonradicality, in that example, of the Bautin ideal. See for instance, Roussarie [22] for a discussion about the cyclicity of the weak-foci in given families and the role of the radicality of the ideal formed by the Lyapunov quantities. Clearly the cyclicity of a weak-focus has a strongly dependence with the perturbed family where it is considered. Here we always perturb inside the general class of polynomials of given degree n.

As we have mentioned, the maximum order is three for quadratic systems and it is five for the cubic systems without quadratic terms, see [3, 4, 25]. For general cubic system, this maximum number would be larger than or equal to 11,  see [5, 6, 29, 30]. For $n=4$ and 5 the maximal order of a weak-focus is not less than 21 and 28 respectively, see [11, 16]. For general even number n, the authors of [2] showed that a planar system of degree n can have a weak-focus of order $n^2-n$. This result was improved by [17, 21] saying that for every integer $n\ge 3$, there exists a polynomial differential system of degree n having a weak-focus of order $n^2-1,$ when n is even, or $(n^2-1)/2,$ when n is odd. The main idea to prove the above results is the computation of cyclicity of the monodromic singularity of a certain class of systems under polynomial perturbations. That is, they can not provide the concrete expression of the systems which have the mentioned focus order.

Usually it is very difficult to find a concrete system with arbitrary degree that exhibits a weak-focus of high order. For the concrete system, even with a simple form, it is also very hard to obtain the focus order for any degree. In fact, the most excellent result of [21] is a theorem which says that for every n there exists a real value $\sigma _n$ such that equation

$$\begin{aligned} \dot{z}=iz+z^n- z\bar{z}^{n-1}+i \sigma _n \bar{z}^n \end{aligned}$$

(8)

has a focus at the origin with focus order $n^2-n$ when n is even and $n+1$ is a prime number or it is an integer power $p^m$ of a prime number p. The authors believe that this conclusion can be extended to general n but nobody has been able to prove it.

Clearly Eq. (8) does not exhibit the highest weak-focus order. Qiu and Yang [21] find other equations which seem possess weak-foci of higher order. They are respectively

$$\begin{aligned} \dot{z}=iz-\frac{n}{n-2}z^n+z\bar{z}^{n-1}+i \tau _n \bar{z}^n, \end{aligned}$$

(9)

and

$$\begin{aligned} \dot{z}=iz+\frac{n}{n-2}z^n+z\bar{z}^{n-1}+(1+i \tilde{\tau }_n)\bar{z}^n. \end{aligned}$$

(10)

It is shown that for $n=6,8,10,12,14,16,18$ (resp. $n=7,9,11,13,15,17,19$) there exist values $\tau _n$ (resp. $\tilde{\tau }_n$) such Eq. (9) (resp. (10)) has a weak-focus at the origin with order $n^2+n-2$ [resp. $(n^2+n-2)/2$].

To the best of our knowledge, for odd number n, until now the highest weak-focus order increases in the main speed of $n^2/2$. One main purpose of this paper is devote to finding a system whose weak-focus order increases in the main speed of $n^2$. Our second main result is

Theorem 1.3

For every integer $3\le n\le 100$, the origin of equation

$$\begin{aligned} \dot{z}=iz+ \bar{z}^{n-1}+z^n \end{aligned}$$

(11)

is a stable (unstable) weak-focus of order $(n-1)^2$ when n is even (odd).

In the above theorem it is assumed that $n\le 100$ simply because we have checked these cases, see the Appendix. However, we have a strong conjectural feeling that the conclusion holds for arbitrary n. Unfortunately we can not prove the conjecture in an analytical way.

Equation (11) differs from Eqs. (8)–(10) and the equations in [17] in some aspects. The first is that (11) has the nonhomogeneous nonlinear terms, while all the equations investigated in both [17, 21] have homogeneous nonlinearities. The second is that (11) has a simpler form, taking into account the number of monomials and their coefficients. The third is that the order, $(n-1)^2,$ does not depend on the parity of the degree. The inspiration for obtaining Eq. (11) comes from [9], where the center problem for polynomial systems with two monomial nonlinearities is considered.

We remark that if an equation has homogeneous nonlinear terms, then its weak-focus order “jump” in the step by step Lyapunov quantities computation. More precisely, if $p_n(z, \bar{z})$ is a homogeneous polynomial of degree n and $L_k$ is the k-Lyapunov quantity of equation $\dot{z}=i z+p_n(z, \bar{z})$ at the origin, then $L_k\equiv 0$ when $2k/(n-1)$ is not an integer, see [27]. This property make, in general, the calculation of weak-focus order easier than the nonhomogeneous cases. But, in these cases and for higher n, the number of monomials and their coefficients makes this problem unmanageable for our computers.

Usually the weak-focus of high order is one of best method to produce high cyclicity examples under perturbation. Therefore Eqs. (9) and (11) are good candidates to provide good lower bounds of M(n) for even n and for odd n respectively. In this paper we will study the cyclicity of these two classes of equations under polynomial perturbation of degree n for some concrete n.

The rest of the present paper is organized as follows. In Sect. 2 we provide a simple computational approach to deal with the cyclicity of a weak-focus. We extend the approach of Christopher, see [6], originally developed for the center cyclicity problem, to weak-foci. Section 3 is devote to the proof of Theorem 1.1 for $n=4,6$ and 8. We also check for $n=20,22,\ldots ,34$ that Eq. (9) has a weak-focus of order $n^2+n-2$. In Sect. 4 we first check the validity of Theorem 1.3. Finally we study the cyclicity of the weak-focus of (11) for $n=3,4,\ldots , 8.$

2 Christopher’s Method in Calculating the Cyclicity of Weak-Focus

In practice the computation of Lyapunov constants from the return map is not the most efficient way to proceed. Instead we will apply the method which turns out to be equivalent. According to [18, 23], there is an analytic positive definite function $V(z,\bar{z})$ in a neighborhood of the origin such that $X(V)=\sum _{k=0}^\infty V_kr^{2k+2}$, where $r^2=z\bar{z}$ and X is the vector field associated to Eq. (6). That is, X(V) is the rate of change of V along the orbits of (6). The coefficient $V_k$ is called the k-Lyapunov constant of (6) at the origin. We recall that they are polynomials in the coefficients of $p_n$ in (6), when $V_0=2\lambda _1=0$.

Although the choice of V is not unique, from [24] we know that $V_k$ is determined modulo $V_1, \ldots ,V_{k-1}$. In fact, $V_k$ is equivalent to L(k) modulo the previous L(j).

Since the ideal, I, generated by the Lyapunov constants $V_j$ has a finite number of generators, we can let m(n) be the minimum number of such constants that generate I,  and let $\tilde{V}_1, \tilde{V}_2, \ldots , \tilde{V}_{m(n)}$ be these generators. If $\tilde{V}_0, \tilde{V}_1, \tilde{V}_2, \ldots , \tilde{V}_{m(n)}$ have alternate signs and $0<|\tilde{V}_0|\ll |\tilde{V}_1|\ll |\tilde{V}_2| \ll \cdots \ll |\tilde{V}_{m(n)}|,$ then Eq. (6) has at least m(n) limit cycles bifurcating from the origin, see [23].

Usually it is very difficult to find the number m(n) and the corresponding generators $\tilde{V}_0, \tilde{V}_1,$ $\ldots ,$ $\tilde{V}_{m(n)}$. But if we can choose Lyapunov constants $V_0,$ $V_{p_1},$ $V_{p_2},$ $\ldots ,$ $V_{p_k}$ (where $V_0=2\lambda _1$) independent with respect to the parameters, then we can produce k limit cycles because by suitable choice of the parameters we can have that $0<|V_0|\ll |V_{p_1}|\ll |V_{p_2}|\ll \cdots \ll |V_{p_k}|$ and that $V_0, V_{p_1}, V_{p_2}, \ldots , V_{p_k}$ have alternate signs. Hence, in a small enough neighborhood of the origin, the return map has k simple zeros and thus (6) has k limit cycles.

However, for general polynomial systems, the computation of the Lyapunov constants from $X(V)=\sum _{k=0}^\infty V_kr^{2k+2}$ is still very complicated. Recently, Christopher has considered a simple computational approach to estimate the cyclicity of centers, see the following result.

Theorem 2.1

[6] Suppose that $\mathbf {s}\in K$ (where K denote the corresponding parameter space of a family of polynomial systems) is a point on the center variety and that the first k of the L(j)’s have independent linear parts [with respect to the expansion of L(j) about $\mathbf {s}$], then $\mathbf {s}$ lies on a component of the center variety of codimension at least k and there are bifurcations which produce $k-1$ limit cycles locally from the center corresponding to the parameter value $\mathbf {s}$.

The above result provides a powerful approach to calculate the cyclicity of a center. Indeed, Christopher [6] considers the cubic center $C_{31}$ in Zoladek’s classification [29]. A direct computation shows that the linear parts of $L(1), L(2), \ldots , L(11)$ [$L(0)=2\pi \lambda _1$ already] are independent in the parameters and therefore 11 limit cycles can bifurcate from this center. This confirm the result of [29]. Applying Christopher’s approach, Giné [11] found a quartic system with 21 limit cycles bifurcating from a center. Recently, in [12], a quintic system with 28 limit cycles surrounding only one singularity is given.

If one check carefully the proof of Theorem 2.1, it is easy to see that the same conclusion holds if we replace the center with a weak-focus.

Proposition 2.2

Suppose that at $\mathbf {\lambda }\in K$, Eq. (6) has a weak-focus with focus order k. If $L(k_1), L(k_2), \ldots , L(k_{\ell -1})$ $(0<k_1<\cdots <k_{\ell -1}<k)$ have independent linear parts (with respect to the expansion of L(j) about $\mathbf {\lambda }$), then there are bifurcations which produce $\ell$ limit cycles locally from the weak-focus corresponding to the parameter value $\mathbf {\lambda }$.

Remark 2.3

Under the hypothesis of Proposition 2.2, we have actually $\ell +1$ linear independent Lyapunov quantities which begin at $L(0)=2\pi \lambda _1$ and end at L(k) with $L(k)\ne 0$ at the parameter value $\mathbf {\lambda }$. Therefore we can also get from [23] that there are bifurcations which produce $\ell$ limit cycles.

In the next two sections we will apply Proposition 2.2 to study the cyclicity of weak-foci. It is worth emphasizing that we have successfully unfolded some concrete systems such that the number of limit cycles is the same that the corresponding weak-focus order. All is done, in general, using the linear terms of Lyapunov quantities with respect to the parameters. Therefore our work further confirm the value of the Christopher’s approach. We also study some other systems which are need to be considered the quadratic terms in the parameters. The reader is referred to Theorem 3.1 of [6] for more details of high order perturbations.

3 Cyclicity of the Weak-Focus of Eq. (9)

As we have commented before, when we perturb in the analytic class, the order and the cyclicity of a weak-focus coincide, see [22]. But this can not be true if we restrict our study to some class, for example if the polynomial perturbations have the same degree that the vector field with a weak-focus of a prescribed order. Consequently for looking high cyclicity monodromic points the main tool is to find a weak-focus with high order. Until now, in a polynomial system of degree n for even number $n\ge 4,$ the highest known weak-focus order is $n^2+n-2$. In this section we will study the number of limit cycles bifurcating from three polynomial systems of the form (9) with degrees $n=4,6,8,$ under general polynomial perturbation of the same degree. We will prove that the cyclicity and the weak-focus order coincide for the quartic family. Moreover, when we perturb (9) for $n=6$ and 8 we provide lower bounds for the cyclicity of the weak-focus for these degrees. In particular we will obtain $M(6)\ge 39$ and $M(8)\ge 63.$ This will be the first part of the proof of Theorem 1.1. In the next section we will finish it.

Proof of Theorem 1.1 for even degree cases

The proof is based on Proposition 2.2. Let $V^{\ell }_m$ be the linear part of the m-Lyapunov constant $V_m$ with respect to the perturbation parameters. In [21], it was shown that the origin of Eqs. (2), (3) and (5) has a weak-focus of order 18, 40,  and 70,  respectively.

• (a) Consider the general perturbation of Eq. (2) in the class of the quartic polynomials without constant and linear terms:

  $$\begin{aligned} \dot{z}=iz-2z^4+z\bar{z}^{3}+ i\sqrt{\frac{52278}{20723}} \, \bar{z}^4 +\sum \limits _{j+k=2}^4 (e_{j,k}+i f_{j,k})z^j\bar{z} ^k. \end{aligned}$$

  (12)

  Here $e_{j,k}$ and $f_{j,k}$ are small real parameters.

  By direct computation, we obtain the expressions of $V^{\ell }_1, \ldots , V^{\ell }_{17}$. Straightforward computations show that the Jacobian matrix of $V^{\ell }_1, \ldots ,V^{\ell }_{17}$ with respect to the parameters has rank 17. This yields that $V^{\ell }_1, \ldots ,V^{\ell }_{17}$ are linearly independent. Since Eq. (2) has a weak-focus at the origin with order 18, it follows from Proposition 2.2 that if we adding the linear perturbation $\lambda _1z$ to (12) then 18 limit cycles can be obtained. Therefore, the cyclicity of the weak-focus of Eq. (2) is 18, under general quartic polynomial perturbations.

• (b) Consider the general perturbations of Eq. (3) in the class of polynomials of degree 6

  $$\begin{aligned} \dot{z}=iz-\frac{3}{2}z^6+z\bar{z}^{5}+\sqrt{\frac{963010778697180}{958721342366881}} \, i \bar{z}^6 +\sum \limits _{j+k=2}^6 (e_{j,k}+f_{j,k}i)z^j\bar{z} ^k,\nonumber \\ \end{aligned}$$

  (13)

  where $e_{j,k}, f_{j,k}$ are small real parameters.

Straightforward computations show that:

• (i) Equation (3) has a weak-focus at the origin with focus order 40.

• (ii) The Jacobian matrix of $\{V^{\ell }_1, V^{\ell }_{2}, \ldots , V^{\ell }_{39}\}{\setminus } \{V^{\ell }_3,V^{\ell }_{38},\}$ with respect to the parameters has rank 37.

• (iii) $V^{\ell }_{38}$ is a linear combination of $V^{\ell }_{8}$, $V^{\ell }_{13},$ $V^{\ell }_{18},$ $V^{\ell }_{23},$ $V^{\ell }_{28},$ $V^{\ell }_{33}.$

• (iv) $V^{\ell }_3$ vanishes identically. But when we vanish all the parameters that appear in the other $V^{\ell }_m$, the quadratic part of the third Lyapunov constant $V_3$ is a positive definite function in two new parameters, which do not appear in the other $V^{\ell }_m.$

Consequently, adding the linear perturbation term $\lambda _1 z$ to Eq. (13), we obtain at least 39 limit cycles. In particular, we have at least 40 independent Lyapunov constants (remember that the first one is $V_0=2 \lambda _1$) which are all the $V_m\ (0\le m\le 40)$ except $V_{38}.$ Unfortunately we are unable to obtain the second order of all $V_j$ to check if $V_{38}$ is independent of $V_1, V_{2}, \ldots , V_{37},\ V_{39}$ or not.

• (d) Finally consider the general perturbation of Eq. (5) in the class of polynomials of degree 8

  $$\begin{aligned} \dot{z}=iz-\frac{4}{3}z^8+z\bar{z}^{7}+i\tau _8 \bar{z}^8 +\sum \limits _{j+k=2}^8 (e_{j,k}+f_{j,k}i)z^j\bar{z}^k, \end{aligned}$$

  (14)

  where $\tau _8$ is defined under (5) and $e_{j,k}$ and $f_{j,k}$ are small real parameters.

Straightforward computations show that:

• (i) Equation (5) has a weak-focus at the origin with order 70.

• (ii) The Jacobian matrix of $\{V^{\ell }_1,\ldots ,V^{\ell }_{69}\}{\setminus }\{V^{\ell }_4,V^{\ell }_5,V^{\ell }_{11},V^{\ell }_{29},V^{\ell }_{36},V^{\ell }_{60},V^{\ell }_{67}\}$ with respect to the parameters has rank 62.

• (iii) $V^{\ell }_{4},$ $V^{\ell }_{5},$ and $V^{\ell }_{11}$ vanish identically.

• (iv) $V^{\ell }_{29}$ and $V^{\ell }_{36}$ are both linear combinations of $V^{\ell }_{1}$, $V^{\ell }_{8},$ $V^{\ell }_{15},$ and $V^{\ell }_{22}.$

• (v) $V^{\ell }_{60}$ and $V^{\ell }_{67}$ are both linear combinations of $V^{\ell }_{18}$, $V^{\ell }_{25},$ $V^{\ell }_{32},$ $V^{\ell }_{39},$ $V^{\ell }_{46},$ and $V^{\ell }_{53}.$

Therefore, in a similar way as in the previous cases, we have at least 62 independent Lyapunov constants $\{V_1,\ldots ,V_{69}\}{\setminus }\{V_4,V_5,V_{11},V_{29},V_{36},V_{60},V_{67}\}$. By adding the linear perturbation $\lambda _1z$ to Eq. (14), we obtain at least 63 limit cycles which bifurcate from the origin. $\square$

At the end of this section, we extend Proposition 1 of [21] to higher degree.

Proposition 3.1

For every $n=20,22,24,\ldots , 34$, there exists a real constant $\tau _n$ such that equation

$$\begin{aligned} \dot{z}=iz-\frac{n}{n-2}z^n+z\bar{z}^{n-1}+i \tau _n \bar{z}^n, \end{aligned}$$

(15)

has a weak-focus at the origin of order $n^2+n-2$.

We have checked the above result in the same way of [21] by using the method developed in [10]. For the sake of brevity we will not provide the detailed proof in this paper nor the explicit expression of all values of the constants $\tau _n$ because of the huge size of them.

4 Cyclicity of the Weak-Focus of Eq. (11)

In this section we present high order weak-focus for polynomial systems of odd degree. This will be the natural candidate systems to obtain high cyclicity. As we have mentioned, among the existing literature, the highest known weak-focus order is $(n^2+n-2)/2$ for polynomial systems of odd degree n. Although this conclusion has only been confirmed for $n\le 19$. In this section we will first provide a very simple polynomial equation of degree n with a weak-focus of order exactly $(n-1)^2$ at the origin for $n\le 100$. This order improve the previous results for all odd $n\ge 5.$ However, we are unable to prove analytically the conclusion for general n nor check, with a computer, the validity for higher values of n due to the computational difficulties. The proof of Theorem 1.3 is standard and hence it is omitted here.

Let us consider the cyclicity of Eq. (11) under general polynomial perturbation for some concrete values of degree n. The following result summarizes the obtained lower bounds for the cyclicity for $3\le n \le 8.$ In particular this prove the remaining case of Theorem 1.1(c).

Theorem 4.1

Under general polynomial perturbations of degree n, we have that

• (a) for $n=3,4,5$, the cyclicity of the origin as a weak-focus of Eq. (11) is $(n-1)^2$;

• (b) for $n=6,7,8$, there are at least $n^2-3n+6$ limit cycles which bifurcate from the origin of Eq. (11).

Proof

Consider the general perturbation of Eq. (11)

$$\begin{aligned} \dot{z}=iz+ \bar{z}^{n-1}+z^n+\sum \limits _{j+k=2}^n (e_{j,k}+i f_{j,k})z^j\bar{z} ^k, \end{aligned}$$

(16)

where $e_{j,k}$ and $f_{j,k}$ are small real numbers.

Notice that Theorem 1.3 guaranties that only the first $(n-1)^2$ Lyapunov constants are necessary to be computed. We denote by $V^{\ell }_m$ the linear part of each m-Lyapunov constant $V_m$ with respect to all the perturbation parameters $e_{j,k}, f_{j,k}$. For every Eq. (16) with $n=3,4,\ldots , 8$, by direct calculation we obtain the expressions of $V^{\ell }_m$ for $m=1,\ldots ,(n-1)^2.$ Here we only provide the expressions for the case $n=3$. The expressions for the other values of n are omitted due to the huge size of them.

$$\begin{aligned} V^{\ell }_{{1}}&=2e_{{2,1}},\\ V^{\ell }_{{2}}&=\frac{10}{3}e_{{1,1}}-\frac{4}{3}e_{{2,0}}-\frac{8}{3}e_{{2,1}}-2f_{{1,2}},\\ V^{\ell }_{{3}}&=-\frac{3}{4}e_{{0,3}}-{\frac{25}{18}e_{{1,1}}}+\frac{5}{9}e_{{2,0}}-{\frac{26}{9}e_{{2,1}}}+\frac{5}{2}f_{{0,3}}+{\frac{21}{4}f_{{1,1}}}-\frac{3}{2} f_{{2,0}},\\ V^{\ell }_{{4}}&=2+4e_{{0,2}}-{\frac{24}{5}e_{{0,3}}}-{\frac{1391}{135}e_{{1,1}}}-\frac{16}{3}e_{{1,2}}+{\frac{362}{135} e_{{2,0}}}-{\frac{8294}{135}e_{{2,1}}}\\&\quad +6e_{{3,0}}-\frac{7}{3}f_{{0,3}}+{\frac{94}{15}f_{{1,1}}}+6f_{{1,2}}+{\frac{16}{15} f_{{2,0}}}. \end{aligned}$$

Let R(n) be the rank of the Jacobian matrix of $V^{\ell }_1, V^{\ell }_{2}, \ldots ,V^{\ell }_{(n-1)^2-1}$ with respect to the parameters. Straightforward computations show that:

• (i) for $n=3,4,$ and 5 $R(n)=(n-1)^2-1$;

• (ii) for $n=6$, we have $V^{\ell }_3=0$ and $R(6)=23$;

• (iii) for $n=7$, we have $V^{\ell }_4=0,$ $8V^{\ell }_3+9V^{\ell }_9=0,$ and $R(7)=33$;

• (iv) for $n=8$, we have $V^{\ell }_4=V^{\ell }_5=V^{\ell }_{11}=0$ and $R(8)=45$.

For $n=3,4,5$, according to statement (i), we conclude that $V^{\ell }_1, V^{\ell }_{2}, \ldots ,V^{\ell }_{(n-1)^2-1}$ are linearly independent. Finally, adding the linear perturbation terms, by Proposition 2.2, we obtain $(n-1)^2$ limit cycles bifurcating from the origin. For these degrees the cyclicity and the order of the weak-focus coincide.

For each $n=6,7,8$, using statements (ii)–(iv) and adding the linear perturbation terms, we get from Proposition 2.2 that at least 24, 34, and 46 limit cycles bifurcate from the origin. This complete the proof. $\square$

Notice that, from the above proof, to check if the cyclicity coincide or not with the order of the weak-focus for $n=6,7,$ and 8 we should study higher order terms, not only the linear ones. But we are unable to do, due to the computational difficulties. As a direct corollary of Theorem 4.1 we have that $M(7)\ge 34.$

5 Final Remarks

We would like to point out that by Theorem 1.1 ($n=4$) and Theorem 4.1 ($n=3,4,5$), in some cases the precise cyclicity can be obtained by computing the linear part of the Lyapunov constant with respect to the parameters. This actually suggest that in some cases Proposition 2.2 provide a simple way to compute the cyclicity of a weak-focus.

On the other hand, although the order of the weak-focus of Eqs. (3) and (5) are 40 and 70 respectively, we have not proved the existence of the total number of the expected limit cycles. We have not been able to obtain all the second order terms, because of the size of them, necessary to complete the higher order study developed in [6].

The unperturbed Eqs. (2), (3) and (5) are special cases of family (15). When perturbations of this equation are considered for higher values of n,  then two obstacles arise. The first is that the difference between the order of the weak-focus and the number of independent linear parts of Lyapunov constants increase with n (2, 7, 15 for $n=6,8,10,$ respectively). The second is that the number of Lyapunov constants such that the linear part vanish also increases (1, 3, 6 for $n=6,8,10,$ respectively). Similar phenomena occur with (11). For Eq. (4) the number of limit cycles using the linear parts method, 34, is two less than the order of the weak-focus, 36.

Moreover, as we have partially done for (13), the quadratic parts of the Lyapunov constants with respect to the parameters were impossible to get for $n\ge 8.$ This is the reason that we did not obtain more limit cycles for system (14). Therefore, if we want an effective proof that guaranties $n^2+n-2$ limit cycles emerging from a weak-focus for $n\ge 6$, Eq. (15) are not so good candidates because of the difficulties in the computations. Much more if we consider that in [16] the existence of systems with weak-foci of order $n^2+n-2$ are done for $4\le n\le 13.$ But they are not explicit, that is, nobody knows which is the concrete system that have the weak-focus with that prescribed cyclicity. And this is not the objective of the present paper.

Appendix

All the computations of this paper are done with Maple except Theorem 1.3 where we have used Pari, see [26]. The algorithm to get the first nonvanishing Lyapunov quantity is written below. We note that it is specially designed for system (11) and, consequently, can not be used in general. Its simplicity is due to the fact that the number of monomials is so small and fixed. Finally, just to show the magnitude of the computations, we remark that the calculation of the last case ($n=100$) needed around 14 h and the total RAM memory of our computer.¹ Moreover, the Lyapunov quantity is a negative rational which is the quotient of two integers of 6209 and 6016 digits, respectively.