Introduction

In many industrial clusters such as, electronics, communication, aerospace, biomedical devices, defense and automotive, miniaturization of the products have recently become a global trend, which requires advanced manufacturing technologies at micron level. Microforming is a plastic deformation procedure for the production of parts having at least two dimensions at micron scale. At this scale there are various factors affecting the deformation behavior, process performance, and the quality of micro-formed parts (see e.g. [11, 14, 36]) for an overview).

In addition to geometry, tooling design, process parameter configuration and deformation conditions, the microstructure, the grain and the specimen size play a crucial role in the plastic behavior of the material (see e.g. [18, 37, 39] for a detailed review). Size effect manifests itself through two important mechanisms at micron scale, namely the size of the grains leading to intrinsic size effect and the size of the specimen restricting the number of grains and leading to statistical/specimen size effect. The fundamental reason behind the intrinsic size effect is the dislocation-grain boundary interaction which could result in transmission/accumulation of dislocations depending on the orientation of the grain itself and the misorientation with respect to the neighboring grains. The accumulation of dislocations is naturally more likely to occur in a specimen with small grains, which makes plastic deformation more difficult to occur resulting in an increase of yield stress and the hardening. If the grain size is kept constant and the size of the specimen is changed then the number of grains in each specimen would be different and the statistical size effect would come into play. For the small specimens at micron level the number of grains would be quite small and each grain’s crystallographic property would play crucial role in the macroscopic plastic behavior of the material. Eventually both size effect mechanisms govern the mechanical behavior during plastic deformation procedures at small scale.

Various theories have been developed for the modeling of macro scale plastic deformation during conventional metal forming processes and many of these frameworks are implemented in commercial finite element simulation tools. In all these local plasticity and damage models, the specimen size and the grain size do not enter the frameworks. Therefore, these classical simulations are not able to capture the effect of the size on the mechanical response of the material. As introduced above shortly, on the scale of several micrometers and below, crystalline materials behave differently from their bulk equivalent due to micro-structural effects (e.g. grain size, lattice defects and impurities), gradient effects and surface constraints (see [16]) for an extensive review). These effects could lead to stronger or weaker material response depending on the size and unique micro-structural features of the material. It has been a challenge to establish models taking into account the microstructural phenomena. Crystal plasticity framework incorporated into FEM has been a key micromechanically motivated modeling approach to simulate the anisotropic material behavior in both single and polycrystalline specimens. It has also been used in statistical/specimen size effect polycrystal simulations (see e.g. [12, 27]), yet the model lacks the length scale in its formulation and the intrinsic size effect can not be modeled. Both size effects can only be modeled simultaneously through a non-local strain gradient crystal plasticity framework. Even though there are a number of non-local crystal plasticity studies focussing these effects (see e.g. [47, 48]) a detailed study on microstructures with different number of grains, grain size, boundary conditions and deformation rate is still missing. Moreover, there have been various studies addressing the size effect issue experimentally and also modeling the behavior with flow stress models (see e.g. [4, 13, 19, 23]). However most of the models do not go beyond the flow stress studies and there is a need for finite element simulations of the specimen through a non-local model which is capable of resolving the strain gradients at the grain boundaries.

Current paper studies both the intrinsic and the statistical size effects through a strain gradient polycrystalline plasticity framework developed for microstructural patterning in single crystals in [42, 43] and used for different microstructure evolution phenomena in [20, 21]. Different specimen and grain sizes are considered using Voronoi tessellation, where the polycrystalline aggregate is generated using probability theory. There are more advanced options for creating physical representative microstructure as well, such as digital material representation (DMR) (see e.g. [22, 24, 33]), where the microstructure morphology can be represented through microscopy imaging, or via simpler methods such as cellular automata, Monte Carlo methods, and Voronoi tessellation . For the sake of simple analysis of microstructures with different number of grains Voronoi method is employed here. Applying the constitutive model to 2D (plane strain) polycrystalline structure, the micro tensile tests for various microstructures are numerically simulated by finite element method (FEM) in Abaqus software through the developed implicit user element subroutine. Even though the 2D simulations introduce an out of plane constraint, the qualitative observations obtained in this study do not change through a 3D extension, yet it would make the analysis more realistic.

The attention is focused on the effect of different boundary conditions and rates on the spatial deformation evolution and the macroscopic size-dependent behavior of the material. Some recent studies address the influence of the boundary conditions in micro scale specimens through strain gradient models (see e.g. [9, 28]), however conclusions are mostly drawn for bi-crystals or specimens with very restricted number of grains or grain shapes (see [3]). A thorough study considering different microstructural parameters and grain boundary conditions has not yet been conducted. The current study illustrates the intrinsic size-effect for various microstructures with different grain size and grain number as well as the statistical effect, which fades away with the increasing number of grains. The advantage of the current study is that the strain gradient crystal plasticity framework is directly implemented into a commercial software and the realistic simulations of the microstructures with various grain numbers, size and rates could easily be conducted. The preliminary results on this study have been presented in the conferences and related proceedings (see e.g. [44,45,46]) however a complete work on the effect of grain boundary conditions, the grain size, the sample size and the loading rate has not been published yet neither by the authors nor in the literature. It is crucial to note that the current study considers full size specimens at micron level and addresses the intrinsic and specimen size effect though a nonlocal crystal plasticity framework. Therefore the analysis is quite different than the local crystal plasticity studies considering the polycrystalline response through RVEs (see e.g. [1, 7, 8, 25, 30,31,32, 35]) and nonlocal crystal plasticity studies taking into account RVE of one type (see e.g. [10]).

The paper is organized as follows. First, in “Constitutive model” section, the strain gradient crystal plasticity model is shortly presented. Then in “Numerical examples” section, a detailed numerical analysis of both intrinsic and statistical size effects is studied where different microstructures analyzed focusing on the influence of the boundary conditions and the deformation rate. Finally, in “Conclusion and Discussion” section the concluding remarks are summarized.

Constitutive model

The constitutive model in this paper is developed originally as a non-convex model for deformation patterning modeling in single crystals (see [39]). Here, the convex counter-part of the model is employed to model size effect prediction in metallic materials. The model is based on the additive decomposition of the strain into elastic and plastic components and the plastic slip field evolution is governed by the slip law,

$$ \dot{\gamma}^{\alpha} = \dot{\gamma}_{0}^{\alpha} \left( |\tau^{\alpha} + \mathbf{{\nabla}} \cdot \mathbf{{\xi}}^{\alpha}|/{s^{\alpha}} \right)^{\frac{1}{m}} \text{sign}(\tau^{\alpha} + \mathbf{{\nabla}} \cdot \mathbf{{\xi}}^{\alpha}) $$
(1)

where \(\tau ^{\alpha }=\mathbf {\sigma }:\mathbf {P}^{\alpha }\) is the resolved Schmid stress on the slip systems with \(\mathbf {{P}}^{\alpha } = \frac {1}{2} (\mathbf {{s}}^{\alpha } \otimes \mathbf {{n}}^{\alpha } + \mathbf {{n}}^{\alpha } \otimes \mathbf {{s}}^{\alpha })\), the symmetrized Schmid tensor, where s αand \(\mathbf {{n}}^{\alpha }\) are the unit slip direction vector and unit normal vector on slip system \(\alpha \), respectively and \(\mathbf {{\xi }}^{\alpha }\) is the microstress vector ξ α = ∂ ψ ∇γ /∂ ∇ γ α = A ∇ γ α bringing the plastic slip gradients into the plasticity formulation. A is a scalar quantity, which includes an internal length scale parameter, and in this work it is defined as \(A = E R^{2} / (16(1-\nu ^{2}))\) where R is a typical length scale for dislocation interactions. In these types of models the internal length scale could be related to different microstructural features and the value would vary, e.g. [26] relates it to dislocation spacing, and [38] to grain size. In the following example we relate R to a certain percentage of the grain size to study its influence. The average grain size and the mesh size govern the magnitude of the internal length scale parameter chosen here. In fact, the mesh size should be smaller than the internal length scale parameter A standing in front of the gradient term.

For the solution of initial boundary value problems a fully coupled finite element solution algorithm is employed where both the displacement u and the plastic slips \(\gamma ^{\alpha }\) are considered as primary variables. These fields are determined in the solution domain by solving simultaneously the linear momentum balance and the slip evolution (1) for \(m = 1\) and constant slip resistance, which constitute the local strong form of the balance equations:

$$ \begin{array}{rrr} \boldsymbol{\nabla} \cdot \boldsymbol{\sigma} &=& \boldsymbol{0}\\ \dot{\gamma}^{\alpha} - \frac{\dot{\gamma}^{\alpha}_{0}}{s^{\alpha}} \, \tau^{\alpha} - \frac{\dot{\gamma}^{\alpha}_{0}}{s^{\alpha}} \,\boldsymbol{\nabla} \cdot \boldsymbol{\xi}^{\alpha} + \frac{\dot{\gamma}^{\alpha}_{0}}{s^{\alpha}} \frac{\partial \psi_{\gamma}}{\partial \gamma^{\alpha}} &=&0 \end{array} $$
(2)

The variational expressions representing the weak forms of the governing equations given above are obtained through a multiplication by weighting functions \(\delta _{\boldsymbol {u}}\) and \(\delta _{\gamma }^{\alpha }\) and integration over the domain \({\Omega }\), which is subdivided into finite elements, where the unknown fields of the displacement and slips and the associated weighting functions within each element are approximated by their nodal values multiplied with the interpolation shape functions. Then the weak forms of the balance equations are linearized with respect to the variations of the primary variables \(\underline {\boldsymbol {u}}\) and \(\underline {\gamma }^{\alpha }\) and solved by means of a Newton-Raphson solution scheme for the increments of the displacement field \({\Delta } \boldsymbol {u}\) and the plastic slips \({\Delta } \gamma ^{\alpha }\). The procedure results in a system of linear equations which can be written in the following matrix format,

$$ \left[ \begin{array}{cc} \underline{K}^{uu} & \underline{K}^{u \gamma} \\ \underline{K}^{\gamma u} & \underline{K}^{\gamma \gamma} \end{array} \right] \; \left[ \begin{array}{c} {\Delta} \underline{\boldsymbol{u}} \\ {\Delta} \underline{\gamma}^{\alpha} \end{array} \right] \; = \; \left[ \begin{array}{c} -\underline{R}^{u} + \underline{R}^{ext}_{u} \\ - \underline{R}^{\gamma} + \underline{R}^{ext}_{\gamma} \end{array} \right] $$
(3)

where \(\underline {K}^{uu}, \underline {K}^{u \gamma }, \underline {K}^{\gamma u}\) and \(\underline {K}^{\gamma \gamma }\) represent the global tangent matrices while \(\underline {R}^{u}\) and \(\underline {R}^{\gamma }\) are the global residual columns. The contributions \(\underline {R}^{ext}_{u}\) and \(\underline {R}^{ext}_{\gamma }\) originate from the boundary terms. This framework is implemented as a user element Fortran subroutine in Abaqus software and the postprocessing is conducted through a Python script developed by the authors to convert the data into a file that could be read by the finite element software. A detailed finite element implementation of the model as a user element is presented in [40]. Note that, the global degrees of freedom in this framework are the displacement and the plastic slips, in terms of which the boundary conditions are defined. There are two types of conditions that could be used at grain boundaries during polycrystal simulations. The first one is the soft boundary condition for the plastic slip which does not restrict the transfer of dislocations to the neighboring grain, and the other one is the hard boundary condition which blocks the transmission of the dislocations through grain boundaries resulting in the boundary layer development in terms of plastic slip and the related stress concentrations at the grain boundaries.

Numerical examples

Numerical examples address both statistical/specimen size effect and the intrinsic size effect of polycrystalline specimen at micron scale having microstructure with \(5, 20, 50\) and 110 grains obtained through Voronoi tessellation (see Fig. 1).

Fig. 1
figure 1

5, 20, 50 and 110 grain model

Full size image

The initial average grain size in these simulations are set to \(D_{av}= 150\mu m\). Then the effect of the grain size is analyzed through a scaling operation using the internal length scale parameter, which would give values from \(100\mu m\) to \(375\mu m\). Horizontal tensile specimens are considered. Displacement is applied to the right edge in the global +x direction, resulting in macroscopic \(\big \langle \varepsilon _{11}\big \rangle = 2.5 \%\). The symbol \(\big \langle \big \rangle \) represents the Macaulay bracket, indicating a macroscopically averaged value. The left edge is constrained in the x direction and rigid body movement is prevented by fixing the bottom left corner of the model in global y direction.

The material parameters, presented in Table 1, are not directly related to any specific engineering material, rather used to demonstrate the strain gradient effects in the polycrstalline aggregates. Crystallographic orientations of grains are randomly distributed (0-360). Two slip systems (120, 60) are considered in the following examples. The slip resistance and reference slip rate are chosen as average values representing metallic alloys.

Table 1 Material properties of the strain gradient crystal plasticity model
Full size table

The specimen is discretized with a quadrilateral mesh where linear and quadratic shape functions are used for plastic slip field and displacement field respectively. As noted before shortly, the mesh size is directly related to the internal length scale parameter and it should be smaller than the internal length scale. The heterogenous microstructure evolution occurs in the vicinity of the grain boundaries. Therefore a non-uniform mesh is used which gets finer closer to the GBs (see e.g. our recent conference proceedings, [44, 46]) for the detailed mesh discussion and representation.

The intrinsic size effect could be analyzed through a change in the grain size or a change in the internal length scale parameter, where both would influence the macroscopic constitutive behavior and the spatial evolution of the plastic strain in the same manner. Therefore, this effect is studied through different \(D_{av}/R\) ratio values. A small \({D_{av}/R}\) value represents a microstructure with small grain size or large internal length scale parameter, which induces large internal stresses penalizing high plastic slip gradients. This behavior results in a more spread geometrically necessary dislocation distribution and therefore the boundary layer thickness is increased. In other words dislocations in small grains would have more possibility to interact with a grain boundary, which results in more dislocation accumulation at the grain boundary and this would increase the thickness of the boundary layer. A classical crystal plasticity framework does not include the plastic slip gradients, therefore a dislocation accumulation or boundary layer evolution cannot be observed. This would result in a sudden change of plastic deformation from one grain to another and it is certainly not physical.

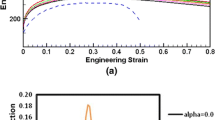
Figure 2 illustrates the intrinsic size effect on the constitutive behavior of a specimen having a microstructure with 5 grains and different \(D_{av}/R\) ratios for both hard and soft boundary conditions. Note that in these curves, as well as in the upcoming stress-strain figures, the volume average of quantities are plotted. As expected and discussed previously, the case with the smaller grain size shows stiffer response. The macroscopic yielding of the material is not influenced by the grain boundary conditions, however there is substantial difference in the case of hardening.

Fig. 2
figure 2

Intrinsic size effect on the macroscopic stress strain response for both soft (left) and hard (right) boundary conditions

Full size image

In Fig. 3(left) and (right) the effect of the random orientation on the global constitutive behavior is presented for soft and hard boundary conditions respectively for 30 randomly oriented grain systems. The bandwidth of the scatter for the soft boundary condition is slightly larger than the hard boundary condition. In the soft case the plastic slips are not restricted at the grain boundaries and the mismatch of orientation is reflected more pronounced at the macroscopic constitutive response. In the case for hard boundary conditions, the plastic slip is enforced to be zero at the grain boundaries, which is a strong condition reducing the effect of orientation mismatch. The randomness of the orientation introduces a statistical effect, which is prominent at the microstructures with low number of grains. The cases with higher number of grains will be discussed in the following where the behavior converges to the isotropic material behavior with increasing number of grains.

Fig. 3
figure 3

Orientation effect on the macroscopic response (for 30 different randomly oriented cases) for soft grain boundary conditions (left), and for hard grain boundary conditions (right)

Full size image
Fig. 4
figure 4

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with hard grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.004 s^{-1}\)

Full size image

In Fig. 4 the local von Mises stress and equivalent plastic strain distributions are plotted for different \(D_{av}/R\) ratios to illustrate the effect of the grain size at a relatively low strain rate, \(\dot {\varepsilon }= 0.004 s^{-1}\). The plastic slip at all grain boundaries are constrained to reach zero level, which induces the evolution of the boundary layer. For small \(D_{av}/R\) values, representing the case with small grain boundaries, wider grain boundary layer corresponding to more distributed geometrically necessary dislocation density are observed. Same influence is observed for the stress evolution at the grain boundaries and more pronounced stress concentration is obtained for the small grain case.

Same example with soft grain boundary conditions are addressed in Fig. 5. The grain size effect on the equivalent plastic strain and equivalent stress distribution is same with the hard boundary case. In this case the stress concentrations at the grain boundary occurs solely due to orientation mismatch since there is no constraint on the plastic slip evolution at the grain boundaries. Note that in all simulations in this work only two slip systems \((60^{o} \text {and} 120^{o})\) are considered and increasing the number of slip systems does not cause a major change in the results for the current plane strain problem.

Fig. 5
figure 5

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with soft grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.004 s^{-1}\)

Full size image

In Figs. 6 and 7 the spatial field evolution studied in Figs. 4 and 5 addressed again with a higher deformation rate, i.e. \(\dot {\varepsilon } = 0.1 s^{-1}\). Comparison of Figs. 4 and 6 reveals that increasing the rate of deformation reduces the thickness of the boundary layer or in other words during high rate of deformation the microstruture forming around the grain boundary does not have enough time to evolve, therefore it is thinner. On the other hand the comparison of the stress values reveals that the stresses obtained at the higher deformation rate reaches much higher levels which is obvious in both small and large grain cases. This makes the grain structure less evident in the plastic strain field plot in Fig. 7 for the case with soft boundary conditions, which is not observed for the stress field evolution.

Fig. 6
figure 6

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with hard grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.1 s^{-1}\)

Full size image
Fig. 7
figure 7

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with soft grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.1 s^{-1}\)

Full size image

After the discussion of the statistical and intrinsic size effect in the samples with very restricted number of grains, the cases with higher number of grains is addressed in the following. Firstly, the intrinsic size effect reflecting the influence of the grain size on the macroscopic constitutive response is similar to the case presented in Fig. 2 for the microstructure with 5 grains and it will not be repeated for other microstructures with higher number of grains. In Figs. 8 and 9 the statistical size effect is presented for samples including 50 and 110 randomly oriented grains respectively for both soft and hard grain boundary conditions. As expected, the effect disappears with increasing number of grains and the behavior converges to isotropic material behavior. The large scatter observed in Fig. 3 due to statistical size effect diminishes with the increasing number of grains (see e.g. [2, 5, 6] for a detailed experimental discussion on the statistical effect). The statistical size effect almost disappears at the case with 110 grains. The transition from the anisotropic behavior of single crystal to isotropic behavior of polycrystalline material happens to occur when the the specimen length is about 10 times or higher of the grain diameter (see e.g. [37]), which is illustrated with the numerical examples here. The comparison of the grain boundary conditions reveal that the scatter observed due to the randomness of the grains decreases slightly in the case of hard grain boundary conditions.

Fig. 8
figure 8

Orientation effect on the macroscopic response for soft grain boundary conditions (left), and for hard grain boundary conditions (right) for a specimen with 50 grains

Full size image
Fig. 9
figure 9

Orientation effect on the macroscopic response for soft grain boundary conditions (left), and for hard grain boundary conditions (right) for a specimen with 110 grains

Full size image

Next, the microstructure evolution study conducted for 5 grains is repeated for the case with 110 grains where the orientation is randomly distributed again. Figures 10 and 11 illustrate the effect of the hard and soft boundary conditions in small and large grained samples through local distribution of equivalent plastic strain and the von Mises stress. The stress and strain inhomogeneity is evident at the grain boundaries in all cases due to the misorientation of the neighboring grains. The limiting values of the stress distribution is edited in the snapshots in order to point out the differences between different cases. The grain boundary layer thickness is obviously larger and the grain structure is more evident for the case with small grain size (the figures on the right) for both hard and soft boundary conditions in Figs. 10 and 11 respectively. Moreover, the stress concentration is higher for the case with small grains and also for the case with hard boundary conditions. The strain localization occurs randomly depending on the orientation distribution. While the stress concentration and the grain boundary thickness occurs solely due to orientation mismatch for soft boundary case, the evolution of these fields is completely controlled by the zero slip condition for the hard boundary cases. This is only possible through a gradient theory where the plastic slip or dislocation density field is considered to be a degree of freedom during finite element solution procedure. However the real behavior of the grain boundary is in between these two limiting cases. The behavior of the grain boundary approaches to the case of hard grain boundary for the large orientation mismatch and converges to the soft grain boundary for the small orientation mismatch. Therefore a proper grain boundary model is needed for a more realistic description (see e.g. [15, 17, 28, 29, 34]).

Fig. 10
figure 10

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with hard grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.004 s^{-1}\)

Full size image
Fig. 11
figure 11

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with soft grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.004 s^{-1}\)

Full size image

The influence of the deformation rate is discussed as well for the case with 110 grains in Figs. 12 and 13 for both hard and soft grain boundary conditions respectively. The aforementioned observations for the grain size and grain boundary conditions remains valid in this case as well. However in the case with higher deformation rates the stress concentration at the grain boundaries reaches to much higher values while the grain boundary thickness is much smaller. As discussed previously for the case with 5 grains in this study and for the the evolution of other types of intragranular microsturctures in previous studies (see e.g. [20, 39, 43]) the microstructures do not have sufficient time to evolve during high deformation rate loading, resulting in a narrow grain boundary layer in this case. The current constitutive framework is highly viscous due to the \(m = 1\) choice in the slip law, and it is considerably higher than the realistic metallic response. However it helps to present clearly the rate effect on the microstructure evolution and the macroscopic constitutive response. For more realistic simulations to compare with experimental behavior of metallic alloys the proper value of m should be identified. Moreover depending on the material, the effect of the temperature should be taken into account as well. The slip resistance and the plastic slip system activity depends on the temperature and at higher temperature levels additional slip systems might be activated which influences the plastic behavior of the material (see e.g. [41]). However, the purpose of the current work is to illustrate both the macroscopic and microscopic plastic behavior of polycrystalline metallic materials qualitatively during microforming processes in a simplest possible way through an advanced micromechanical model, which is only possible through some simplifications. Yet, the study gives clear messages on the plastic behavior of metallic materials with restricted amount of grains. Note that the framework is developed in the small strain context, and the applied strain level is quite low. However, since the primary concern here is the microplasticity rather than damage and fracture behavior, the model does not prevent us from obtaining important conclusions. For failure analysis finite strain extension of the model and simulations at higher strain levels would be needed.

Fig. 12
figure 12

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with hard grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.1 s^{-1}\)

Full size image
Fig. 13
figure 13

Local equivalent plastic strain (top) and equivalent stress distribution (bottom) with soft grain boundary conditions for large (left) D a v /R = 400 and small (right) D a v /R = 40 values representing large and small grain sized specimens at \(\dot {\varepsilon }= 0.1 s^{-1}\)

Full size image

Conclusion and Discussion

This study addresses the intrinsic and the statistical size effects in micron scale polycrystalline metallic specimens under plastic deformation through a non-local (strain gradient) crystal plasticity framework. In samples including limited number of grains the statistical effect due to random grain orientation is quite dominating since the individual grain behavior plays crucial role in material response and there is huge scatter in stress-strain curves. As the number of grains is increased the scatter band decreases. Moreover, a detailed study on the effect of the grain boundary conditions, grain size and the deformation rate on the local response is presented as well. It is observed that hard conditions at the grain boundaries yield not only increase in the hardening behavior but also slight decrease in the scatter due to random orientation distribution. The stress concentration due to orientation mismatch is evident in all cases with soft and hard boundary conditions, which increases with hard grain boundary conditions and higher deformation rate. The thickness of the boundary layer developed due to zero slip (hard grain boundary) condition increases with the reduction in grain size and decreases with higher deformation rates. Moreover the stress values at the grain boundary increases with the decrease in grain size and with the increase in loading rate. Various observations are presented for both macroscopic constitutive response and local stress and strain evolution during the plastic deformation of micron scale sized specimen with different number of grains and grain size, which has been missing in the literature. One of the important aspects of the current study is that the pre-processing, modeling and the post-processing of the simulations are automated in the commercial software Abaqus with python scripts and user element routine (UEL). After certain upgrades of the model in hardening and extension to 3D, the researchers can directly use the model for various forming operations. Even though we do not present such simulations in the current work, a perspective in that direction is presented clearly. The capability of the current model in obtaining intrinsic evolution of stress concentration in the grain boundary region for different grain size and deformation rate offers rather physical modeling opportunity of inter-granular cracking phenomenon. Insertion of cohesive zone elements in the region with certain traction-separation relation would lead to simple but micromechanically motivated modeling of mechanical opening and sliding at grain boundaries.