Discrete mesoscopic modeling for the simulation of woven-fabric reinforcement forming

Abstract

A discrete modeling approach is proposed to simulate woven-fabric reinforcement forming via explicit finite element analysis. The tensile behaviour of the yarns is modeled by truss, beam or seatbelt elements, and the shearing behaviour of the fabric is incorporated within shell or membrane elements. This method is easy to set up using the user-defined material subroutine capabilities of explicit finite element programs. In addition, the determination of the material parameters is straightforward from conventional tensile and shear-frame tests. The proposed approach has been implemented in the ABAQUS and LS-DYNA explicit finite element programs. Two types of fabric, a plain-weave and a twill-weave Twintex® (commingled polypropylene and glass fibres) were characterized and used to validate the modeling approach. For this validation, shear-frame and bias-extension tests have been modeled, and the finite element results are compared to experimental data. The determination of experimental shear angle contours was possible via Digital Image Correlation (DIC). The finite element results from ABAQUS and LS-DYNA are similar and agree well with the experimental data. As an example of the capabilities of the method, the deep drawing of a hemisphere is simulated using both finite elements programs.

Introduction

The use of woven-fabric reinforced composites in the aerospace and automotive industries is growing, and a reliable simulation tool for fabric forming is needed to assist in the design of parts and in the design of the associated processing methods. Processes such as Resin Transfer Moulding (RTM) [1] and thermostamping/thermoforming [2, 3] are promising for producing high-volume low-cost composite parts. By using composites made with these processes, the automotive industry can realize improved fuel economy through vehicle weight reduction by replacing the currently used steel and aluminum parts with polymer composites and have the added benefit of a corrosion-resistant material without an increase in the manufacturing time.

A reliable simulation will help to explore the optimum processing conditions in which the part can be formed without defects such as wrinkles or tearing while maintaining a cycle time that is as short as possible. In addition, the simulation tool can provide the positions of the fabric constituents after forming which is of great importance for structural analysis of the formed part. Such structural analyses could include modal analysis, stiffness and damage tolerance.

For a woven fabric, the two main modes of deformation at the mesoscopic scale (as opposed to the microscale, i.e. the scale of the fibers) are the stretching of the fibers and the in-plane shearing of the fabric. The in-plane shearing results in a change of the angle between the warp and weft yarns. The tensile deformation of the yarns is primarily a result of the uncrimping of the yarns. After the yarns have “stretched” to their limit, then in-plane shearing is the principal mode of deformation during the draping of a three-dimensional (3D) shape.

Numerous testing methods have been developed to characterize the tensile behaviour (uniaxial and biaxial tensile tests [4]) and the in-plane shear behaviour (shear frame and bias-extension tests [5]). The typical tensile behaviour starts with a nonlinear “decrimping” due to the undulations of the yarns within the woven fabric, followed by a linear behaviour, corresponding to the elastic deformation of the fibers. During in-plane shearing, the fabric will first undergo an initial stage with low shear resistance up to the so-called locking angle where the lateral yarn compression starts to build up. As a result of the yarn compression, the shear resistance will significantly increase above the locking angle [6].

The finite element method is very amenable to the development of a simulation tool for woven-fabric composites because it can account for the mechanical behaviour of the fabric and the complex boundary conditions (such as the effect of a binder). Geometrical methods such as the fishnet draping models generally do not have this ability and thus are more suited to simulate handmade draping [7].

Several families of methods have been developed. Boisse et al. [7] have reviewed many of these and have classified these as continuous, discrete and semi-discrete approaches. In the continuous approach, the fabric is homogenized and considered as a continuum. Conventional shell or membrane elements are used, but special considerations of solid mechanics are used to track the evolution of the principal load paths over the fabric within each element. The fabric is initially orthotropic as the yarns are initially mutually perpendicular, but as the fabric shears the material becomes anisotropic. A large volume of work has also been done on discrete modeling, i.e. models where individual components of the fabric such as the fibers or yarns are considered. To maintain reasonable computing time, the models are generally limited to the scale of the yarns. A trellis of truss, beam or spring elements is used to describe the woven fabric. The incorporation of the in-plane shearing resistance over this trellis can be done by the addition of diagonal truss elements [8, 9] or shell or membrane elements [10, 11]. The semi-discrete approach has been introduced recently and appears to be promising. Specific 4-node and 3-node finite elements that consider the mesoscale components of the woven fabric (the yarns) have been developed to model the specific mechanical behaviour of the fabric [4, 12]. The continuous and semi-discrete models can be very challenging to implement into commercially available finite element packages. In contrast, discrete methods are generally easy to set up [8, 9]. Apart from a few exceptions, e.g. a model by Yu [13, 14] and a recent continuous model developed by Willems [15], material parameters cannot generally be directly deduced from testing results, and an identification step is needed [15]. This identification step involves the simulation of tensile and shear tests to tune the material parameters to match the experimental data.

In the current study, a discrete approach based on an explicit finite element formulation using a hypoelastic description is proposed. The explicit formulation was chosen because it is the best suited formulation for forming simulations due to its computing time efficiency and relatively robust contact algorithm. In developing this method, the objective was to keep a relatively simple description and to have a scheme that can be implemented within popular commercially available explicit finite element packages that allow for the linking of user-defined material subroutines with the explicit solver. To demonstrate this ability, the model was implemented within two commercial explicit codes, ABAQUS and LS-DYNA. In addition, the proposed model allows a direct identification of the material parameters from simple tensile and shear tests of the fabric.

The following aspects are presented in this paper:

• Mathematical description of the model,

• Material characterization and determination of the parameters,

• Validation of the shear response on a single mesh unit and a shear frame simulation,

• Validation of the model on a more complex state of deformation (i.e. on a bias-extension test), using Digital Image Correlation to determine the experimental shear strain field.

• Forming simulation of a three dimensional (3-D) shape.

Model description

Principle

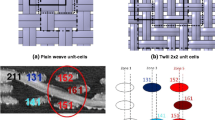
A discrete description of the fabric is built using a mesh of 1-D and 2-D elements (Fig. 1). The 1-D elements account for the tensile contribution of the yarns to the fabric material behavior and automatically capture the evolution of the orientation of the principal load paths as the yarns rotate. The 2-D elements account only for the shearing resistance of the fabric and have no tensile stiffness. Appropriate nonlinear constitutive equations are associated with the 1-D and 2-D elements via user-defined material subroutines to capture the mechanical behavior of the fabric.

Fig. 1

Principle of the discrete mesoscopic modeling using a combination of 1-D and 2-D elements

User-defined material subroutines

To model large deformation and strains, explicit commercial codes such as ABAQUS and LS-DYNA can employ nonlinear constitutive laws. The material behavior may or may not be rate dependent. For the current investigation, a rate-independent hypoelastic material response was used. The evolution of the stress-strain state uses the Hughes and Winget formula for the stress update [16, 17] and expressing this process in Voigt notation:

$$ \sigma_i^{t + 1} = \sigma_i^t + \Delta \sigma_i^{t + 1} $$

(1)

$$ \Delta \sigma_i^{t + 1} = C_{ij} .\Delta \varepsilon_j^{{t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}} $$

(2)

where $\Delta \sigma_i^{t + 1}$ is the stress increment at time step t + 1, C _ij is the constitutive matrix which is a function of the strain state and $\Delta \varepsilon_j^{{t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}}$ is the midpoint strain increment obtained from the integration of the strain-rate tensor. In this paper, the conventional finite element formulation of representing the state of stress as a vector σ _i is used such that the relationship between the stress tensor entries σ ₁₁ , σ ₂₂ (in-plane normal stresses) and σ ₁₂ (in-plane shear stress) and the stress vector entries are σ ₁  = σ ₁₁ , σ ₂  = σ ₂₂ and σ ₄  = σ ₁₂ and likewise for the strains. Finite element packages such as ABAQUS and LS-DYNA allow the user to link custom constitutive models with the overall solver to update the stress (Eq. 2) via user-defined material subroutines. The strain increment, $\Delta \varepsilon_j^{{t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}}$, is given by the solver to the user-defined material subroutine that subsequently returns the corresponding stress increment to the solver. The stress update is made in the local reference frame for the element, i.e. a co-rotational frame that rotates with the element. The summation of the strain increments give a logarithmic (or true) strain in the principal-stretch directions [18].

Case of 1-D elements

For 1-D elements, Eq. 2 reduces to:

$$ \Delta \sigma_1^{t + 1} = C_{11} \left( {\varepsilon_1 } \right).\Delta \varepsilon_1^{{t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}} $$

(3)

where C ₁₁ is the tangent tensile modulus and is a function of ε _1, the axial strain in the yarn. This tangent modulus is easily found from the slope of the experimental tensile stress-true strain data of the fabric.

Case of 2-D “shear” element

The incorporation of the in-plane shear behaviour in a shell/membrane element for finite-strain analysis is more challenging than the tensile behaviour of the 1-D elements. Two reference frames as depicted in Fig. 2 have to be considered. The e _i unit vectors define the local orthogonal reference frame, i.e. the Green-Nagdhi frame that rotates with the material, and the g _i basis vectors form a nonorthogonal frame that follows the yarn directions:

Fig. 2

Schematic representation of the different coordinate systems used

$$ \vec{g}_i = \underline{\underline{F}} .\vec{g}_i^0 = \underline{\underline{F}} .\vec{e}_i^0 $$

(4)

where $\underline{\underline{F}}$ is the deformation gradient tensor known at each time increment.

The stress can be expressed in terms of its contravariant coordinates $\tilde{\sigma }^i$ in g _i . Experimentally, during a shear frame test, the normal components of the stress $\tilde{\sigma }^1$ and $\tilde{\sigma }^2$ are equal to zero and the shear component of the stress $\tilde{\sigma }^4$ is a function of the logarithmic or true engineering shear strain $\gamma_4^L$ expressed in the orthogonal coordinate system e _i :

$$ \tilde{\sigma }^4 = f\left( {\gamma_4^L } \right) $$

(5)

where $\tilde{\sigma }^4$ is equal to the normalized shear force F_sh [5, 19] divided by the thickness of the fabric. The logarithmic definition of strain is used to be consistent with finite element codes that use the logarithmic strains for the summation of the strain increments. The shear strain $\gamma_4^L$ can be obtained from the logarithmic strains in the principal stretch directions $\varepsilon_I^L$ and $\varepsilon_{II}^L$ by a 45° Mohr’s circle transformation. In the case of a shear frame test, a geometrical analysis leads to the expression of $\gamma_4^L$ as a function of the geometric shear angle γ:

$$ \gamma_4^L = \varepsilon_I^L - \varepsilon_{II}^L = - \ln \left( {\tan \left( {{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.} \!\lower0.7ex\hbox{$4$}} - {\raise0.7ex\hbox{$\gamma $} \!\mathord{\left/ {\vphantom {\gamma 2}}\right.} \!\lower0.7ex\hbox{$2$}}} \right)} \right) $$

(6)

The tangent shear modulus C _sh is defined as follows:

$$ C_{sh} \left( {\gamma_4^L } \right) = \frac{{d\tilde{\sigma }^4 }}{{d\gamma_4^L }} $$

(7)

At each time increment t, the in-plane shear behaviour of the woven fabric can thus be captured by the following constitutive equation:

$$ \left[ {\Delta \tilde{\sigma }^4 } \right]_{{\;t + 1}} = C_{sh} \left( {\gamma_4^L } \right).\left[ {\Delta \gamma_4 } \right]_{{\;t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}} $$

(8)

with $\left[ {\Delta \gamma_4 } \right]_{{\;t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}} = 2.\left[ {\Delta \varepsilon_4 } \right]_{{\;t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}}$ (where γ ₄ and ε ₄ denote the engineering and tensorial shear strains, respectively).

This constitutive equation uses the strain increment $\Delta \varepsilon_4^{{t + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}}$ expressed in e _i as it is given by the finite element solver to the user-defined material subroutine. However, the stress increment is expressed in terms of the g _i basis while it needs to be returned to the finite element solver in the e _i basis at the end of the user-defined subroutine. The relationship between $\Delta \sigma_i$ the Cartesian stress increment components in e _i and $\Delta \tilde{\sigma }^i$ the contravariant stress increment components in g _i is obtained from a geometric analysis of Fig. 2 [20]:

$$ \left[ {\begin{array}{*{20}c} {\Delta \sigma_1 } \\ {\Delta \sigma_2 } \\ {\Delta \sigma_4 } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos^2 \alpha } & {\cos^2 \left( {\alpha + \theta } \right)} & {2.\cos \alpha \cos \left( {\alpha + \theta } \right)} \\ {\sin^2 \alpha } & {\sin^2 \left( {\alpha + \theta } \right)} & {2.\sin \alpha \sin \left( {\alpha + \theta } \right)} \\ {\sin \alpha \cos \alpha } & {\sin \left( {\alpha + \theta } \right)\cos \left( {\alpha + \theta } \right)} & {\sin \left( {2\alpha + \theta } \right)} \\ \end{array} } \right].\left[ {\begin{array}{*{20}c} {\Delta \tilde{\sigma }^1 } \\ {\Delta \tilde{\sigma }^2 } \\ {\Delta \tilde{\sigma }^4 } \\ \end{array} } \right] $$

(9)

where α is the angle between e ₁ and g ₁ and θ is the angle between g ₁ and g ₂ . These angles can be determined within the user subroutine via the deformation gradient $\underline{\underline{F}}$.

The 1-D elements carry the stress in the g ₁ and g ₂ directions and consequently $\Delta \tilde{\sigma }^1 = \Delta \tilde{\sigma }^2 = 0$ within the 2-D element. Thus, the stress increments are returned to the solver in the e _i basis using:

$$ \begin{array}{*{20}c} {\Delta \sigma_1 = 2.\cos \alpha \cos \left( {\alpha + \theta } \right).\Delta \tilde{\sigma }^4 } \\ {\Delta \sigma_2 = 2.\sin \alpha \sin \left( {\alpha + \theta } \right).\Delta \tilde{\sigma }^4 } \\ {\Delta \sigma_4 = \sin \left( {2\alpha + \theta } \right).\Delta \tilde{\sigma }^4 } \\ \end{array} $$

(10)

Material characterization

Two Twintex® fabrics (commingled fiberglass/polypropylene fibres) were characterized for use in the proposed model. The two fabrics differ in their weaving, the first one is a plain weave and will be referred as PW; and the second is a twill weave and will be referred as TW. These fabrics were donated by Vetrotex (now owned by Owens Corning) and are part of a benchmark exercise [5].

The properties needed for modeling purposes are listed in Table 1. The effective cross section of the yarns, A _yarn , assumes no voids between the fibres and is determined using the following equation [21]:

Table 1 Fabric data

$$ A_{yarn} = \frac{{\rho_{yarn} }}{{VF_{glass} \cdot \rho_{glass} + \left( {1 - VF_{glass} } \right) \cdot \rho_{PP} }} $$

(11)

where VF _glass is the glass volume fraction (35%), ρ _yarn is the yarn linear density, and ρ _glass and ρ _PP are the glass and polypropylene densities, respectively. The yarn interval is used to define the meshing: the mesh unit is based on a 4.92 mm × 4.92 mm square shell for the PW and on a 2.44 mm × 5.1 mm rectangular shell for the TW. The crimp ratio corresponds to the difference between the length of the yarn before being woven into the fabric and the length of the fabric that takes into account the yarn undulation.

Tensile characterization

Unaxial tensile tests of single yarns were performed on an INSTRON 4464 machine with a 2-kN load cell to determine their stiffness. Then, knowing the crimp ratio, the nonlinear tensile behaviour of the yarn within the fabric was assessed. Pneumatic cord and yarn grips were used, and the gauge length was set to be approximately one meter to minimize the effect of the deformation in the grips. The use of a strain gauge was not possible due to the specific nature of the tested material. The displacement rate was 5 mm/s. The true definition of strain was used, i.e. $\varepsilon = \ln \left( {1 + l/l_0 } \right)$where l is the measured length of the sample and l ₀ is the initial length. The effective cross section of the yarn, A _yarn, , was used for the stress calculation.

The effective stiffness of the yarns was determined from the slope of the stress/true-strain curves. The stress-strain behaviour of the yarn within the fabric was fit with a 4th-order polynomial extrapolation for the decrimping section of the stress-strain curve. The resulting stress-strain curves are presented in Fig. 3. Only the uniaxial behaviour was considered in this study. While the biaxial effect, i.e. the effect of tension in the lateral yarn direction, is well known [4], one intent of the research was to explore whether or not the lateral-tension effect was significant. The good correlation between a bias-extension test and the associated simulation will show that for the fabrics considered in this work the biaxial effects were not significant. The tangent tensile moduli, C ₁₁ , were determined from these curves as a function of the strain, ε ₁ , and are presented in Table 2.

Fig. 3

Yarn tensile behaviour including the extrapolated decrimping portion of the stress-strain curve

Table 2 Tangent tensile modulus C ₁₁ (ε ₁ )

In-plane shearing characterization

The shear frame test was used to characterize the in-plane shearing behaviour of the fabrics. This test consists of shearing a piece of fabric via a pin-jointed frame mounted in a conventional testing machine. The tests were performed on the same machine used for tensile testing (INSTRON 4464). The geometry chosen for the specimen, i.e. a cross with yarns removed in the arms, is shown in Fig. 4. The length of the frame L _F is 216 mm and the length of the fabric L _f is 120 mm. The specimen was sheared at the rate of 2 mm/s. A mechanical conditioning consisting of five pre-test shearing runs was applied. The mechanical conditioning reduces the effect of undesired tension in the yarns that could arise from a misalignment of the yarns [5, 22, 23].

Fig. 4

Geometry of the shear frame. Free yarns have been removed in the “arms” of the specimen

The normalized shear force F _sh and the shear angle γ were determined from the crosshead displacement δ and the total load on the frame F by the following equations [5, 19]:

$$ \gamma = \frac{\pi }{2} - 2.\arccos \left( {\frac{\delta }{{2.L_F }} + \frac{{\sqrt 2 }}{2}} \right) $$

(12)

$$ F_{sh} = \frac{{L_F }}{{L_f^2 }}\frac{F}{{2\cos \left( {{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.} \!\lower0.7ex\hbox{$4$}} - {\raise0.7ex\hbox{$\gamma $} \!\mathord{\left/ {\vphantom {\gamma 2}}\right.} \!\lower0.7ex\hbox{$2$}}} \right)}} $$

(13)

The underlying assumptions made here are that the shear angle is uniform over the entire sample and equal to the frame angle. These two assumptions have been investigated for these two fabrics by two research groups (including UMass Lowell) via Digital Image Correlation (DIC) [23, 24]. Notably, it has been shown that the difference between the DIC measured shear angle and the frame angle never exceed 3° within the 0–40° range, regardless of the sample geometry (a square fabric sample with cross yarns removed from the arms or a large sample with corner cuts). Thus, the aforementioned assumptions are reasonable, in particular considering the relatively high standard deviation observed on this test.

The shear stress $\tilde{\sigma }^4$ (expressed in the g _i basis) is equal to the normalized shear force F _sh divided by the thickness of the fabric (the thickness after consolidation reported in Table 1 is used). Experimental shear stress versus $\gamma_4^L$ curves are displayed in Fig. 5. The tangent shear modulus $C_{sh} \left( {\gamma_4^L } \right)$is obtained by fitting a 4th-order polynomial to the shear stress vs. $\gamma_4^L$ experimental data and differentiating it. Results are presented in Table 3.

Fig. 5

In-plane shear behaviour from shear-frame tests. Average of five tests for each fabric. Error bars represent one standard deviation

Table 3 Tangent shear modulus $C_{sh} \left( {\gamma_4^L } \right)$

Implementation and validation of the shear response

The proposed method has been implemented via user-defined material subroutines in the explicit finite element codes ABAQUS and LS-DYNA. In ABAQUS B31 beams and T3D2 trusses and in LS-DYNA trusses and seatbelt elements have been used to model the yarns. The LS-DYNA seatbelt element has zero compressive stiffness and is very efficient in terms of computational time compared to a beam element. To account for the lack of compression in the seatbelt elements in LS-DYNA, compressive-only elements were added to account for that contribution to the mechanical behaviour. However, like trusses, these seatbelt and compression elements have no flexural rigidity and hence will not be suitable for the modeling of fabric bending behaviour. Similarly, the in-plane shear behaviour can potentially be captured using either shell or membrane elements.

The models require the use of a hybrid mesh. A hybrid mesh can be created with ABAQUS CAE or a preprocessor such as HyperMesh using merge options. However, the building of such a mesh in one of these preprocessors can be tricky and time consuming. For the current research, a FORTRAN code was written to generate the meshes of the fabrics.

The use of the hybrid mesh eliminates the option for using an automatic adaptive mesh refinement scheme during the finite element soluton. However, this mesh approach does not dictate a specific mesh definition, and the authors have explored using “coarser” meshes, where the sizes of the shell (or membrane) and beam (or truss) elements have been increased. To compensate for this reduced number of elements, the effective cross-sectional area and bending stiffness (for beams) of the yarns is increased proportionally. Such studies have shown that the method can be run with a “coarser” mesh and give equally good results. Likewise, the mesh can be refined to consider the forming of the fabric over small features. Thus, a “mesh refinement” can be accomplished to explore whether or not a solution has converged to the “best” solution.

Pure shear of a unit cell of fabric

The model was first studied for a single finite element unit cell of PW fabric subjected to pure shearing. The responses given by the ABAQUS S4R shell, ABAQUS M3D4R membrane, LS-DYNA Belytschko-Tsay shell (type 2) and LS-DYNA Hughes-Liu shell (type 6) have been investigated and compared with the analytical calculation of the response (Fig. 6). LS-DYNA elements type 2 and 6 were defined as membrane elements, i.e. with a single integration point through the thickness.

Fig. 6

Accuracy of the response obtained for the shearing of a single unit cell using various element types

As expected, on this simple model free from bending or transverse shear, shell element (ABAQUS S4R) and membrane elements (ABAQUS M3D4R and LS-DYNA shell type 6) give the same responses that appear to be acceptable up to a 45° shear angle. These elements will be generally aceptable for composite reinforcement forming simulations as the fabric locking angles rarely exceed 45°. However, the LS-DYNA shell type 2 element gives an erroneous response after a shearing of only 15° and consequently should not be used for simulations involving high shearing. This result confirms the importance of this initial test on a representative unit cell when incorporating the model into a new code. Indeed, very high shearing with no deformation in the principal axes is a very specific deformation mode and some shell/membrane element formulations do not account correctly for this kind of deformation.

Shear-frame test simulation

The experimental shear frame test used to determine the material parameters was simulated to provide validation of the approach used to incorporate the shearing behavior. A finite element model of the shear-frame test was built, including the “arms” of the specimens. The procedure used for completing the shear-frame testing required the removal of the free yarns in the arms of the specimens (Fig. 4), so only 1-D elements were used to model the arms. The frame was modeled using four aluminum trusses with a cross section of 500 mm². For the fabric, truss elements have been preferred to beam elements and seatbelt elements for minimizing the required computation time and considering that the bending of the beams should be insignificant for this in-plane mode of deformation. The simulation results obtained with the ABAQUS S4R elements, the ABAQUS M3D4R elements and the LS-DYNA shell type 6 are compared with the experimental data for the PW and TW fabrics in Figs. 7 and 8, respectively. The shear-frame simulations correlate well with the experimental data for both fabric tests. These simulations demonstrate the validity of the direct parameter identification as well as the in-plane shear-behaviour implementation.

Fig. 7

Model/Experiment comparison for PW shear frame test. Error bars represent one standard deviation

Fig. 8

Model/Experiment comparison for TW shear frame test. Error bars represent one standard deviation

Bias-extension test simulation

After successfully showing that the approach correctly captured the nonlinear shearing behaviour, its ability to simulate a more complex state of deformation was demonstrated via a bias-extension test simulation. This experiment consists of a tensile test of the fabric pulled in its bias direction, i.e. the yarns oriented at 45° to the tensile direction. A typical sample geometry is a rectangle having its length equal to twice its width. This geometry leads to a specific strain field involving three different zones with 0°, γ/2 and γ shearing angles. It is sometimes used as an easy way to evaluate the shearing properties of fabrics [5, 25]. This test is particularly interesting for validation purposes as it involves combined shearing and tension, as well as rigid rotation of some shell / membrane elements. The simulation-experiment comparison presented here includes the use of Digital Image Correlation to obtain the experimental shear-strain field.

Experimental

A bias-extension test was performed on an INSTRON 4464 tensile machine equipped with hydraulic grips. Samples of “16 yarns” were used with an aspect ratio of two between the length and width. The PW fabric samples were approximately 115 mm × 230 mm, and the TW samples were 120 mm × 240 mm.

The shear strain field was recorded during the tests using a three-dimensional (3-D) DIC technique. The ARAMIS® software was used in 3-D mode with two digital cameras. The strain measurement is based on subset windows (or facets) that are tracked during the deformation by a correlation algorithm. The centre coordinates of the facets are then used to determine the strains. Sufficient contrast is needed, so a speckle pattern is generally applied on the surface.

For the Twintex fabrics used in this study, the surface preparation involved the application of a very thin layer of white matte paint to reduce the light reflection of the fabric and then the application of a pattern with a marker. It was established in other testing that the paint does not affect the in-plane shear behaviour of the fabric. The pattern and the facet size were carefully chosen to record only the macroscopic deformation of the fabric, and not, for example, the movement of the fibres within the yarns (Fig. 9).

Fig. 9

Pattern, facet size and overlap used for DIC computation

Results

The PW and the TW bias-extension tests were simulated. For ABAQUS/Explicit, the B31 beam and the S4R shell or M3D4R membrane elements were used, and for the LS-DYNA simulation, the seatbelt and the shell type 6 elements were used. The shear-angle contours and the load-versus-displacement plots are compared to experimental data.

The shear-angle contours after 30 mm of displacement, obtained experimentally via DIC and from the simulations, are displayed in Figs. 10 and 11 for the PW and TW fabrics, respectively. It is noted that experimentally the boundaries for the three different theoretical zones do not exhibit as sharp a transition as it is shown for the boundaries in the simulations. Part of this effect could come from the lack of resolution of the DIC system, due to the choice of a relatively large facet size (this choice has been motivated by the coarse weave of the fabric, see Fig. 9). However, part of it is undoubtedly real: yarns do not exhibit a marked angle at a transition zone as is the case in the simulation where the yarns are pinned. While the model, because of its pin-jointed nature, allows yarns to have a marked angle, the actual yarns are continuous and can only bend along a smooth curve as shown in Fig. 12. For the TW fabric, the ABAQUS model using the shell elements exhibits a relatively smooth transition between the different shear zones leading to a contour shape that is very close to the experimental one.

Fig. 10

Shear angle contours in degrees during PW bias extension from finite element simulations and DIC measurements at 30 mm of crosshead displacement

Fig. 11

Shear angle contours in degrees during TW bias extension from finite element simulations and DIC measurements at 30 mm of crosshead displacement

Fig. 12

Detail of the actual direction of the yarns from the DIC

For a quantitative comparison, the shear angles in the center zone were averaged and plotted versus crosshead displacement in Fig. 13 for the PW and Fig. 14 for the TW. The ideal kinematic angle $\gamma_{kin}$ is also plotted. In the case of a sample with a length to width ratio of two, it can be computed as [19, 26]:

Fig. 13

Comparison of the average shear angles in the central zone for the PW fabric

Fig. 14

Comparison of the average shear angles in the central zone for the TW fabric

$$ \gamma_{kin} = \frac{\pi }{2} - 2\cos^{- 1} \left( {\frac{{W + \delta }}{{W\sqrt 2 }}} \right) $$

(14)

where δ is the crosshead displacement and W is the initial width of the sample.

The angles compare fairly well between the models and the experiments up to 25° (less than 3° difference) and then start to diverge. The experimental angles are lower than the ones observed in the simulation results. It is noted that the average shear angle is similar for all the simulations while some differences in the shear angle contours are observed among the various simulations.

Comparisons of the load-displacement curves are shown in Figs. 15 and 16. The PW bias-extension simulation agrees well with the experimental data up to 25–30° and then overestimates the load observed from the test. In light of the difference between the model and the experiment seen in Fig. 13, this result was expected: the overestimation of the shear angles above 25° leads logically to an overestimation of the load.

Fig. 15

PW bias-extension test: comparison of the load-displacement curves from experiment and simulation. Error bars represent one standard deviation over three tests

Fig. 16

TW bias-extension test: comparison of the load-displacement curves from experiment and simulation. Error bars represent one standard deviation over four tests

At large crosshead displacement, lower shear angles as shown by the experimental data could be due to the appearance of yarn sliding. Indeed, this phenomenon is commonly observed during bias-extension testing [26, 27] and is not taken into account in the models because of their pin-jointed nature. During a bias-extension test, the yarns are clamped only on one side, and consequently some of them can slide. Only the friction prevents them from sliding, and when the load to overcome this friction is developed within the fabric, sliding occurs.

The comparison of the experimental and simulation load-displacement curves for the TW fabric shows good agreement at large crosshead displacement, suggesting that the sliding is less marked for this fabric. This observation appears to be realistic because this fabric has a tighter weave than the PW fabric, and this tighter weave creates increased friction between the yarns which leads to increased sliding resistance.

From these experimental-simulation comparisons, it is concluded that the model proposed captures correctly the fabric behavior during a bias-extension test up to the appearance of yarn sliding. This sliding phenomenon is particularly marked during bias-extension test but may not necessarily be as high during an actual stamping process.

The comparison between the different simulations using different element types and finite element solvers is also interesting. Even if it is observed that the two different types of 2-D elements used in ABAQUS lead to slightly different results, the various simulations agree reasonably well with the experimental data.

Hemisphere forming simulation

The deep drawing of a hemisphere was simulated to show the capabilities of the model for a 3-D shape forming and to further compare the results obtained from the ABAQUS and LS-DYNA codes. The hemispherical geometry depicted in Fig. 17 was used. The total force applied on the binder was 650N, and the friction coefficient between the fabric and the tools was set to 0.3. The PW material data at room temperature was used. One ABAQUS model used B31 beam elements combined with S4R shell elements and another ABAQUS model used M3D4R membrane elements. The LS-DYNA model used seatbelt elements and Hughes-Liu shells (type 6). The shear angle contours after a 90-mm punch displacement from the ABAQUS model using shell elements and the LS-DYNA model are shown in Fig. 18. The two contours are essentially the same, and the characteristic final shape for this type of draping is obtained.

Fig. 17

Deep drawing of a hemisphere: geometry of the tools

Fig. 18

Shear angle contour comparison between a LS-DYNA Hughes-Liu shells and b ABAQUS S4R shells

To compare the fabric mechanical responses, the punch reaction forces were extracted from the simulation results. The punch forces as function of the displacement are shown in Fig. 19. The ABAQUS model using the membrane elements did not converge sufficiently to run this hemispherical-punch simulation to completion. While being more efficient in terms of computing time on planar simulations, the ABAQUS membrane element appears to be less robust than the ABAQUS shell elements and can lead to a nonconvergence of the analysis for 3-D shape forming simulations in some cases. However, the resulting punch force is higher when using shell elements compared to membrane elements due to the addition of bending and transverse shear stiffness.

Fig. 19

Punch force comparison for an hemisphere deep drawing

Bending stiffness

It was shown that 1-D and 2-D finite elements with and without bending stiffness can be used for the in-plane deformation of the fabrics. The modeling scheme was subsequently applied to the stamping of a hemispherical dome. However, the importance of the bending contributions associated with shell and beam elements to the overall mechanical behavior was not explored in detail in this paper due to the lack of experimental data at this time. The bending contributions will be investigated and reported in a future paper.

Conclusion

A mesoscopic method for the modeling of woven-fabric composites has been presented. The model uses standard elements available within commercial finite element codes and links the specific material behavior to the finite element solver via user-supplied subroutines. The necessary material constants can be derived from simple tensile tests of yarns and shear tests of woven fabrics. The ability for the mesoscopic approach to capture the mechanical behavior of woven fabrics was demonstrated for a shear-frame test, a bias-extension test and for the thermostamping of a hemisphere. The determination of experimental shear angle contours was examined using Digital Image Correlation. The finite element results agreed very well with the experimentally observed shear angles and load-deflection curves. When implementing the proposed method in other finite element packages, care should be taken for the choice of the two-dimensional elements and validation tests on simple models should be conducted to verify that the chosen elements are suitable.