Introduction

Pathologies such as congenital heart disease, hypertension, valvular disease, and myocardial infarction cause the heart to grow and remodel. In many cases, this remodeling contributes to the deterioration of cardiac function and the development of heart failure [1, 2]. Thus, increases in ventricular mass, diameter, and wall thickness [3,4,5,6] have all been associated with poor clinical prognosis.

Since remodeling of the ventricle is often progressive, the most pertinent clinical questions surrounding disorders that induce remodeling tend to be prognostic. Clinicians often face difficult decisions not only about the type of treatment but also about the timing, constantly weighing the trade-offs of delaying vs. performing a given repair at a specific time in an individual patient. For example, patients with mitral or aortic insufficiency are at increased risk for heart failure. Surgical repair or replacement of the valve can arrest or even reverse ventricular remodeling and preserve or restore function [6]. Because these benefits diminish with disease progression, early intervention has been associated with lower onset of heart failure rates and higher long-term survival [7, 8]. On the other hand, not all patients require intervention, and in some, the risks and complications (such as endocarditis, atrial or even ventricular fibrillation, embolic/bleeding events, and eventual deterioration of a prosthetic valve) will outweigh the benefits. Similar dilemmas exist for clinicians treating patients with congenital heart abnormalities. For example, high levels of pulmonary vascular resistance and low birth weight increase the risks associated with early surgical intervention for infants with single ventricles, but prolonged overloading of their single ventricle gradually reduces the efficacy of surgery [9]. Often, infants with single ventricle abnormalities develop heart failure so rapidly that surgery is no longer advised. Thus, in many situations, the ability to reliably predict growth and remodeling of the heart in individual patients could be a valuable tool for clinicians in anticipatory management, allowing them to predict both whether and when the benefits of intervention outweigh the risks.

Computational models are promising tools for integrating patient-specific data to generate meaningful predictions. In the past two decades, there has been considerable progress in the development of models capable of predicting cardiac remodeling in the setting of hypertension, valvular disease, and other pathologies. These models typically rely on mathematical equations, termed “growth laws,” that predict remodeling based on changes in one or more local mechanical inputs. These laws are grounded in experimental observations that hemodynamic perturbations known to cause myocardial hypertrophy also alter the stress and strain within the myocardium. Although this approach is broadly consistent with experimental evidence that cardiac myocytes can sense and respond to changes in mechanics, the models are typically phenomenologic, derived from fitting data rather than attempting to represent the underlying myocyte biology.

We recently compared how eight published growth laws responded to reported changes in mechanics following the onset of pressure (aortic constriction) and volume overload (mitral regurgitation or fistula) in dogs [10]. Three of these growth laws captured most features of the observed eccentric and concentric growth patterns. Of these, the growth law proposed by Kerckhoffs et al. [11] has shown particular promise in simulating growth and remodeling in clinically relevant situations, including pressure overload, volume overload, and dyssynchrony associated with left bundle branch block [11, 12]. However, this model was originally implemented in a complex, anatomically realistic finite-element model fully coupled to a closed loop model of circulatory hemodynamics; simulating 1 month of growth required 3 weeks on a Linux cluster with 12 Intel XeonX5650 6-core 2.66 GHz processors. The time required both to construct and to run patient-specific versions of this model would likely limit its clinical application. Therefore, we sought to develop and implement a version of the Kerckhoffs law in a much simpler framework in order to reduce the time required to customize and run the model. To this end, we simplified the law and coupled it to a compartmental model of the ventricles and circulation, fit growth parameters using two published studies of pressure and volume overload, and tested the predictive capacity of the parameterized model against independent studies of pressure overload, volume overload, and post-infarction remodeling.

Methods

We simulated left ventricular mechanics across a range of overload states using a time-varying elastance compartmental model connected to a circuit model of the circulation. Strains were estimated from LV compartmental volumes assuming a simple spherical geometry, and used to drive growth in a strain-based growth law adapted from Kerckhoffs [11]. We simulated multiple published studies of hemodynamic overload in dogs, in each case matching the reported hemodynamics and then predicting growth. We fitted growth parameters to two published canine studies—one of pressure overload [13] and one of volume overload [14] – and tested the ability of the parameterized model to predict growth in three independent studies of pressure overload [15], volume overload [16], and post-infarction remodeling [17].

Compartmental Model of the Ventricles and Circulation

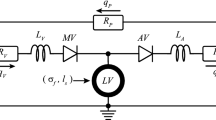
A model of the ventricles and circulation similar to that employed by Santamore and Burkhoff [18] was used to simulate hemodynamics throughout the cardiac cycle. In this model (Fig. 1), the ventricles were simulated using time-varying elastances. The left ventricular end-diastolic and end-systolic pressure–volume relationships were defined by

$$ {P}_{ES}=E\ast \left({V}_{ES}-{V}_0\right) $$
(1)
$$ {P}_{ED}=B\ast \exp \left[A\ast \left({V}_{ED}-{V}_0\right)\right]-B $$
(2)

respectively, where E was the end-systolic elastance of the ventricle, V0 was the unloaded volume of the ventricle, and A and B were coefficients describing the exponential shape of the end-diastolic pressure–volume relationship (EDPVR). We assumed the same end-diastolic parameters for the right and left ventricles and set the end-systolic elastance of the right ventricle to 43% of that for the left [18]. The systemic and pulmonary vessels were represented by capacitors in parallel with resistors. Pressure-sensitive diodes simulated the valves. Stressed blood volume, SBV, was defined as the total blood volume contained in the circulatory capacitors plus ventricles. As discussed in detail below, we varied systemic arterial resistance, stressed blood volume, and left ventricular passive and active properties to match hemodynamic data from the studies we simulated; all other circulatory parameters were held constant at baseline values throughout all simulations (Supplemental Table 1). We implemented this model in MATLAB as a series of differential equations for changes in the volume of each compartment (left ventricle, systemic arteries, systemic veins, right ventricle, pulmonary arteries, and pulmonary veins) at 5000 time points over the cardiac cycle. A 16-GB RAM, 64-bit operating system, and 3.4-GHz Intel Core i7-3770 running MATLAB 2012B ran all simulations.

Fig. 1
figure 1

Schematic of the circuit model used to simulate the pressure-volume behavior of the cardiovascular system. Systemic and pulmonic circuits consisted of a characteristic resistance (R cs and R cp ), arterial resistance (SVR and R ap ), resistance to venous return (R vs and R vp ), arterial compliance (C as and C ap ), and venous compliance (C vs and C vp ), respectively. Pressures sensitive diodes (TV, PV, MV, and AV) respresented the tricuspid, pulmonary, mitral, and aortic valves, respectively. Elements highlighted in red were added or altered in order to simulate hemodynamic overload. An increase in SVR simulated aortic occlusion, a decrease in the backflow resistance of the mitral valve (MVBR) simulated mitral valve regurgitation, and dividing the left ventricle (LV) into active and passive compartments (MI) simulated myocardial infarction

Full size image

Simulation of Control and Acute Hemodynamics

We simulated three different types of experimental perturbations known to produce different patterns of LV hypertrophy: pressure overload, volume overload, and myocardial infarction. An increase in the systemic vascular resistance, SVR, replicated the hemodynamic changes typical of pressure overload induced through aortic constriction. Since the experimental studies considered here created volume overload through the induction of mitral regurgitation, a resistor allowing backflow across the mitral valve (MVBR) enabled mitral regurgitation. Myocardial infarction was simulated using the approach of Sunagawa et al. [19] in which the damaged left ventricle was functionally divided into two compartments: the noninfarcted, contractile compartment, and the infarcted, non-contractile compartment. At any time point during the cardiac cycle, the compartment volumes added to the total LV volume and their pressures were the same. Sunagawa showed that this simple approach replicates measured pressure–volume behavior across a wide range of infarct sizes remarkably well.

Before simulating LV hypertrophy for each of the studies considered here, we tuned the circulatory parameters in the model to match hemodynamics and LV dimensions reported at baseline and immediately following the induction of aortic constriction, mitral regurgitation, or myocardial infarction (acute). Reported heart rate and infarct size were prescribed directly. We assumed acute hemodynamic perturbation did not change the end-diastolic or end-systolic LV pressure–volume relationships and therefore, only one set of unknown LV parameters (A, B, V0, and E) was required for each study. In contrast, we assumed that systemic vascular resistance and stressed blood volume could vary rapidly following creation of hemodynamic overload, treating both baseline and acute values for these parameters as unknowns (SVRcontrol, SVRacute, SBVcontrol, and SBVacute). For volume overload studies, an additional unknown parameter controlling the severity of mitral valve regurgitation (MVBRacute) was also determined. Thus, tuning baseline and acute hemodynamics for each study considered required identifying 8 or 9 (for volume overload) parameters.

Table 1 shows the control and acute hemodynamic data reported by each study (mean ± standard deviation); results highlighted in pink were used to tune circulatory model parameters. In general, end-diastolic and end-systolic pressures and volumes in the baseline and acutely overloaded states (EDPcontrol, ESPcontrol, EDVcontrol, ESVcontrol, EDPacute, ESPacute, EDVacute, ESVacute, n = 8 values)—plus the measured regurgitant fraction for volume overload studies—should provide enough information to tune the 8–9 unknown parameters specified in the previous paragraph. However, no study reported exactly these volumes and pressures. All studies reported measurements that could be used to estimate LV end-diastolic pressure (end-diastolic pressure, pulmonary capillary wedge pressure, or mean left atrial pressure), some measurement of blood pressure during systole (maximum LV pressure, mean arterial pressure, or systolic blood pressure), and some measurement of LV volume during systole (end-systolic LV volume, minimum LV volume, or stroke volume). Except for Nagatomo et al. [15], all studies also reported maximum LV volume or dimensions (see Supplement). Since Nakano et al. and Nagatomo et al. reported similar stroke volumes, the end-diastolic pressure volume relationship from Nakano was used for both.

Table 1 Model results and experimental data for all studies. Highlighted model values were used to tune control and acute circulatory parameters (pink), match unloaded thickness (blue), or fit growth parameters (green). An asterisk indicates model predictions more than one standard deviation away from the reported mean
Full size table

We estimated model parameters simultaneously using the fminsearch function in MATLAB. Differences between measured and predicted hemodynamic values were normalized by the reported standard deviation to compute Z scores, and mean squared error (MSE) in Z score was minimized. In order to reduce the complexity of the optimization, for any choice of V0, the diastolic parameters A and B were computed directly from end-diastolic pressure–volume data (Eq. 1) prior to optimization.

For each study, E, SBVcontrol, and SBVacute were initially set to values reported by Santamore and Burkhoff [18], while SVRcontrol and SVRacute were initialized by dividing the reported mean arterial or peak systolic pressure by the product of stroke volume and heart rate. We initialized V0 at a value that produced an end-diastolic stretch, λ, of 1.44 ± 0.24 relative to a completely unloaded state [10] in our thin-walled spherical model. Finally, for volume overload studies, MVBRacute was initialized at 1 mmHg*s/ml.

To explore the uniqueness of the parameter sets identified by our optimization procedure, we performed a sensitivity analysis on the estimated parameter set for the Kleaveland volume overload study [14]. We systematically varied each parameter between 50 and 150% of its optimized value and examined the shape of the objective function projected onto every possible two-parameter plane (Fig. 2).

Fig. 2
figure 2

(a) Mean squared error (MSE) in Z scores computed as V0 and SVRcontrol were varied between 50 and 150% of their optimized values with all other parameters set to their optimized values. Changes in either parameter greater than 15% pushed error above 0.04. (b) By contrast, many combinations of V0 and E produced MSE values below 0.04. (c, d) Repeating the simulations from panels (a, b) using an augmented objective function provided a unique optimum for all parameters including V0 and E

Full size image

At MSE values below 0.04 (darkest colors in panels A and B), hemodynamic parameters were within an average of 0.2 standard deviations of their reported mean; in most cases, variations of any one parameter of more than 15% pushed the objective function outside this range. For example, Fig. 2a shows similar dependence of MSE on V0 and SVRcontrol, with relatively few combinations of the two parameters that hold it below 0.04. Plots of the solution space for all other model parameter pairs had a similar shape except for V0 and E (Fig. 2b). Here, many different combinations of values yielded similarly low error. As a quantitative reflection of this error landscape analysis, we computed the area of each graph with MSE values less than 0.04. For the V0 and E pair, the area was 0.16, whereas the average for all other parameter pairs was 0.04 ± 0.04 (Supplemental Table 2). We concluded from this analysis that additional information or constraints are necessary in order to obtain unique, repeatable values for all parameters including V0 and E.

We therefore augmented our objective function using additional data from the literature regarding the physiologic values of end-diastolic stretch relative to an unloaded state [10], which varies with choice of V0, and the peak rate of LV pressure rise [20,21,22,23,24,25,26,27,28,29,30], which varies with E. Supplemental Table 3 gives the modified objective functions; we chose to give these literature-based terms half the weight of the data terms. Figure 2c, d show contour plots for the same projections shown in Fig. 2a, b, using the augmented objective function; including the literature terms constrained the range of acceptable values for V0 and E without negatively impacting identification of other parameters (Supplemental Table 2).

Strain-Based Ventricular Growth Law

The growth law proposed by Kerckhoffs et al. [11] for myocyte hypertrophy employed two different local strain measures as inputs to the growth equations. The stimulus for growth along the axis of the myofibers, s l , was driven by changes in the maximum fiber strain, which typically occurred at end diastole. The stimulus for fiber radial growth, s t , was driven by changes in principal strain in the cellular cross-sectional plane, which typically occurred at end systole. Therefore, they computed strain within the plane of the ventricular wall in the direction along the axis of the myofibers, E ff , and perpendicular to the myofibers, E cc . They also determined strain along the radius of the myofibers (across the ventricular wall), E rr , and cross-fiber radial shear, E cr . To construct approximations of the required strain component inputs in our compartmental model, we treated the left ventricle as a thin-walled spherical pressure vessel with an initial unloaded radius r0 and an initial unloaded thickness h0. Using the loaded radius, r, and thickness, h, of the spherical ventricle, we computed E ff  = E cc  = 0.5 ∗ (r/r0 ∗ 1/Fg, fi)2 − 0.5, E rr  = 0.5 ∗ (h/h0 ∗ 1/Fg, ri)2 − 0.5, and assumed E cr  = 0. Fg, fi and Fg, ri indicate the growth stretches (ratio of grown to original length in the unloaded state) in the fiber and radial directions for growth step i. The stimulus for axial myofiber growth

$$ {s}_l=\max \left({E}_{ff}\right)-{E}_{f,\mathrm{set}} $$
(3)

was unchanged when implemented in the compartmental model, but that for radial myofiber growth was simplified to

$$ {s}_t=-\max \left({E}_{rr}\right)+{E}_{r,\mathrm{set}} $$
(4)

where Ef, set and Er, set indicated the homeostatic setpoints at which no growth occurs. The growth law proposed by Kerkhoffs et al. assumed that increased fiber strain stimulated growth in the fiber direction, while increased strain perpendicular to the fibers stimulated growth in both the crossfiber and radial directions. Given the simple spherical geometry employed here, we assumed that crossfiber growth was equal to fiber growth:

$$ {F_{g,f}}^{i+1}={F_{g,c}}^{i+1}=\left\{\begin{array}{cc}{F_{g,f}}^i\ast \sqrt{\frac{f_{ff,\max }}{1+\exp \left(-{f}_f\ast \left({s}_l-{s}_{l,50}\right)\right)}+1}& {s}_l\ge 0\\ {}{F_{g,f}}^i\ast \sqrt{\frac{-{f}_{ff,\max }}{1+\exp \left({f}_f\ast \left({s}_l+{s}_{l,50}\right)\right)}+1}& {s}_l<0\end{array}\right.\kern0.5em $$
(5)
$$ {F_{g,r}}^{i+1}=\left\{\begin{array}{cc}{F_{g,r}}^i\ast \left[\frac{f_{rr,\max }}{1+\exp \left(-{r}_{f,\mathrm{positive}}\ast \left({s}_t-{s}_{t,50,\mathrm{positive}}\right)\right)}+1\right]& {s}_t\ge 0\\ {}{F_{g,r}}^i\ast \left[\frac{-{f}_{rr,\max }}{1+\exp \left({r}_{f,\mathrm{negative}}\ast \left({s}_t+{s}_{t,50,\mathrm{negative}}\right)\right)}+1\right]& {s}_t<0\end{array}\right.. $$
(6)

Equations (5) and (6) prescribed sigmoidal functions such that the parameters fff, max and frr, max dictated the maximum and minimum growth allowed within a single step. The slope of the sigmoid was specified by f f , rf, positive, and rf, negative, and there was a small nearly quiescent region near the setpoints specified by sl, 50, st, 50, positive, and st, 50, negative. As part of the growth parameter fitting process, we relaxed Kerckhoffs’ assumption that [rf, positive = rf, negative and st, 50, positive = st, 50, negative]. Additionally, we did not employ limiting terms to restrict the total magnitude of change in the growth stretches.

Within the growth law, eight parameters are used to compute ventricular growth: sl, 50, st, 50, positive, st, 50, negative, f f , rf, positive, rf, negative, fff, max, and frr, max. We used the changes in ED thickness reported by Sasayama et al. [13] at 9 and 18 days of growth to fit st, 50, positive and rf, positive since pressure overloading predominantly induces LV thickening. Similarly, we used the maximum LV volume at 1 and 3 months reported by Kleaveland et al. [14] to fit sl, 50 and f f because volume overload induces substantial LV dilation. Kleaveland also reported LV thinning, which enabled us to fit st, 50, negative and rf, negative using their reported changes in ED thickness. Finally, we set fff, max and frr, max to 0.1. In all simulations one growth time step in the model corresponded to 1 day of ventricular growth. After each growth time step, we ran the circulation model until it reached steady state (the compartmental volumes at the beginning and end of the cardiac cycle were within 0.1 ml of each other).

Implementation of Growth in Compartmental Model

We fitted growth parameters using data from a pressure overload study by Sasayama et al. [13] and a volume overload study by Kleaveland et al. [14], then tested the ability of the parameterized model to predict growth reported in three independent canine studies: a pressure overload study by Nagatomo et al. [15], a volume overload study by Nakano et al. [16], and a post-infarction remodeling study by Jugdutt et al. [17]. While all other growth parameters were held constant across all simulations, since the studies used dogs of different weights and reported a wide range of control left ventricular volumes (ranging from 24 to 68 ml), we computed homeostatic setpoint values for each study to ensure that no growth occurred under baseline conditions. The left ventricle was modeled as a spherical pressure vessel with an initial unloaded cavity volume V01 and an initial unloaded cavity radius \( {r}_0={\left(\frac{3{V_0}^1}{4\pi}\right)}^{1/3} \). We assumed that acute hemodynamic overload did not alter the LV wall volume and determined the unloaded LV thickness using the reported change in end-diastolic thickness following acute overload. Two studies did not report an acute change in thickness (Nakano and Nagatomo); in those cases, we used values from the next most similar study (Kleaveland and Sasayama, respectively).

We assumed growth did not change the intrinsic material properties of the myocardium [31] and thus held the relationship between stress and stretch in the myocardium constant. For a thin-walled spherical pressure vessel, hoop stress is determined by pressure, radius, and thickness: σ = P ∗ r/(2 ∗ h). At each growth step, we computed the cavity radius at end diastole and end systole, r ED and r ES , assuming a spherical geometry using the steady-state cavity volumes. We computed the corresponding end-diastolic and end-systolic thicknesses, h ED and h ES by holding the LV wall volume constant throughout the cardiac cycle. Using Eqs. (1) and (2), respectively, the hoop stress at end systole and end diastole were

$$ {\sigma}_{\mathrm{hoop}, ED}=\frac{r_{ED}}{2{h}_{ED}}\ast {B}^i\ast \left(\exp \left[{A}^i\ast \left({V}_{ED}-{V_0}^i\right)\right]-1\right)\ \mathrm{and} $$
(7)
$$ {\sigma}_{\mathrm{hoop}, ES}=\frac{r_{ES}}{2{h}_{ES}}\ast {E}^i\ast \left({V}_{ES}-{V_0}^i\right). $$
(8)

To maintain a constant relationship between hoop stress and stretch at end diastole and end systole as the ventricle grows, the parameters that govern the pressure-volume behavior of the ventricle (Ai, Bi, Ei, and V0i) must be altered. Therefore, we rewrote the stress equations in terms of stretches:

$$ {\sigma}_{\mathrm{hoop}, ED}=\frac{r_{ED}}{r_0}\ast \frac{h_0}{h_{ED}}\ast \frac{{F_{g,r}}^i}{{F_{g,f}}^i}\ast b\ast \left(\exp \left[a\ast {\left(\frac{r_{ED}}{r_0}\ast \frac{1}{{F_{g,f}}^i}\right)}^3-a\right]-1\kern0.5em \right) $$
(9)
$$ {\sigma}_{\mathrm{hoop}, ES}=\frac{r_{ES}}{r_0}\ast \frac{h_0}{h_{ES}}\ast \frac{{F_{g,r}}^i}{{F_{g,f}}^i}\ast e\ast \left[{\left(\frac{r_{ES}}{r_0}\ast \frac{1}{{F_{g,f}}^i}\right)}^3-1\right] $$
(10)

where a, b, and e are material parameters that governed the nonlinear relationships between circumferential and radial stretches and hoop stress at end diastole and end systole. Note that r0 and h0 always refer to the initial unloaded dimensions of the ventricle (prior to any growth). Under the assumption that the material properties a, b, and e are unchanged with growth, growth-induced changes in the LV compartmental parameters Ai, Bi, Ei, and V0i can be determined directly:

$$ {V_0}^i=\frac{4\pi }{3}\ast {\left({r}_0\ast {F_{g,f}}^i\right)}^3, $$
(11)
$$ {A}^i=a\ast \frac{3}{4\pi}\ast {\left(\frac{1}{r_0\ast {F_{g,f}}^i}\right)}^3, $$
(12)
$$ {B}^i=2\ast b\ast \frac{h_0\ast {F_{g,r}}^i}{r_0\ast {F_{g,f}}^i},\mathrm{and} $$
(13)
$$ {E}^i=\frac{3}{2\pi}\ast e\ast \frac{h_0\ast {F_{g,r}}^i}{{\left({r}_0\ast {F_{g,f}}^i\right)}^4}\kern0.5em . $$
(14)

Most parameters in the circulation model were held constant at their acute overload values during growth simulations, with three exceptions. All studies reported heart rate at each time point, so we prescribed heart rate throughout growth by linearly interpolating between reported values. We also used reported changes in mean arterial pressure (or in some cases systolic pressures) to estimate the evolution of systemic vascular resistance. Finally, for the volume overload studies, we prescribed the mitral valve backflow resistance such that regurgitant fraction followed the reported trajectory.

Results

Our goal was to test the ability of a relatively simple model that combines a compartmental representation of the ventricles and circulatory system with a phenomenologic growth law to predict left ventricular (LV) growth across a spectrum of hemodynamic states. We fitted growth parameters to a pressure overload study from Sasayama et al. [13] and a volume overload study from Kleaveland et al. [14]. Then, we tested the predictive capability of the parameterized growth model against three independent studies: a pressure overload study from Nagatomo et al. [15], a volume overload study from Nakano et al. [16], and a post-infarction remodeling study from Jugdutt et al. [17]. As detailed below, we were able match reported control and acute hemodynamics within one standard deviation (SD) for all studies, and to fit growth parameters to simultaneously match reported growth in the Sasayama (PO) and Kleaveland (VO) studies. This parameterized model then correctly predicted reported growth in all three independent studies used for validation.

Simulation of Control and Acute Hemodynamics

Using the optimization approach described under “Methods,” we were able to match reported pressures, volumes, and/or dimensions for all control and acute overload studies within one SD. Supplemental Table 4 shows the final optimized circulation parameters for each study, and Table 1 shows the comparison between measured and modeled pressures, volumes, and dimensions.

Simulations of Left Ventricular Growth (Fitting Studies)

The growth parameters shown in Table 2 produced changes in ED volume (Fig. 3a, b) and ED wall thickness (Fig. 3c, d) that fell within 1 SD of reported values throughout the course of both the pressure and volume overload fitting simulations. Furthermore, during simulated growth, all reported hemodynamic values such as end-diastolic pressure (EDP) remained within 1 SD of their reported means even though no further adjustments were made to the circulation in order to match them (Table 1). The model predicted wall thickening (Fg, r > 1) with very little dilation (Fg, f ≈ 1) in simulated pressure overload (Fig. 3e), and substantial dilation and a small amount of wall thinning for simulated volume overload (Fig. 3f). For the pressure and volume overload simulations, the computation times to complete 18 and 90 days of growth were 72.7 and 161.2 s, respectively.

Table 2 Growth parameters utilized for all studies
Full size table
Fig. 3
figure 3

The predicted maximum LV volume (a and b) and the ratio of ED thickness to control ED thickness (c and d) throughout growth for the simulations of pressure and volume overload used to fit growth parameters [13, 14]. Evolution of growth stretches (e and f) for these simulations matched typical patterns of growth following pressure and volume overload. Black and red dots indicate control and acute dimensional values tuned using the circulatory model, respectively, and experimental data are shown in gray, mean ± SD

Full size image

Simulations of Left Ventricular Growth (Validation Studies)

When we matched acute hemodynamics and prescribed the evolution of systemic vascular resistance and heart rate (see “Methods”) from the independent pressure overload validation study by Nagatomo and simulated growth without adjusting any growth parameters, the model predicted an increase in LV mass within 1 SD of experimental data throughout growth (Fig. 4a, Table 1). Additionally, the stroke volume, end-diastolic pressure, and maximum LV pressure all remained within 1 SD of the experimental data throughout simulated growth (Fig. 4b c, d, Table 1). The computation time to simulate 10 days of growth was 54.6 s.

Fig. 4
figure 4

The change in LV mass (a), stroke volume (b), end-diastolic pressure (c), and maximum LV pressure (d) throughout growth for the simulation of an independent pressure overload study used to validate the growth model [15]. Black and red dots indicate control and acute values tuned using the circulatory model, respectively, and experimental data are shown in gray, mean ± SD

Full size image

When we matched acute hemodynamics and prescribed the evolution of systemic vascular resistance, heart rate, and regurgitant fraction from the independent volume overload validation study by Nakano, the model predicted a maximum LV volume and ED wall thickness ratio within 1 SD after 90 days (Fig. 5a, b, Table 1). At 90 days, the ejection fraction was within 1 SD of the reported mean; however, the model predicted a systolic pressure that was too high and an end-diastolic pressure that was too low (Fig. 5c, d, Table 1). The computation time to simulate 90 days of growth was 146.1 s.

Fig. 5
figure 5

The change in maximum LV volume (a), ED thickness (b), end-diastolic pressure (c), and systolic blood pressure (d) throughout growth for the simulation of an independent volume overload study used to validate the growth model [16]. Black and red dots indicate control and acute dimensional values tuned using the circulatory model, respectively, and experimental data are shown in gray, mean ± SD

Full size image

Lastly, when we matched acute hemodynamics and prescribed the evolution of systemic vascular resistance and heart rate from the independent myocardial infarction study by Jugdutt, the model predicted increases in maximum LV volume and the ED wall thickness of the noninfarcted region that were within 1 SD of experimental data throughout growth (Fig. 6a, b, Table 1). Additionally, end-diastolic pressure and mean arterial pressure both remained within 1 SD of the experimental data throughout simulated growth (Fig. 6c, d, Table 1). The computation time to simulate 6 weeks of growth was 255.1 s.

Fig. 6
figure 6

The change in maximum LV volume (a), ED thickness in the remote noninfarcted region of the LV (a), end-diastolic pressure (c), and mean arterial pressure (d) throughout growth for the simulation of an independent myocardial infarction study used to validate the model [17]. Black and red dots indicate control and acute values tuned using the circulatory model, respectively, and experimental data are shown in gray, mean ± SD

Full size image

Discussion

We sought to develop a computational model of left ventricular growth and remodeling in response to hemodynamic overload that can be customized and run quickly enough to make its eventual use in clinical decision-making practical. We adapted a previously published phenomenologic growth law, integrated it with a compartmental model of the ventricles and circulation, and showed that the model could predict the time course of remodeling following experimental pressure overload, volume overload, and myocardial infarction in dogs. Three features of the work reported here support the feasibility of applying similar models in a clinical setting to individual patients. First, we were able to automatically customize model parameters based on hemodynamic data that are accessible in clinical settings, such as arterial pressures, pulmonary capillary wedge pressure (obtained by catheterization), and LV dimensions (measured by ultrasound). Second, the current model requires just 6 min to simulate 3 months of growth and remodeling. Third, after its growth parameters were fitted to data from experimental studies of pressure (PO) and volume overload (VO), the model could predict not only results from independent studies of PO and VO but also remodeling in response to other conditions such as myocardial infarction.

Customizing Hemodynamics

Phenomenologic growth laws use changes in mechanics to predict the rate of growth and remodeling. Thus, accurate predictions of the time course of growth require accurate matching of the hemodynamic perturbations that precipitate it. Thus, we expect that patient-specific tuning of hemodynamic parameters will be an essential step in clinical applications of growth models such as the one presented here. While some of the hemodynamic parameters in the model presented here—such as heart rate and systemic vascular resistance—can be directly measured or easily estimated for each subject, other parameters—such as the stressed blood volume—are very difficult to measure and therefore must be estimated from other measurable data through some sort of optimization routine. In this study, we generated an algorithm to automatically tune model parameters for the left ventricle and circulatory system to match measured control and acute hemodynamics by minimizing the error in reported control and acute levels of maximum LV volume, minimum LV volume, end-diastolic pressure, and a measurement of systolic pressure. With one exception discussed under “Customizing Material Properties,” below, we found the error landscape for this optimization to be very well-suited to automatic parameter identification (Fig. 2, Supplemental Table 2). Using the built-in fminsearch function in MATLAB, our automatic tuning algorithm required 1 h of computation time, but it should be fairly straightforward to reduce this time substantially.

When simulating growth retrospectively, we had the advantage of knowing how hemodynamic variables change over time and prescribed the evolution of heart rate, systemic vascular resistance, and mitral valve regurgitation based on these data. When making prospective predictions in the clinical context, however, future hemodynamic conditions will be uncertain. We therefore repeated each of the three validation simulations holding all hemodynamic parameters constant at acute overload levels to more closely simulate a typical prospective prediction. Perhaps surprisingly, in these alternate simulations all of the predicted LV dimensions remained within 1 SD of the experimental means. However, predicted hemodynamics matched data less well in some cases. Conversely, even our original simulations probably omitted some hemodynamic changes that actually occurred over the course of the studies simulated here. For example, in simulated volume overload, our predicted EDP was at the low end of the experimental range in the fitting study and below 1 SD of the mean for the validation study (Table 1). Given the known physiology of long-term volume overload and the fact that one of these studies reported pulmonary congestion in the study animals, it seems likely that stressed blood volume increased during the course of these studies, a factor we ignored because we did not have sufficient data to include it. Overall, the fact that correctly predicting growth in the studies simulated here required a good match to acute hemodynamics but much less data on their subsequent evolution is likely due to the fact that the acute perturbations were much bigger than subsequent adjustments. When applying growth models to specific clinical problems, it will be important to conduct comprehensive sensitivity analyses to understand when long-term changes in hemodynamics are important to track and incorporate into growth predictions, and when (as in our study) they are less essential.

Customizing Geometry

Interestingly, most published growth modeling studies have paid less attention to quantitatively matching hemodynamic loading than the present study, but have employed much more realistic representations of left ventricular geometry. Realistic geometries are now relatively easy to obtain in a clinical setting using MRI or CT. Yet, translating these images into a finite-element mesh typically requires some user intervention in the segmentation and assembly pipeline, adding to the time required to customize the model for a specific patient. One implication of our results is that for some conditions such as global pressure or volume overload, detailed representations of left ventricular geometry may not be essential for predicting the time course of growth. Additionally, since geometrically simpler models require only a few measurements (LV diameter and thickness) that are easily obtained from echocardiography, using such models could reduce imaging time and cost.

On the other hand, when modeling cardiac growth and remodeling, it is essential to account for how geometric changes feed back to influence LV function. For example, the same active myofiber stress translates to much lower pressures in a dilated, thin-walled heart compared to a heart with a normal geometry. One advantage of finite-element models is that they account for these geometric effects automatically, since they specify force generation at the myofiber or single-element level and integrate over the mesh to determine the corresponding cavity pressure. Here, we used a time-varying elastance model of ventricular contraction, which required us to modify the governing diastolic and systolic pressure-volume relationships to account for changes in geometry as remodeling progressed. We did this by developing analytic expressions based on the relationships between strain and volume and stress and pressure in a thin-walled sphere. Clearly, the heart is not a thin-walled sphere, and stresses estimated using formulas for a thin-walled sphere are not very accurate. Yet, this limitation did not impair our ability to predict growth-related changes in passive or active chamber properties, likely because relative changes in radius and wall thickness have similar relative impacts on stress in simpler and more complex cardiac geometries.

Finally, the growth law employed here was originally implemented in a finite element model and prescribed the same amount of growth in the radial and cross-fiber directions. The spherical model only has two directions (circumferential and radial), which means it cannot simulate changes in LV shape that might arise from differential growth in the fiber and cross-fiber directions. This limitation did not seem to diminish the ability of the model to predict ventricular dilation or thickening in response to global hemodynamic overload, but our approach would be inappropriate for applications where predicting shape change is of interest. In cases where more complex geometric or biophysical predictions are desired, models like the one presented here may be valuable as part of a multi-level modeling strategy (e.g., [32]) expediting parameter fitting and reducing computation time.

Customizing Material Properties

Myocardial material properties are particularly difficult to measure on a patient-specific basis. In this respect, the simpler geometry we employed is well-suited to clinical applications, because there is no need to determine multiple different material parameters governing fiber, cross-fiber, and shear properties. On the other hand, the estimation of unloaded volume proved more difficult than expected, echoing experiences with estimating unloaded geometry in finite-element models. The unloaded state is an artificial model construct that cannot be observed in vivo, but the choice of this state strongly influences model strains and therefore the performance of strain-based growth laws. When developing our automatic parameter tuning algorithm, we discovered that many combinations of unloaded volume and maximal LV elastance were compatible with each dataset. Upon closer examination, we determined a clear trade-off in unloaded volume and contractility: increasing unloaded volume reduced end-diastolic stretch but increased maximum pressure generation, while decreasing contractility reduced maximum pressure generation but increased end-diastolic stretch. We therefore augmented the objective function using literature values for control end-diastolic stretch and maximum pressure generation to constrain the choice of V0 and E.

We held ventricular material properties constant in all simulations presented here, but in cases where these properties are known to change it is easy to take this into account. For example, when simulating the volume overload validation study, our model predicted a mean arterial pressure after 3 months of growth that was much higher than reported. However, the authors of the study reported a 50% reduction in end-systolic stiffness at 3 months. This finding suggests that intrinsic myocardial contractility may have diminished due to the onset of heart failure, which would indeed reduce arterial pressures if included in the model. When we decreased intrinsic myocardial contractility linearly during the growth time period by a total of 50%, the predictions for ventricular dilation and thickening remained within 1 SD of the data, and the error in the predicted systolic arterial pressure was reduced by 6%. End-diastolic pressure remained well below 1 SD of the data, however, suggesting that multiple parameters would have to change over time to match all of the hemodynamic data from this study. Another situation where material properties clearly change is in a healing infarct. In the myocardial infarction validation study simulated here, Jugdutt et al. reported that after 6 weeks of growth, the hydroxyproline content of the infarct region at its border and center were fourfold and tenfold greater, respectively, than in the posterior ventricular wall, suggesting that the infarct region stiffened during growth. When we simulated this stiffening by increasing b, the material parameter associated with ED stiffness, in the infarct region by sevenfold, the average error in the predicted end-diastolic and end-systolic volumes were reduced by 7 and 13%, respectively, without altering predicted changes in LV thickness or hemodynamics in the noninfarcted compartment (Supplemental Figure 1). As discussed for hemodynamic parameters in the previous section, this finding suggests that the initial loss of contractile function in the infarct region generates bigger changes in stretch in the noninfarcted myocardium than subsequent gradual stiffening of the infarct, and is therefore more important in driving predicted remodeling.

Limitations

A major limitation of phenomenologic models is that they must be specifically validated (and sometimes re-parameterized) for each new situation prior to use. Thus, any clinical application of the approach described here must be preceded by careful retrospective validation in an appropriate patient population. Because growth laws of the type employed here are based on the ability of myocytes to sense and respond to stretch, special caution is warranted in any situation where the inherent responsiveness of myocytes to stretch is changing. Thus, different growth parameters might be needed to predict remodeling in patients treated with beta-blockers (which modulate intracellular hypertrophic signaling) or in patients transitioning to heart failure (where beta-adrenergic responsiveness is changing). In general, we found it was not necessary to change the material properties of the myocardium to correctly predict growth for the experiments modeled here; however, there may be pathologies such as myocardial fibrosis that change not only material properties but also the local mechanical signals sensed by the myocytes. Furthermore, it remains to be seen whether an approach similar to the one described here can handle the regional heterogeneity observed in hypertrophic cardiomyopathy or electrical dyssynchrony. Although intuition might suggest that such cases will require more geometrically sophisticated models, the two-compartment model of infarction described here performed surprisingly well, and Walmsley et al. have successfully reproduced many aspects of LV dyssynchrony using a multi-compartment model [33].

Conclusion

The ability to reliably predict growth and remodeling of the heart in individual patients could have widespread clinical applications. Ideally, growth models intended for clinical use should capture ventricular growth across a range of different hemodynamic conditions yet be fast enough to construct and run that they can support decision-making on the time scale of a hospital admission or even office visit. The compartmental growth model presented here was able to capture both the time course and distinct patterns of hypertrophy following aortic constriction, mitral valve regurgitation, and myocardial infarction for up to 3 months with simulation times of just a few minutes, suggesting promise for future clinical application.