Introduction

The dynamics of sediment suspensions in tidal estuaries and basins have been studied extensively during the past few decades. Postma (1967) described the movement and distortion of tidal currents and their relationship with sedimentary processes in tidal estuaries and established the importance of tidal asymmetry and settling lag in entrapment of particles. Tidal asymmetry indicates differences of amplitude and duration between flood and ebb tides. The major part of the asymmetry of the tide curve can be represented by superposition of the leading tide and overtides (Dyer 1997). The dominance of flood or ebb can be predicted by the phase difference between the overtide and leading tide (Speer and Aubrey 1985).

Groen (1967) developed a quantitative model to explain the net sediment flux following the direction of flooding caused by a longer ebbing period. Ridderinkhof (1997) applied Groen’s approach to study tidally averaged transport of bed-load and suspended sediment and showed that the direction of net transport of both modes is determined dominantly by the phase of the M4 current relative to the M2 current. Dronkers (1986) investigated the relationship between tidal asymmetry and estuarine morphology and found that tidal velocity asymmetry affects residual transport of suspended sediment, and sediment infill is favored by flood-dominated tidal waves. Using an idealized model of a tidal embayment, Schuttelaars and de Swart (1996) showed that the introduction of overtides in the forcing results in more complex dynamics. Depending on the phase difference between the overtide and the leading tide, the tidal embayment could be exporting or importing sediment. Friedrichs et al. (1998) reached similar conclusions with regard to funnel-shaped tidal estuaries and proposed the importance of settling and scour lags, particularly as the lags interact with along-channel width convergence. Also, they pointed out that a zero net transport of sediment requires along-channel variation in bed erodibility.

Settling lag is the time taken for suspended sediment concentration (SSC) to respond to changing current velocity (Pritchard 2005) and is important in determining the direction of net sediment flux. Prandle (2004) described settling lag using an exponential function with a half-life time. It is found that the phase lag of sediment concentration relative to velocity will be close to 90° for large half-life time and to 0° for small half-life time. Using a numerical model, Bass et al. (2002) examined the influences of settling, advection, and local erosion on temporal evolution of depth-averaged sediment concentration. They found that the phase difference between SSC and current speed increases with decreasing settling velocity when horizontal advection is neglected.

Pritchard (2005) constructed semianalytical solutions for sediment transport in an idealized tidal embayment. The results suggested that settling lag is usually a more important process than scour lag and emphasized that horizontal advection is crucial in predicting the direction of net sediment transport. The contributions of local and nonlocal (advection) processes can be distinguished by examining the frequency components of the SSC variation (Weeks et al. 1993; Bass et al. 2002). However, general expressions for the horizontal gradient of SSC are usually unavailable due to insufficient observation data.

In this study, we model a tidal embayment with a simple geometry that provides an idealized analog of tidal estuaries and basins. This idealized study does not consider sediment properties such as flocculation, deflocculation, and variation in bed erodibility. Both analytic and numerical models are applied. We try to parameterize the horizontal gradient of SSC based on the results from a primitive-equation numerical model, solve the nonlinear sediment transport equation, and provide an analytical solution of SSC “at a point.” The main aim of this paper is to present quantitative expressions of phase differences between SSC and tidal current and describe how tidal asymmetry and settling lag determine the direction of net sediment transport.

One of the most distinctive features in partially and well-mixed estuaries is the presence of a turbidity maximum, which is a region near the upper limit of salt intrusion where concentrations of suspended materials in the channel are the greatest. The hydrodynamic mechanisms proposed for the occurrence of the maxima are estuarine gravitational circulation and tidal asymmetry of velocity and mixing (Postma 1967; Allen et al. 1980; Geyer 1993; Jay and Musiak 1994, Burchard and Baumert 1998). Thus, the estuarine turbidity maximum can be considered as consisting of two components: a gravitational circulation-induced component and tidally induced component. When tidal amplitudes are small compared to the mean water depth (which is fulfilled in this study), density-driven and tidal currents can be separated linearly (Ianniello 1977). Therefore, the numerical model can simulate the tidal turbidity maximum even though fresh water sources are excluded. The other objective of this paper is to explore the occurrence of the tidally induced turbidity maximum in short tidal embayments.

The paper is structured as follows: In the “Model Description” section, we describe the embayment geometry and the analytic model. Also, the configuration of the numerical model is provided. In the “Results” section, numerical model results are presented and an approximate expression for horizontal gradient of depth-averaged SSC is obtained. Solutions of the analytic model are derived and validated using the numerical model results. In the “Discussion” section, quantitative expressions of phase differences between SSC and velocity are provided and examined with numerical results. The effects of tidal asymmetry and settling lag on residual sediment transport are elucidated. In addition, a possible process for the formation of tidal turbidity maximum is described. Finally, we summarize our study in the “Summary and Conclusions” section.

Model Description

Model Geometry

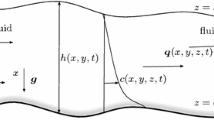
The tidal embayment is restricted to simple and idealized conditions. The geometry of the idealized embayment is considered to be of a rectangular shape, ignoring variation in width (Fig. 1). The embayment is narrow compared to its length so that it can be simplified to a two-dimensional system (a vertical slice along the channel). The length of the embayment is much shorter than the tidal wave length, and its hydrodynamics can be described with simple analytic models (Schuttelaars and De Swart 1996; Prandle 2004; Pritchard 2005). The channel has free communication with the adjacent sea at its mouth, x = 0, and has a reflecting wall at its head, x = L. The local Cartesian coordinates are shown in Fig. 1, bottom panel, in which x increases inland along the channel and z is the vertical coordinate. The height of the mean sea level relative to the bottom boundary is H, which is constant along the channel.

Fig. 1
figure 1

Schematic of an idealized embayment (length not to scale). The upper panel shows the plan view of the tidal embayment; the lower panel shows a vertical–longitudinal section along the center line of the channel. The dashed lines represent high and low tidal elevations

Full size image

Numerical Model Setup

The regional ocean modeling system (ROMS) is used in this study. ROMS is a free-surface, hydrostatic, primitive-equation ocean model, which uses stretched, terrain-following vertical coordinates and orthogonal curvilinear horizontal coordinates on an Arakawa C grid (Shchepetkin and McWilliams 2005). Warner et al. (2005) incorporated a sediment transport module into ROMS, which simulates sediment suspension, advection, and deposition processes.

The model domain is 50 km long and is horizontally discretized with 100 along-channel and three cross-channel cells (Table 1). Grid resolution is uniformly distributed. The vertical dimension is discretized with 20 sigma layers and vertical stretching parameters allow increased resolution near the surface and bottom boundaries. The head (eastern end) of the channel is closed with a wall. The model is forced by a S2 tide at the mouth. The Flather boundary condition is applied for barotropic momentum. Baroclinic momentum and tracers are allowed to radiate through the open boundary using the Orlanski scheme. The flow is homogeneous in temperature and salinity. The vertical eddy viscosity and diffusivity are computed using the k–ω turbulence closure.

Table 1 Model parameters
Full size table

Sediment is introduced into the water column by erosion from the bed on which sediment is uniformly distributed. Initial SSC in the water column is zero. Erosion rate is parameterized with bottom shear stress (τ b) and a bed erodibility constant (E 0), which is spatially uniform and user-defined. Settling velocity (w s) is set to be constant. The model starts from rest and runs for 10 days.

Analytic Model

For a single-sized sediment with a constant settling velocity, the one-dimensional depth-averaged equation describing sediment transport in the water column is given by

$$\frac{{\partial HC}}{{\partial t}} + u\frac{{\partial HC}}{{\partial x}} = E_{\text{r}} - D_{\text{p}} $$
(1)

where C denotes the depth-averaged SSC, u is the depth-averaged horizontal velocity, E r is the erosion rate, and D p is the deposition rate. The horizontal diffusion term is neglected because it is usually much smaller than the horizontal advection term. Therefore, temporal variation of C is mainly controlled by local (erosion and deposition) and nonlocal (advective) processes. In this study, the tidal amplitude is considered much smaller than the mean water depth so that the fluctuation of the water surface is neglected in the total water depth.

Erosion and deposition rates are parameterized using approaches similar to those carried out in ROMS. Erosion rate is taken to be proportional to the bottom shear stress, τ b (Warner et al. 2005):

$$E_{\text{r}} = E_0 \left( {1 - \varphi } \right)\frac{{\tau _{\text{b}} - \tau _{{\text{ce}}} }}{{\tau _{{\text{ce}}} }}\,{\text{where }}\tau _{\text{b}} >\tau _{{\text{ce}}} $$
(2)

where ϕ is the porosity of the top bed layer and τ ce is the critical shear stress for erosion. For this study, τ ce is assumed to be much smaller than τ b and is neglected from the numerator (τ b –τ ce) in Eq. 2. Bottom shear stress, τ b, is related to u with a drag coefficient, C d , such that

$$E_{\text{r}} = Mu^2 ,\,M = E_0 \left( {1 - \varphi } \right)\frac{{\rho C_{\text{d}} }}{{\tau _{{\text{ce}}} }}$$
(3)

where M takes constant, which implies that the bed erodibility is spatially uniform. The relation (Eq. 3) assumes continuous erosion and neglects the effect of scour lag such that Eq. 1 can be solved analytically. This simplification does generate discrepancy between numerical and analytical results. We use a relatively strong tide (tidal amplitude is 1 m) to make this effect (error) small. The deposition rate follows the concept of continuous deposition (Sanford and Chang 1997), which is also applied in ROMS as

$$D_{\text{p}} = w_{\text{s}} C_{\text{b}} ,\quad C_{\text{b}} = EC$$
(4)

where C b is the SSC near bed and E is a coefficient that adjusts C to C b. The coefficient, E is always larger than 1.0 and is expected to increase with increasing settling velocity. By assuming a Rouse profile, E can be related to Rouse number, B (Bass et al. 2002)

$$E = \frac{{H\left( {1 - B} \right)}}{{z_0^B \left( {H^{1 - B} - z_0^{1 - B} } \right)}},\;B = \frac{{\sigma w_{\text{s}} }}{{\kappa \sqrt {C_{\text{d}} } u}}$$
(5)

where z 0 is a reference height, κ is the von Karman constant, and σ is the Schmidt number. The parameters M and E are assumed constant in the analytic model and their value will be obtained using the numerical results when the analytic model is compared with the numerical model.

Although erosion and deposition rates can be parameterized explicitly, the horizontal gradient of C is generally unknown. Certain previous studies have assumed a constant horizontal gradient of C in shelf and coastal environments (Weeks et al. 1993; Bass et al. 2002). However, this simplification has not been verified in a tidal embayment. In this study, we will try to find an approximation of the concentration gradient based upon numerical results and provide an analytical solution of Eq. 1.

Results

Longitudinal Velocity

Due to the simple geometry of the embayment, it can be represented as a two-dimensional section along its length. Numerical results from the middle section of the channel are chosen for analysis. To identify the leading tide and overtides, spectral analysis was carried out for the longitudinal section (Fig. 2, top panel). In order to display all frequencies on the same scale, the power of each frequency is normalized using a simple linear transformation

$$s' = {{\left( {s - \overline s } \right)} \mathord{\left/ {\vphantom {{\left( {s - \overline s } \right)} {\sigma _{\text{s}} }}} \right. \kern-\nulldelimiterspace} {\sigma _{\text{s}} }}$$
(6)

where s′ is the normalized value of power (s), \(\overline s \) is the mean power of all the frequencies, and σ s is the standard deviation of all frequencies.

Fig. 2
figure 2

Spectral and harmonic analysis for longitudinal velocity from the numerical model. The top panel shows longitudinal distribution of the power spectrum (normalized using Eq. 6); the lower three panels show results from the harmonic analysis with the frequencies S2, S4, and S6. The second panel shows amplitudes and the third panel shows phases of the three components, respectively; the fourth panel shows the mean

Full size image

The results show that S2 is the leading tide, and that overtides S4 and S6 are minor components and weak. Frequencies of semi-, quarter-, and sixth-diurnal are chosen for harmonic analysis (Fig. 2, bottom three panels). The amplitude of S2 is much stronger than S4 and S6, and amplitudes of all three components decrease, nearly linearly, from mouth to head. The phases are almost constant along the channel. Phase differences between S4 and S2 are approximately −25°, which is indicative of a flood-dominated tidal wave. The residual current is the Eulerian mean flow, which will not be equal to zero when Stokes drift is important.

Some analytical solutions have been proposed to describe longitudinal velocities in tidal embayments. Using a perturbation method, Ianniello (1977) derived two-dimensional solutions of tidally induced residual currents for a rectangular channel, while Friedrichs et al. (1998) provided solutions for funnel-shaped tidal estuaries. Because the length of the idealized tidal embayment is shorter than the tidal wave length, the equations of motion can be simplified and the so-called “pumping flow” solution provides a good approximation (Schuttelaars and De Swart 1996):

$$u = u_0 \left( {1 - \frac{x}{L}} \right)\cos \omega t$$
(7)

where u is the longitudinal velocity, which is assumed to be a cosine wave with constant amplitude (u 0 ) at the mouth, L is the length of the channel, and ω is the semidiurnal frequency. The solution shows that the tidal velocity decreases approximately linearly from mouth to head. Another important feature of the short tidal embayment is that velocity is cotidal along the channel. These characteristics are similar to that in the numerical model. Therefore, the “pumping flow” can provide an appropriate solution of the longitudinal velocity for a single harmonic component. According to the harmonic analysis of the numerical results, a linear combination of the analytical solutions for leading tide and overtides is a reliable approximation for u in the tidal embayment. At a point, u can be approximately expressed as

$$u = u_{\text{a}} \cos \omega t + \varepsilon u_{\text{a}} \cos \left( {2\omega t + \phi _0 } \right)$$
(8)

where u a denotes the amplitude of semidiurnal component, ɛ is the relative strength of the overtide compared with the leading tide, and ϕ 0 is the phase difference between the two tidal components. Here, the third harmonic is not included because it does not strongly contribute to net suspended sediment transport (Friedrichs et al. 1998).

Horizontal Gradient of Depth-Averaged Sediment Concentration

In tidally dominated estuaries, the horizontal gradient of sediment concentration cannot be assumed constant because of the periodic movement of tidal waves. Frequencies of the horizontal gradient of C are examined using a power spectral analysis (Fig. 3, top panel). S2 is the dominant frequency while S4 and S6 are minor components. At the transition zone (7–10 km), the quarter-diurnal frequency is the most significant. Therefore, the frequencies S2 and S4 are taken for harmonic analysis (Fig. 3, bottom three panels). The amplitudes of harmonic components, particularly the S2, are much stronger in the area near the mouth than in the remaining section (considered the interior section). The mean of the concentration gradient shows a pattern opposite to that of the amplitude of the harmonics. The amplitude of the mean is small in the near-mouth area and becomes large in the interior section. To simply describe the longitudinal distribution of the horizontal concentration gradient, we assume

$$\frac{{\partial C}}{{\partial x}} = N\cos \left( {\omega t + \phi } \right) + N_0 $$
(9)

where, N is the amplitude of the semidiurnal component, N 0 represents the mean of the gradient, and ϕ is the phase difference between \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) and the velocity of the leading tide. This relation is an appropriate approximation of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) in the embayment except in the transition zone, where both S2 and S4 components are important. This insufficiency will be taken into account in the interpretation of model results.

Fig. 3
figure 3

Spectral and harmonic analysis for the horizontal gradient of depth-averaged sediment concentration from the numerical model. The top panel shows longitudinal distribution of the power spectrum (normalized using Eq. 6); the lower three panels show results from the harmonic analysis with the frequencies S2 and S4. The second panel shows amplitudes and the third panel shows phases of the two components, respectively; the fourth panel shows the mean

Full size image

Temporal Variation of Depth-Averaged Sediment Concentration

Although the horizontal pattern of u shows a linear distribution, the general expressions of N and N 0 along the channel are still not available. Instead of directly obtaining one-dimensional solutions, we first solve Eq. 1 at a point and then apply it to the entire tidal embayment using the results of u a , N, and N 0 obtained from harmonic analysis of the numerical results. Substituting Eqs. 8 and 9 into Eq. 1, C at a point is obtained:

$$\begin{array}{*{20}c} {C = {\underbrace {\frac{{M'u^{2}_{a} }}{{2{\sqrt {E'^{2} w^{2}_{s} + 4\omega ^{2} } }}}}_{{A1}}}\sin {\left( {2\omega t + \phi _{2} } \right)}{\underbrace { - \frac{{Nu_{a} }}{{2{\sqrt {E'^{2} w^{2}_{s} + 4\omega ^{2} } }}}}_{{A2}}}\sin {\left( {2\omega t + \phi _{2} + \phi } \right)}} \\ {{\underbrace { - \frac{{N_{0} u_{a} }}{{{\sqrt {E'^{2} w^{2}_{s} + \omega ^{2} } }}}}_{{A3}}}\sin {\left( {\omega t + \phi _{1} } \right)}{\underbrace { + \frac{{M'u^{2}_{a} - Nu_{a} \cos \phi }}{{2E'ws}}}_{{A4}}}} \\ {{\underbrace { + \frac{{\varepsilon M'u^{2}_{a} }}{{{\sqrt {E'^{2} w^{2}_{s} + 9\omega ^{2} } }}}}_{{A5}}}\sin {\left( {3\omega t + \phi _{3} + \phi _{0} } \right)}{\underbrace { - \frac{{\varepsilon Nu_{a} }}{{2{\sqrt {E'^{2} w^{2}_{s} + 9\omega ^{2} } }}}}_{{A6}}}\sin {\left( {3\omega t + \phi _{3} + \phi _{0} + \phi } \right)}} \\ {{\underbrace { - \frac{{\varepsilon N_{0} u_{a} }}{{{\sqrt {E'^{2} w^{2}_{s} + 4\omega ^{2} } }}}}_{{A7}}}\sin (2\omega t + \phi _{2} + \phi _{0} )} \\ {{\underbrace { + \frac{{\varepsilon M\prime u^{2}_{a} }}{{{\sqrt {E'^{2} w^{2}_{s} + \omega ^{2} } }}}}_{{A8}}}\sin {\left( {\omega t + \phi _{1} + \phi _{0} } \right)}{\underbrace { - \frac{{\varepsilon Nu_{a} }}{{2{\sqrt {E'^{2} w^{2}_{s} + \omega ^{2} } }}}}_{{A9}}}\sin {\left( {\omega t + \phi _{1} + \phi _{0} - \phi } \right)}} \\ { + D\exp {\left( { - E'wst} \right)} + O{\left( {\varepsilon ^{2} } \right)}} \\ {\tan \phi _{1} = \frac{{E'w_{s} }}{\omega },\tan \phi _{3} = \frac{{E'w_{s} }}{{3\omega }},\tan \phi _{2} = \frac{{E'w_{s} }}{{2\omega }},M' = \frac{M}{H},E' = \frac{E}{H}} \\ \end{array} $$
(10)

where D is an integral constant. When the evolution of C tends to be steady, the term Dexp(−E’w s t) becomes trivial and can be neglected. In the solution, high-order terms O(ɛ 2) that contain frequency 4ω are omitted. The lower-order terms include harmonic frequencies from ω to 3ω.

The first four terms in the solution are contributions from the leading tide S2, while the last five terms represent the effects of the overtide S4. Contributions of local and nonlocal processes can be readily identified for each term: A1 is local resuspension, A2 and A3 represent the contribution of horizontal advection, and A4 is the mean that results from local erosion and the harmonic component of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\). The overtide does not contribute to the mean. Local erosion by overtides produces harmonic components with frequencies ω and 3ω (A8 and A5). The mean of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) generates frequency 2ω (A7), while the harmonic of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) yields frequencies ω and 3ω (A9 and A6). It is noticed that both local and nonlocal processes can generate semi- and quarter-diurnal components.

To evaluate the contribution of each mechanism, amplitudes of the nine terms (A1–A9) are plotted in Fig. 4, top panel. The A4 component is approximately 0.8 kg m−3 in the first 5 km and decreases to zero at the head. Contributions of the leading tide are generally larger than those of the overtide. S2 and S4 are the major harmonics, while contributions from S6 are small. The semidiurnal component is mainly composed of A3 and A8, while the major quarter-diurnal component consists of A1 and A2. To compare the amplitudes of the semi- and quarter-diurnal components, the two major terms for each frequency are combined using the relation

$$\begin{array}{*{20}c} {a\sin \alpha + b\sin {\left( {\alpha + \beta } \right)} = {\sqrt {a^{2} + b^{2} + 2ab\cos \beta } }\sin {\left( {\alpha + \frac{\beta }{2} + \phi '} \right)},} \\ {\tan \phi ' = \frac{{b - a}}{{a + b}}\tan \frac{\beta }{2}} \\ \end{array} $$
(11)
Fig. 4
figure 4

Longitudinal distributions of depth-averaged sediment concentration from the analytic model. The upper panel shows amplitudes of the nine major terms; the lower panel shows amplitudes of S2 and S4 components

Full size image

The S4 component dominates the near-mouth area, while the S2 component is significant in the interior section (Fig. 4, bottom panel). Both terms are important in the transition zone. The general trend is that the major frequency of C shifts from 2ω to ω from the mouth to the head of the channel.

To examine the analytical solution, spectral analysis is carried out for C as obtained from the numerical model (Fig. 5, top panel). The results show that S4 is more important in the near-mouth area, while S2 is more significant in the interior section. Higher frequencies are very small. From harmonic analysis, the distributions of the amplitudes of the S2 and S4 components (Fig. 5, second panel) are similar to the analytical solution (Fig. 4, bottom panel). The distribution of the mean (Fig. 5, bottom panel) is almost identical to that of A4 (Fig. 4, top panel). The phase of the S4 component decreases in the near-mouth area and tends to be constant in the interior section (the last 15 km is not taken into account). The phase of S2 fluctuates only slightly along the channel, except for the deviation of the first five points, which may be caused by the boundary condition of tracers (Fig. 5, third panel). Also, this may produce the distinct discrepancy in S2 and S4 amplitudes between numerical and analytic models in the near-mouth area. Because SSC is not specified in the open boundary, SSC computed inside the modeling domain radiates through the open boundary during ebb tides, and water with zero SSC comes into the modeling domain during flood tides. This treatment of the open boundary may result in a loss of sediment in the near-mouth area. However, in general, the analytical solution of C is consistent with the numerical results.

Fig. 5
figure 5

Spectral and harmonic analysis for depth-averaged sediment concentration from the numerical model. The first panel shows the longitudinal distribution of the power spectrum (normalized using Eq. 6); the lower three panels show results from the harmonic analysis with the frequencies S2 and S4. The second panel shows amplitudes and the third panel shows phases of the two components, respectively; the fourth panel shows the mean

Full size image

Discussion

Phase Relationships Between Sediment Concentration and Tidal Current

A phase difference is usually observed between peaks in sediment concentration and current velocity during a tidal cycle. The phase difference is crucial in determining the direction of residual sediment flux and can be produced by a variety of processes, such as threshold lag, settling lag, and erosion lag (Dyer 1997). Because consolidation is not included in the analytic and numerical models, here, the phase difference represents the settling lag.

Sediment resuspension is related to square of velocity. The quarter-diurnal components in Eq. 10 are selected to determine the phase lag between C and the current speed of the leading tide. As shown in Fig. 4, the quarter-diurnal components are mainly determined by terms A1 and A2, so that the phase lag (ϕ) is obtained from the combination of A1 and A2 using Eq. 11:

$$\Phi = \phi _2 + \frac{\phi }{2} + \phi ' - \frac{\pi }{2},\quad \tan \phi ' = \frac{{A2 - A1}}{{A1 + A2}}\tan \frac{\phi }{2}$$
(12)

The π/2 exists because u is assumed to be a cosine function. In the formula, ϕ 2 represents the local contribution (local phase lag), and ϕ is the nonlocal contribution (nonlocal phase lag). When the local process is evaluated, ϕ equates to \(\phi _2 - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\) and is mainly determined by w s . If w s is very small, ϕ 2 tends to zero, and C is, thus, out of phase with the current speed. On the other hand, if w s is very large, ϕ 2 tends toward π/2, so that C is in phase with the current speed. This relation indicates that if sediment settles quickly enough, then the near bed concentration of locally resuspended sediment is generally in phase with current speed. If the sediment settles more slowly, it may be delayed in settling to the bed, resulting in a lag in C relative to current speed. If E and ω are assumed constant, the local phase lag increases as w s decreases. This conclusion agrees with the previous studies (Bass et al. 2002; Prandle 2004).

Physically, ϕ 2 represents ET tide/2T sett, a ratio between tidal period (T tide) and the sediment settling time (T sett), which is the time taken for a sediment particle to settle from surface to bottom. Also, ϕ 2 is the ratio of the deposition rate to the horizontal advection term, representing the relative importance of settling lag and tidal timescale. The nondimensional parameter ET tide/2T sett has been recognized in previous studies. Friedrichs et al. (1998) pointed out that the relative importance of advection is represented by the ratio of the sediment response timescale to the tidal timescale. The sediment response time can be expected to approximately equal the vertical settling distance divided by the suspended sediment fall velocity. Pritchard (2005) applied this nondimensional parameter in his analytic model to represent the ratio of the tidal timescale to the timescale over which sediment concentrations respond to changes in erosion and deposition rates. He found that the semitidal signal of local erosion and deposition becomes dominant when the parameter is very large.

From the expression of ϕ 2 (Eq. 10), the local phase lag is also controlled by the parameter E, which is a function of Rouse number (Eq. 5) and is thus related to the current velocity. Because the amplitude of u decreases from mouth to head (Fig. 2, second panel), B and E increase from mouth to head and ϕ 2 also increases (Fig. 6, top panel). In the calculation, u includes the sum of the amplitudes of the leading tide and overtide. Since ϕ 2 is relatively small, C tends to be out of phase of current speed if nonlocal processes are excluded. The nonlocal phase lag is not only related to ϕ, for which an explicit expression is generally not available, but is also related to the strength of local erosion (A1) and horizontal advection (A2). Accordingly, it is difficult to find general conclusions for the effect of nonlocal phase lag. Here, numerical results are used to examine Eq. 12. ϕ is obtained from harmonic analysis of u (Fig. 2, third panel) and \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) (Fig. 3, third panel). It decreases in the near-mouth area and tends to be constant in the interior section (Fig. 6, middle panel). ϕ is obtained from harmonic analysis of the current speed and C (Fig. 6, bottom panel). The ϕ calculated using Eq. 12 has a distribution similar to that from numerical results, which decreases from approximately −50° to −90° in the near-mouth area to about −90° in the interior section (Fig. 6, bottom panel). The discrepancy between analytic and numerical models may be caused by open boundary conditions and harmonic analysis. In the interior section, C is almost out of phase with current speed, indicating that local phase lag dominates this section. Thus, the ϕ from the analytic model shows a trend similar to ϕ 2. In the near-mouth area, ϕ is closely related to ϕ because the harmonic of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) is significant.

Fig. 6
figure 6

Longitudinal distribution of phase lags. The upper panel shows local phase lag from the analytic model; the middle panel shows phase difference between the horizontal gradient of depth-averaged sediment concentration and the semidiurnal component of tidal current speed from the numerical model; the lower panel shows phase differences between the depth-averaged sediment concentration and the quarter-diurnal component of tidal current speed

Full size image

Residual Flux of Suspended Sediment

Using the available solution of C (Eq. 10) and the approximation of u (Eq. 8), the residual sediment flux over a semidiurnal tidal cycle, T, is obtained

$$\begin{array}{*{20}c} {\frac{1}{T}{\int\limits_0^T {uCdt} } = - \frac{{N_{0} u^{2}_{{\text{a}}} \sin \phi _{1} }}{{2{\sqrt {E'^{2} w^{2}_{{\text{s}}} + \omega ^{2} } }}}{\underbrace { + \frac{{\varepsilon M'u^{3}_{{\text{a}}} \sin {\left( {\phi _{1} + \phi _{0} } \right)}}}{{2{\sqrt {E'^{2} w^{2}_{{\text{s}}} + \omega ^{2} } }}}}_{{r2}}}{\underbrace { + \frac{{\varepsilon M'u^{3}_{{\text{a}}} \sin {\left( {\phi _{2} - \phi _{0} } \right)}}}{{4{\sqrt {E'^{2} w^{2}_{{\text{s}}} + 4\omega ^{2} } }}}}_{{r3}}}} \\ {{\underbrace { - \frac{{\varepsilon Nu^{2}_{{\text{a}}} \sin {\left( {\phi _{1} + \phi _{0} - \phi } \right)}}}{{4{\sqrt {E'^{2} w^{2}_{{\text{s}}} + \omega ^{2} } }}}}_{{r4}}}{\underbrace { - \frac{{\varepsilon Nu^{2}_{{\text{a}}} \sin {\left( {\phi _{2} - \phi _{0} + \phi } \right)}}}{{4{\sqrt {E'^{2} w^{2}_{{\text{s}}} + 4\omega ^{2} } }}}}_{{r5}}}} \\ \end{array} $$
(13)

In the solution, higher-order terms O(ɛ 2) and the transient terms, which include D, are omitted. The first term, r1 shows the contribution from the leading tide due to the mean of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\). The last four terms are generated by the overtide. Terms r2 and r3 represent local resuspension, while r3 and r4 indicate contributions from the harmonic of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\). The term r1 is the major component (Fig. 7, top panel). The pair r2 and r3 and pair r4 and r5 decrease from mouth to head and show mirror image relationships. The overtide generates an outward net sediment flux in the near-mouth area and an inward net sediment flux in the interior section (Fig. 7, middle panel). According to the analytic model, the total net flux is negative near the mouth and becomes positive from x = 5 km (Fig. 7, bottom panel). The results from the numerical model show a trend similar to the analytic model, but with a discrepancy in the near-mouth area. This may be caused by the open boundary condition and insufficient approximation of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) in the transition zone.

Fig. 7
figure 7

Residue sediment flux from the analytic model. The upper panel shows amplitudes of the five components of residual sediment flux; the middle panel shows residual sediment flux generated by the overtide; the lower panel shows comparison of residual sediment flux between the analytic and numerical models

Full size image

The direction of net sediment flux produced by the leading tide is determined by the mean of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) because sin ϕ 1 is always positive. If the mean gradient is positive, the net flux is outward. If the mean gradient is negative, the embayment is importing sediment. From Fig. 7, top panel, r1 is positive in almost the whole embayment, which is consistent with the distribution of mean \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\).

The overtide contribution from local erosion (r2 and r3) is controlled by both local phase lag and ϕ 0. The local phase lag is related to settling velocity, while ϕ 0 determines tidal asymmetry. The tidal current is flood-dominated for \({{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2} <\phi _0 <{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\) and ebb-dominated for \(\phi _0 <- {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\) and \(\phi _0 >{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\). Rearranging r2 and r3, we obtain

$$\begin{array}{*{20}c} {r2 + r3 = \varepsilon M'u^{3}_{a} \left\{ {{\left[ {\frac{{E'w_{{\text{s}}} }}{{E'^{2} w^{2}_{{\text{s}}} + \omega ^{2} }} + \frac{{E'w_{{\text{s}}} }}{{2{\left( {E'^{2} w^{2}_{{\text{s}}} + 4\omega ^{2} } \right)}}}} \right]}\cos \phi _{0} } \right.} \\ { + \left. {{\left[ {\frac{\omega }{{E'^{2} w^{2}_{{\text{s}}} + \omega ^{2} }} - \frac{\omega }{{E'^{2} w^{2}_{{\text{s}}} + 4\omega ^{2} }}} \right]}\sin \phi _{0} } \right\}} \\ \end{array} $$
(14)

Notice that the contents of the two square brackets are always positive. The sign of the whole term depends on cos ϕ 0 and sin ϕ 0. When E’w s is much larger than ω, the second square bracket term tends toward zero; thus, the sign of r2 + r3 is determined by cos ϕ 0. Under this condition, flood-dominated tides generate inward net sediment flux and ebb-dominated tides yield outward residual sediment flux. When E’w s is much smaller than ω, the first square bracket term tends to be trivial, so that the sign of r2 + r3 is determined by sin ϕ 0. In this situation, both flood-dominated and ebb-dominated tides can yield an importing or exporting residual sediment flux depending on ϕ 0. With increasing w s , r2 + r3 shifts form from sin ϕ 0 to cos ϕ 0 (Fig. 8). The zero flux line in the figure can be used to determine critical grain size of sediment that is trapped in the embayment. Pritchard (2005) described how the net sediment flux varies with the exchange rate parameter and with the phase of the imposed overtide. The relation shown in Fig. 8 confirms and is consistent with the results from the nonadvective sediment transport model proposed by Pritchard (2005).

Fig. 8
figure 8

Contours of residual sediment flux as a function of sediment settling velocity and phase between overtide (S4) velocity and leading tide (S2) velocity. The amplitude of the residual sediment flux is normalized using Eq. 6. Positive values indicate import of sediment; negative represents export of sediment

Full size image

Using the same approach, r4 + r5 can be rearranged in similar form as r2 + r3, in which ϕ 0 is replaced by ϕ 0–ϕ. The sign of term r4 + r5 is controlled by sin(ϕ 0–ϕ) and cos(ϕ 0–ϕ). A relation between w s and ϕ 0–ϕ similar to that in Fig. 8 is available but is not shown here. Because the general expression of ϕ is unknown, impacts of nonlocal processes on net sediment flux cannot be presented in a general expression. From this analysis, we see that residual flux of suspended sediment is determined by the local phase lag (settling lag), ϕ 0 (tidal asymmetry), and nonlocal processes. A local mode is not sufficient to predict the direction of sediment flux.

Limitation of the Parameterization of Horizontal SSC Gradient

An important presumption of this study is that \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) may be parameterized with the combination of a semidiurnal harmonic and a mean (Eq. 9). This parameterization is sensitive to settling velocity. A range of settling velocities from 0.05 to 2 mm/s was selected and tested in the numerical experiments. Two particular cases are shown in Fig. 9. In general, the longitudinal distributions of semi- and quarter-diurnal harmonic components and mean gradient show similar patterns and fulfill the parameterization of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\). The quarter-diurnal component becomes significant as settling velocity increases, particularly in the interior section (Fig. 9, top right panel). Therefore, the quarter-diurnal harmonic is required in the parameterization of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) for coarse sediment. Since this study mainly focuses on suspended sediment, which mainly consists of fine-grained sediment, Eq. 9 could be a valid parameterization for the horizontal gradient of depth-averaged SSC. The treatment of the open boundary (Orlanski scheme) affects the SSC, and thus its gradient, near the mouth. Therefore, the near-mouth area has to be excluded from the comparison between analytic and numerical models. Due to the limitations of the parameterization of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\), the analytic model is valid only for an idealized tidal embayment but needs further study for extension to real environments.

Fig. 9
figure 9

Sensitivity of the horizontal gradient of depth-averaged SSC to settling velocity. Shown are results from harmonic analysis of numerical experiments with setting velocities of 0.1 mm/s (left column) and 1.0 mm/s (right column). The two upper panels show amplitude of S2 and S4 components; the two lower panels show means

Full size image

Tidal Turbidity Maximum: Importance of Tidal Excursion

If nonlocal transport is neglected, the magnitude of C is proportional to the velocity squared (see A1 in Eq. 10). Because the amplitude of u decreases from mouth to head, the magnitude of C is similarly expected to decrease up-estuary (Fig. 10, top panel). Because velocity is cotidal along the channel, the longitudinal distribution of C will maintain the same spatial pattern and its amplitude will vary periodically with time. Thus, the maximum SSC always appears at the mouth, and a tidal turbidity maximum cannot develop and migrate landward in the channel. If horizontal advection is included, however, the turbidity maximum generated at the mouth migrates upstream to a point and then returns to the mouth during a tidal period. A complete cycle of the migration is shown in Fig. 10. Because of the migration of the tidal turbidity maximum, spatial distribution of SSC in the near-mouth area varies significantly over a tidal cycle, whereas SSC near the head of the channel does not change significantly. Thus, horizontal advection plays an important role in the near-mouth area, while local processes dominate the interior section. This is consistent with the longitudinal distribution of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\).

Fig. 10
figure 10

Migration of the tidal turbidity maximum over a semidiurnal tidal cycle. Five particular snapshots are shown. The unit of SSC is kg/m3

Full size image

Occurrence of a tidal turbidity maximum is traditionally explained by tidal asymmetry, which is important in determining the direction of residual sediment flux and may favor the entrapment of sediment. However, model results suggest that the tidal turbidity maximum is not a residual phenomenon but, rather, a persistent feature. The residual sediment flux directly contributes to the tendency of SSC \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}\) but does not directly determine the spatial distribution of SSC that also relies on initial SSC before the temporal increment.

Schubel (1968) pointed out that the estuarine turbidity maximum can be related to local resuspension by tidal currents and waves. Allen et al. (1980) showed that, without density stratification, the tidal turbidity maximum is, in reality, an “erosion maximum,” located in the estuary where the power dissipated by the tidal currents on the estuary bottom attains a maximum. Also, they suggested that the turbidity maximum extends upstream to the head of tidal excursion. According to the numerical results presented herein, the tidal turbidity maximum in a short embayment is mainly determined by the maximum tidal current amplitude, and tidal propagation produces an oscillating migration of the turbidity maximum in the channel. In reality, oceanic and riverine sediment sources and variable bed erodibility will result in more complicated behavior of the tidal turbidity maximum (Ganju et al. 2004).

The farthest distance that the tidal turbidity maximum can reach is related to the tidal excursion measured from the mouth of the embayment (this assumes that the highest velocities are at the mouth). The trajectory of a water particle, x w, starting from the mouth in the embayment is related to velocity by

$$\frac{{dx_{\text{w}} }}{{dt}} = u_0 \left( {1 - \frac{{x_{\text{w}} }}{L}} \right)\cos \omega t$$
(15)

Integrating the equation, and using the initial condition: t = 0, x w = 0, we obtain

$$x_{\text{w}} = L - L\exp \left( { - \frac{{u_0 }}{{L\omega }}\sin \omega t} \right)$$
(16)

Given the geometry and coordinates of the embayment, the length of tidal excursion equates to the maximum value of x w. Using the u 0 of the leading tide (0.85 ms−1, Fig. 2, second panel), the maximum x w is 5.5 km (if u 0 is 1.0 ms−1 for the sum of all three tidal constituents, the maximum x w is 6.4 km), which is much smaller than the value (8.5 km) shown in Fig. 10, third panel. Because of the settling lag, maximum C does not coincide with the maximum current. In order to estimate the migration of tidal turbidity maximum, the phase lag (ϕ) between C and current speed is incorporated into Eq. 15 and the trajectory of tidal turbidity maximum (x c) is obtained

$$x_{\text{c}} = L - L\exp \left\{ { - \frac{{u_0 }}{{L\omega }}\left[ {\sin \left( {\omega t + \Phi } \right) - \sin \left( \Phi \right)} \right]} \right\}$$
(17)

According to Eq. 17, ϕ is crucial in determining the migration of the tidal turbidity maximum. If ϕ is −40° (roughly estimated from Fig. 6, bottom panel), the maximum x c is about 8.8 km, which is close to the numerical result.

Summary and Conclusions

A short tidal embayment with simple geometry provides an idealized analog of tidal estuaries and basins. As such, it can be used for preliminary understanding of suspended sediment transport processes. The relationship of sediment concentration with tidal current velocity and tidal velocity asymmetry are crucial in determining the direction of net sediment transport, which affects long-term evolution of bed morphology. Insights from analytic models can be used to identify the dominant mechanisms of sediment transport. However, insufficient information makes it difficult to obtain analytical solutions. This is particularly true with respect to the parameterization of the horizontal advection term. In contrast, a primitive-equation numerical model can provide full solutions of hydrodynamics and sediment transport, but it needs guidance in data interpretation. In this study, we use both numerical and analytic models to overcome mutual disadvantages.

The numerical results show that the amplitude of the longitudinal velocity decreases nearly linearly from the mouth to the head of the channel and its phase is constant along the channel. By spectral and harmonic analysis, the horizontal gradient of sediment concentration can be approximately expressed with the combination of the first harmonic and mean. This parameterization is valid for fine-grained sediment. The harmonic dominates the near-mouth area, while the mean is important in the interior section. Using the approximation of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) and velocity, a solution of the analytic model is obtained. Neglecting higher-order terms O(ɛ 2), the nine major terms in the solution represent interactions between tidal movement (the leading tide and first-order overtide) and three sediment transport processes, namely, local resuspension, and harmonics and means of horizontal advection. Frequencies of these terms range from ω to 3ω. Evaluation of the harmonic components shows that semi- and quarter-diurnal frequencies are dominant components. This is supported by harmonic analysis of numerical results. The quarter-diurnal frequency is significant near the mouth, while the semidiurnal component dominates the interior area.

The phase difference between depth-averaged sediment concentration and tidal current speed is determined by local and nonlocal phase lags. The local phase lag is a function of the ratio between tidal period and settling time. It increases with decreasing settling velocity. The nonlocal phase lag is determined by the phase difference between sediment concentration and tidal velocity and the relative strength of local erosion and horizontal advection. The residual sediment flux consists of a leading tide and overtide components. The direction of the former is determined by the mean of \({{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\), while the latter includes both local and nonlocal contributions. The direction of local residual sediment flux is controlled by the phase difference between the overtide and leading tide (tidal velocity asymmetry) and sediment settling velocity (settling lag). For relatively large settling velocities, flood-dominant tidal currents produce sediment infill, while ebb-dominant tidal currents lead to the export of sediment. For relatively fine sediment, both flood- and ebb-dominant tidal currents can yield import or export of sediment. The introduction of nonlocal sediment transport results in more complicated relations.

The numerical model presents a periodic migration of the tidal turbidity maximum. The tidal turbidity maximum in a short embayment appears to be determined by the maximum tidal current amplitude, and tidal propagation produces the migration of turbidity maximum in the channel. The farthest distance that the tidal turbidity maximum can reach is related to the tidal excursion measured from the mouth of the embayment. Settling lag may cause the location of the tidal turbidity maximum to deviate from the upstream limit of the tidal excursion.