Abstract
In this paper, we define and study a canonical Hardy–Littlewood-type maximal operator associated with the one-dimensional generalized Fourier transform. For this operator to which covering methods do not apply, we construct a geometric maximal operator, which controls pointwise the canonical maximal operator, and for which we can use the machinery of real analysis to obtain a maximal theorem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In Dunkl’s theory, the role of orthogonal groups, which provide the underlying structure of the classical Fourier transform, is replaced by finite Coxeter groups, the partial derivatives are replaced by differential–difference operators (Dunkl’s operators) and the Lebesgue measure is replaced by a weighted Lebesgue measure whose weight is invariant under the action of Coxeter groups.
More recently, Kobayashi, Ørsted, and the first author [7] gave a far reaching extension of the classical situation by constructing a generalized Fourier transform \({\mathcal {F}}_{k,a}\) commuting with finite Coxeter groups and it acts on a Hilbert space deforming \(L^2({\mathbb {R}}^N).\) The deformation parameters consist of a real parameter \(a>0\) coming from the interpolation of the minimal unitary representations of two different reductive Lie groups and a real parameter k coming from Dunkl’s theory. We pin down that the unitary operator \({\mathcal {F}}_{k,a}\) includes some known integral transforms as special cases:
the Euclidean Fourier transform [21] (\(a=2,\)\(k\equiv 0\));
the Hankel transform [23] (\(a=1,\)\(k\equiv 0\));
the Dunkl transform [17] (\(a=2,\)\(k>0\)).
The theory of \({\mathcal {F}}_{k,a}\) has a rich structure parallel to that of Fourier analysis, which allows us to extend several classical results to this setting (see, e.g., [7, 9,10,11,12, 18, 22]). There are still many problems to be solved and the theory is still at its infancy.
The background of this paper is a translation operator and a convolution structure developed recently by the first author in [5] for the one-dimensional generalized Fourier transform \({\mathcal {F}}_{k,1}\), with \(k>1/4\), and giving rise to a class of signed hypergroups. In this setting, we define a Hardy–Littlewood-type maximal operator and we prove weak-type and strong-type estimates for it. Maximal operators are important tools for treatment of problems related to the pointwise convergence of parametrized families of operators (whose basic example is the Lebesgue differentiation theorem) and for the theory of singular integrals. The fundamental Hardy–Littlewood maximal inequality has a long and rich history; see, e.g., the seminal work [20] and the recent survey [16] (and references therein).
For \(k> {1/4},\) let \({\mathcal {M}}_k\) be the Hardy–Littlewood maximal operator canonicaly defined for suitable functions f by
where the measure \(d\mu _k(y):=2^{-1} \Gamma ( {{2k } } )^{-1}|y|^{2k-1}dy\) and \(T_x^k\) is the translation operator introduced in [5] (see Sect. 2 for more details). The crucial result about \({\mathcal {M}}_k\) is to show the weak-type (1, 1) estimate. To do so, we define a more handy operator
where the interval \(I(x,r):=]\big (\max \{0, \sqrt{|x|}-\sqrt{|r|}\}\big )^2, \big (\sqrt{|x|}+\sqrt{|r|}\big )^2[.\) The core relationship between \({\mathcal {M}}_k\) and \({\mathbb {M}}_k\) is the pointwise inequality
and therefore the weak-type (1, 1) estimate for \({\mathcal {M}}_k\) follows from the one for \({\mathbb {M}}_k.\) Now, the proof of the weak-type (1, 1) estimate for \({\mathbb {M}}_k\) depends heavily on a covering lemma of Vitali-type for the intervals I(x, r). We provide a proof of the lemma to highlight the (non-obvious) engulfing property and the doubling property of I(x, r) and \(\mu _k\). The main issue is that when you multiply r in I(x, r) by a constant \(c>0\), then I(x, r) and I(x, cr) do not share the same center and could overlap randomly. Lastly, by means of Marcinkiewicz interpolation, we get the assertion that \({\mathbb {M}}_k\), and therefore \({\mathcal {M}}_k\), is strong-type (p, p) for all \(1<p\leqslant \infty .\)
As we shall see, our strategy of constructing the more convenient maximal operator \({\mathbb {M}}_k\) follows from the fact that we have to bypass some problems occurring with the structure of the translation operators and preventing us from proceeding directly by standard techniques. The key point in the construction of \({\mathbb {M}}_k\) is a sharp estimate for \(T^k_x(\chi _{{}_{]-r,r[}};\,\cdot \,)\). This approach is in the spirit of similar results in Dunkl’s setting (see [1, 2, 13, 14]) or hypergroups theory (see [8, 15]).
Our exposition is organized in the following way. In Sect. 2, we briefly outline some results on the one-dimensional generalized Fourier transform \({\mathcal {F}}_{k,1},\) and we show a covering lemma for the intervals I(x, r). In Sect. 3, we give a sharp estimate for \(T_x^k(\upchi _{]-r,r[}; \,\cdot \,)\), which is crucial in the construction of \({\mathbb {M}}_k\). Finally, the maximal theorems for the various maximal functions are established in Sect. 4.
Throughout the paper, the notation \(X \lesssim Y\) indicates that \(X\leqslant c Y\) with a positive constant c independent of significant quantities.
2 Preliminaries and a Covering Lemma of Vitali-Type
2.1 Preliminaries
Let \(k>0.\) Define the measure
on \({\mathbb {R}}\) and the kernel
where
denotes the normalized Bessel function. We pin down that \(|B_k(x,y)|\leqslant 1.\) The one-dimensional generalized Fourier transform (denoted in the Introduction by \({\mathcal {F}}_{k,1}\)) is given by (see [6, 7] §5))
for appropriate function f on \({\mathbb {R}}.\)
For \(p<\infty ,\) let \(L^p(d\mu _k)=L^p({\mathbb {R}}, d\mu _k(x)),\) and let \(\Vert \cdot \Vert _{L_k^p}\) denote the associated norm. For \(p=\infty ,\)\(\Vert \cdot \Vert _{L_k^\infty }\) is simply the usual \(\Vert \cdot \Vert _{\infty }.\) From [7], Theorems 5.1 and 5.3], it is known that \({\mathcal {F}}_k\) is an involutive unitary operator on \(L^1(d\mu _k)\) and that there exists a unique isometry on \(L^2(d\mu _k)\) that coincides with \({\mathcal {F}}_k\) on \(L^1\cap L^2(d\mu _k).\)
Intimately connected with the generalized Fourier transform are the translation operator and the convolution product defined and studied recently by the first author in [5]. Under the assumption that \(k>1/4\) and for a locally integrable function f on \({\mathbb {R}}\) with respect to \(d\mu _k,\) the translation operator is defined by
where the function \(z\mapsto K_{\mathrm{L}}^k ( x, y, z)\) is compactly supported on
we refer the reader to [5] for an explicit expression of the kernel \(K_{\mathrm{L}}^k ( x, y, z).\) From now on, we will always assume that \(k>1/4\). The translation operator mainly satisfies \(T_x^k(f;0)=f(x),\)\(T_x^k (f; y)=T_y^k (f; x)\) and \(T_x^k (B_k(\lambda , \,\cdot \,); y)=B_k(\lambda , x)B_k(\lambda ,y).\) The convolution product of two convenient functions f and g is then defined by

The convolution  carries a new commutative signed hypergroup in the sense of [24] or [25]. Moreover, its restriction to the space of even functions gives the convolution structure associated to the integral transform \(T_l\) in [23, (6.1.4)] (with \(l=0\) and \(m=2k+1\) in the authors’ notation).
carries a new commutative signed hypergroup in the sense of [24] or [25]. Moreover, its restriction to the space of even functions gives the convolution structure associated to the integral transform \(T_l\) in [23, (6.1.4)] (with \(l=0\) and \(m=2k+1\) in the authors’ notation).
The following theorem collects several useful results on the translation operator and the convolution product.
Theorem 2.1
(see [5], Theorem 3.3]) The following statements hold:
- (1)
For all \(1\leqslant p\leqslant \infty \) and \(f\in L^p(d\mu _k),\) we have \(\Vert T_x^k(f;\,\cdot \,)\Vert _{L_k^p}\lesssim \Vert f\Vert _{L_k^p}\) with \(x\in {\mathbb {R}}.\)
- (2)
If \(f\in L^p(d\mu _k),\)\(1\leqslant p\leqslant 2\) and \(x\in {\mathbb {R}},\) then \({\mathcal {F}}_{k}(T_x^k(f;\,\cdot \,))(y)=B_k(y, x) {\mathcal {F}}_{k}(f)(y)\) for almost every \(y\in {\mathbb {R}}.\)
- (3)
(Young inequality) For p, q, r such that \(1\leqslant p,q,r\leqslant \infty \) and \(1/p+1/q-1=1/r,\) and for \(f\in L^p(d\mu _k)\) and \(g\in L^q(d\mu _k),\) the convolution product
 is a well-defined element in \(L^r(d\mu _k)\) and
is a well-defined element in \(L^r(d\mu _k)\) and 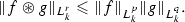
- (4)
For p, q, r such that \(1\leqslant p,q,r\leqslant 2\) and \(1/p+1/q-1=1/r,\) and for \(f\in L^p( d\mu _k)\) and \(g\in L^q(d\mu _k),\) we have
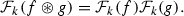 In particular
In particular  is associative in \(L^1(d\mu _k).\)
is associative in \(L^1(d\mu _k).\)
2.2 A Covering Lemma of Vitali-Type
Below we will state and then show a covering lemma of Vitali-type which will play a crucial role in the proof of the main result of the paper. For \(x\in {\mathbb {R}}\) and \(r>0,\) let
These intervals I(x, r) are intimately related to the support (2.6) of the kernel \(K_{\mathrm{L}}^k \) defining the translation operator \(T_x^k.\)
The main properties of those intervals are the engulfing property and the doubling property. Engulfing property, which is far from being obvious for I(x, r), states that if two intervals intersect, one is contained in some dilated form of the other one. The doubling property simply allows us to exploit the first property. Let us begin with the doubling property.
Lemma 2.2
The measure \(\mu _k\) is doubling for the intervals I(x, r) in the sense that:
- (1)
\(0<\mu _k(I(x,r))<\infty \) for all I(x, r).
- (2)
\( \mu _k\bigl (I(x,2r)\bigr )\lesssim \mu _k\bigl (I(x,r)\bigr ) \) for all \(x \in {\mathbb {R}}\) and \(r>0.\)
Proof
Part (1) is obvious. We divide the proof of part (2) in three cases.
Assume first that \(\sqrt{|x|}\leqslant \sqrt{r}\). Then we have
$$\begin{aligned} \mu _k\bigl (I(x,2r)\bigr )=\int _{0}^{(\sqrt{|x|}+\sqrt{2r})^2}d\mu _k(z)=\frac{1}{4k\Gamma (2k)}\bigl (\sqrt{|x|}+\sqrt{2r}\bigr )^{4k}\lesssim \bigl (\sqrt{|x|}+\sqrt{r}\bigr )^{4k}, \end{aligned}$$and thus
$$\begin{aligned} \mu _k\bigl (I(x,2r)\bigr ) \lesssim \mu _k\bigl (I(x,r)\bigr ). \end{aligned}$$Now assume that \(\sqrt{r}\leqslant \sqrt{|x|}\leqslant \sqrt{2r}\). On the one hand, we have
$$\begin{aligned} \mu _k\bigl (I(x,2r)\bigr )=\int _{0}^{(\sqrt{|x|}+\sqrt{2r})^2}d\mu _k(z)=\frac{1}{4k\Gamma (2k)}\bigl (\sqrt{|x|}+\sqrt{2r}\bigr )^{4k}\lesssim r^{2k}. \end{aligned}$$On the other hand, we have
$$\begin{aligned} \mu _k\bigl (I(x,r)\bigr )=\int _{(\sqrt{|x|}-\sqrt{r})^2}^{(\sqrt{|x|}+\sqrt{r})^2}d\mu _k(z)\geqslant \int _{(3-2\sqrt{2})r}^{4r}d\mu _k(z)=\frac{4^{2k}-\bigl (3-2\sqrt{2}\bigr )^{2k}}{4k\Gamma (2k)}r^{2k}. \end{aligned}$$Thus,
$$\begin{aligned} \mu _k\bigl (I(x,2r)\bigr ) \lesssim \mu _k\bigl (I(x,r)\bigr ). \end{aligned}$$The remaining case is \(\sqrt{|x|}\geqslant \sqrt{2r}\). A change of variables gives
$$\begin{aligned} \mu _k\bigl (I(x,2r)\bigr )=\frac{1}{\Gamma ( {{2k } }) }\int _{\sqrt{|x|}-\sqrt{2r}}^{\sqrt{|x|}+\sqrt{2r}}z^{4k-1}dz\leqslant \frac{2\sqrt{2r}}{\Gamma ( {{2k } }) }\bigl (\sqrt{|x|}+\sqrt{2r}\bigr )^{4k-1}, \end{aligned}$$
while
The assumption \(\sqrt{|x|}\geqslant \sqrt{2r} \) implies \(7\bigl (\sqrt{|x|}-\sqrt{r}\bigr )\geqslant \sqrt{|x|}+\sqrt{2r},\) and therefore
\(\square \)
Now we state the covering lemma which will highlight the engulfing property of the intervals I(x, r).
Lemma 2.3
Let E be a \(\mu _k\)-measurable subset of \({\mathbb {R}}^*_+\) covered by a finite collection of intervals \(\{I(x_j,r_j)\}_{1\leqslant j \leqslant n}\). Then, there exists disjoint subcollection \(I(x_{n_1},r_{n_1}),\ldots ,I(x_{n_\ell },r_{n_\ell })\) of these intervals which satisfy
Proof
The selection process is the standard one (see, e.g., [27]). One can select the interval with the biggest diameter in the collection, denote it as \(I(x_{n_1},r_{n_1}),\) and then remove all other intervals that intersect with \(I(x_{n_1},r_{n_1}).\) Repeat this procedure until one runs out of intervals. After this greedy algorithm, one ends up with a subcollection of disjoint intervals, namely \(I(x_{n_1},r_{n_1}),\ldots , I(x_{n_\ell },r_{n_\ell }),\) and each interval in the collection \(I(x_1,r_1),\ldots , I(x_n,r_n)\) is either selected or removed.
In view of the doubling property proved in the previous lemma, to establish the inequality (2.8), it suffices to prove that each interval \(I(x_j, r_j)\) that has been removed is included in some \(I(x_{n_\imath }, c\, r_{n_\imath }),\)\(1\leqslant \imath \leqslant \ell ,\) for some positive constant \(c\geqslant 1.\)
Let \(I(x_j, r_j)\) be one of the intervals that have been removed. Then, from the above algorithm, there exists a smallest \(\imath \), \(1\leqslant \imath \leqslant \ell ,\) such that \(I(x_j, r_j)\cap I(x_{n_\imath }, r_{n_\imath }) \not = \emptyset \) and \({{\,\mathrm{diam}\,}}( I(x_j, r_j))\leqslant {{\,\mathrm{diam}\,}}( I(x_{n_\imath }, r_{n_\imath })).\) We claim that there exists a constant \(c\geqslant 1\) such that \(I(x_j, r_j)\subset I(x_{n_\imath }, c\, r_{n_\imath }).\) We divide the proof of the claim into two cases.
\(\bullet \) First case: Assume that \(I(x_j,r_j)=\bigl ]0,\bigl (\sqrt{|x_j|}+\sqrt{r_j}\bigr )^2\bigr [\).
− If \(I(x_{n_\imath },r_{n_\imath })=\bigl ]0,\bigl (\sqrt{|x_{n_\imath }|}+\sqrt{r_{n_\imath }}\bigr )^2\bigr [\), then the condition on the diameters of \(I(x_j,r_j)\) and \(I(x_{n_\imath },r_{n_\imath })\) implies that \(I(x_j,r_j)\subset I(x_{n_\imath },r_{n_\imath }).\)
− If \(I(x_{n_\imath },r_{n_\imath })=\bigl ]\bigl (\sqrt{|x_{n_\imath }|}-\sqrt{r_{n_\imath }}\bigr )^2,\bigl (\sqrt{|x_{n_\imath }|}+\sqrt{r_{n_\imath }}\bigr )^2\bigr [\), then, based on the relationship between \(I(x_j, r_j)\) and \(I(x_{n_\imath },r_{n_\imath })\), we have
Thus,
which implies \(\sqrt{|x_{n_\imath }|} (\sqrt{|x_{n_\imath }|}-6\sqrt{r_{n_\imath }})\leqslant 0.\) That is \(\sqrt{|x_{n_\imath }|}-6\sqrt{r_{n_\imath }}\leqslant 0.\) In these circumstances, the interval \(I(x_{n_\imath }, 36 r_{n_\imath })\) is in the form \( \bigl ]0, \bigl (\sqrt{|x_{n_\imath }|}+6\sqrt{r_{n_\imath }}\bigr )^2\bigr [\) and it contains \(I(x_j, r_j),\) since \(\bigl (\sqrt{|x_j|}+\sqrt{r_j}\bigr )^2 \leqslant \bigl (\sqrt{|x_{n_\imath }|}+\sqrt{r_{n_\imath }}\bigr )^2 \leqslant \bigl (\sqrt{|x_{n_\imath }|}+6\sqrt{r_{n_\imath }}\bigr )^2. \)
\(\bullet \) Second case: Assume that \(I(x_j,r_j)=\bigl ]\bigl (\sqrt{|x_j|}-\sqrt{r_j}\bigr )^2,\bigl (\sqrt{|x_j|}+\sqrt{r_j}\bigr )^2\bigr [\).
− First, we consider the case \(I(x_{n_\imath },r_{n_\imath })=\bigl ]0,\bigl (\sqrt{|x_{n_\imath }|}+\sqrt{r_ {n_\imath }}\bigr )^2\bigr [\). In other words, here we consider the case \(\sqrt{|x_{n_\imath }|}\leqslant \sqrt{r_ {n_\imath }}.\) We will assume that
Otherwise, i.e., if \((\sqrt{|x_j|}+\sqrt{r_j})^2\leqslant (\sqrt{|x_{n_\imath }|}+\sqrt{r_{n_\imath }})^2\), then there is nothing to do since obviously we have \(I(x_j,r_j)\subset I(x_{n_\imath },r_{n_\imath }).\) From \({{\,\mathrm{diam}\,}}( I(x_j, r_j))\leqslant {{\,\mathrm{diam}\,}}( I(x_{n_\imath }, r_{n_\imath }))\), we have the inequality below:
In view of (2.9) and the fact that we are considering the case \(\sqrt{|x_{n_\imath }|}\leqslant \sqrt{r_ {n_\imath }},\) we get
Therefore, \(I(x_j,r_j)\subset I(x_ {n_\imath },8r_ {n_\imath })\). Here \(I(x_ {n_\imath },8r_ {n_\imath })=\bigl ]0, \bigl (\sqrt{|x_ {n_\imath }|}+\sqrt{8r_ {n_\imath }}\bigr )^2\bigr [\) due to the fact that \(\sqrt{|x_{n_\imath }|}\leqslant \sqrt{r_ {n_\imath }} \leqslant \sqrt{8 r_ {n_\imath }} .\)
− Now we consider the case \(I(x_{n_\imath },r_{n_\imath })=\bigl ]\bigl (\sqrt{|x_{n_\imath }|}-\sqrt{r_{n_\imath }}\bigr )^2,\bigl (\sqrt{|x_{n_\imath }|}+\sqrt{r_{n_\imath }}\bigr )^2\bigr [\).
If we consider the sub-case where
then there is nothing to do since \(I(x_j, r_j)\subset I(x_{n_\imath },r_{n_\imath }).\)
Let us consider the second possible sub-case
Using the diameter property, we get
which implies
Now, if \(\sqrt{|x_{n_\imath }|}\leqslant 3\sqrt{r_{n_\imath }},\) then \(I(x_{n_\imath }, 9r_{n_\imath }) = \big ]0, \bigl (\sqrt{|x_{n_\imath }|}+3\sqrt{r_{n_\imath }}\bigr )^2\big [\) and by (2.11) we have \(I(x_j,r_j)\subset I(x_{n_\imath },9r_{n_\imath })\). For the remaining case, i.e., \(\sqrt{|x_{n_\imath }|}\geqslant 3\sqrt{r_{n_\imath }},\) the interval \(I(x_{n_\imath }, 3r_{n_\imath }) \) takes the form \(\bigl ] \bigl (\sqrt{|x_{n_\imath }|}-3\sqrt{r_{n_\imath }}\bigr )^2 , \bigl (\sqrt{|x_{n_\imath }|}+3\sqrt{r_{n_\imath }}\bigr )^2\bigr [,\) and the fact that \(I(x_j,r_j)\subset I(x_{n_\imath },9r_{n_\imath })\) follows from (2.10) and (2.11).
The last possible sub-case is
The diameter property together with (2.12) yields
In particular,
Now, if \(\sqrt{|x_{n_\imath }|} \leqslant 6\sqrt{r_{n_\imath }},\) then \(I (x_{n_\imath }, 36 r_{n_\imath }) = \bigl ]0, \bigl (\sqrt{|x_{n_\imath }|}+6\sqrt{r_{n_\imath }}\bigr )^2\bigr [\) and we have \(I(x_j,r_j)\subset I(x_{n_\imath },36r_{n_\imath }).\) In the case where \(\sqrt{|x_{n_\imath }|} \geqslant 6\sqrt{r_{n_\imath }},\) the interval \(I(x_{n_\imath },36r_{n_\imath })\) is given by \(\bigl ] \bigl (\sqrt{|x_{n_\imath }|}-6\sqrt{r_{n_\imath }}\bigr )^2, \bigl (\sqrt{|x_{n_\imath }|}+6\sqrt{r_{n_\imath }}\bigr )^2 \bigr [\), and the fact that \(I(x_j,r_j)\subset I(x_{n_\imath },36r_{n_\imath })\) follows from (2.12) and (2.13) since \(\sqrt{|x_{n_\imath }|}\bigl (\sqrt{|x_{n_\imath }|}-6\sqrt{r_{n_\imath }}\bigr )\geqslant \bigl (\sqrt{|x_{n_\imath }|}-6\sqrt{r_{n_\imath }}\bigr )^2\).
In conclusion, we have shown that for every unselected interval \(I(x_j, r_j),\) one can find a constant factor (say 36) to enlarge \(I(x_{n_\imath }, r_{n_\imath })\) to contain \(I(x_j, r_j).\) Consequently, in the light of the doubling property of the measure \(\mu _k\) (see Lemma 2.2), we get
\(\square \)
3 A Sharp Estimate for the Generalized Translation Operator
In this section, we will prove a crucial control of the translate of the characteristic function \(\upchi _{r}\) of the interval \(]-r,r[,\) with \(r>0.\) This estimate, which will play a key role in the proof of the main result of the paper, might be of some interest in its own right.
The main result of this section is the following statement.
Theorem 3.1
For every \(x \in {\mathbb {R}}^*\) and for almost every \(y \in {\mathbb {R}}^*,\) we have
where the interval I(x, r) is as in (2.7).
The proof of Theorem 3.1 relies heavily on the statement below.
Proposition 3.2
For every \(x \in {\mathbb {R}}^*\) and for almost every \(y \in {\mathbb {R}}^*,\) the following pointwise estimates holds true
The proof of the above proposition needs three lemmas.
Lemma 3.3
For every \(x,y \in {\mathbb {R}}^*\), we have
Proof
By (2.2) we have
where \(J_\nu \) is the Bessel function in (2.3). Now, the desired inequality follows immediately from the following well-known estimate (see, e.g., [3, p. 238])
\(\square \)
Lemma 3.4
The generalized Fourier transform of the characteristic function \(\upchi _r\) satisfies
and
Proof
For the proof of (3.1) we used the fact that \(|B_k(x,y)|\leqslant 1.\) To derive (3.2) we shall compute \({\mathcal {F}}_k(\upchi _r)(x)\) first. Clearly we have
Above we have used (see, e.g., [19, p. 427])
Now the inequality (3.2) follows from the fact that \(\sup _{u\geqslant 0}\,u^{1/2}|J_\nu (u)|<+\infty .\)\(\square \)
For \(t>0\) and \(x \in {\mathbb {R}}\), let \(q_t(x):=t^{-2k} e^{-{{\vert x\vert }\over t}}\). The function \(q_t\) generalizes the fundamental solution for the classical heat equation; see [4] for more details. The third lemma needed to prove Proposition 3.2 is the following:
Lemma 3.5
For \(t>0\), the function \(q_t\) satisfies \(\displaystyle {\Vert q_t \Vert _{L_k^1}=1}\) and
Proof
The first statement is obvious. For the second one, we write
To conclude, it is enough to invoke the following formula (see (4.11.25) p. 222 in [3]):
\(\square \)
We now turn to the proof of Proposition 3.2.
Proof of Proposition 3.2
We divide the proof in two cases.
\(\bullet \) First, we assume that \(\sqrt{|x|}\leqslant 2\sqrt{r}\). By Theorem 2.1 we have
Thus, the proposition holds in the first case.
\(\bullet \) In the second case, we assume that \(\sqrt{|x|}\geqslant 2\sqrt{r}\). In this circumstance we will assume in addition that y satisfies \((\sqrt{|x|}-\sqrt{|y|})^2\leqslant r,\) otherwise \(T^k_x(\upchi _r;y)=0\) due to the support (2.6) of the translation operator.
Let \(t>0\). By Theorem 2.1 we have  Further, since the translation operator is bounded, it follows
Further, since the translation operator is bounded, it follows  for all x. Furthermore, Hölder’s inequality and Plancherel’s theorem for \({\mathcal {F}}_k\) imply
for all x. Furthermore, Hölder’s inequality and Plancherel’s theorem for \({\mathcal {F}}_k\) imply

That is  As a consequence, the function
As a consequence, the function  which is equal to
which is equal to  belongs to \(L^1(d\mu _k)\) (recall that \(|B_k(x,y)|\leqslant 1\) for all \(x,y\in {\mathbb {R}}\)). In conclusion,
belongs to \(L^1(d\mu _k)\) (recall that \(|B_k(x,y)|\leqslant 1\) for all \(x,y\in {\mathbb {R}}\)). In conclusion,  and
and  belong to \(L^1(d\mu _k)\), which allow us to rewrite, by inversion formula and Lemma 3.5, the translation
belong to \(L^1(d\mu _k)\), which allow us to rewrite, by inversion formula and Lemma 3.5, the translation  as
as

where
Let us estimate first \(I^{(1)}\). By Lemma 3.3 and inequality (3.1), we obtain
In view of the following observation
we get
To estimate \(I^{(2)}\), we use Lemma 3.3 and inequality (3.2) to get
Using again the observation (3.3) we deduce that
In conclusion, for all \(t>0,\) we have

On the other hand, the Plancherel theorem for \({\mathcal {F}}_k\) implies that  goes to \(\upchi _r\) as \(t\rightarrow 0,\) in the \(L_k^2\)-sense. Thus, the \(L_k^2\)-boundedness of the translation operator implies
goes to \(\upchi _r\) as \(t\rightarrow 0,\) in the \(L_k^2\)-sense. Thus, the \(L_k^2\)-boundedness of the translation operator implies

in the \(L_k^2\)-sense. Now, by a standard argument, the inequality (3.6) leads to
This finishes the proof of Proposition 3.2.\(\square \)
We can now turn to the proof of Theorem 3.1.
Proof of Theorem 3.1
Let \(x \in {\mathbb {R}}^*\) and \(r>0\).
First, let us assume that \(\sqrt{|x|}\leqslant \sqrt{r}\). On the one hand, we have
$$\begin{aligned} \mu _k\bigl (I(x,r)\bigr )= & {} \int _0^{(\sqrt{|x|}+\sqrt{r})^2}d\mu _k(z)\leqslant \int _0^{4r}d\mu _k(z)\\= & {} {{2^{4k-1}}\over {\Gamma (2k+1)}}r^{2k}= 2^{4k-1} \mu _k\bigl (]-r,r[\bigr ). \end{aligned}$$On the other hand, for all \(x,y\in {\mathbb {R}},\)
$$\begin{aligned} \vert T^k_x(\upchi _r;y)\vert \leqslant \Vert T^k_x(\upchi _r;\,\cdot \,)\Vert _{L_k^\infty } \lesssim \Vert \upchi _r\Vert _{L_k^\infty }<\infty . \end{aligned}$$Thus, we can choose a constant \(C_k\) large enough so that
$$\begin{aligned} \vert T^k_x(\upchi _r;y)\vert \leqslant C_k \frac{\mu _k\bigl (]-r,r[\bigr )}{\mu _k\bigl (I(x,r)\bigr )}. \end{aligned}$$Let us now consider the case \(\sqrt{|x|}>\sqrt{r}\). In this circumstance,
$$\begin{aligned} \mu _k\bigl (I(x,r)\bigr )= & {} \int _{(\sqrt{|x|}-\sqrt{r})^2}^{(\sqrt{|x|}+\sqrt{r})^2}d\mu _k(z)\\= & {} \frac{1}{\Gamma (2k)}\int _{\sqrt{|x|}-\sqrt{r}}^{\sqrt{|x|}+\sqrt{r}}z^{4k-1}dz\lesssim \sqrt{r}\bigl (\sqrt{|x|}+\sqrt{r}\bigr )^{4k-1}. \end{aligned}$$
Since \(\sqrt{|x|}>\sqrt{r}\) and \(\mu _k \bigl (]-r,r[ \bigr ) =\Gamma (2k+1)^{-1} r^{2k},\) the above inequality gives
That is
To conclude the proof one needs to use Proposition 3.2. \(\square \)
4 Hardy–Littlewood-Type Maximal Theorem
In terms of the generalized translation operator, we define the maximal function \({\mathcal {M}}_k f\) by
where f is a locally integrable function on \({\mathbb {R}}\) with respect to the measure \(\mu _k.\)
The main result of the paper is the following maximal theorem of Hardy–Littlewood-type for \({\mathcal {M}}_k\).
Theorem 4.1
Let f be a locally integrable function on \({\mathbb {R}}\) with respect to the measure \(\mu _k.\)
- (1)
(Weak-type (1, 1)estimate) If \(f \in L^1(d\mu _k)\), then for every \(\lambda >0\),
$$\begin{aligned} \mu _k\Bigl (\Bigl \{x \in {\mathbb {R}}: \;{\mathcal {M}}_kf(x)>\lambda \Bigr \}\Bigr )\leqslant \frac{c_k}{\lambda }\Vert f\Vert _{L^1_k}, \end{aligned}$$where \(c_k\) is a constant independent of f and \(\lambda \).
- (2)
(Strong-type (p, p) estimate) If \(f \in L^p(d\mu _k)\) with \(1<p\leqslant +\infty \), then \({\mathcal {M}}_kf \in L^p(d\mu _k)\) and
$$\begin{aligned} \bigl \Vert {\mathcal {M}}_kf\bigr \Vert _{L^p_k}\leqslant c_{k,p} \Vert f\Vert _{L^p_k}, \end{aligned}$$where \(c_{k,p}\) is a constant independent of f.
To prove the above theorem, the idea is to construct a more convenient maximal operator \({\mathbb {M}}_k\) which will control pointwise \({\mathcal {M}}_k\) and then Theorem 4.1 will be a consequence of the assertion that \({\mathbb {M}}_k\) is of weak-type (1, 1) and bounded on \(L^p(d\mu _k)\) for \(1<p\leqslant \infty .\)
For a locally integrable function f on \({\mathbb {R}}\) with respect to the measure \(\mu _k,\) we define the maximal function \({\mathbb {M}}_kf\) by
where the interval I(x, r) is as in (2.7).
We first prove that \({\mathbb {M}}_k\) is a larger operator than \({\mathcal {M}}_k\).
Proposition 4.2
Let \(f \in L^1_{\mathrm {loc}}(d\mu _k)\). For every \(x \in {\mathbb {R}}\), we have
Proof
For \(x=0\), the statement is obvious, since \(T_0^k(f;y)=f(y)\) and \(I(0,r)=]0,r[\). Assume that \(x\not =0.\) Due to the support (2.6) of \(T_x^k\), observe that
This observation together with Theorem 3.1 leads to
Now the pointwise inequality is immediate. \(\square \)
In the light of the above statement, to get Theorem 4.1 it suffices to establish its analogue for the maximal operator \({\mathbb {M}}_k.\) To do so, we will use the covering Lemma 2.3.
Theorem 4.3
Let f be a locally integrable function on \({\mathbb {R}}\) with respect to the measure \(\mu _k.\)
- (1)
(Weak-type (1, 1) estimate) If \(f \in L^1(d\mu _k)\), then for every \(\lambda >0\),
$$\begin{aligned} \mu _k\Bigl (\Bigl \{x \in {\mathbb {R}}: {\mathbb {M}}_kf(x)>\lambda \Bigr \}\Bigl )\lesssim \frac{1}{\lambda }\Vert f\Vert _{L^1_k}. \end{aligned}$$ - (2)
(Strong-type (p, p) estimate) If \(f \in L^p(d\mu _k)\) with \(1<p\leqslant +\infty \), then \({\mathbb {M}}_kf \in L^p(d\mu _k)\) and
$$\begin{aligned} \bigl \Vert {\mathbb {M}}_kf \bigr \Vert _{L^p_k}\lesssim \Vert f\Vert _{L^p_k}. \end{aligned}$$
Proof
To start off the proof, it is easy to see that \({\mathbb {M}}_k\) is bounded on \(L^\infty (d\mu _k)\). When \(1<p<\infty ,\) the proof combines the weak-type (1, 1) estimate (i.e., the first statement), the \(L^\infty _k\)-boundedness, and the Marcinkiewicz interpolation theorem (see, e.g., [26, p. 21]). Therefore, the proof of the theorem boils down to showing the first statement.
For \(\lambda >0\), we define the set
From the definition (4.1) of \({\mathbb {M}}_k\), it follows that for any \(x\in {\mathbb {R}}_\lambda ^{+}\) there exists \(r_x>0\) such that
Let K be a compact subset of \({\mathbb {R}}_\lambda ^+.\) Since \(K \subset \cup _{x \in K}I(x,r_x),\) then, by compactness there exists a finite subcover \(I(x_1, r_1), \ldots I(x_n, r_n)\) of K. Using Lemma 2.3 we find a subcollection of pairwise disjoint intervals \(I(x_{n_1},r_{n_1}), \ldots , I(x_{n_\ell },r_{n_\ell }) \) such that
Since for every \(x_{n_\imath },\)\(\mu _k (I(x_{n_\imath },r_{n_\imath })) \) satisfies (4.2), then we may rewrite (4.3) as
Above we have used the disjoint property of the intervals \((I(x_{n_\imath },r_{n_\imath }))_{1\leqslant {\imath } \leqslant \ell }\). Since this inequality holds for every compact subset \(K\subset {\mathbb {R}}_{\lambda }^+,\) the inner regularity of the weighted Lebesgue measure yields
Finally, using the fact that
where
and the fact that \({\mathbb {M}}_kf(-x)={\mathbb {M}}_kf(x),\) we deduce that
This finishes the proof of the first statement, and consequently, as explained at the beginning of the demonstration, the proof of Theorem 4.3. \(\square \)
Now, Theorem 4.1 follows immediately by putting Proposition 4.2 and Theorem 4.3 together.
References
Abdelkefi, C.: Dunkl operators on \(\mathbb{R}^d\) and uncentered maximal function. J. Lie Theory 20(1), 113–125 (2010)
Abdelkefi, C., Sifi, M.: Dunkl translation and uncentered maximal operator on the real line. Int. J. Math. Math. Sci. 2007, 9 (2007)
Andrews, G., Askey, R., Roy, R.: Special Functions. Encyclopedia of Mathematics and its Applications, p. 71. Cambridge University Press, Cambridge (1999)
Ben Saïd, S.: Strichartz estimates for Schrodinger-Laguerre operators. Semigr. Forum 90(1), 251–269 (2015)
Ben Saïd, S.: A product formula and a convolution structure for a \(k\)-Hankel transform on \(\mathbb{R}\). J. Math. Anal. Appl. 463(2), 1132–1146 (2018)
Ben Saïd, S., Kobayashi, T., Ørsted, B.: Generalized Fourier transforms \(\cal{F}_{k, a}\). C. R. Math. Acad. Sci. Paris 347(19–20), 1119–1124 (2009)
Ben Saïd, S., Kobayashi, T., Ørsted, B.: Laguerre semigroup and Dunkl operators. Compos. Math. 148(4), 1265–1336 (2012)
Bloom, W.R., Xu, Z.: The Hardy-Littlewood maximal function for Chébli-Trimèche hypergroups. In: Applications of Hypergroups and Related Measure Algebras (Seattle, WA, 1993), Contemp. Math., Amer. Math. Soc., Providence, RI, 183: 45–70, (1995)
De Bie, H.: The kernel of the radially deformed Fourier transform. Integral Transforms Spec. Funct. 24(12), 1000–1008 (2013)
De Bie, H., Ørsted, B., Somberg, P., Souček, V.: Dunkl operators and a family of realizations of \({{\mathfrak{o}}}{{\mathfrak{s}}}{{\mathfrak{p}}}(1|2)\). Trans. Am. Math. Soc. 364(7), 3875–3902 (2012)
De Bie, H., Oste, R., Van der Jeugt, J.: Generalized Fourier transforms arising from the enveloping algebras of \({{\mathfrak{s}}}{{\mathfrak{l}}}(2)\) and \({{\mathfrak{o}}}{{\mathfrak{s}}}{{\mathfrak{p}}}(1|2)\). Int. Math. Res. Not. IMRN 15, 4649–4705 (2016)
De Bie, H., Pan, L., Constales, D.: Explicit formulas for the Dunkl dihedral kernel and the \((k, a)\)-generalized Fourier kernel. J. Math. Anal. Appl. 460(2), 900–926 (2018)
Deleaval, L.: Fefferman-Stein inequalities for the \({\mathbb{Z}}_2^d\) Dunkl maximal operator. J. Math. Anal. Appl. 360(2), 711–726 (2009)
Deleaval, L.: Dunkl kernel and Dunkl translation for a positive subsystem of orthogonal roots. Adv. Pure Appl. Math. 4(3), 107–137 (2013)
Deleaval, L.: Vector-valued theorem for the uncentered maximal operator on Bessel-Kingman hypergroups. Glasg. Math. J. 56(1), 43–51 (2014)
Deleaval, L., Guédon, O., Maurey, B.: Dimension free bounds for the Hardy-Littlewood maximal operator associated to convex sets. Ann. Fac. Sci. Toulouse Math. 27(1), 1–198 (2018)
Dunkl, C.F.: Hankel transforms associated to finite reflection groups. In: Proceedings of the Special Session on Hypergeometric Functions on Domains of Positivity, Jack Polynomials and Applications (Tampa, FL, 1991), Contemp. Math., 138, 123–138 (1992)
Gorbachev, D.V., Ivanov, V.I., Tikhonov, S.Y.: Pitt’s inequalities and uncertainty principle for generalized Fourier transform. Int. Math. Res. Not. IMRN 23, 7179–7200 (2016)
Grafakos, L.: Classical Fourier Analysis. Volume 249 of Graduate Texts in Mathematics, 2nd edn. Springer, New York (2008)
Hardy, G.H., Littlewood, J.E.: A maximal theorem with function-theoretic applications. Acta Math. 54(1), 81–116 (1930)
Howe, R.: The oscillator semigroup. In: The Mathematical Heritage of Hermann Weyl, (Durham, NC, 1987), Proceedings of Symposia in Pure Mathematics, ed. R. O. Wells Jr (American Mathematical Society, Providence, RI), 48, 61–132 (1988)
Johansen, T.R.: Weighted inequalities and uncertainty principles for the \((k, a)\)-generalized Fourier transform. Int. J. Math. 27(3), 44 (2016)
Kobayashi, T., Mano, G.: The inversion formula and holomorphic extension of the minimal representation of the conformal group. In: Li, J.S., Tan, E.C., Wallach, N., Zhu, C.B. (eds.) Harmonic Analysis, Group Representations, Automorphic Forms and Invariant Theory: In Honor of Roger Howe, pp. 159–223. World Scientific, Singapore (2007)
Rösler, M.: Convolution algebras which are not necessarily positivity-preserving. In: Applications of Hypergroups and Related Measure Algebras (Seattle, WA, 1993), Contemp. Math., Amer. Math. Soc., Providence, RI, 183, 299–318 (1995)
Ross, K.A.: Hypergroups and signed hypergroups. In: Harmonic Analysis and Hypergroups (Delhi, 1995), Trends Math., Birkhauser Boston, Boston, MA, 77–91: (1998)
Stein, E.M.: Singular integrals and differentiability properties of functions. Princeton Mathematical Series, p. 30. Princeton University Press, Princeton (1970)
Stein, E.M.: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press, Princeton (1993)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
SBS is thankful to UAEU for the Start-up Grant No. 31S375.
Rights and permissions
About this article
Cite this article
Ben Saïd, S., Deleaval, L. A Hardy–Littlewood Maximal Operator for the Generalized Fourier Transform on \({\mathbb {R}}\). J Geom Anal 30, 2273–2289 (2020). https://doi.org/10.1007/s12220-019-00183-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-019-00183-6



 is a well-defined element in
is a well-defined element in 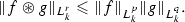
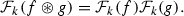 In particular
In particular  is associative in
is associative in