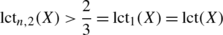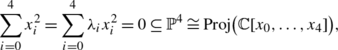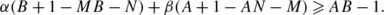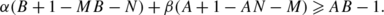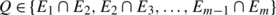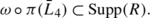Computing α-Invariants of Singular del Pezzo Surfaces

Abstract

We prove a new local inequality for divisors on surfaces and utilize it to compute α-invariants of singular del Pezzo surfaces, which implies that del Pezzo surfaces of degree one whose singular points are of type $\mathbb{A}_{1}$, $\mathbb{A}_{2}$, $\mathbb{A}_{3}$, $\mathbb{A}_{4}$, $\mathbb{A}_{5}$, or $\mathbb{A}_{6}$ are Kähler-Einstein.

We assume that all varieties are projective, normal, and defined over ℂ.

1 Introduction

Let X be a Fano variety with at most quotient singularities (a Fano orbifold).

Theorem 1.1

[37]

If dim(X)=2 and X is smooth, then

An important role in the proof of Theorem 1.1 is played by several holomorphic invariants, which are now known as α-invariants. Let us describe their algebraic counterparts.

Let D be an effective ℚ-divisor on the variety X. Then the number

is called the log canonical threshold of the divisor D (see [21, Definition 8.1]). Put

for every n∈ℕ. For small n, the number lct _n (X) is usually not very hard to compute.

Example 1.2

[28]

If X is a smooth surface in ℙ³ of degree 3, then

The number lct _n (X) is denoted by α _n (X) in [38].

Remark 1.3

It follows from [27, Lemma 4.8] that the set

is finite (cf. [23]). Thus, there exists a divisor B∈|−nK _X | such that lct _n (X)=c(X,B/n)∈ℚ.

If the variety X is smooth, then it is proved by Demailly (see [6, Theorem A.3]) that

where α(X) is the α-invariant introduced by Tian in [36]. Put lct(X)=inf{lct _n (X)∣n∈ℕ}.

Conjecture 1.4

[38, Question 1]

There is an n∈ℕ such that lct(X)=lct _n (X).

The proof of Theorem 1.1 uses (at least implicitly) the following result.

Theorem 1.5

[10, 36]

The Fano orbifold X is Kähler–Einstein if

Note that there are many well-known obstructions to the existence of Kähler–Einstein metrics on smooth Fano manifolds and Fano orbifolds (see [14, 15, 25, 34]).

Example 1.6

If X≅ℙ(1,2,3), then X is not Kähler–Einstein (see [15, 34]).

Let us describe one more α-invariant that took its origin in [37].

Let $\mathcal{M}$ be a linear system on the variety X. Then the number

is called the log canonical threshold of the linear system $\mathcal{M}$ (cf. [21, Theorem 4.8]). Put

for every n∈ℕ. The number lct _n,2(X) is denoted by α _n,2(X) in [8] and [41]. Note that

$$ \mathrm{lct} (X )=\mathrm{inf} \bigl\{ \mathrm{lct}_{n,2} (X )\mid n\in\mathbb{N} \bigr\},$$

(1)

and it follows from [21, Theorem 4.8] that lct _n (X)⩽lct _n,2(X) for every n∈ℕ.

Remark 1.7

It follows from [27, Lemma 4.8] and [21, Theorem 4.8] that the set

is finite. Thus, there is a pencil $\mathcal{B}$ in |−nK _X | such that the equality $\mathrm{lct}_{n,2}(X)=\mathrm{c}(X,\mathcal{B}/n)$. Then

if there exist at most finitely many effective ℚ-divisors D ₁,D ₂,…,D _r on the variety X such that

and D ₁∼_ℚ D ₂∼_ℚ⋯∼_ℚ D _r ∼_ℚ−K _X .

The importance of the number lct _n,2(X) is due to the following conjecture.

Conjecture 1.8

(cf. [8, Theorem 2], [41, Theorem 1])

Suppose that

for every n∈ℕ. Then X is Kähler–Einstein.

Note that Conjecture 1.8 is not much stronger than Theorem 1.5 by (1).

Example 1.9

Suppose that X is a smooth hypersurface in ℙ^m of degree m⩾3. Then

for every n∈ℕ by [2]. The equality lct _n (X)=1−1/m holds ⇔ the hypersurface X contains a cone of dimension m−2 (see [2, Theorem 1.3], [2, Theorem 4.1], [13, Theorem 0.2]). Then

by Remark 1.7, [2, Remark 1.6], [2, Theorem 4.1], [2, Theorem 5.2], and [13, Theorem 0.2], because X contains at most finitely many cones by [9, Theorem 4.2]. If X is general, then

by [3, 5, 33]. Thus, if X is general, then it is Kähler–Einstein by Theorem 1.5.

The assertion of Conjecture 1.8 follows from [8, Theorem 2] and [41, Theorem 1] under an additional assumption that the Kähler–Ricci flow on X is tamed (see [8] and [41]).

Theorem 1.10

[8, 41]

If dim(X)=2, then the Kähler–Ricci flow on X is tamed.

Corollary 1.11

Suppose that dim(X)=2 and

for every n∈ℕ. Then X is Kähler–Einstein.

Two-dimensional Fano orbifolds are called del Pezzo surfaces.

Remark 1.12

Del Pezzo surfaces with quotient singularities are not classified (cf. [20]). But

• del Pezzo surfaces with canonical singularities are classified (see [18]),

• del Pezzo surfaces with 2-Gorenstein quotient singularities are classified (see [1]),

• smoothable del Pezzo surfaces with quotient singularities of Picard rank 1 are classified (see [17]).

Del Pezzo surfaces with canonical singularities form a very natural class of del Pezzo surfaces.

Problem 1.13

Describe all Kähler–Einstein del Pezzo surface with canonical singularities.

Recall that if X is a del Pezzo surface with canonical singularities, then

• either the inequality $K_{X}^{2}\geqslant 5$ holds,

• or one of the following possible cases occurs:

  • the equality $K_{X}^{2}=1$ holds and X is a sextic surface in ℙ(1,1,2,3),

  • the equality $K_{X}^{2}=2$ holds and X is a quartic surface in ℙ(1,1,1,2),

  • the equality $K_{X}^{2}=3$ holds and X is a cubic surface in ℙ³,

  • the equality $K_{X}^{2}=4$ holds and X is a complete intersection in ℙ⁴ of two quadrics.

Let us consider few examples to illustrate the expected answer to Problem 1.13.

Example 1.14

Suppose that X is a sextic surface in ℙ(1,1,2,3) such that its singular locus consists of singular points of type $\mathbb{A}_{1}$ or $\mathbb{A}_{2}$. Arguing as in the proof of [3, Lemma 4.1], we see that

for every n∈ℕ. Thus, the surface X is Kähler–Einstein by Corollary 1.11.

Example 1.15

Suppose that X is a quartic surface in ℙ(1,1,1,2) such that its singular locus consists of singular points of type $\mathbb{A}_{1}$ or $\mathbb{A}_{2}$. Then X is Kähler–Einstein by [16, Theorem 2].

Example 1.16

Suppose that X is a cubic surface in ℙ³ that is not a cone. Then

• if X is smooth, then X is Kähler–Einstein by Theorem 1.1,

• if Sing(X) consists of one point of type $\mathbb{A}_{1}$, then it follows from [35, Theorem 5.1] that

  

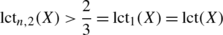
  for every n∈ℕ, which implies that X is Kähler–Einstein by Corollary 1.11,

• if the cubic surface X has a singular point that is not a singular point of type $\mathbb{A}_{1}$ or $\mathbb{A}_{2}$, then the surface X is not Kähler–Einstein by [11, Proposition 4.2].

Example 1.17

Suppose that X is a complete intersection in ℙ⁴ of two quadrics. Then

• if X is smooth, then X is Kähler–Einstein by Theorem 1.1,

• if X is Kähler–Einstein, then X has at most singular points of type $\mathbb{A}_{1}$ (see [19]),

• it follows from [24] or [16, Theorem 44] that X is Kähler–Einstein if it is given by

  

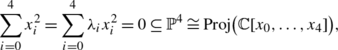
  and X has at most singular points of type $\mathbb{A}_{1}$, where (λ ₀:λ ₁:λ ₂:λ ₃:λ ₄)∈ℙ⁴.

Keeping in mind Examples 1.14, 1.15, 1.16, 1.17, [4, Example 1.12], and [26, Table 1], it is very natural to expect that the following answer to Problem 1.13 is true (cf. Example 1.6).

Conjecture 1.18

If the orbifold X is a del Pezzo surface with at most canonical singularities, then the surface X is Kähler–Einstein ⇔ it satisfies one of the following conditions:

• $K_{X}^{2}=1$ and Sing(X) consists of points of type $\mathbb{A}_{1}$, $\mathbb{A}_{2}$, $\mathbb{A}_{3}$, $\mathbb{A}_{4}$, $\mathbb{A}_{5}$, $\mathbb{A}_{6}$, $\mathbb{A}_{7}$, or $\mathbb{D}_{4}$,

• $K_{X}^{2}=2$ and Sing(X) consists of points of type $\mathbb{A}_{1}$, $\mathbb{A}_{2}$, or $\mathbb{A}_{3}$,

• $K_{X}^{2}=3$ and Sing(X) consists of points of type $\mathbb{A}_{1}$, or $\mathbb{A}_{2}$,

• $K_{X}^{2}=4$ and Sing(X) consists of points of type $\mathbb{A}_{1}$,

• the surface X is smooth and $6\geqslant K_{X}^{2}\geqslant 5$,

• either X≅ℙ² or X≅ℙ¹×ℙ¹.

In this paper, we prove the following result.

Theorem 1.19

Suppose that X is a sextic surface in ℙ(1,1,2,3). Then

for every n∈ℕ if Sing(X) consists of points of type $\mathbb{A}_{1}$, $\mathbb{A}_{2}$, $\mathbb{A}_{3}$, $\mathbb{A}_{4}$, $\mathbb{A}_{5}$ or $\mathbb{A}_{6}$.

Corollary 1.20

Suppose that X is a sextic surface in ℙ(1,1,2,3) such that its singular locus consists of singular points of type $\mathbb{A}_{1}$, $\mathbb{A}_{2}$, $\mathbb{A}_{3}$, $\mathbb{A}_{4}$, $\mathbb{A}_{5}$, or $\mathbb{A}_{6}$. Then X is Kähler–Einstein.

It should be pointed out that Corollary 1.20 and Examples 1.14, 1.15, 1.16, 1.17 illustrate a general philosophy that the existence of Kähler–Einstein metrics on Fano orbifolds is related to an algebro-geometric notion of stability (see [11, 12, 39, Theorem 4.1]).

Remark 1.21

If X is a sextic surface in ℙ(1,1,2,3) with canonical singularities, then either

or Sing(X) consists only of points of type $\mathbb{A}_{1}$ and $\mathbb{A}_{2}$ (see [40]).

What is known about α-invariants of del Pezzo surfaces with canonical singularities?

Theorem 1.22

[3]

If X is a smooth del Pezzo surface, then lct(X)=lct₁(X).

Theorem 1.23

[3, 31]

If X is a del Pezzo surface with canonical singularities, then

in the case when $K_{X}^{2}\geqslant 3$.

Theorem 1.24

[31]

If X is a quartic surface in ℙ(1,1,1,2) with canonical singularities, then

In this paper, we prove the following result (cf. Example 1.14).

Theorem 1.25

Suppose that X is a sextic surface in ℙ(1,1,2,3) with canonical singularities, let ω:X→ℙ(1,1,2) be a natural double cover, and let R be its branch curve in ℙ(1,1,2). Then

It should be pointed out that if X is a del Pezzo surface with at most canonical singularities, then all possible values of the number lct₁(X) are computed in [28–30].

Example 1.26

If X is a sextic surface in ℙ(1,1,2,3) with canonical singularities, then

• lct₁(X)=1/6 ⇔ the surface X has a singular point of type $\mathbb{E}_{8}$,

• lct₁(X)=1/4 ⇔ the surface X has a singular point of type $\mathbb{E}_{7}$,

• lct₁(X)=1/3 ⇔ the surface X has a singular point of type $\mathbb{E}_{6}$,

• lct₁(X)=1/2 ⇔ the surface X has a singular point of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{D}_{7}$ or $\mathbb{D}_{8}$,

• lct₁(X)=2/3 ⇔ the following two conditions are satisfied:

  • the surface X has no singular points of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{D}_{7}$, $\mathbb{D}_{8}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$,

  • there is a curve in |−K _X | that has a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$,

• lct₁(X)=3/4 ⇔ the following three conditions are satisfied:

  • the surface X has no singular points of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{D}_{7}$, $\mathbb{D}_{8}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$,

  • there is no curve in |−K _X | that has a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$,

  • there is a curve in |−K _X | that has a cusp at a point in Sing(X) of type $\mathbb{A}_{1}$,

• lct₁(X)=5/6 ⇔ the following three conditions are satisfied:

  • the surface X has no singular points of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{D}_{7}$, $\mathbb{D}_{8}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$,

  • there is no curve in |−K _X | that have a cusp at a point in Sing(X),

  • there is a curve in |−K _X | that has a cusp,

• lct₁(X)=1 ⇔ there are no cuspidal curves in |−K _X |.

A crucial role in the proofs of both Theorems 1.25 and 1.19 is played by a new local inequality that we discovered. This inequality is a technical tool, but let us describe it now.

Let S be a surface, let D be an arbitrary effective ℚ-divisor on the surface S, let O be a smooth point of the surface S, let Δ₁ and Δ₂ be reduced irreducible curves on S such that

and the divisor Δ₁+Δ₂ has a simple normal crossing singularity at the smooth point O∈Δ₁∩Δ₂, let a ₁ and a ₂ be some non-negative rational numbers. Suppose that the log pair

is not Kawamata log terminal at O, but (S,D+a ₁Δ₁+a ₂Δ₂) is Kawamata log terminal in a punctured neighborhood of the point O.

Theorem 1.27

Let A,B,M,N,α,β be non-negative rational numbers. Then

in the case when the following conditions are satisfied:

• the inequality αa ₁+βa ₂⩽1 holds,

• the inequalities A(B−1)⩾1⩾max(M,N) hold,

• the inequalities α(A+M−1)⩾A ²(B+N−1)β and α(1−M)+Aβ⩾A hold,

• either the inequality 2M+AN⩽2 holds or

  

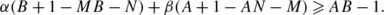
Corollary 1.28

Suppose that

for some integer m such that m⩾3. Then

Proof

To prove the required assertion, let us put

and let us check that all hypotheses of Theorem 1.27 are satisfied.

We have αa ₁+βa ₂⩽1 by assumption. We have

since m⩾3. We have

since m⩾3. We have α(1−M)+Aβ=2⩾2=A and 2M+AN=0⩽2.

Thus, we see that all hypotheses of Theorem 1.27 are satisfied. Then

by Theorem 1.27. □

For the convenience of the reader, we organize the paper in the following way:

• in Sect. 2, we collect auxiliary results,

• in Sect. 3, we prove Theorem 1.27,

• in Sect. 4, we prove Theorem 4.1,

• in Sect. 5, we prove Theorem 5.1,

• in Sect. 6, we prove Theorem 6.1.

By Remark 1.21, both Theorems 1.19 and 1.25 follow from Theorems 4.1, 5.1, and 6.1.

2 Preliminaries

Let S be a surface with canonical singularities, and let D be an effective ℚ-divisor on S. Put

where D _i is an irreducible curve, and a _i ∈ℚ_>0. We assume that D _i ≠D _j ⇔i≠j.

Suppose that (S,D) is log canonical, but (S,D) is not Kawamata log terminal.

Remark 2.1

Let $\bar{D}$ be an effective ℚ-divisor on the surface S such that

and the log pair $(S,\bar{D})$ is log canonical, where $\bar{a}_{i}$ is a non-negative rational number. Put

where α is well defined and α⩽1. Then $\alpha=1\iff D=\bar{D}$. Suppose that $D\ne \bar{D}$. Put

and choose k∈{1,…,r} such that $\alpha=a_{k}/\bar{a}_{k}$. Then $D_{k}\not\subset\mathrm{Supp}(D^{\prime})$ and $D^{\prime}\sim_{\mathbb{Q}} \bar{D}\sim_{\mathbb{Q}} D$, but the log pair (S,D′) is not Kawamata log terminal.

Let LCS(S,D) be the locus of log canonical singularities of the log pair (S,D) (see [6]).

Theorem 2.2

[22, Theorem 17.4]

If −(K _S +D) is nef and big, then LCS(S,D) is connected.

Take a point P∈LCS(S,D). Suppose that LCS(S,D) contains no curves that pass through P.

Lemma 2.3

Suppose that $P\not\in\mathrm{Sing}(S)$ and $P\not\in\mathrm{Sing}(D_{1})$. Then

Proof

The log pair $(S, D_{1}+\sum_{i=2}^{r}a_{i}D_{i})$ is not log canonical at P, since a ₁<1. Then

by [22, Theorem 17.6]. □

Let $\pi\colon \bar{S}\to S$ be a birational morphism, and let $\bar{D}$ be a proper transform of D via π. Then

where E _i is an irreducible π-exceptional curve, and e _i ∈ℚ. We assume that E _i =E _j ⇔i=j.

Suppose, in addition, that the birational morphism π induces an isomorphism

Remark 2.4

The log pair $(\bar{S},\bar{D}+\sum_{i=1}^{s}e_{i}E_{i})$ is not Kawamata log terminal at a point in $\bigcup_{i=1}^{s}E_{i}$.

Suppose that S is singular at P, and either P is a singular point of type $\mathbb{D}_{n}$ for some n∈ℕ_⩾4, or the point P is a singular point of type $\mathbb{E}_{m}$ for some m∈{6,7,8}.

Lemma 2.5

Suppose that $E_{1}^{2}=E_{2}^{2}=\cdots=E_{s}^{2}=-2$. Then e ₁=1 if

Proof

This follows from [32, Proposition 2.9], because (S∋P) is a weakly exceptional singularity (see [32, Example 4.7], [7, Example 3.4], [7, Theorem 3.15]). □

Lemma 2.6

Suppose that S is a sextic surface in ℙ(1,1,2,3) that has canonical singularities, and suppose that D∼_ℚ−K _X . Let μ be a positive rational number such that either

or μ=2/3 and D is not a curve in |−K _X | with a cusp at a point in Sing(S) of type $\mathbb{A}_{2}$. Then

the locus LCS(S,μD) contains no points of type $\mathbb{A}_{1}$ or $\mathbb{A}_{2}$, and |LCS(S,μD)|⩽1.

Proof

This follows from Theorem 2.2 and the proof of [3, Lemma 4.1]. □

Most of the described results are valid in much more general settings (cf. [22] and [21]).

3 Local Inequality

The purpose of this section is to prove Theorem 1.27.

Let S be a surface, let D be an arbitrary effective ℚ-divisor on the surface S, let O be a smooth point of the surface S, let Δ₁ and Δ₂ be reduced irreducible curves on S such that

and the divisor Δ₁+Δ₂ has a simple normal crossing singularity at the smooth point O∈Δ₁∩Δ₂, let a ₁ and a ₂ be some non-negative rational numbers. Suppose that the log pair

is not Kawamata log terminal at O, but (S,D+a ₁Δ₁+a ₂Δ₂) is Kawamata log terminal in a punctured neighborhood of the point O. In particular, we must have a ₁<1 and a ₂<1.

Let A,B,M,N,α,β be non-negative rational numbers such that

• the inequality αa ₁+βa ₂⩽1 holds,

• the inequalities A(B−1)⩾1⩾max(M,N) hold,

• the inequalities α(A+M−1)⩾A ²(B+N−1)β and α(1−M)+Aβ⩾A holds,

• either the inequality 2M+AN⩽2 holds or

  

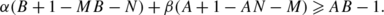
Lemma 3.1

The inequalities A+M⩾1 and B>1 holds. The inequality

holds. The inequality β(1−N)+Bα⩾B holds. The inequalities

and α(2−M)B+β(1−N)(A+1)⩾B(A+1) hold.

Proof

The inequality B>1 follows from the inequality A(B−1)⩾1. Then

because 2B⩾B+1. Similarly, we see that A+M⩾1, because

and B+N−1⩾0. The inequality β(1−N)+Bα⩾B follows from the inequalities

because A+1⩾2−M.

Let us show that the inequality

holds. Let L ₁ be the line in ℝ² given by the equation

and let L ₂ be the line that is given by the equation

where (x,y) are coordinates on ℝ². Then L ₁ intersects the line y=0 at the point

and L ₂ intersects the line y=0 at the point (A/(1−M),0). But

which implies that α(2−M)B+β(1−N)(A+1)⩾B(A+1) if

where (α ₀,β ₀) is the intersection point of the lines L ₁ and L ₂. But

where Δ=2AB−ABM−A+AM−1+M+NA−NAM+N−NM. But

because A(B−1)⩾1, which implies that A ² β ₀(B+N−1)⩾α ₀(A+M−1).

Finally, let us show that the inequality

holds. Let $L^{\prime}_{1}$ be the line in ℝ² given by the equation

where (x,y) are coordinates on ℝ². Then $L^{\prime}_{1}$ intersects the line y=0 at the point

and L ₂ intersects the line y=0 at the point (A/(1−M),0). But

which implies that α(B+1−MB−N)+β(A+1−AN−M)⩾AB−1 if

where (α ₁,β ₁) is the intersection point of the lines $L^{\prime}_{1}$ and L ₂. Note that

where Δ′=AB−1−ABM+AM+2M−NAM−M ².

To complete the proof, it is enough to show that the inequality

holds. This inequality is equivalent to the inequality

which is true, because M⩽1 and AN+2M−2⩽0. □

Let us prove Theorem 1.27 by reductio ad absurdum. Suppose that the inequalities

hold. Let us show that this assumption leads to a contradiction.

Lemma 3.2

The inequalities a ₁>(1−M)/A and a ₂>(1−N)/B hold.

Proof

It follows from Lemma 2.3 that

which implies that a ₁>(1−M)/A. Similarly, we see that a ₂>(1−N)/B. □

Put m ₀=mult _O (D). Then m ₀ is a positive rational number.

Remark 3.3

The inequalities m ₀<M+Aa ₁−a ₂ and m ₀<N+Ba ₂−a ₁ hold.

Lemma 3.4

The inequality m ₀+a ₁+a ₂<2 holds.

Proof

We know that m ₀+a ₁+a ₂<M+(A+1)a ₁ and m ₀+a ₁+a ₂<N+(B+1)a ₂. Then

which implies that m ₀+a ₁+a ₂<2 by Lemma 3.1. □

Let π ₁:S ₁→S be the blow-up of the point O, and let F ₁ be the π ₁-exceptional curve. Then

where D ¹, $\Delta^{1}_{1}$, $\Delta^{1}_{2}$ are proper transforms of the divisors D, Δ₁, Δ₂ via π ₁, respectively. Then

is not Kawamata log terminal at some point O ₁∈F ₁ (see Remark 2.4), where m ₀+a ₁+a ₂⩾1.

Lemma 3.5

Either $O_{1}=F_{1}\cap\Delta^{1}_{1}$ or $O_{1}=F_{1}\cap\Delta^{1}_{2}$.

Proof

Suppose that $O_{1}\not \in\Delta^{1}_{1}\cup\Delta^{1}_{2}$. Then m ₀=D ¹⋅F ₁>1 by Lemma 2.3. But

because m ₀<M+Aa ₁−a ₂ and m ₀<N+Ba ₂−a ₁. On the other hand, we have

because αa ₁+βa ₂⩽1 and AB−1>0. But we already proved that m ₀>1. Thus, we see that

which is impossible by Lemma 3.1. □

Lemma 3.6

The inequality $O_{1}\ne F_{1}\cap\Delta^{1}_{1}$ holds.

Proof

Suppose that $O_{1}=F_{1}\cap\Delta^{1}_{1}$. It follows from Lemma 2.3 that

which implies that a ₁>(2−M)/(A+1). Then

because a ₂>(1−N)/B by Lemma 3.2. Thus, we see that

which is impossible by Lemma 3.1. □

Therefore, we see that $O_{1}=F_{1}\cap\Delta^{1}_{2}$. Then the log pair

is not Kawamata log terminal at the point O ₁. We know that 1>m ₀+a ₁+a ₂−1⩾0.

We have a blow-up π ₁:S ₁→S. For any n∈ℕ, consider a sequence of blow-ups

such that π _i+1:S _i+1→S _i is a blow-up of the point $F_{i}\cap\Delta^{i}_{2}$ for every i∈{1,…,n−1}, where

• we denote by F _i the exceptional curve of the morphism π _i ,

• we denote by $\Delta^{i}_{2}$ the proper transform of the curve Δ₂ on the surface S _i .

For every k∈{1,…,n} and for every i∈{1,…,k}, let D ^k, $\Delta^{k}_{1}$, and $F^{k}_{i}$ be the proper transforms on the surface S _k of the divisors D, Δ₁ and F _i , respectively. Then

where π=π _n ∘⋯∘π ₂∘π ₁ and $m_{i}=\mathrm{mult}_{O_{i}}(D^{i})$ for every i∈{1,…,n}. Then the log pair

$$ \Biggl(S_{n},D^{n}+a_{1} \Delta^{n}_{1}+a_{2}\Delta^{n}_{2}+ \sum_{i=1}^{n} \Biggl(a_{1}+ia_{2}-i+ \sum_{j=0}^{i-1}m_{j} \Biggr)F^{n}_{i} \Biggr) $$

(2)

is not Kawamata log terminal at some point of the set $F^{n}_{1}\cup F^{n}_{2}\cup\cdots\cup F^{n}_{n}$ (see Remark 2.4).

Put $O_{k}=F_{k}\cap\Delta^{k}_{2}$ for every k∈{1,…,n}.

Lemma 3.7

For every i∈{1,…,n}, we have

and (2) is Kawamata log terminal at every point of the set $(F^{n}_{1}\cup F^{n}_{2}\cup\cdots\cup F^{n}_{n})\setminus O_{n}$.

Since mult _O (D⋅Δ₂)<N+Ba ₂−a ₁ by assumption, it follows from Lemma 3.7 that

which implies that n⩽(N+Ba ₂)/(1−a ₂). On the other hand, the assertion of Lemma 3.7 holds for arbitrary n∈ℕ. So, taking any n>(N+Ba ₂)/(1−a ₂), we obtain a contradiction.

We see that to prove Theorem 1.27, it is enough to prove Lemma 3.7.

Let us prove Lemma 3.7 by induction on n∈ℕ. The case n=1 is already done.

We may assume that n⩾2. For every k∈{1,…,n−1}, we may assume that

the singularities of the log pair

are Kawamata log terminal along $(F^{k}_{1}\cup F^{k}_{2}\cup\cdots\cup F^{k}_{k})\setminus O_{k}$ and not Kawamata log terminal at O _k .

Lemma 3.8

The inequality a ₂>(n−N)/(B+n−1) holds.

Proof

The singularities of the log pair

are not Kawamata log terminal at the point O _n−1. Then it follows from Lemma 2.3 that

which implies that a ₂>(n−N)/(B+n−1). □

Lemma 3.9

The inequalities $1>a_{1}+na_{2}-n+\sum_{j=0}^{n-1}m_{j}\geqslant 0$ hold.

Proof

The inequality $a_{1}+na_{2}-n+\sum_{j=0}^{n-1}m_{j}\geqslant 0$ follows from the fact that the log pair

is not Kawamata log terminal at the point O _n−1.

Suppose that $a_{1}+na_{2}-n+\sum_{j=0}^{n-1}m_{j}\geqslant 1$. Let us derive a contradiction.

It follows from Remark 3.3 that m ₀+a ₂⩽M+Aa ₁. Then

which implies that a ₁⩾(n+1−Mn)/(nA+1). But a ₂>(n−N)/(B+n−1) by Lemma 3.8. Then

where α(1−M)/A+β⩾1 by assumption. Therefore, we see that

where n⩾2. But A+M>1 and B+N>1 by Lemma 3.2, since a ₁<1 and a ₂<1. Then

but A ²(B+N−1)β⩽α(A+M−1) by assumption. Then

which implies that βA(B+N−1)>α(B−1)(A+M−1). Then

because A ²(B+N−1)β⩽α(A+M−1) by assumption. Then we have α≠0 and A(B−1)<1, which is impossible, because A(B−1)⩾1 by assumption. □

Lemma 3.10

The log pair (2) is Kawamata log terminal at every point of the set

Proof

Suppose that there is a point Q∈F _n such that

but (2) is not Kawamata log terminal at the point Q. Then the log pair

is not Kawamata log terminal at the point Q as well. Then

by Lemma 2.3, because $a_{1}+na_{2}-n+\sum_{j=0}^{n-1}m_{j}<1$ by Lemma 3.9. Then

because m ₀<M+Aa ₁−a ₂ and m ₀<N+Ba ₂−a ₁ by Remark 3.3. We have

because αa ₁+βa ₂⩽1 and AB−1>0. But m ₀>1. Thus, we see that

which contradicts our initial assumptions. □

Lemma 3.11

The log pair (2) is Kawamata log terminal at the point $F_{n}\cap F^{n}_{n-1}$.

Proof

Suppose that (2) is not Kawamata log terminal at $F_{n}\cap F^{n}_{n-1}$. Then the log pair

is not Kawamata log terminal at the point $F_{n}\cap F^{n}_{n-1}$ as well. Then

by Lemma 2.3, because $a_{1}+(n-1)a_{2}-(n-1)+\sum_{j=0}^{n-2}m_{j}<1$. Note that

which implies that m ₀+a ₂<Aa ₁+M. Then

which gives a ₁>(n+1−nM)/(An+1).

Now arguing as in the proof of Lemma 3.9, we obtain a contradiction. □

The assertion of Lemma 3.7 is proved. The assertion of Theorem 1.27 is proved.

4 One Cyclic Singular Point

Let X be a sextic surface in ℙ(1,1,2,3) with canonical singularities such that |Sing(X)|=1, let ω:X→ℙ(1,1,2) be the natural double cover, let R be its ramification curve in ℙ(1,1,2), and suppose that Sing(X) consists of one singular point of type $\mathbb{A}_{m}$, where m∈{1,…,8}.

Theorem 4.1

The following equality holds:

and if lct(X)=2/3, then there is a unique effective ℚ-divisor D on X such that D∼_ℚ−K _X and

By Theorem 1.5, Corollary 1.11, and Remark 1.7, we obtain the following two corollaries.

Corollary 4.2

If m⩽6, then lct _n,2(X)>2/3 for every n∈ℕ.

Corollary 4.3

If m⩽6, then X is Kähler–Einstein.

In the rest of this section, we will prove Theorem 4.1.

Let D be an arbitrary effective ℚ-divisor on the surface X such that

and put μ=c(X,D). To prove Theorem 4.1, it is enough to show that

and if μ=lct(X)=2/3, then D is uniquely defined. Note that lct₁(X)⩾5/6 if m⩾3 (see [30]).

Let us prove Theorem 4.1. By Lemma 2.6, we may assume that m⩾3 and μ<lct₁(X). Then

by Lemma 2.6. Put P=Sing(X).

Let $\pi\colon\bar{X}\to X$ be a minimal resolution, let E ₁,E ₂,…,E _m be π-exceptional curves such that

let C be the curve in |−K _X | such that P∈C, and let $\bar{C}$ be it proper transform on $\bar{X}$. Then

and the curve C is irreducible. We may assume that D≠C, because μ⩾lct₁(X) if D=C.

By Remark 2.1, we may assume that $C\not\subset\mathrm{Supp}(D)$.

Let $\bar{D}$ be the proper transform of the divisor D on the surface $\bar{X}$. Then

where a _i is a non-negative rational number. Then the log pair

$$ \Biggl(\bar{X},\mu\bar{D}+\sum _{i=1}^{m}\mu a_iE_i \Biggr) $$

(3)

is not Kawamata log terminal (by Remark 2.4). On the other hand, we have

where all intersections $\bar{D}\cdot E_{1}, \bar{D}\cdot E_{2}, \ldots, \bar{D}\cdot E_{m}$ are non-negative. Moreover, we have

where the intersection $\bar{D}\cdot\bar{C}$ is non-negative, since $C\not\subset\mathrm{Supp}(D)$ by assumption. Hence, we have

$$ \left\{\begin{array}{l@{\quad}l} \displaystyle a_1\geqslant \frac{a_2}{2}, \\[7pt] a_2\geqslant \displaystyle\frac{a_1+a_3}{2}, \\[7pt] a_3\geqslant \displaystyle\frac{a_2+a_4}{2}, \\[7pt] \vdots \\[7pt] a_{m-1}\geqslant\displaystyle \frac{a_{m-2}+a_m}{2}, \\[7pt] a_m\geqslant\displaystyle\frac{a_{m-1}}{2}, \\[7pt] 1\geqslant a_1+a_m. \\ \end{array} \right. $$

(4)

It should be pointed out that at least one inequality in (4) must be strict, since $\bar{D}\cdot E_{i}>0$ for at least one i∈{1,…,m}, because P∈Supp(D). Then a _i >0 for some i∈{1,…,m}.

Note that a ₁⩾a ₂/2 by (4). Similarly, it follows from (4) that

which implies that a ₂⩾2a ₃/3. Arguing in the same way, we see that

for every k∈{1,…,m−1} (use (4) and induction on k). Using symmetry, we see that

for every k∈{1,…,m−1}. In particular, the inequality a _k >0 holds for every k∈{1,…,m}, since we already know that a _i >0 for some i∈{1,…,m}.

Lemma 4.4

Suppose that μa _i <1 for every i∈{1,…,m}. Then

• there exists a point

  

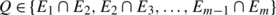
  such that the log pair (3) is not Kawamata log terminal at Q,

• the log pair (3) is Kawamata log terminal outside of the point Q,

• if μ<(m+1)/(2m−2), then Q≠E ₁∩E ₂ and Q≠E _m−1∩E _m .

Proof

It follows from Remark 2.4 and Theorem 2.2 that there is a point $Q\in \bigcup_{i=1}^{m}E_{i}$ such that the log pair (3) is not Kawamata log terminal at Q and is Kawamata log terminal elsewhere.

Suppose that Q∈E ₁ and $Q\not\in E_{2}$. Then

by Lemma 2.3. Taking (4) into account, we get

and adding all these inequalities together we get

which implies that a ₁+a _m >1. However, the latter is impossible, since a ₁+a _m ⩽1 by (4).

We see that if Q∈E ₁, then Q=E ₁∩E ₂. Similarly, we see that Q=E _m−1∩E _m if Q∈E _m .

Suppose that Q∈E _i and $Q\not\in E_{j}$ for every j≠i. Then i≠1 and i≠m. We have

by Lemma 2.3. Taking (4) into account, we get

and adding all these inequalities together we get

which implies that a ₁+a _m >1. However, the latter is impossible, since a ₁+a _m ⩽1 by (4).

Thus, we see that there is k∈{1,…,m−1} such that Q=E _k ∩E _k+1.

Suppose that μ<(m+1)/(2m−2). Let us show that k≠1 and k≠m−1.

Due to symmetry, it is enough to show that k≠1. Recall that m⩾3.

Suppose that k=1. Then Q=E ₁∩E ₂. Take $\bar{\mu}\in\mathbb{Q}$ such that $(m+1)/(2m-2)>\bar{\mu}>\mu$ and

is not Kawamata log terminal at Q and is Kawamata log terminal outside of the point Q. Then

by (4), since a ₁≠0 and a ₂≠0. On the other hand, we have

since $\mu<\bar{\mu}$. Therefore, it follows from Corollary 1.28 that

which implies that a ₂(m−2)>a ₃(m−1), since $\mu<\bar{\mu}$. But we proved earlier that

which is impossible, since a ₂(m−2)>a ₃(m−1). Thus, we see that k≠1. □

If m=3, then it follows from (4) that a ₁⩽3/4, a ₂⩽1, a ₃⩽3/4.

Corollary 4.5

If m=3, then μ⩾lct₁(X)⩾5/6.

Lemma 4.6

Suppose that m=4. Then μ⩾lct₂(X)=4/5.

Proof

There is a unique smooth irreducible curve $\bar{Z}\subset\bar{X}$ such that

and $E_{2}\cap E_{3}\in\bar{Z}$ (cf. the proof of Lemma 6.8). Put $Z=\pi(\bar{Z})$. Then

To complete the proof, it is enough to show that μ⩾4/5. Suppose that μ<4/5.

By Remark 2.1, we may assume that $Z\not\subset\mathrm{Supp}(D)$, because Z is irreducible.

It follows from (4) that a ₁⩽4/5, a ₂⩽6/5, a ₃⩽6/5, a ₄⩽4/5.

Put Q=E ₂∩E ₃. Then it follows from Lemma 4.4 that (3) is not Kawamata log terminal at the point Q and is Kawamata log terminal outside of the point Q. Then

by Lemma 2.3. Similarly, we see that

which implies that a ₂>5/6 and a ₃>5/6.

Let $\xi\colon\tilde{X}\to\bar{X}$ be a blow-up of the point Q, let E be the exceptional curve of the blow-up ξ, and let $\tilde{D}$ be the proper transform of the divisor $\bar{D}$ on the surface $\tilde{X}$. Put $\delta=\mathrm{mult}_{Q}(\bar{D})$.

Let $\tilde{E}_{1}$, $\tilde{E}_{2}$, $\tilde{E}_{3}$, $\tilde{E}_{4}$ be the proper transforms on $\tilde{X}$ of E ₁, E ₂, E ₃, E ₄, respectively. Then

$$ \bigl(\tilde{X},\mu\tilde{D}+\mu a_2\tilde{E}_2+\mu a_3\tilde{E}_3+ (\mu a_2+\mu a_3+\mu \delta-1 )E \bigr)$$

(5)

is not Kawamata log terminal at some point O∈E.

Let $\tilde{Z}$ be the proper transform on $\tilde{X}$ of the curve $\bar{Z}$. Then

which implies that δ+a ₂+a ₃⩽2. We have μa ₂+μa ₃+μδ−1⩽2μ−1⩽3/5, which implies that (5) is Kawamata log terminal outside of the point O by Theorem 2.2. We have

which implies that δ⩽1. If $O\not\in\tilde{E}_{2}\cup\tilde{E}_{3}$, then

by Lemma 2.3. Thus, we see that either $O=\tilde{E}_{2}\cap E$ or $O=\tilde{E}_{3}\cap E$.

Without loss of generality, we may assume that $O=\tilde{E}_{2}\cap E$. By Lemma 2.3, one has

since δ+a ₂+a ₃⩽2 and a ₃>5/6. The obtained contradiction concludes the proof. □

Let τ be a biregular involution of the surface $\bar{X}$ that is induced by the double cover ω.

Lemma 4.7

Suppose that m=5. Then there exists a unique curve Z∈|−2K _X | such that

and either D=Z/2 or μ>2/3.

Proof

Let $\alpha\colon\bar{X}\to\breve{X}$ be a contraction of the curves $\bar{C}$, E ₅, E ₄, E ₃. Then

and $\breve{X}$ is a smooth del Pezzo surface such that $K_{\breve{X}}^{2}=5$, which implies that there is a smooth irreducible rational curve $\breve{L}_{2}$ on the surface $\breve{X}$ such that $\breve{L}_{2}\cdot\alpha(E_{2})=1$ and $\breve{L}_{2}\cdot \breve{L}_{2}=-1$.

Let $\bar{L}_{2}$ be the proper transform of the curve $\breve{L}_{2}$ on the surface $\bar{X}$. Then $\bar{L}_{2}\cdot \bar{L}_{2}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{2}=E_{3}\cdot \bar{L}_{2}=E_{4}\cdot \bar{L}_{2}=E_{5}\cdot \bar{L}_{2}=\bar{C}\cdot\bar{L}_{2}=0$.

Let $\beta\colon\bar{X}\to\check{X}$ be a contraction of the curves $\bar{L}_{2}$, $\bar{C}$, E ₅, E ₄. Then

and $\check{X}$ is a smooth del Pezzo surface such that $K_{\check{X}}^{2}=5$, which implies that there is an irreducible smooth curve $\check{L}_{3}\subset\check{X}$ such that $\check{L}_{3}\cdot\beta(E_{3})=1$ and $\check{L}_{3}\cdot\check{L}_{3}=-1$ (cf. the proof of Lemma 6.7).

Let $\bar{L}_{3}$ be the proper transform of the curve $\check{L}_{3}$ on the surface $\bar{X}$. Then $\bar{L}_{3}\cdot \bar{L}_{3}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{3}=E_{2}\cdot \bar{L}_{3}=E_{4}\cdot \bar{L}_{3}=E_{5}\cdot \bar{L}_{3}=\bar{C}\cdot\bar{L}_{3}=0$.

If $\tau(\bar{L}_{3})=\bar{L}_{3}$, then $2\pi(\bar{L}_{3})\sim -2K_{X}$, but $\pi(\bar{L}_{3})$ is not a Cartier divisor.

Put $Z=\pi(\bar{L}_{3}+\tau(\bar{L}_{3}))$. Then Z∼−2K _X and c(X,Z)=1/3. We see that lct₂(X)⩽2/3.

Suppose that D≠Z/2. To complete the proof, it is enough to show that μ>2/3.

Suppose that μ⩽2/3. Let us derive a contradiction. It follows from (4) that

By Remark 2.1, without loss of generality we may assume that $\pi(\bar{L}_{3})\not\subset\mathrm{Supp}(D)$. Then

which implies that a ₃⩽1.

Put Q=E ₂∩E ₃. By Lemma 4.4, we may assume that (3) is not Kawamata log terminal at the point Q and is Kawamata log terminal outside of the point Q. Then

by Lemma 2.3, which implies that a ₃>9/8 by (4). But a ₃⩽1. □

Lemma 4.8

Suppose that m=6. Then there exists a unique curve Z∈|−2K _X | such that

and either D=Z/2 or μ>2/3.

Proof

Let $\alpha\colon\bar{X}\to\breve{X}$ be a contraction of the curves $\bar{C}$, E ₆, E ₅, E ₄, and E ₃. Then

and $\breve{X}$ is a smooth del Pezzo surface such that $K_{\breve{X}}^{2}=6$, which implies that there is a smooth irreducible rational curve $\breve{L}_{2}$ on the surface $\breve{X}$ such that $\breve{L}_{2}\cdot\alpha(E_{2})=1$ and $\breve{L}_{2}\cdot \breve{L}_{2}=-1$.

Let $\bar{L}_{2}$ be the proper transform of the curve $\breve{L}_{2}$ on the surface $\bar{X}$. Then $\bar{L}_{2}\cdot \bar{L}_{2}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{2}=E_{3}\cdot \bar{L}_{2}=E_{4}\cdot \bar{L}_{2}=E_{5}\cdot \bar{L}_{2}=E_{6}\cdot \bar{L}_{2}=\bar{C}\cdot\bar{L}_{2}=0$.

Let $\beta\colon\bar{X}\to\check{X}$ be a contraction of the curves $\bar{L}_{2}$, $\bar{C}$, E ₆, E ₅, and E ₄. Then

and $\check{X}$ is a smooth del Pezzo surface such that $K_{\check{X}}^{2}=6$, which implies that there are irreducible smooth rational curves $\check{L}_{3}$ and $\check{L}_{2}^{\prime}$ on the surface $\check{X}$ such that

and $\check{L}_{3}\cdot\check{L}_{3}=\check{L}_{2}^{\prime}\cdot\check{L}_{2}^{\prime}=-1$. Let $\bar{L}_{3}$ and $\bar{L}_{2}^{\prime}$ be the proper transforms of the curves $\check{L}_{3}$ and $\check{L}_{2}^{\prime}$ on the surface $\bar{X}$, respectively. Then $\bar{L}_{3}\cdot \bar{L}_{3}=\bar{L}_{2}^{\prime}\cdot \bar{L}_{2}^{\prime}=-1$ and

which implies that $\bar{C}\cdot\bar{L}_{3}=\bar{C}\cdot\bar{L}_{2}^{\prime}=0$, and $E_{i}\cdot \bar{L}_{3}=E_{j}\cdot \bar{L}_{2}^{\prime}=0$ for every i≠3 and j≠2,

Put $\bar{L}_{4}=\tau(\bar{L}_{3})$, $\bar{L}_{5}=\tau(\bar{L}_{2})$, $\bar{L}_{5}^{\prime}=\tau(\bar{L}_{2}^{\prime})$. Then $\bar{C}\cdot\bar{L}_{4}=\bar{C}\cdot\bar{L}_{5}=\bar{C}\cdot\bar{L}_{5}^{\prime}=0$ and

which implies that $E_{i}\cdot\bar{L}_{5}=E_{i}\cdot\bar{L}_{5}^{\prime}=E_{j}\cdot \bar{L}_{4}=0$ for every i≠5 and j≠4.

Put $L_{3}=\pi(\bar{L}_{3})$, $L_{4}=\pi(\bar{L}_{4})$, $L_{2}=\pi(\bar{L}_{2})$, $L_{2}^{\prime}=\pi(\bar{L}_{2}^{\prime})$, $L_{5}=\pi(\bar{L}_{5})$, $L_{5}^{\prime}=\pi(\bar{L}_{5}^{\prime})$. Then

and c(X,L ₃+L ₄)=1/3, which implies that lct₂(X)⩽2/3.

Note that $\mathrm{c}(X,L_{2}+L_{5})=\mathrm{c}(X,L_{2}^{\prime}+L_{5}^{\prime})=1/2$.

Suppose that D≠(L ₃+L ₄)/2. To complete the proof, it is enough to show that μ>2/3.

Suppose that μ⩽2/3. Let us derive a contradiction.

It follows from (4) that a ₁⩽6/7, a ₂⩽10/7, a ₃⩽12/7, a ₄⩽12/7, a ₅⩽10/7, a ₆⩽6/7.

By Remark 2.1, without loss of generality we may assume that $\bar{L}_{4}\not\subset\mathrm{Supp}(D)$. Then

which gives us a ₄⩽1. Similarly, we may assume that either $\bar{L}_{2}\not\subset\mathrm{Supp}(D)$ or $\bar{L}_{5}\nobreak\not\subset\nobreak\mathrm{Supp}(D)$, which implies that either a ₂⩽1 or a ₅⩽1, respectively.

Let us show that $L_{2}+L_{2}^{\prime}+L_{3}\sim -3K_{X}$. We can easily see that

which implies that $L_{2}+L_{2}^{\prime}+L_{3}\sim_{\mathbb{Q}} -3K_{X}$, since Pic(X)≅ℤ³ and

but $L_{2}+L_{2}^{\prime}+L_{3}$ is a Cartier divisor, which implies that $L_{2}+L_{2}^{\prime}+L_{3}\sim -3K_{X}$.

Since $\mathrm{c}(X,L_{2}+L_{2}^{\prime}+L_{3})=1/4$, we may assume that Supp(D) does not contain at least one curve among L ₂, $L_{2}^{\prime}$, and L ₃ by Remark 2.1, which implies that either a ₂⩽1 or a ₃⩽1.

It follows from (4) and a ₄⩽2 that μa _i <1 for every i. By Lemma 4.4, there exists a point

such that (3) is not Kawamata log terminal at the point $Q\in\bar{X}$, but it is Kawamata log terminal elsewhere. Take k∈{2,3,4} such that Q=E _k ∩E _k+1. It follows from Lemma 2.3 that

which is impossible by (4), since a ₄⩽1, and either a ₂⩽1 or a ₃⩽1. □

Lemma 4.9

Suppose that m=7. Then the following conditions are equivalent:

• the curve R is irreducible,

• the surface $\bar{X}$ contains an irreducible curve $\bar{L}_{4}$ such that $\bar{L}_{4}\cdot \bar{L}_{4}=-1$ and $\bar{L}_{4}\cdot E_{4}=1$.

• the surface $\bar{X}$ contains an irreducible curve $\bar{L}_{4}$ such that $\bar{L}_{4}\cdot \bar{L}_{4}=-1$, $\bar{L}_{4}\cdot E_{4}=1$ and

  

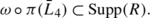
Proof

Suppose that $\bar{X}$ has an irreducible curve $\bar{L}_{4}$ such that $\bar{L}_{4}\cdot \bar{L}_{4}=-1$ and $\bar{L}_{4}\cdot E_{4}=1$. Then

where $L_{4}=\pi(\bar{L}_{4})$. Then $\tau(\bar{L}_{4})=\bar{L}_{4}$ and ω(L ₄)⊂Supp(R), because

Suppose now that the curve R is reducible. Let us show that the surface $\bar{X}$ contains an irreducible curve $\bar{L}_{4}$ such that $\bar{L}_{4}\cdot \bar{L}_{4}=-1$ and $\bar{L}_{4}\cdot E_{4}=1$.

Let $\eta\colon\bar{X}\to\bar{X}^{\prime}$ be a contraction of the curve $\bar{C}$. Then there is a commutative diagram

where π′ is a minimal resolution, ϕ is an anticanonical embedding, ψ is a projection from ϕ∘ω(P), and ω′ is a double cover branched at ψ∘ϕ(R). Note that X′ is a del Pezzo surface and $K_{X^{\prime}}^{2}=2$.

The morphism π′ contracts the smooth curves η(E ₂), η(E ₃), η(E ₄), η(E ₅), and η(E ₆). But

and X′ has a singularity of type $\mathbb{A}_{5}$ at the point η(E ₂). Put P′=η(E ₂).

Put R′=ψ∘ϕ(R). Then R′ is reducible, since R is reducible.

Since $\mathrm{Sing}(\mathbb{P}(1,1,2))\not\in R$, one of the following cases holds:

• either ϕ(R) is a union of a smooth conic and an irreducible quartic,

• or the curve ϕ(R) is a union of three different smooth conics.

The case when the curve ϕ(R) consists of a union of three different smooth conics is impossible, since the surface X′ has a singularity of type $\mathbb{A}_{5}$ at the point P′=Sing(X′).

We see that the curve ϕ(R) is a union of a smooth conic and an irreducible quartic curve, which easily implies that R′ is a union of a line L and an irreducible cubic curve Z. Then

because X′ has a singularity of type $\mathbb{A}_{5}$ at the point P′. Then $\bar{X}$ contains a curve $\bar{L}_{4}$ such that

and $\bar{L}_{4}$ is irreducible. Then $\bar{L}_{4}\cdot \bar{L}_{4}=-1$ and $\bar{L}_{4}\cdot E_{4}=1$. □

The proof of Lemma 4.9 can be simplified using the results obtained in [31, Sect. 2].

Lemma 4.10

Suppose that m=7 and R is irreducible. Then μ⩾lct₃(X)=3/5.

Proof

Arguing as in the proofs of Lemmas 4.7 and 4.8, we see that there is an irreducible smooth rational curve $\bar{L}_{2}$ on the surface $\bar{X}$ such that $\bar{L}_{2}\cdot \bar{L}_{2}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{2}=E_{3}\cdot \bar{L}_{2}=E_{4}\cdot \bar{L}_{2}=E_{5}\cdot \bar{L}_{2}=E_{6}\cdot \bar{L}_{2}=E_{7}\cdot \bar{L}_{2}=\bar{C}\cdot\bar{L}_{2}=0$.

Put $\bar{L}_{5}=\tau(\bar{L}_{2})$. Then $\bar{L}_{5}\cdot \bar{L}_{5}=-1$ and $-K_{\bar{X}}\cdot \bar{L}_{5}=E_{5}\cdot\bar{L}_{5}=1$, which implies that

Since the branch curve R is reducible by Lemma 4.9, one can show that there exists an irreducible smooth rational curve $\bar{L}_{3}$ on the surface $\bar{X}$ such that $\bar{L}_{3}\cdot \bar{L}_{3}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{3}=E_{2}\cdot \bar{L}_{3}=E_{4}\cdot \bar{L}_{3}=E_{5}\cdot \bar{L}_{3}=E_{6}\cdot \bar{L}_{3}=E_{7}\cdot \bar{L}_{3}=\bar{C}\cdot\bar{L}_{3}=0$.

Put $\bar{L}_{6}=\tau(\bar{L}_{2})$, $\bar{L}_{5}=\tau(\bar{L}_{3})$, $L_{2}=\pi(\bar{L}_{2})$, $L_{3}=\pi(\bar{L}_{4})$, $L_{5}=\pi(\bar{L}_{5})$ and $L_{6}=\pi(\bar{L}_{6})$. Then

which implies that L ₂+2L ₃∼−3K _X . Indeed, we have L ₂+2L ₃∼_ℚ−3K _X , since

and Pic(X)≅ℤ³. But L ₂+2L ₃ is a Cartier divisor, which implies that L ₂+2L ₃∼−3K _X .

We have c(X,L ₂+2L ₃)=3/15 and L ₂+2L ₃∼−3K _X , which implies that lct₃(X)⩽3/5.

To complete the proof, it is enough to show that μ⩾3/5.

Suppose that μ<3/5. Let us derive a contradiction.

By Remark 2.1, we may assume that the support of the divisor $\bar{D}$ does not contain at least one component of every curve $\bar{L}_{2}+\bar{L}_{6}$, $\bar{L}_{2}+2\bar{L}_{3}$, $\bar{L}_{3}+\bar{L}_{5}$. But

which implies that a _i ⩽1 if $\bar{L}_{i}\not\subset\mathrm{Supp}(\bar{D})$. Therefore, either a ₃⩽1 or a ₂⩽1 and a ₅⩽1.

If a ₃⩽1, then it follows from (4) that

If a ₂⩽1 and a ₅⩽1, then it follows from (4) that

By Lemma 4.4, there exists k∈{2,3,4,5} such that (3) is not Kawamata log terminal at the point E _k ∩E _k+1 and is Kawamata log terminal outside of E _k ∩E _k+1.

Put Q=E _k ∩E _k+1. Then it follows from Lemma 2.3 that

which is impossible by (4), since we assume that either a ₃⩽1 or a ₂⩽1 and a ₅⩽1. □

Lemma 4.11

Suppose that m=7 and R is reducible. Then μ⩾lct₂(X)=1/2.

Proof

By Lemma 4.9, the surface X contains an irreducible curve $\bar{L}_{4}$ such that

and $-\bar{L}_{4}\cdot \bar{L}_{4}=\bar{L}_{4}\cdot E_{4}=1$. Then $-K_{\bar{X}}\cdot\bar{L}_{4}=1$, which implies that

Put $L_{4}=\pi(\bar{L}_{4})$. Then 2L ₄∼−2K _X and

which implies that lct₂(X)⩽c(X,L ₄)=1/2.

To complete the proof, it is enough to show that μ⩾1/2.

Suppose that μ<1/2. Let us derive a contradiction.

By Remark 2.1, we may assume that $L_{4}\not\subset\mathrm{Supp}(D)$. Then

which implies that a ₄⩽1. Thus, it follows from (4) that

It follows from Lemma 4.4 that there exists a point

such that $\mathrm{LCS}(\bar{X},\mu\bar{D}+\sum_{i=1}^{7}\mu a_{i}E_{i})=Q$.

Without loss of generality, we may assume that either Q=E ₂∩E ₃ or Q=E ₃∩E ₄.

If Q=E ₃∩E ₄, then it follows from Lemma 2.3 that

which together with (4) imply that a ₄>1, which is a contradiction.

If Q=E ₂∩E ₃, then it follows from Lemma 2.3 that

which together with (4) immediately leads to a contradiction. □

Lemma 4.12

Suppose that m=8. Then μ⩾lct₃(X)=1/2.

Proof

Arguing as in the proofs of Lemmas 4.7 and 4.8, we see that there is an irreducible smooth rational curve $\bar{L}_{3}$ on the surface $\bar{X}$ such that $\bar{L}_{3}\cdot \bar{L}_{3}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{3}=E_{2}\cdot \bar{L}_{3}=E_{4}\cdot \bar{L}_{3}=E_{5}\cdot \bar{L}_{3}=E_{6}\cdot \bar{L}_{3}=E_{7}\cdot \bar{L}_{3}=\bar{C}\cdot\bar{L}_{3}=0$.

Put $\bar{L}_{6}=\tau(\bar{L}_{3})$. Then $\bar{L}_{6}\cdot \bar{L}_{6}=-1$ and $-K_{\bar{X}}\cdot \bar{L}_{6}=E_{6}\cdot\bar{L}_{6}=1$, which implies that

Put $L_{3}=\pi(\bar{L}_{3})$ and $L_{6}=\pi(\bar{L}_{6})$. Then 3L ₃∼3L ₆∼−3K _X . On the other hand, we have

which implies c(X,L ₃)=c(X,L ₆)=1/2. Then lct₃(X)⩽1/2.

To complete the proof, it is enough to show that μ⩾1/2.

Suppose that μ<1/2. Let us derive a contradiction.

By Remark 2.1, we may assume that $\mathrm{Supp}(\bar{D})$ does not contain $\bar{L}_{3}$ and $\bar{L}_{6}$. Then

which implies that a ₃⩽1. Similarly, we have a ₆⩽1. Then it follows from (4) that

By Lemma 4.4, there exists k∈{2,3,4,5,6} such that (3) is not Kawamata log terminal at the point E _k ∩E _k+1 and is Kawamata log terminal outside of the point E _k ∩E _k+1.

Put Q=E _k ∩E _k+1. Then it follows from Lemma 2.3 that

which is impossible by (4), since a ₃⩽1 and a ₆⩽1. □

The assertion of Theorem 4.1 is proved.

5 One Non-Cyclic Singular Point

Let X be a sextic surface in ℙ(1,1,2,3) with canonical singularities such that |Sing(X)|=1, and Sing(X) consists of a singular point of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{D}_{7}$, $\mathbb{D}_{8}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$.

Theorem 5.1

The following equality holds:

Corollary 5.2

The inequality lct(X)⩽1/2 holds.

In the rest of this section, we will prove Theorem 5.1.

Let D be an effective ℚ-divisor on X such that D∼_ℚ−K _X . We must show that

To prove Theorem 5.1, put μ=c(X,D).

Suppose that μ<lct₁(X). Then LCS(X,μD)=Sing(X) by Lemma 2.6. Put P=Sing(X).

Let $\pi\colon\bar{X}\to X$ be a minimal resolution, let E ₁,E ₂,…,E _m be irreducible π-exceptional curves, let C be the curve in |−K _X | such that P∈C, and let $\bar{C}$ be its proper transform on $\bar{X}$. Then

where n _i ∈ℕ. Without loss of generality, we may assume that E ₃⋅∑ _i≠3 E _i =3. Then

By Remark 2.1, we may assume that $C\not\subset\mathrm{Supp}(D)$, since the curve C is irreducible.

Let $\bar{D}$ be the proper transform of the divisor D on the surface $\bar{X}$. Then

where a _i is a non-negative rational number. Then

which implies that $(\bar{X},\mu\bar{D}+\sum_{i=1}^{m}\mu a_{i}E_{i})$ is not Kawamata log terminal (see Remark 2.4).

Lemma 5.3

The equality μa ₃=1 holds.

Proof

The equality μa ₃=1 follows from Lemma 2.5. □

Lemma 5.4

Suppose that P is not a point of type $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$. Then

and P is either a point of type $\mathbb{D}_{7}$ or is a point of type $\mathbb{D}_{8}$.

Proof

Without loss of generality, we may assume that the diagram

shows how the π-exceptional curves intersect each other. Then

which implies that $\bar{C}\cdot E_{m-1}=1$ and $\bar{C}\cdot E_{i}=0\iff i\ne m-1$. Then

$$ \left\{\begin{aligned} &1-a_{m-1}=\bar{D}\cdot \bar{C}\geqslant 0, \\ &2a_1-a_3=\bar{D}\cdot E_{1}\geqslant 0, \\ &2a_2-a_3=\bar{D}\cdot E_{2}\geqslant 0, \\ &2a_3-a_1-a_2-a_3=\bar{D}\cdot E_{3}\geqslant 0, \\[-3pt] &\vdots \\[-3pt] &2a_{m-1}-a_{m-2}-a_m=\bar{D}\cdot E_{m-1}\geqslant 0, \\ &2a_m-a_{m-1}=\bar{D}\cdot E_{m}\geqslant 0, \\ \end{aligned} \right. $$

(6)

which easily implies that a ₃⩽2 if m⩽6. But μa ₃=1 and μ<lct₁(X)=1/2 by Lemma 5.3, which implies that either m=7 or m=8.

Arguing as in the proofs of Lemmas 4.7 and 4.8, we may assume that there is an irreducible smooth rational curve $\bar{L}_{1}$ on the surface $\bar{X}$ such that $\bar{L}_{1}\cdot \bar{L}_{1}=-1$ and

which implies that $\bar{C}\cdot\bar{L}_{1}=0$ and $E_{i}\cdot \bar{L}_{1}=0\iff i\ne 1$.

Let ω:X→ℙ(1,1,2) be the natural double cover given by |−2K _X |, and let τ be a biregular involution of the surface $\bar{X}$ that is induced by ω. Put $\bar{L}_{2}=\tau(\bar{L}_{1})$. If m=7, then

and $\bar{L}_{2}\cdot \bar{L}_{2}=-1$, which implies that $\bar{C}\cdot\bar{L}_{2}=0$ and $E_{i}\cdot \bar{L}_{2}=0\iff i\ne 2$.

Put $L_{1}=\pi(\bar{L}_{1})$ and $L_{2}=\pi(\bar{L}_{2})$. Then L ₁+L ₂∼−2K _X . If m=7, then

which implies that c(X,L ₁+L ₂)=1/5 and lct₂(X)⩽2/5. If m=7, then

by (6). But μa ₃=1 by Lemma 5.3. Then μ⩾2/5 if m=7, which is exactly what we need.

We may assume that m=8. Then $\bar{L}_{2}=\bar{L}_{1}$ and

which implies that lct₂(X)⩽c(X,L ₁)=1/3. But a ₃⩽1/3 by (6) and μa ₃=1 by Lemma 5.3, which implies that μ⩾1/3, which completes the proof since lct₂(X)⩾lct(X). □

To complete the proof of Theorem 5.1, we may assume that P is a point of type $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$.

Without loss of generality, we may assume that the diagram

shows how the π-exceptional curves intersect each other. It is well known (cf. [29, 30]) that

• if m=6, then $\bar{C}\cdot E_{4}=1$, which implies that and $\bar{C}\cdot E_{i}=0\iff i\ne 4$,

• if m=7, then $\bar{C}\cdot E_{1}=1$, which implies that and $\bar{C}\cdot E_{i}=0\iff i\ne 1$,

• if m=8, then $\bar{C}\cdot E_{8}=1$, which implies that and $\bar{C}\cdot E_{i}=0\iff i\ne 8$.

Put k=4 if m=6, put k=1 if m=7, put k=8 if m=8. Then

$$ \left\{\begin{aligned} &1-a_{k}=\bar{D}\cdot \bar{C}\geqslant 0, \\ &2a_1-a_3=\bar{D}\cdot E_{1}\geqslant 0, \\ &2a_2-a_3-a_1=\bar{D}\cdot E_{2} \geqslant 0, \\ &2a_3-a_2-a_4-a_5=\bar{D}\cdot E_{3}\geqslant 0, \\ &2a_4-a_3=\bar{D}\cdot E_{4}\geqslant 0, \\ &2a_5-a_3-a_6=\bar{D}\cdot E_{5}\geqslant 0, \\ &\vdots \\ &2a_{m-1}-a_{m-2}-a_m=\bar{D}\cdot E_{m-1}\geqslant 0, \\ &2a_m-a_{m-1}=\bar{D}\cdot E_{m}\geqslant 0, \\ \end{aligned} \right. $$

(7)

which implies that a ₃<n ₃. But n ₃=1/lct₁(X) and μa ₃=1 by Lemma 5.3. Then μ⩾lct₁(X).

The assertion of Theorem 5.1 is proved.

6 Many Singular Points

Let X be a sextic surface in ℙ(1,1,2,3) with canonical singularities such that |Sing(X)|⩾2.

Theorem 6.1

The following equality holds:

and if there exists an effective ℚ-divisor D on the surface X such that D∼_ℚ−K _X and

then either D is an irreducible curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$, or the divisor D is uniquely defined and it can be explicitly described.

Let D be an arbitrary effective ℚ-divisor on the surface X such that

and put μ=c(X,D). To prove Theorem 6.1, it is enough to show that

and if μ=lct(X)=2/3, then we have the following two possibilities:

• either D is a curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$,

• or the divisor D is uniquely defined and it can be explicitly described.

Lemma 6.2

If Sing(X) has a point of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$, then μ⩾lct₁(X).

Proof

Suppose that Sing(X) has a point of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$, but μ<lct₁(X). Then

and LCS(X,μD) consists of a point in Sing(X) that is not of type $\mathbb{A}_{1}$ or $\mathbb{A}_{2}$ by Lemma 2.6.

If the locus LCS(X,μD) is a singular point of the surface X of type $\mathbb{D}_{4}$, $\mathbb{D}_{5}$, $\mathbb{D}_{6}$, $\mathbb{E}_{6}$, $\mathbb{E}_{7}$, or $\mathbb{E}_{8}$, then arguing as in the proof of Theorem 5.1, we immediately obtain a contradiction.

By Remark 1.21, the locus LCS(X,μD) must be a singular point of the surface X of type $\mathbb{A}_{3}$, and we can easily obtain a contradiction arguing as in the proof of Corollary 4.5. □

Lemma 6.3

Suppose that Sing(X) consists of points of type $\mathbb{A}_{1}$, $\mathbb{A}_{2}$, or $\mathbb{A}_{3}$. Then μ⩾lct₁(X). If

then D is a curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$.

Proof

This follows from Lemma 2.6 and the proof of Corollary 4.5. □

By Remark 1.21 and Lemmas 6.2 and 6.2, we may assume that

which implies that there is a point P∈Sing(X) that is a point of type $\mathbb{A}_{m}$ for m∈{4,5,6,7}.

Let $\pi\colon\bar{X}\to X$ be a minimal resolution, let E ₁,E ₂,…,E _m be π-exceptional curves such that

and π(E _i )=P for every i∈{1,…,m}, let C be the unique curve in |−K _X | such that P∈C, and let $\bar{C}$ be the proper transform of the curve C on the surface $\bar{X}$. Then

and $\bar{C}\cdot E_{2}=\bar{C}\cdot E_{3}=\cdots=\bar{C}\cdot E_{m-1}=0$. Note that $\bar{C}\cong\mathbb{P}^{1}$ and $\bar{C}\cdot\bar{C}=-1$.

Let $\bar{D}$ be the proper transform of D on the surface $\bar{X}$. Then

where a _i is a non-negative rational number. Then

$$ \left\{\begin{aligned} &1-a_1-a_m= \bar{D}\cdot\bar{C}\geqslant 0, \\ &2a_1 - a_2=\bar{D}\cdot E_{1}\geqslant 0, \\ &\vdots \\ &2a_{m-1}-a_{m-2}-a_m=\bar{D}\cdot E_{m-1}\geqslant 0, \\ &2a_m - a_{m-1}=\bar{D}\cdot E_{m}\geqslant 0. \\ \end{aligned} \right. $$

(8)

Let $\eta\colon\bar{X}\to\bar{X}^{\prime}$ be a contraction of the curve $\bar{C}$. Then there is a commutative diagram

where ω and ω′ are natural double covers π′ is a minimal resolution, ϕ is an anticanonical embedding, and ψ is a projection from ϕ∘ω(P). Put P′=η(E ₂). Then P′∈Sing(X′).

Remark 6.4

The birational morphism π′ contracts the smooth curves η(E ₂),η(E ₃),…,η(E _m−1), and π′∘η contracts all π-exceptional curves that are different from the curves E ₁,E ₂,…,E _m .

Let R be the branch curve in ℙ(1,1,2) of the double cover ω. Put R′=ψ∘ϕ(R).

Lemma 6.5

Suppose that m=7. Then μ⩾lct₂(X)=1/2.

Proof

Let $\alpha\colon\bar{X}\to\breve{X}$ be a contraction of the irreducible curves $\bar{C}$, E ₇, E ₆, E ₅, E ₄, E ₃, and E ₂, and let F be the π-exceptional curve such that π(F) is a point of type $\mathbb{A}_{1}$. Then

Let $\breve{L}_{2}$ be the fiber of the projection $\breve{X}\to\mathbb{P}^{1}$ such that $\alpha(\bar{C})\in\breve{L}_{2}$, and let $\bar{L}_{2}$ be the proper transform of the curve $\breve{L}_{2}$ on the surface $\bar{X}$ via α. Then $\bar{L}_{2}\cdot \bar{L}_{2}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{2}=E_{3}\cdot \bar{L}_{2}=E_{4}\cdot \bar{L}_{2}=E_{5}\cdot \bar{L}_{2}=E_{6}\cdot \bar{L}_{2}=E_{7}\cdot \bar{L}_{2}=\bar{C}\cdot\bar{L}_{2}=0$.

Let $\beta\colon\bar{X}\to\check{X}$ be a contraction of the curves $\bar{L}_{2}$, E ₂, $\bar{C}$, E ₇, E ₆, E ₅, E ₄. Then

and $\check{X}$ is a smooth del Pezzo surface such that $K_{\check{X}}^{2}=8$. Then $\check{X}\cong\mathbb{P}^{1}\times \mathbb{P}^{1}$.

Let $\check{L}_{4}$ be the curve in |β(F)| such that $\beta(E_{4})\in \check{L}_{4}$, and let $\bar{L}_{3}$ be its proper transform on the surface $\bar{X}$ via β. Then one can easily check that $\bar{L}_{4}\cdot \bar{L}_{4}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{4}=E_{2}\cdot \bar{L}_{4}=E_{3}\cdot \bar{L}_{4}=E_{5}\cdot \bar{L}_{4}=E_{6}\cdot \bar{L}_{4}=E_{7}\cdot \bar{L}_{4}=\bar{C}\cdot\bar{L}_{4}=F\cdot\bar{L}_{4}=0$.

Put $L_{4}=\pi(\bar{L}_{4})$. Then one can easily check that

which implies that c(X,L ₄)=1/2. But 2L ₄∼−2K _X , which implies that lct₂(X)⩽1/2.

Arguing as in the proof of Lemma 4.9, we see that ω(L ₄)⊂Supp(R).

Arguing as in the proof of Lemma 4.11 and using (8), we see that μ⩾lct₂(X)=1/2. □

Lemma 6.6

Suppose that m=6. Then μ⩾lct₂(X)=2/3, and if μ=2/3, then

• either D is a curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$,

• or the divisor D is uniquely defined and can be explicitly described.

Proof

Let $\alpha\colon\bar{X}\to\breve{X}$ be a contraction of the curves $\bar{C}$, E ₆, E ₅, E ₄, E ₃, E ₂. Then $\breve{X}$ is a smooth surface such that $K_{\breve{X}}^{2}=7$, and −K _X is nef. There is a birational morphism $\gamma\colon\breve{X}\to\hat{X}$ such that

and γ is a blow-down of a smooth irreducible rational curve that does not contain the point $\alpha(\bar{C})$.

Let $\hat{L}_{2}$ be the fiber of the projection $\hat{X}\to\mathbb{P}^{1}$ such that $\gamma\circ\alpha(\bar{C})\in\hat{L}_{2}$, and let $\bar{L}_{2}$ be the proper transform of the curve $\hat{L}_{2}$ on the surface $\bar{X}$ via γ∘α. Then $\bar{L}_{2}\cdot \bar{L}_{2}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{2}=E_{3}\cdot \bar{L}_{2}=E_{4}\cdot \bar{L}_{2}=E_{5}\cdot \bar{L}_{2}=E_{6}\cdot \bar{L}_{2}=\bar{C}\cdot\bar{L}_{2}=0$.

Let $\beta\colon\bar{X}\to\check{X}$ be a contraction of the curves $\bar{L}_{2}$, $\bar{C}$, E ₆, E ₅, E ₄, and let F be the π-exceptional curve such that π(F) is a point of type $\mathbb{A}_{1}$. Then

and $\check{X}$ is a smooth del Pezzo surface such that $K_{\check{X}}^{2}=6$. Thus, there exists an irreducible smooth rational curve $\check{L}_{3}$ on the surface $\check{X}$ such that $\check{L}_{3}\cdot\check{L}_{3}=-1$, $\check{L}_{3}\cdot\beta(E_{3})=1$, and $\check{L}_{3}\cdot\beta(F)=0$.

Let $\bar{L}_{3}$ be the proper transform of the curve $\check{L}_{3}$ on the surface $\bar{X}$. Then $\bar{L}_{3}\cdot \bar{L}_{3}=-1$ and

which implies that $E_{1}\cdot \bar{L}_{3}=E_{2}\cdot \bar{L}_{3}=E_{4}\cdot \bar{L}_{3}=E_{5}\cdot \bar{L}_{3}=E_{6}\cdot \bar{L}_{3}=\bar{C}\cdot\bar{L}_{3}=F\cdot \bar{L}_{3}=0$.

Put $\bar{L}_{4}=\tau(\bar{L}_{3})$ and $\bar{L}_{5}=\tau(\bar{L}_{2})$. Then $\bar{C}\cdot\bar{L}_{4}=\bar{C}\cdot\bar{L}_{5}=0$ and

which implies that $E_{i}\cdot\bar{L}_{5}=E_{j}\cdot \bar{L}_{4}=0$ for every i≠5 and j≠4.

Put $L_{3}=\pi(\bar{L}_{3})$, $L_{4}=\pi(\bar{L}_{4})$, $L_{2}=\pi(\bar{L}_{2})$ and $L_{5}=\pi(\bar{L}_{5})$. Then

which implies that c(X,L ₃+L ₄)=1/3 and c(X,L ₂+L ₅)=1/2. Then lct₂(X)⩽2/3. But

which implies that c(X,2L ₂+L ₃)=1/4. Then 2L ₂+L ₃∼_ℚ−3K _X , since Pic(X)≅ℤ² and

but 2L ₂+L ₃ is a Cartier divisor, which implies that 2L ₂+L ₃∼−3K _X .

If D is not a curve in |−K _X | and D≠(L ₃+L ₄)/2, then arguing as in the proof of Lemma 4.8, we easily see that μ>2/3, since we can use (8). The lemma is proved (see Example 1.26). □

Lemma 6.7

Suppose that m=5. Then μ⩾lct₂(X)=2/3, and if μ=2/3, then

• either D is a curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$,

• or the divisor D is uniquely defined and can be explicitly described.

Proof

The curve R′ has an ordinary tacnodal singularity at the point ω′(P′), which implies that there exists a line L′⊂ℙ² such that either L′⊂Supp(R′) or $L^{\prime}\not\subset\mathrm{Supp}(R^{\prime})$ and

There are irreducible smooth rational curves $L^{\prime}_{3}$ and $L^{\prime}_{4}$ on the surface X′ such that

and $L^{\prime}_{3}=L^{\prime}_{4}\iff L^{\prime}\subset\mathrm{Supp}(R^{\prime})$. Note that neither $L^{\prime}_{3}$ nor $L^{\prime}_{4}$ contains a point in Sing(X′)∖R′.

Let $\bar{L}^{\prime}_{3}$ be the proper transform of the curve $L^{\prime}_{3}$ on the surface $\bar{X}^{\prime}$. Then

and $\bar{L}^{\prime}_{3}\cdot\eta(E_{3})=1$. Let $\bar{L}^{\prime}_{4}$ be the proper transform of the curve $L^{\prime}_{4}$ on the surface $\bar{X}^{\prime}$. Then

and $\bar{L}^{\prime}_{4}\cdot\eta(E_{3})=1$. One can also check that $\bar{L}^{\prime}_{3}\cap\bar{L}^{\prime}_{4}=\varnothing$ if $\bar{L}^{\prime}_{3}\ne\bar{L}^{\prime}_{4}$.

Let $\bar{L}_{3}$ and $\bar{L}_{4}$ be the proper transforms of the curves $\bar{L}^{\prime}_{3}$ and $\bar{L}^{\prime}_{4}$ on the surface $\bar{X}$, respectively, and let us put $L_{3}=\pi(\bar{L}_{3})$ and $L_{4}=\pi(\bar{L}_{4})$. Then

and $\mathrm{c}(X, \bar{L}_{3}+\bar{L}_{4})=1/3$, which implies that lct₂(X)⩽2/3.

If $D\ne (\bar{L}_{3}+\bar{L}_{4})/2$, then (8), the proof of Lemma 4.7, and Lemma 2.6 imply that

and if μ=2/3, then D is a curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$. □

Lemma 6.8

Suppose that m=4. Then

and if μ=2/3, then D is a curve in |−K _X | with a cusp at a point in Sing(X) of type  $\mathbb{A}_{2}$.

Proof

The point ω′(P′) is an ordinary cusp of the curve R′. Then there is a line L′⊂ℙ² such that

Let Z′ be a curve in X′ such that ω′(Z′)=L′ and −K _X′⋅Z′=2. Then

and Z′ is irreducible curve that has an ordinary cusp at the point R′.

Let $\bar{Z}^{\prime}$ be the proper transform of the curve Z′ on the surface $\bar{X}^{\prime}$. Then Z′ is smooth and

Let $\bar{Z}$ be the proper transform of the curve $\bar{Z}^{\prime}$ on the surface $\bar{X}$. Put $Z=\pi(\bar{Z})$. Then

and E ₂∩E ₃∈Z. Then c(X,Z)=2/5, which implies that lct₂(X)⩽4/5.

Arguing as in the proof of Lemma 4.6 and using Lemma 2.6 and (8), we see that

and if μ=2/3, then D is a curve in |−K _X | with a cusp at a point in Sing(X) of type $\mathbb{A}_{2}$. □

The assertion of Theorem 6.1 is proved.