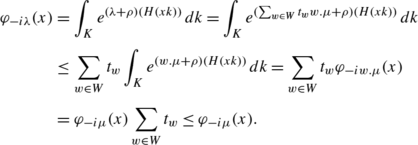Multipliers on Locally Symmetric Spaces

Abstract

We prove an analogue of the Hörmander–Mikhlin multiplier theorem on a class of locally symmetric spaces improving the results of Lohoué and Marias (Math. Ann. 343:639–667, 2009).

1 Introduction and Statement of the Results

Let κ be a tempered distribution on ℝⁿ and let m be its Fourier transform. The Hörmander–Mikhlin multiplier theorem, [26, 39], in its simple version, asserts that the convolution operator Tf=f∗κ is a bounded operator on L ^p(ℝⁿ), 1<p<∞, provided that m satisfies the symbol estimates

$$ \sup_{\xi \in \mathbb{R}^{n}}|\xi |^{\vert \alpha \vert }\bigl|\partial^{\alpha }m(\xi )\bigr|<+\infty , \text{ } $$

for all multi-indices α with |α|≤[n/2]+1, where [t] is the integer part of t∈ℝ.

This theorem has been generalized in various geometric contexts; see, for example, [1–4, 6, 8–10, 13, 15, 17, 19, 22, 28, 30, 31, 33–35, 37, 38, 40–42] and the references therein. In the present work we deal with multipliers on a class of locally symmetric spaces and we improve the results of [35].

For the statement of the results, we need to introduce some notation first. Let G be a real semisimple Lie group, connected, noncompact, with finite center and K be a maximal compact subgroup of G. We denote by X the Riemannian symmetric space G/K.

Let $\mathfrak{g}$ and $\mathfrak{k}$ be the Lie algebras of G and K. Also let $\mathfrak{p}$ be the subspace of $\mathfrak{g}$ which is orthogonal to $\mathfrak{k}$ with respect to the Killing form. The Cartan decomposition is $\mathfrak{g=k\oplus p}$.

Let $\mathfrak{a}$ be an abelian maximal subspace of $\mathfrak{p}$, $\mathfrak{a}^{\ast }$ its dual, and let $\varSigma \subset \mathfrak{a}^{\ast }$ be the root system of ($\mathfrak{g}$, $\mathfrak{a}$). We denote by W the Weyl group associated with Σ. Choose a set Σ ⁺ of positive roots. Let ρ be the half-sum of positive roots counted with multiplicity. We denote by C _ρ the convex hull in $\mathfrak{a}^{\ast }$ generated by w.ρ, w∈W.

Let us denote by $\mathcal{CO}_{p} ( X )$ the Banach algebra of bounded linear operators T on L ^p(X), 1≤p<∞, which are translation invariant under G. Then $\mathcal{CO}_{2} ( X )$ is isomorphic to the algebra $L^{\infty } ( \mathfrak{a}^{\ast } )^{W}$ of all W-invariant bounded measurable functions on $\mathfrak{a}^{\ast }$ [4, 10]. The isomorphism T↔m is given by

$$ \mathcal{H} ( Tf ) ( \lambda ) =m ( \lambda ) \mathcal{H}f ( \lambda ) ,\quad f\in L^{2} ( X ) ,\ \lambda \in\mathfrak{a}^{\ast }, $$

(1)

where $\mathcal{H}f$ is the spherical Fourier transform of f. We denote by T _m the operator associated with m by (1). Note that (1) is equivalent to

$$ T_{m}f ( x ) = ( f\ast \kappa ) ( x ) =\int_{G}f ( g ) \kappa \bigl( g^{-1}x \bigr)\,dg,\quad x\in G,\ f\in C_{0}^{\infty } ( X ) , $$

where κ is the inverse spherical Fourier transform of m in the sense of tempered distributions.

Further, $\mathcal{CO}_{p} ( X ) \subset \mathcal{CO}_{2} ( X )$, 1≤p<∞, and so every $T_{m}\in \mathcal{CO}_{p} ( X )$ is of the form (1). The corresponding functions $m:\mathfrak{a}^{\ast }\longrightarrow \mathbb{C}$ are called the Fourier multipliers of L ^p(X) and they are denoted by $\mathcal{M}_{p}$.

In their pioneer work [10], Clerc and Stein observed that in the case of symmetric spaces of noncompact type, every $m\in \mathcal{M}_{p}$ extends to a W-invariant bounded holomorphic function inside the tube $\mathcal{T}^{v}=\mathfrak{a}^{\ast }+ivC_{\rho }$, where v=|(2/p)−1|, p∈(1,∞).

Let v∈ℝ₊, N∈ℕ. We say that $m\in \mathcal{M}( v,N )$, if

• (i) m is analytic inside the tube $\mathcal{T}^{v}$ and

• (ii) for all multi-indices α, with |α|≤N, ∂ ^α m(λ) extends continuously to the whole of $\mathcal{T}^{v}$ with

  $$ \bigl( 1+\vert \lambda \vert ^{2} \bigr)^{\vert \alpha \vert /2}\bigl \vert \partial^{\alpha }m ( \lambda ) \bigr \vert <\infty ,\quad \lambda \in \mathcal{T}^{v}. $$

  (2)

In [4], Anker proved that if $m\in \mathcal{M} ( v,N )$ with v=|(2/p)−1|, p∈(1,∞), and N=[(v/2)dimX]+1, then T _m is bounded on L ^p(X).

Note that if $m\in \mathcal{M}_{p}$, then m is a holomorphic function inside the tube $\mathcal{T}^{v}$, [10], and Anker obtained the optimal width of the tube $\mathcal{T}^{v}$ of analyticity.

In [35], the authors proved a multiplier theorem on locally symmetric spaces. More precisely, let Γ be a discrete, torsion-free subgroup of G and let us denote by M the locally symmetric space Γ∖X=Γ∖G/K. The quotient M equipped with the projection of the canonical Riemannian structure of X becomes a Riemannian manifold. It is worth observing that M may not have bounded geometry, for its injectivity radius may be equal to 0, [11].

Let $m\in L^{\infty } ( \mathfrak{a}^{\ast } )^{W}$ and let us denote by κ its inverse spherical transform. Consider the operator

$$ S_{\kappa }u ( x ) =\int_{G}u ( \overline{g} ) \kappa \bigl( g^{-1}x \bigr)\,dg,\quad x\in G,\ u\in C_{0}^{\infty }( M ) , $$

where $\overline{g}$ is the class of g∈G in M.

We set

$$ n=\dim X,\qquad a=\dim \mathfrak{a}, $$

(3)

and we denote by λ ₀≥0 the bottom of the L ²-spectrum of the Laplacian on M.

In [35, Theorem 2] we proved that if p ₀>2 and $m\in \mathcal{M}( \tau ( p_{0} ) ,N_{0} )$ with

$$ \tau ( p_{0} ) >\frac{1}{2} \biggl( 1-\frac{2\lambda_{0}}{\vert \rho \vert ^{2}p_0} \biggr)^{1/2}\quad\text{and}\quad N_{0}= \bigl[ n+ ( a/2 ) \bigr] +1, $$

(4)

then S _κ is bounded on L ^p(M) for $p\in [ p_{0}^{\prime },p_{0} ]$, where $p_{0}^{\prime }$ is the conjugate of p ₀.

In the present work, we deal again with the L ^p-boundedness of S _κ by adopting a different approach, and we improve the results of [35, Theorem 2] for a class of locally symmetric spaces. The crucial point of this approach is an estimate of the L ^p norm of the operator S _κ . More precisely, in Sect. 3, we prove that for a class of locally symmetric spaces there exists a suitable vector η _Γ on the Euclidean sphere S(0,(|ρ|²−λ ₀)^1/2) of $\mathfrak{a}^{\ast }$ such that

$$ \Vert S_{\kappa }\Vert _{p\rightarrow p}\leq \int_{G} \bigl \vert \kappa ( g ) \bigr \vert \varphi_{-i\eta _{\varGamma }} ( g )^{s ( p ) }\,dg,\quad p\in ( 1,\infty ) , $$

(5)

where $\varphi_{-i\eta _{\varGamma }} ( g )$ is a spherical function of index η _Γ and s(p)∈(0,1). Note that the analogue of (5) in [4, Proposition 7] is obtained by using the Herz majorizing principle; however, this is no longer true in the present context.

To prove (5), we shall write L ²(Γ∖G) as a direct integral as we did in [35]. More precisely, let us denote by $\widehat{G}$ the unitary dual of G and by R the right regular representation of G on L ²(Γ∖G):

$$ R ( g ) h ( \overline{y} ) =h ( \overline{yg} ),\quad g\in G,\ h\in L^{2} ( \varGamma \backslash G ) . $$

Since G is a connected Lie group, it is of type I, [20]. It follows that

$$ L^{2} ( \varGamma \backslash G ) =\int_{\widehat{\varGamma \backslash G}}^{\oplus }H_{\pi _{\zeta }}\,d\mu ( \zeta ) ,\qquad R ( g ) =\int_{\widehat{\varGamma \backslash G}}^{\oplus } \pi_{\zeta } ( g ) \,d\mu ( \zeta ) , $$

(6)

where $\widehat{\varGamma \backslash G}\subset \widehat{G}$, μ is a positive measure on $\widehat{G}$, $\zeta \rightarrow H_{\pi _{\zeta }}$ is a μ-measurable field of Hilbert spaces, and ζ→π _ζ is a μ-measurable field of unitary and irreducible representations of G on $H_{\pi _{\zeta }}$, [12].

Recall that $\widehat{G}$ is equipped with the Fell topology [21], and denote by π ₀ the trivial representation.

We say that the pair (G,Γ) possesses property (I) if either

• (i) Γ is a lattice, i.e., Γ∖G has finite volume, or

• (ii) $\operatorname{vol} ( \varGamma \backslash G ) =\infty$ and either the trivial representation π ₀ does not appear in the decomposition (6), or if it appears, then it is isolated in $\widehat{\varGamma \backslash G}$.

In Sect. 3 we prove estimate (5) under the assumption that (G,Γ) has property (I).

Let us make a few comments about property (I). A criterion for the appearance of π ₀ in the decomposition (6) is amenability. Recall that π ₀ is weakly contained in the representation R if $\pi_{0}\in \widehat{\varGamma \backslash G}$, [12, p. 157], and that Γ∖G is amenable if π ₀ is weakly contained in R, [14, p. 44].

Note that a semisimple Lie group is unimodular. So, if Γ is a lattice, then the canonical measure μ on Γ∖G is positive and G invariant, [29, Theorem 8.36]. Thus, μ determines a right invariant mean on L ^∞(Γ∖G) and Γ∖G is amenable, [14].

Recall that G has Kazhdan’s property (T) if π ₀ is isolated in $\widehat{G}$, [21]. Note that G has (T) iff G has no simple factors locally isomorphic to SO(n,1) or SU(n,1), [21, Chap. 2]. Thus, if G has (T) then (G,Γ) possesses property (I) for all discrete subgroups Γ.

Recall also that G is non-amenable and that Γ∖G is non-amenable if Γ is amenable, [14, Exposé no 1]. Thus $\pi_{0}\notin \widehat{\varGamma \backslash G}$ and (G,Γ) has property (I). Note that if Γ is finitely generated and has subexponential growth, then Γ is amenable, [7, 18].

We now state our results. For p∈(1,∞) set

$$ v_{\varGamma } ( p ) =2\min \bigl( ( 1/p ) , \bigl( 1/p^{\prime } \bigr) \bigr) \frac{\vert \eta_{\varGamma }\vert }{\vert \rho \vert }+\bigl \vert ( 2/p ) -1\bigr \vert , $$

(7)

where p′ is the conjugate of p.

Set b=n−a, and let b′ be the smallest integer ≥b/2. Let

$$ N= [ a/2 ] +b^{\prime }+1. $$

(8)

Theorem 1

Assume that (G,Γ) possesses property (I). Let v _Γ (p), p∈(1,∞) and N be as above. If $m\in \mathcal{M} ( v,N )$, with v>v _Γ (p), then the operator S _κ is bounded on L ^p(M).

Next, we treat the case where estimates of the bottom λ ₀ of the L ²-spectrum of −Δ on M are known. This is the case when G has trivial center and no compact factors, [32].

Fix x ₀∈X and let R>0. Set

$$ n_{R}=\# \bigl\{ \gamma \in \varGamma :d ( x_{0},\gamma x_{0} ) <R \bigr\} . $$

The critical exponent δ(Γ) of Γ is given by

$$ \delta ( \varGamma ) =\limsup_{R\rightarrow \infty }\frac{\log n_{R}}{R}. $$

We set

$$ \rho_{m}=\min_{H\in \overline{\mathfrak{a}_{+}},\text{ }\vert H\vert =1}\rho ( H ) . $$

Using the estimates of λ ₀ obtained by Leuzinger (cf. [32] and Sect. 2.3 for details), Theorem 1 implies the following corollary.

Corollary 2

Assume that G has trivial center and no compact factors and that (G,Γ) possesses property (I). If $m\in \mathcal{M}( v,N )$, then the operator S _κ is bounded on L ^p(M), wherever v satisfies:

• (i) If δ(Γ)∈[0,ρ _m ], then v>|(2/p)−1|, p∈(1,∞);

• (ii) If δ(Γ)∈[ρ _m ,ρ _m +|ρ|], then

  $$ v>2\min \bigl( ( 1/p ) , \bigl( 1/p^{\prime } \bigr) \bigr) \frac{\delta ( \varGamma ) -\rho_{m}}{\vert \rho \vert }+\bigl \vert ( 2/p ) -1\bigr \vert ;\quad \mbox{\textit{and}} $$

• (iii) v=1, when δ(Γ)∈[ρ _m +|ρ|,2|ρ|].

We wish to add here a few comments about the result of this paper and the main points of the proof.

In the context of non-compact symmetric spaces, the multiplier theorem for convolution operators has been treated in [4, 6, 10, 27, 28, 38, 40, 41]. The pioneer work was done by Clerc and Stein in [10]. Sharp results concerning the L ^p boundedness, p∈(1,∞), or the weak type (1,1) have been proved in [4, 28, 38]. Anker’s result [4] is improved by Inonescu [28], who deals with multipliers that are allowed to have singularities on the boundary of the tube $\mathcal{T}^{v}$ of analyticity.

In Theorem 1, we deal with multipliers in the class $\mathcal{M}( v,N )$, where N=[a/2]+b′+1 and v>v _Γ (p). Note that N=[n/2]+2 if a is even and b odd, and N=[n/2]+1 otherwise. As it is mentioned in [4, Proposition 7], the number N above is the best that one can get by a direct kernel estimate. Recall that the sharp result is N=[(v/2)n]+1, [4, Theorem 1] and it is obtained by using some heavy machinery of function space theory.

Next, note that v _Γ (p) is always larger than |(2/p)−1|, which is the optimal width of the tube of analyticity in the case of symmetric spaces [4, 10]. It is important to note that if λ ₀= |ρ|², then v _Γ (p)>|(2/p)−1|, i.e., v _Γ (p) is optimal. Note that if G is as in Corollary 2 and $\operatorname{vol} ( M ) <\infty$, then λ ₀=0. Thus v _Γ (p)=1.

In the context of locally symmetric spaces Γ∖X, the first result is obtained in [36], in the case when X is the real hyperbolic space ℍⁿ. We have already mentioned that a multiplier theorem is given in [35] in the general context of locally symmetric spaces. In [15], the results of [35] are improved in the particular case when X has rank one.

Using (4), (7), and (8), one can check that Theorem 1 above improves Theorem 2 of [35], while in the case when X has rank one, the results of Corollary 2 are weaker than the results of [15], except in the case of claim (i) where both are optimal.

To prove our results, we divide as usual the kernel κ of the operator S _m into two pieces: κ=κ ⁰+κ ^∞, with $\operatorname{supp} ( \kappa^{0} ) \subset B ( 0,2 )$ and $\operatorname{supp} ( \kappa^{\infty } ) \subset B ( 0,1 )^{c}$. Denote by $S_{\kappa }^{0}$ and by $S_{\kappa }^{\infty }$ the corresponding operators.

The continuity of $S_{\kappa }^{0}$ for all p∈(1,∞) is proved in [35, Proposition 13]. This is carried out by observing that $S_{\kappa }^{0}$ can be defined as an operator on the group G, and then by the local result of [4] we conclude its boundedness on L ^p(G), p∈(1,∞). The continuity of $S_{\kappa }^{0}$ on L ^p(M) follows by applying Herz’s Theorem A [25].

The crucial step for the proof of the boundedness of $S_{\kappa }^{\infty }$ is to obtain the estimate (5) of the norm $\Vert S_{\kappa }^{\infty }\Vert _{p\rightarrow p}$. To conclude the proof of Theorem 1, we prove that if $m\in \mathcal{M} ( v,N )$ then the integral in (5) is finite. For this we follow closely [4, Proposition 5].

In Sect. 2, we recall the basic notions and tools we need for the proof of the results. In Sect. 3, we first prove the existence of the spherical function $\varphi_{-i\eta _{\varGamma }}$ appearing in (5) and then we obtain the estimate (5). In Sect. 4, we give the proof of Theorem 1.

Throughout this article the different constants will always be denoted by the same letter c.

2 Preliminaries

We recall first some basic facts about Fourier analysis on symmetric spaces of noncompact type; for details, see [4, 5, 16, 24, 35].

Denote by $\mathfrak{g}$ and $\mathfrak{k}$ the Lie algebras of G and K. Let $\mathfrak{p}$ be the subspace of $\mathfrak{g}$ which is orthogonal to $\mathfrak{k}$ with respect to the Killing form. Then we have the Cartan decomposition $\mathfrak{g=k\oplus p}$.

We fix a maximal abelian subspace $\mathfrak{a}$ of $\mathfrak{p}$ and we denote by $\mathfrak{a}^{\ast }$ (resp., $\mathfrak{a}_{\mathbb{C}}^{\ast }$) the real (resp., complex) dual of $\mathfrak{a}$.

Let $\varSigma \subset \mathfrak{a}^{\ast }$ be the root system of ($\mathfrak{g}$, $\mathfrak{a}$). We denote by W the Weyl group associated with Σ. Choose a set Σ ⁺ of positive roots. Let $\mathfrak{a}^{+}\subset \mathfrak{a}$ be the corresponding positive Weyl chamber and let $\overline{\mathfrak{a}_{+}}$ be its closure. We denote by $\mathfrak{a}_{+}^{\ast }$ and $\overline{\mathfrak{a}_{+}^{\ast }}$ the corresponding cones in $\mathfrak{a}^{\ast }$.

Let A be the analytic subgroup of G with Lie algebra $\mathfrak{a}$. Then A is closed in G and the exponential map is an isomorphism from $\mathfrak{a}$ onto A. We put $A^{+}=\exp \mathfrak{a}_{+}$; its closure in G is $\overline{A^{+}}=\exp \overline{\mathfrak{a}_{+}}$. The Cartan decomposition is $G=K(\overline{A^{+}})K=K(\exp \overline{\mathfrak{a}_{+}})K$. If x∈G, then according to the Cartan decomposition, it is written as x=k ₁(expH)k ₂. The A-component is uniquely determined modulo W; in particular, it is well defined in $\overline{A^{+}}$.

According to the Cartan decomposition, the Haar measure on G is written as

$$ \int_{G}f ( g )\,dg=c\int_{K}dk_{1} \int_{\mathfrak{a}^{+}}\delta ( H ) \,dH\int_{K}f \bigl( k_{1} ( \exp H ) k_{2} \bigr) \,dk_{2}, $$

(9)

where

$$ \delta ( H ) =\prod_{\alpha \in \varSigma ^{+}}\sinh^{m_{\alpha }}\alpha ( H ) , $$

with $m_{\alpha }=\dim \mathfrak{g}_{\alpha }$ and

$$ \mathfrak{g}_{\alpha }= \bigl\{ X\in \mathfrak{g}: [ H,X ] =\alpha ( H ) X \text{ for all }H\in \mathfrak{a} \bigr\} $$

is the root space associated with α∈Σ ⁺.

Note that

$$ \delta ( H ) \leq ce^{2\rho ( H ) },\quad H\in \mathfrak{a}_{+}. $$

(10)

Setting $\mathfrak{n}=\sum_{\alpha \in \varSigma ^{+}}\mathfrak{g}_{\alpha }$, the Iwasawa decomposition is $\mathfrak{g}=\mathfrak{k\oplus a\oplus n}$ and G=KAN. The map (k,a,n)⟶kan is a global diffeomorphism from K×A×N onto G.

Let k, expH, and n be the components of x∈G in K, $\exp \mathfrak{a}$, and N respectively, according to the Iwasawa decomposition $G=K ( \exp \mathfrak{a} ) N$. Then the Haar measure on G is given by

$$ \int_{G}f ( g )\,dg=c\int_{K}dk\int _{\mathfrak{a}}e^{2\rho ( H ) }\,dH\int_{N}f \bigl( k ( \exp H ) n \bigr) \,dn. $$

2.1 Spherical Functions

Denote by D(G) the set of all left-invariant differential operators on G, and by D _K (G) the set of operators in D(G) which are right invariant under K. A complex function φ on G is said to be a spherical function if φ is a K-bi-invariant eigenfunction of each operator in D _K (G) and φ(0)=1. In the case of symmetric spaces of noncompact type, a classical theorem of Harish-Chandra asserts that the spherical functions on G are exactly the functions

$$ \varphi_{\lambda } ( x ) =\int_{K}e^{ ( i\lambda +\rho ) ( H ( xk ) ) }\,dk,\quad x\in G,\ \lambda \in \mathfrak{a}_{\mathbb{C}}^{\ast }, $$

(11)

where H(xk) is the component of xk in $\mathfrak{a}$ according to the Iwasawa decomposition $G=K\exp \mathfrak{a}N$, [24, p. 418].

Further,

$$ \varphi_{\lambda }=\varphi_{\nu }\quad\mbox{iff}\quad\nu =w\lambda,\quad \mbox{for some } w\in W. $$

(12)

Below we collect some properties of spherical functions we shall need for the proof of our results.

• (i) The function φ _λ (x) is C ^∞ in x and holomorphic in λ.

• (ii) If $\lambda \in \overline{\mathfrak{a}_{+}^{\ast }}$, then

  $$ -\varDelta \varphi_{-i\lambda }= \bigl( -\vert \lambda \vert ^{2}+ \vert \rho \vert ^{2} \bigr) \varphi_{-i\lambda }. $$

  (13)

• (iii) For $H\in \overline{\mathfrak{a}_{+}}$,

  $$ e^{-\rho ( H ) }\leq \varphi_{0} ( \exp H ) \leq c \bigl( 1+\vert H \vert \bigr)^{a}e^{-\rho ( H ) }, $$

  (14)

  for some constants c, a>0, [24].

• (iv) The spherical function φ _λ is bounded if and only if λ belongs to the tube $\mathcal{T}_{1}=\mathfrak{a}^{\ast }+iC_{\rho }$, [24, Theorem 8.1].

• (v) Let $\mu \in \overline{\mathfrak{a}_{+}^{\ast }}$, and let C _μ be the convex hull of the points w.μ, w∈W. If λ∈C _μ , then

  $$ \varphi_{-i\lambda }\leq \varphi_{-i\mu }. $$

  (15)

  Indeed, λ is written as ∑ _w∈W t _w w.μ with t _w ≥0 and ∑ _w∈W t _w ≤1. By the convexity of the exponential, (11), and (12), we get that

  

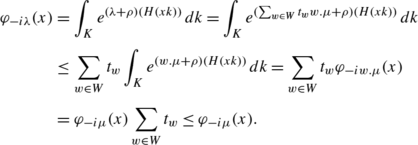
• (vi) For $H\in \overline{\mathfrak{a}_{+}}$ and $\lambda \in \overline{\mathfrak{a}_{+}^{\ast }}$,

  $$ 0<\varphi_{-i\lambda } ( \exp H ) \leq e^{\lambda ( H ) }\varphi_{0} ( \exp H ) , $$

  (16)

  [16, Proposition 4.6.1]. Combining (16) and (iii), we get that

  $$ 0<\varphi_{-i\lambda } ( \exp H ) \leq c \bigl( 1+\vert H\vert \bigr)^{a}e^{\lambda ( H ) -\rho ( H ) }. $$

  (17)

• (vii) Spherical functions are in fact matrix coefficients of spherical representations of G. In particular, if π is an irreducible unitary and spherical representation of G on a Hilbert space $\mathcal{H}$, we denote by $\mathcal{H}_{\pi }$ the one-dimensional space of vectors in $\mathcal{H}$ which are fixed under each π(k), k∈K. If e is a unit vector in $\mathcal{H}_{\pi }$, then the matrix coefficient

  $$ \varphi_{\pi } ( x ) := \bigl\langle e,\pi ( x ) e \bigr \rangle_{\mathcal{H}_{\pi }},\quad x\in G, $$

  is a spherical function on G, [24, Theorem 3.7]. Therefore, by the afore-mentioned theorem of Harish-Chandra there is a $\lambda_{\pi }=\xi_{\pi }+i\eta_{\pi }\in \mathfrak{a}_{\mathbb{C}}^{\ast }$, such that $\varphi_{\pi } ( x ) =\varphi_{\lambda _{\pi }} ( x )$.

Further, φ _π (x) is a positive definite function, [24, Theorem 1.5]. This in particular implies that φ _π (x) is bounded. Therefore, by [23] we have η _π ∈C _ρ and

$$ \bigl \vert \varphi_{\pi } ( x ) \bigr \vert \leq \varphi_{-i\eta _{\pi }} ( x ) ,\text{ \ }x\in G. $$

(18)

2.2 The Spherical Fourier Transform

Let us denote by S(K∖G/K) the Schwartz space of K-bi-invariant functions on G. The spherical Fourier transform $\mathcal{H}$ is defined by

$$ \mathcal{H}f ( \lambda ) =\int_{G}f ( x ) \varphi_{\lambda } ( x ) \,dx,\quad\lambda \in \mathfrak{a}^{\ast },\ f\in S ( K\backslash G/K ) . $$

Let $S ( \mathfrak{a}^{\ast } )$ be the usual Schwartz space on $\mathfrak{a}^{\ast }$ and let us denote by $S ( \mathfrak{a}^{\ast } )^{W}$ the subspace of W-invariants in $S ( \mathfrak{a}^{\ast } )$. Then, by a celebrated theorem of Harish-Chandra, $\mathcal{H}$ is an isomorphism between S(K∖G/K) and $S ( \mathfrak{a}^{\ast } )^{W}$ and the following inversion formula holds:

$$ \bigl( \mathcal{H}^{-1}f \bigr) ( x ) =c\int_{\mathfrak{a}^{\ast }}f ( \lambda ) \varphi_{-\lambda } ( x ) \frac{d\lambda }{\vert \mathbf{c} ( \lambda ) \vert ^{2}},\quad x\in G,\ f\in S \bigl( \mathfrak{a}^{\ast } \bigr)^{W}. $$

(19)

Here, c(λ) is the Harish-Chandra function; a simple proof of this result is given by Anker in [5].

Note that c(λ) satisfies the estimate

$$ \bigl \vert \mathbf{c} ( \lambda ) \bigr \vert ^{-2}\leq c \bigl( 1+ \vert \lambda \vert ^{2} \bigr)^{ ( n-a ) /2}:= \langle \lambda \rangle^{n-a}. $$

(20)

The Plancherel theorem for the spherical Fourier transform asserts that $\mathcal{H}$ is an isometry between L ²(K∖G/K) and $L^{2} ( \mathfrak{a}^{\ast },d\nu )$, where dν(λ)=|c(λ)|⁻²  dλ.

The Abel transform $\mathcal{A}$ is defined by

$$ \mathcal{A}f ( H ) =e^{\rho ( H ) }\int_{N}f \bigl( ( \exp H ) n \bigr) \,dn,\quad H\in \mathfrak{a},\ f\in S ( K\backslash G/K ) . $$

We denote by $\mathcal{F}$ the Euclidean Fourier transform

$$ \mathcal{F}g ( \lambda ) =\int_{\mathfrak{a}}g ( H ) e^{-i\lambda ( H ) }\,dH,\quad\lambda \in \mathfrak{a}^{\ast }. $$

Then the diagram

$$ \begin{array}{ccc} & S ( \mathfrak{a}^{\ast } )^{W} & \\ \overset{\mathcal{H}}{\nearrow } & & \overset{\mathcal{F}}{\nwarrow } \\ S ( K\backslash G/K ) & \overset{\mathcal{A}}{\longrightarrow } & S ( \mathfrak{a} )^{W}\end{array} $$

(21)

is commutative and each arrow is an isomorphism.

We set

$$ V_{r}= \bigl\{ H\in \mathfrak{a}:\vert H\vert \leq r \bigr\} ,\qquad U_{r}=K ( \exp V_{r} ) K\subset G,\quad r>0. $$

Helgason has proved that the Abel transform is an isomorphism between $C_{0}^{\infty } ( K\backslash\allowbreak G/K )$ and $C_{0}^{\infty } ( \mathfrak{a} )^{W}$ such that

$$ \operatorname{supp}f\subset U_{r}\text{ \ iff \ }\operatorname{supp} \mathcal{A}f\subset V_{r}. $$

(22)

2.3 The L ²-Spectrum of the Laplacian on M

The bottom λ ₀ of the L ²-spectrum of −Δ on M=Γ∖X is defined by

$$ \lambda_{0}=\inf \bigl\{ \langle -\varDelta f,f \rangle ;f\in C_{0}^{\infty } ( M ) ,\Vert f\Vert _{2}=1\bigr\}. $$

We always have that 0≤λ ₀≤|ρ|²; also the bottom of the L ²-spectrum of −Δ on X is |ρ|².

If G has no compact factors and its center is trivial, then Leuzinger has obtained the following estimates of λ ₀, [32]:

• (i) If δ(Γ)∈[0,ρ _m ], then

  $$ \lambda_{0}=\vert \rho \vert ^{2}. $$

• (ii) If δ(Γ)∈[ρ _m ,|ρ|], then

  $$ \vert \rho \vert ^{2}- \bigl( \delta ( \varGamma ) - \rho_{m} \bigr)^{2}\leq \lambda_{0}\leq \vert \rho \vert ^{2}. $$

• (iii) If δ(Γ)∈[|ρ|,2|ρ|], then

  $$ \max \bigl\{ 0;\vert \rho \vert ^{2}- \bigl( \delta ( \varGamma ) - \rho_{m} \bigr)^{2} \bigr\} \leq \lambda_{0}\leq \vert \rho \vert ^{2}- \bigl( \delta ( \varGamma ) -\vert \rho \vert \bigr)^{2}. $$

3 Estimates of the Norm of the Operator S _κ

If g∈G, then $\overline{g}$ denotes its class {gk:k∈K} in X, but also its class {γgk:γ∈Γ,k∈K} in M. Furthermore, if $u\in C_{0}^{\infty } ( M )$, then u is left Γ-invariant and right K-invariant. Then u can be considered as a function defined on G/K or on G, and it will be always denoted by the same letter u.

Let $m\in L^{\infty } ( \mathfrak{a}^{\ast } )^{W}$ and let κ be its inverse spherical transform. In this section we prove the estimate (5) of the L ^p-norm of the operator

$$ S_{\kappa }u ( x ) =\int_{G}u ( \overline{g} ) \kappa \bigl( g^{-1}x \bigr)\,dg,\quad x\in G,\ u\in C_{0}^{\infty } ( M ) . $$

It is straightforward to check that if u is left Γ-invariant and κ is K-bi-invariant then S _κ u inherits these invariances, therefore S _κ may be thought of as an operator on functions on M.

3.1 The Spherical Function $\protect\varphi_{-i\protect\eta_{\varGamma }}$

In this section, we shall prove the existence of the spherical function $\varphi_{-i\eta _{\varGamma }}$ appearing in the estimate (5) by exploiting the representation theory of G and specifically property (I).

Let $\widehat{G}_{K}$ be the unitary dual of G and let $( \widehat{\varGamma \backslash G} )_{K}$ be a subset of $\widehat{G}_{K}$.

Proposition 3

There exists an $\eta_{\varGamma }\in C_{\rho }\cap \overline{\mathfrak{a}_{+}^{\ast }}$ such that for all representations π in $( \widehat{\varGamma \backslash G} )_{K}\backslash \{ \pi_{0} \}$ the matrix coefficient φ _π of π satisfies the estimate

$$ \bigl \vert \varphi_{\pi } ( g ) \bigr \vert \leq \varphi_{-i\eta _{\varGamma }} ( g ) ,\quad g\in G. $$

(23)

For the proof, we first need to fix some notation. We first fix a positive Weyl chamber $\mathfrak{a}_{+}$ in $\mathfrak{a}$ and denote by α ₁,…,α _a , $a=\dim \mathfrak{a}$, the simple roots. Then

$$ \mathfrak{a}_{+}= \bigl\{ H\in \mathfrak{a}:\alpha_{j} ( H ) >0,\text{ }j\leq a \bigr\} . $$

Let H ₁,…,H _a be the basis of $\mathfrak{a}$ dual to the basis α ₁,…,α _a of $\mathfrak{a}^{\ast }$. Then H _j are the edges of the closed Weyl chamber $\overline{\mathfrak{a}_{+}}$.

For $\alpha \in \mathfrak{a}_{\mathbb{C}}^{\ast }$, let $H_{\alpha }\in \mathfrak{a}_{\mathbb{C}}$ be the root vector associated with α, i.e., the vector determined by (H,H _α )=α(H), $H\in \mathfrak{a}$. We denote by J the isomorphism α⟶H _α , and by $\mathfrak{a}_{+}^{\ast }$ the positive Weyl chamber associated with $\mathfrak{a}_{+}$ via J:

$$ \mathfrak{a}_{+}^{\ast }= \bigl\{ \eta \in \mathfrak{a}^{\ast }: ( \eta ,\alpha_{j} ) = ( H_{\eta },H_{\alpha _{j}} ) >0,\ j\leq a \bigr\} . $$

If $\eta \in \mathfrak{a}_{+}^{\ast }$, let C _η be the convex hull of the points s.η, s∈W. Then J(C _η ) is the convex hull of the points H _sη , s∈W.

We finally set

$$ Q_{e} ( \eta ) = \bigl\{ H\in \mathfrak{a}_{+}: ( H,H_{j} ) < ( H_{\eta },H_{j} ) ,\ j\leq a \bigr\} , $$

(24)

and

$$ Q_{s} ( \eta ) =sQ_{e} ( \eta ) ,\quad s\in W. $$

In [23, Lemma 2.5] it is proved that

$$ J ( C_{\eta } ) =\bigcup_{s\in W}\overline{Q_{s}} ( \eta ) . $$

(25)

Proof of Proposition 3

Recall that the matrix coefficient φ _π of a representation in $\widehat{G}_{K}$ is a bounded spherical function. Then by (18), there is a $\lambda_{\pi }=\xi_{\pi }+i\eta_{\pi }\in \mathfrak{a}^{\ast }+iC_{\rho }$, such that $\varphi_{\pi } ( x ) =\varphi_{\lambda _{\pi }} ( x )$ and

$$ \bigl \vert \varphi_{\pi } ( x ) \bigr \vert \leq \varphi_{-i\eta _{\pi }} ( x ),\quad x\in G\text{.} $$

We set

$$ \widetilde{Q}_{1}= \bigl\{ \eta_{\pi }\in C_{\rho }: \pi \in ( \widehat{\varGamma \backslash G} )_{K}\backslash \{ \pi_{0} \} \bigr\} . $$

(26)

To now prove the proposition, it is sufficient to show that

$$ \widetilde{Q}_{1}\subset C_{\eta _{\varGamma }}. $$

(27)

Indeed, if (27) holds true, then as it is already mentioned in Sect. 2.1 (v), we have that for all $\eta \in C_{\eta _{\varGamma }}$,

$$ \varphi_{-i\eta } ( g ) \leq \varphi_{-i\eta _{\varGamma }} ( g ) ,\quad g\in G. $$

The proof of (27) will be given in steps.

Step 1. Construction of η _Γ . We set $Q_{1}=J ( \widetilde{Q}_{1} )$; by (25), if $\eta \in \widetilde{Q}_{1}\cap C_{\rho }$ then $H_{\eta }\in Q_{1}\cap ( \bigcup_{s\in W}\overline{Q_{s}} ( \rho ) )$.

Assume first that $H_{\eta }\in Q_{1}\cap \overline{Q_{e}} ( \rho )$. By (24), the projections (H _η ,H _j ) of H _η on the edges H _j of $\overline{\mathfrak{a}_{+}}$, satisfy

$$ ( H_{\eta },H_{j} ) \leq ( H_{\rho },H_{j} ) =\rho ( H_{j} ),\quad j=1,\ldots,a. $$

(28)

Set

$$ \lambda_{j}^{e}=\sup_{H_{\eta }\in Q_{1}\cap \overline{Q_{e}} ( \rho ) } ( H_{j},H_{\eta } ). $$

(29)

Assume next that $H_{\eta }\in Q_{1}\cap \overline{Q_{s}} ( \rho )$, s∈W, s≠e. Then $H_{s^{-1}\eta }\in \overline{Q_{e}} ( \rho )$. Set

$$ \lambda_{j}^{s}=\sup_{H_{s^{-1}\eta }\in Q_{1}\cap \overline{Q_{e}} ( \rho ) } ( H_{j},H_{s^{-1}\eta } ) \leq \rho ( H_{j} ),\quad j=1,\ldots,a. $$

(30)

Finally, let

$$ \lambda_{j}^{\varGamma }=\sup_{s\in W}\lambda_{j}^{s},\quad j=1,\ldots,a. $$

(31)

Then by (29) and (30) we have

$$ \lambda_{j}^{\varGamma }\leq \rho ( H_{j} ) ,\quad j=1,\ldots,l. $$

(32)

Consider the vector $H_{\eta _{\varGamma }}$ with projections on the edges H _j of $\overline{\mathfrak{a}_{+}}$ given by

$$ ( H_{\eta _{\varGamma }},H_{j} ) =\lambda_{j}^{\varGamma },\quad j=1,\ldots,a. $$

Then by (32), $H_{\eta _{\varGamma }}\in \overline{Q_{e}} ( \rho )$, i.e., $\eta_{\varGamma }\in C_{\rho }\cap \overline{\mathfrak{a}_{+}^{\ast }}$.

Step 2. Proof of (27). Assume first that $H_{\eta }\in Q_{1}\cap \overline{Q_{e}} ( \rho )$. Then, by (29) and (31),

$$ ( H_{\eta },H_{j} ) \leq \lambda_{j}^{e} \leq \lambda_{j}^{\varGamma }= ( H_{\eta _{\varGamma }},H_{j} ),\quad j=1,\ldots,a, $$

i.e., $H_{\eta }\in \overline{Q_{e}} ( \eta_{\varGamma } )$.

Next, if $H_{\eta }\in Q_{1}\cap \overline{Q_{s}} ( \rho )$, then $H_{s^{-1}\eta }\in Q_{1}\cap \overline{Q_{e}} ( \rho )$. Thus, by (30) and (31),

$$ ( H_{s^{-1}\eta },H_{j} ) \leq \lambda_{j}^{s} \leq \lambda_{j}^{\varGamma }= ( H_{\eta _{\varGamma }},H_{j} ),\quad j=1,\ldots,a. $$

Thus $H_{s^{-1}\eta }\in \overline{Q_{e}} ( \eta_{\varGamma } )$, i.e., $H_{\eta }\in \overline{Q_{s}} ( \eta_{\varGamma } )$ and the proof of (27) is complete. □

3.2 Estimate of the L ²-Norm of the Operator S _κ

In this section, we obtain an estimate of the L ²-norm of S _κ . Note that we can always assume that $m\in S ( \mathfrak{a}^{\ast } )^{W}$. Then, from diagram (21) it follows that κ∈S(K∖G/K). Therefore, in the proof of the estimates we can always replace the kernel κ by a positive function $\psi \in C_{0}^{\infty } ( K\backslash G/K )$.

Proposition 4

If ψ is a positive function in S(K∖G/K), then

$$ \Vert S_{\psi }\Vert _{2\rightarrow 2}\leq \int_{G} \psi ( g ) \varphi_{-i\eta _{\varGamma }} ( g )\,dg, $$

(33)

where $\varphi_{-i\eta _{\varGamma }} ( g )$ is defined in Proposition 3.

Proof

We set

$$ I ( f,h ) =\int_{\varGamma \backslash G}h ( \overline{x} ) S_{\psi }f ( \overline{x} ) \,d\overline{x},\quad f,h\in C_{0}^{\infty } ( \varGamma \backslash G ) . $$

Then, since the functions in L ²(M) are simply the elements of L ²(Γ∖G) which are right K-invariants, (33) will follow from the estimate

$$ \bigl \vert I ( f,h ) \bigr \vert \leq \biggl( \int_{G} \psi ( g ) \varphi_{-i\eta _{\varGamma }} ( g )\,dg \biggr) \Vert f\Vert _{L^{2} ( \varGamma \backslash G ) } \Vert h\Vert _{L^{2} ( \varGamma \backslash G ) }. $$

(34)

But it is straightforward to check that

$$ I ( f,h ) =\int_{G}\psi ( g ) \bigl\langle f,R ( g ) h \bigr\rangle_{L^{2} ( \varGamma \backslash G ) }\,dg, $$

(35)

where R is the right regular representation of G.

Recall that from the decomposition (6) of R it follows that the coefficient matrix $\langle f,R ( g ) h \rangle_{L^{2} ( \varGamma \backslash G ) }$ is written as

$$ \bigl\langle f,R ( g ) h \bigr\rangle_{L^{2} ( \varGamma \backslash G ) }=\int_{\widehat{\varGamma \backslash G}} \bigl\langle f_{\zeta },\pi_{\zeta } ( g ) h_{\zeta } \bigr \rangle_{H_{\pi _{\zeta }}}\,d\mu ( \zeta ) . $$

(36)

Next, using that ψ is K-bi-invariant, one can prove as in [35, Lemma 9] that in the expression (35) we may assume that f and h are K-invariant. This implies that the representations π _ζ appearing in (36) are spherical, [35, p. 656]. Therefore,

$$ \bigl\langle f,R ( g ) h \bigr\rangle_{L^{2} ( \varGamma \backslash G ) }=\int_{ ( \widehat{\varGamma \backslash G} ) _{K}} \bigl\langle f_{\zeta },\pi_{\zeta } ( g ) h_{\zeta } \bigr \rangle_{H_{\pi _{\zeta }}}\,d\mu ( \zeta ) , $$

(37)

where $( \widehat{\varGamma \backslash G} )_{K}=$ $\widehat{\varGamma \backslash G}\cap \widehat{G}_{K}$.

Let us now proceed to the proof of the estimate (34). We distinguish two cases.

First assume that $\operatorname{vol} ( \varGamma \backslash G ) =\infty$. By the assumption that (G,Γ) satisfies property (I), it follows that if π ₀ appears in (37), it is isolated in $( \widehat{\varGamma \backslash G} )_{K}$ and one may prove as in [35, Lemma 10], that μ({π ₀})=0. Combined with (37), this gives

$$ \bigl\langle f,R ( g ) h \bigr\rangle_{L^{2} ( \varGamma \backslash G ) }=\int_{ ( \widehat{\varGamma \backslash G} ) _{K}\backslash \{ \pi _{0} \} } \bigl\langle f_{\zeta },\pi_{\zeta } ( g ) h_{\zeta } \bigr \rangle_{H_{\pi _{\zeta }}}\,d\mu ( \zeta ) . $$

(38)

From (35) and (38) it follows that

(39)

Next, by Proposition 3 there exists $\eta_{\varGamma }\in C_{\rho }\cap \overline{\mathfrak{a}_{+}^{\ast }}$ such that for all $\pi_{\zeta }\in ( \widehat{\varGamma \backslash G} )_{K}\backslash \{ \pi_{0} \}$,

$$ \bigl \vert \varphi_{\pi _{\zeta }} ( g ) \bigr \vert \leq \varphi_{-i\eta _{\varGamma }} ( g ) ,\quad g\in G. $$

(40)

Putting together (39) and (40), we obtain the estimate (34).

Assume now that $\operatorname{vol} ( \varGamma \backslash G ) <\infty$. Then Γ∖G is amenable and $\pi_{0}\in \widehat{\varGamma \backslash G}$. Let $P_{0}:L^{2} ( \varGamma \backslash G ) \longrightarrow H_{\pi _{0}}$ be the projection P ₀(h)=h ₀. Thus P ₀ is continuous. But constants belong to L ²(Γ∖G). So, P ₀ is continuous on L ²(Γ∖G). Write S _ψ =S _ψ P ₀+S _ψ (I−P ₀). Then

$$ ( S_{\psi }P_{0} ) ( h ) ( x ) =P_{0} ( h ) ( x ) \int_{G}\psi ( g )\,dg,\quad x\in G. $$

Thus S _ψ P ₀ is continuous on L ²(Γ∖G). So, to prove the boundedness of S _ψ on L ²(Γ∖G) it suffices to prove the continuity of S _ψ (I−P ₀). This allows us to replace h by h−h ₀ in (35) and obtain that

$$ \bigl\langle f,R ( g ) ( h-h_{0} ) \bigr\rangle =\int _{ ( \widehat{\varGamma \backslash G} ) _{K}\backslash \{ \pi _{0} \} } \bigl\langle f_{\zeta },\pi_{\zeta } ( g ) ( h_{\zeta }-h_{0} ) \bigr\rangle_{H_{\pi _{\zeta }}}\,d\mu ( \zeta ) , $$

(41)

since $\langle f_{0},\pi_{0} ( g ) ( h_{0}-h_{0} ) \rangle_{H_{\pi _{0}}}=0$.

Using (41) and arguing as in (39) we obtain that

$$ \bigl \vert I ( f,h-h_{0} ) \bigr \vert \leq \biggl( \int _{G}\psi ( g ) \varphi_{-i\eta _{\varGamma }} ( g )\,dg \biggr) \Vert f\Vert _{L^{2} ( \varGamma \backslash G ) }\Vert h-h_{0}\Vert _{L^{2} ( \varGamma \backslash G ) }. $$

This complete the proof the proposition. □

By using the heat semigroup on M, we shall prove that η _Γ belongs to the sphere S(0,(|ρ|²−λ ₀)^1/2) of $\mathfrak{a}^{\ast }$.

Denote by $p_{t}^{X}$ the heat kernel on X and set

$$ S_{p_{t}^{X}}f ( x ) =\int_{G}p_{t}^{X} \bigl( g^{-1}x \bigr) f ( \overline{g} )\,dg,\quad f\in C_{0}^{\infty } ( M ) . $$

Lemma 5

Let $P_{t}^{M}$, t>0, be the heat semigroup on M. Then

$$ S_{p_{t}^{X}}f=P_{t}^{M}f,\quad t>0,\ f\in C_{0}^{\infty} ( M ) . $$

Proof

Recall that the heat kernel $p_{t}^{M}$ on M is given by

$$ p_{t}^{M} ( \overline{x},\overline{y} ) =\sum _{\gamma \in \varGamma }p_{t}^{X} ( x,\gamma y ) =\sum _{\gamma \in \varGamma }p_{t}^{X} \bigl( ( \gamma y )^{-1}x \bigr) . $$

Using the fact that the measure $d\bar{g}$ on Γ∖X satisfies

$$ \int_{X}f ( g )\,dg=\int_{\varGamma \backslash X} \biggl( \sum_{\gamma \in \varGamma }f ( \overline{\gamma g} ) \biggr) \,d\bar{g} $$

and bearing in mind that if $f\in C_{0}^{\infty } ( M )$, then f is left Γ-invariant and right K-invariant, we get that

On the other hand, using the fact that f is right K-invariant, we get

and the proof is complete. □

Lemma 6

Let η _Γ be as in Proposition 3. Then

$$ \eta_{\varGamma }\in C_{\rho }\cap S \bigl( 0, \bigl( \vert \rho \vert ^{2}-\lambda_{0} \bigr)^{1/2} \bigr) . $$

Proof

Since $e^{-\lambda _{0}t}$ is the biggest eigenvalue of $P_{t}^{M}$, we have that

$$ \bigl \Vert P_{t}^{M}\bigr \Vert _{2\rightarrow 2}=e^{-\lambda _{0}t}. $$

(42)

On the other hand, it follows from Proposition 4, Lemma 5, and (13) that

(43)

since $\varphi_{-i\eta _{\varGamma }} ( 0 ) =1$.

From (42), it follows that in the expression (43) we can choose η _Γ such that λ ₀=|ρ|²−|η _Γ |² or η _Γ ∈S(0,(|ρ|²−λ ₀)^1/2). □

3.3 Estimate of the L ^p-Norm of the Operator S _ψ

The estimate of the L ^p-norm of S _ψ will follow from Proposition 4 and complex interpolation.

Proposition 7

If $\psi \in C_{0}^{\infty } ( K\backslash G/K )$, then for p∈(1,∞),

$$ \Vert S_{\psi }\Vert _{p\rightarrow p}\leq \int_{G} \bigl \vert \psi ( g ) \bigr \vert \varphi_{-i\eta _{\varGamma }} ( g )^{s ( p ) }\,dg, $$

where

$$ s ( p ) =2\min \bigl( ( 1/p ) , \bigl( 1/p^{\prime } \bigr) \bigr) . $$

(44)

Proof

Consider the analytic family of operators $S_{\psi _{z}}$ with kernels

$$ \psi_{z} ( g ) =\bigl \vert \psi ( g ) \bigr \vert \varphi_{-i\eta _{\varGamma }} ( g )^{s ( p ) -z},\quad z\in \mathbb{C} \text{.} $$

If $\operatorname{Re}z=1$, then by Proposition 4, $S_{\psi _{z}}$ is bounded on L ² and

Similarly, if $\operatorname{Re}z=0$, then $S_{\psi _{z}}$ is bounded on L ¹ and

$$ \Vert S_{\psi _{z}}\Vert _{1\rightarrow 1}\leq \int_{G} \bigl \vert \psi ( g ) \bigr \vert \varphi_{-i\eta _{\varGamma }} ( g )^{s ( p ) }\,dg. $$

The conclusion for 1<p<2 follows by complex interpolation. The case p>2 follows by duality. □

4 Proof of Theorem 1

We start by performing a kernel decomposition. Let ζ be a K-bi-invariant function in G with compact support, and define

$$ \kappa^{0}=\zeta \kappa,\qquad \kappa^{\infty }= ( 1-\zeta ) \kappa . $$

Denote by $S_{\kappa }^{0}$ and $S_{\kappa }^{\infty }$ the operators with kernels κ ⁰ and κ ^∞.

As it is mentioned in the Introduction, the boundedness of $S_{\kappa }^{0}$ on L ^p follows exactly as in [35, Proposition 13]. It therefore remains to prove the L ^p-boundedness of $S_{\kappa }^{\infty }$. According to Proposition 7, for p∈(1,∞) we have that

(45)

where s is defined in (44).

Therefore, to finish the proof of Theorem 1 we have to show that if $m\in \mathcal{M} ( v,N )$, then the integral above is finite.

To prove (45) we follow the proof of Proposition 5 in [4]. For the sake of completeness, we state this proof below. It will be given in steps.

Step 1. The modification of the kernel on the Abel transform side. To estimate the integral in (45), we shall estimate κ ^∞ over concentric shells. Let

$$ V_{r}= \bigl\{ H\in \mathfrak{a}:\vert H\vert \leq r \bigr\} $$

be the Euclidean ball in $\mathfrak{a}$ and set

$$ V_{r}^{+}=V_{r}\cap \overline{ \mathfrak{a}_{+}}= \bigl\{ H\in \overline{\mathfrak{a}_{+}}:\vert H\vert \leq r \bigr\} , $$

and

$$ U_{r}= \bigl\{ x=k_{1} ( \exp H ) k_{2}\in G:k_{1},k_{2}\in K,H\in V_{r}^{+} \bigr\} =K \bigl( \exp V_{r}^{+} \bigr) K. $$

Using the Cartan decomposition $G=K\exp \overline{\mathfrak{a}_{+}}K$, the integral in (45) is written as

$$ I:=\sum_{j\geq 1}\int_{U_{j+1}\backslash U_{j}}\bigl \vert \kappa^{\infty } ( g ) \bigr \vert \varphi_{-i\eta _{\varGamma }} ( g )^{s}\,dg=\sum_{j\geq 1}I_{j}. $$

(46)

To estimate the integrals I _j we follow Anker [4, p. 606], and modify the kernel κ ^∞ on the Abel transform side by removing the frequencies in V _j . For that, we need a family of W-invariant cut-off functions $\omega_{j}^{\infty }$, j=1,2,… . Let ω ^∞∈C ^∞(ℝ) with ω ^∞≡0 on (−∞,0] and ω ^∞≡1 on [1,∞). Consider the functions

$$ \omega_{j}^{\infty } ( H ) =\prod_{w\in W} \omega^{\infty } \bigl( j-(w.\rho) ( H ) \bigr) ,\quad H\in \mathfrak{a}. $$

These satisfy the following.

• (i) $\omega_{j}^{\infty }\in C^{\infty } ( \mathfrak{a} )^{W}$, with $\omega_{j}^{\infty }\equiv 1$ on V _j−1, and $\omega_{j}^{\infty }\equiv 0$ on $V_{j}^{c}$.

• (ii) $\vert \partial^{\alpha }\omega_{j}^{\infty }\vert \leq c$, for all multi-indices α.

Set $\ell =\mathcal{F}^{-1}m=\mathcal{A}\kappa$. Since κ∈S(K∖G/K), according to diagram (21), $\ell \in S ( \mathfrak{a} )^{W}$. Write

$$ \ell =\omega_{j}^{\infty }\ell + \bigl( 1-\omega_{j}^{\infty } \bigr) \ell =\omega_{j}^{\infty }\ell +\varOmega_{j}^{\infty } \ell . $$

We set $\ell_{j}^{\infty }=\varOmega_{j}^{\infty }\ell$. Since $\ell_{j}^{\infty }\in S ( \mathfrak{a} )^{W}$, then $\mathcal{A}^{-1}\ell_{j}^{\infty }=\kappa_{j}^{\infty }\in S ( K\backslash G/K )$ and $\mathcal{F}\ell_{j}^{\infty }=m_{j}^{\infty }\in S ( \mathfrak{a}^{\ast } )^{W}$.

Since $\operatorname{supp} ( \ell_{j}^{\infty } ) \subset V_{j}^{c}$, by the support’s conservation property (22) of Abel’s transform, we get that $\kappa_{j}^{\infty }=\kappa$ on $U_{j}^{c}$, i.e., the modification does not affect the values of κ ^∞ on the shell U _j+1∖U _j . This allows us to replace κ by $\kappa_{j}^{\infty }$ in the integral I _j appearing in (46) and write

$$ I_{j}=\int_{U_{j+1}\backslash U_{j}}\bigl \vert \kappa_{j}^{\infty } ( g ) \bigr \vert \varphi_{-i\eta _{\varGamma }} ( g )^{s}\,dg. $$

Step 2. Estimation of I _j . By Cauchy–Schwarz’s inequality we have

$$ I_{j}\leq \biggl( \int_{U_{j+1}\backslash U_{j}} \varphi_{-i\eta _{\varGamma }} ( g )^{s}\,dg \biggr)^{1/2}\bigl \Vert \kappa_{j}^{\infty }\bigr \Vert _{2}. $$

(47)

By the estimate (16) of $\varphi_{-i\eta _{\varGamma }}$ and (14) we get

(48)

since s∈(0,1) and $\operatorname{vol} ( V_{j+1}^{+}\backslash V_{j}^{+} ) \leq j^{a-1}$.

From (48) and (47) we get that

$$ I_{j}\leq ce^{v\vert \rho \vert j}j^{ ( a-1 ) /2}\bigl \Vert \kappa_{j}^{\infty }\bigr \Vert _{2}, $$

(49)

for every

where v _Γ (p) is defined in (7).

Step 3. Estimation of $\Vert \kappa_{j}^{\infty }\Vert _{2}$. We set b=n−a, and let b′ be the smallest integer ≥b/2. Set N=[a/2]+b′+1. We shall prove that

$$ \bigl \Vert \kappa_{j}^{\infty }\bigr \Vert _{2}\leq cj^{-N}e^{-v\vert \rho \vert j}. $$

(50)

Recall that $\kappa_{j}^{\infty }=\mathcal{H}m_{j}^{\infty }$. By Plancherel’s theorem for the spherical Fourier transform and the estimate |c(λ)|⁻²≤c〈λ〉^b, we obtain

(51)

since b′≥b/2.

Now, the estimation of the integral above is a purely Euclidean problem. Bearing in mind that $m_{j}^{\infty }=\mathcal{F}\ell_{j}^{\infty }$ and using Plancherel’s theorem for the Euclidean Fourier transform, we obtain that

(52)

since $\ell_{j}^{\infty }=\varOmega_{j}^{\infty }\ell$ and $\operatorname{supp}( \varOmega_{j}^{\infty } ) \subset \mathfrak{a}\backslash V_{j-1}$.

As in [4, p. 607] we now set

$$ \operatorname{Cosh}_{v\rho } ( H ) =\frac{1}{\vert W\vert }\sum_{w\in W}e^{v ( w.\rho ) ( H ) },\quad H\in \mathfrak{a}. $$

Since |H|≥cj and $\operatorname{Cosh}_{v\rho } ( H ) \geq ce^{v\vert \rho \vert j}$ if $H\in \mathfrak{a}\backslash V_{j}$, it follows that

(53)

We observe here that the analyticity of m(λ) in the tube $\mathcal{T}^{v}=\mathfrak{a}^{\ast }+ivC_{\rho }$, allows us to change the path of the integration and obtain that the Euclidean Fourier transform of the function

$$ H\longrightarrow \otimes^{\gamma } ( iH ) \operatorname{Cosh}_{v\rho } ( H ) \partial^{\alpha }\ell ( H ) \text{ } $$

is given by

$$ \partial_{\lambda }^{\gamma } \biggl\{ \frac{1}{\vert W\vert }\sum_{w\in W}\otimes^{\alpha } \bigl( \lambda +iv ( w.\rho ) \bigr) m \bigl( \lambda +iv ( w.\rho ) \bigr) \biggr\} . $$

(54)

Combining (52), (53), (54), using the W-invariance of m, and the Euclidean Plancherel theorem, we obtain that

(55)

Finally, using the symbol estimates (2) for m(λ), from (55) it follows that

$$ \biggl( \int_{\mathfrak{a}}\bigl \vert \partial^{\alpha } \ell_{j}^{\infty } ( H ) \bigr \vert ^{2}\,dH \biggr)^{1/2}\leq c\int_{\mathfrak{a}^{\ast }} \langle \lambda \rangle^{2 ( b^{\prime }-N ) }\,d\lambda . $$

(56)

Putting together (51), (52), and (56), we get

This completes Step 3.

Step 4. End of proof of Theorem 1. Putting together the estimates (49) and (50) we have that

since N−(a−1)/2>1.