A Spaceborne Gravity Gradiometer Concept Based on Cold Atom Interferometers for Measuring Earth’s Gravity Field

Abstract

We propose a concept for future space gravity missions using cold atom interferometers for measuring the diagonal elements of the gravity gradient tensor and the spacecraft angular velocity. The aim is to achieve better performance than previous space gravity missions due to a very low white noise spectral behavior and a very high common mode rejection, with the ultimate goals of determining the fine structures of the gravity field with higher accuracy than GOCE and detecting time-variable signals in the gravity field better than GRACE.

Introduction

Launched in 2002, the Gravity Recovery and Climate Experiment (GRACE) mission (Tapley et al. 2004) measures changes in the Earths gravity field, exploiting low-low satellite-to-satellite tracking (SST) using microwave K/Ka-band ranging and, like for CHAMP launched in 2000 (Reigber et al. 1999), high-low SST using GPS. The Gravity field and steady-state Ocean Circulation Explorer (GOCE) satellite (Floberghagen et al. 2011), launched in 2009, exploits high-low SST using GPS and, for the first time, gravity gradiometry. Continuing these successful gravity mission series, GRACE Follow-On (launch planned in 2017) will exploit low-low SST using K/Ka-band ranging and, as a demonstrator, laser ranging as well as high-low SST (Sheard et al. 2012). Future mission concepts like GRACE 2 or ESAs Next Generation Gravity Mission focus on low-low SST using laser ranging (Silvestrin et al. 2012). Electrostatic gravity gradiometers approach their ultimate performances, even if some improvement could be realized (Zhu et al. 2013).

In the past decades, it has been shown that atomic quantum sensors have the potential to drastically increase the performance of inertial measurements (Peters et al. 2001; Sorrentino et al. 2014). These inertial sensors present a very low and spectrally white noise as opposed to classical accelerometers, which present colored noise. Recent results in different labs show that it is possible to build a reliable system for using atom interferometry on vehicles (Wu 2009; Bidel et al. 2013) and for space applications (Yu et al. 2006; Sorrentino et al. 2010; Geiger et al. 2011). These last developments prove that this technology, which is already suitable on ground vehicles, is competitive with classic inertial sensors. Some developments already worked in zero-g environment in the drop tower facility in Bremen, Germany (Müntinga et al. 2013), or in a 0g plane (Geiger et al. 2011) and are the state-of-the-art of compact setups aiming for spaceborne platform. Depending on the application current developments are now limited to a single component measurement (Sorrentino et al. 2014), or limited to a short interaction time due to gravity field on the ground (Jiang et al. 2013), or dedicated to fundamental physics such as Weak Equivalence Principle (Sorrentino et al. 2010; Bonin et al. 2013) or the detection of gravitational waves (Barrett et al. 2013).

We propose here a concept using cold atom interferometers for measuring all diagonal elements of the gravity gradient tensor and the full spacecraft angular velocity in order to achieve better performance than the GOCE gradiometer over a larger part of the spectrum, with the ultimate goals of determining the fine structures and time-variable signals in the gravity field better than today. This concept relies on a high common mode rejection (Bonin et al. 2013) and a longer interaction time due to micro gravity environment, which will a provide better performance than any other cold atom interferometer on the ground, as already shown by a spectacular amelioration of the sensitivity using high fountain (Dickerson et al. 2013).

Principle of an Atom Interferometer

Although the wave nature of matter has been known since de Broglie, practical applications of matter waves have not been forthcoming until the appropriate techniques were devised and combined to cool, trap and manipulate atom ensembles and atom beams. These techniques have been continuously refined over nearly three decades resulting in the field of (cold) atom interferometry (AI) and the development of a host of laboratory instruments operating as inertial sensors or used for fundamental physics experiments.

Environmental vibrations, gravity fluctuations, and the presence of gravity effects that curb the interferometer interaction time currently limit the performance of atom interferometers on the ground. The operation of an atom interferometer in space under suitable conditions, i.e. in microgravity environment, will enable hitherto unachievable performance and allow for ultra precise measurements not possible on the ground. At low altitude residual drag can still exist but provided it is compensated to less than few mN this should not affect the measurements as the vibrations are rejected.

Atom interferometry will enable the realization of inertial and gravity sensing payloads with unprecedented sensitivity. Future Earth gravity missions will require gradiometers with sensitivity in the order of $1\;mE/\sqrt {Hz}$ (1 E = 10⁻⁹ s ⁻²) over a wide spectral range. Atom interferometers with a baseline in the range of 1 meter are expected to meet this requirement and can be used for the realization of next-generation gravity gradiometer payloads (Silvestrin et al. 2012). The main advantages of this technology are a flat noise power spectral density even for low frequency measurements with very good repeatability, no hard moving parts and an intrinsically accurate measurement thanks to the stability of the atom transitions.

Atom interferometers rely on the wave-particle duality, which allows matter waves to interfere, and on the superposition principle. They can be sensitive to inertial forces. We present here the principle of a Chu-Bordé interferometer with ⁸⁷ Rb, which can be extended to any kind of inertial sensors such as a gravimeter (Peters et al. 2001), a gyroscope (Canuel et al. 2006) or a gravity gradiometer (Sorrentino et al. 2014). In a Chu-Bordé interferometer the test mass is a cloud of cold atoms, which is obtained from a Magneto-Optical Trap (MOT) by laser cooling and trapping techniques. This cloud of cold atoms is released from the trap and its acceleration due to external forces is measured by an atom interferometry technique. A Chu-Bordé interferometer consists in a sequence of three equally spaced Raman laser pulses (Kasevich and Chu 1991), which drive stimulated Raman transitions between two stable states of the atoms. In the end, the proportion of atoms in the two stable states depends sinusoidally on the phase of the interferometer Φ, which is proportional to the acceleration of the atoms along the Raman laser direction of propagation. The Chu-Bordé interferometer in a double diffraction scheme (see Fig. 1) allows to enlarge the sensitivity by a factor 2, and to suppress at first order parasitic effects such as light shift, magnetic field, as the atoms remain in the same internal state (Lévèque et al. 2009; Giese et al. 2013). Phase shifts of this effects will be detailed in Section 1.

Fig. 1

(Color online) The double diffraction scheme for one cloud of atoms. Figure from (Tino et al. 2013)

In presence of an acceleration a = a _M + γ(z−z _M ) the trajectories of the atoms can be calculated using the Euler-Lagrange equation. In micro-gravity, a _M is the acceleration experienced by the inertial reference, which is the mirror in Fig. 1. z and z _M are the position of the atom cloud and the mirror, respectively, in the instrument frame. We decide by convention z _M = 0. The gradient force is $\gamma =V_{zz}-{\Omega }^{2}$, where V _zz is the diagonal element of the gravity gradient tensor along z-axis defined by the Raman laser, and ${\Omega }^{2}={\omega _{x}^{2}}+{\omega _{y}^{2}}$ is the rotation rate of the instrument. The initial position of the atom is z _A , with an initial velocity v ₀ along z. A Raman pulse (called π/2 Raman pulse) of duration $\tau _{s}=\frac {\pi }{{\Omega }_{eff}\sqrt {2}}$, where Ω _eff is the Rabi effective frequency, produces a coherent superposition between two momentum states. Due to the Raman interaction, the clouds of atoms receive a 2 photons recoil velocity in the opposite direction. $\frac {\hbar k_{eff}}{2m}$ is the 2 photons recoil velocity due to Raman interaction (Lévèque et al. 2009), where m is the mass of the atom and $k_{eff}\approx \frac {8\pi }{\lambda }$ is the effective wave vector of the Raman transition. After free falling during a time T the atoms are positioned at z _B and z _D . A 4 photons recoil velocity in opposite direction via a so-called π pulse (of duration $\tau _{m}=\sqrt {2}\pi /{\Omega }_{eff}$) is then given and after a time $T^{\prime }$ a last π/2 pulse is given to the atoms to recombine the atom interferometers at positions z _C and $z_{C^{\prime }}$ (see Fig. 1).

$$ \begin{array}{l l} z_{A}=z_{0} \\ \begin{array}{l l}z_{B}=&\frac{a_{M}}{\gamma}+\left( z_{0}-\frac{a_{M}}{\gamma}\right)\cdot ch\left(\sqrt{\gamma}T\right) \\&+\left(\frac{v_{0}}{\sqrt{\gamma}}+\frac{\hbar k_{eff}}{2m\sqrt{\gamma}}\right)\cdot sh\left(\sqrt{\gamma}T\right) \end{array}\\ \begin{array}{l l}z_{D}=&\frac{a_{M}}{\gamma}+\left( z_{0}-\frac{a_{M}}{\gamma}\right)\cdot ch\left(\sqrt{\gamma}T\right)\\&+\left(\frac{v_{0}}{\sqrt{\gamma}}-\frac{\hbar k_{eff}}{2m\sqrt{\gamma}}\right)\cdot sh\left(\sqrt{\gamma}T\right) \end{array}\\ \begin{array}{l l}z_{C}=&\frac{a_{M}}{\gamma}+\left( z_{0}-\frac{a_{M}}{\gamma}\right)\cdot ch\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)\\&+\left(\frac{v_{0}}{\sqrt{\gamma}}+\frac{\hbar k_{eff}}{2m\sqrt{\gamma}}\right)\cdot sh\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)\\&-\frac{\hbar k_{eff}}{m\sqrt{\gamma}}sh\left(\sqrt{\gamma}T^{\prime}\right)\end{array}\\ \begin{array}{l l}z_{C^{\prime}}=&\frac{a_{M}}{\gamma}+\left( z_{0}-\frac{a_{M}}{\gamma}\right)\cdot ch\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)\\&+\left(\frac{v_{0}}{\sqrt{\gamma}}-\frac{\hbar k_{eff}}{2m\sqrt{\gamma}}\right)\cdot sh\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)\\&+\frac{\hbar k_{eff}}{m\sqrt{\gamma}}sh\left(\sqrt{\gamma}T^{\prime}\right)\end{array} \end{array} $$

(1)

The matter wave phase at the end of the interferometer is given by (Bordé 2001):

$$ \begin{array}{l l} \begin{array}{l l}{\Phi} &= \frac{{\Phi}_{ABDC}+{\Phi}_{ABDC^{\prime}}}{2}\\&=k_{eff}\left(z_{C^{\prime}}-z_{B}-z_{D}+z_{A}\right)+\frac{1}{2}k_{eff}\left(z_{C}-z_{C^{\prime}}\right) \\ &=k_{eff}\left[\begin{array}{l l}\left( z_{0}-\frac{a_{M}}{\gamma}\right)\cdot \left(\begin{array}{l l}1+ch\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)\\-2ch\left(\sqrt{\gamma}T\right)\end{array}\right)\\+\frac{v_{0}}{\sqrt{\gamma}}\cdot \left(sh\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)-2sh\left(\sqrt{\gamma}T\right)\right)\end{array}\right] \\ &\approx k_{eff} \left[\left( z_{0}-\frac{a_{M}}{\gamma}\right)\left(\gamma T^{2}+\frac{7}{12}\gamma^{2}T^{4}\right)+v_{0}\gamma T^{3}\right]\end{array} \end{array} $$

(2)

It is possible to suppress a _M by measuring simultaneously different atom interferometers (Sorrentino et al. 2014; Dickerson et al. 2013). On Fig. 2 as the inertial reference being common to the 4 different atom interferometers, the high common rejection cancels the vibration noise and combining Φg ₁ and Φg ₂ (or Φg ₃ and Φg ₄) we can precisely measure the rotation rate ω _x , knowing precisely $\vec {v}$ along y-axis. This is due to the measurement of the Coriolis effect $2\vec {\Omega }\times \vec {v}$ along z-axis. Combining Φg ₁ and Φg ₃ (or Φg ₂ and Φg ₄) allows to measure γ, relying on the precise knowledge of the distance between the atom clouds. Applying this measurements in the 3 orthogonal directions (see Section 1), the full angular velocity $\vec {\Omega }$ is simultaneously measured, thus we have direct access to all diagonal elements of the gravity gradient tensor V _xx ,V _yy ,V _zz .

Fig. 2

(Color online) Combining 4 atom interferometers to measure both gravity gradient and rotation rate

Due to force gradient, the interferometer is not perfectly closed. The distance at the end of the interferometer is proportional to the 4 photons recoil velocity $4v_{rec}=\frac {\hbar k_{eff}}{m}$:

$$ \begin{array}{l l}{\Delta} z&=z_{C}-z_{C^{\prime}}\\ &=\frac{\hbar k_{eff}}{m\sqrt{\gamma}}\cdot\left[sh\left(\sqrt{\gamma}\left(T+T^{\prime}\right)\right)-2sh\left(\sqrt{\gamma}T^{\prime}\right)\right]\\&\approx 4v_{rec}\gamma T^{3} \end{array} $$

(3)

As in optical interferometers we introduce a coherence length of the atoms, which is defined by the wavelength of De Broglie, directly dependent on the temperature Θ of the atoms.

$$ \lambda_{DB}=\frac{h}{\sqrt{2\pi mk_{B}{\Theta}}} $$

(4)

For example Table 1 reports the different coherence lengths needed, in relation to the temperature.

Table 1 Type of cold atom clouds needed for different interrogation time

A Bose Einstein Condensate (BEC) is required for T = 5 s. Even if it is possible to close the interferometer by changing $T^{\prime }$ (Roura et al. 2014), the maximum temperature estimated by the extension of the cloud of the atoms, has to be lower than 10 nK which corresponds to a cloud extension of 1 mm/s. To avoid loss of contrast due to the initial velocity distribution of the atom source, a point source interferometry (PSI) scheme (Dickerson et al. 2013) should be used to simultaneously detect the differential acceleration of 2 clouds of atoms. As the scheme relies on differential acceleration measurements between two correlated, simultaneously operated atom interferometers (separated by a baseline d), then the error per measurement on the gravity gradient is:

$$ \sigma_{\gamma}=\sigma_{\Phi}\cdot\frac{1}{k_{eff}}\cdot\frac{1}{T^{2}}\cdot\frac{\sqrt{2}}{d} $$

(5)

The error on the phase is $\sigma _{\Phi }=\frac {1}{SNR}$. The signal to noise ratio (SNR) depends on the detection system and the standard quantum limit (SQL). It is possible to reject the detection noise by a very low noise detection system (Biedermann et al. 2009), but some time is necessary until the interferometer output ports are separated for simultaneous detection. For a separation of 2.5 cm, 1 s is needed before detection. Limited by the SQL means that the SNR is proportional to the square root of the number N of atoms in the interferometer. With typically N = 10⁶ atoms, it is reasonable to assume a phase noise due to the detection at the level of 1 mrad as current state of the art.

Concept of a Spaceborne Gravity gradiometer Based on Laser-Cooled Atom Interferometry

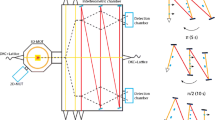
Figure 3 describes the gravity gradiometer concept in one dimension. This one-dimensional concept consists in measuring one diagonal element of the gravity tensor (V _zz ) and the rotation rate along the x-axis. It can be extended to the other two dimensions in order to obtain the full diagonal elements of the gravity gradient tensor and the full angular rate vector.

Fig. 3

(Color online) Scheme of the vacuum chamber (not drawn to scale; orientative sizing). The red arrows represent the Raman lasers for the interferometry part; the blue arrows represent the light pulse giving the transverse velocity v _trans ; the green arrows represent the light pulses guiding the atoms from the cooling room to the interferometer room; the blue rectangle is the mirror, which will be the inertial reference

Preparation of the 4 Cold Atoms Test Masses

Two clouds of atoms are symmetrically prepared along the y-axis. In order to reach ultra-high vacuum inside the vacuum chamber and the high atom number required for efficient evaporative cooling, the MOT is loaded from a 2D-MOT flux (Schoser et al. 2002). The atoms are launched along y-axis with a precise velocity $\left |\left |\vec {v}\right |\right |=v_{trans}$ corresponding to 2 cycling transitions resulting in a 4 photons recoil velocity (v _trans = 4.v _rec = 2.5 cm/s). The laser providing this recoil moment is represented by a blue arrow in Fig. 3 and is common to the 2 MOTs. This will define the longitudinal axis for the rotation measurement. As the cloud of atoms is moving along y-direction, it is possible to load a new MOT for the following measurement while preparing the BEC: the moving atoms are first stopped by an opposite 2 cycling transition, then the BEC is prepared before first mentioned recoil laser is used to simultaneously move the second MOT in preparation and the BEC. Then a high recoil laser pulse (Chiow et al. 2011) splits each cloud of atom in two and brings the 4 clouds to the interferometer rooms (green arrows in Fig. 3) along the z-axis. This defines the gradient axis. A second high recoil pulse brings them back to a parallel launch. With a 100 recoils velocity pulse it is thus possible to bring the atoms in the 50 cm separated interferometer rooms in 0.8 s. As the interferometer time can be assumed to be 2T = 10 s, the distance between two counter-propagating BEC is 25 cm in the interferometer sequence.

In order to reach 10⁶ atoms at the end of each interferometer, the proposed source system is beyond current state of the art and will require a further detailed study, as many losses can occur after loading MOT, evaporating process and high recoil laser pulse.

Interferometer Sequence

The Chu-Bordé interferometer is realized by using a double diffraction scheme with two counter-propagating Raman lasers (red arrows in Fig. 3). It is thus possible to have a gradiometer by measuring the acceleration of two clouds of cold atoms from two MOTs separated by d = 50 cm. The use of counter-propagating atomic clouds allows measurements of the rotation rate along the x-axis (rotation axis).

As the interferometer is then delocalized it is also possible to prepare cold atoms during the interferometric sequence and then reduce the cycling time below the time of the interferometer measurement. It is thus possible to have a quasi-continuous measurement by launching atoms at a high frequency, limited by the time T _cycle to produce cold atoms. Thus the interferometer will produce measurements for f < 1/T _cycle . Best performances reported up to date are a BEC of 10⁴ atoms loaded in 1 s (van Zoest et al. 2010). We can expect for future experiments a BEC of few 10⁶ atoms loaded in T _cycle = 1 s (Müntinga et al. 2013), on condition that no parasitic stray will perturb the preparation of the BEC, especially from the near MOT loading.

According to Eq. 5 and considering that the interferometer noise is limited by the quantum projection noise with N = 10⁶ atoms, the sensitivity that can be reached is given by the following expression, for f < 1/(2T):

$$ \begin{array}{l l} {\Delta}\gamma=\frac{\sqrt{2}}{\sqrt{N}\cdot k_{eff}\cdot d\cdot T^{2}}\cdot \sqrt{T_{cycle}}=3.5\;mE/\sqrt{Hz} \\ {\Delta}\omega=\frac{1}{2\cdot \sqrt{N}\cdot k_{eff}\cdot v_{trans}\cdot T^{2}}\cdot \sqrt{T_{cycle}}=25\;prad.s^{-1}/\sqrt{Hz} \end{array} $$

(6)

As the time between each measurement is shorter than the interferometer time, for 1/(2T) < f < 1/T _cycle the sensitivity is increased by a factor (2T.f)^1/2 (see Fig. 4).

Fig. 4

(Color online) Comparison between classical (GOCE)/quantum concepts for a space gradiometer

Extension to the Three Directions

The scheme shown on Fig. 3 has to be duplicated in the 3 directions to have all diagonal elements of the gravity gradient tensor V _xx ,V _yy ,V _zz and the angular rate vector $\vec {\Omega }$.

In order to avoid any overlap between the different laser pulses the π pulse in the middle of the interferometer can not be done anymore. Instead, having 4 Raman pulses for the interferometer sequence allows duplicating this one-dimensional concept in the three directions and then measuring the full diagonal elements of the gravity gradient tensor and the full angular rate vector.

Fig. 5

(Color online) Time sequence for measuring the diagonal elements of the gravity tensor and the rotation rates. The arrows indicate one point measurement

The height of each interferometer is v _rec .T = 20 cm. This can be reduced by a factor 2 by implementing a Ramsey-Bordé interferometer with four pulses π/2 separated by T1 = 2.5 s, T2 = 5 s, T3 = T1 = 2.5 s, in which case the sensitivity is degraded by a factor 4/3, thus:

$$ \begin{array}{l l} {\Delta}\gamma=4.7\;mE/\sqrt{Hz} \\ {\Delta}\omega=35\;prad.s^{-1}/\sqrt{Hz} \end{array} $$

(7)

Due to losses at the second and third pulse, 4.10⁶ atoms have to be loaded before the interferometer to achieve this sensitivity. Moreover the orientation of the magnetic field in the different parts of the system implies a careful shielding to avoid crosstalk between the fields as:

• The bias fields during interferometry must be in the direction of the Raman beams.

• The bias field for launching atoms after 3D-MOT field and the BEC after evaporation must be perpendicular to the splitting field which moves the atoms into the two interferometry zones.

To avoid any overlap between the different laser functions the time sequences also have to be very well controlled, as follows on Fig. 6.

Fig. 6

(Color online) Time sequence for measuring the diagonal elements of the gravity tensor and the rotation rates. The arrows indicate one point measurement

External Noise Sources

Gravity measurement by atom interferometry is an absolute measurement, as the interferometric phase only relies on atomic transitions. Thus other phase contributions have to be very well determined to reach the desired high sensitivity. These phase contributions have different origins:

• Energy modification of the hyperfine structure of the Rubidium (Zeeman effect, AC Stark shift).

• Axis of measurement (Wavefront curvature of the Raman laser, verticality of the axis).

• Non-gravitational forces (Centrifugal acceleration, Coriolis force).

As the atoms are sensitive to the magnetic field, for a Chu-Bordé interferometer the dependence is proportional to the gradient of the magnetic field along the interferometer: δ Φ = α⋅B ₀⋅∇B⋅L⋅T where α = 2π.575 Hz/G ² for ⁸⁷ Rb m _F = 0, B ₀ = 1 mG is the magnetic field applied during the interferometer sequence to avoid Zeeman transitions (Peters et al. 2001) and L is the longitudinal length of the interferometer.

Due to matter-light interaction during Raman pulses, the AC Stark shift affects also the energy of the Rb. The first order phase shift is given by Peters et al. (2001):

$$ {\Delta}{\Phi}^{AC}=\frac{\delta_{4}^{AC}-\delta_{1}^{AC}}{{\Omega}_{eff}} $$

(8)

$\delta _{1}^{AC}$ (resp. $\delta _{4}^{AC}$) is the Stark shift during the first (resp. last) pulse. With a well-defined ratio between the intensity of the Raman lines I ₁ and I ₂ it is thus possible to cancel this effect (Peters et al. 2001).

Using the double diffraction scheme allows us to suppress these effects on the energy levels as the atoms remain in the same state, on condition that there is no magnetic field gradient and the Raman intensities do not fluctuate during the interferometer sequence.

Due to the expansion of the cloud of atoms, the wavevector defined by the Raman lines is not the same for different class of velocity of the atoms (Louchet-Chauvet et al. 2011), the error in acceleration on each cloud is at first order $\frac {{\sigma _{v}^{2}}}{R}$ where R is the wavefront curvature of the laser and σ _v = 1 mm/s for a temperature of the cloud Θ = 10 nK. For differential measurements, the error on the phase is $\delta \phi =k_{eff}T^{2}{\sigma _{v}^{2}}\frac {\delta R}{R^{2}}$ where δR is the differential wavefront curvature of the lasers.

The axis of the Raman laser has to be well determined as the measurement is done along this axis. The relative error on the gravity gradient is half of the square of the angle error of the axis (attitude control of the laser direction), i.e. $\theta <2\sqrt {\Delta \gamma /\gamma }$.

Finally, using the interferometer as a gradiometer cancels common mode vibrations, and using it as a gyroscope leads to know the Coriolis force (considering v _⊥ < σ _v ), thus the centrifugal force that is a systematic effect on the gravity gradient measurement.

The Table 2 gives the required maximum incertitude to reach on these different contributions on the interferometric phase, in order to get below a sensitivity of 1 mrad phase noise.

Table 2 External sources and minimum knowledge of these sources to achieve 1 mrad noise on the interferometric phase

Conclusion and Outlook

A concept of gravity gradiometer based on cold atom interferometer techniques is proposed. This instrument allows reaching sensitivity of $3.5\;mE/\sqrt {Hz}$, with the promise of a flat noise power spectral density also at low frequency, and a very high accuracy on rotation rates. New techniques allow us to go beyond the SQL limit with squeezed state or Information-recycling beam splitters (Gross and squeezing 2012; Haine 2013). At best it is possible to reach the Heisenberg limit, i.e. to have a SNR proportional to N. The phase noise could be extended at best to 1 μrad with these new techniques (Gross and squeezing 2012; Haine 2013), on condition than other noise sources can be consistent with this limit.

Estimation of the Earth gravity field model from the new gravity gradiometer concept has to be evaluated taking into account different system parameters such as attitude control, altitude of the satellite, time duration of the mission, etc., which is the subject of a separate analysis.

In the meantime as long as this gravity gradiometer concept is not yet available, hybridization between quantum and classical techniques could be an option to improve the performance of accelerometers on next generation gravity missions. This could be achieved as it is realized in frequency measurements where quartz oscillators are phase locked on atomic or optical clocks (Vanier 1979). This technique could correct the spectrally colored noise of the electrostatic accelerometers in the lower frequencies.