On prime degree isogenies between K3 surfaces

Abstract

We classify prime order isogenies between algebraic K3 surfaces whose rational transcendental Hodge structures are not isometric. The morphisms of Hodge structures induced by these isogenies are correspondences by algebraic classes on the product fourfolds; however, they do not satisfy the hypothesis of the well-known Mukai–Nikulin theorem. As an application we describe isogenies obtained from K3 surfaces with an action of a symplectic automorphism of prime order.

1 Introduction

Let X and Y be two complex projective K3 surfaces. The Hodge conjecture predicts that every Hodge class $Z\in \mathrm{{H}}^4(Y\times X, \mathbb Q)\cap \mathrm{{H}}^{2,2}(Y\times X)$ is algebraic (see e.g. [3, §6.4]). By Künneth decomposition, the question reduces to the study of the Hodge classes Z in $\mathrm{{H}}^2(Y,\mathbb Q)\otimes \mathrm{{H}}^2(X,\mathbb Q)$. This data is equivalent to a morphism $\phi$ of weight two rational Hodge structures between $\mathrm{{H}}^2(Y,\mathbb Q)$ and $\mathrm{{H}}^2(X,\mathbb Q)$, where $\phi$ is nothing else than the correspondence induced by the class Z. Since the rational transcendental lattice of a K3 surface has an irreducible Hodge structure of weight two, the morphism $\phi$ decomposes as the sum of a Hodge morphism $\phi _{\mathrm{{T}}}$ between the rational transcendental lattices $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$, which is either trivial or an isomorphism, and a morphism $\phi _{\mathrm{{NS}}}$ between the rational Néron–Severi lattices $\mathrm{{NS}}(Y)_\mathbb Q$ and $\mathrm{{NS}}(X)_\mathbb Q$. The morphism $\phi _\mathrm{{NS}}$ is automatically induced by an algebraic correspondence by the Lefschetz theorem on (1, 1)-classes, so the question finally reduces to the algebraicity of the correspondence $\phi _\mathrm{{T}}$.

There is a wide literature on the topic, especially when $X=Y$ (see e.g. [5, 6, 10–13, 15, 16, 19, 20]). One of the most famous results is due to Mukai [16, Corollary 1.10] and Nikulin [19]: if ${{\mathrm{rk}}}\mathrm{{NS}}(Y)\ge 5$ and if $\phi _\mathrm{{T}}$ is an isometry, then $\phi _\mathrm{{T}}$ is algebraic. A generalization of this result to any projective K3 surfaces has been recently announced by Buskin [4]. Here the term “isometry” means isometry of rational quadratic spaces. However the Hodge conjecture predicts that any homomorphism of rational transcendental Hodge structures of K3 surfaces is induced by an algebraic cycle, without requiring that it is an isometry. The question addressed in this paper is thus the following: can non-isometric rational transcendental Hodge structures of K3 surfaces be related by an algebraic correspondence? An example was given by van Geemen and the second author in [9, Proposition 2.5] where the Hodge isomorphism between the rational transcendental lattices is induced by an isogeny of degree two between a K3 surface X and the minimal resolution Y of its quotient by a symplectic involution. This example was a motivation for us to study more in general the Hodge isomorphisms induced by isogenies between K3 surfaces in the context of the Hodge conjecture.

As noted by Morrison [13], the term “isogeny”, when applied to K3 surfaces, has several conflicting definitions in the literature. In this paper we follow the definition of Inose [10]: an isogeny between two complex projective surfaces X and Y is a rational map of finite degree $\gamma :X\dashrightarrow Y$. Following Inose [10], the rational map $\gamma$ induces an isomorphism of rational Hodge stuctures $\gamma ^*:\mathrm{{H}}^2(Y,\mathbb Q)\rightarrow \mathrm{{H}}^2(X,\mathbb Q)$ given by an algebraic correspondence, whose component $\gamma ^*_\mathrm{{T}}:\mathrm{{T}}_{Y,\mathbb Q}\rightarrow \mathrm{{T}}_{X,\mathbb Q}$ can be described in geometric terms; in particular, one has ${{\mathrm{rk}}}\mathrm{{T}}_X={{\mathrm{rk}}}\mathrm{{T}}_Y$. The morphism $\gamma ^*_\mathrm{{T}}$ is not an isometry but it is a dilation with a scale factor p (see Sect. 2). Equivalently, $\gamma ^*_\mathrm{{T}}$ is an isometry between $\mathrm{{T}}_{Y,\mathbb Q}(p)$ (where the intersection form is multiplied by p) and $\mathrm{{T}}_{X,\mathbb Q}$. If $\mathrm{{T}}_{Y,\mathbb Q}(p)$ happens to be isometric to $\mathrm{{T}}_{Y,\mathbb Q}$, then $\gamma ^*_\mathrm{{T}}$ is closely related to an isometry of rational Hodge structures (a Hodge isometry for short): roughly speaking, $\gamma ^*_\mathrm{{T}}$ becomes an isometry after a (nonisometric) base change. The main result of this paper is a precise condition on $\mathrm{{T}}_Y$ so that there exists no isometry (in particular no Hodge isometry) between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$.

Theorem 1.1

Let $\gamma :X\dashrightarrow Y$ be an isogeny of prime order p between complex projective K3 surfaces X and Y. Then ${{\mathrm{rk}}}\mathrm{{T}}_{Y,\mathbb Q}={{\mathrm{rk}}}\mathrm{{T}}_{X,\mathbb Q}=:r$ and

• 1. If r is odd, there exist no isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$.

• 2. If r is even, there exists an isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$ if and only if $\mathrm{{T}}_{Y,\mathbb Q}$ is isometric to $\mathrm{{T}}_{Y,\mathbb Q}(p)$. This property is equivalent to the following:

  • (a) If $p=2$: for every prime number q congruent to 3 or 5 modulo 8, the q-adic valuation $\nu _q(\det \mathrm{{T}}_Y)$ is even.

  • (b) If $p>2$: for every prime number $q >2$, $q \ne p$, such that p is not a square in $\mathbb F_q$, the number $\nu _q(\det \mathrm{{T}}_Y)$ is even and the following equation holds in $\mathbb F_p^*/(\mathbb F_p^*)^2$:

    $$\begin{aligned} {{\mathrm{res}}}_p (\det \mathrm{{T}}_Y) = (-1)^{\frac{r(r-1)}{2} + \nu _p(\det \mathrm{{T}}_Y)}, \end{aligned}$$

    where ${{\mathrm{res}}}_p(\det \mathrm{{T}}_Y)$ is the residue of $\det \mathrm{{T}}_Y$ modulo p (see definition in Sect.  3).

The proof is given in Sect. 3 using several results coming from lattice theory and the theory of Witt groups that are recalled in Sect. 2. This result suggests that there is a large family of isogenies $\gamma$ that produce algebraic correspondences between nonisometric rational transcendental Hodge structures of K3 surfaces, so that the Hodge conjecture holds in this context without Mukai–Nikulin’s isometric condition. To construct concrete examples one can generalize the example given in [9, Proposition 2.5] to K3 surfaces with a symplectic automorphism of prime order:

Corollary 1.2

Let $\sigma$ be a symplectic automorphism of prime order p on a complex projective K3 surface X and let Y be the minimal resolution of the quotient $X/\langle \sigma \rangle$, which is a K3 surface with a degree p isogeny $\gamma :X\dashrightarrow Y$. If ${{\mathrm{rk}}}\mathrm{{T}}_X$ is odd, then there exists no isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$.

Note that the condition ${{\mathrm{rk}}}\mathrm{{T}}_{X}$ odd corresponds to the generic surface in the moduli space of K3 surfaces with a symplectic automorphism of order p (see Sect. 4). This corollary is a direct consequence of Theorem 1.1 since it is a special case of Inose’s construction. In Sect. 5 we give a different and completely self contained proof (the necessary background is given in Sect. 4). This second proof is of independent interest since it uses deep geometric properties of symplectic automorphisms on K3 surfaces: the key is to show the existence of a commutative diagram of blow-ups and contractions from which the properties of $\gamma ^*_\mathrm{{T}}$, and consequently of the rational quadratic spaces $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$ can be deduced by geometric arguments without using Witt theory. This diagram has been studied by Morrison [14] and van Geemen–Sarti [9] for $p=2$ and by Tan [25] for $p=3,5$. To our knowledge, the construction of the diagram for $p=7$ is new.

To conclude this paper, we discuss in Sect. 6 some classical and interesting examples of isogenies.

2 Preliminaries

2.1 Lattices

A lattice L is a free $\mathbb Z$-module of finite rank equipped with a nondegenerate integral quadratic form with integer values. The determinant of the bilinear form (computed with respect to any basis) is called the discriminant of the lattice L and is denoted ${{\mathrm{disc }}}L$.

If $M \subset L$ is a sublattice of the same rank, the quotient L / M has finite order and we have

$$\begin{aligned} {{\mathrm{disc }}}M = {{\mathrm{disc }}}L \cdot [L:M]^2. \end{aligned}$$

(1)

A sublattice $M \subset L$ is primitive if L / M is free. Then $M \oplus M^\perp$ has finite index in L and

$$\begin{aligned} {{\mathrm{disc }}}M \cdot {{\mathrm{disc }}}M^\perp = {{\mathrm{disc }}}L \cdot [L:M\oplus M^\perp ]^2. \end{aligned}$$

(2)

For any lattice L, we denote by L(n) the lattice L whose quadratic form is multiplied by $n\in \mathbb Z^*$ and by $L_\mathbb Q$ the $\mathbb Q$-vector space $L \otimes \mathbb Q$ with the induced rational quadratic form.

2.2 Classification of rational quadratic forms

We recall some classical material for which we refer to [23]. Two quadratic forms $\varphi$ and $\varphi '$ with coefficients in a field $\mathbb K$ are equivalent if there exists a linear isomorphism between them. Equivalently, their associated matrices Q and $Q'$ in any bases are congruent, i.e. there exists an invertible matrix A with coefficients in $\mathbb K$ such that $Q'= A^\top Q A$. In particular, when these quadratic forms are nondegenerate this implies that

$$\begin{aligned} \det Q \equiv \det Q'\mod (\mathbb Q^*)^2. \end{aligned}$$

(3)

This basic property will be very useful in the sequel to detect which dilations associated to isogenies cannot be related to an isometry.

Given $a_1,\ldots ,a_n\in \mathbb K$ we denote by $\langle a_1,\ldots ,a_n\rangle$ the quadratic form

$$\begin{aligned} (x_1,\ldots ,x_n)\mapsto a_1x_1^2+\cdots +a_nx_n^2. \end{aligned}$$

(4)

If the characteristic of $\mathbb K$ is different from two, any equivalence class of a quadratic form contains a representative in diagonal form (4).

Any quadratic form $\varphi$ decomposes as

$$\begin{aligned} \varphi \cong \langle 0\rangle ^{\oplus k}\oplus \langle 1, -1 \rangle ^{\oplus \ell } \oplus \varphi _a \end{aligned}$$

where $\ell \in \mathbb N$ is uniquely determined and $\varphi _a$ is the anisotropic part of $\varphi$, well-defined up to equivalence. Two regular quadratic forms $\varphi$ and $\psi$, not necessarily of the same dimension, are Witt-equivalent if their anisotropic parts $\varphi _a$ and $\psi _a$ are equivalent. The Witt-equivalence class of $\varphi$, resp. $\langle a_1, \ldots , a_n \rangle$, is denoted by $[\varphi ]_W$, resp. $\langle a_1, \ldots , a_n \rangle _W$. The orthogonal sum operation $\oplus$ defines the group law of the Witt group $W(\mathbb K)$ of Witt-equivalence classes of regular quadratic forms on $\mathbb K$.

The discriminant of a regular quadratic form $\varphi$ of dimension n is

$$\begin{aligned} \Delta (\varphi ) := (-1)^{\frac{n(n-1)}{2}} \det (\varphi ) \in \mathbb K/(\mathbb K^*)^2, \end{aligned}$$

it depends only on the Witt-equivalence class of $\varphi$. For any $r \in \mathbb Q^*$ and any prime number q, we denote by $\nu _q(r)$ the q-adic valuation of r. Writing $r = q^{\nu _q(r)} \frac{s}{t}$ where s and t are integers prime to q, the residue of r modulo q is by definition

$$\begin{aligned} {{\mathrm{res}}}_q(r) := \bar{s} \bar{t}^{-1} \in \mathbb F_q^* \end{aligned}$$

and then we set

$$\begin{aligned} \partial _q (r) := {\left\{ \begin{array}{ll} 0 &{} \text {if } \nu _q(r) \text { is even} \\ {{\mathrm{res}}}_q(r) &{} \text {if } \nu _q(r) \text { is odd.} \end{array}\right. } \end{aligned}$$

For any q, there exists a unique group homomorphism

$$\begin{aligned} \bar{\partial }_q :W(\mathbb Q) \rightarrow W(\mathbb F_q) \end{aligned}$$

such that

$$\begin{aligned} \bar{\partial }_q (\langle a_1,\ldots , a_n \rangle _W) = \langle \partial _q (a_1),\ldots ,\partial _q(a_n) \rangle _W \quad \forall a_1,\ldots ,a_n\in \mathbb Q^*. \end{aligned}$$

We recall below two classical results of Witt theory. The signature of a regular rational quadratic form $\varphi$ of dimension n is the pair $(r_{(+)},r_{(-)})$ where $r_{(+)}$ (resp. $r_{(-)}$) is the number of positive (resp. negative) eigenvalues of $\varphi$ as a real quadratic form (in particular $n=r_{(+)} + r_{(-)}$).

Proposition 2.1

[23, Ch.5, Corollary 3.6] Two regular rational quadratic forms $\varphi$ and $\psi$ are equivalent if and only if they have the same signature over $\mathbb R$ and if for every prime number q:

$$\begin{aligned} \bar{\partial }_q([\varphi ]_W) = \bar{\partial }_q([\psi ]_W). \end{aligned}$$

Proposition 2.2

[23, Ch.2, §3] Two regular quadratic forms on a finite field are Witt-equivalent if and only if their dimensions have the same parity and their discriminants are equal.

For any regular rational quadratic form $\varphi$ and any prime number q, the parity of the q-adic valuation of the determinant of $\varphi$ is an invariant of the Witt-equivalence class of $\varphi$. We thus define

$$\begin{aligned} \delta _q:W(\mathbb Q)\rightarrow \mathbb Z/2\mathbb Z,\quad \delta _q(\varphi )= \nu _q(\det (\varphi )) \mod 2. \end{aligned}$$

In particular, expressions like $s^{\delta _q(\varphi )}$, with $s \in \mathbb K^*$, are well defined in $\mathbb K^*/(\mathbb K^*)^2$.

2.3 Hodge theory for products of K3 surfaces

Let M be a smooth complex compact Kähler manifold. Its cohomology with complex coefficients admits a Hodge decomposition

$$\begin{aligned} \mathrm{{H}}^k(M,\mathbb C)=\bigoplus _{p+q=k} \mathrm{{H}}^{p,q}(M)\quad \forall k\in \mathbb N\end{aligned}$$

where $\mathrm{{H}}^{p,q}(M)$ is the space of classes of differential (p, q)-forms. Every smooth codimension k subvariety $Z\subset X$ admits a fundamental class [Z] in cohomology and it is easy to see that $[Z]\in \mathrm{{H}}^{k,k}(M)$. Conversely, denote

$$\begin{aligned} \mathrm{{Hdg}}^k(M):=\mathrm{{H}}^{2k}(M,\mathbb Q)\cap \mathrm{{H}}^{k,k}(M) \end{aligned}$$

the group of Hodge classes of degree 2k on M. The Hodge conjecture predicts that if M is projective, then every Hodge class is a linear combination with rational coefficients of cohomology classes of algebraic subvarieties of M.

Let X be a projective K3 surface. The intersection product, denoted $\langle -,-\rangle _X$ in the sequel, gives the second cohomology space $\mathrm{{H}}^2(X,\mathbb Z)$ the structure of an even unimodular lattice of rank 22 and signature (3, 19), isometric to $U^{\oplus 3}\oplus E_8^{\oplus 2}$, where U is the hyperbolic plane and $E_8$ is the unique even unimodular negative definite lattice of rank 8. The $\mathbb Q$-vector space $\mathrm{{H}}^2(X ,\mathbb Q):=\mathrm{{H}}^2(X,\mathbb Z)\otimes \mathbb Q$ carries a weight two Hodge structure

$$\begin{aligned} \mathrm{{H}}^2(X,\mathbb Q)\otimes \mathbb C=\mathrm{{H}}^2(X,\mathbb C)=\mathrm{{H}}^{2,0}(X)\oplus \mathrm{{H}}^{1,1}(X)\oplus \mathrm{{H}}^{0,2}(X) \end{aligned}$$

where the space $\mathrm{{H}}^{2,0}(X)$ of global holomorphic 2-forms is one-dimensional, $\mathrm{{H}}^{1,1}(X)$ is 20-dimensional and $\mathrm{{H}}^{0,2}(X)=\overline{\mathrm{{H}}^{2,0}(X)}$. Inside $\mathrm{{H}}^2(X,\mathbb Z)$ there are two distinguished sublattices: the Néron Severi lattice $\mathrm{{NS}}(X):=\mathrm{{H}}^{1,1}(X)\cap \mathrm{{H}}^2(X,\mathbb Z)$ and the transcendental lattice $\mathrm{{T}}_X:=\mathrm{{NS}}(X)^\perp$. Since X is projective, its hyperplane section is an integral 1-codimensional cycle, hence $\rho (X):={{\mathrm{rk}}}\mathrm{{NS}}(X)\ge 1$. By the Hodge index theorem $\mathrm{{NS}}(X)$ has signature $(1,\rho (X)-1)$. The rational transcendental lattice $\mathrm{{T}}_{X,\mathbb Q}:=\mathrm{{T}}_X\otimes \mathbb Q$ admits a weight two Hodge structure $\mathrm{{T}}_{X,\mathbb C}=\mathrm{{T}}^{2,0}_X\oplus \mathrm{{T}}^{1,1}_X\oplus \mathrm{{T}}^{0,2}_X$ given by $\mathrm{{T}}_X^{p,q}:=\mathrm{{H}}^{p,q}(X)\cap \mathrm{{T}}_{X,\mathbb C}$, where $\mathrm{{T}}_X^{2,0}$ and $\mathrm{{T}}_X^{0,2}$ are one-dimensional and $\mathrm{{T}}_X^{1,1}$ contains no nonzero rational class. It follows easily that $\mathrm{{T}}_{X,\mathbb Q}$ is an irreducible Hodge structure (see e.g. [8, Lemma 1.7]).

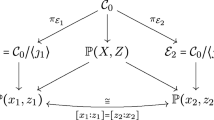
Assume that $M=Y\times X$ is a product of two projective K3 surfaces X and Y. By the Lefschetz theorem on (1, 1)-classes, $\mathrm{{Hdg}}^1(M)=\mathrm{{NS}}(M)_\mathbb Q$ so it contains only algebraic classes and by the Hard Lefschetz theorem $\mathrm{{Hdg}}^3(M)$ thus contains also only algebraic classes. So the Hodge conjecture remains open for $\mathrm{{Hdg}}^2(M)$. By Künneth decomposition, the question is non trivial only for classes living in $\mathrm{{H}}^{2,2}(M)\cap (\mathrm{{H}}^2(Y,\mathbb Q)\otimes \mathrm{{H}}^2(X,\mathbb Q))$. We have

$$\begin{aligned} \mathrm{{H}}^2(Y,\mathbb Q)\otimes \mathrm{{H}}^2(X,\mathbb Q)\cong \mathrm{{H}}^2(Y,\mathbb Q)^\vee \otimes \mathrm{{H}}^2(X,\mathbb Q)\cong {{\mathrm{Hom}}}(\mathrm{{H}}^2(Y,\mathbb Q),\mathrm{{H}}^2(X,\mathbb Q)). \end{aligned}$$

Denoting by $\pi _Y$, resp. $\pi _X$, the projection of $Y\times X$ onto Y, resp. X, the last isomorphism identifies a class $[Z]\in \mathrm{{H}}^2(Y,\mathbb Q)\otimes \mathrm{{H}}^2(X,\mathbb Q)$ with the correspondence $[Z]_*:x\mapsto \pi _{X*}(\pi _Y^*x\cdot [Z])$. It is easy to check that this correspondence is compatible with the Hodge structures if and only if $[Z]\in \mathrm{{H}}^{2,2}(M)$.

Decomposing $\mathrm{{H}}^2(X,\mathbb Q)=\mathrm{{NS}}(X)_{\mathbb Q}\oplus \mathrm{{T}}_{X,\mathbb Q}$, and similarly for Y, since the Hodge structure of the rational Néron–Severi lattice has weight zero and those of the rational transcendental lattice is irreducible of weight two, there are no nonzero homomorphisms of Hodge structures between them. It follows that every morphism of Hodge structures $\phi \in {{\mathrm{Hom}}}_\mathrm{{Hdg}}(\mathrm{{H}}^2(Y,\mathbb Q),\mathrm{{H}}^2(X,\mathbb Q))$ decomposes as $\phi =\phi _\mathrm{{NS}}+\phi _\mathrm{{T}}$ where $\phi _\mathrm{{NS}}\in {{\mathrm{Hom}}}_\mathrm{{Hdg}}(\mathrm{{NS}}(Y)_\mathbb Q, \mathrm{{NS}}(X)_\mathbb Q)$ and $\phi _\mathrm{{T}}\in {{\mathrm{Hom}}}_\mathrm{{Hdg}}(\mathrm{{T}}_{Y,\mathbb Q}, \mathrm{{T}}_{X,\mathbb Q})$ is either zero or an isomorphism. The morphism $\phi$ is the correspondence by a class $[Z]\in \mathrm{{H}}^{2,2}(M)\cap (\mathrm{{H}}^2(Y,\mathbb Q)\otimes \mathrm{{H}}^2(X,\mathbb Q))$. The morphism $\phi _\mathrm{{NS}}$ is the correspondence by the component of [Z] in $\mathrm{{NS}}(Y)_\mathbb Q\otimes \mathrm{{NS}}(X)_\mathbb Q$, which is automatically algebraic. Finally the study of the algebraic cycles in $\mathrm{{Hdg}}^2(Y\times X)$ reduces to the study of morphisms of rational Hodge structures between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$ that come from algebraic correspondences. Conversely, any such morphism extends to an element of ${{\mathrm{Hom}}}_\mathrm{{Hdg}}(\mathrm{{H}}^2(Y,\mathbb Q),\mathrm{{H}}^2(X,\mathbb Q))$ by projection and inclusion. We can thus formulate the Hodge conjecture for a product of complex projective K3 surfaces $Y\times X$ as follows: is every morphism in ${{\mathrm{Hom}}}_{\mathrm{{Hdg}}}(\mathrm{{T}}_{Y,\mathbb Q},\mathrm{{T}}_{X,\mathbb Q})$ given by an algebraic correspondence?

2.4 Correspondences induced by isogenies

Let $\gamma :X\dashrightarrow Y$ be an isogeny between two complex projective K3 surfaces X and Y, i.e. a rational map of finite degree n. By elimination of indeterminacy there exists a birational morphism $\beta :\widetilde{X}\rightarrow X$ and a morphism $\widetilde{\gamma }:\widetilde{X}\rightarrow Y$ which resolves the indeterminacies of $\gamma$, i.e. $\widetilde{\gamma }=\gamma \circ \beta$:

(5)

The composition of the correspondences by the graphs $\Gamma _\beta$ of $\beta$ and $\Gamma _{\widetilde{\gamma }}$ of $\widetilde{\gamma }$ produces a morphism

$$\begin{aligned} \gamma ^*:=[\Gamma _{\beta }]_*\circ [\Gamma _{\widetilde{\gamma }}]^*:\mathrm{{H}}^*(Y,\mathbb Z)\rightarrow \mathrm{{H}}^*(X,\mathbb Z) \end{aligned}$$

which is easily identified with the correspondence $[\Gamma ]^*$ by the graph

$$\begin{aligned} \Gamma :=\left\{ (\beta (x),\widetilde{\gamma }(x))\,|\,x\in \widetilde{X}\right\} \subset X\times Y \end{aligned}$$

which gives an algebraic class in $\mathrm{{Hdg}}^2(Y\times X)$. Symmetrically, the composition of correspondences

$$\begin{aligned} \gamma _*:=[\Gamma _{\widetilde{\gamma }}]_*\circ [\Gamma _{\beta }]^*:\mathrm{{H}}^*(X,\mathbb Z)\rightarrow \mathrm{{H}}^*(Y,\mathbb Z) \end{aligned}$$

is the correspondence $[\Gamma ]_*$. Once restricted to the second cohomology groups, the morphisms $\gamma _*$ and $\gamma ^*$ are adjoint to each other for the intersection product.

Consider the composed morphism

$$\begin{aligned} \gamma _*\gamma ^*=[\Gamma _{\widetilde{\gamma }}]_*\circ [\Gamma _{\beta }]^*\circ [\Gamma _{\beta }]_*\circ [\Gamma _{\widetilde{\gamma }}]^*=\widetilde{\gamma }_*\beta ^*\beta _*\widetilde{\gamma }^*. \end{aligned}$$

Note that $\widetilde{\gamma }$ is generically finite of degree n and that since $\beta$ is a sequence of blow-ups, $\beta ^*:\mathrm{{H}}^2(X,\mathbb Z)\rightarrow \mathrm{{H}}^2(\widetilde{X},\mathbb Z)$ is an inclusion. To study the restriction of $\gamma _*\gamma ^*$ to $\mathrm{{T}}_Y$ we need a geometric description of the restriction of $\gamma ^*$ to $\mathrm{{T}}_Y$, which is explained by Inose [10, §1] as follows. Fix a set of curves $C_i$, resp. $D_j$, whose classes generate $\mathrm{{NS}}(\widetilde{X})$, resp. $\mathrm{{NS}}(Y)$, and let N be a reducible curve in Y which contains in its support all the images $\widetilde{\gamma }(C_i)$ and the curves $D_j$. Take an element $t\in \mathrm{{T}}_Y$ and denote by $\tau \in \mathrm{{H}}_2(Y,\mathbb Z)$ its Poincaré dual. By assumption we have $\int _{N_i} t=0$ for any irreducible component $N_i$ of N, hence by a standard transversality argument we can take the curve N to meet $\tau$ transversally, so that here $\tau \cap N=\emptyset$. It follows from the definition that $\gamma ^*(t)$ is the Poincaré dual of $\beta (\widetilde{\gamma }^{-1}(\tau ))$. As a consequence, since $\widetilde{\gamma }$ is generically finite of degree n we have (see Inose [10, Proposition 1.1])

$$\begin{aligned} (\gamma _*\gamma ^*)_{|\mathrm{{T}}_Y}=n\,\mathrm{{id}}_{\mathrm{{T}}_Y} \end{aligned}$$

from which follows by adjunction that

$$\begin{aligned} \langle \gamma _\mathrm{{T}}^*(x),\gamma _\mathrm{{T}}^*(y)\rangle _X=\langle x,\gamma _{\mathrm{{T}}*}\gamma _\mathrm{{T}}^*(y)\rangle _Y=n\,\langle x,y\rangle _Y \quad \forall x,y\in \mathrm{{T}}_Y. \end{aligned}$$

In particular ${{\mathrm{rk}}}(\mathrm{{T}}_Y)={{\mathrm{rk}}}(\mathrm{{T}}_X)$ and $\gamma _\mathrm{{T}}^*$ is a dilation with scale factor n. We denote also by $\gamma ^*_\mathrm{{T}}:\mathrm{{T}}_{Y,\mathbb Q}\rightarrow \mathrm{{T}}_{X,\mathbb Q}$ its $\mathbb Q$-linear extension, which is thus an isomorphism of rational Hodge structures induced by an algebraic cycle, but not an isometry. So the Hodge conjecture is verified for $\gamma ^*_\mathrm{{T}}$ even if it does not satisfy the hypothesis of the Mukai–Nikulin theorem. Our aim in this paper is to study those isogenies between projective K3 surfaces whose transcendental rational Hodge structures are not isometric at all.

3 Proof of Theorem 1.1

The proof of Theorem 1.1 is decomposed into four slightly more general Propositions of independent interest: assertion (1) is proven in Proposition 3.1, assertion (2) is proven in Proposition 3.2 and the equivalences of assertion  (2) with either assertion (2a) or assertion (2b) is proven in Propositions 3.4 and 3.5.

Proposition 3.1

Let $\gamma :X\dashrightarrow Y$ be an isogeny of degree n between two complex projective K3 surfaces. Assume that n is not a square in $\mathbb Q^*$ and that ${{\mathrm{rk}}}\mathrm{{T}}_X$ is odd. Then there exists no isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$.

Proof

As explained in Sect. 2.4, the morphism $\gamma ^*_\mathrm{{T}}:\mathrm{{T}}_Y\rightarrow \mathrm{{T}}_X$ is a dilation with scale factor n, hence $\gamma ^*_\mathrm{{T}}:\mathrm{{T}}_Y(n)\hookrightarrow \mathrm{{T}}_X$ is an embedding of lattices of the same rank r. It follows that

$$\begin{aligned}{}[\mathrm{{T}}_X:\mathrm{{T}}_Y(n)]^2=\frac{{{\mathrm{disc }}}\mathrm{{T}}_Y(n)}{{{\mathrm{disc }}}\mathrm{{T}}_X}=n^r \frac{{{\mathrm{disc }}}\mathrm{{T}}_Y}{{{\mathrm{disc }}}\mathrm{{T}}_X}. \end{aligned}$$

Assuming that $\mathrm{{T}}_{Y,\mathbb Q}$ is isometric to $\mathrm{{T}}_{X,\mathbb Q}$, Eq. (3) gives:

$$\begin{aligned} {{\mathrm{disc }}}\mathrm{{T}}_Y \equiv {{\mathrm{disc }}}\mathrm{{T}}_X \mod (\mathbb Q^*)^2. \end{aligned}$$

Combining these two formulas we deduce that $n^r$ is a square in $\mathbb Q^*$. Since by hypothesis n is not a square in $\mathbb Q^*$, this can happen only if r is even.

Proposition 3.2

Let $\gamma :X\dashrightarrow Y$ be an isogeny of degree n between two complex projective K3 surfaces. Then there exists an isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$ if and only if $\mathrm{{T}}_{Y,\mathbb Q}$ is isometric to $\mathrm{{T}}_{Y,\mathbb Q}(n)$.

Proof

As explained in Sect. 2.4, the morphism $\gamma ^*_\mathrm{{T}}:\mathrm{{T}}_Y\rightarrow \mathrm{{T}}_X$ is a dilation with scale factor n, hence it is an isometry between $\mathrm{{T}}_{Y,\mathbb Q}(n)$ and $\mathrm{{T}}_{X,\mathbb Q}$ (that we still denote $\gamma ^*_\mathrm{{T}}$ by abuse of notation):

If there exists an isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{Y,\mathbb Q}(n)$, then composed with $\gamma ^*_\mathrm{{T}}$ it gives an isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$, and vice versa.

Remark 3.3

The statement is symmetric in X and Y, it is equivalent to “$\mathrm{{T}}_{X,\mathbb Q}(n)$ is isometric to $\mathrm{{T}}_{X,\mathbb Q}$”. Indeed, $\mathrm{{T}}_{Y,\mathbb Q}(n)\cong \mathrm{{T}}_{X,\mathbb Q}$ if and only if ${\mathrm{{T}}_{Y,\mathbb Q}\cong \mathrm{{T}}_{X,\mathbb Q}(n)}$ since $\mathrm{{T}}_{X,\mathbb Q}(n^2)\cong \mathrm{{T}}_{X,\mathbb Q}$.

The following proposition proves assertion (2) of Theorem 1.1 by taking $\varphi$ equal to the rational quadratic form of $\mathrm{{T}}_{Y,\mathbb Q}$. We follow the notation of Sect. 2.2. Recall that for any rational quadratic form $\varphi = \langle a_1, \ldots , a_n \rangle$ and any $m\in \mathbb Z^*$, we put $\varphi (m) := \langle m a_1, \ldots , m a_n \rangle$.

Proposition 3.4

Let $\varphi$ be a regular rational quadratic form of dimension n. Then $\varphi$ and $\varphi (2)$ are equivalent if and only if n is even and for every prime number q congruent to 3 or 5 modulo 8, one has $\delta _q(\varphi )$=0.

Proof

We can assume, up to equivalence, that

$$\begin{aligned} \varphi = \langle a_1,\ldots , a_{m_1}, 2\,b_1, \ldots , 2 \, b_{m_2} \rangle , \end{aligned}$$

where $m_1 + m_2 = n$ and $a_i, b_j$ are square-free odd integers. Then $\varphi (2)$ is equivalent to

$$\begin{aligned} \psi := \langle 2\, a_1,\ldots , 2\, a_{m_1}, b_1 \ldots , b_{m_2} \rangle . \end{aligned}$$

Clearly, $\varphi$ and $\psi$ have the same signature. Moreover,

$$\begin{aligned} \bar{\partial }_2 ([\varphi ]_W) = \langle \bar{1} \rangle _W^{\oplus m_2} \quad \text {and} \quad \bar{\partial }_2 ([\psi ]_W) = \langle \bar{1} \rangle _W^{\oplus m_1}; \end{aligned}$$

hence, by Proposition 2.2 we have that $\bar{\partial }_2 ([\varphi ]_W)$ is Witt-equivalent to $\bar{\partial }_2 ([\psi ]_W)$ if and only if $m_1$ and $m_2$ have the same parity, or equivalently if n is even.

Let q be an odd prime number. We denote by k the number of coefficients $a_i$ and $b_j$ which are not divisible by q. Since $\partial _q(2\,r)=2\partial _q(r)$ for all $r \in \mathbb Q^*$, the quadratic forms $\bar{\partial }_q([\varphi ]_W)$ and $\bar{\partial }_q([\psi ]_W)$ have both dimension $n-k$. If $k=n$ obviously $\delta _q(\varphi )=0$. Otherwise

$$\begin{aligned} \Delta (\bar{\partial }_q ([\varphi ]_W))&=(-1)^{\frac{(n-k)(n-k-1)}{2}}2^{n_1}\prod _i\text {}^\prime \partial _q( a_i)\prod _j\text {}^\prime \partial _q(b_j)\\ \Delta (\bar{\partial }_q ([\psi ]_W))&=(-1)^{\frac{(n-k)(n-k-1)}{2}}2^{n_2}\prod _i\text {}^\prime \partial _q( a_i)\prod _j\text {}^\prime \partial _q(b_j) \end{aligned}$$

where $n_1=\nu _q\left( \prod _{j=1}^{m_2}b_j\right)$ and $n_2=\nu _q\left( \prod _{i=1}^{m_1}a_i\right)$ are the numbers of coefficients $b_j$ (resp. $a_i$) that are divisible by q and $\prod \text {}^\prime$ means the product of the non-zero elements. These two discriminants are equal in $\mathbb F_q^*/(\mathbb F_q^*)^2$ if and only if $2^{n_1-n_2}$ is a square in $\mathbb F_q$. If $q\equiv \pm 1\mod 8$ this is true by the second supplement to the law of quadratic reciprocity. Otherwise q is congruent to 3 or 5 modulo 8 and $2^{n_1-n_2}$ is a square in $\mathbb F_q$ if and only if $n_1-n_2$ is even, or equivalently if

$$\begin{aligned}\delta _q(\varphi )=n_1+n_2\mod 2\equiv 0 \mod 2. \end{aligned}$$

Under these conditions $\bar{\partial }_q ([\varphi ]_W)$ and $\bar{\partial }_q ([\psi ]_W)$ are Witt-equivalent for any q by Proposition 2.2, hence $\varphi$ and $\varphi (2)$ are equivalent by Proposition 2.1. $\square$

Proposition 3.5

Let $\varphi$ be a regular rational quadratic form of dimension n and let $p >2$ be a prime number. Then $\varphi$ and $\varphi (p)$ are equivalent if and only if n is even and the following conditions are satisfied:

• 1. for every prime number $q >2$, $q \ne p$, such that p is not a square in $\mathbb F_q$, one has $\delta _q(\varphi )=0$;

• 2. the following equation holds in $\mathbb F_p^*/(\mathbb F_p^*)^2$:

  $$\begin{aligned} {{\mathrm{res}}}_p (\det (\varphi )) = (-1)^{\frac{n^2-n}{2} + \delta _p(\varphi )}. \end{aligned}$$

Proof

Up to equivalence we can assume that

$$\begin{aligned} \varphi = \langle a_1, \ldots , a_{m_1}, p b_1, \ldots , p b_{m_2} \rangle , \end{aligned}$$

where $m_1+m_2=n$ and $a_i$, $b_j$ are square-free integers not divisible by p. Then $\varphi (p)$ is equivalent to

$$\begin{aligned} \psi := \langle p a_1, \ldots , p a_{m_1}, b_1, \ldots , b_{m_2} \rangle . \end{aligned}$$

Clearly $\varphi$ and $\psi$ have the same signature and $\bar{\partial }_2([\varphi ]_W) = \bar{\partial }_2([\psi ]_W)$ since $p>2$.

Let q be an odd prime number different from p. By a similar argument as in the proof of Proposition 3.4 we see that $\bar{\partial }_q([\varphi ]_W)$ and $\bar{\partial }_q([\psi ]_W)$ have the same dimension and that their discriminants are automatically equal when p is a square in $\mathbb F_q^*$. Otherwise they are equal if and only if ${\delta _q(\varphi )}=0$.

Finally for $q=p$ we have

$$\begin{aligned} \bar{\partial }_p ([\varphi ]_W) = \langle \bar{b}_1, \ldots , \bar{b}_{m_2} \rangle _W \quad \text {and} \quad \bar{\partial }_p ([\psi ]_W) = \langle \bar{a}_1, \ldots , \bar{a}_{m_1} \rangle _W. \end{aligned}$$

The dimensions $m_1$ and $m_2$ of these forms have the same parity if and only if n is even. Their discriminants are equal if and only if the following equation holds in $\mathbb F_p^*/(\mathbb F_p^*)^2$:

$$\begin{aligned} (-1)^{\frac{m_1(m_1-1)}{2}} \prod _{i=1}^{m_1} a_i = (-1)^{\frac{m_2(m_2-1)}{2}} \prod _{j=1}^{m_2} b_j \end{aligned}$$

or equivalently

$$\begin{aligned} \prod _{i=1}^{m_1} a_i\prod _{j=1}^{m_2} b_j = (-1)^{\frac{m_1(m_1-1)+m_2(m_2-1)}{2}}. \end{aligned}$$

(6)

We have $\det (\varphi ) = p^{m_2} \prod _{i=1}^{m_1} a_i \prod _{j=1}^{m_2} b_j$, so

$$\begin{aligned} \nu _p(\varphi )=m_2\quad \text { and }\quad {{\mathrm{res}}}_p(\det (\varphi )) = \prod _{i=1}^{m_1} a_i \prod _{j=1}^{m_2} b_j. \end{aligned}$$

Substituting $m_1 = n - m_2$ and using that $(-1)^n =1$ since n is even, we see that equation (6) is equivalent to

$$\begin{aligned} {{\mathrm{res}}}_p (\det (\varphi )) = (-1)^{\frac{n^2-n}{2} + \delta _p(\varphi )}. \end{aligned}$$

$\square$

4 Isogenies induced by symplectic automorphisms of K3 surfaces

Let X be a complex K3 surface with an automorphism $\sigma$ of prime order p leaving invariant the symplectic two-form of X; such an automorphism is called symplectic. It is well-known (see [18]) that $p\in \{ 2, 3, 5, 7\}$. Symplectic automorphisms of order 2, often called Nikulin involutions (see [14, Definition 5.1]), have been intensively studied. Since the local action of $\sigma$ at a fixed point is given by a matrix

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} \omega &{} 0\\ 0&{} \bar{\omega }\end{array} \right) , \end{aligned}$$

where $\omega$ is a primitive p-th root of the unity, and $\bar{\omega }$ is its complex conjugate, the automorphism $\sigma$ has only isolated fixed points; we denote their number by $\lambda$. By Nikulin [18, Theorem 4.5] the number $\lambda$ depends only on the order p and is given by $\lambda = \frac{24}{p+1}$. Moreover if X is generic in the moduli space of K3 surfaces with a symplectic automorphism of order p then:

$$\begin{aligned} {{\mathrm{rk}}}\mathrm{{NS}}(X)=\lambda (p-1)+1,\quad {{\mathrm{rk}}}\mathrm{{T}}_X=21-\lambda (p-1), \end{aligned}$$

so generically ${{\mathrm{rk}}}\mathrm{{T}}_X$ is odd.

The quotient surface $\bar{Y}:= X/\langle \sigma \rangle$ contains $\lambda$ singular points of type $A_{p-1}$, which are the images of the fixed points in X. Therefore its minimal resolution $Y \rightarrow \bar{Y}$ contains $\lambda$ configurations of $(-2)$-curves of type $A_{p-1}$. Since the automorphism $\sigma$ acts symplectically on X, the surface Y is again a K3 surface (see e.g. [18, Proof of Theorem 4.5]) and we get a degree p isogeny

$$\begin{aligned} \gamma :X\dashrightarrow Y. \end{aligned}$$

We give a precise description of the resolution of indeterminacies $\beta :\widetilde{X}\rightarrow X$ of the map $\gamma$ (see diagram (5) of Sect. 2.4) generalizing [14, Section 3]. Denote by $p_1,\ldots , p_{\lambda }$ the singular points on $\bar{Y}$, by $E_i^1,\ldots , E_i^{p-1}$ the $(-2)$-curves of the $A_{p-1}$ graph on the singularity $p_i$ with the properties

$$\begin{aligned} \left( E_i^j\right) ^2= & {} -2,\\ \left( E_i^j,E_i^{j+1}\right)= & {} 1, \quad j=1,\ldots , p-2,\\ \left( E_i^j,E_i^{k}\right)= & {} 0, \quad \text{ for } \text{ all } k\not = j+1 \ \mathrm{and}\ j-1.\\ \end{aligned}$$

Let $M_p$ be the smallest primitive sublattice of the lattice $\mathrm{{H}}^2(Y,\mathbb Z)$ that contains all the curves $E_i^j$ for $i=1,\ldots , \lambda$ and $j=1,\ldots , p-1$. By Nikulin, [18, Proposition 7.1, Theorem 7.2] the lattice $M_p$ contains exactly one divisible class of the form $\eta /p$ where $\eta$ is a linear combination of the $E_i^j$. Since $\mathrm{{NS}}(Y)$ is a primitive sublattice of $\mathrm{{H}}^2(Y,\mathbb Z)$, the lattice $M_p$ is a sublattice of $\mathrm{{NS}}(Y)$. An explicit expression for $\eta$ is given in [18, Section 6, 1a), p. 116 and Definition 6.2] as follows. Put:

$$\begin{aligned} \delta _i:= \sum _{j = 1}^{p-1} j E^j_i, \end{aligned}$$

the class $\eta$ can be written

$$\begin{aligned} \eta =\sum _{i=1}^\lambda a_i \delta _i \end{aligned}$$

where

$$\begin{aligned} (a_1,\ldots ,a_{8})&=(1,\ldots ,1)\text { if } p=2\\ (a_1,\ldots ,a_{6})&=(1,\ldots ,1)\text { if } p=3\\ (a_1,a_2,a_3,a_4)&=(1,1,2,2)\text { if } p=5\\ (a_1,a_2,a_3)&=(1,2,3)\text { if } p=7. \end{aligned}$$

By [1, I§17] there exists a cyclic covering $\bar{\gamma }:\bar{X}\rightarrow Y$ of order p ramified on $\eta$. If $p=2$ then $\bar{X}$ is the blow-up of X at the fixed points of $\sigma$. In particular $\bar{X}=\widetilde{X}$ is smooth and we have a commutative diagram (see [9] or [14, Section 3]):

If $p>2$ the situation is more complicated since $\bar{X}$ has Hirzebruch–Jung singularities over the singular points of $\eta$ (see [1, I§17, III§2] for their description). We denote by $\varepsilon :\widetilde{X} \rightarrow \bar{X}$ the minimal resolution of the singularities of $\bar{X}$. The preimage on the surface $\widetilde{X}$ of each $A_{p-1}$-configuration has the following dual graph:

The self-intersection numbers of the curves can be obtained by a straightforward calculation with continuous fractions following [1, Theorem III.5.1]. For example for $p = 3$ we have a singularity of type $A_{3,1}$ on $\bar{X}$ over the point of intersection of $E_i^1$ and $E_i^2$ for each $i = 1,\ldots ,\lambda$. After resolving it one obtains a curve $F_i$ with self-intersection $-3$. Denote by $\widetilde{\gamma }:\widetilde{X}\rightarrow Y$ the composition $\bar{\gamma }\circ \varepsilon$. Since $(\widetilde{\gamma }^*E_i^j)^2 = 3(E_i^j)^2 = -6$ and $\widetilde{\gamma }^*E_i^j = 3\tilde{E}_i^j + F_i$, we get

$$\begin{aligned} -6 = \left( \widetilde{\gamma }^*E_i^j\right) ^2 = 9 \left( \tilde{E}_i^j\right) ^2 + 6\left( \tilde{E}_i^j,F_i\right) + F_i^2 = 9 \left( \tilde{E}_i^j\right) ^2 +6-3 \end{aligned}$$

so the strict transforms $\tilde{E}_i^j$ have self-intersection $-1$. In the cases $p = 5$ or $p=7$ the computation is similar.

Contracting these configurations to smooth points we obtain the map $\beta :\widetilde{X} \rightarrow X$, and the following commutative diagram:

(7)

Similar diagrams are described by Tan [25] in a more general setting.

The map $\beta$ can be easily described by appropriate blow-ups. For instance if $p=3$, to get a smooth quotient Y one has to blow-up three times each of the fixed points on X (two blow-ups are on the exceptional curve that we obtain after the first blow-up), so that the pullback of the order three automorphism $\sigma$ has no isolated fixed points on the exceptional set and the quotient surface is smooth. The configuration of the exceptional curves after the three blow-ups is the same as in the graph described above and the surface that we get is clearly $\widetilde{X}$. This works in a similar way for $p=5$ or $p=7$.

5 A geometric proof of Corollary 1.2

Let $\sigma$ be a symplectic automorphism of prime order p on a complex projective surface X. Let Y be the minimal resolution of $X/\langle \sigma \rangle$ and let $\gamma :X\dasharrow Y$ be the associated isogeny (see Sect. 4). Corollary 1.2 is a direct consequence of Theorem 1.1, or more precisely Proposition 3.1. In this section, we give a different proof based upon the geometric properties of the automorphism, generalizing [9, Proposition 2.5].

The invariant sublattice $\mathrm{{H}}^2(X,\mathbb Z)^\sigma$ is primitive in $\mathrm{{H}}^2(X,\mathbb Z)$, we denote

$$\begin{aligned} M:=(\mathrm{{H}}^2(X,\mathbb Z)^{\sigma })^\perp \end{aligned}$$

its orthogonal complement in $\mathrm{{H}}^2(X,\mathbb Z)$. Since $\sigma$ acts symplectically on X one has $M \subset \mathrm{{NS}}(X)$. By [18, Proposition 10.1] (see also [7, 9]) we have

$$\begin{aligned} {{\mathrm{rk}}}M = \lambda (p - 1) \quad \text {and} \quad {{\mathrm{disc }}}M = p^\lambda . \end{aligned}$$

In particular, ${{\mathrm{rk}}}M$ is always even. Denote

$$\begin{aligned} V := \mathrm{{H}}^2(X,\mathbb Z)^\sigma \cap \mathrm{{NS}}(X)=M^\perp \cap \mathrm{{NS}}(X) \end{aligned}$$

the orthogonal complement of M in $\mathrm{{NS}}(X)$. Using formula (2) we obtain

$$\begin{aligned} \quad p^\lambda {{\mathrm{disc }}}V \equiv {{\mathrm{disc }}}\mathrm{{NS}}(X) \mod (\mathbb Q^*)^2. \end{aligned}$$

(8)

Recall (see Sect. 4) that $M_p$ denotes the minimal primitive sublattice of $\mathrm{{NS}}(Y)$ that contains the curves $E^j_i$. Its rank is ${{\mathrm{rk}}}M_p=\lambda (p-1)={{\mathrm{rk}}}M$. Since $M_p$ is an overlattice of the lattice generated by the curves $E^j_i$, whose discriminant is $p^\lambda$, formula (1) gives

$$\begin{aligned} {{\mathrm{disc }}}M_p \equiv p^\lambda \mod (\mathbb Q^*)^2. \end{aligned}$$

More precisely by [18, Proposition 10.1] we have ${{\mathrm{disc }}}M_p=p^{\lambda -2}$. Put

$$\begin{aligned} W := M_p^\perp \cap \mathrm{{NS}}(Y) \subset \mathrm{{NS}}(Y) \end{aligned}$$

and note that ${{\mathrm{rk}}}W={{\mathrm{rk}}}V$. Using formula (2) we get

$$\begin{aligned} p^\lambda {{\mathrm{disc }}}W \equiv {{\mathrm{disc }}}\mathrm{{NS}}(Y) \mod (\mathbb Q^*)^2. \end{aligned}$$

(9)

Consider the morphism of Hodge structures $\gamma ^*:=\beta _*\widetilde{\gamma }^*:\mathrm{{H}}^2(Y,\mathbb Z)\rightarrow \mathrm{{H}}^2(X,\mathbb Z)$ and its restriction to W. One has $\mathrm{{H}}^2(\widetilde{X},\mathbb Z) \cong \mathrm{{H}}^2(X,\mathbb Z)\oplus \bigoplus _i \langle C_i \rangle$, where the curves $C_i$ are all the curves contracted by $\widetilde{\gamma }$. The map

$$\begin{aligned} \beta _*:\mathrm{{H}}^2(\widetilde{X},\mathbb Z) \cong \mathrm{{H}}^2(X,\mathbb Z)\oplus \bigoplus _i\langle C_i \rangle \rightarrow \mathrm{{H}}^2(X,\mathbb Z) \end{aligned}$$

is the projection onto the first factor. For any $u\in W$, one has

$$\begin{aligned} (\widetilde{\gamma }^*u, C_i) = (u, \widetilde{\gamma }_* C_i) = 0 \end{aligned}$$

since $\widetilde{\gamma }_*C_i$ is either 0 or one of the curves $E^j_i$. It follows that $\gamma ^*$ maps W injectively in V. Moreover

$$\begin{aligned} \langle \beta _* \widetilde{\gamma }^* x, \beta _* \widetilde{\gamma }^* y\rangle _X = \langle \widetilde{\gamma }^* x, \widetilde{\gamma }^* y\rangle _{\widetilde{X}} = p\,\langle x,y\rangle _Y\quad \forall x,y\in W. \end{aligned}$$

Since ${{\mathrm{rk}}}W={{\mathrm{rk}}}V$, it follows that the restriction $\gamma ^*:W_\mathbb Q\rightarrow V_\mathbb Q$ is an isomorphism and a dilation with scale factor p of rational quadratic spaces. Thus we have

$$\begin{aligned} {{\mathrm{disc }}}V \equiv p^{{{\mathrm{rk}}}W} {{\mathrm{disc }}}W \mod (\mathbb Q^*)^2. \end{aligned}$$

(10)

If $\mathrm{{T}}_{X,\mathbb Q}$ and $\mathrm{{T}}_{Y,\mathbb Q}$ are isometric, then ${{\mathrm{disc }}}\mathrm{{T}}_X \equiv {{\mathrm{disc }}}\mathrm{{T}}_Y\mod (\mathbb Q^*)^2$. Since the K3 lattice is unimodular, this implies that ${{\mathrm{disc }}}\mathrm{{NS}}(X) \equiv {{\mathrm{disc }}}\mathrm{{NS}}(Y)\mod (\mathbb Q^*)^2$. Putting together Eqs. (8), (9) and (10) we obtain

$$\begin{aligned} p^{{{\mathrm{rk}}}W} \equiv 1 \mod (\mathbb Q^*)^2. \end{aligned}$$

Since ${{\mathrm{rk}}}W={{\mathrm{rk}}}\mathrm{{NS}}(X)-\lambda (p-1)$ and $\lambda (p-1)$ is even, we finally get

$$\begin{aligned} p^{{{\mathrm{rk}}}\mathrm{{NS}}(X)} \equiv 1 \mod (\mathbb Q^*)^2. \end{aligned}$$

Since p is prime this is possible if and only if ${{\mathrm{rk}}}\mathrm{{NS}}(X)={{\mathrm{rk}}}\mathrm{{NS}}(Y)$ is even, or equivalently if ${{\mathrm{rk}}}\mathrm{{T}}_X$ is even. This proves Corollary 1.2.

6 Examples

6.1 Nikulin involutions

A K3 surface X admits a Shioda–Inose structure if there is a Nikulin involution $\iota$ on X with rational quotient map $\gamma :X\dashrightarrow Y$ such that Y is a Kummer surface and $\gamma _*$ induces an integral Hodge isometry between $\mathrm{{T}}_X(2)$ and $\mathrm{{T}}_Y$ (see [14, Definition 6.1]). By [14, Corollary 6.4] a K3 surface of Picard number $\rho (X):={{\mathrm{rk}}}\mathrm{{NS}}(X)$ equal to 19 or 20 always admits such a structure, so these surfaces come in a natural way with an isogeny of degree 2 to another K3 surface. If $\rho (X)=19$ then Theorem 1.1 says that there exists no isometry between $\mathrm{{T}}_{Y,\mathbb Q}$ and $\mathrm{{T}}_{X,\mathbb Q}$. If $\rho (X)=20$, using Remark 3.3 we see that $\mathrm{{T}}_{X,\mathbb Q}$ and $\mathrm{{T}}_{Y,\mathbb Q}$ are isometric rational quadratic forms if and only if $\mathrm{{T}}_{X,\mathbb Q}(2)\cong \mathrm{{T}}_{X,\mathbb Q}$. It is not difficult in this case to produce several examples where they are not isometric. Recall that there is a bijection between positive definite even integral matrices of the form

$$\begin{aligned} Q:=\left( \begin{matrix} 2a&{}\quad b\\ b&{} \quad 2c \end{matrix}\right) , \end{aligned}$$

with $a,b,c\in \mathbb Z$, $d:=4ac-b^2>0$, $a,c>0$, $-a\le b\le a\le c$ and transcendental lattices of K3 surfaces of Picard number 20 (see [24, Theorem 4]). Over $\mathbb Q$ the form Q is equivalent to the rational quadratic form $\varphi _Q=\langle 2a, \frac{d}{2a}\rangle$. By Proposition 3.4, if the determinant $d=\det (\mathrm{{T}}_X)$ is divisible by a prime number q congruent to 3 or 5 modulo 8 with an odd exponent then $\mathrm{{T}}_{X,\mathbb Q}(2)$ is not isometric to $\mathrm{{T}}_{X,\mathbb Q}$, so by Theorem 1.1 the rational lattice $\mathrm{{T}}_{X,\mathbb Q}$ is not isometric to $\mathrm{{T}}_{Y,\mathbb Q}$. We give some explicit examples below using well-known K3 surfaces.

6.2 The Fermat quartic

Let F be the Fermat quartic $x^4+y^4+z^4+t^4=0$. Its transcendental lattice is given by the quadratic form

$$\begin{aligned} \mathrm{{T}}_F = \left( \begin{matrix} 8 &{}\quad 0 \\ 0 &{}\quad 8 \end{matrix}\right) \end{aligned}$$

which is equivalent over $\mathbb Q$ to the rational quadratic form $\varphi _F := \langle 2, 2 \rangle$. We have $\det (\varphi _F)=2^2$ so for q congruent to 3 or 5 modulo 8 the q-adic valuation of the determinant is always 0. By Theorem 1.1 we get $\varphi _F \cong \varphi _F(2)$.

The surface F also admits a symplectic automorphism of order three given by the 3-cycle $(x,y,z,t)\mapsto (y,z,x,t)$ (see [17]). We see that $\mathrm{{T}}_{F,\mathbb Q}(3)$ is not isometric to $\mathrm{{T}}_{F,\mathbb Q}$: since $\det (\varphi _F)=2^2$, the second condition of Proposition 3.5 is

$$\begin{aligned} 2^2={{\mathrm{res}}}_3(\det (\varphi _F))=-1, \end{aligned}$$

which is not true in $\mathbb F_3^*/(\mathbb F_3^*)^2$.

6.3 The Schur quartic

Let S be the Schur quartic $x^4-xy^3=z^4-zt^3$. Its transcendental lattice is given by the quadratic form

$$\begin{aligned} \mathrm{{T}}_S = \left( \begin{matrix} 8 &{}\quad 4 \\ 4 &{}\quad 8 \end{matrix}\right) \end{aligned}$$

which is equivalent over $\mathbb Q$ to the rational quadratic form $\varphi _S := \langle 2, 6 \rangle$. We have $\det (\varphi _S)=3\cdot 2^2$ so the 3-adic valuation of the determinant is odd. By Theorem 1.1 we get $\varphi _S \not \cong \varphi _S(2)$.

The surface S admits a symplectic automorphism of order three, for instance $(x:y:z:t)\mapsto (x:\omega y: z:\bar{\omega } t)$ where $\omega$ is a primitive third root of the unity. Here $\mathrm{{T}}_{S,\mathbb Q}(3)$ is equivalent to $\langle 6, 18 \rangle \cong \langle 6, 2\rangle$ so it is isometric to $\mathrm{{T}}_{S,\mathbb Q}$.

6.4 Surfaces with many nodes

In [2, 21] the authors describe one-dimensional families of K3 surfaces obtained as special quotients of pencils of surfaces in $\mathbb P^3$ that contain surfaces with many nodes. In particular, looking in [22, Table 1], the K3 surfaces X in the one-dimensional families admit a Shioda–Inose structure, so a symplectic involution and a rational quotient Y as described in Sect. 6.1. Applying our criteria one can compute that $\mathrm{{T}}_{X,\mathbb Q}$ is not isometric to $\mathrm{{T}}_{Y,\mathbb Q}$ for all the K3 surfaces in the families described in the lines 1, 3, 4 of the table.

6.5 Kummer surfaces

One standard way to produce isogenies that do not come from symplectic automorphisms is to use Kummer surfaces (see e.g. [11]). Let A be a complex abelian surface and $\Gamma$ a subgroup of prime order p of the group $A[p]\cong (\mathbb Z/p\mathbb Z)^{\oplus 4}$ of p-torsion points of A. Denoting $B:=A/\Gamma$ we have a degree p morphism $g:A\longrightarrow B$. It is easy to see that g induces an order p isogeny between the Kummer surfaces associated to A and B, denoted $\gamma :{{\mathrm{Km}}}(A)\dashrightarrow {{\mathrm{Km}}}(B)$:

where the vertical arrows are the birational quotients by the involutions $(-\mathrm{{id}})$ with 16 fixed points. At least for $p>7$ this isogeny can certainly not be induced by a symplectic automorphism of order p on ${{\mathrm{Km}}}(A)$ and non-symplectic automorphisms do not produce such maps.