1 Introduction

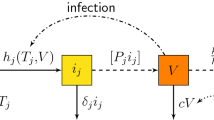
There is a huge number of works in the existing literature; proposing and studying virus infection mathematical models; we invite the reader to see for example [1, 3, 5, 7, 8, 14, 15, 23, 25, 26, 33] and the references therein. In the particular case of an HIV infection, the corresponding model is usually divided into three classes; namely uninfected cells, T, infected cells, i and free virus particles, V.

In order to establish a more realistic HIV model, many authors have considered the age state in their models, as for example in [6, 16, 24, 27, 34]. This was done with the aim to make distinction between cells, so the infection age that is time since cell is infected, is introduced in the subpopulation of infected cells, which makes, among other considerations, a variation of the mortality in this class.

Another important aspect to be considered, is the infection function, which represents the interaction between the virus and the uninfected cells. Frequently, this interaction is described by a bilinear function (mass action) or some standard functions. However these cited functions are not always a good representation of this complicated phenomenon [11, 12, 32].

It is established that the process and the evolution of these infections, are governed by partial differential equations, and thus it is not obvious to study the global properties of their solutions, see [4, 20,21,22, 31].

One of the leading works, modeling age-structured HIV-1 infection treatment with bilinear interaction was proposed by Nelson et al. [24], where the local stability of equilibria was established. More recently, Wang et al. [34], and Yang et al. [35] have introduced an age structured HIV infection model with a nonlinear interaction. In [34], the rate infection function that is considered is \(\dfrac{T(t)V(t)}{1+\alpha V(t)}\) and in [35], the authors considered, the Beddington–DeAngelis infection function, namely \(\dfrac{T(t)V(t)}{1+\alpha _1T(t)+\alpha _2 V(t)}.\) In these two papers, the global asymptotic stability of the equilibria is proved, using suitable Lyapunov functions.

Motivated by these works, we propose and investigate an age-structured HIV infection model with a very general nonlinear infection function,

$$\begin{aligned} \left\{ \begin{array}{lll} T'(t)=A- dT(t)-f(T(t),\quad V(t)) \;\;\ t \ge 0,\\ i_t(t,a)+i_a(t,a)=-\delta (a) i(t,a), \\ V'(t)=\int _0^{\infty } p(a)i(t,a)da-cV(t), \end{array} \right. \end{aligned}$$
(1.1)

with the boundary and initial conditions

$$\begin{aligned} \left\{ \begin{array}{lll} i(t,0)=f(T(t),\quad V(t)), \\ T(0)=T_0\ge 0, \quad V(0)=V_0 , \\ i(0,.)=i_0(.)\in L_{+}^{1}(\mathbb {R}^{+}). \end{array} \right. \end{aligned}$$
(1.2)

Here, T(t),  i(t, a) and V(t) are the populations of uninfected cells, infected cells with infection age a and free virus at time t respectively. The functions \(\delta (a),\) p(a),  are respectively, the age-dependent per capita death, the viral production rate of infected cells with age a. The parameters c,  d,  are respectively the clearance rate of virus and the death rate of uninfected cells. The parameter A represent the entering flux into the target cells in class T.

The novelty of our work is to propose a general Lyapunov functional that ensures global stability of equilibria; and this is done for a large class of infection functions, some of them being untreated in the literature as the family of functions \(f(T,V)=\dfrac{TV}{1+\alpha V^n}\) with \(0\le n\le 1,\) numerically illustrated in the last example in this paper.

Next, it will be assumed that :

  • The function \(\delta (a) \ge \delta _0>0\) for almost every \(a\ge 0\) and \(\delta \in L_{+}^{\infty }(\mathbb {R}^{+}).\)

  • The function p is assumed to belong to the set \(L_{+}^{\infty }(\mathbb {R}^{+})\setminus {\{0\}}\), and \( p^{max}:=ess\sup _{a\in \mathbb {R}^{+}} p(a)\) for almost every \(a\ge 0\).

  • The parameters A,  d and c are supposed to be positive.

We present now our basic assumptions for the infection function f and notations that will be used from now on.

We suppose that the infection response function f satisfies :

  • \(f(\cdot p,V)\) is increasing for \(V> 0.\) Moreover \(f(0,V)=f(T,0)=0\) for all \(T, V\ge 0,\)

  • The function \(\dfrac{\partial f}{\partial V}(.,0)\) is continuous positive on every compact set K.

  • The function f is locally Lipschitz continuous in T and V,  with a Lipschitz constant \(L>0,\) i.e. for every \(C>0\) there exists some \(L:=L_C>0\) such that

    $$\begin{aligned} |f(T_2,V_2)-f(T_1,V_1)|\le L(|T_2-T_1|+|V_2-V_1|), \end{aligned}$$
    (1.3)

    whenever \(0\le T_2,T_1, V_2, V_1\le C.\)

Let us define the functional space \(X:=\mathbb {R}\times L^{1}(\mathbb {R}^{+})\times \mathbb {R}\) equipped with the norm

$$\begin{aligned} ||(T,i,V)||_{X}=|T|+\int _0^{\infty }|i(a)|da+|V|, \quad T,V \in \mathbb {R},\quad i\in L^1(\mathbb {R}^{+}). \end{aligned}$$

Moreover, \(X_{+}=\mathbb {R}^{+}\times L_{+}^{1}(\mathbb {R}^{+})\times \mathbb {R}^{+}\) denote the positive cone of X.

Throughout this paper, we denote the probability that an infected cell survives to age a, by \(\Pi (a):\)

$$\begin{aligned} \begin{array}{lll} \Pi (a)=e^{-\int _0^a\delta (\theta )d\theta }, \end{array} \end{aligned}$$
(1.4)

and thus

$$\begin{aligned} N=\int _0^{\infty }p(a)\Pi (a)da. \end{aligned}$$
(1.5)

represents the total number of viral particles produced by an infected cell in its life span.

For the model (1.1), the number \(R_0\) of secondary infections produced by a single infected cell during its lifetime [10] is defined by

$$\begin{aligned} R_0=\dfrac{N}{c}\dfrac{\partial f}{\partial V}\left( \frac{A}{d},0\right) . \end{aligned}$$
(1.6)

Next, we set \(\Phi (t,a)=(T(t),i(t,a),V(t)),\) \(\Phi _0(a)=\left( T_0, i_0(a),V_0\right) \)

$$\begin{aligned} |\Phi (t,.)|=|T(t)|+\int _0^{\infty }|i(t,a)|da+|V(t)|. \end{aligned}$$

We begin by stating the following theorem, its proof is standard, see for instance [35].

Theorem 1.1

Assume that (1.3) holds and let us suppose \( (T_0,i_{0}(.),V_0) \in X_{+}.\) Then there exists a unique non-negative solution \( (T,i,V) \in C^{1}(\mathbb {R}^{+})\times C(\mathbb {R}^{+}; L^{1}(\mathbb {R^{+}}))\times C^{1}(\mathbb {R}^{+})\) of problem (1.1)–(1.2). Moreover, we have the following estimates,

$$\begin{aligned} T(t)+\int _0^{\infty }i(t,a)da\le & {} \max \left\{ \dfrac{A}{\alpha }, ||i_0||_1+T_0\right\} :=\theta ,\\ V(t)\le & {} \max \left\{ V_0,\dfrac{p^{max}}{c}\theta \right\} , \end{aligned}$$

for all \(t\ge 0,\) with \(\alpha := \min \{d,\delta _0\}.\) Moreover

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\left( T(t)+\int _0^{\infty }i(t,a)da\right) \leqslant \dfrac{A}{d}, \end{aligned}$$

and

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }V(t) \leqslant \dfrac{p^{max}A}{c\alpha }. \end{aligned}$$

Finally,

$$\begin{aligned} \liminf _{t\rightarrow \infty } T(t)\ge \Lambda , \end{aligned}$$
(1.7)

with \(\Lambda :=\dfrac{A}{d+L},\) and L is a Lipschitz constant defined in (1.3).

The rest of this paper is organized as follows: The next section focuses on proving the existence of compact attractor and determining the total trajectories. Then, we will prove that the infection-free equilibrium is globally asymptotically stable whenever \(R_0\le 1.\) Finally, we will investigate the global dynamic of the infection equilibrium, whenever it exists. Observe that the Lyapunov functional that will ensure the global stability is constructed independently of the choice of the infection function, and is valid for almost all usual functions; bilinear or nonlinear as Holling or Beddington.

2 Global compact attractor and total trajectories

We begin by writing the problem (1.2) in the form of a Volterra type equation,

$$\begin{aligned} i(t,a)=\left\{ \begin{array}{lll} \Pi (a) f(T(t-a),V(t-a)), \;\;\ t>a\ge 0,\\ \dfrac{\Pi (a)}{\Pi (a-t)}i_0(a-t), \;\;\ a>t\ge 0. \end{array} \right. \end{aligned}$$
(2.1)

Now, it is not difficult to show the existence of a continuous semiflow

$$\begin{aligned} \Phi (t,(T_0,i_0(.),V_0))=(T(t),i(t,.),V(t)), \end{aligned}$$
(2.2)

with (T, i, V) is solution of the autonomous problem (1.1)–(1.2).

We choose \(X=\mathbb {R}^{+}\times L^{1}(\mathbb {R}^{+})\times \mathbb {R}^{+}\) endowed with the natural norm \(||(T,i,V)||_X=|T|+||i||_1+|V|.\)

The following theorem state the existence of a compact attractor of all bounded sets of X, (the concept of global attractor is presented in e.g. [19],[28, 30]).

Theorem 2.1

The semiflow \(\Phi \) has a compact attractor \(\mathbf {A}\) of bounded sets of X.

Proof

By Theorem 1.1, the semiflow \(\Phi \) is point-dissipative and eventually bounded on bounded sets on X.

Hence, from Theorem 2.33 in [28], we only need to show the asymptotic smoothness of \(\Phi \) to complete the proof. In order to prove this property, we apply Theorem 2.46 in [28]. We define

$$\begin{aligned} \Theta _1(t,(T_0,i_0(.),V_0))=(0,w_1(t,.),0), \end{aligned}$$

as

$$\begin{aligned} w_1(t,a)=\left\{ \begin{array}{lll} 0, \;\;\ t>a,\\ \dfrac{\Pi (a)}{\Pi (a-t)}i_0(a-t) , \;\;\ a>t, \end{array} \right. \end{aligned}$$
(2.3)

and \(\Theta _2(t,(T_0,i_0(.),V_0))=(T(t),w_2(t,.),V(t))\) with

$$\begin{aligned} w_2(t,a)=\left\{ \begin{array}{lll} \Pi (a)f(T(t-a),V(t-a)), \;\;\ t>a,\\ 0, \;\;\ a>t. \end{array} \right. \end{aligned}$$
(2.4)

Notice that

$$\begin{aligned} \Phi (t,(T_0,i_0(a),V_0))=\Theta _1(t,(T_0,i_0(a),V_0))+\Theta _2(t,(T_0,i_0(a),V_0)). \end{aligned}$$

Now let C be a bounded closed subset of initial data in X,  that is forward invariant under \(\Phi .\) First, in view of Theorem 1.1 observe that

$$\begin{aligned} T(t)+\int _0^{\infty }i(t,a)da+V(t)\le \tilde{M},\quad \text{ for } \text{ all } \quad t\ge 0, \end{aligned}$$

with \(\tilde{M}=\max \{\dfrac{A}{\alpha }, ||i_0||_1+T_0\}+\max \{V_0,\dfrac{p^{max}}{c}\max \{\dfrac{A}{\alpha }, ||i_0||_1+T_0\}\}.\)

Then \(\Theta _1\) satisfies,

$$\begin{aligned} ||\Theta _1||\le & {} e^{-\delta _0 t}||i_0||_1,\\\le & {} \tilde{M}e^{-\delta _0 t}, \end{aligned}$$

hence \(\Theta _1\rightarrow 0\) as \(t\rightarrow \infty \) uniformly for all initial data in C. We set

$$\begin{aligned} I_h= & {} \int _0^{\infty }|w_2(t+a+h)-w_2(t+a)|da,\\= & {} \int _0^{t-h}|\Pi (a+h)f(T(t-a-h),V(t-a-h))\\&\quad -\Pi (a)f(T(t-a),V(t-a))|da\\&\quad +\int _{t-h}^{t}|\Pi (a)f(T(t-a),V(t-a))|da, \end{aligned}$$

we claim that \(I_h\rightarrow 0\) as \(h\rightarrow 0\) uniformly for all initial data in C. Notice that the second term of \(I_h\) tends to 0 uniformly for all initial data in C. So by setting

$$\begin{aligned} I^1_h= & {} \int _0^{t-h}|\Pi (a+h)f(T(t-a-h),V(t-a-h))\\&-\Pi (a)f(T(t-a),V(t-a))|da, \end{aligned}$$

and applying the Lipschitz condition of f,  namely (1.3) we have

$$\begin{aligned} I^1_h\le & {} L\int _0^{t-h}\Pi (a+h)\left( |T(t-a-h)-T(t-a)|+|V(t-a-h){-}V(t-a)|\right) da\\&+ f^{\infty }\int _0^{t-h}|\Pi (a+h)-\Pi (a)|da, \end{aligned}$$

with \(f(T,V)\le f^{\infty }\) for all \((T,V)\in K\) where K is a compact. Now observe that

$$\begin{aligned} |T'(t)|\le A+d\tilde{M}+f^{\infty }, \end{aligned}$$

and

$$\begin{aligned} |V'(t)|\le (p^{max}+c)\tilde{M}, \end{aligned}$$

for all \(t\ge 0.\) Therefore we easily conclude that \(I^{1}_h\) tends to 0 as h tends to 0, uniformly for all initial data in C. This completes the proof. \(\square \)

Further, we describe the total trajectories of system (1.1), that are solutions of (1.1) defined for all \(t\in \mathbb {R}.\) These extended solutions play an important role in proving the global asymptotic stability of equilibria.

We consider \(\bar{\phi }\) a total \(\Phi -\)trajectory, \(\bar{\phi }(t)=(T(t),i(t,.),V(t)).\) Then by a straightforward calculation, see also [2, 28] we obtain, for all \(t\in \mathbb {R},\)

$$\begin{aligned} \left\{ \begin{array}{lll} T'(t)=A-dT(t)-f(T(t),V(t)),\\ i(t,a)=\Pi (a)f(T(t-a),V(t-a)),\\ V'(t)=\int _0^{\infty }p(a)i(t,a)da-cV. \end{array} \right. \end{aligned}$$
(2.5)

Our next result relies on properties of the total trajectory, related to the compact attractor \(\mathbf {A}.\)

Lemma 2.2

For all \((T_0,i_0,V_0)\in \mathbf {A},\) we have,

$$\begin{aligned}&T_0+\int _0^{\infty }i_0(a)da+V_0\le \dfrac{A}{\alpha } \left( 1+\dfrac{p^{max}}{c}\right) ,\;\ \text{ with }\;\ \alpha :=\min {\{d,\delta _0\}} \\&\quad i_0(a)\le \Gamma \Pi (a),\\&\quad T_0 \ge \Lambda ,\quad \text{ with }\quad \Lambda :=\dfrac{A}{d+L}, \end{aligned}$$

where L is the Lipschitz constant defined in (1.3) and \(\Gamma \) is a positive constant.

Proof

First, we set

$$\begin{aligned} I(t):=\int _0^{\infty }i(t,a)da= & {} \int _0^{\infty }\Pi (a)f(T(t-a),V(t-a)),\\= & {} \int _{-\infty }^{t}\Pi (t-\sigma )f(T(\sigma ),V(\sigma ))d\sigma . \end{aligned}$$

Differentiating this last equation and using the definition of \(\Pi \) we get,

$$\begin{aligned} I'(t)=f(T(t),V(t))-\int _{\infty }^{t}\delta (t-\sigma ) \Pi (t-\sigma )f(T(\sigma ),V(\sigma ))d\sigma . \end{aligned}$$

using \(\delta (a)\ge \delta _0,\) and from the equation of T in (2.5),

$$\begin{aligned} T'(t)+I'(t)= & {} A-dT(t)-\delta _{0}\int _{-\infty }^{t} \Pi (t-\sigma )f(T(\sigma ),V(\sigma ))d\sigma ,\\\le & {} A-dT(t)-\delta _0\int _{0}^{\infty }\Pi (\sigma )f(T(t-\sigma ),V(t-\sigma ))d\sigma ,\\\le & {} A-dT(t)-\delta _0I(t),\\\le & {} A-\alpha (T(t)+I(t)), \end{aligned}$$

with \(\alpha :=\min {\{d,\delta _0\}}.\) Now integrating this last inequality over the interval (r, t) we obtain

$$\begin{aligned} (T(t)+I(t))e^{\alpha t}\le (T(r)+I(r))e^{\alpha r}+\dfrac{A}{\alpha }\left( e^{\alpha t}-e^{\alpha r}\right) . \end{aligned}$$

Letting r goes to \(-\infty \) we get

$$\begin{aligned} T(t)+I(t)\le \dfrac{A}{\alpha } \;\ \text{ for } \text{ all }\;\ t \in \mathbb {R}. \end{aligned}$$
(2.6)

Moreover from the equation of V in (2.5) we have

$$\begin{aligned} V'(t)\le & {} p^{max}I(t)-cV(t),\\\le & {} \dfrac{Ap^{max}}{\alpha }-cV(t), \end{aligned}$$

thus, a straightforward computation leads to,

$$\begin{aligned} V(t)\le \dfrac{Ap^{max}}{\alpha c} \;\ \text{ for } \text{ all }\;\ t\in \mathbb {R}. \end{aligned}$$
(2.7)

Therefore, adding (2.6) and (2.7) we find,

$$\begin{aligned} T(t)+I(t)+V(t)\le \dfrac{A}{\alpha }\left( 1+\dfrac{p^{max}}{c}\right) \;\ \text{ for } \text{ all }\;\ t\in \mathbb {R}. \end{aligned}$$

In addition since T and V belong to a compact subset, and f is a continuous function, then there exists a positive constant \(\Gamma \) such that

$$\begin{aligned} i(t,a)\le \Gamma \Pi (a), \;\ \text{ for } \text{ all } \;\ t\in \mathbb {R} \;\ \text{ and } \text{ all } \;\ a\in \mathbb {R^{+}}. \end{aligned}$$

Finally, concerning the lower bound of T,  using the Lipschitz hypothesis of f,

$$\begin{aligned} T'(t)\ge A-dT(t)-LT(t), \end{aligned}$$

after integration,

$$\begin{aligned} T(t)\ge \dfrac{A}{d+L} \;\ \text{ for } \text{ all } \;\ t\in \mathbb {R}. \end{aligned}$$

This completes the proof.\(\square \)

3 The global stability of the infection-free equilibrium

This section is devoted to prove the global asymptotic stability of the infection-free equilibrium. Throughout this section we suppose that :

  • \(\mathbf {(H1)}\) the function f is concave with respect to V.

We observe that the system (1.2) always has an infection-free equilibrium \((\dfrac{A}{d},0,0).\)

Theorem 3.1

Suppose that (H1) holds. Then, the disease free equilibrium \((\dfrac{A}{d},0,0)\) is globally asymptotically stable whenever \(R_0\le 1.\)

Proof

Let us define the function \(\psi \) as

$$\begin{aligned} \psi (a)=\dfrac{1}{N\Pi (a)}\int _{a}^{\infty }p(\sigma )\Pi (\sigma )d\sigma , \end{aligned}$$

which is solution of the following problem

$$\begin{aligned} \left\{ \begin{array}{lll} \psi '(a)=\delta (a)\psi (a)- \dfrac{p(a)}{N}, \quad {a > 0,} \\ \psi (0)=1. \end{array} \right. \end{aligned}$$
(3.1)

Then for \(x:=(T_0,i_0(.),V_0)\in \mathbf A ,\) we consider as the Lyapunov functional

$$\begin{aligned} U(x)=U_1(x)+U_2(x)+\dfrac{V_0}{N}, \end{aligned}$$

where

$$\begin{aligned} U_1(x)=T_0-\int _{\frac{A}{d}}^{T_0}\lim \limits _{V\rightarrow 0}\dfrac{f\left( \frac{A}{d},V\right) }{f(\eta ,V)}d\eta -\dfrac{A}{d}, \end{aligned}$$

and

$$\begin{aligned} U_2(x)=\int _0^{\infty }\psi (a)i_0(a)da. \end{aligned}$$

Let \(\chi : \mathbb {R}\rightarrow \mathbf {A}\) be a total \(\Phi -\)trajectory, \(\chi (t)=(T(t),i(t,.),V(t)),\) \(T(0)=T_0,\) \(i(0,a)=i_0(a),\) and \(V(0)=V_0\) with (T(t), i(t, a), V(t)) is solution of problem (2.5).

$$\begin{aligned} \dfrac{d}{dt}U_1(\chi (t))= & {} \left( 1-\lim \limits _{V\rightarrow 0^{+}} \dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}\right) \left( A-dT(t)-f(T(t),V(t))\right) ,\\= & {} d\left( 1-\lim \limits _{V\rightarrow 0^{+}}\dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}\right) \left( \dfrac{A}{d}-T(t)\right) \\&-f(T(t),V(t))\left( 1-\lim \limits _{V\rightarrow 0^{+}}\dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}\right) . \end{aligned}$$

Next,

$$\begin{aligned} U_2(\chi (t))=\int _0^{\infty }\psi (a)i(t,a)da, \end{aligned}$$

from the expression of i in (2.5) we have

$$\begin{aligned} U_2(\chi (t))=\int _0^{\infty }\phi _1(a)\xi (t-a)da, \end{aligned}$$

with

$$\begin{aligned} \begin{array}{lll} \xi (t)=f(T(t),V(t)),\;\ \text{ and }\;\ \phi _1(a)=\psi (a)\Pi (a). \end{array} \end{aligned}$$
(3.2)

Following the same arguments as in the proof of Lemma 9.18 in [28] we can show that \(U_2\) is absolutely continuous and

$$\begin{aligned} \dfrac{d}{dt}U_2(\chi (t))=\phi _1(0)\xi (t)+\int _0^{\infty }\phi _1'(a)\xi (t-a)da, \end{aligned}$$

thus, in view of (3.2) it yields,

$$\begin{aligned} \dfrac{d}{dt}U_2(\chi (t))= & {} \psi (0)f(T(t),V(t))\\&+\int _0^{\infty }\left( \psi '(a)-\delta (a)\psi (a)\right) \Pi (a)f(T(t-a),V(t-a))da, \end{aligned}$$

from this, and (3.1) we obtain,

$$\begin{aligned} \dfrac{d}{dt}U_2(\chi (t))=f(T(t),V(t))-\int _0^{\infty }\dfrac{p(a) \Pi (a)}{N}f(T(t-a),V(t-a))da. \end{aligned}$$

Now we analyze \(U':=U_1'+U_2'+\dfrac{V'}{N},\) then by using (2.5), adding and subtracting \(V\dfrac{\partial f}{\partial V}(\dfrac{A}{d},0)\) we obtain

$$\begin{aligned} \dfrac{d}{dt}U(\chi (t))= & {} d\left( 1-\lim \limits _{V\rightarrow 0^{+}} \dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}\right) \left( \dfrac{A}{d}-T(t)\right) \\&+f(T(t),V(t))\lim \limits _{V\rightarrow 0^{+}}\dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}-V\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right) \\&+ V\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right) -c\dfrac{V}{N}, \end{aligned}$$

by the definition of \(R_0\) observe that,

$$\begin{aligned} \dfrac{\partial f}{\partial V}\left( \frac{A}{d},0\right) =\dfrac{cR_0}{N}, \end{aligned}$$

thus,

$$\begin{aligned} \dfrac{d}{dt}U(\chi (t))= & {} d\left( 1-\lim \limits _{V\rightarrow 0^{+}} \dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}\right) \left( \dfrac{A}{d}-T(t)\right) \\&+f(T(t),V(t))\lim \limits _{V\rightarrow 0^{+}}\dfrac{f\left( \dfrac{A}{d},V\right) }{f(T(t),V)}-V\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right) \\&+\,c\dfrac{V}{N}(R_0-1), \end{aligned}$$

On the other hand, we compute

$$\begin{aligned} f(T,V)\lim \limits _{V\rightarrow 0^{+}}\dfrac{f\left( \dfrac{A}{d},V\right) }{f(T,V)} -V\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right)= & {} f(T,V) \dfrac{\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right) }{\dfrac{\partial f}{\partial V}(T,0)}-V\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right) ,\\= & {} \dfrac{\dfrac{\partial f}{\partial V}\left( \dfrac{A}{d},0\right) }{\dfrac{\partial f}{\partial V}(T,0)}\left( f(T,V)-V\dfrac{\partial f}{\partial V}(T,0)\right) , \end{aligned}$$

finally the concavity of f with respect to V ensures that

$$\begin{aligned} f(T,V)-V\dfrac{\partial f}{\partial V}(T,0)\le 0. \end{aligned}$$

Hence, using the fact that \(\dfrac{\partial f}{\partial V}(.,0)\) is continuous positive on every compact set K and \(R_0\le 1\) we get

$$\begin{aligned} \dfrac{d}{dt}U(\chi (t))\le 0. \end{aligned}$$

Further, notice that, \(\dfrac{d}{dt}U(\chi (t))=0\) implies that \(T(t)=\dfrac{A}{d}.\) Let Q be the largest invariant set, for which \(\dfrac{d}{dt}U(\chi (t))=0.\) Then in Q we must have \(T(t)=\dfrac{A}{d}\) for all \(t\in \mathbb {R}.\) We substitute this into the equation of T in (2.5) we get \(V(t)=0\) for all \(t\in \mathbb {R}\) and thus, from the equation of i in (2.5) we obtain \(i(t,.)=0\) for all \(t\in \mathbb {R}.\) Then the largest invariant set with the property that \(\dfrac{d}{dt}U(\chi (t))=0\) is \((\dfrac{A}{d},0,0)\) (LaSalle’s Invariant Principle). Now, since \(\mathbf {A}\) is compact, the \(\omega (x)\) and \(\alpha (x)\) are non-empty, compact, invariant and attract \(\chi (t)\) as \(t\rightarrow \pm \infty ,\) respectively. We know that U is constant on the \(\omega (x)\) and \(\alpha (x),\) and thus \(\omega (x)=\alpha (x)=\{(\dfrac{A}{d},0,0)\}.\) Consequently \(\lim \limits _{t\longrightarrow \pm \infty }\chi (t)=(\dfrac{A}{d},0,0)\) and

$$\begin{aligned} \lim \limits _{t\longrightarrow - \infty }U(\chi (t))=\lim \limits _{t\longrightarrow + \infty }U(\chi (t))=U\left( \dfrac{A}{d},0,0\right) . \end{aligned}$$

Since \(U(\chi (t))\) is a decreasing function of t,  we obtain \(U(\chi (t))=U(\dfrac{A}{d},0,0)\) for all \(t\in \mathbb {R},\) and thus \(\chi (t)=(\dfrac{A}{d},0,0)\) for all \(t\in \mathbb {R}.\) In particular \((T_0,i_0(.),V_0)=(T(0),i(0,.),V(0))=(\dfrac{A}{d},0,0).\) Therefore the attractor \(\mathbf {A},\) is the singleton set formed by the disease free equilibrium \((\dfrac{A}{d},0,0).\) By Theorem 2.39 in [28], the infection-free equilibrium is globally asymptotically stable.\(\square \)

4 Existence of infection equilibrium states and uniform persistence

In this section, we first ensures the existence of a positive equilibrium states and next, we establish the strongly uniform persistence of the solution to problem (1.2).

Lemma 4.1

Let \(\lim \limits _{V\rightarrow 0^{+}}\dfrac{f(\dfrac{A}{d},V)}{f(T,J)}>1\) for \(T\in [0,\dfrac{A}{d}).\) Then, if \(R_0>1,\) system (1.1)–(1.2) has positive equilibrium states .

Proof

An infection equilibrium is a fixed point of the semiflow \(\Phi \),

$$\begin{aligned} \Phi (t,(T^{*},i^{*},V^{*}))=(T^{*},i^{*},V^{*}), \;\ \text{ with } \;\ i^{*}\ne 0,\;\ \forall t\ge 0. \end{aligned}$$

From (2.1), we obtain

$$\begin{aligned} i^{*}(a)=\left\{ \begin{array}{lll} \Pi (a) f(T^{*},V^{*}), \quad 0<a<t,\\ \dfrac{\Pi (a)}{\Pi (a-t)}i^{*}(a-t), \quad a>t, \end{array} \right. \end{aligned}$$
(4.1)

and

$$\begin{aligned} \left\{ \begin{array}{lll} A=dT^{*}+f(T^*,V^*),\\ cV^{*}=\int _0^{\infty }p(a)i^{*}(a)da. \end{array} \right. \end{aligned}$$
(4.2)

First remark that if \(i^{*}(a)\) is given by the first case in (4.1), it also satisfies the second case. Indeed, for \(t<a<2t\) we have

$$\begin{aligned} i^{*}(a-t)=\Pi (a-t) f(T^{*},V^{*}), \end{aligned}$$

and thus

$$\begin{aligned} i^{*}(a)= & {} \dfrac{\Pi (a)}{\Pi (a-t)}i^{*}(a-t),\\= & {} \dfrac{\Pi (a)}{\Pi (a-t)}\Pi (a-t) f(T^{*},V^{*}),\\= & {} \Pi (a)f(T^{*},V^{*}). \end{aligned}$$

Now we proceed by iteration in order to prove the result. Therefore

$$\begin{aligned} i^{*}(a)=\Pi (a)f(T^{*},V^{*}), \quad \forall a\ge 0. \end{aligned}$$
(4.3)

Combining the equations (4.2) and (4.3) we get,

$$\begin{aligned} \left\{ \begin{array}{lll} A=d T^*+f(T^*,V^*), \\ \dfrac{N}{c}f(T^*,V^*)=V^*. \end{array} \right. \end{aligned}$$
(4.4)

with N is defined in (1.5). Following the same arguments as [17, 18] we prove the existence of positive equilibrium states.\(\square \)

We emphasis now on the uniform persistence see for instance [13, 19, 28, 29]; for this purpose we apply Theorem 5.2 in [28].

We first make the following assumptions on the infection function f.

We suppose that there exists a positive equilibrium \((T^{*},V^{*})\) verifying (4.4) such that for all \(T>0\) we have

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{x}{V^{*}}< \dfrac{f(T,x)}{f(T,V^{*})}< 1 \quad \text{ for }\;\ 0<x< V^{*},\\ 1<\dfrac{f(T,x)}{f(T,V^{*})}< \dfrac{x}{V^{*}} \quad \text{ for }\;\ x> V^{*}. \end{array} \right. \end{aligned}$$
(4.5)

There exists \(\varepsilon >0\) and there exists \(\eta >0\) such that for all \(T\in [\dfrac{A}{d}-\varepsilon ,\dfrac{A}{d}+\varepsilon ]\) we have

$$\begin{aligned} \dfrac{f(T,V_1)}{V_1}\ge \dfrac{f(T,V_2)}{V_2}, \end{aligned}$$
(4.6)

for all \(0< V_1 \le V_2\le \eta .\)

Finally we suppose that

$$\begin{aligned} V_0+\int _{0}^{\infty }i_0(a)da>0. \end{aligned}$$
(4.7)

Remark 4.2

If the function f is increasing and concave with respect to V then (4.5) and (4.6) are clearly verified.

We define a persistence function \(\rho : X\rightarrow \mathbb {R}^{+}\) by

$$\begin{aligned} \rho (T_0,i_0(.),V_0)=V_0+\int _0^{\infty }i_0(a)da, \end{aligned}$$

then

$$\begin{aligned} \rho (\Phi (t,x))=V(t)+\int _0^{\infty }i(t,a)da, \end{aligned}$$

with \(x=(T_0,i_0(.),V_0).\)

The following lemma affirm that the hypothesis (H1) in Theorem 5.2. [28] holds.

Lemma 4.3

Under assumption (4.7), the function \(\rho (\phi (t))\) is positive on \(\mathbb {R},\) with \(\phi \) is a total \(\Phi -\)trajectory defined in (2.5).

Proof

We claim that \(V(t)>0\) for all \(t\in \mathbb {R}\) with V is defined in (2.5). Indeed, suppose first that there exists \(r\in \mathbb {R}\) such that \(V(t)=0\) for all \(t\le r.\) So for \(t>r\) we have

$$\begin{aligned} V'(t)=\int _r^tp(t-\sigma )\Pi (t-\sigma )f(T(\sigma ),V(\sigma ))d\sigma -cV(t). \end{aligned}$$

We show, in this case, that \(V(t)=0\) for all \(t\in \mathbb {R}.\) Assume by contradiction that there exists \(t_1>0\) such that \(V(t_1)=0,\) \(V'(t_1)>0\) and \(V(t)=0\) for all \(t\le t_1.\) Thus

$$\begin{aligned} 0<V'(t_1)=\int _r^{t_1}p(t_1-\sigma )\Pi (t_1-\sigma )f(T(\sigma ),V(\sigma ))d\sigma =0, \end{aligned}$$

consequently, \(V(t)=0\) for all \(t\in \mathbb {R},\) in addition, using the definition of i in (2.5) we get \(V(t)+\int _0^{\infty }i(t,a)da=0\) for all \(t\in \mathbb {R}\). However from (4.7), this is not possible, so there exists sequence \((t_n)_n\) and \(t_n\rightarrow -\infty \) such that \(V(t_n)>0.\) On the other hand remark that, by integration the equation of V over \((t_n,t)\),

$$\begin{aligned} V(t)e^{ct}=V(t_n)e^{ct_n}+\int _{t_n}^{t}\int _{-\infty }^{s}e^{cs}p (s-\sigma )\Pi (s-\sigma )f(T(\sigma ),V(\sigma ))d\sigma ds, \end{aligned}$$

now it is easily to conclude that \(V(t)>0\) for all \(t\in \mathbb {R}.\) Hence we conclude.\(\square \)

Now we are ready to prove the strong uniform persistence of the disease.

Theorem 4.4

Suppose (4.6), (4.7) hold. Then there exists some \(\varepsilon >0\) such that

$$\begin{aligned} \liminf _{t\rightarrow \infty } \rho (\Phi (t,x))>\varepsilon , \end{aligned}$$

for all nonnegative solutions of (1.2) provided that \(R_0>1.\)

Proof

By Theorem 5.2. in [28], and Lemma 4.3, the solution of problem (1.1)–(1.2) is strongly uniformly persistent if it is weakly uniformly persistent.

Suppose that the disease is not uniformly weakly persistent, that is, there exists an arbitrarily small \(\varepsilon >0\) such that

$$\begin{aligned} \limsup _{t\rightarrow \infty } \rho (\Phi (t,x))<\varepsilon , \end{aligned}$$

so,

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }V(t)=0\quad \text{ and } \quad \lim \limits _{t\rightarrow \infty }\int _0^{\infty }i(t,a)da=0. \end{aligned}$$

Next, we set \(\lim \inf \limits _{t\rightarrow \infty }T(t)=T_{\infty },\) using the fluctuation method see for instance [30], there exists a sequence \((t_k)_k\) such that \(\lim \limits _{t_k\rightarrow \infty }T'(t_k)= 0\) and \(\lim \limits _{t_k\rightarrow \infty }T(t_k)=T_{\infty }.\)

First, in view of the continuity of the function f we have

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }f(T(t),V(t))=0. \end{aligned}$$

Combining this with the equation of T in (1.1), we have (for large t)

$$\begin{aligned} 0\ge & {} A-dT_{\infty }- \varepsilon , \end{aligned}$$

therefore,

$$\begin{aligned} T_{\infty }\ge \dfrac{A}{d}-\theta (\varepsilon ), \end{aligned}$$

with \(\theta (\varepsilon )=\dfrac{\varepsilon }{d}\). Now since \(R_0>1,\) then there exists \(\varepsilon _1>0\) so small and \(\lambda :=\lambda _{\varepsilon _1}>0\) such that

$$\begin{aligned} \dfrac{f\left( \frac{A}{d}-\theta (\varepsilon _1),\varepsilon _1\right) }{\varepsilon _1}\dfrac{1}{c} \int _0^{\infty }\Pi (a)p(a)e^{-\lambda a}da>1. \end{aligned}$$

We set

$$\begin{aligned} \alpha _{\varepsilon _1}:=\dfrac{f\left( \frac{A}{d}-\theta (\varepsilon _1),\varepsilon _1\right) }{\varepsilon _1}\int _0^{\infty }\Pi (a)p(a)e^{-\lambda a}da-c>0. \end{aligned}$$
(4.8)

On the other hand, we introduce the following auxiliary problem

$$\begin{aligned} \left\{ \begin{array}{lll} \phi '(a)=(\delta (a)+\lambda )\phi (a)-p(a),\\ \phi (0)=\int _0^{\infty }\Pi (a)p(a)e^{-\lambda a}da. \end{array} \right. \end{aligned}$$
(4.9)

The solution of this problem is given by

$$\begin{aligned} \phi (a)=\int _a^{\infty }p(\sigma )e^{-\int _a^{\sigma } \delta (s)ds}e^{-\lambda (\sigma -a)}d\sigma . \end{aligned}$$

In addition, remarking that the function \(\phi \) is uniformly bounded, more precisely

$$\begin{aligned} \phi (a)\le \dfrac{||p||_{\infty }}{\delta _0+\lambda }. \end{aligned}$$

Now we analyze de derivative of \(I_1(t):=\int _0^{\infty }\phi (a)i(t,a)da+V(t),\) so by a simple calculation using (4.9) we obtain,

$$\begin{aligned} I_1'(t)= & {} i(t,0)\phi (0)+\lambda \int _0^{\infty }(\phi '(a) -\delta (a)\phi (a))i(t,a)da\\&+\int _0^{\infty }p(a)i(t,a)da-cV(t),\\= & {} f(T(t),V(t))\phi (0)+\lambda \int _0^{\infty }\phi (a)i(t,a)da-cV(t). \end{aligned}$$

Now for t so large and the monotonicity of f with respect to T,  we have,

$$\begin{aligned} f(T(t),V(t))\ge f\left( \frac{A}{d}-\theta (\varepsilon _1),V(t)\right) . \end{aligned}$$

On the other hand, since \(V(t)\le \varepsilon _1\) then using (4.6) we get

$$\begin{aligned} \dfrac{f(T,V)}{V}\ge & {} \dfrac{f\left( \frac{A}{d}-\theta (\varepsilon _1),V\right) }{V},\\\ge & {} \dfrac{f\left( \frac{A}{d}-\theta (\varepsilon _1),\varepsilon _1\right) }{\varepsilon _1}. \end{aligned}$$

Therefore

$$\begin{aligned} I_1'(t)\ge & {} \left( \dfrac{f\left( \frac{A}{d}-\theta (\varepsilon _1),\varepsilon _1\right) }{\varepsilon _1} \phi (0)-c\right) V(t)+\lambda \int _0^{\infty }\phi (a)i(t,a)da,\\\ge & {} \alpha _{\varepsilon _1}V+\lambda \int _0^{\infty }\phi (a)i(t,a)da,\\\ge & {} \beta _{\varepsilon _1}I_1(t), \end{aligned}$$

with \(\beta _{\varepsilon _1}=\min \{\alpha _{\varepsilon _1},\lambda \}\) where \(\alpha _{\varepsilon _1}\) is defined in (4.8).

Finally

$$\begin{aligned} I_1(t)\ge \left( \int _0^{\infty }\phi (a)i_0(a)da+V_0\right) e^{\theta _{\varepsilon _1}t}, \end{aligned}$$

hence due to (4.7) \(I_1(t)\rightarrow +\infty \) which is a contradiction with the boundedness of V and \(\int _0^{\infty }\phi (a)i(t,a)da\). The result is reached. \(\square \)

Let \(X_0\) be a subset defined as

$$\begin{aligned} X_0=\left\{ (T_0,i_0(.),V_0)\in X_{+} ; \int _0^{\infty }i_0(a)da+V_0=0\right\} . \end{aligned}$$

From Theorem 5.7 in [28] we have the following result

Theorem 4.5

Under the assumptions (4.6), (4.7), there exists a compact attractor \(\mathbf {A_1}\) that attracts all solutions with initial condition belonging to \(X_{+}\setminus X_0.\) Furthermore \(\mathbf {A_1}\) is \(\rho -\) uniformly positive, i.e., there exists some \(\gamma >0\) such that,

$$\begin{aligned} \int _0^{\infty }i_0(a)da+V_0\ge \gamma \;\ \text{ for } \text{ all } \;\ (T_0,i_0(.),V_0)\in \mathbf {A_1}. \end{aligned}$$
(4.10)

5 The global stability and uniqueness of the infection steady state

In this section, we discuss the global stability of the infection equilibrium \((S^{*},v^{*}(.),i^{*}(.))\) of system (2.5). Before stating the main result of this section, we need the following estimate, which guarantees that all solutions of (2.5) with initial data satisfying (4.7), are bounded away from 0. We will use a simple modification of the idea proposed in the proof of Claim 5.3 in [9].

Proposition 5.1

Assume (4.6), (4.7) hold. Then, there exist positive constants \(\alpha \) and \(\Gamma \) such that, for all \((T_0,i_0(.),V_0)\in \mathbf {A_1},\)

$$\begin{aligned} V_0>\alpha \;\ \text{ and }\;\ \dfrac{i_0(a)}{i^{*}(a)}\ge \Gamma , \;\ a\ge 0. \end{aligned}$$

Proof

Since \(\mathbf {A_1}\) is invariant, then, there exists a total trajectory \(\Psi :\mathbb {R}\rightarrow \mathbf {A_1},\) \(\Psi (t)=(T(t),i(t,.),V(t))\) with \(T(0)=T_0,\) \(i(0,a)=i_0(a)\) and \(V(0)=V_0.\) Suppose by contradiction that \(\liminf \limits _{t\rightarrow \infty }V(t)=0,\) then there exists a sequence \(t_n\rightarrow \infty \) such that \(V(t_n)\rightarrow 0.\) We set \(T_n(t)=T(t+t_n),\) \(V_n(t)=V(t+t_n)\) and \(i_n(t,.)=i(t+t_n,.).\) Then up to a subsequence one may assume that \((T_n(t),V_n(t),i_n(t,.))\rightarrow (\tilde{T}(t),\tilde{V}(t),\tilde{i}(t,.))\) locally uniformly with \(((\tilde{T}(t),\tilde{V}(t),\tilde{i}(t,.))\) is a solution of (2.5) such that \(\tilde{V}(0)=0.\) Now employing the same argument as in the proof of lemma 4.3 we reach a contradiction with (4.10) and \(\tilde{V}(0)=0.\) Moreover,

$$\begin{aligned} i(t,a)=\Pi (a)f(T(t-a),V(t-a)), \end{aligned}$$

due to Lemma 2.2, and (4.3) there exists \(\Gamma >0\) such that,

$$\begin{aligned} \dfrac{i(t,a)}{i^{*}(a)}:=\dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}\ge \Gamma ,\;\ t\in \mathbb {R}, \;\ a\ge 0, \end{aligned}$$

\(\square \)

Now we are able to state the main result of this section.

Theorem 5.2

Under the assumptions of (4.5), (4.6), (4.7), the problem (2.5) has a unique positive infection equilibrium \((T^{*},i^{*}(a),V^{*})\) which is globally asymptotically stable in \(X_{+}\setminus X_0\).

Proof

Let \(\Psi : \mathbb {R}\rightarrow \mathbf {A_1}\) be a total \(\Phi -\)trajectory, \(\Psi (t)=(T(t),i(t,.),V(t)),\) \(T(0)=T_0,\) \(i(0,a)=i_0(a),\) and \(V(0)=V_0,\) with (T(t), i(t, a), V(t)) is solution of problem (2.5).

We set,

$$\begin{aligned} H(y)=y-ln(y)-1, \end{aligned}$$

and

$$\begin{aligned} \phi (a)=\dfrac{f(T^{*},V^{*})}{N}\int _a^{\infty }p(\sigma )\Pi (\sigma )d\sigma , \end{aligned}$$

with N is defined in (1.5).

Then, for \(x:=(T_0,i_0(.),V_0)\in \mathbf {A_1},\) we consider the following Lyapunov functional

$$\begin{aligned} W(x)=W_1(x)+W_2(x)+W_3(x), \end{aligned}$$

with,

$$\begin{aligned} W_1(x)=T_0-T^*-\int ^{T_0}_{T^*}\dfrac{f(T^*,V^*)}{f(\eta ,V^*)}d\eta , \end{aligned}$$
$$\begin{aligned} W_2(x)=\int _0^{\infty }H(\dfrac{i_0(a)}{i^{*}(a)})\phi (a)da, \end{aligned}$$

and

$$\begin{aligned} W_3(x)=\dfrac{f(T^{*},V^{*})}{c}H\left( \dfrac{V_0}{V^{*}}\right) . \end{aligned}$$

By analyzing the derivative of \(W_1,\) using the definition of the positive steady state in (4.4) we have,

$$\begin{aligned} \dfrac{d}{dt}W_1(\Psi (t))= & {} \left( 1-\dfrac{f\left( T^{*},V^{*}\right) }{f(T(t),V^{*})}\right) (A-dT(t)-f(T(t),V(t)))\\= & {} d\left( 1-\dfrac{f(T^{*},V^{*})}{f(T(t),V^{*})}\right) (T^*-T)\\&+\,\left( 1-\dfrac{f(T^{*},V^{*})}{f(T(t),V^{*})}\right) (f(T^{*},V^{*})-f(T(t),V(t))). \end{aligned}$$

Now, concerning \(W_2.\) Following the same arguments as in the proof of Lemma 9.18 in [28] and (2.5) we find,

$$\begin{aligned} \dfrac{d}{dt}W_2(\Psi (t))= & {} H\left( \dfrac{f(T(t),V(t))}{f(T^{*},V^{*})}\right) \phi (0)+\int _0^{\infty }H\left( \dfrac{i(t,a)}{i^{*}(a)}\right) \phi '(a)da,\\= & {} H\left( \dfrac{f(T(t),V(t))}{f(T^{*},V^{*})}\right) f(T^{*},V^{*}) -\dfrac{f(T^{*},V^{*})}{N}\\&\times \int _0^{\infty } H\left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}\right) p(a)\Pi (a)da. \end{aligned}$$

Using the definition of H we have

$$\begin{aligned} H\left( \dfrac{f(T(t),V(t))}{f(T^{*},V^{*})}\right)= & {} \dfrac{f(T(t),V(t))}{f(T^{*},V^{*})}-\ln \left( \dfrac{f(T(t),V(t))}{f(T^{*},V^{*})}\right) -1,\\= & {} \dfrac{f(T(t),V(t))}{f(T^{*},V^{*})}-\ln \left( \dfrac{f(T(t),V(t))}{f(T(t),V^{*})}\right) -\ln \left( \dfrac{f(T(t),V^{*})}{f(T^{*},V^{*})}\right) -1, \end{aligned}$$

thus,

$$\begin{aligned} \dfrac{d}{dt}W_2(\Psi (t))= & {} f(T(t),V(t))-f(T^{*},V^{*})\ln \left( \dfrac{f(T(t),V(t))}{f(T(t),V^{*})}\right) \\&-f(T^{*},V^{*}) \ln \left( \dfrac{f(T(t),V^{*})}{f(T^{*},V^{*})}\right) \\&-f(T^{*},V^{*})-\dfrac{f(T^{*},V^{*})}{N}\\&\times \int _0^{\infty } H\left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}\right) p(a)\Pi (a)da. \end{aligned}$$

Next, for \(W_3\) we get,

$$\begin{aligned} \dfrac{d}{dt}W_3(\Psi (t))= & {} \dfrac{f(T^{*},V^{*})}{cV^{*}} (1-\dfrac{V^{*}}{V(t)})\left( \int _0^{\infty }p(a)i(t,a)da-cV\right) ,\\= & {} \dfrac{f(T^{*},V^{*})}{cV^{*}}(1-\dfrac{V^{*}}{V(t)}) \left( \int _0^{\infty }p(a)\Pi (a)f(T(t-a),\right. \\&\left. V(t-a))da-cV\right) . \end{aligned}$$

From (4.4) namely, \(cV^{*}=Nf(T^{*},V^{*})\) we obtain,

$$\begin{aligned} \dfrac{d}{dt}W_3(\Psi (t))= & {} f(T^{*},V^{*})\left( 1-\dfrac{V^{*}}{V(t)}\right) \int _0^{\infty }\left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})} -\dfrac{V}{V^{*}}\right) \\&\dfrac{p(a)\Pi (a)}{N}da, \end{aligned}$$

hence, for \(W=W_1+W_2+W_3\) we get,

$$\begin{aligned} \dfrac{d}{dt}W(\Psi (t))= & {} d\left( 1-\dfrac{f(T^{*},V^{*})}{f(T(t),V^{*})}\right) (T^*-T(t))+f(T^{*},V^{*})\\&\left( -\ln \left( \dfrac{f(T(t),V^{*})}{f(T^{*},V^{*})} -\dfrac{f(T^{*},V^{*})}{f(T(t),V^{*})}+1\right) \right) \\&+f(T^{*},V^{*})\left\{ H\left( \dfrac{f(T(t),V(t))}{f(T(t),V^{*})}\right) \right. \\&\left. -\int _0^{\infty }H\left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}\right) \dfrac{p(a)\Pi (a)}{N}da\right\} \\&+f(T^{*},V^{*})(1-\dfrac{V^{*}}{V(t)})\int _0^{\infty } \left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}-\dfrac{V}{V^{*}} \right) \\&\dfrac{p(a)\Pi (a)}{N}da. \end{aligned}$$

Observe that the function \(-ln(x)-\dfrac{1}{x}+1\le 0,\) for all \(x>0,\) then the first two terms of the above equation are negative. Next we will claim that the last term is negative. For this we set,

$$\begin{aligned} D(t):= & {} H\left( \dfrac{f(T(t),V(t))}{f(T(t),V^{*})}\right) -\int _0^{\infty }H \left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}\right) \dfrac{p(a)\Pi (a)}{N}da\\&+\,\left( 1-\dfrac{V^{*}}{V(t)}\right) \int _0^{\infty }\left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}-\dfrac{V}{V^{*}}\right) \dfrac{p(a)\Pi (a)}{N}da. \end{aligned}$$

Let us consider a time t such that \(\dfrac{V(t)}{V^*}<1,\) then, from the hypothesis (4.5) we have,

$$\begin{aligned} \dfrac{V(t)}{V^*}<\dfrac{f(T(t),V(t))}{f(T(t),V^{*})}<1. \end{aligned}$$

Hence, since \(H(1)=0\) and H is decreasing in (0, 1),  it yields,

$$\begin{aligned} H\left( \dfrac{V(t)}{V^*}\right) >H\left( \dfrac{f(T(t),V(t))}{f(T(t),V^{*})}\right) , \end{aligned}$$

thus,

$$\begin{aligned} D(t)\le & {} \int _0^{\infty }\left\{ H\left( \dfrac{V(t)}{V^{*}}\right) -H\left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})}\right) \right. \\&\left. +\,H'\left( \dfrac{V(t)}{V^{*}}\right) \left( \dfrac{f(T(t-a),V(t-a))}{f(T^{*},V^{*})} -\dfrac{V(t)}{V^{*}}\right) \right\} \dfrac{p(a)\Pi (a)}{N}da. \end{aligned}$$

Now since H is a convex function then,

$$\begin{aligned} H(b)-H(a)+H'(b)(a-b)\le 0,\;\ \text{ for } \text{ all }\;\ a,b \; \text{ positive }, \end{aligned}$$

so,

$$\begin{aligned} D(t)\le 0. \end{aligned}$$

For other values of t i.e. \(\dfrac{V(t)}{V^*}>1,\) again from (4.5), and by taking into account that H is an increasing function over \((1,\infty )\) we also arrive to prove that \(D(t)\le 0\). Consequently,

$$\begin{aligned} \dfrac{d}{dt}V(\Psi (t))\le 0,\quad \forall t\in \mathbb {R}. \end{aligned}$$

Further, \(\dfrac{d}{dt}V(\Psi (t))=0\) implies that \(T(t)=T^{*}.\) Now we look for the largest invariant set Q for which \(\dfrac{d}{dt}V(\Psi (t))=0.\) In Q,  we must have \(T(t)=T^{*}\) for all \(t\in \mathbb {R}.\) First, according to equations of T and \(T^{*}\) in (2.5) and (4.1) it is clear that,

$$\begin{aligned} V(t)=V^{*}, \;\ \text{ for } \text{ all } \;\ t\in \mathbb {R}, \end{aligned}$$

and finally in view of (2.5),

$$\begin{aligned} i(t,.)=i^{*}(.), \;\ \text{ for } \text{ all } \;\ t\in \mathbb {R}, \end{aligned}$$

Following the same arguments as in the proof of Theorem 3.1 we conclude the global asymptotic stability of the infection equilibrium. Uniqueness is a direct consequence of the fact that \(\frac{d}{dt}V(\Psi (t))=0\) holds only on the line \(T=T^{*}.\) This ends the proof of the theorem.\(\square \)

6 Example and numerical simulations

In this section, we propose some mathematical models describing a virus dynamics to illustrate the different results obtained in the previous sections. We also realize some numerical simulations for each example.

Example 1

Let f be the Beddington–DeAngelis function

$$\begin{aligned} f(T,V)= \frac{\beta T~V}{1+\alpha _1 T+\alpha _2 V}. \end{aligned}$$

We replace the function f in system (1.1), we obtain

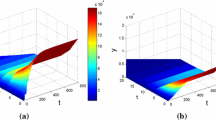
$$\begin{aligned} \left\{ \begin{array}{lll} T'(t)=A- dT(t)- \displaystyle \frac{\beta T(t)V(t)}{1+\alpha _1 T(t) +\alpha _2 V(t)} \quad t \ge 0,\\ i_t(t,a)+i_a(t,a)=-\delta (a) i(t,a), \\ V'(t)=\int _0^{\infty } p(a)i(t,a)da-cV(t), \end{array} \right. \end{aligned}$$

where \(\beta , \alpha _1\) and \(\alpha _2\) are positive constants, we denote by \(\beta \) the rate of infection, \(\alpha _1\) and \(\alpha _2\) represent the Beddington–DeAngelis infection rate, for more details about this system, we refer to [35] (Figs. 1, 2).

Fig. 1
figure 1

a The evolution of the solution T and V with respect to time. b The age distribution of i with respect to time and infection age

Full size image
Fig. 2
figure 2

a The evolution of the solution T and V with respect to time. b The age distribution of i with respect to time and infection age

Full size image

The function f satisfies all hypothesis defined in the first part, and by theorems 3.1 and 5.2, we obtain the following result:

  • If \(R_0 \leqslant 1\), the disease free equilibrium is globally asymptotically stable.

  • If \(R_0>1\), the positive infection equilibrium is globally asymptotically stable.

The number \(R_0\) of this model is defined by

$$\begin{aligned} R_0 = \displaystyle \frac{A N \beta }{c (d+ \alpha _1 A)}. \end{aligned}$$

We give the following values to some parameters to do the numerical simulations of this model,

$$\begin{aligned}&\displaystyle A=4, \quad d=0.04, \quad c=1, \quad \delta =0.2, \quad \beta = 0.1, \quad \alpha _1=0.1, \quad \alpha _2=0.2.\\&\displaystyle p(a)=\left\{ \begin{array}{lll} 0 \qquad \text { if }\, \, t\leqslant \tau , \\ 0.5 \quad \text { if }\,\, t> \tau . \end{array} \right. \end{aligned}$$

with the initial conditions

$$\begin{aligned} T_0=50, \qquad V_0=25, \qquad i_0(t)=10 e^{-0.1t}. \end{aligned}$$

We take different values of \(\tau \) to simulate all possible cases of the asymptotic dynamics of system (1), when \(\tau =6\), then \(R_0=0.6676 > 1,\)

And when \(\tau =1\), then \(R_0=1.8146 > 1\),

Example 2

We choose the following function f for our second example

$$\begin{aligned} f(T,V)= \displaystyle \frac{ \beta TV }{ (1+\alpha V^n)}=h(V).T \end{aligned}$$

the function h being defined as

$$\begin{aligned} h(x)= \displaystyle \frac{ \beta x }{1+ \alpha x^n} \qquad \text {with } 0 \leqslant n \leqslant 1. \end{aligned}$$
(6.1)
Fig. 3
figure 3

Graphical representation of the function h with \(\beta =0.1\) and \(\alpha =0.2\)

Full size image
Fig. 4
figure 4

a The evolution of the solution T and V with respect to time. b The age distribution of i with respect to time and infection age

Full size image

for a special case \(n=1\) and \(n=0\), function h is similar to Holling type I and II functional response (Figs. 3, 4, 5).

We can see that the function f satisfies all the assumptions made in the previous sections.

The number \(R_0\) is defined by

$$\begin{aligned} R_0 = \displaystyle \frac{A N \beta }{c d}. \end{aligned}$$

The choice of the parameter \(A=2, \quad d=0.1, \quad c=1, \quad \delta =0.3, \quad \beta = 0.1, \quad \alpha _1=0.2 \text { and } n=0.8.\) Letting \(\tau \) free in

$$\begin{aligned} p(a)=\left\{ \begin{array}{lll} 0 \qquad \text { if }\, \, t\leqslant \tau , \\ 0.5 \quad \text { if }\, \, t> \tau . \end{array} \right. \end{aligned}$$

with the initial conditions

$$\begin{aligned} T_0=10, \qquad V_0=5, \qquad i_0(t)=3 e^{-0.1t}. \end{aligned}$$

We change the values of \(\tau \) in order to have \(R_0 \leqslant 1\) or to have \(R_0>1.\) If we choose \(\tau =5\), then \(R_0=0.7162 < 1\),

And if we choose \(\tau =1\), then \(R_0=2.3779 > 1\),

Fig. 5
figure 5

a The evolution of the solution T and V with respect to time. b The age distribution of i with respect to time and infection age

Full size image

Remark 6.1

We made the choice to let \(\tau \) free, and to discuss with respect to its different values. One can choose to fix \(\tau \) and let any other parameter free, this will lead us the same conclusion provided that either \(R_0\le 1\) or \(R_0>1.\)

7 Conclusion

In this paper we have considered an age-structured HIV infection model with a very general nonlinear infection function,

$$\begin{aligned} \left\{ \begin{array}{lll} T'(t)=A- dT(t)-f(T(t),\quad V(t)) \;\;\ t \ge 0,\\ i_t(t,a)+i_a(t,a)=-\delta (a) i(t,a), \\ V'(t)=\int _0^{\infty } p(a)i(t,a)da-cV(t), \end{array} \right. \end{aligned}$$

with the boundary and initial conditions

$$\begin{aligned} \left\{ \begin{array}{lll} i(t,0)=f(T(t),\quad V(t)), \\ T(0)=T_0\ge 0,\quad V(0)=V_0 , \\ i(0,.)=i_0(.)\in L_{+}^{1}(\mathbb {R}^{+}). \end{array} \right. \end{aligned}$$

This kind of problems is widely treated in the literature for particular choices of f, our main contribution consists in considering a very general class of infection functions f(T(t), V(t)), observe that the assumptions made on f are not restrictive, as almost all types of usual infection functions fulfill them. We propose a Lyupunov function for these problems, confirming the results obtained by previous works and showing new ones as for the case of \(f(T,V)=\dfrac{TV}{1+\alpha V^n}\) with \(0\le n\le 1.\)

Even if a lot is biologically known about the virus evolution in its current form, however the interaction between uninfected cells and the virus is a very complicated phenomenon, in addition a virus can mutate, and develop other ways to contaminate cells than those known till now, hence the relevance of considering a function f in its most general form to prevent any possible behavioral change of the virus.

Our results are illustrated by numerical simulations, we have chosen some examples that are untreated in the existing the literature, we made the distinction between the cases \(R_0 \le 1\) and \(R_0 >1.\)

As a good perspective to the present work, one can include a treatment or a vaccination function with different strategies of vaccination; and study the asymptotic behavior of the solutions to the considered model.